Basic mathematical concepts

4 Crucial Basic Math Concepts

Search my site:

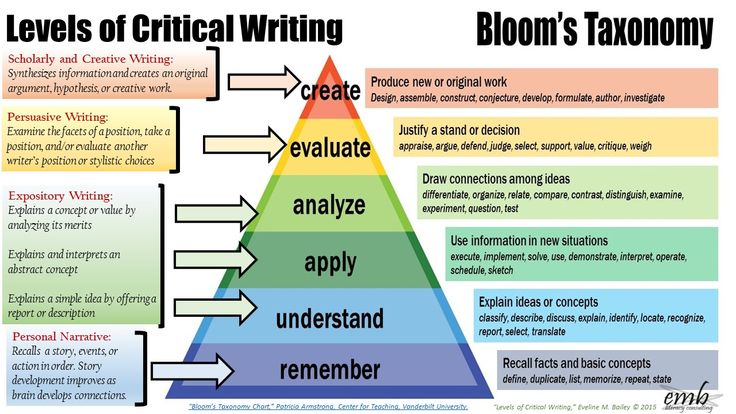
Your child's success in learning Math depends on mastering these five crucial concepts. They are essential for building a strong foundation in Math. They help your child understand and make sense of numbers and problem-solving; they strengthen his or her number sense.

The good news is that it is very easy to help your child understand these concepts. The key is to practice a few minutes several times a day. Make it a family affair so your child does not feel overly stressed. Your child or children will remember the lessons better if they had fun with it.

1.   Understanding Numbers

The first concept your child must master is knowing how to read, write and understand numbers. Print out 2 sets of the number chart here.  Use one set as a reference.  Cut out the individual numbers from the second set.

Some ideas for you:

-  read and write numbers

-  recite a list of numbers forwards and backwards

-  what number comes before or next

-  arrange numbers in order (start with consecutive numbers)

-  even and odd numbers

Print out this set of place numbers for older children.

2.   More, Less or Equal

The next important concept in Math is to know how 2 numbers compare; whether one  number is more, less or equal to another number.

Numbers represent quantity. Your child must first understand these types of questions.

1. Amanda has 12 stickers.  Benjamin has 9 stickers.  Who has more stickers?
2. Jack has 35 stamps.  Alan has 19 stamps.  Who has fewer stamps?
3. Sam has 107 balloons.  Jodie has 90 balloons.  Who has more balloons?  How many more?
4. Charlie is 30-years-old. Mary is 17-years-old.  Who is younger?  How many years younger?
   

Followed by these types of questions:

1. Rodney has $3 more than Janice. How much money does Rodney have if Janice has $26?
2. I have 7 fewer pencils than books.   How many books do I have if I have 20 pencils?
3. John spent $11 less than Mark.  How much did they spend altogether if Mark spent $15?
   

And these types of questions:

1. 5 pencils cost the same as 2 books.  Which is more expensive, the pen or the book?
2. 6 apples cost the same as 10 oranges.  What is the cost of 1 apple if 1 orange costs $0.60?
3. Mary and James have the same amount of money.  Mary spent half of her money.  James spent one-third of his money.  Who spent more money?
   

No matter how difficult the questions get, they can all be broken down into simple comparisons of more, less or equal.

3.  Knowing Which Operation to Use

In Basic Maths there are actually only 4 operations your child needs to know: addition, subtraction, multiplication and division.  Here are some clues to help your child decide which of these to use.  Print the following graphic for your child to use as a guide.

4.   Different Ways to Get to the Answer

When it comes to Math, many children assume there is only one way or method to use to come up with the correct answer. If your child does not understand the teacher's method, he or she assumes that it is because he or she too stupid to understand.

You must help your child realize that there can be different ways of understanding a problem and different strategies can be used to find the answer. However, though the strategies may differ, the answer to the question must always be the same.

Play this family game: Write out simple word problems on cards. Read out a problem, then each person explains how he or she comes up with the answer.

Example

Mary has 9 sweets. She bought a few more sweets and now she has 13 sweets. How many sweets did Mary buy?

Some methods of solving:

1. Say '9' then count '10, 11, 12, 13' on your fingers. Since you used 4 fingers to count, the answer is 4.
2. Draw 9 circles in a row. Draw 13 circles in a second row below the first, making sure you line them up exactly. Compare the two rows and point out there are 4 extra circles in the second row. The answer is 4.
3. Write the numbers 1 to 13 on a number line. Point out that after the number 9, there are 4 more numbers to reach the number 13.  The answer is 4.
   

Play this game often and your child will become more flexible and logical in his or her thinking. He or she will automatically look for different ways to solve a hard problem. This will surely help in tackling complicated Math problems later on in school. Teach your child to ask "Is there another way of solving?" when he or she cannot understand one explanation.

This will help them realize that failure to understand does not mean they are cannot learn Math.

After your child has mastered this Math concept, introduce deliberate mistakes in your reasoning to see if your child can spot and correct them.

But do this only after your child has thoroughly understood the different strategies or you'll only end up confusing your child.

For older children, you can help them understand the properties of the different operations of addition, subtraction, multiplication and division.

Sometimes the order that these operations are used does not matter.  Sometimes it does.  Discuss the different strategies to find out when order matters, and when it doesn't.

Example

Max bought 3 boxes of pencils.  Each box contains 12 pencils.  He gave 5 pencils to his brother and 8 pencils to his sister.  How many pencils does Max have left?

Methods of solving:

1. To find the total number of pencils at first, you can multiple (3 x 12) or add (12 + 12 + 12).
2. To find the number of pencils left, you can add first (5 + 8) and then subtract
   (36 - 13).
3. Or you can subtract only (36 - 5 - 8).

I hope these strategies help your child excel in Maths.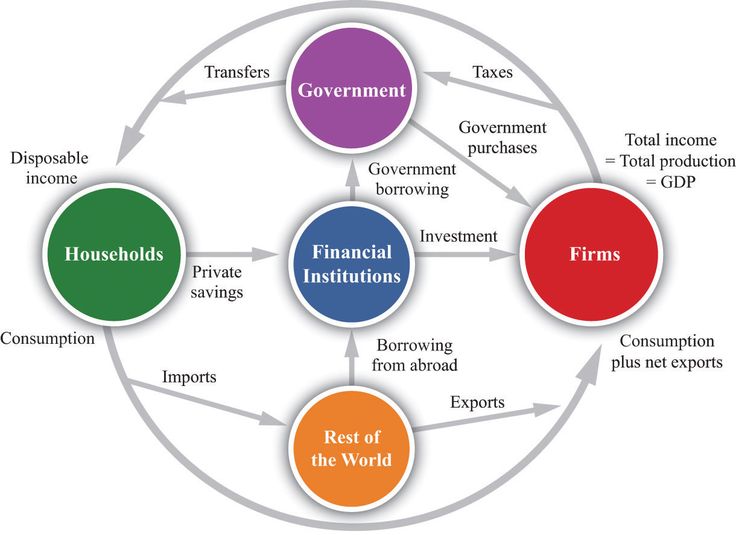   Share them with other parents whose children struggle with Maths.

Basic Concepts in Mathematics | Sciencing

••• Rechenrahmen image by Yvonne Bogdanski from Fotolia.com

Updated April 24, 2017

By Erin Schreiner

Upon entering school, students begin to develop their basic math skills. Mathematics makes it possible for students to solve simple number based problems. Through the use of math, students can add up store purchases, determine necessary quantities of objects and calculate distances. While the discipline of math does become quite complex, there are some basic math skills that every student can and should learn during their math education program.

Number Sense

The first mathematics skill that students learn is basic number sense. Number sense is the order and value of numbers. Through the use of their number sense, students can recall that ten is more than five and that positive numbers indicate a greater value than their negative counterparts. Students commonly begin learning number sense skills in pre-school, and continue developing a more complex understanding of the concept throughout elementary school. Teachers introduce this skill to students by having them order digits and complete basic counting activities. They extend their knowledge by introducing the concept of the greater than and less than symbols and explaining what the use of each indicates.

Addition and Subtraction

The first mathematical operation that students learn is addition, followed closely by subtraction. Students begin studying these skills through the use of manipulatives, or physical tools that represent objects, as early as pre-school, and continue building their skills, adding and subtracting ever larger numbers through elementary school. When the skills are initially introduced, students perform rudimentary calculations using single digits. Later in their study, they practice applying these skills through the completion of story problems.

Multiplication and Division

After developing a complex understanding of addition and subtraction, students move on to studying multiplication and division. Depending on the student’s math achievement level, he may begin studying these operations as early as first grade. As with addition, students' study of these operations begins with single digit calculations. As they develop their multiplication and division skills, the problems become increasingly complex, involving larger numbers.

Decimals and Fractions

After students develop a strong understanding of number sense, they explore fractional numbers or numbers that lay between whole digits. Commonly this study begins in first grade with the exploration of basic fractions including ½ and ¼. After learning fractions, including how to add, subtract, divide and multiply non-whole numbers in fraction form, students study decimals. A strong understanding of fractions and decimals is vital, as students will use these non-whole numbers extensively as they continue their math study.

Related Articles

References

• NCTM: National Standards by Grade
• National Council for the Teachers of Mathematics: Math Skills

About the Author

Erin Schreiner is a freelance writer and teacher who holds a bachelor's degree from Bowling Green State University. She has been actively freelancing since 2008. Schreiner previously worked for a London-based freelance firm. Her work appears on eHow, Trails.com and RedEnvelope. She currently teaches writing to middle school students in Ohio and works on her writing craft regularly.

Photo Credits

Rechenrahmen image by Yvonne Bogdanski from Fotolia.com

Basic Concepts of Mathematics — Mathematical Structures Minor — National Research University Higher School of Economics

Course page

Reading: 1-2 2nd year module
Prerequisites: none
Labor intensity: 5 credits

64 class hours:

• 32 lecture hours;
• 32 hours of seminars.

Control forms:

• exam;
• 1 test;
• 10 homework assignments.

Teachers

Kirichenko Valentina Alekseevna

Department of Mathematics: Associate Professor

About the course

Purpose of the course:

Master the key mathematical concepts used in modern mathematics and its many applications. Starting from the concepts of school mathematics familiar to everyone, such as number, line, function, we will get their far-reaching generalizations, such as rings, fields, vector spaces, transformation groups, operators. Students will also learn about the aims, problems, and methods of mathematics, from set theory to the beginnings of algebra, geometry, and analysis.

The following topics will be discussed in the course:

1. What is a number? Natural numbers: Peano's axioms and the method of mathematical induction. Real numbers: Dedekind sections, Cauchy sequences. Complex numbers, quaternions, octaves, p-adic numbers. Generalizations: rings, fields, algebras.
2. What is planimetry? Hilbert's formal method: axiom systems of Euclidean geometry from Euclid to Hilbert and Kolmogorov. Groups of motions of the plane and space. Generalizations: linear space axioms, linear operators, bases, dimension, classical groups.
3. What is a set? Sets, functions and mappings. Combinatorics: Dirichlet principle and Newton's binomial. Binary relations, equivalence and order relations. Countable sets, uncountable sets. Cantor's Diagonal Method and the Paradoxes of Naive Set Theory.

Homework and seminar tasks:

• DZ1 Seminar1
• DZ2 Workshop2
• DZ3 Seminar3
• DZ4 Seminar4
• DZ5
• DZ6 Seminar5
• DZ7 Seminar6
• DZ8 Seminar7
• DZ9 Workshop8
• DZ10 Seminar9

Lecture notes (2nd module):

• Lectures_until_30_11

Literature:

1. V. I. Arnold, Huygens and Barrow, Newton and Hooke, the first steps in mathematical analysis and catastrophe theory, from involute to quasicrystals. M., Nauka, 1989
2. D. Hilbert, S. Cohn-Vossen, Visual geometry. M.-L., ONTI, 1936
3. G. Gindikin. Stories about physicists and mathematicians. M., MTSNMO, 2006
4. A.A. Kirillov. What is a number? M., Fizmatlit, 1993
5. R. Courant, G. Robbins What is mathematics? M., MTSNMO, 2013
6. A. Shen. On "mathematical rigor" and the school course in mathematics, M.: MTsNMO, 2006.

Additional reading

S.V. Fomin. Number systems, 5th ed., M., Nauka, 1987

I.V. Arnold. Theoretical arithmetic, M., Uchpedgiz, 1938

A. Shen. Mathematical induction, 3rd ed., M., MTsNMO, 2007

G.E. Shilov. Simple gamma (device of a musical scale), Fizmatgiz, 1963

D. Hilbert. Foundations of Geometry, L., "The Sower", 1923

Euclid. Nachala, St. Petersburg, 1819

V. Yu. Protasov. Maxima and minima in geometry, Library "Mathematical Education", Issue 3, MCNMO, 2005

N.Ya. Vilenkin. Theory of sets, 4th ed., M., MTsNMO, 2007

Other minor courses:

• Computability and complexity
• Logic
• Graphs and topology

Basic mathematical concepts

The FEMP methodology in the system of pedagogical sciences is designed to help prepare preschool children for the perception and assimilation of mathematics - one of the most important subjects in school and the comprehensive development of the child.

The FEMT technique has a specific, purely mathematical terminology .

This is:

- set;

- number;

- counting and computing activities;

- value;

- geometric figures;

- time;

- space.

SET is a collection of objects that are considered as a whole . The world in which a person lives is represented by a variety of sets: a lot of stars in the sky, plants, animals around him, a lot of different sounds, parts of his own body.

Sets are made up of elements. The elements of the set are the objects that make up the set. These can be real objects (things, toys, drawings), as well as sounds, movements, numbers, etc. .

The elements of a set can be not only individual objects, but also their combinations . For example, when counting in pairs, triplets, tens. In these cases, the elements of the set are not one object, but two, three, ten - a set.

Thus, sets are considered as a set , a set , a collection of any objects and objects, united by a common, for all, characteristic property .

Any property can be considered as belonging to some objects.

Attention!

If you need help writing a paper, we recommend that you contact professionals. Over 70,000 authors are ready to help you right now. Free corrections and improvements. Find out the value of your work.

Calculation costGuaranteesReviews

For example, has the property of being red some flowers, berries, cars and other items. The property of being round is possessed by the moon, the ball, the wheels of bicycles and cars, parts of various machines and machine tools, etc.

Thus, each property is associated with a set (objects) that have this property. It is also said that the set is characterized by the given property — or the set is given indicating a characteristic property.

Under the characteristic property of a set is understood such a property, which all objects belonging to a given set (elements of this set) have, and not a single object that does not belong to it, i.e. this item is not its element.

If some set A is specified by specifying the characteristic property P , then this is written as follows:

A = { x | P ( x )}

and reads like this: “ A is the set of all x such that x has the property P ”, or, in short, “A is the set of all having property P ". When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property.