Cardinal number of a set
Cardinal Numbers - Meaning, Examples, Sets
Cardinal numbers are numbers that are used for counting. They are also known as natural numbers or cardinals. A set of cardinal numbers starts from 1 and it goes on up to infinity. We use cardinal numbers to answer the question "how many?". For example, how many students are going to the school picnic? The answer could be any number like 20, 23, 30, etc. So, all these numbers come in the category of cardinal numbers. In this article, we will explore the world of cardinal numbers and understand the difference between cardinal and ordinal numbers.
| 1. | What are Cardinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Cardinal Numbers from 1 to 100 |
| 4. | Cardinal Numbers of a Set |
| 5. | FAQs on Cardinal Numbers |
What are Cardinal Numbers?
A cardinal number describes or represents how many of something are present. Example 2 apples, 5 flowers, etc. It quantifies an object. It does not have values as fractions or decimals. Cardinal numbers are counting numbers, they help to count the number of items. Let's have a look at cardinal numbers examples. Ana wants to count the number of people standing in a queue at a billing counter. Can you help her? Ana started to count using Natural numbers.
Ana counted 1, 2, 3, 4, and 5. There are 5 people standing in a queue at the billing counter. Counting numbers are cardinal numbers! Now, Let's consider another example, Noah kept eight apples in a basket. The number eight denotes how many apples are there in the basket, irrespective of their order.
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on. The smallest cardinal number is 1 as 0 is not used for counting, so it is not a cardinal number.
Difference Between Cardinal and Ordinal Numbers
All the natural numbers are also referred to as cardinal numbers.
Cardinal numbers are used for counting. While an ordinal number is a number that denotes the position or place of an object. Example: 1st, 2nd, 3rd, 4th, 5th, etc. Ordinal numbers are used for ranking. Here is an example that explains cardinal and ordinal numbers:
In the above image, we can see a team of 4 workers on the construction site. This is an example of cardinal numbers.
In the above image, we can see the position of the runners in the running event. First, second, third, and so on. This is an example of ordinal numbers. Let's discuss ordinal and cardinal number differences in the table below:
| Cardinal Numbers | Ordinal Numbers |
|---|---|
| They are counting numbers that represent quantity. | They are based on the rank or position of an object in a given list or order. |
Cardinal numbers give us the answer of 'how many?'. |
Ordinal numbers give us the answer of 'where'. For instance, where does the object lies in the list? |
| Examples are 1, 2, 3, 4, 5, 10, etc. | Examples are 1st, 2nd, 3rd, 4th, 5th, 10th, etc. |
List of Cardinal Numbers from 1 to 100
Given below are the basic and most important cardinal numbers, which form the base for other counting numbers.
| 1 - One | 6 - Six |
| 2 - Two | 7 - Seven |
| 3 - Three | 8 - Eight |
| 4 - Four | 9 - Nine |
| 5 - Five | 10 - Ten |
| 10 - Ten | 60 - Sixty |
| 20 - Twenty | 70 - Seventy |
| 30 - Thirty | 80 - Eighty |
| 40 - Forty | 90 - Ninety |
| 50 - Fifty | 100 - Hundred |
Given below is the list of all cardinal numbers from 1 to 100.
It will also help you to see how we write cardinal numbers in words like 21- twenty-one.
Cardinal Numbers of a Set
In the case of a set, the cardinal number is the total number of elements present in it. In other words, the number of distinct elements present in a set is the cardinal number of the set. The cardinal number of a set A is represented as n(A). For example, the cardinal number of set W = {1, 3, 5, 7, 9} is n(W)=5, as there are 5 elements in it.
Think Tank:
- Maria wrote January 1, 2020, as today’s date in her notebook. Does the number 1 in the date, represent a cardinal number?
- There are _______ people in the line ahead of me. I am the 7th person in the line.
Important Notes:
- Cardinal numbers help us to count the number of things or people in or around a place or a group.
- The collection of all the ordinal numbers can be denoted by the cardinal.
- Cardinal numbers can be written as words such as one, two, three, etc.
- Cardinal numbers tell how many items, whereas ordinal numbers show position or ranking.
Related Articles
Check out these interesting articles to know more about cardinal numbers and its related articles.
- Ordinal Numbers
- Whole Numbers
- Natural Numbers
- Difference Between Natural and Whole Numbers
Cardinal Numbers Examples
-
Example 1: Kate has a list of numbers as shown - 7, 8th, 10, Two, Fourth, 2nd. Identify the cardinal numbers.
Solution:
7, 10 and two help us in counting, whereas 8th, fourth and 2nd helps us in identifying the position. Thus, 7, 10, and two are cardinal numbers.
-
Example 2: Help Ryan, to calculate the number of vowels in "NUMBERS".
Also, identify the number of alphabets used to form this word.Solution:
(i) We know that a, e, i, o, and u are the vowels and in the given word u and e are used. Therefore, 2 vowels are used to form this number (2 is the required cardinal number).
(ii) We start counting from N to S, we see that "Numbers" has 7 alphabets in all. Therefore, a total of 7 alphabets are required to form the given word and here 7 is a cardinal number.
go to slidego to slide
Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations with Cuemath.
Book a Free Trial Class
Practice Questions on Cardinal Numbers
go to slidego to slidego to slide
FAQs on Cardinal Numbers
What is a Cardinal Number Example?
Cardinal numbers are used for counting. Some examples of cardinal numbers are 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 100, etc.
In our daily life, we use cardinal numbers a lot. Even a small child uses this mathematical concept without knowing the term for it. They do count how many toys they have, how many people are there around them, how many friends they have, how many subjects do they study at school, etc.
What is the Smallest Cardinal Number?
The smallest cardinal number is 1 (one) as whenever we count, we always start from 1.
How do you Find Cardinal Numbers?
Cardinal numbers can be found by counting. We start by 1 and then go on as per the number sequence.
How is Cardinal Number Different from the Ordinal Number?
Cardinal numbers are numbers that represent the number of items(quantity) while ordinal numbers represent the rank or position of an item in the given list.
What is a Cardinal Number in Sets?
In set A, if there are a total of 25 elements then 25 is the cardinal number of set A represented by n(A).
Can Cardinal Numbers Negative?
No, cardinal numbers cannot be negative.
They are positive integers or natural numbers, as we always count the number of items starting from number 1, and then it goes up to infinity.
Is Zero a Cardinal Number?
No, 0 is not a cardinal number as cardinal numbers represent quantity, and 0 means nothing or no quantity.
What is the Biggest Cardinal Number?
There are infinite natural numbers. Therefore, there are as many cardinal numbers as natural numbers. There can be no generalization of the biggest natural number and so does for the biggest cardinal number.
Cardinal numbers
A cardinal number is a natural number that is used to represent how many of something there are in a group. Cardinality is studied as a part of set theory.
Given a set of objects, A, the cardinal number of the set, n(A), is the number of elements in the set. Given the set A = {1, 2, 3}, there are 3 elements, so the cardinal number is n(A) = 3. Another way to say this is that the cardinality of the set is 3.
Example
Given the following sets of numbers: {1, 2, 3}, {4, 5, 6}, {7, 8, 9}, {10, 11, 12}, determine the cardinality of each set.
Although the numbers in each set of numbers above are different, they all have the same cardinality: 3.
We can also count that there are 4 sets of 3 numbers; 4 is another cardinal number.
One real life example of a cardinal number is a team. A soccer team has 11 players on the field at any one time, a baseball team has 9, and so on. Players on the team may have the jersey numbers 11 and 9, but those numbers wouldn't be considered cardinal numbers, because they aren't actually counting anything, and are instead used as identification; these types of numbers are known as nominal numbers.
Properties of cardinal numbers
Cardinal numbers are used for counting, so fractions, decimals, negative numbers, etc., are not considered cardinal numbers, only natural numbers. Also, the cardinality of a set can only be determined if the set is finite, since the cardinality is dependent on the number of elements in the set; a set with infinite elements cannot be counted, so we cannot find the cardinality of an infinite set.
0 is also not included in the cardinal numbers. If a given set is empty, or A = {}, the cardinality of the set is 0.
Cardinal arithmetic follows many of the same rules and shares a number of properties of arithmetic operations with natural numbers. For example, cardinal addition is also associative and commutative. Cardinal multiplication also follows the respective rules for associativity and commutativity in ordinary multiplication.
There are various other properties of cardinal numbers, these are just a few.
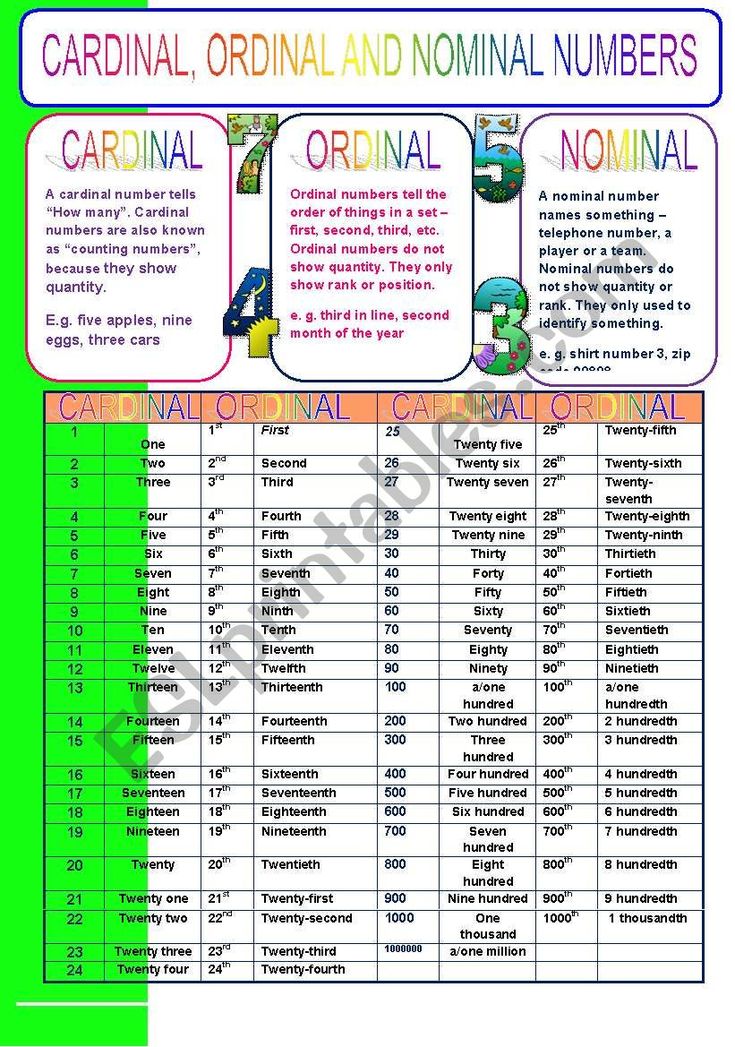
Cardinal, ordinal, and nominal numbers
These three types of numbers are often discussed together since it is necessary to understand them in order to effectively communicate using numbers. Briefly, a nominal number differs from a cardinal number in that nominal numbers are only used for identification purposes, typically to distinguish elements within a set of similar objects. They do not represent a count of something as cardinal numbers do.
Ordinal numbers, unlike cardinal or nominal numbers, tell us something about order, rank, or position.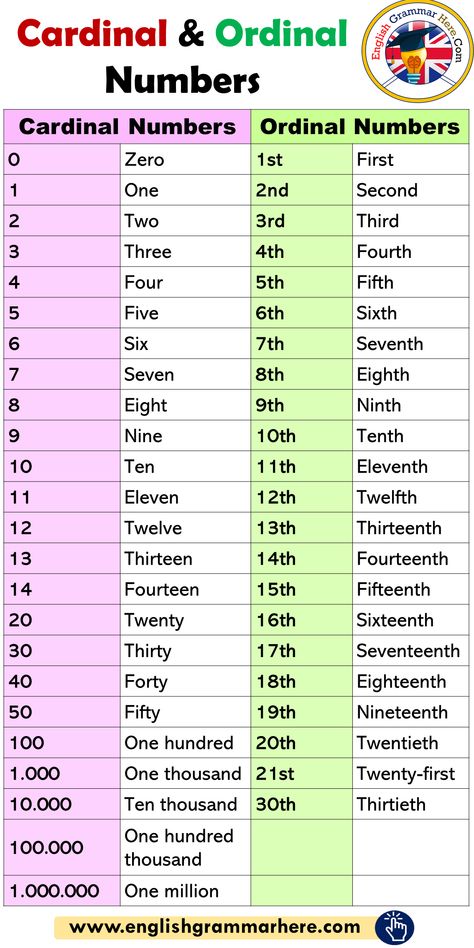
They can be identified by using terms such as first, second, third, and fourth to represent the cardinal numbers 1, 2, 3, and 4.
As an example that includes the use of all three types of numbers, imagine that there are 15 people running in a race. 15 is a cardinal number. The participants in the race are assigned the numbers 1-15 depending on when they registered for the race. Their respective numbers are nominal numbers. Only the three people who finish the race fastest get a prize based on whether they ranked first, second, or third. First, second, and third are ordinal numbers.
cardinal number | it's... What is a cardinal number?
Aleph-zero, the smallest infinite cardinal.
Cardinal number or shortly cardinal in set theory is an object that characterizes the cardinality of a set. The cardinal number of any set A is denoted as | A | or Card A .
For a finite set A, the cardinal number |A| is a natural number, which means the number of elements of this set.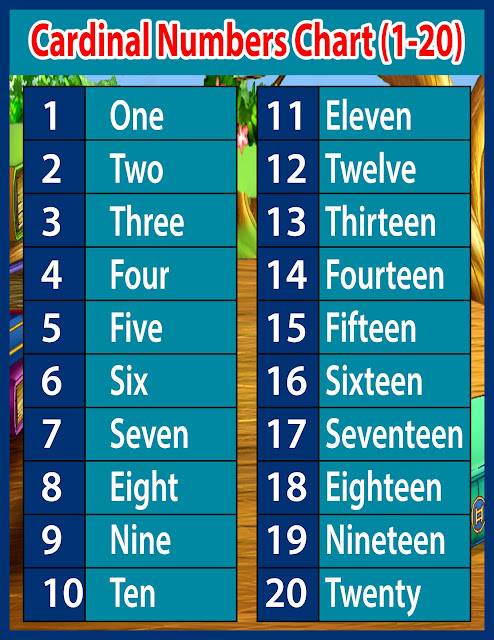
For infinite sets, the cardinal number is a generalization of the concept of the number of elements.
Although the cardinal numbers of infinite sets are not reflected in natural numbers, they can be compared. Let A and B be infinite sets, then the following four cases are logically possible:
- A ~ B and | A |=| B |.
- There is a one-to-one correspondence between the set A and some own subset B' of set B . Then they say that the cardinality of the set A is not greater than the cardinality of the set B and write | A |≤| B |.
- The set A is equivalent to some subset of the set B , and vice versa, the set B is equivalent to some subset of the set A , that is, A ~ B' ⊆ B0009 B ~ A' ⊆ A . According to the Cantor-Bernstein theorem, in this case, A ~ B is fulfilled, i.
e. | A |=| B |. - There is no one-to-one correspondence between set A and any subset of set B and there is also no one-to-one correspondence between set B and any subset of set A . It follows from this that the cardinalities of the sets A and B are not comparable.
However, deeper research in set theory has shown that, relying on the axiom of choice, it is possible to prove the impossibility of the existence of the fourth case.
Thus, the cardinalities of any two sets A and B are always comparable. That is, for cardinal numbers | A | and | B | arbitrary sets A and B , one of the three relations holds: | A |=|B|, | A |≤| B | or | B |≤| A |. If | A |≤| B |, but the set A is not equivalent to the set B , then | A |<| B |.
|
Contents
|
Aleph numbers
Cardinal number of set N all natural numbers (and hence any countable set) are denoted by (read "aleph-zero").
The cardinal number of continuum sets is denoted c or ("aleph-one"). The following cardinal numbers in ascending order denote Cantor proved that there is no set of the greatest cardinality, that is, there is no greatest cardinal number.
The Continuum Hypothesis
The Continuum Hypothesis states that there is no set whose cardinal number lies between the cardinal number of the set of natural numbers and the cardinal number of the set of real numbers , that is, < < .
See also
- Power of set
- Ordinal number
- Cantor-Bernstein theorem
- Continuum hypothesis
References
- Hans Hahn, Infinity , Part IX, Chapter 2, Volume 3 of The World of Mathematics . New York: Simon and Schuster, 1956.
- Paul Halmos, Naive set theory . Princeton, NJ: D. Van Nostrand Company, 1960. Reprinted by Springer-Verlag, New York, 1974. ISBN 0-387--6 (Springer-Verlag edition).
- Weisstein, Eric W. Cardinal Number at Wolfram MathWorld .
- Cardinality at ProvenMath formal proofs of the basic theorems on cardinality.
- Undergraduate Set Theory more proofs about cardinality - includes proof of infinite cardinal addition in Section 4.2.
Power of the set, cardinal number (cardinal) of the set Discrete Mathematics....
Hi, You will learn about the power of the set, Let's analyze its main types and features of use. There will be many more detailed examples and descriptions. In order to better understand what is cardinality of a set, cardinal number of a set, cardinal number, cardinal, I highly recommend reading everything from the Discrete Mathematics category. Set Theory. Graph Theory. Combinatorics..
set cardinality , the cardinal number of a set (lat.
cardinalis ← cardo “the main circumstance; basis; heart”) is a characteristic of sets (including infinite ones), generalizing the concept of the number (number) of elements of a finite set.
This concept is based on natural ideas about comparing sets:
- Any two sets, between whose elements a one-to-one correspondence (bijection) can be established, contain the same number of elements (have the same cardinality, are equivalent).
- Conversely, equivalent sets must allow such a one-to-one correspondence.
- Part of the set does not exceed the full set in cardinality (that is, in the number of elements).
Before the construction of the theory of cardinality of sets, sets differed in terms of features: empty/non-empty and finite/infinite, and finite sets also differed in the number of elements. Infinite sets could not be compared.
Cardinality of sets allows infinite sets to be compared. For example, countable sets are the "smallest" infinite sets.
The cardinality of a set is denoted by . Sometimes there are notations , and .
block diagram of the algorithm for determining the cardinality of a set
In set theory, the cardinal number or cardinal is called an object that characterizes the cardinality of a set. The cardinal number of any set A is denoted as | A | or Card A .
For a finite set A, the cardinal number |A| is a natural number, which means the number of elements of this set. For infinite sets, the cardinal number is a generalization of the concept of the number of elements.
Although the cardinal numbers of infinite sets are not reflected in natural numbers, they can be compared. Let A and B be infinite sets, then the following four cases are logically possible:
- A ~ B and | A |=| B |.
- There is a one-to-one correspondence between the set A and some own subset B' of the set B .
Then they say that the cardinality of the set A is not greater than the cardinality of the set B and write | A |≤| B |.
- The set A is equivalent to some subset of the set B , and vice versa, the set B is equivalent to some subset of the set A , that is, A ~ B' ⊆ B0242 and B ~ A' ⊆ A . According to the Cantor-Bernstein theorem, in this case, A ~ B is fulfilled, i.e. | A |=| B |.
- There is no one-to-one correspondence between set A and any subset of set B , and there is also no one-to-one correspondence between set B and any subset of set A . It follows from this that the cardinalities of the sets A and B are not comparable.
However, deeper research in set theory has shown that, relying on the axiom of choice, it is possible to prove the impossibility of the existence of the fourth case.
Thus, the cardinalities of any two sets A and B are always comparable. That is, for cardinal numbers | A | and | B | arbitrary sets A and B , one of the three relations holds: | A |=|B|, | A |≤| B | or | B |≤| A |. If | A |≤| B |, but the set A is not equivalent to the set B , then | A |<| B |.
Definition
Assuming the axiom of choice to be true, the cardinality of a set is formally defined as the smallest ordinal number , under which a bijective correspondence can be established between and. This definition is also called the von Neumann distribution of cardinal numbers.
If the axiom of choice is not accepted, then a different approach is required. The very first definition of the cardinality of a set (it is implicit in Cantor's work and explicitly stated in Frege, as well as in Principia Mathematica) is the class of all sets that are equivalent in cardinality.
In axiomatic systems based on the theory of ZFC, such a definition is inapplicable, since for non-empty such a collection is too large to fit the definition of a set. More precisely, if , then there is an injective mapping of the universal set into , under which each set goes to , whence, by virtue of the axiom of the size restriction, it follows that is a proper class. This definition can be used in type theory and "new foundations" [en] , as well as in related axiomatic systems. In the case of ZFC, the definition can be used by restricting the collection to the least rank equivalent sets (this trick, proposed by Dana Scott, works because the collection of objects that have a given rank is a set).
The formal order among cardinal numbers is introduced as follows: means that the set can be injectively mapped to . According to the Cantor-Bernstein theorem, it follows from the pair of inequalities and that . The axiom of choice is equivalent to the statement that for any sets and , at least one of the inequalities or .
A set is called Dedekind infinite [en] if it has a proper subset such that . Otherwise, the set is called Dedekind finite. Finite cardinal numbers coincide with ordinary natural numbers - in other words, the set is finite if and only if for some natural . All other sets are infinite. Subject to the axiom of choice, one can prove that the Dedekind definitions coincide with the standard ones. In addition, it can be proved that the cardinality of the set of natural numbers (alef-zero, or aleph-0 - the name is derived from the first letter of the Hebrew alphabet) is the smallest infinitely large cardinal number, that is, in any infinite set there is a subset of cardinality. The cardinal number next in order is denoted, and so on, the number of alephs is infinite. Any ordinal number corresponds to a cardinal number, and in this way any infinitely large cardinal number can be described.
Related definitions
- The cardinality of the set of natural numbers is denoted by the symbol ("aleph-zero").
A set is called infinite if its cardinality is (not less than the cardinality of the set of natural numbers), so countable sets are the "smallest" of infinite sets. The next cardinal numbers in ascending order are denoted (where the index runs through all ordinal numbers). Among the cardinal numbers, there is no largest: for any set of cardinal numbers, there is a cardinal number that is greater than all elements of this set.
- Sets that are equivalent to the set of all real numbers are said to have the cardinality of the continuum, and the cardinality of such sets is denoted by the symbol . The assumption that , is called the continuum hypothesis.
- For powers, as in the case of finite sets, there are concepts: "equality", "greater", "less". That is, for any sets and only one of the three is possible:
- , or and are equivalent;
- , or is more powerful than , that is, it contains a subset that is equally powerful, but not equally powerful;
- , or more powerful - in this case, contains a subset that is equivalent to , but not equally powerful.
- The situation in which and are not equivalent and in none of them there is a part that is equivalent to the other is impossible. This is indicated by the site https://intellect.icu. This follows from Zermelo's theorem. Otherwise, this would mean the existence of incomparable powers (which is possible in principle if one does not accept the axiom of choice).
- The situation in which and is impossible by the Cantor-Bernstein theorem.
- Sets and are called equivalent to if there exists a one-to-one mapping of a set onto a set .
Examples
- A set is called finite if it is equivalent to a segment of the natural series for some non-negative integer . The number expresses the number of elements in the finite set. For , the set contains no elements (empty set). If , then there is no injective mapping from to (the Dirichlet principle), and hence there is no bijection between them. Therefore, the sets and have different cardinalities.
- A set is called countable if it is equivalent to the set of all natural numbers . The countable sets are:
- Set for any natural . Conformity: .
- Set of . Conformity: .
- The set of integers . Correspondence is obtained by comparing the terms of the series with its partial sums (the terms of the series are taken without taking into account the sign).
- Set of pairs of natural numbers .
- The set of rational numbers is mapped injectively into a set (an irreducible fraction of the form corresponds to a pair of numbers ). Therefore, the set of rational numbers is at most countable. But since it contains the set of natural numbers, it is not less than countable. By the Cantor-Bernstein theorem, it is countable.
- Infinite sets not equivalent to the set are called uncountable. According to Cantor's theorem, the set of infinite sequences composed of the digits 0 and 1 is uncountable. The cardinality of this set is called the continuum.
- The cardinality of the set of real numbers is equal to the continuum.
Properties
- Two finite sets are equivalent if and only if they consist of the same number of elements. That is, for a finite set, the concept of power coincides with the usual concept of quantity.
- For infinite sets, the cardinality of the set can be the same as the cardinality of its own subset, for example .
- Moreover, a set is infinite if and only if it contains an equally powerful proper (that is, not coinciding with the main set) subset.
- Any infinite set is equivalent to the set of all its finite subsets.
- Cantor's theorem The set of all subsets of the set A has more power than A , or .
- In particular, there exists a set more powerful than any given one.
- Using the Cantor square, one can also prove the following useful statement: The Cartesian product of an infinite set A with itself is equivalent to A .
- Cartesian product power:
- Inclusion-exclusion formula for two and three sets:
- Power of the symmetric difference of two and three sets:
Arithmetic of cardinal numbers
Ordinary arithmetic operations on natural numbers can be generalized to the case of cardinal numbers. It can also be shown that in the case of finite cardinal numbers these operations coincide with the corresponding arithmetic operations on numbers. In addition, operations on cardinal numbers retain many of the properties of ordinary arithmetic operations.
The next cardinal number
Subject to the axiom of choice, for each cardinal number it is possible to determine the number following it, and there are no other cardinal numbers between and. If of course, then the next cardinal number is the same as . In the case of infinite, the next cardinal number is different from the next ordinal number.
Addition of cardinal numbers
If the sets and have no common elements, then the sum of cardinalities is determined by the cardinality of their union. If there are common elements, the original sets can be replaced by non-intersecting sets of the same cardinality — for example, by replacing with , and with .
Neutrality of zero regarding the addition:
Association:
CommetTativity:
Monotony (failure) addition to both arguments:
The sum of two infinite cardinal numbers can be easily calculated with the observation of the axiom of the choice . If one of the numbers or is infinite, then
Subtraction
Subject to the axiom of choice for any infinite cardinal number and arbitrary cardinal number, the existence of , for which , is equivalent to the inequality . This is unique (and coincides with ) if and only if .
Multiplication of fundamental numbers
The work of two cardinal numbers is expressed through the decartion of the sets:
Octos of zero:
Unit relative to multiplication:
9000 (non-decreasing) multiplication with respect to both arguments:
Distributivity of multiplication with respect to addition:
By analogy with addition, the product of two infinite cardinal numbers can be easily calculated if the axiom of choice is observed.
If the numbers and are nonzero and at least one of them is infinite, then
Division
Subject to the axiom of choice, for any pair of cardinal numbers and , where is infinite and not equal to zero, the existence of , for which , is equivalent to the inequality . This is unique (and coincides with ) if and only if .
Exponentiation of cardinal numbers
Exponentiation is defined as follows:
,
where denotes the set of all functions from to .
(in particular), see the empty function
Monotony:
We note that it is the power of Bulean and, therefore, for any set (see Cantor's Diagonal Method). This implies that among the cardinal numbers there is no largest (since for any cardinal number, a larger number can be specified). In fact, the class of all cardinal numbers is proper (although in some axiomatizations of the theory, the set of this cannot be proved - such, for example, is the system of "New Foundations" [en]).
All subsequent statements in this section rely on the axiom of choice.
If and are finite numbers greater than 1, and is an infinite cardinal number, then If the cardinal number is infinite, and finitely different from zero, then .
If and , and at least one of them is infinite, then
.
Using Koenig's theorem, we can prove that for any infinite cardinal number the following inequalities hold:
,
where denotes confinality .
Extracting roots
Subject to the axiom of choice, for any infinite cardinal and finite cardinal there exists a cardinal number such that , and .
Logarithms
Subject to the axiom of choice, a cardinal number that satisfies the condition , given infinite and finite , does not always exist. If such exists, then it is infinite and less than , and any finite cardinal number will also satisfy the equality .
The logarithm of an infinite cardinal number is the smallest cardinal number that satisfies the condition.
Despite the fact that the logarithms of infinitely large cardinal numbers lack some of the properties that are characteristic of the logarithms of positive real numbers, they turn out to be useful in certain areas of mathematics - in particular, in the study of cardinal invariants of topological spaces.
Continuum hypothesis
According to the continuum hypothesis, there are no other cardinal numbers between and. The cardinal number is also denoted and represents the cardinality of the continuum (that is, the set of real numbers). In this case . The generalized continuum hypothesis denies the existence of cardinal numbers strictly between and for any infinite set of . The continuum hypothesis is independent of the standard axiomatization of set theory, i.e. the Zermelo-Fraenkel axiom system combined with the axiom of choice (see Zermelo-Fraenkel set theory).
See also
- Ordinal number
-
TRANSFINITE NUMBER
In general, my friend, you have overcome reading this article about the cardinality of the set.
