Different shape of maths
Shapes – Definition with Examples
What are Shapes?
In geometry, a shape can be defined as the form of an object or its outline, outer boundary or outer surface.
Everything we see in the world around us has a shape. We can find different basic shapes such as the two-dimensional square, rectangle, and oval or the three-dimensional rectangular prism, cylinder, and sphere in the objects we see around us. These geometric shapes appear in objects we see as credit cards, bills and coins, finger rings, photo frames, dart boards, huts, windows, magician’s wands, tall buildings, flower pots, toy trains, and balloons.
Different Types of Shapes
Shapes can be classified into open and closed shapes.
| In geometry, an open shape can be defined as a shape or figure whose line segments and/or curves do not meet. They do not start and end at the same point. | In geometry, a closed shape can be defined as an enclosed shape or figure whose line segments and/or curves are connected or meet. |
Closed geometric shapes can further be put into two broad categories, namely two-dimensional and three-dimensional shapes.
| The 2-Dimensional shape is flat. | A 3-Dimensional Shape is a solid shape. |
| It has two dimensions, that is, length and width. | It has two dimensions, that is, length, width, and depth. |
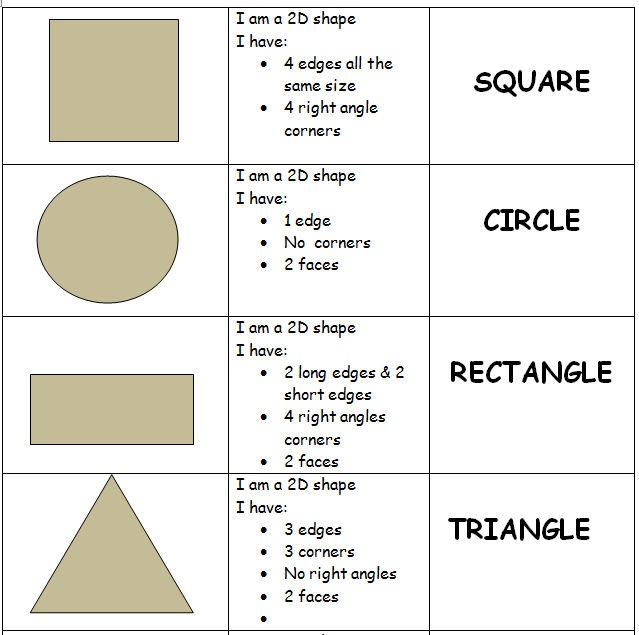
Here’s a list of 2-D or two-dimensional shapes with their names and pictures:
| Two-Dimensional Geometric Shapes |
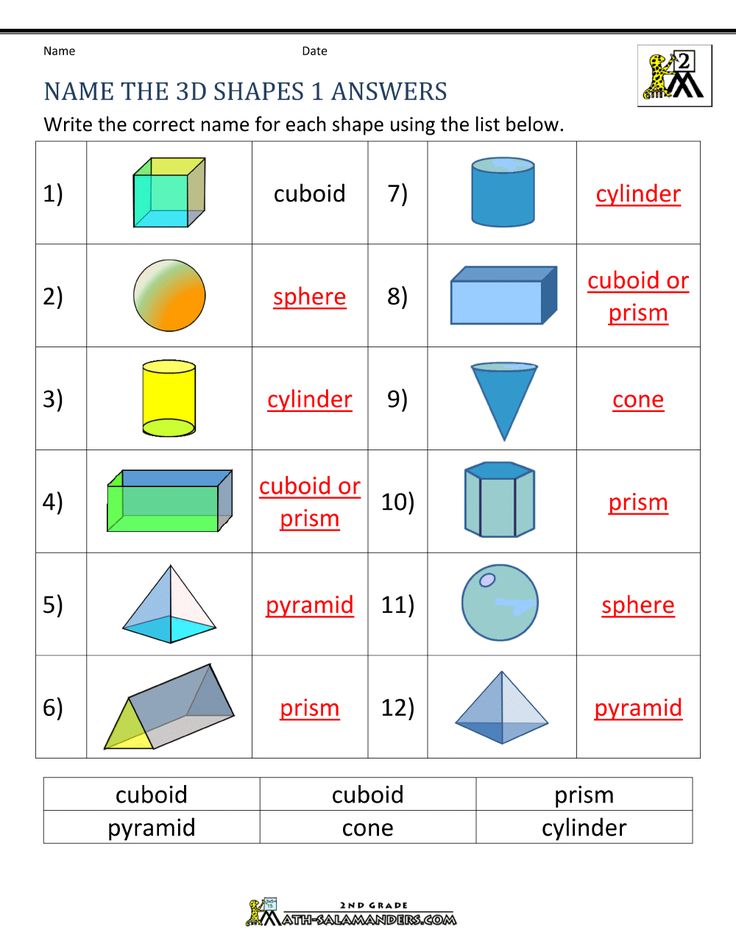
Here’s a list of 3-D or three-dimensional shapes with their names and pictures:
| Three-Dimensional Geometric Shapes |
The color, overall size, and orientation called the non-defining attributes of a two-dimensional or three-dimensional shape do not define or affect the shape in any way. These attributes can change without any effect on the shape.
On the other hand, defining attributes such as the number of sides (parallel or non-parallel, straight or curved), vertices, edges, and faces of a shape, whether the shape is open or closed, and the angle measures determine the shape of a two-dimensional or three-dimensional object. Any change in these defining attributes will change the shape.
Solved Examples on Shapes
Example 1: Name the shapes.
- A polygon with 6 sides.
- Outline of a door.
- When you fold square corner to corner.
- A square and a triangle on top of it.
Solution:
- Hexagon
- Rectangle or quadrilateral
- Triangle
- Pentagon
Example 2: Classify the given letters as open shape or closed shape.
C, D, L, M, O, S, U, V, Z
Solution:
Open shape: C, L, M, S, U, V, Z
Closed shape: D, O
Example 3: Identify the solid shape of given objects.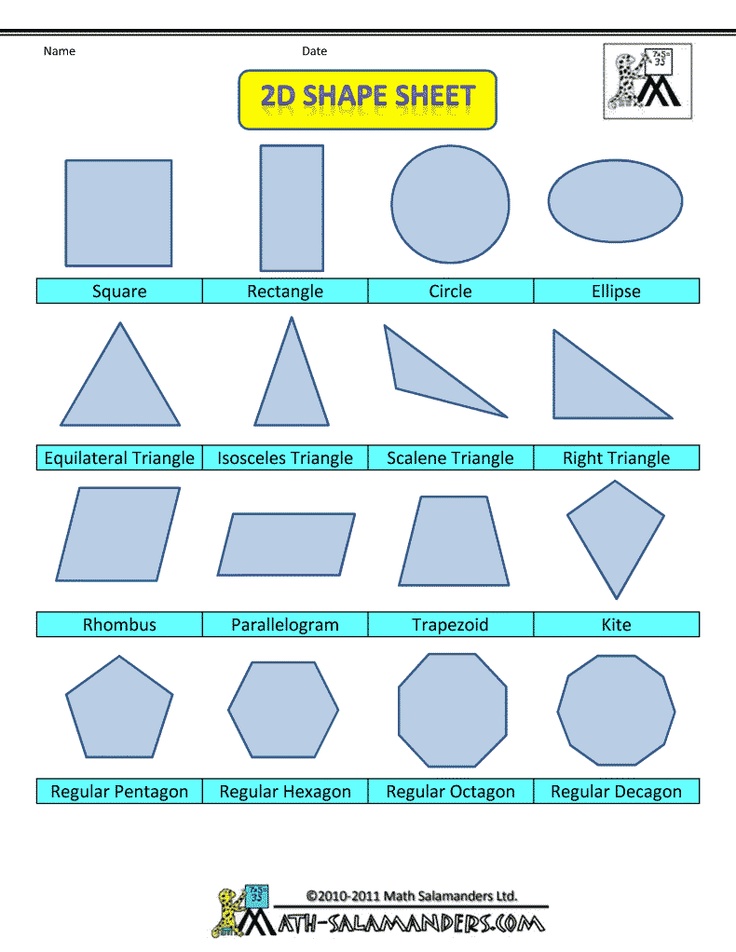
- Globe
- Book
- Cold drink can
- Dice
Solution:
- Sphere
- Cuboid
- Cylinder
- Cube
Example 4: Why is the crescent-shaped moon not a polygon?
Solution:
Crescent shape moon is not a polygon as it has curved lines.
Practice Problems
1
What is 8-sided polygon known as?
hexagon
heptagon
octagon
quadrilateral
Correct answer is: octagon
A polygon with 8 sides is known as octagon.
2
How many dimensions does a solid shape have?
1
2
3
depends on the shape
Correct answer is: 3
All solid shapes are 3-dimensional shapes.
3
Which of the following statements is incorrect?
closed shapes can have only straight sides.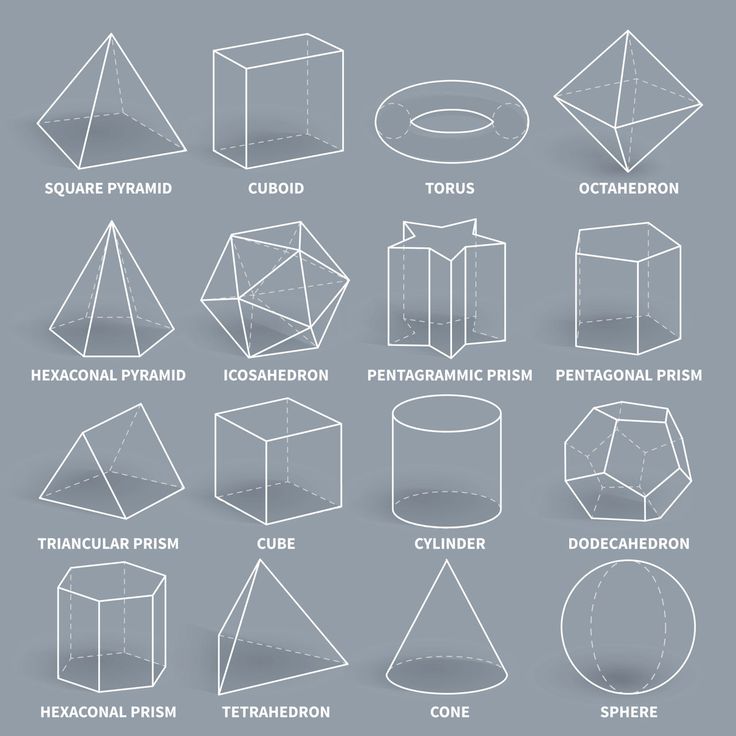
closed shapes have definite area.
start and end point of a closed shape are the same.
start and end point of a open shape are the different.
Correct answer is: closed shapes can have only straight sides.
Closed shapes are shapes whose start and end points are the same. It is not necessary that it is formed by only straight sides.
Different Shape Names (with Useful List, Types) • 7ESL
Pin
Are you looking for different shape names in English? Here you will find a list of shapes with different types and useful example sentences. If you work in a business that requires the use of mathematics, for example then it would be very important that you are aware of the English names for shapes.
However, this may not be the only reason that you need to learn this information. When taking part in day-to-day conversations, you will need to learn the shape names in order to describe something or be able to understand what someone is talking about, for example, if a person tells you about ‘the square plate.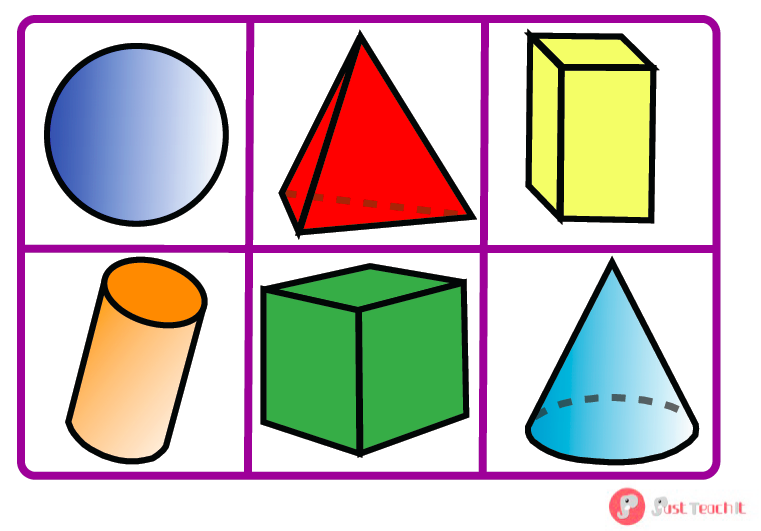 ’ Here, you can learn shape names and further expand your vocabulary.
’ Here, you can learn shape names and further expand your vocabulary.
Table of Contents
Shapes
What Are Shapes?
Shapes are geometric figures, or the pattern an outline falls into. Shapes are often drawn (whether by ink, pencil, or digitally), but they occur in life, also. Frequently, people picture 2D (two-dimensional, or flat) images when they hear the word “shapes,” so most of the objects listed in this lesson will be 2D shapes, but some will be 3D as well.
Different Types of Shapes
There are many, many different types of shapes, and there are names for basically all of them. The following list focuses on more common shapes that you’re more likely to encounter or to need or want to know the name of.
Shape names with pictures
Pin
Two-Dimensional (Flat) Shapes
- Circle: A circle is an equally round shape. Picture the lid of a jar, flat, from above.
 That is a circle. The wheels on a car are circular, as well. So are the holes in most lined paper and notebooks.
That is a circle. The wheels on a car are circular, as well. So are the holes in most lined paper and notebooks. - Oval: An oval is basically a circle that’s been a little squished. The cups of over-the-ear headphones are generally referred to as oval. So is the profile of an egg. Some make a distinction between circles that have been squished in the middle versus circles that have been squished at the top, the former being called an ellipse, but common usage treats both as ovals.
- Rectangle: A rectangle is a shape with four sides, made up of two sets of parallel lines, with four right angles (90 degree angles; picture a capital L). It doesn’t matter whether the sets of sides are the same length. Picture a plain piece of printing paper. This is a rectangle, with one set of sides (generally the top and bottom) shorter than the other set of sides (generally the left and right).
- Square: A square is a very specific type of rectangle, one with four equal sides.
 Some boxes have a square footprint. Origami paper is square.
Some boxes have a square footprint. Origami paper is square. - Triangle: A triangle is a shape with three straight sides. These sides can be any length, with any degree of angle, as long as the three sides are joined at their ends. Many warning signs are triangular. A slice of a round pizza is mostly triangular (the crust is a little too rounded to be perfect).
- Pentagon: A pentagon is a shape with five sides. A basic drawing of a house, with two lines for the roof, a line for each side, and a line for the bottom is generally a pentagon.
Shapes with more sides are generally named based on how many sides they have. A hexagon has six sides, heptagon has seven, and an octagon has eight.
Three-Dimensional Shapes
Three-dimensional shapes are ones that aren’t just flat on paper, but also take up room vertically. Only a few are really commonly named.
- Sphere: A sphere is a 3D circle, like a ball.
- Cube: A cube is a 3D square, like a box.
- Pyramid: A pyramid is a 3D triangle. The giant structures in Egypt are pyramids, as is the Luxor in Las Vegas.
Shape Names
It’s important to build a good vocabulary, in any language. The more words you know and understand, the better you can communicate. Even if you don’t use the words often, understanding them allows you to follow along with a conversation, even if it ventures a little outside of your comfort zone. This lesson is specifically focused on different types of shapes.
List of Shapes- Nonagon
- Octagon
- Heptagon
- Hexagon
- Triangle
- Scalene triangle
- Right triangle
- Parallelogram
- Rhombus
- Square
- Pentagon
- Circle
- Oval
- Heart
- Cross
- Arrow
- Cube
- Cylinder
- Star
- Crescent
The math student measured each side of the nonagon until he had measurements for all nine edges.
Pin
OctagonThe sectional shape is a quarter of an octagon.
Pin
HeptagonThe pagoda has a base of heptagon.
Pin
HexagonA hexagon is a six – sided figure.
Pin
TriangleThe sum of all the angles of a triangle is 180 degrees.
Pin
Scalene triangleA scalene triangle is a triangle that has three unequal sides.
Pin
Right triangleThe hypotenuse is the longest side of a right triangle.
Pin
ParallelogramThese are the opposite sides of the parallelogram.
Pin
RhombusA rhombus is a simple quadrilateral whose four sides all have the same length.
Pin
SquareThe interior angles of a square are right angles or angles of 90 degrees.
Pin
PentagonDraw a pentagon, a regular five-sided figure.
Pin
CircleThe students sit in a circle on the floor.
Pin
OvalThe shape of the earth is an oval.
Pin
HeartThe pool was in the shape of a heart.
Pin
CrossThe cross is the symbol of Christianity.
Pin
ArrowIt flew straight as an arrow.
Pin
CubeThe box was cube-shaped.
Pin
CylinderThe cylinder is rotated 180 degrees.
Pin
StarShe cuts these paper into star-shaped.
Pin
CrescentHe has a crescent–shaped knife.
Pin
Shapes | PictureLearn different shapes with images to improve and expand your vocabulary, especially shapes and colors vocabulary words in English.
PinShapes: Different Shape Names (with Useful List, Types)Shapes Names VideoThere are shapes everywhere, and so references to them happen frequently. Hopefully, after this lesson, you’re feeling prepared to deal with shapes!
Hopefully, after this lesson, you’re feeling prepared to deal with shapes!
Mathematicians have created a new geometry
April 16, 2019 13:15
Source: Newspaper.ru
Mathematicians from Moscow State University, together with foreign specialists, laid the foundations of Nijenhuis geometry, a branch of mathematics that is closely related to integrable systems, algebra, differential geometry, and mathematical physics. Papers (1 and 2), supported by a RSF grant, can be found at arXiv.org and are now being prepared for publication in the world's leading mathematical journals.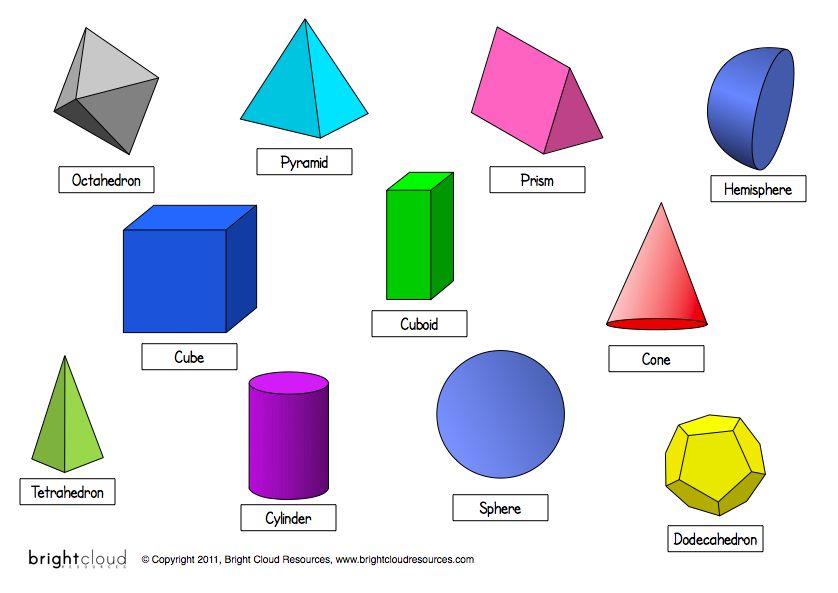
Geometry is at the heart of modern physics. So, for example, Albert Einstein's theory of relativity is connected with pseudo-Riemannian geometry. In this geometry, information about the geometric structure is written in the form of a matrix - the elements of the object that mathematicians study are enclosed in a table. In such a table, all elements have two numbers - the number of the row where it is written, and the number of the column. Just like in Excel.
The components, that is, the values of the table elements, change from point to point. If the dimension of space, for example, is three (length, width and height), then the size of such a matrix is 3 by 3, that is, it has 9 parameters. An additional condition is imposed on the matrix - symmetry. This means that the elements of the matrix that are symmetrical with respect to the diagonal are the same. This means that the number of parameters is not 9, but 6. Albert Einstein formulated his theory of relativity precisely in terms of pseudo-Riemannian geometry - this is its mathematical toolkit. He combined space and time to form a four-dimensional object, so his matrix is 4 by 4. In turn, Einstein's equation describes gravity in terms of the components of the matrix. It is this problem that astrophysicists solve numerically when they try to describe the behavior of physical objects in the vicinity of black holes.
This means that the number of parameters is not 9, but 6. Albert Einstein formulated his theory of relativity precisely in terms of pseudo-Riemannian geometry - this is its mathematical toolkit. He combined space and time to form a four-dimensional object, so his matrix is 4 by 4. In turn, Einstein's equation describes gravity in terms of the components of the matrix. It is this problem that astrophysicists solve numerically when they try to describe the behavior of physical objects in the vicinity of black holes.
Pictures: construction of a neighborhood of a singular point Nijenhuis operator. Source: study authors
Another geometry that is used in classical mechanics and partly in quantum mechanics is called Poisson geometry. In it, all geometric information is contained in a matrix, which in this case is not symmetric, but skew-symmetric. This means that in place of ij in this matrix there is the same function as in ji, only taken with a minus sign.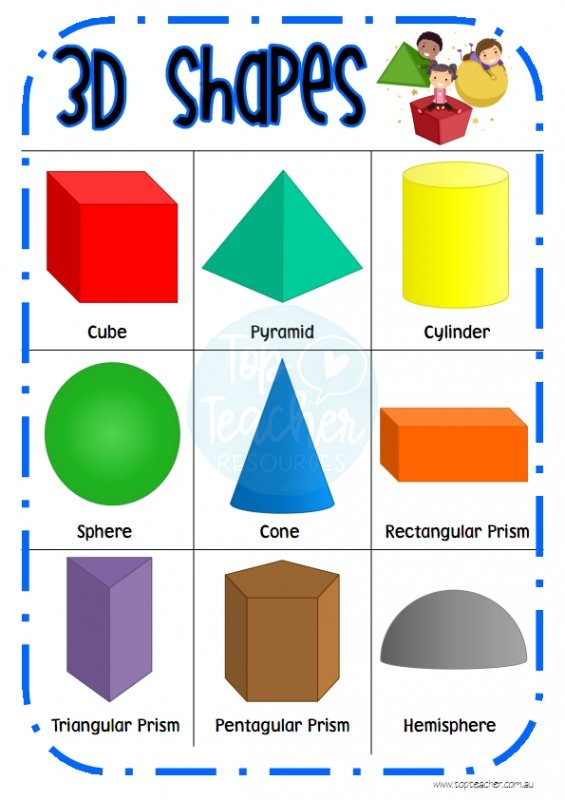 Additional conditions are imposed on the components of this matrix - the system of differential Jacobi identities.
Additional conditions are imposed on the components of this matrix - the system of differential Jacobi identities.
Poisson geometry first appeared as a tool in the theory of dynamical systems. Now it is used, for example, in the theory of deformation quantization, for the creation of which the famous French mathematician of Russian origin Maxim Kontsevich received the Fields Prize and twice the Miller Prize (once for the physical part, the other time just for the corresponding mathematical tools). This theory allows a comprehensive approach to the transition from classical to quantum physics. Today, there are many issues in this direction that are being actively studied.
“In our work, we turned to geometry, where information about the structure is also contained in the matrix. An important difference is what kind of matrix it is, - explains Andrey Konyaev , Ph.D. Lomonosov . - Traditionally, matrices in mathematics are used to write three different objects - a bilinear form, a 2-vector and an operator.
They are written as matrices because these objects are called tensors and are correctly transformed when changing coordinates. In pseudo-Riemannian geometry, a bilinear form appears, in Poisson geometry, a 2-vector, and in a new geometry, which is called Nijenhuis, we are talking about operators.”
Photo: research participant Andrey Konyaev (Moscow State University). Source: study authors
Imagine ordinary matter: a piece of tablecloth or a towel. It is made up of twisted threads. Some of the threads go, conditionally, from left to right, and some - from top to bottom. If the tablecloth has seen the views, then it has hooks, ties. A two-dimensional space with the Niinehuis operator is something similar - threads are stretched through each point. In this sense, the splitting theorem tells how the weaving of our “tablecloth” is locally arranged, and the study of singular points (the linearization theorem) tells what the simplest knots and hooks are.
Picture: Evgeny Zeleny
Some conditions are also imposed on the matrix in Nijenhuis geometry, which were discovered by Albert Nijenhuis back in the 50s of the last century. Despite the fact that this object has been at the disposal of mathematicians for the last 60 years, it was considered as a kind of auxiliary object for solving other problems.
A similar situation was with Poisson geometry in the 70s of the last century until several mathematicians managed to lay the foundation of Poisson geometry. This foundation is a certain set of basic theorems that reveal the richness of the structure and demonstrate the potential for its study.
One such scientist was Alan Weinstein. He managed to prove the so-called splitting theorem and lay the foundations of linearization - both of these mathematical ideas later turned into whole directions.
“In new papers, it was possible to obtain results similar in depth - the splitting theorem for Niinehuis operators, as well as to formulate and in some cases solve the linearization problem.
In the same works, we demonstrated deep connections between our results and other areas of mathematics and mathematical physics,” says Konyaev.
Tags
Mathematics, Special project
Physical and mathematical reality / Sudo Null IT News
This article is the second part of the synopsis of the book “Our mathematical universe. In Search of the Fundamental Nature of Reality" (author Max Tegmark).
The incredible effectiveness of mathematics in the natural sciences is something bordering on mysticism, because there is no rational explanation for this fact.
Eugene Wigner (1960)
The idea that the universe is in some sense mathematical goes back at least to the Pythagoreans and gave rise to centuries of discussion among physicists and philosophers. Galileo argued that the universe is a "majestic book" written in the language of mathematics. Nobel Prize winner in physics Eugene Wigner insisted in the 1960s that "the incredible effectiveness of mathematics in the natural sciences" needs to be explained.
Nobel Prize winner in physics Eugene Wigner insisted in the 1960s that "the incredible effectiveness of mathematics in the natural sciences" needs to be explained.
If you look around. Where is all this mathematics that we are going to do? Isn't mathematics the science of numbers? You will probably come across several numbers , such as the time on the clock, but these are only symbols invented and depicted by people, so they are unlikely to reflect the mathematical essence of the Universe in any deep sense.
Galileo speaks of geometric figures like circles and triangles as mathematical. You see, you are surrounded by geometric patterns or figures? (The design of objects in different shapes doesn't count.) But try throwing a pebble and see what a beautiful shape nature gives to its trajectory. Galileo made a discovery: the trajectory of any object has the same shape, called an inverted parabola. Moreover, the shape of this parabola can be described by a simple equation: x = y 2 , where x is the horizontal position, y is the vertical position. Depending on the initial speed and direction, this shape can stretch both vertically and horizontally, but it always remains a parabola.
Moreover, the shape of this parabola can be described by a simple equation: x = y 2 , where x is the horizontal position, y is the vertical position. Depending on the initial speed and direction, this shape can stretch both vertically and horizontally, but it always remains a parabola.
When we watch objects orbit in space, we discover another repeating shape, the ellipse. An ellipse is just a stretched circle. Depending on the initial speed, the direction of the orbiting object and the mass around which it moves , the shape of this orbit can be stretched or inclined, but always remains an ellipse.
Gradually, people discovered many other repetitive forms and patterns in nature, covering not only movement and gravity, but also such different areas as electricity, magnetism, light, heat, chemistry, radioactivity and subatomic particles. These patterns add up to the laws of physics. Like the shape of an ellipse, these laws can be described using mathematical equations (Fig. 1).
1).
Equations are not the only hint of mathematics hidden in nature: there are also numbers . Tegmark is not referring to the creations of human hands, like pagination in a book, but to numbers that express the fundamental properties of our physical reality. How many pencils can you arrange so that they are all perpendicular (at an angle 90°) to each other? Three. Where did the number 3 come from? We call it the dimension of space, , but why are there exactly 3 dimensions, and not 2, 4, or 42? Why are there (as far as scientists can tell) exactly six types of quarks in our universe ? There are many other "built-in" integers that describe what type of elementary particles exist. There are also values encoded in nature , which are not integers and require fractional values to be written.
Does this include the number that appears on the scale display when you stand on it? No, since it is a measure of something (your mass), that the day from days changes, and therefore is not a fundamental property of our Universe.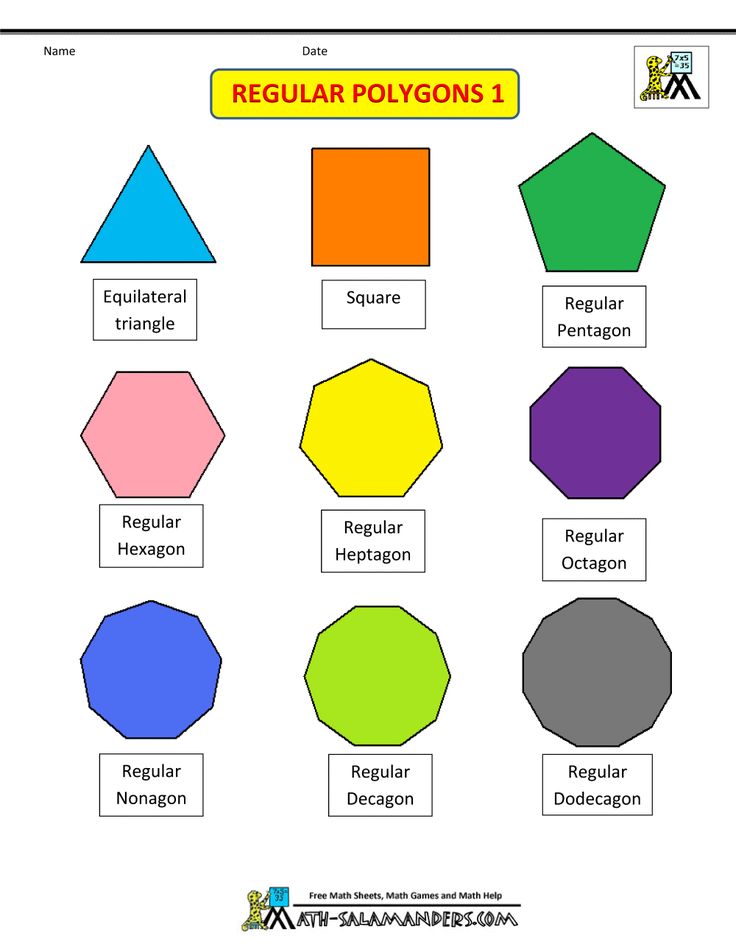 What can be said about the proton mass (1.672622 × 10 –27 kg) or the mass of an electron (9.109382 × 10 –31 kg), which seem to be constant in time? They also don't count, since are measured in kilograms, and this is an arbitrary unit of mass invented by people. But if you divide one of those two numbers by the other, you get something truly fundamental: a proton is about 1836.15267 times as massive as an electron. The value 1836.15267 is the dimensionless number , similar to π or √2, in the sense that its value does not depend on any human units such as grams, meters, seconds, or volts. Why is this value so close to 1836? Why not 2013? The simple answer is that scientists do not know this.
What can be said about the proton mass (1.672622 × 10 –27 kg) or the mass of an electron (9.109382 × 10 –31 kg), which seem to be constant in time? They also don't count, since are measured in kilograms, and this is an arbitrary unit of mass invented by people. But if you divide one of those two numbers by the other, you get something truly fundamental: a proton is about 1836.15267 times as massive as an electron. The value 1836.15267 is the dimensionless number , similar to π or √2, in the sense that its value does not depend on any human units such as grams, meters, seconds, or volts. Why is this value so close to 1836? Why not 2013? The simple answer is that scientists do not know this.
There is something purely mathematical in our universe, and the closer we look, the more mathematics we seem to see. As for the natural constants, there are hundreds of thousands of dimensionless numbers measured in different areas of physics: from the ratio of the masses of elementary particles to the ratios of the characteristic wavelengths of light emitted by various molecules.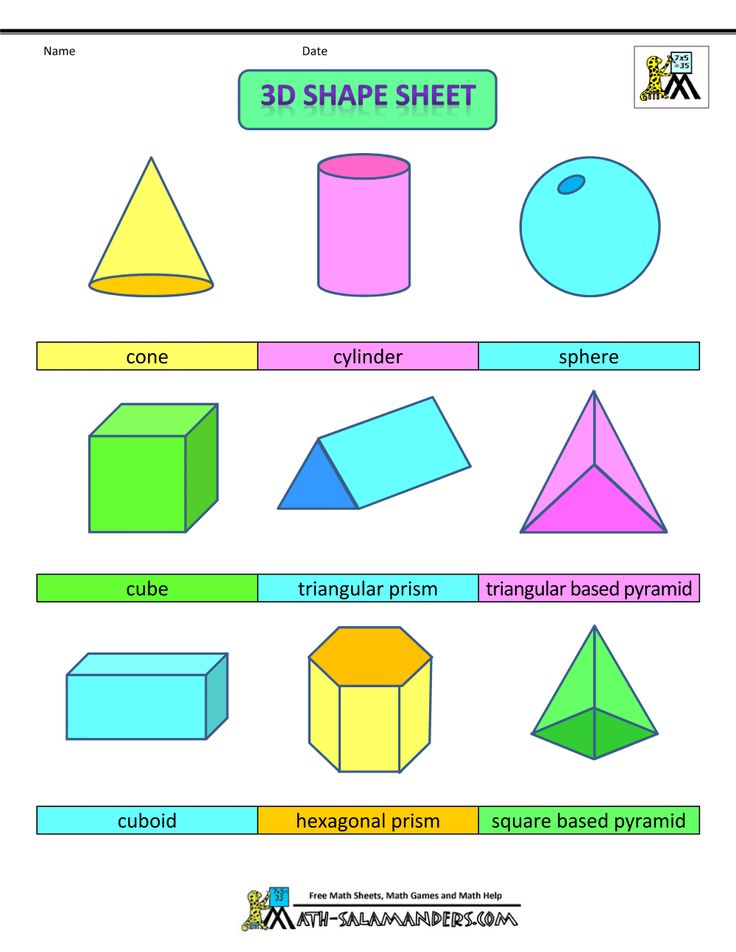 With computers powerful enough to solve the equations that describe the laws of nature, every one of these numbers can be determined. Some calculations and measurements are extremely complex and have not yet been done, and when they can, then, perhaps, the numbers in theory and experiment will not match. This sort of discrepancy has happened more than once in the past and has usually been resolved in one of three ways:
With computers powerful enough to solve the equations that describe the laws of nature, every one of these numbers can be determined. Some calculations and measurements are extremely complex and have not yet been done, and when they can, then, perhaps, the numbers in theory and experiment will not match. This sort of discrepancy has happened more than once in the past and has usually been resolved in one of three ways:
-
Someone has found an error in the experiment.
-
Someone has found an error in the calculations.
-
Has anyone found an error in our laws of physics.
In the latter case, it was usually possible to find more fundamental laws of physics - as when replacing Newton's equations for gravity with Einstein's, it was possible to explain why Mercury does not orbit the Sun in a perfect ellipse. In all cases, the feeling that there is something mathematical in nature only intensified.
Additional evidence
What to do with all these hints of the presence of mathematics in our physical world? Most physicists are accustomed to the fact that nature is, for some reason, described by mathematics, at least approximately, and accept this as a fact.
Why is mathematics so successful in describing nature? As Wigner said: it requires an explanation. We are constantly confronted with evidence that indicates that mathematics does not simply describe nature. In some respects, nature is mathematical:
-
The very fabric of our physical world, its space, is a purely mathematical entity in the sense that all the inherent properties of space—number of dimensions, curvature, and topology—are mathematical.
-
The "stuffing" of our physical world consists of elementary particles, which, in turn, are purely mathematical objects in the sense that all their inherent properties (for example, charge, spin) are mathematical.
-
There is something, perhaps even more fundamental than our three-dimensional space with particles in it, and that is the wave function and the infinite-dimensional Hilbert space in which it lives. Particles can be created and destroyed, and also be in several places at the same time, but there was and always will be only one wave function moving through Hilbert space in accordance with the Schrödinger equation.
 Both the wave function and the Hilbert space are purely mathematical entities.
Both the wave function and the Hilbert space are purely mathematical entities.
Mathematical Universe Hypothesis
It occurred to Tegmark one evening in 1990 that our reality is not only mathematically described, but is mathematics in a very specific sense. Not some aspects of it, but the whole, including ourselves.
Before going into details, here is the logical structure he uses to think about it. First, there are two hypotheses. The first, the External Reality Hypothesis (ERH), seems harmless: There is an external physical reality completely independent of people . The second, the Mathematical Universe Hypothesis (GMH), looks much more radical: Our external physical reality is a mathematical structure .
Secondly, Tegmark has a proof that, given a sufficiently broad definition of mathematical structure, the second hypothesis follows from the first hypothesis.
The first assumption, the external reality hypothesis, is not seriously disputed: most physicists agree with this old idea. Assuming that an external reality exists, the goal of physical theories is to describe how it works. The most successful theories, such as general relativity and quantum mechanics, describe only a part of this reality: gravity or, say, the behavior of subatomic particles. But the Holy Grail of theoretical physics is a "theory of everything", a comprehensive description of reality.
Assuming that an external reality exists, the goal of physical theories is to describe how it works. The most successful theories, such as general relativity and quantum mechanics, describe only a part of this reality: gravity or, say, the behavior of subatomic particles. But the Holy Grail of theoretical physics is a "theory of everything", a comprehensive description of reality.
Reduced baggage allowance
If we accept that reality exists independently of human beings, then for its description to be complete, it must also be correctly defined for non-human beings - say aliens or supercomputers - who are not familiar with human concepts. In other words, such a description should be expressed in a form devoid of any human "baggage" like the concepts "particle", "observation" and other natural language words.
At the same time, all physical theories contain two components: mathematical equations and "baggage" - words that explain how these equations are related to what we observe and intuitively understand. Deriving consequences from the theory, we invent new concepts and words for them, for example, atoms, molecules, stars, because they are convenient to use. It is important to remember, however, that these concepts are invented by people. In principle, everything can be computed without "baggage". Hypothetical perfect a supercomputer is able to calculate how the state of the universe changes over time, without "human" interpretation, simply calculating how all particles will move or how the wave function will change.
Deriving consequences from the theory, we invent new concepts and words for them, for example, atoms, molecules, stars, because they are convenient to use. It is important to remember, however, that these concepts are invented by people. In principle, everything can be computed without "baggage". Hypothetical perfect a supercomputer is able to calculate how the state of the universe changes over time, without "human" interpretation, simply calculating how all particles will move or how the wave function will change.
Another remarkable fact is that it is often possible to mathematically predict the existence of entities worthy of a name from the equations that govern their parts. In this way, it is possible to predict the entire "Lego-like" hierarchy of structures, from elementary particles to atoms to molecules, as well as all objects at every level, which people have given memorable names. For example, if you solve the Schrödinger equation for five or fewer quarks, it turns out that there are only two ways in which they can be fairly stably organized: either as clumps of two up quarks and one down quark, or as clumps of two down quarks and one top. People for the sake of convenience added names for these two types of bunches to their "baggage": protons and neutrons .
For example, if you solve the Schrödinger equation for five or fewer quarks, it turns out that there are only two ways in which they can be fairly stably organized: either as clumps of two up quarks and one down quark, or as clumps of two down quarks and one top. People for the sake of convenience added names for these two types of bunches to their "baggage": protons and neutrons .
Tegmark considers such composite objects as emergent in the sense that they arise as solutions of equations describing more fundamental objects. Their emergence is an elusive property, since historically scientific progress on has mostly gone in the opposite direction. Thus, people learned about stars before before they realized that they are composed of atoms; learned about atoms before they knew they were are made up of electrons, protons, and neutrons, and so on. For every emergent object that is important to us, people have collected "baggage" in the form of new concepts.
Emergence and accumulation of human "baggage" of the same nature are seen in fig. 2. The figure shows a rough diagram of the organization of scientific theories into a genealogical tree, in which each theory can be derived from more fundamental ones. All these theories have two components: mathematical equations, as well as words that explain how the equations relate to what we observe. At each level of the hierarchy of theories, new concepts are introduced because they are convenient and capture the essence of what is happening, without recourse to a higher, more fundamental theory. All these concepts are introduced by people: in principle, everything can be deduced from the fundamental theory at the top of the tree, although such extreme reductionism is usually useless in practice. Roughly speaking, as you move down on the tree, the number of words increases, and equations - decreases, almost reaching zero in such extremely applied areas as medicine or sociology.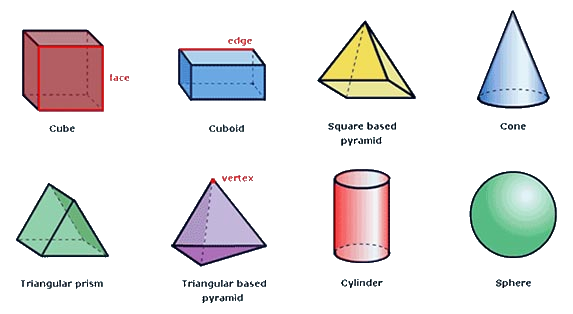 On the contrary, theories close to the close to the top are highly mathematized, and physicists find it difficult to describe concepts in a form that is accessible to the layman, if at all possible.
On the contrary, theories close to the close to the top are highly mathematized, and physicists find it difficult to describe concepts in a form that is accessible to the layman, if at all possible.
Something is missing: there is no holistic theory that combines gravity and quantum mechanics. The TV ("theory of everything") would be a complete description of the external physical reality that is assumed to exist in the external reality hypothesis. A full description should be free of any "baggage", that is, it should not contain any concepts. In other words, it must be a purely mathematical theory without explanations or "postulates". So an infinitely intelligent mathematician should be able to derive the entire tree of theories (Fig. 2) from these equations alone, extracting from them the properties of the physical reality they describe, the properties of its inhabitants, their perception of the world, and even the words they invent. All this inevitably leads to the question: is it really possible to find a description of external reality in which there would be no "baggage"?
Modern mathematics is a formal study of structures that can be defined in a purely abstract way, without human "baggage".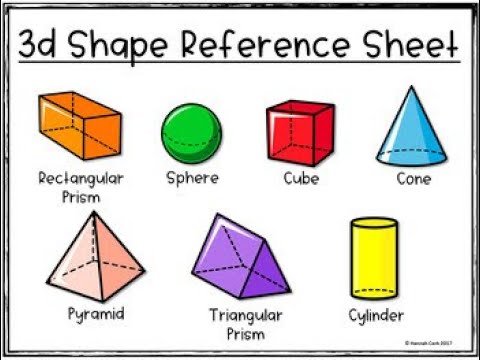 Think of mathematical symbols as mere labels with no intrinsic content. The notation used to indicate entities and their relationships is irrelevant; integers have only those properties that bind them together. That is, we do not invent mathematical structures: we discover them, but only invent notations to describe them.
Think of mathematical symbols as mere labels with no intrinsic content. The notation used to indicate entities and their relationships is irrelevant; integers have only those properties that bind them together. That is, we do not invent mathematical structures: we discover them, but only invent notations to describe them.
So, two main conclusions:
-
The hypothesis of external reality implies that the "theory of everything" (a complete description of our external physical reality) does not contain "baggage".
-
Something that has a description completely free of "baggage" is nothing but a mathematical structure.
From these theses follows the hypothesis of the mathematical Universe, that is, the statement that the external physical reality, described by means of the “theory of everything”, is a mathematical structure. If you believe in an external reality independent of humans, then you must also believe that our physical reality is a mathematical structure.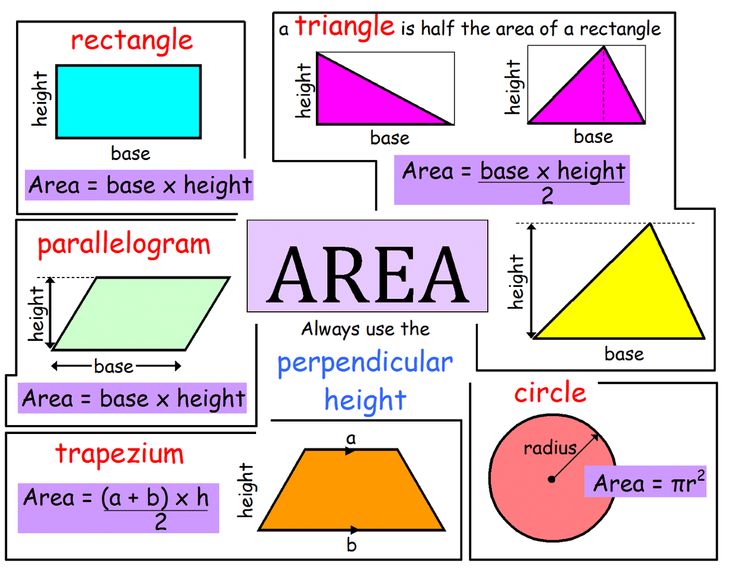 In other words, we live in a gigantic mathematical entity—perhaps much more complex than the entities with intimidating names like Calabi-Yau manifolds, tensor bundles, or Hilbert spaces that appear in cutting-edge modern physics theories. Everything in our world is purely mathematical - including ourselves.
In other words, we live in a gigantic mathematical entity—perhaps much more complex than the entities with intimidating names like Calabi-Yau manifolds, tensor bundles, or Hilbert spaces that appear in cutting-edge modern physics theories. Everything in our world is purely mathematical - including ourselves.
"Luggage" and equivalent descriptions
So people add "baggage" to their descriptions. Now let's look from the other side: how mathematical abstraction can get rid of "baggage", "exposing" things to their very essence.
An abstract game of chess does not depend on the color or shape of the pieces, on whether the moves are described by the movements of the pieces on a physically existing board, on a stylized computer image, or using algebraic chess notation - it is still the same game. Similarly, the mathematical structure does not depend on the symbols that are used to describe it (Fig. 3).
Fig. 3. Let's take a closer look at how we describe abstract entities. First of all, the description must be concrete, so one must invent objects, words, symbols, corresponding to the abstract idea. So, in the USA, a chess piece that moves diagonally is called a bishop. Secondly, it is obvious that this name is arbitrary and others would be just as good. Indeed, this figure is called fou ("fool") in French, strelec ("shooter") in Slovak, löpare ("runner") in Swedish, fil ("elephant") in Persian.
First of all, the description must be concrete, so one must invent objects, words, symbols, corresponding to the abstract idea. So, in the USA, a chess piece that moves diagonally is called a bishop. Secondly, it is obvious that this name is arbitrary and others would be just as good. Indeed, this figure is called fou ("fool") in French, strelec ("shooter") in Slovak, löpare ("runner") in Swedish, fil ("elephant") in Persian.
Any words, concepts, or symbols that appear in some but not all equivalent descriptions are obviously optional, and therefore "baggage". But if we want to define the essence of a chess game, how much "baggage" can we throw away? A lot, obviously: computers can play chess without any understanding of human language or concepts like color, texture, sizes, and names of pieces. To fully understand how far we can go, we need to give strict definition of equivalence: Two descriptions are equivalent if there is a correspondence between them that preserves all relations.
Chess uses abstract entities (pieces and squares on the board) and relationships between them. One of the relationships a piece can have with a square is that the first is on top of the second. Another relation a piece can have to the square, , is that it is allowed to move to it. Two central illustrations for fig. 3 are, by our definition, equivalent: there is a correspondence between three-dimensional and two-dimensional pieces and boards, so that any three-dimensional piece worth on a certain square corresponds to a two-dimensional piece on the corresponding square.
When computers play chess, they usually use other abstract descriptions of positions, which are patterns of zeros and ones in memory. So what is left after of how we get rid of "baggage"? What exactly is described by equivalent descriptions? Chess game, 100% cleared.
"Luggage" and mathematical structures
The analyzed case with abstract chess pieces, fields on the board and relations between them is an example of a much more general concept - mathematical structure. A mathematical structure is a set of abstract entities with relationships between them.
A mathematical structure is a set of abstract entities with relationships between them.
Figure 4 (left) describes mathematical structures with four entities linked by a like relationship. The essence of Philip is represented by an image with many internal properties, such as hair color. On the contrary, the essence of mathematical structures is completely abstract, which suggests that they do not have any intrinsic properties whatsoever.
Consider the more rigorous description shown in the middle figure. It is equivalent to the first one, , because if you match according to the following dictionary: Philip = 1, Alexander = 2, ski = 3, skateboard = 4, like = R, all relations are preserved.
On the right side of fig. 4 is the third equivalent description of our mathematical structure using a four-by-9 numerical table.0087 four. In a table, a value of 1 indicates that a relationship (likes) exists between the element corresponding to the given row and the element corresponding to the given column.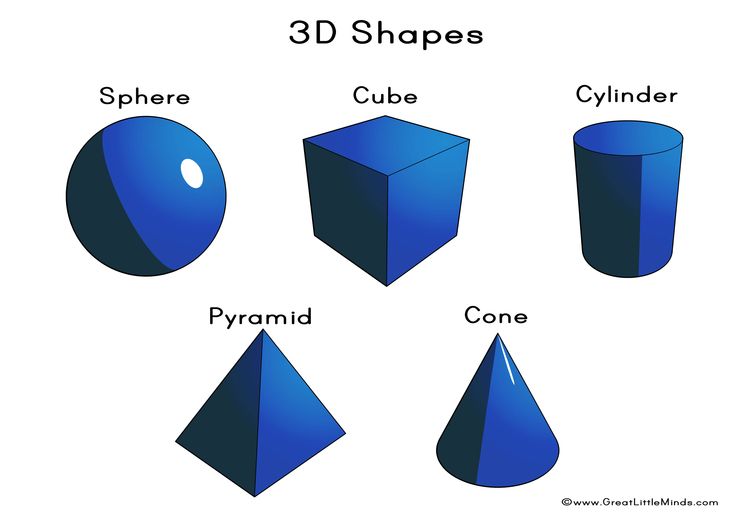 Let's say that the fact that there is a 1 in the third column of the first row means that "Philip likes skis."
Let's say that the fact that there is a 1 in the third column of the first row means that "Philip likes skis."
As a result, there is only one unique mathematical structure, which is described in all these ways. So, any concrete description of a mathematical structure carries "baggage", but the structure itself does not contain it. It is important not to confuse the description with what exactly is being described: even the seemingly most abstract description of a mathematical structure is not the structure itself. It would be more correct to say that the structure corresponds to the class of all its equivalent descriptions. In table. 1 gives a summary of the relationships between the key concepts associated with the idea of a mathematical universe.
Tab. 1.
| Mathematical Universe Cheat Sheet | ||
| "Baggage" | Concepts and words invented by people for convenience, which are not necessary to describe the external physical reality. | |
| Mathematical structure | A set of abstract entities with relationships between them. Can be described in a baggage-independent way. | |
| Equivalence | Two descriptions of a mathematical structure are equivalent if there is a correspondence between them that preserves all relationships. If two mathematical structures have equivalent descriptions, then they are the same structure. | |
| Symmetry | A property that remains unchanged during transformation. For example, a perfect sphere does not change when rotated. | |
| External reality hypothesis | There is an external physical reality, completely independent of people. | |
| Hypothesis of the mathematical Universe | External physical reality is a mathematical structure. | |
| Computable Universe Hypothesis | Our physical reality is a mathematical structure defined by a computable function. | |
| The hypothesis of a finite universe | Our physical reality is a finite (finite) mathematical structure. | |
Symmetry and other mathematical properties
However, according to the popular definition, mathematics is “the formal study of mathematical structures” (from the cube, integers to exotic, like Banach spaces). One of the most important tasks of mathematicians in the study of mathematical structures is a proof of theorems about their properties. But what kind of properties can a mathematical structure have if its entities and relationships are not allowed to have any intrinsic properties?
Consider the mathematical structure described on the left side of Fig.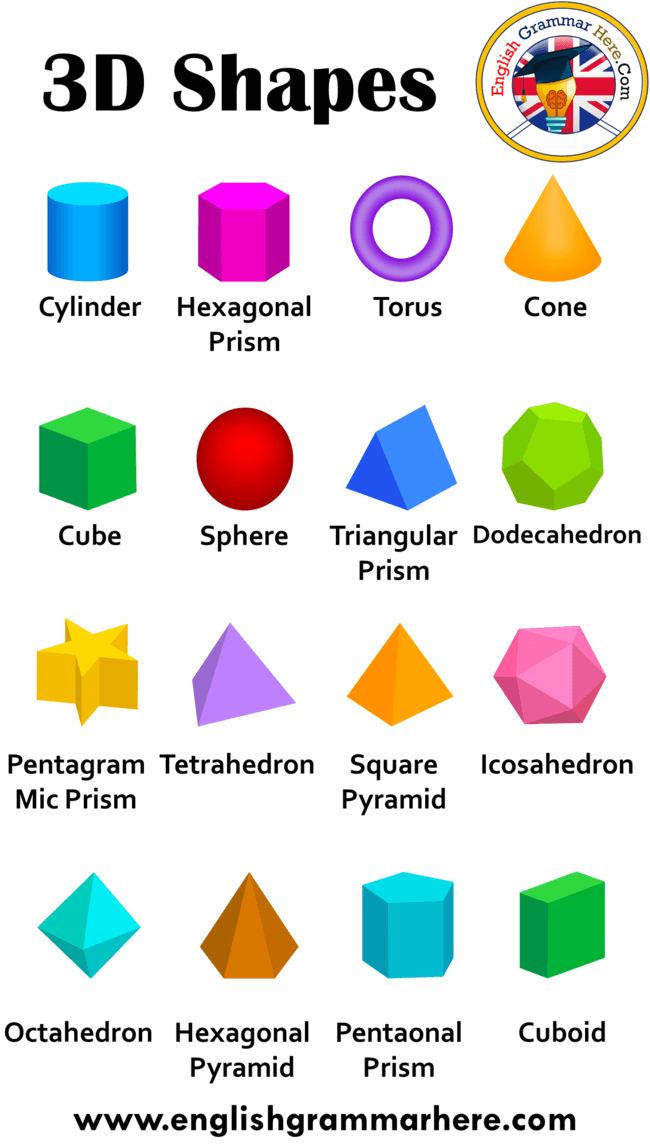 5. There is no relationship between the entities in it, so there is nothing that would allow to distinguish one of these entities from any other. This means that this mathematical structure does not have any properties, except for the power - the number of entities in it. Maths call this mathematical structure "a set of eight elements", and its only property is the presence of eight elements.
5. There is no relationship between the entities in it, so there is nothing that would allow to distinguish one of these entities from any other. This means that this mathematical structure does not have any properties, except for the power - the number of entities in it. Maths call this mathematical structure "a set of eight elements", and its only property is the presence of eight elements.
Middle image in fig. 5 describes another eight-element mathematical structure that includes their relationships. One of the descriptions of this structure is that its elements are vertices of a cube, and the relations determine which which vertices are connected by edges. Remember, however, that one should not confuse a description with what is being described: the mathematical structure has no properties of its own (such as size, color, texture, or composition) - it only contains eight related entities that you can optionally interpret as the vertices of a cube . On the right side of Fig. 5 shows an equivalent definition of this mathematical structure without reference to geometric concepts like "cube", "vertex" or "edge".
On the right side of Fig. 5 shows an equivalent definition of this mathematical structure without reference to geometric concepts like "cube", "vertex" or "edge".
But if the entities within this structure do not have their own properties, then can the structure itself have such properties ? Yes - this is symmetry (Table 1). In physics, something is said to have symmetry if it stays the same when you transform it in a certain way.
The famous sore point of philosophy is the problem of infinite regress. For example, if we say that the properties of diamond are explained by the properties and arrangement of carbon atoms in it, the properties of carbon atoms are explained by the properties and arrangement of protons, neutrons and electrons in them, and the properties of protons are explained by the properties and arrangement of quarks in them, it seems that we are doomed forever to try to explain the properties of these constituents. The Mathematical Universe Hypothesis offers a radical solution to this problem: at a lower level, reality is a mathematical structure, so that its parts have no intrinsic properties at all. In other words, it follows from the hypothesis of the mathematical Universe that we live in a relational reality, that is, the properties of the surrounding world are determined not by the properties of the primary “building blocks” of which it is composed, but by relations between "blocks". The outer physical reality is thus something more than the sum of its parts. It can have many interesting properties, although its parts have no properties of their own at all.
The Mathematical Universe Hypothesis offers a radical solution to this problem: at a lower level, reality is a mathematical structure, so that its parts have no intrinsic properties at all. In other words, it follows from the hypothesis of the mathematical Universe that we live in a relational reality, that is, the properties of the surrounding world are determined not by the properties of the primary “building blocks” of which it is composed, but by relations between "blocks". The outer physical reality is thus something more than the sum of its parts. It can have many interesting properties, although its parts have no properties of their own at all.
Every mathematical structure can be analyzed for symmetry, and many have interesting symmetries. One of the most important discoveries in physics was the presence of built-in symmetries in our physical reality. Thus, the laws of physics have rotational symmetry, that is, there is no preferred direction in the Universe that can be would be called "up". They also appear to have translational symmetry (with respect to shear), meaning there is no particular place that could be called the center of space. In the XX century many symmetries of nature were discovered. They underlie Einstein's theories of relativity, quantum mechanics, and the Standard Model of elementary particles.
They also appear to have translational symmetry (with respect to shear), meaning there is no particular place that could be called the center of space. In the XX century many symmetries of nature were discovered. They underlie Einstein's theories of relativity, quantum mechanics, and the Standard Model of elementary particles.
Symmetry properties so important for physics appear precisely because of the absence of their own properties in the "building blocks" of reality. If points in three-dimensional space had properties that would make some points intrinsically different from others, space would lose its rotational and translational symmetry. “Less is more” in the sense that the fewer properties the points have, the more symmetries the space has.
If the hypothesis of the mathematical Universe is correct, then our Universe is a mathematical structure, and from its description an infinitely intelligent mathematician should be able to deduce all physical theories.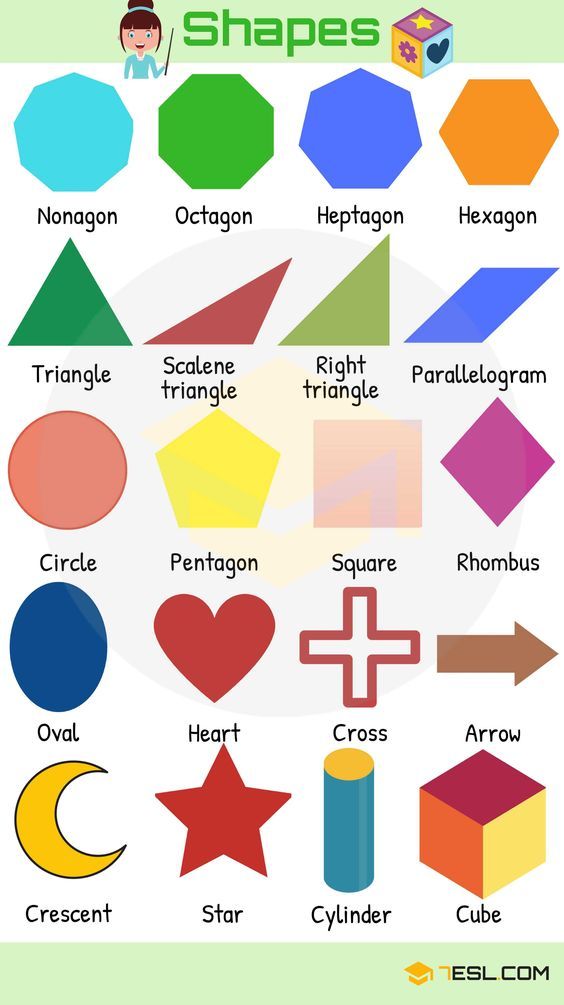 How exactly will he do it? Scientists don't know. No Tegmark I am sure that his first step would be to determine the symmetries of this mathematical structure.
How exactly will he do it? Scientists don't know. No Tegmark I am sure that his first step would be to determine the symmetries of this mathematical structure.
Summary
-
Physicists continue to discover forms, patterns and patterns in nature that can be described by mathematical equations.
-
The fabric of our physical reality contains dozens of dimensionless numbers, from which, in principle, it is possible to calculate all measurable constants.
-
Some physical entities, such as empty space, elementary particles, and the wave function, appear to be purely mathematical in the sense that all of their inherent properties are mathematical.
-
The External Reality Hypothesis (ERH), that there is an external physical reality completely independent of humans, is accepted by most physicists.
-
With a sufficiently broad definition of mathematics, the hypothesis of the mathematical Universe (GMH) follows from the GWR, stating that our physical world is a mathematical structure.

-
This means that our physical world is not only described by mathematics, but is also a mathematical structure, which makes us self-conscious parts of a giant mathematical entity.
-
A mathematical structure is an abstract set of entities with relationships between them. These entities do not have "baggage": other than these relationships, they do not have any properties.
-
A mathematical structure can have interesting properties, such as symmetries, even though neither the entities it contains nor the relationships between them have properties of their own.
-
GLM solves the infamous infinite regression problem. It lies in the fact that the properties of nature can only be explained by the properties of its parts, which require further explanation, and so on ad infinitum: the properties of nature arise not from the properties of its most fundamental "building blocks" (which have no properties), but from the relations between "blocks".
Conclusion
This synopsis touches on only part of the justification that the external physical reality is a mathematical structure. This really sounds crazy, however, as Tegmark wrote, this is just a warm-up. In subsequent chapters, Tegmark deals with the consequences and testable predictions that follow from the hypothesis of a mathematical universe, and things will get even crazier there. In addition, Tegmark will come to the inevitable conclusion about a new multiverse so huge that even the level III multiverse in quantum mechanics will pale in comparison.
The hypothesis of a mathematical universe raises three questions at once:
-
What exactly is the mathematical structure?
-
How exactly can our physical world be a mathematical structure ?
-
Does this statement make any testable predictions?
In this abstract, the first question was raised. You can familiarize yourself with the second and third in the original (the second question is the chapter “Is time illusory?”, The third question is the chapter “Level IV Multiverse”).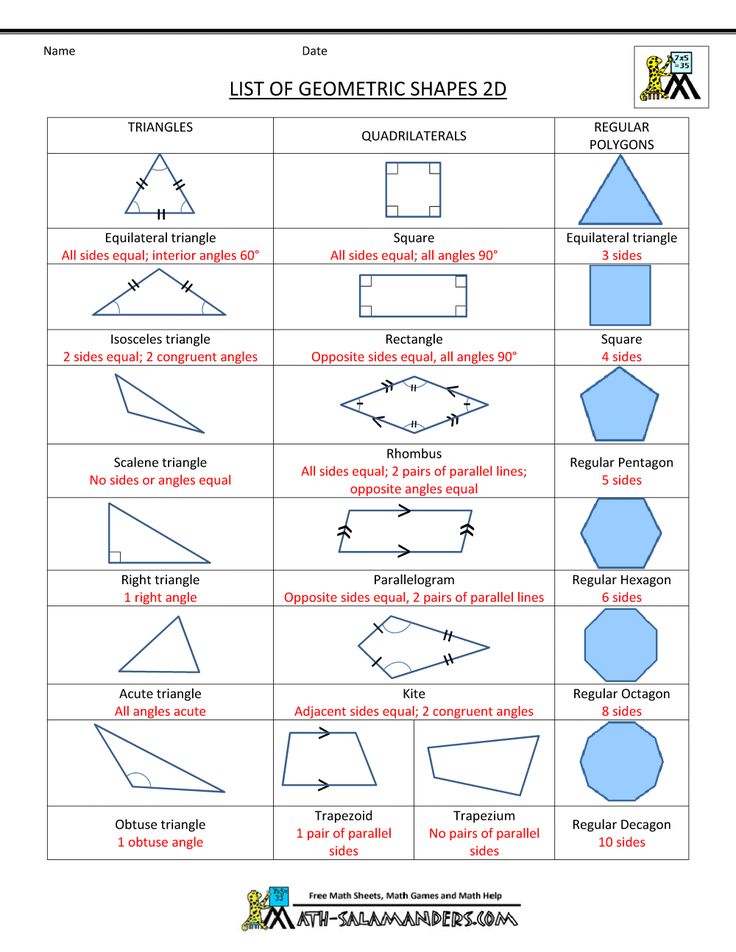


 Tegmark argues that this follows from the external reality hypothesis.
Tegmark argues that this follows from the external reality hypothesis.