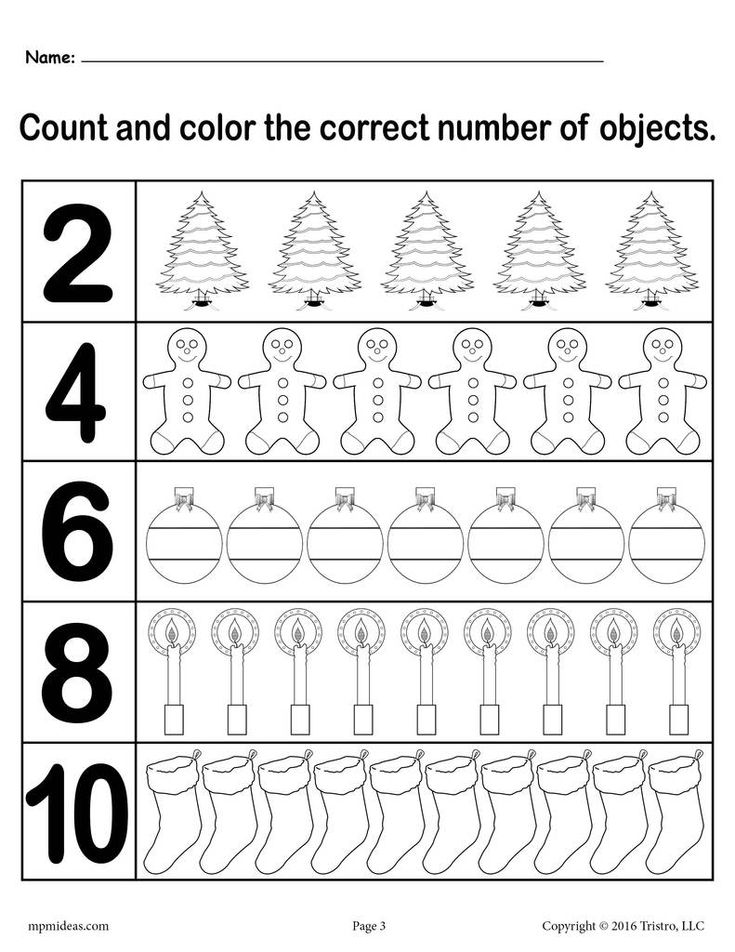
Learn how to count numbers

How Children Learn to Count

• Education
• Maths Tips
• 5 and under

Counting is easily taken for granted but there's a lot of fascinating research into how we learn to count - and there's more to it than you may think.

The mathematical brain

It’s first worth considering where our capacity to do mathematics comes from.

Neuropsychologist Brian Butterworth in his book “The Mathematical Brain” suggests we’re born with an innate sense of number hard-wired into our brain and he attributes this to a small region of the brain behind the left ear he calls "the number module". He compares this idea to colour – in the same way we perceive the “greenness” of a leaf we can also perceive the “twoness” or “threeness” of a group of objects.

Take counting. Like times tables and algebra, we tend to think it's something kids have to be taught. Wrong, says Butterworth - it's an instinct. Sure, we have to learn the names and symbols of numbers to develop that instinct, but, because the number module is hardwired into the brain, basic counting comes naturally.

Remote tribes can count even when they have no words for numbers. In maths as in language he believes, "kids start off with little starter kits" And their maths starter kit is the number module.

There are other theories too - such as maths being an extension of our spatial awareness – but there’s something nice in the idea of a “little maths starter kit”.  

A Word of warning - All this doesn't mean a child is predestined to be either good at maths or not. Far from it, we’re all born ready to learn maths – and it’s what happens in the first 10 years or so that sets us up.

Counting with toddlers

Research suggest that toddlers - even as young as 12 months - have a sense of how many there are in a set - up to around three objects. This comes from their innate sense of number.

Counting is learned when the toddler starts making the connection between this innate sense of "how many there are" and the language we use to count "one, two, buckle my shoe". This is the first stage in learning maths and it's the building block for many early concepts.

Should parents count with their toddlers? Absolutely, using a variety of real objects. And since counting and language are interlinked reading to your toddlers is equally, if not more, important.

Counting - early learning milestones

Here are some stages of learning to count that you may notice your child going through at ages 3 to 5:

• Recognising how many objects are in a small set without counting. So if you show your child four apples they won't have to count them to tell you there's four.
• Knowing the "number words" from one to ten and their order.
• Know the sequence regardless of which number they start on. So if you say "start counting at four" they will count "four, five . ." as opposed to always counting from one.
• Conservation of quantity - This is where children realise that the number of objects in a set stays the same unless any are added or removed. So if they count six cans of beans in a straight line, then you rearrange the beans ( in front of their eyes ) into say two stacks of three - they will realise there's still six without recounting.
• Counting non-visible objects - your child will realise they can count things they can't touch or even see - such as sounds, members of someone else's family, or even ideas.
• Cardinality, not to be confused with carnality - This is knowing that the last number counted is equal to the quantity of the set. If your child counts six oranges 1,2,3,4,5,6 and then you ask "how many oranges are there"? and they count them again then they haven't grasped "cardinality".

Counting on - as a step towards adding

Learning to add comes as an extension of counting. Here are some stages a child goes through to make this connection:

• Counting all - For 3 + 5, children will count "one, two, three" and then "one, two, three, four, five"  to establish the quantity of the sets to be added – for example, three fingers on one hand and five fingers on the other. The child will then count all the objects "one, two, three, four, five, six, seven, eight"
• Counting on from the first number - Some children come to realise that it is not necessary to count the first number to add. They can start with three, and then count on another five to get the solution. Using finger counting, the child will no longer count out the first set, but start with the word ‘Three’, and then use a hand to count on the second added: ‘Four, five, six, seven, eight’.
• Counting on from the larger number -  It's more efficient when the smaller of the two numbers is counted. The child now selects the biggest number to start with which is "five", and then counts on "six, seven, eight".
• The final stage isn't really counting - it's where learners know their number facts and skip the time-consuming counting altogether.

Number lines are great visual tools for making this connection between "counting on" and addition or subtraction - we use them in Komodo a lot. Here's an earlier blog article all about number lines.

Beyond basic counting

Counting is the first mathematical pattern learners encounter. From here they soon begin to count backwards which is a step towards subtraction and they'll also count in twos, fives and tens which are a foundation for multiplication.

The next big step is the idea of place value and counting to base 10. Learners often make this leap simply because it's an obvious and efficient way to count large numbers. In Komodo, we use practice examples like this to help learners make the connection to counting in tens and ones.

It's easy to forget that counting is a key concept in maths with many stages before it's mastered. There's certainly a lot more to it than one, two, three!

I'm Ged, Co-founder of Komodo, ex-maths teacher and dad. If you have any questions please get in touch.

About Komodo - Komodo is a fun and effective way to boost primary maths skills. Designed for 5 to 11 year olds to use in the home, Komodo uses a little and often approach to learning maths (15 minutes, three to five times per week) that fits into the busy routine. Komodo users develop fluency and confidence in maths - without keeping them at the screen for long.

Find out more about Komodo and how it helps thousands of children each year do better at maths - you can even try Komodo for free.

Related Posts

Mindset - the path to mastery

People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.

Top tips to de-stress homework time

Homework can be a trigger for some of the worst fights and arguments that we have with our children. Here are some solutions that can help reduce tensions and get homework done without arguments.

When Do Kids Start Counting to 10?

Feb 12, 2022 Counting to 10 is a major developmental milestone to which many parents look forward. But, at what point should your child start to learn numbers, and when should they be able to count to 10?

In This Article

• When Should My Toddler Learn to Count to 10?
  • Do you feel like your child should be counting by now?
• When Do Children Understand Basic Math Concepts?
• 9 Early Math Games for Kids Learning to Count to 10
  • 1. Coin counting game
  • 2. Magnetic fishing game
  • 3. Songs about numbers
  • 4. Get active while counting
  • 5. Speech Blubs’ “Numbers and Me” section

Math is all around us and from the moment children start exploring the world, they are learning. Whether they are identifying shapes, recognizing patterns, or predicting events, these are all mathematical concepts that develop as a child ages. But, at what age do children start to understand numbers?

The truth is, children will recite numbers before they actually understand the concept behind them. Though every child is different, most toddlers will be able to count to 10 by the time they are two-years-old. At this point in time they are probably repeating them mostly by memory and have yet to understand what they actually mean.

This concept is known as “rote” counting. Rote counting is when a child can say numbers in order, and is mostly learned through hearing the numbers repeatedly said out loud by others. 

Take this free cutting-edge 3-minute quiz. You will find out if your child is on track with his milestones and receive a free report with a personalized plan of learning. Speech Blubs is full of activities to encourage speech development!

View this post on Instagram

A post shared by Speech Blubs (@speechblubs)

When rote counting to 10, children may be able to cite numbers in order or may jump from number to number randomly. The more they hear others count, the more confident they will become in reciting the proper number orders. 

Note: Don’t panic if your child is not able to count to 10 by the time they are 2-years-old. This is the average age that children learn to count, but is by no means definitive.

All children learn at their own pace and some will learn more quickly than others. You can help your child learn numbers by working with them on a regular basis and engaging in toddler math activities.

We mentioned above that even though most toddlers can cite their numbers by 2, they don’t necessarily understand the concept behind them.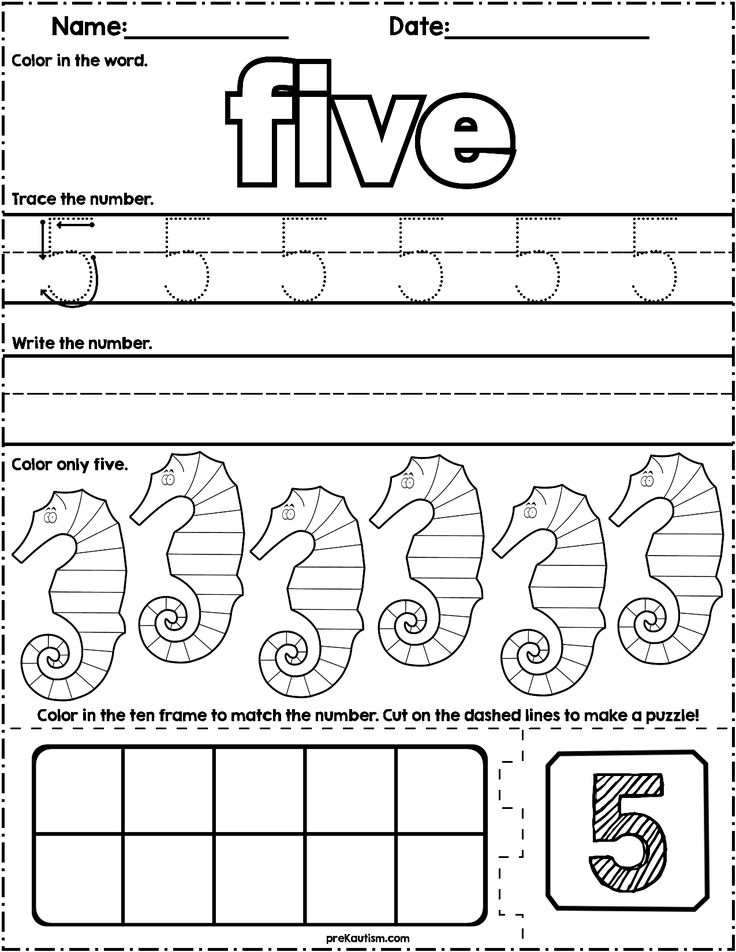 Children don’t actually start to understand the concepts of counting until between 2-4 years of age. 

The first sign that your child is starting to understand the concept behind numbers is with a skill known as one-to-one correspondence. You will often see this during playtime. One-to-one correspondence is when children start to group objects, pointing to each one as they count them. Again, this math skill is often learned by copying others. 

The next stage is understanding what these numbers represent. For example, if you count “one,” “two,” “three” cars, then there are three cars total in that group.

Once children start to understand this concept, the next stage is pairing numbers with their written numerals. Most children can start to understand this pairing by their preschool years, or 3-4 years of age. 

Other mathematical concepts that are usually developed by the preschool years include the ability to recognize shapes, use classifications (height, size, etc. ), use spatial awareness for puzzles, and start predicting cause and effect relationships. 

Learn Numbers With Speech Blubs!

Take this quiz and get a report on your child’s milestones and a personalized learning plan.

Start the Assessment

9 Early Math Games for Kids Learning to Count to 10

Here are some early math games for kids that you can do with your toddler to help them learn numbers and to count to 10:

1.

If you give a toddler a beautiful toy, what will they want to play with? A box. This is because toddlers love “real-life” toys and often prefer them to plastic kids’ toys.

With a toddler, things like boxes, pots, and pans, and money will attract more attention than any toddler toy – so why not utilize this to your advantage?

To encourage counting for preschoolers, let them count coins. At the same time, you can work on sorting the coins by size and on learning the different values of the coins. Each of these are mathematical concepts that will develop over time, but that you can encourage by practicing regularly.

You can purchase magnetic fishing games at almost any store that sells children’s toys.

These games are exactly what you would think they are – children use a magnetic pole to go “fishing” for magnetic fish.

Encourage your child to count the number of fish as they catch them. Not only will this encourage counting, but it will also help them with their hand-eye coordination.

Children love to sing and dance, and singing songs together is a great way to enhance learning. It is a perfect math game for kids, since they won’t even know they are learning! And when it comes to counting to 10, there are many songs out there that can help your child learn.

All you have to do is search YouTube for “number songs,” and you can choose from a long list of catchy tunes to help your child learn their numbers – and have a blast while doing it.  

When it comes to learning, we always like to encourage you to get your children outside. And when it comes to mathematics, nature is one of the most educational places your child can be.

Why? Because there are examples of math all over – the symmetry of a snowflake, the pattern of a pinecone, the geometry of a honeycomb, the height of different trees – math is everywhere you look. Of course, you can’t expect your toddler to understand the geometry of a honeycomb, but you can encourage them to count outdoors. **You also might check out Jon Scieszka’s bestseller, The Math Curse, for a fun story about a child who encounters math in everyday activities.

Go for a walk, choose a piece of nature (i.e., a tree), and see how many you can count on your way.

Learn Numbers With Speech Blubs!

Take this quiz and get a report on your child’s milestones and a personalized learning plan.

Start the Assessment

Speech Blubs is a speech therapy app that can help toddlers and young children to work on their speech. It can be used by all children, including those at a “typical” developmental level, and those with developmental speech delays due to conditions like autism or other learning disabilities. 

The NUM8ER5 AND M3 section of the app puts elementary numerical concepts on the tips of children’s tongues. It is a great early math game that you can use to teach counting to preschoolers.

Speech therapists will tell you that as children learn, the brain processes mathematical and linguistic stimulus in completely different locations of the brain. But, by doing exercises that target both of these neural centers simultaneously, you can help pave new neural networks within the brain. 

When using Speech Blubs, children’s participation will be rewarded with fun facts that show how various numbers appear within the world, on our bodies, and within society in general. Regular updates of fresh and new content keep the app exciting and interesting for young ones. 

Remember, however, that while the app works to help kids learn numbers and the concepts behind them, children always reap the most benefits when their parents participate. In return, it’s important that you make time to laugh along, mimic the speech models with your child, and extend the ideas on the app into the real world so that they can gain more context.

The more time you spend doing toddler activities and using the Speech Blubs app with your child, the more benefits they will receive from it.  

Teach numbers with Speech Blubs! Our fun section, NUM8ERS & M3 will help your toddler learn counting and develop his number sense in no time!

6.

Draw numbers from 1 to 10 on large pieces of paper. Tape them on the objects around the playroom or in your living room. For example, one can be on a chair, two can be on the couch, three in the corner, four on the wall, five at the window, etc.  When you shout out a number, your child has to go to that number and point to any object they represent! If they struggle you can give them clues. This activity is best for kids aged 3 or 4 when they have already learned the numbers by rote. It is also fun physical activity if you tell them they have to be as fast as possible or if you have more kids in the room who can compete to arrive first at the right number.

Find more ideas in this video about Number Recognition Preschool Activities:

7.

For this one, you need masking tape. Tape the shape of a number on a big piece of paper and ask your little one to trace them with colored pencils or sharpies. Besides the number writing practice, this activity is also great for working on their fine motor skills! If they like it, it can keep them occupied while you take some time off, prepare a meal, etc.

8. Sort the Colorful Mini Pom-Poms

Take an egg carton, and write a number in each of the egg compartments. Color each with a specific color. Now find objects to fit in the egg compartment that are the same color. This can be paper clips or small fluffy pom-poms you can get in the dollar store. Now match the number of pom-poms with the number and color in an egg compartment. For example, 1 yellow pom-pom, 2 red pom-poms, 3 green pom-poms, etc. Give your toddler the exact number of pom-poms for each color! Mix them up, and ask your child to sort them. They will be sorting for hours, learning colors and numbers at the same time.

9. Count with Legos

If you have Legos or any other toy building bricks at home, you can simply count them and learn numbers. Write numbers from one to 10 on a piece of paper. Below each number write a square or a box. Ask your child to put one Lego brick in the box under the number one, two under the number two, three under the number three, and so on. This will teach your child to compare what is less and what is more. You can also ask them: “Is one less than two? If I have two lego bricks, do I have more than one?” Don’t be too bothered with right or wrong answers (you can model to them what is right), the point is to just get them familiar with comparisons.

Learn Numbers With Speech Blubs!

Take this quiz and get a report on your child’s milestones and a personalized learning plan.

Start the Assessment

How to learn to quickly count any numbers in your mind: mental counting techniques

Mental counting is an activity that fewer and fewer people are bothering with nowadays. It is much easier to get a calculator on your phone and calculate any example.

But is it really so? In this article, we will present math hacks that will help you learn how to quickly add, subtract, multiply and divide numbers in your mind. Moreover, operating not with units and tens, but with at least two-digit and three-digit numbers.

After mastering the methods in this article, the idea of ​​reaching for a calculator on your phone doesn't seem so good anymore. After all, you can not waste time and calculate everything in your mind much faster, but at the same time stretch your brains and impress others (of the opposite sex).

So, welcome to the exciting world of computing! We have collected tips from our authors on how to improve mental arithmetic and become a math hero and genius. By the way, if you are interested in mathematics, you can read the article "Limits for dummies" in our blog.

Warning! If you are an ordinary person and not a child prodigy, then it will take training and practice, concentration and patience to develop mental numeracy. At first, everything can turn out slowly, but then things will go smoothly, and you can quickly count any numbers in your head.

Gauss and mental counting

One of the mathematicians with a phenomenal speed of mental counting was the famous Carl Friedrich Gauss (1777-1855). Yes, yes, the same Gauss who came up with the normal distribution.

In his own words, he learned to count before he could speak. When Gauss was 3 years old, the boy looked at his father's payroll and declared, "The calculations are wrong." After the adults checked everything, it turned out that little Gauss was right.

In the future, this mathematician reached considerable heights, and his works are still actively used in theoretical and applied sciences. Until his death, Gauss did most of his calculations in his head.

Here we will not deal with complex calculations, but start with the simplest.

Adding numbers in your head

To learn how to add large numbers in your head, you need to be able to accurately add numbers up to 10 . Ultimately, any complex task comes down to performing a few trivial actions.

Most often, problems and errors occur when adding numbers with "going through 10 ". When adding (and even when subtracting), it is convenient to use the technique of “reliance on a dozen”. What's this? First, we mentally ask ourselves how much one of the terms is missing before 10 , and then add to 10 the difference remaining up to the second term.

For example, let's add the numbers 8 and 6 . To get 8 from 8 , 2 is missing. Then to 10 it remains to add 4=6-2 . As a result, we get: 8+6=(8+2)+4=10+4=14

The main trick with adding large numbers is to break them into bit parts, and then add these parts together.

Let's add two numbers: 356 and 728 . The number 356 can be represented as 300+50+6 . Similarly, 728 would be 700+20+8 . Now add up:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Mental subtraction

Subtracting numbers will also be easy. But unlike addition, where each number is divided into bit parts, when subtracting, you only need to “break” the number that we subtract.

For example, how much is 528-321 ? We divide the number 321 into bit parts and get: 321=300+20+1 .

Now counting: 528-300-20-1=228-20-1=208-1=207

Try to visualize addition and subtraction. At school, everyone was taught to count in a column, that is, from top to bottom. One way to restructure thinking and speed up counting is not to count from top to bottom, but from left to right, breaking numbers into place parts.

Mental multiplication

Multiplication is the repeated repetition of a number. If you need to multiply 8 by 4 , this means that the number 8 must be repeated 4 times.

8*4=8+8+8+8=32

Since all complex problems are reduced to simpler ones, you need to be able to multiply all single-digit numbers. There is an excellent tool for this - multiplication table . If you do not know this table by heart, then we strongly recommend that you first learn it and only then take up the practice of mental counting. In addition, there is, in fact, nothing to learn there.

Multiplication of multi-digit numbers by single digits

First, practice multiplication of multi-digit numbers by single digits. Let's multiply 528 by 6 . We divide the number 528 into digits and go from the oldest to the youngest. We multiply first and then add the results.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

By the way! For our readers, there is now a 10% discount on any kind of work

Multiplication of two-digit numbers

There is nothing complicated here either, only the load on short-term memory is a little more.

Multiply 28 and 32 . To do this, we reduce the whole operation to multiplication by single-digit numbers. Let's represent 32 as 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Another example. Multiply 79 by 57 . This means that you need to take the number " 79 " 57 times. Let's break the whole operation into stages. First we multiply 79 by 50 , and then - 79 by 7 .

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Multiply by 11

Here's a quick mental counting trick that will help you multiply any two-digit number by 11 at phenomenal speed.

To multiply a two-digit number by 11 , add two digits of the number together, and enter the resulting amount between the digits of the original number. The resulting three-digit number is the result of multiplying the original number by 11 .

Check and multiply 54 by 11 .

• 5+4=9
• 54*11=594

Take any two-digit number, multiply it by 11 and see for yourself - this trick works!

Squaring

Another interesting method of mental counting is to quickly and easily square two-digit numbers. It's especially easy to do this with numbers that end in 9.0033 5 .

The result starts by multiplying the first digit of the number by the one following it in the hierarchy. That is, if this digit is denoted by n , then the next digit in the hierarchy will be n+1 . The result ends with the square of the last digit, i. e. the square of 5 .

Let's check! Let's square the number 75 .

• 7*8=56
• 5*5=25
• 75*75=5625

Division of numbers in the mind

It remains to deal with division. In fact, this is the inverse operation of multiplication. With the division of numbers up to 100 , there should be no problems at all - after all, there is a multiplication table that you know by heart.

Single digit division

When dividing multidigit numbers by single digits, it is necessary to select the largest possible part that can be divided using the multiplication table.

For example, there is a number 6144 that needs to be divided by 8 . We recall the multiplication table and understand that the number 5600 will be divided by 8 . Let's imagine the example as follows:

6144:8=(5600+544):8=700+544:8

Further, from the number 544 we also select the largest possible number, which is divisible by 8 . We have:

544: 8 = (480+64): 8 = 60+64: 8

It remains to divide 64 by 8 and get the result, folding all the results of the division

64:8=8

6144:8=700+60+8=768

Two-digit division

When dividing by a two-digit number, you must use the rule of the last digit of the result when multiplying two numbers.

When multiplying two multi-digit numbers, the last digit of the multiplication result always coincides with the last digit of the result of multiplying the last digits of these numbers.

For example, multiply 1325 by 656 . As a rule, the last digit in the resulting number will be 0 , since 5*6=30 . Indeed, 1325*656=869200 .

Now, armed with this valuable information, let's consider division by a two-digit number.

What is 4424:56 ?

Initially, we will use the fitting method and find the limits within which the result lies. We need to find the number that when multiplied by 56 will give 4424 . Intuitively, let's try the number 80.

56*80 = 4480

means the desired number less than 80 and clearly more than 70 . Let's determine its last digit. Her product of 6 must end with 4 . According to the multiplication table, the results 4 and 9 work for us. It is logical to assume that the result of division can be either the number 74 or 79 . Checking:

79*56=4424

Done, solution found! If the number 79 did not come up, the second option would certainly be correct.

Useful tips

In conclusion, here are some useful tips that will help you quickly learn mental counting:

• Remember to exercise every day;
• do not quit training if the result does not come as quickly as you would like;
• download the mobile application for mental counting: this way you don't have to come up with examples for yourself;
• read books on methods of rapid mental counting. There are different mental counting techniques, and you can learn the one that works best for you.

The benefits of mental counting are undeniable. Practice, and every day you will count faster and faster. And if you need help in solving more complex and multi-level tasks, contact the student service specialists for fast and qualified help!

How to learn to count mentally | Mathematics Club

⬑ More articles

According to many, counting in your head is no longer relevant nowadays, because every smartphone, computer and laptop has a calculator. However, the calculator will not accompany you with every step you take, but you need to count constantly and a lot. The ability to count in the mind is a very necessary skill even in the 21st century. And even more so, schoolchildren need it to solve examples in mathematics from a difficult school curriculum. And it will be very useful for them to be able to count quickly, without resorting to electronic devices.

Experience and constant training play an important role in the development of any ability, but the skill of mental calculation does not consist only of experience. This can be proved by people who can count much more complex examples in their heads: for example, multiply and divide three- and four-digit numbers, find sums and differences of huge examples.

What does a person need to know and do in order to repeat this?

• Firstly, concentration , or the ability to briefly keep several things in mind at the same time.

• Secondly, algorithms , special calculation methods and mathematical tricks that greatly facilitate the process of mental counting.

• Third, practice . Constant training and the gradual complication of the tasks to be solved will improve the speed and quality of oral counting.

It is important to note that it is the practice that has the highest value of . Without sufficient experience, you will not be able to quickly apply convenient algorithms that are suitable for certain situations. And remember that the maximum effect will be achieved with the optimal use of all three constituting . You can train all aspects of this skill at once in the online mental counting simulator.

Attention and concentration

To calculate mentally as fast as possible, you need to be able to concentrate on a specific example. This skill is useful not only for performing mathematical operations, but also for solving any life problems. There are several ways to improve your attentiveness and ability to concentrate:

When counting in your mind, it is important to clearly imagine the problem being solved - render it. You need to memorize intermediate results not by ear, but as they look in the record, for example, on paper. There are many ways to train this perception, and part of the visualization of the solution comes with experience.

Try to always find something interesting in your routine, turning the action into a game . So do some parents who want their child to do some boring work.

A huge number of people always want to "be better" than the opponent. That's why competitiveness is another way to develop your mindfulness. In the oral account, you can find an opponent for yourself and try to surpass him in this.

Another factor that creates excitement when counting can be a struggle with oneself when a certain result is achieved, that is, personal records . They can be set, for example, in counting speed, in the number of solved examples and in their accuracy of answers.

Finally, the maximum concentration can be achieved by spontaneous enthusiasm for the process of counting. As an example, while reading, you stop thinking about the objects around you, people, situations, and completely immerse yourself in the book. Precisely genuine interest in something can make you become more attentive in this matter.

Of course, all these methods must be worked out and practiced. Various visual memory simulators and mindfulness improvements can help with this.

Simple arithmetic patterns

The solution to any problem of complexity always comes down to the application of basic principles, and it is these principles and patterns that will allow you to quickly perform various kinds of operations. There is a certain set of such rules and patterns that need to be brought to automatism with the help of various online math simulators.

Subtract 7, 8, 9 . To subtract 9 from any number, you need to subtract 10 from it and add 1. To subtract 8 from any number, you need to subtract 10 from it and add 2. To subtract 7 from any number, you need to subtract 10 from it and add 3. If usually If you think differently, then for the best result you need to get used to this new way.

Multiplication table . For quick mental counting, it would be good to know the multiplication table perfectly, which is the basis of counting. If you still have problems with this, you can use the online Multiplication Table Trainer.

Multiply by 2 . To multiply non-round numbers by 2, try rounding them to the nearest more convenient number. So 139×2 is easier to calculate if you first multiply 140 by 2 (140×2=280), and then subtract 1×2=2 (that's 1 you need to add to 139 to get 140). Total: 140×2-1×2=280-2=278.

Divided by 2 . Despite the fact that multiplication and division by 2 is quite easy for many, in difficult cases, also try to round numbers. For example, to divide 198 by 2, you must first divide 200 (which is 198+2) by 2 and subtract 2 divided by 2. Total: 198:2=200:2-2:2=100-1=99.

Division and multiplication by 4 and 8 . Division (or multiplication) by 4 and by 8 are two or three division (or multiplication) by 2. It is convenient to perform these operations sequentially. For example, 46x4=46x2x2=92x2=184.

Multiplying by 5 and 25 . Multiplying by 5 and dividing by 2 are practically the same, so always multiply by 5 by dividing the number by 2 and multiplying by 10: 88×5=88:2×10=440. Multiplying by 25 corresponds to dividing by 4 (and then multiplying by 100). So 120x25 = 120:4x100 = 30x100 = 3000.

Multiply by 9 . You can quickly multiply any number by 9 as follows: first multiply this number by 10, and then subtract the number itself from the result. For example: 89×9=890-89=801.

Multiply by 11 . To multiply any two-digit number by 11, you need to enter the sum of the first and second digits between the first and second digits of the multiplied number. For example: 23×11= 2 (2+3) 3 = 253. Or if the sum of the numbers in the center is greater than 10: 29×11 = 2 (2+9) 9 = 2 (11) 9 = 319.

And finally , it is useful to know the division of multiples of 10 by multiples of two: 1000 = 2x500 = 4x250 = 8x125 = 16x62.5.

More sophisticated techniques

The efficiency of mental multiplication of some two-digit numbers can be higher due to fewer steps if special algorithms are used. Below are three special techniques, including the introduction and use of the reference number.

Squaring the sum and square the difference

To square a two-digit number, you can use the formulas for the square of the sum or the square of the difference. For example:

23 ² = (20+3) ² = 20 ² +2 × 3 × 20+3 ² = 400+120+9 = 529

9000 ² = ( 70-1) ² = 70 ² - 70×2×1 + 1 ² = 4 900-140+1 = 4 761

Squaring numbers ending in 5

numbers ending in 5, you need to multiply the number up to the last five by the sum of the same number and one. Add 25 to the result. Here are some examples:

25 ² = (2 × (2+1)) 25 = 625

85 ² = (8 × (8+1)) 25 = 7 225

155 ² = (15×(15+1)) 25 = (15×16)25 = 24025

Pivot Number

The most popular technique for multiplying large numbers in the mind is to use what is called a Pivot Number. The reference number for multiplication is the number to which both factors are close and by which it is convenient to multiply. And the method of using this number depends on whether the factors are greater or less than itself.

Both factors are less than the reference . Let's say we want to multiply 48 by 47. These numbers are close enough to 50 that it's convenient to use 50 as a reference number. Then we proceed as follows: from 47 we subtract as much as 48 to 50 is not enough (or from 48 we subtract as much as 47 to 50 is not enough), multiply the result by the reference number and add to it the product of the differences of the reference number with each factor. Illustrative example:

(48–(50-47))×50 + (50-47)×(50-48) = 2250 + 6 = 2256

Both factors are greater than the reference . You need to act in the same way, but do not subtract the deficiency, but add the excess:

(51+(63-50)) × 50 + (63-50) × (51-50) = 3200 + 13 = 3213

One the multiplier is less, the other is greater than the reference .

Learn more

• 
  1St graders learning
• 
  What are social skills
• 
  Children and meditation
• 
  Helping kids with sight words
• 
  When did the three little pigs come out
• 
  Sing the alphabet
• 
  What are vowel sounds
• 
  Game where you sound out words
• 
  Bed time fairy tales
• 
  Bedtime story short funny
• 
  Thumb in a pie