Home » Misc » Pre k math skills

Pre k math skills


The Most Important Math Concepts Kids Learn in Pre-K

Although there’s a lot of emphasis placed on emergent reading, experts show that pre-k math skills are just as important for your child’s learning development.

Understanding what skills your child will be exposed to as a math beginner will give you an idea of what concepts you can emphasize in fun, easy ways at home!

Fortunately, kids are exposed to many math concepts from a very young age — putting puzzles together, sorting objects, and even playing with building blocks. These activities all help build a good foundation for math.

In this article, we’ll take you through the most important pre-k math concepts so you can encourage and motivate your budding mathematician!

Table Of Contents

  • What Are The Components Of Pre-K Math?
  • Basic Pre-K Math Checklist
  • Pre-K Math Development
  • 9 Fun Pre-K Math Activities

What Are The Components Of Pre-K Math?

There are five basic components of pre-k math. They act like umbrella terms, each with many different elements hidden inside their broad concepts.

Your child will become acquainted with all of these essential concepts when they begin learning pre-k math.

1) Numbers And Counting

Children typically start with the bedrock of math — numbers! They’ll learn number names and how to write numbers, typically beginning with 1-10.

Counting is not easy business! While your child learns how to count — first with physical objects, then conceptually — they are bound to make mistakes here and there. This is perfectly all right. Counting will take time to master.

Most of kids’ initial exposure will be through representational counting. This could mean counting the number of strawberries in their lunch box, how many blocks are on the floor, and so on. These counting activities will set the stage for a strong foundation in counting.

By understanding that numbers represent objects, your child will begin to understand one-to-one correspondence (each object counted gets its own number and only that number) as well as the counting principle that when counting the number of objects, the last number counted equals the amount present.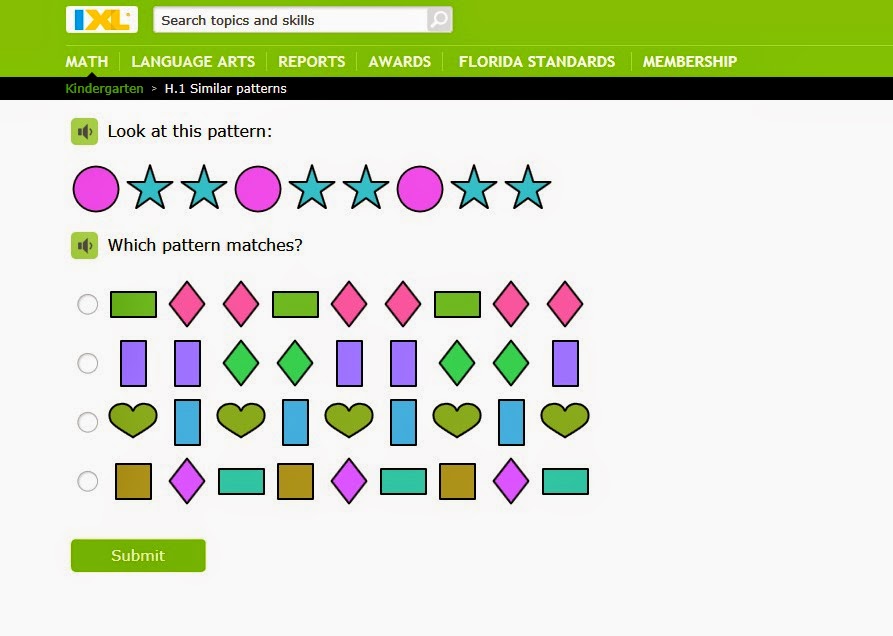

Over time, a child’s reliance on physical objects for counting will decrease. They’ll depend more on conceptual counting as their skills develop.

This conceptual counting is called “number sense.” They’ll understand that quantities, whether tangible or theoretical, are countable. They’ll also learn that numbers can be compared: two or more numbers can have a more-than, less-than, or same-as number relationship.

There are many fun ways to get your child comfortable with numbers and counting at home without making it feel burdensome.

Here are a few simple yet effective strategies you can try:

  • Encourage your child to touch and count objects they see in everyday life — for example, a bunch of bananas or a stack of books.
  • After they count a set of objects, help them write down the corresponding number on a piece of paper.
  • Have your child compare different items using the appropriate language. For example, “Let’s count the number of blueberries and strawberries on the plate. Are there more strawberries than blueberries?”
  • Hang a simple number line on the wall or tape one to your refrigerator. Throughout the day, point to each number with your child and count from 1-10 together.
  • Ask your child to help set the table by counting out the right number of forks and spoons. Once they have collected them, they can count them again as they put one at each place setting.

These simple activities allow children to make sense of numbers. And the more they practice counting principles outside of the classroom, the more they’ll realize how relevant they are to everyday life.

2) Addition And Subtraction

Once your child has a firm grasp on counting and is developing number sense, they’ll explore the relationships between numbers more often. Describing how numbers are the same or different will lead into learning how to combine two numbers to make a new number!

Similar to the last concept, children will typically learn how to add and subtract by relying on counting activities with tangible objects. For example, you could set up two separate groups of apples and ask how many you will have if you join them together.

The first group may have three apples, while the second group has two apples. At first, many children will count one group and then start over to count the second group. It is a good idea to count both groups individually and then bring them together and count the total amount.

This is their first introduction to addition! The same idea works for subtracting. What happens when you begin with five apples and then take away two of them?

“Taking away” objects may be a little harder for your child to master at first. This is why many children will remove apples first and then count the remaining apples rather than counting backward.

To help, practice counting backward together. Pretend to be a rocket ship, and start counting down from five to one, gradually increasing the beginning number each time. After you get to one, shout, “Blastoff!” and jump into the air as high as you can. This fun game can help your child become more comfortable with counting down.

Pictures can also help your child master addition and subtraction concepts. For addition practice, present one sheet of paper with three apples and another with two. Then say, “Count the apples on both pieces of paper. How many apples do you have total?”

For subtraction problems, present this scenario: “On our paper, we have five apples total. How many apples will you see if I cover up two of them?” Then, count the remaining apples together.

Pictures are an effective way for your child to visualize mathematical problems. But, if you prefer not to draw, you can also use real objects instead. You could get out several apples (stuffed animals, cups, or whatever) and count them. Then, use those items for math practice.

Remember that adding and subtracting are basically making comparisons between numbers or establishing relationships between them. There are many strategies a child might use to solve a problem, which is a good thing since our main goal is to help children think mathematically.

3) Geometry And Spatial Reasoning

Shapes are everywhere in our world, which will be one of your greatest assets when it comes to teaching your child about shapes and spatial reasoning.

They’ll start out by learning about the basic 2-D shapes that are used in math: squares, triangles, circles, rectangles, rhombuses, and ovals. Learning how to draw these basic shape illustrations can be helpful for their learning process.

Some of these shapes you’ll be able to reference easily in your day-to-day life. This will help reinforce your child’s understanding of the shapes after their initial introduction.

For example, when making breakfast with your child, you could hold up a plate and ask them, “What shape is this? Do you think it’s a square or a circle?”

Other shapes, like triangles or rhombuses, may be a little harder to find hanging around. Challenge your child to find these shapes in nature. Are there any flower petals in your garden that are shaped like triangles (or an aloe vera plant hanging in their windowsill)?

Encourage your child to be creative with identifying shapes! It will help them with learning geometry in the long run.

Next, learning 3-D shapes will come after learning 2-D shapes. Like their flatter cousins, 3-D shapes are all around the world, too! Your child’s soccer ball is a sphere; the paper towel roll in the kitchen is a cylinder.

We recommend learning the basic form of these shapes and how they appear first. Then, you can use the natural 3-D shapes in your child’s environment to reinforce their learning!

Point out shapes when you see them and play a shape version of “I Spy” to practice. If your child has a set of blocks, talk about the different shapes of the blocks. Challenge them to use only one shape to build something. Then, see what they can make by using all of the shapes.

Kids also learn about spatial reasoning by discovering how to describe the shapes they see and play with. They can compare them with dimensional adjectives like “big” and “small,” or characteristics of their shape like “straight” and “curvy.”

This includes the spatial relationship between different objects, too. Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.

4) Sorting And Patterns

We categorize things in our daily lives without even realizing it. Your child probably already does this, too — they may arrange their stuffed animals or toys in a certain way. For example, they may keep farm animals separated from dinosaurs.

Sorting and patterns are related to categorical reasoning. In the same way grocery stores sort out items by their parallel uses, your child will learn how to sort things based on their characteristics and how they are the same or different from other objects.

They’ll sort objects by weight, shape, quantity, texture, color, and other traits, often without even realizing it!

It’s important to note here that sorting and counting aren’t sequential. Your child might begin sorting before they begin counting, in fact.

For instance, if you want your child to sort a bowl of fruit, you can ask them to count all of the strawberries.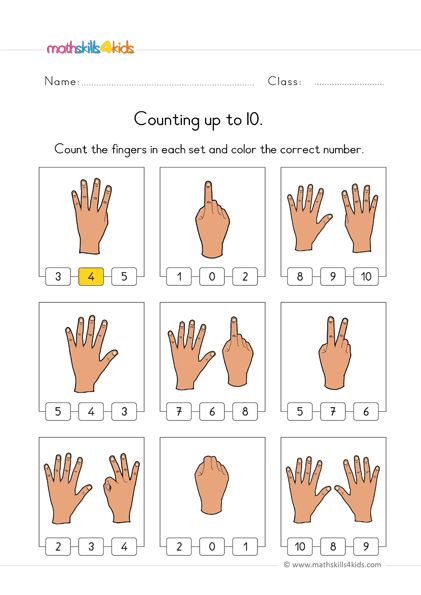 They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.

Once a child has learned to isolate characteristics, they can begin to identify, extend, and even create patterns. Your child will learn how to:

  • Copy a pattern
  • Identify the parts that repeat and continue a pattern
  • Correct a mistake in a pattern
  • Explain a pattern
  • Create their own patterns

To encourage your child to explore patterns, take a few moments to build a pattern for them when you play together. Use whatever materials you have available and create a simple AB pattern, such as truck, car, truck, car.

Next, point to each object. Say its name aloud. Then, when you get to the end of the row, ask them what comes next. If they aren’t sure, grab the next object and put it down. Once you’ve completed one round, start at the beginning and repeat each item to reinforce the pattern.

5) The Language Of Math

Part of learning how to do math means learning how to “speak” math. We don’t mean your child will turn into C-3PO — just that they will learn how to use mathematically correct language, or how to tell a story with math terms.

This can happen in daily life. While picking at an afternoon snack, your younger child may say, “Hey! My brother has more crackers than me!” Then you might agree to “add” to the cookies on the younger child’s plate so that both plates are “equal.”

These skills may be naturally exciting for your child — they’ll feel like they’re learning how to speak “grown up!” Show them how fun it is to incorporate mathematically appropriate language into their daily speech and use it to tell stories about what’s going on around them.

Using words to describe things in their lives will help them give ownership over ideas and observations. Motivate them to think about the order of the world around them and use different words to describe them, such as:

  • More than
  • Less than
  • Shape names
  • Light or heavy
  • Small or big

Mastering math language will help them in their quest to become robust mathematicians! It’ll also help them develop a strong vocabulary so they’re better prepared for kindergarten.

Basic Pre-K Math Checklist

Now that you know some of the concepts your child will be learning in pre-k math, let’s look at some of the skills they’ll build during this time.

  • Rote count to 10
  • Use one-to-one correspondence to count up to 10 objects and tell how many there are altogether
  • Recognize basic shapes (circle, triangle, square)
  • Understand the concept of quantity (more/less)
  • Sort objects by one characteristic
  • Understand and use directional terms, such as up, down, in, out
  • Pick what object goes next in a simple pattern

While these aren’t all of the math skills your child might learn in pre-k, they will give your child a solid mathematical foundation to build on in kindergarten. And they’re all skills you can practice in fun ways!



Pre-K Math Development

As your child grows and learns, they’ll work through three phases of mathematical development: concrete, representational, and abstract. They’ll likely be in the concrete stage at the beginning of pre-k.

During this phase, students need hands-on activities and real-world examples to help them understand mathematical concepts. This is why math manipulatives are so crucial in the early years. It’s also essential to present math concepts in a very concrete way during this stage.

For example, if you’re teaching your child about numbers, don’t just tell them that five is more than three. Instead, show them five objects and three objects, and let them count for themselves. This will help them understand the concept of more and less.

As your child continues to learn and practice a mathematical concept, they can move into the representational phase. Here, students can count pictures or images instead of actual objects. For example, they realize that numbers can be represented by lines or drawings.

Then, they’ll be ready to try the abstract stage. At this point, children understand that numbers can be represented by symbols. They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.

The activities above will help your child to build their understanding of mathematical concepts so they can move through the different stages.

But, in pre-k, it’s important to focus on the process, not the answer. So don’t worry if your child doesn’t get the solution right away. Let them work through the problem and try to figure it out for themselves.

A strong foundation in pre-k math sets children up for success when they start kindergarten. By providing opportunities for them to explore and experiment with math, you can help them develop the skills they need to be successful in school and beyond.

9 Fun Pre-K Math Activities

Now that you’re clear on all of the exciting new math concepts your pre-kindergartener will be exposed to and what skills they’ll practice, let’s talk about some games and activities you can play at home to help your child hone them.

We’ve already discussed some math activities you can incorporate into everyday life. Now, we’re sharing our list of fun games to encourage your young learner to love math even more.

1) What Did I Do?

This game helps reinforce counting, adding, and subtracting. It’s quick to play, so it’s perfect for when you have a few extra minutes.

What You’ll Need
  • Small objects (e.g., paper clips)
What To Do

Place some paper clips (or any other small objects) in your hand, and let your child count how many you have. After they’ve done this, put your hands behind your back and either add or remove some.

Next, show your child the new quantity and ask them to count how many there are now. You can ask your child questions, such as, “Did I add or take away some paper clips?” or “How many did I add or take away?”

For even more fun and learning opportunities, take turns playing the game. And when it’s your turn to guess, it’s OK to guess wrong — “I think you took away 10!… No! I added two!” This back and forth offers lots of laughs and critical thinking for your little mathematician.

Remember that because your child is in pre-k, the concepts of addition and subtraction are still new. Therefore, it’s best to keep the number of objects used in this game low (e.g., 1-10 clips) so they aren’t confused or overwhelmed.

2) Math Tic-Tac-Toe

Add a mathematical twist to the classic game of Tic-Tac-Toe!

What You’ll Need
  • Paper
  • Pencil
  • Ruler
  • Markers (or colored pencils)
What To Do

Start by dividing your sheet of paper into squares by drawing lines (three horizontal by three vertical). In traditional tic-tac-toe, you’d leave these squares blank until the game starts. Not this time.

For this version of the game, you’ll need to fill each box with dots and have your child tell you how many dots are in a box before placing their X or O in it. The first player to get three Xs or Os wins!

The Xs or Os don’t have to be in order at this point, but you can add that requirement as a challenge once your child gets the hang of playing the game.

This activity helps kids work on their counting skills while also incorporating lots of fun.

3) NumberBow

Your child will add numbers to create a beautiful rainbow in this game.

What You’ll Need
  • Two dice
  • Two sheets of paper
  • Colored pencils (or crayons)
  • Pencil
What To Do

Draw two identical rainbow-shaped boards (one on each sheet of paper) with numbered boxes on the rainbows. (You can check out this link for reference.). The aim of the game is to color the numbered boxes in.

To play, each player throws two dice, then adds the numbers from the throw together and colors in the corresponding box on their rainbow.

For example, if your child throws a three and a one, they’d need to add 3+1 and color in the “4” box. If they’ve already colored that box in, they’d have to wait for their next turn. Each player gets 10 turns to have the most colorful rainbow at the end!

While this is an effective game to help your child work on their addition skills, some children might experience difficulty adding larger numbers together (e. g., 5 and 6). If you need to help them, that’s OK!

Remember that exposure and repetition are very beneficial for young learners.

4) Fill The Cup

This game can be challenging for younger children, so if it causes frustration, play other math games until your child is more comfortable with adding and counting.

What You’ll Need
  • Dice
  • Plastic cup
  • Small objects that are easy to count (e.g., paper clips, dried beans, pebbles, etc.)
What To Do

To begin the game, players roll the dice at the same time. The number rolled indicates the number of items you can add to your cup. For example, if you roll a five, you add five dried beans. The goal for your child is to be the first one to fill their cup.

At the pre-kindergarten stage, some children might not be comfortable with the steps needed to play this game (rolling the dice, reading the number aloud, adding the items to the cup). So, before starting, take a few minutes to get them used to the process.

If you notice that it’s still too challenging, you can make it easier by choosing to roll the dice for each other. In this option, you can roll the dice and then help your child read the number and add the right amount of items to their cup.

Whichever variation you choose, this is a fun and engaging way to help children learn numbers and practice counting.

5) Stand Up, Sit Down

Kids enjoy playing this active game where they get to use their bodies and their brains! (Note: This game requires more than one child player, so it’s a great activity for siblings or to do when your child has a friend over.)

What You’ll Need
  • Index cards
  • Marker
What To Do

Write the numbers 1-10 on the index cards (one number per card) and hand three to each participant. Then, say a math equation (or word problem) out loud.

If the answer matches a number they’re holding, the child will stand. If they don’t have the answer, they remain seated.

For example, if the question is, “If I have three dried beans and I throw away one, how many do I have left?”, the child with “2” would then need to stand up and show their card.

The player who has the least number of cards left at the end of five rounds wins. Note: To make it easier, you can give children small items (e.g., blocks, dried beans, paper clips, etc.) to help them count.

Stand Up, Sit Down is also helpful for children learning shapes. Instead of writing numbers on the cards and handing them out, you can draw different 2-D and 3-D shapes that children learn in pre-k (as discussed above) and hand those out.

To play, someone describes a shape and the player who has that shape stands up and says what it is. For example, “If you are holding a shape that has three sides, stand up right now!”

When the child stands up, they’ll need to say that their shape is a triangle, and they get the point. In this version of the game, the player with the most points at the end wins.

Using this game allows children to learn the names and attributes of the different 2-D and 3-D shapes they get exposed to in pre-kindergarten.

6) Who Has More?

This game is perfect for helping kids understand the concepts of more and less, which are critical in early math development.

What You’ll Need
  • A small bowl or container
  • A teaspoon
  • A handful of objects (e.g., buttons, pennies, cereal pieces, etc.)
What To Do

Place the objects in one bowl. Have your child scoop a teaspoon of them out and count them. Then, you do the same and see who got the most. That person’s the winner!

Note: Counting past 10 is difficult at this age, so you’ll want to use big enough items (such as large kidney beans) and stick to a teaspoon for scooping so your child doesn’t end up with more than 10 per spoonful.

7) Read Math Books

Help your child develop a love for math by reading math-related books together.

What You’ll Need
  • A mathematical-themed book to read together (see some recommendations below)
What To Do

Grab one of the following books and snuggle up with your little one for a math-themed storytime. As you read, point out any mathematical concepts in the book.

  • From the Garden by Michael Dahl
  • The Shape of Me and Other Stuff by Dr. Seuss
  • The Button Box by Margarette S. Reid
  • A Pair of Socks by Stuart J. Murphy
  • The Berenstain Bears and the Spooky Old Tree by Stan and Jan Berenstain
  • Pattern Fish by Trudy Harris

When you finish reading, discuss any new math concepts your child learned. You could even do a related activity or two to reinforce what they’ve learned.

8) In The Box

This game helps your child practice prepositions or direction words, like “under,” “behind,” and “in front of.” These concepts are essential for mathematical development as well as reading comprehension.

What You’ll Need
  • A stuffed animal
  • An empty box large enough for the animal to fit inside
What To Do

Ask your child to put the animal inside the box. If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”

Once the animal is in the box, ask them to describe where it is using prepositions. So, they might say, “The animal is in the box.”

Then, take the animal out and place it behind the box. Ask your child to describe its location again. For example, they might say, “The animal is behind the box.”

Next, let them take a turn placing the animal in, on, under, next to, etc. the box. When they’re done, you describe where it is. Continue taking turns as you practice different prepositions.

9) Number Line Race

This game helps kids with number recognition as well as one-to-one correspondence.

What You’ll Need
  • Number cards (we recommend the ones from the HOMER Explore Numbers Kit)
  • A die
What To Do:

Spread the cards out in numerical order, with a bit of space between each one. They should form a line on the floor, though it doesn’t need to be perfectly straight.

Have your child stand on the card with the number one on it. Hand them the die and let them roll it. Call out the number they rolled. Next, ask them to move that many numbers forward, moving from one index card to the next as they count aloud.

If they land on a number that would take them off the end of the line, they start from the beginning for their next throw (each player gets five throws). Then, it’s your turn! Start on one and see how far you can get, too.

The person to end on the card with the highest number is the winner!

Encouraging A Love Of Pre-K Math At Home

Pre-k math isn’t just reserved for pre-k classes. You can help your child explore the exciting world of pre-k math right from your home!

HOMER is always here to help and happy to be your at-home learning partner. Our Learn & Grow app offers tons of opportunities for your child to develop their pre-k math skills from conception to execution.

Our games are personalized to accommodate your child’s specific interests. They include pattern-identification games like Ribbons or shape-building games like the Castle Creator.

Your child can also explore the Shapery Bakery, where they help the cute, cuddly Tisa the Cat by sorting treats based on their shape. All that and so much more can help your child develop their pre-k math skills!

Author

Help Your Child Develop Early Math Skills

Before they start school, most children develop an understanding of addition and subtraction through everyday interactions. Learn what informal activities give children a head start on early math skills when they start school.

Children are using early math skills throughout their daily routines and activities. This is good news as these skills are important for being ready for school. But early math doesn’t mean taking out the calculator during playtime. Even before they start school, most children develop an understanding of addition and subtraction through everyday interactions. For example, Thomas has two cars; Joseph wants one. After Thomas shares one, he sees that he has one car left (Bowman, Donovan, & Burns, 2001, p. 201). Other math skills are introduced through daily routines you share with your child—counting steps as you go up or down, for example. Informal activities like this one give children a jumpstart on the formal math instruction that starts in school.

What math knowledge will your child need later on in elementary school? Early mathematical concepts and skills that first-grade mathematics curriculum builds on include: (Bowman et al., 2001, p. 76).

  • Understanding size, shape, and patterns
  • Ability to count verbally (first forward, then backward)
  • Recognizing numerals
  • Identifying more and less of a quantity
  • Understanding one-to-one correspondence (i.e., matching sets, or knowing which group has four and which has five)

Key Math Skills for School

More advanced mathematical skills are based on an early math “foundation”—just like a house is built on a strong foundation. In the toddler years, you can help your child begin to develop early math skills by introducing ideas like: (From Diezmann & Yelland, 2000, and Fromboluti & Rinck, 1999.)

Number Sense

This is the ability to count accurately—first forward. Then, later in school, children will learn to count backwards. A more complex skill related to number sense is the ability to see relationships between numbers—like adding and subtracting. Ben (age 2) saw the cupcakes on the plate. He counted with his dad: “One, two, three, four, five, six…”

Representation

Making mathematical ideas “real” by using words, pictures, symbols, and objects (like blocks). Casey (aged 3) was setting out a pretend picnic. He carefully laid out four plastic plates and four plastic cups: “So our whole family can come to the picnic!” There were four members in his family; he was able to apply this information to the number of plates and cups he chose.

Spatial sense

Later in school, children will call this “geometry. ” But for toddlers it is introducing the ideas of shape, size, space, position, direction and movement. Aziz (28 months) was giggling at the bottom of the slide. “What’s so funny?” his Auntie wondered. “I comed up,” said Aziz, “Then I comed down!”

Measurement

Technically, this is finding the length, height, and weight of an object using units like inches, feet or pounds. Measurement of time (in minutes, for example) also falls under this skill area. Gabriella (36 months) asked her Abuela again and again: “Make cookies? Me do it!” Her Abuela showed her how to fill the measuring cup with sugar. “We need two cups, Gabi. Fill it up once and put it in the bowl, then fill it up again.”

Estimation

This is the ability to make a good guess about the amount or size of something. This is very difficult for young children to do. You can help them by showing them the meaning of words like more, less, bigger, smaller, more than, less than. Nolan (30 months) looked at the two bagels: one was a regular bagel, one was a mini-bagel. His dad asked: “Which one would you like?” Nolan pointed to the regular bagel. His dad said, “You must be hungry! That bagel is bigger. That bagel is smaller. Okay, I’ll give you the bigger one. Breakfast is coming up!”

Patterns

Patterns are things—numbers, shapes, images—that repeat in a logical way. Patterns help children learn to make predictions, to understand what comes next, to make logical connections, and to use reasoning skills. Ava (27 months) pointed to the moon: “Moon. Sun go night-night.” Her grandfather picked her up, “Yes, little Ava. In the morning, the sun comes out and the moon goes away. At night, the sun goes to sleep and the moon comes out to play. But it’s time for Ava to go to sleep now, just like the sun.”

Problem-solving

The ability to think through a problem, to recognize there is more than one path to the answer. It means using past knowledge and logical thinking skills to find an answer. Carl (15 months old) looked at the shape-sorter—a plastic drum with 3 holes in the top. The holes were in the shape of a triangle, a circle and a square. Carl looked at the chunky shapes on the floor. He picked up a triangle. He put it in his month, then banged it on the floor. He touched the edges with his fingers. Then he tried to stuff it in each of the holes of the new toy. Surprise! It fell inside the triangle hole! Carl reached for another block, a circular one this time…

Math: One Part of the Whole

Math skills are just one part of a larger web of skills that children are developing in the early years—including language skills, physical skills, and social skills. Each of these skill areas is dependent on and influences the others.

Trina (18 months old) was stacking blocks. She had put two square blocks on top of one another, then a triangle block on top of that. She discovered that no more blocks would balance on top of the triangle-shaped block. She looked up at her dad and showed him the block she couldn’t get to stay on top, essentially telling him with her gesture, “Dad, I need help figuring this out. ” Her father showed her that if she took the triangle block off and used a square one instead, she could stack more on top. She then added two more blocks to her tower before proudly showing her creation to her dad: “Dada, Ook! Ook!”

You can see in this ordinary interaction how all areas of Trina’s development are working together. Her physical ability allows her to manipulate the blocks and use her thinking skills to execute her plan to make a tower. She uses her language and social skills as she asks her father for help. Her effective communication allows Dad to respond and provide the helps she needs (further enhancing her social skills as she sees herself as important and a good communicator). This then further builds her thinking skills as she learns how to solve the problem of making the tower taller.

What You Can Do

The tips below highlight ways that you can help your child learn early math skills by building on their natural curiosity and having fun together. (Note: Most of these tips are designed for older children—ages 2–3. Younger children can be exposed to stories and songs using repetition, rhymes and numbers.)

Shape up.

Play with shape-sorters. Talk with your child about each shape—count the sides, describe the colors. Make your own shapes by cutting large shapes out of colored construction paper. Ask your child to “hop on the circle” or “jump on the red shape.”

Count and sort.

Gather together a basket of small toys, shells, pebbles or buttons. Count them with your child. Sort them based on size, color, or what they do (i.e., all the cars in one pile, all the animals in another).

Place the call.

With your 3-year-old, begin teaching her the address and phone number of your home. Talk with your child about how each house has a number, and how their house or apartment is one of a series, each with its own number.

What size is it?

Notice the sizes of objects in the world around you: That pink pocketbook is the biggest. The blue pocketbook is the smallest. Ask your child to think about his own size relative to other objects (“Do you fit under the table? Under the chair?”).

You’re cookin’ now!

Even young children can help fill, stir, and pour. Through these activities, children learn, quite naturally, to count, measure, add, and estimate.

Walk it off.

Taking a walk gives children many opportunities to compare (which stone is bigger?), assess (how many acorns did we find?), note similarities and differences (does the duck have fur like the bunny does?) and categorize (see if you can find some red leaves). You can also talk about size (by taking big and little steps), estimate distance (is the park close to our house or far away?), and practice counting (let’s count how many steps until we get to the corner).

Picture time.

Use an hourglass, stopwatch, or timer to time short (1–3 minute) activities. This helps children develop a sense of time and to understand that some things take longer than others.

Shape up.

Point out the different shapes and colors you see during the day. On a walk, you may see a triangle-shaped sign that’s yellow. Inside a store you may see a rectangle-shaped sign that’s red.

Read and sing your numbers.

Sing songs that rhyme, repeat, or have numbers in them. Songs reinforce patterns (which is a math skill as well). They also are fun ways to practice language and foster social skills like cooperation.

Start today.

Use a calendar to talk about the date, the day of the week, and the weather. Calendars reinforce counting, sequences, and patterns. Build logical thinking skills by talking about cold weather and asking your child: What do we wear when it’s cold? This encourages your child to make the link between cold weather and warm clothing.

Pass it around.

Ask for your child’s help in distributing items like snacks or in laying napkins out on the dinner table. Help him give one cracker to each child. This helps children understand one-to-one correspondence. When you are distributing items, emphasize the number concept: “One for you, one for me, one for Daddy.” Or, “We are putting on our shoes: One, two.”

Big on blocks.

Give your child the chance to play with wooden blocks, plastic interlocking blocks, empty boxes, milk cartons, etc. Stacking and manipulating these toys help children learn about shapes and the relationships between shapes (e.g., two triangles make a square). Nesting boxes and cups for younger children help them understand the relationship between different sized objects.

Tunnel time.

Open a large cardboard box at each end to turn it into a tunnel. This helps children understand where their body is in space and in relation to other objects.

The long and the short of it.

Cut a few (3–5) pieces of ribbon, yarn or paper in different lengths. Talk about ideas like long and short. With your child, put in order of longest to shortest.

Learn through touch.

Cut shapes—circle, square, triangle—out of sturdy cardboard. Let your child touch the shape with her eyes open and then closed.

Pattern play.

Have fun with patterns by letting children arrange dry macaroni, chunky beads, different types of dry cereal, or pieces of paper in different patterns or designs. Supervise your child carefully during this activity to prevent choking, and put away all items when you are done.

Laundry learning.

Make household jobs fun. As you sort the laundry, ask your child to make a pile of shirts and a pile of socks. Ask him which pile is the bigger (estimation). Together, count how many shirts. See if he can make pairs of socks: Can you take two socks out and put them in their own pile? (Don’t worry if they don’t match! This activity is more about counting than matching.)

Playground math.

As your child plays, make comparisons based on height (high/low), position (over/under), or size (big/little).

Dress for math success.

Ask your child to pick out a shirt for the day. Ask: What color is your shirt? Yes, yellow. Can you find something in your room that is also yellow? As your child nears three and beyond, notice patterns in his clothing—like stripes, colors, shapes, or pictures: I see a pattern on your shirt. There are stripes that go red, blue, red, blue. Or, Your shirt is covered with ponies—a big pony next to a little pony, all over your shirt!

Graphing games.

As your child nears three and beyond, make a chart where your child can put a sticker each time it rains or each time it is sunny. At the end of a week, you can estimate together which column has more or less stickers, and count how many to be sure.

References

Bowman, B.T., Donovan, M.S., & Burns, M.S., (Eds.). (2001). Eager to learn: Educating our preschoolers. Washington, DC: National Academy of Sciences.

Diezmann, C., & Yelland, N. J. (2000). Developing mathematical literacy in the early childhood years. In Yelland, N.J. (Ed.), Promoting meaningful learning: Innovations in educating early childhood professionals.  (pp.47–58). Washington, DC: National Association for the Education of Young Children.

Fromboluti, C. S., & Rinck, N. (1999 June). Early childhood: Where learning begins. U.S. Department of Education, Office of Educational Research and Improvement, National Institute on Early Childhood Development and Education. Retrieved on May 11, 2018 from https://www2.ed.gov/pubs/EarlyMath/title.html

 

Formation of elementary mathematical skills in preschoolers | Article (senior group) on the topic:

In the XVIII-XIX centuries. issues of the content and methods of teaching arithmetic to preschool children and the development of ideas about dimensions, measures of measurement, time and space are reflected in the advanced pedagogical systems of education developed by Ya.A. Comenius, I.G. Pestalozzi, K.D. Ushinsky, L.N. Tolstoy, etc. [24]

Mathematics is one of the most difficult subjects in the school cycle. Therefore, in kindergarten today, the child must learn elementary mathematical knowledge. However, the problem of the formation and development of children's mathematical abilities is one of the least developed methodological problems of preschool pedagogy today.

Teaching preschoolers the basics of mathematics is given an important place. This is due to a number of reasons: the beginning of schooling from the age of six, the abundance of information received by the child, increased attention to computerization, the desire to make the learning process more intense. [11]

Traditionally, the problem of assimilation and accumulation of knowledge of a mathematical nature in preschool pedagogy is associated mainly with the formation of ideas about a natural number and actions with it (counting, counting, arithmetic operations and comparison of numbers, measurement of scalar quantities, etc.). The formation of elementary mathematical representations is a means of mental development of the child, his cognitive abilities.

The use of various didactic games contributes to the formation of a child's mathematical concepts. In the game, the child acquires new knowledge, skills and abilities. Games that contribute to the development of perception, attention, memory, thinking, the development of creative abilities are aimed at the mental development of a preschooler as a whole. The mathematical development of a preschooler is a process of qualitative change in the intellectual sphere of the individual, which occurs as a result of the formation of mathematical representations and concepts in the child.

For a long time, the concepts of the initial teaching of number and counting to young children were built either on the basis of speculative theoretical constructions or through empirical experience. Outstanding thinkers of the past (J. A. Comenius, I. G. Pestalozzi, K. D. Ushinsky, L. N. Tolstoy), prominent figures in the field of preschool education abroad (F. Fröbel, M. Montessori) and in our country (E. I. Tikheeva, F. N. Bleher) successfully combined direct work with children with a theoretical understanding of its results. [23]

Teachers of that era, under the influence of the requirements of developing practice, came to the conclusion that it was necessary to prepare children for the assimilation of mathematics. They made certain proposals about the content and methods of teaching children, mainly in a family setting.

Methods for developing ideas about number and form in children were reflected and further developed in the systems of sensory education of the German teacher F. Fredel (1782-1852), the Italian teacher M. Montessori (1870-1952), etc. In general, teaching mathematics in The system of Maria Montessori began with a sensory impression, then a transition was made to understanding the symbol, which made mathematics attractive and accessible even for 3-4-year-old children. [26]

So, the leading teachers of the past, Russian and foreign, recognized the role and necessity of primary mathematical knowledge in the development and upbringing of preschool children, singled out the account as a means of mental development and strongly recommended that children be taught it as early as possible, from about 3 years old .

Mathematical development plays a significant role in the mental development of preschool children. "The mathematical development of preschoolers should be understood as shifts and changes in the cognitive activity of the individual, which occur as a result of the formation of elementary mathematical representations and the logical operations associated with them." Thus, the mathematical development of preschool children is understood as qualitative changes in the forms of their cognitive activity that occur as a result of the formation of elementary mathematical representations and the logical operations associated with them. [23]

Content, organization of the mathematical development of preschoolers, taking into account age-related characteristics in the development of practical actions by children, mathematical connections and patterns, continuity in the development of mathematical abilities are the leading principles in the formation of mathematical concepts. Education in kindergarten is aimed primarily at educating children in the habit of full-fledged logical argumentation of the environment. The experience of teaching indicates that the development of logical thinking of preschoolers is most facilitated by the study of the principles of mathematics. The mathematical style of thinking is characterized by clarity, brevity, dismemberment, accuracy and logic of thought, the ability to use symbolism.

One of the most complex knowledge, skills and abilities included in the content of social experience that the younger generations master is mathematical. They are abstract in nature, operating with them requires the implementation of a system of complex mental actions. In everyday life, in everyday life and in games, the child begins to encounter situations early enough that require the use of, although elementary, but still mathematical solutions (prepare treats for friends, set the table for dolls, divide sweets equally, etc. .), knowledge of such relationships as many, few, more, less, equally, the ability to determine the number of objects in the set, choose the appropriate number of elements from the set, etc. First, with the help of adults, and then on their own, children solve problems that arise. [18]

Thus, already at preschool age, children get acquainted with mathematical content and master elementary computational skills, and the formation of elementary mathematical representations in them is one of the important areas of work for preschool institutions.

The concept of "development of mathematical abilities" is quite complex, complex and multifaceted. It consists of interrelated and interdependent ideas about space, shape, size, time, quantity, their properties and relationships, which are necessary for the formation of "everyday" and "scientific" concepts in a child. [21]

Mathematical development of preschoolers is understood as qualitative changes in the child's cognitive activity that occur as a result of the formation of elementary mathematical concepts and related logical operations.

The mathematical development of preschool children was laid down in the works of L. A. Wenger and today is the most common in the theory and practice of teaching mathematics to preschoolers. The purpose of teaching in the classroom in kindergarten is the assimilation by the child of a certain range of knowledge and skills given by the program. The development of mental abilities in this case is achieved indirectly: in the process of mastering knowledge. This is precisely the meaning of the widespread concept of “developmental education”. The developmental effect of learning depends on what knowledge is communicated to children and what teaching methods are used. [6]

According to V.V. Abashina, the mathematical development of a preschooler is a process of qualitative change in the intellectual sphere of the individual, which occurs as a result of the formation of mathematical representations and concepts in the child.

From the study by EI Shcherbakova, the mathematical development of preschoolers should be understood as shifts and changes in the cognitive activity of the individual, which occur as a result of the formation of elementary mathematical representations and the logical operations associated with them. In other words, the mathematical development of preschool children is a qualitative change in the forms of their cognitive activity that occurs as a result of children mastering elementary mathematical concepts and related logical operations. [25]

Having stood out from preschool pedagogy, the methodology for the formation of elementary mathematical representations has become an independent scientific and educational area. The subject of her research is the study of the main patterns of the process of formation of elementary mathematical representations in preschoolers in the context of public education. The range of tasks of mathematical development solved by the method is quite extensive: [17]

  • scientific substantiation of program requirements for the level of development of quantitative, spatial, temporal and other mathematical representations of children in each age group;
  • determination of the content of the material for preparing a child in kindergarten for learning mathematics at school;
  • improvement of the material on the formation of mathematical representations in the kindergarten program;
  • development and implementation in practice of effective didactic means, methods and various forms and organization of the process of development of elementary mathematical concepts;
  • implementation of continuity in the formation of basic mathematical concepts in kindergarten and the corresponding concepts in school;
  • development of the content of training highly qualified personnel capable of carrying out pedagogical and methodological work on the formation and development of mathematical concepts in children in all parts of the preschool education system;
  • development on a scientific basis of guidelines for parents on the development of mathematical concepts in children in a family setting.

Shcherbakova E.I. among the tasks for the formation of elementary mathematical knowledge and the subsequent mathematical development of children, he singles out the main ones, namely:

  • acquisition of knowledge about set, number, size, form, space and time as the basis of mathematical development;
  • formation of a broad initial orientation in the quantitative, spatial and temporal relations of the surrounding reality;
  • formation of skills and abilities in counting, calculations, measurement, modeling, general educational skills;
  • mastery of mathematical terminology;
  • development of cognitive interests and abilities, logical thinking, general intellectual development of the child. [13]

These tasks are most often solved by the teacher at the same time in each lesson in mathematics, as well as in the process of organizing various types of independent children's activities. Numerous psychological and pedagogical studies and advanced pedagogical experience in preschool institutions show that only properly organized children's activities and systematic training ensure the timely mathematical development of a preschooler. [10]

  1. The content of teaching mathematics to preschoolers

Mathematical development of preschoolers is carried out both as a result of the child's acquisition of knowledge in everyday life, and through targeted training in the classroom to form elementary mathematical concepts. Research and pedagogical experience show that, thanks to the systematic teaching of mathematics to children, they form sensory, perceptual, mental, verbal and other components of general and special abilities.

In the mathematical training provided by the program, along with teaching children to count, developing ideas about the number and number within the first ten, dividing objects into equal parts, much attention is paid to operations with visual material, taking measurements using conditional measures, determining the volume of liquid and bulk bodies, the development of the children's eye, their ideas about geometric shapes, about time, the formation of an understanding of spatial relationships. In the classroom in mathematics, the educator carries out not only educational tasks, but also solves educational ones. The teacher introduces preschoolers to the rules of behavior, educates them in diligence, organization, the habit of accuracy, restraint, perseverance, purposefulness, and an active attitude to their own activities. [15]

The teacher organizes work on the development of elementary mathematical concepts in children in the classroom and outside of class: in the morning, in the afternoon during walks, in the evening; 2 - 3 times a week. Teachers of all age groups should use all types of activities to consolidate mathematical knowledge in children. For example, in the process of drawing, sculpting, and designing, children gain knowledge about geometric shapes, the number and size of objects, and their spatial arrangement; spatial representations, counting skills, ordinal count - in music and physical education classes, during sports entertainment. In various outdoor games, children's knowledge about measurements by conditional measures of the size of objects can be used. To consolidate mathematical concepts, educators widely use didactic games and game exercises separately for each age group. In the summer, the program material in mathematics is repeated and fixed on walks, in games. [9]

Methods of teaching mathematical knowledge are based on general didactic principles: systematic, consistent, gradual, individual approach. The tasks offered to children sequentially, from lesson to lesson, become more complicated, which ensures the availability of learning. When moving on to a new topic, do not forget to repeat the past. Repetition of material in the process of learning new things not only deepens children's knowledge, but also makes it easier to focus on new things. In mathematics classes, educators use various methods (verbal, visual, game) and techniques (storytelling, conversation, description, indication and explanation, questions for children, children's answers, sample, showing real objects, pictures, didactic games and exercises, outdoor games) .

A large place in the work with children of all age groups is occupied by developmental teaching methods. This is the systematization of the knowledge he offers, the use of visual aids (reference samples, the simplest schematic images, substitute objects) for highlighting various properties and relationships in real objects and situations, and the application of a general method of action in new conditions. [22]

The second junior group

In the second junior group, they begin to carry out special work on the formation of elementary mathematical concepts. The further mathematical development of children depends on how successfully the first perception of quantitative relations and spatial forms of real objects is organized.

Work with children of three years old, on the development of elementary mathematical concepts, is mainly aimed at developing ideas about the set. Children are taught to compare two sets, compare elements of one set with elements of another, distinguish between equality and inequality of groups of objects that make up a set. [1]

Children are introduced to the development of preschoolers' initial ideas about the size of objects, contrasting and of the same size in length, width, height, thickness, volume (larger, smaller, equal in size).

Children get their first information about geometric shapes while playing. Based on the accumulated experience, children are introduced to the names of planar geometric shapes (square, circle, triangle). Learn to identify, distinguish and name these figures.

It is advisable to develop spatial representations in a group of children of the fourth year of life using everyday life, routine moments, didactic, outdoor games, morning exercises, music and physical education classes.

Orientation in time involves teaching children the ability to distinguish between parts of the day and call them: morning, evening, day and night.

Middle group

The middle group program is aimed at further development of mathematical concepts in children. It includes learning to count up to 5, comparing two sets expressed by adjacent numbers. An important task is the ability to establish equality and inequality of groups of objects when objects are at different distances from each other, when they are different in size, etc. [5]

The children of the middle group should learn counting techniques: name the numbers in order, correlate each number with only one object, at the end of the count summarize it in a circular motion, learn to distinguish the counting process from the counting total, count with the right hand from left to right, in the counting process call only numerals, to teach children to correctly coordinate numerals with nouns in gender, number, case.

When teaching counting at each lesson, special attention should be paid to such techniques as comparing two numbers, matching, establishing their equality and inequality, overlay techniques and applications. [8]

Senior group

The program of the senior group is aimed at expanding, deepening and generalizing elementary mathematical concepts in children. Children are taught to master the techniques of counting objects, sounds, movements, by touch within 10, count the number of objects according to the model and according to the named number, learn to form numbers by increasing or decreasing by units, equalize sets of objects, subject to quantitative differences between the number of 1, 2 and 3 elements, skills are developed to apply quantitative and ordinal counting, children are introduced to numbers from 0 to 10. [15]

Counting exercises keep getting more difficult. In the process of learning to count, children are introduced to numbers, they are taught to distinguish, name, find, build a row. Children are taught to compare all numbers within 10, they begin to learn to use ordinal numbers for the first time, they are taught to divide the whole into parts.

Preparatory group

In the preparatory group for school, special attention is paid to the development of children's ability to navigate in some hidden essential mathematical relationships, relationships, dependencies: “equal”, “more”, “less”, “whole and part”, dependencies between values, the dependence of the measurement result on the value of the measure, etc. Children master the methods of establishing various kinds of mathematical connections and relationships. They begin to understand that the most accurate ways of establishing quantitative relationships are by counting objects and measuring quantities. Their counting and measurement skills become quite strong and conscious. [6]

The ability to navigate essential mathematical connections and dependencies and mastering the appropriate actions allow preschoolers to raise the visual-figurative thinking to a new level and create prerequisites for the development of their mental activity in general. Children learn to count with their eyes alone, to themselves, they develop an eye, quick reaction to the form.

No less important at this age is the development of mental abilities, independence of thinking, mental operations of analysis, synthesis, comparison, the ability to abstract and generalize, and spatial imagination. Children should be brought up with a steady interest in mathematical knowledge, the ability to use it and the desire to independently acquire it. The program for the development of elementary mathematical representations of the preparatory group for school provides for the generalization, systematization, expansion and deepening of the knowledge acquired by children in previous groups. [11]

  1. The specificity of the formation of preschoolers' ideas

about the multitude and number

At an early age, children accumulate ideas about aggregates consisting of homogeneous and heterogeneous objects. They master a number of practical actions aimed at perceiving the abundance of a multitude of objects.

Children of the first and second years of life learn how to act with groups of homogeneous objects (balls, buttons, rings, etc.). They sort them out, shift them, pour them out, collect them again, lay them out horizontally on the table, in the form of a curved line; perform more complex actions: grouping objects of different numbers in shape, color. [17]

The perception of a plurality of objects and phenomena is facilitated by the entire environment of the child - a multitude of people, familiar and unfamiliar, a multitude of objects, repeated sounds. The child perceives the plurality of objects and phenomena with different analyzers: auditory, visual, kinesthetic, etc.

The formation of initial ideas about the plurality of objects (many) and singularity (one) occurs very early (in the second year of life). An indicator of this is the difference between the singular and plural by children as early as 15-16 months of age. [18]

In the second year of life, children begin to understand the meaning of the words a lot, a little, with a difference between sets of two objects. However, the words many and few do not have a clear quantitative characteristic for them. They also associate the word much with the word big, and the word little with the word small. The word much refers to both the totality of objects and their size. Consequently, quantitative representations in children have not yet differentiated from spatial ones.

Thus, the quantitative side in the totality of objects is not yet a special sign, significant for children of the second year of life (VV Danilova). At this age, there is a perception of many objects as an indefinite plurality, there is an ability to distinguish between the meaning of the word one and many, there is an active mastery of the grammatical forms of the singular and plural. [20]

In the third year of life, the ability to distinguish between groups of objects of different sizes is born. The words one, many, few children correlate with a certain number of objects, perform actions in response to the request of adults: “Bring one ball”, “Give me a lot of pictures”, etc.

By the end of the third year, children master the ability to differentiate not only subject aggregates, but also sets of sounds.

Children at the end of the second - beginning of the third year of life have a desire to create a set of objects themselves. At this age, there is a tendency to "compare" the aggregates, when one object is superimposed on another. But the movements of the children are not yet precise, moreover, the children still do not see the relationships between the compared aggregates, they are mainly interested in the process of splitting the aggregates into separate objects and their combination. [22]

Children of the third year of life in different conditions correctly understand and correlate the words a lot, a little within five objects.

The ability to differentiate sets with more and fewer elements depends on children's education.

In the third year of life, the quantitative side gradually begins to separate from the subject content. Children develop the ability to accept tasks, act as directed, which indicates their intellectual activity and the development of arbitrary thinking.

Gradually, children begin to master the simplest way to compare elements of two sets. They superimpose (apply) objects of one set on objects of another, establishing a one-to-one correspondence between them, and see their equality in quantity. [24]

However, when performing reproduction tasks on their own (filling in the gaps between images), children
often experience errors.

In the third year of life, with gradual systematic learning, children can compare many sounds with many objects.

In the studies of V.V. Danilova, by the age of three there are significant qualitative changes in the perception and comparison of sets by children. In the process of organized actions with sets of objects under the guidance of an adult, children begin to develop the ability to isolate a sign of quantity, regardless of the name of the objects, their qualities and properties. [9]

Thus, under the influence of learning, children show the ability to distinguish between many objects and many sounds, independently create sets from objects, learn the meaning of the words many, few, one, attribute them to the corresponding groups of objects, sounds, movements.

The idea of ​​numbers, their sequence, relationships, place in the natural series is formed in preschool children under the influence of counting and measurement.

Children learning to count is a long and complicated process.

Counting as an activity consists of a number of interrelated components, each of which the child must master: correlating numeral words, called in order, with objects, determining the final number. As a result of this practical activity, a sequence of numbers is mastered. [10]

The early appearance of numerals in the active dictionary of children (1.5 - 2 years old) is not an indicator of the formation of quantitative ideas. These words are borrowed from the speech of adults and used by children during the game.

At an early age, children from the knowledge of numerals, under the influence of training, pass to the assimilation of a sequence of numbers in a limited segment of the natural series. As a rule, these are the numbers 1, 2, 3.

Under the influence of training, they become interested in comparing objects in terms of their size and number. Such behavior mainly characterizes children at the beginning of the third year of life and can be considered as a qualitatively new stage in the development of counting activity. [23]

Having learned the numerals of the first ten, the children easily move on to the second ten, and then they count like this: “Twenty-ten, twenty-eleven”, etc. But as soon as the child is corrected and named the number thirty after twenty-nine, the stereotype is restored and the child continues: “Thirty-one, thirty-two ... thirty-nine,” etc. Some children begin to understand that after twenty-nine, thirty-nine, forty-nine there are special words whose names they do not yet know. In such cases, children pause, waiting for the help of an adult.

However, the auditory image of the natural series of numbers formed in children does not yet indicate that they have mastered counting skills.

In the third year of life, children try to count, showing great interest in counting activities. Mastering the sequence of numbers by children in the process of counting objects, sounds, movements is the content of the next stage in the development of their quantitative representations (for 3-4-year-olds). [15]

Further formation of ideas about the number and the natural series of numbers is carried out under the influence of mastering counting activities on the basis of exercises on the equation of sets of objects by number, comparison of sets and numbers.

By mastering counting, children acquire the ability to determine the number of objects as a result of understanding the final value of a number, to compare sets and numbers with the definition of relationships between them (visually, in a word). Comparison of numbers (on a visual basis) reveals, highlights the quantitative value of the number.

Successful formation of counting activity, especially at the early stages of development, is possible only with the participation of movements, speech, and the interaction of all analyzers.

The motor component (showing counting objects, circular movement of the hand when summing up) goes through its own developmental path: first, the child moves objects, then touches them, then points to objects at a distance, and finally, selects the object only with his eyes, without relying on practical action. In the process of mastering counting, the development of the speech component also occurs: from the loud naming of numeral words in the process of counting, the child proceeds to naming them in a whisper, then only moves his lips and, finally, pronounces them mentally, i. e. in terms of inner speech. [13]

The movement of the eyes and the spoken word perform the function of splitting sets. Gradually, the word and eye movements begin to replace the action of the hand, becoming the main carrier of the counting action.

At the age of 4-5, children learn the sequence and names of numerals, accurately correlate the numeral with each set of objects, regardless of their qualitative features and forms of location, learn the meaning of the last number named when counting as the final one.

Children 4-5 years of age and older often have a very limited understanding of the value of the unit. The unit is associated with some individual object. Under the influence of learning, children master the ability to attribute a unit not only to a separate object, but also to a group. This is the basis for understanding the decimal number system. [8]

At the senior preschool age, children master the measurement. From the practical comparison of objects by measurement, they move on to a quantitative characteristic of it by counting conditional measurements. This activity deepens the concept of number. The number begins to act as the ratio of the whole (measured quantity) to the part (measure).

Under the influence of mastering two types of activity, counting and measurement, children form clear ideas about the place, sequence, quantitative value of the number, its relation to other numbers (within 10). [5]

Thus, the general sequence of development of ideas about number in the period of preschool childhood is as follows: from the perception of plurality (many) and the emergence of the first quantitative ideas (many, one, few) through mastering practical methods for establishing one-to-one correspondence (the same, more , less) to meaningful counting and measurement.

Development of children's mathematical abilities through play activities

Children's play is the main activity in preschool age. In the preschool period, the child's motivation to acquire new knowledge is still not very active, and this is quite natural. But children take play activities seriously, completely immersing themselves in the process for a long time. They try to follow the established rules and strive to achieve the desired result with all their might. This feature of the psychology of preschoolers can be used for learning by presenting educational tasks as games.

What kind of mathematical knowledge can a preschooler get in a playful way

Playing activities at the age of 3-6 years are varied, so an experienced specialist gives all the mathematical knowledge and skills necessary for a future first-grader. In a playful way, the child will master forward and backward counting, learn numbers and learn how to write them, understand the meaning of addition and subtraction and learn how to solve problems using these actions. The curriculum for preschoolers includes an introduction to geometric shapes, the concepts of area and volume. Solving mathematical and logical problems develops the child's mental abilities. He learns to understand the meaning of the task, analyze it, draw up a solution plan and look for non-standard ways of doing it.

The development of children's mathematical abilities through play activities has the following advantages:

  • children are willing to study and complete tasks;
  • does not cause fatigue and loss of concentration, which is observed during normal activities;
  • the learning process causes positive emotions, which awakens the desire for further mastery of knowledge;
  • the mathematical abilities of children are formed, the general outlook develops, speech, coordination of movements, fine motor skills of the hands are improved.

When learning in a playful way, abilities are developed in other areas: communication skills are developed, since children perform some tasks together, helping each other, exchanging thoughts. Joint tasks give rest and provide the development of speed of thinking, coordination of movements, the ability to act in a team

The development of mathematical abilities helps to learn about the world and achieve success

The formation of elementary mathematical representations of abilities at preschool age is important for general development. The ability to understand and evaluate the quantitative characteristics of objects and phenomena makes knowledge about the world around us more complete and deep.

Mathematics requires logical thinking, but not template solutions, therefore it allows developing creativity. Well-developed spatial thinking will be useful for future artists and architects, and the ability to think logically and find beautiful solutions will be useful for future managers, advertising and marketing specialists. It does not matter what type of activity the child chooses - the ability to think clearly, see the task and divide it into components will help him succeed, facilitate the study of all school disciplines.

Education in the form of a game

The form of learning in a game does not cause difficulties and fatigue for the child, but for the teacher such an activity is more difficult than the traditional presentation of material. It is necessary to organize the educational process in such a way that: