What are math concepts
How Math Concepts and Math Skills Work Together and Why You Should Care
Sometimes people use the words “math skills” and “math concepts” interchangeably. They are not the same, but they do go hand and hand. Understanding how new math skills and concepts work together will give you a new perspective on math education and math challenges.
Definition of Skills
Skills are actions. People do them. People master math skills the same way they master musical skills or sports skills. They practice the actions and steps intentionally, correctly and frequently. They may even go to a special place to practice the skill.
Definition of Concepts
Concepts are ideas. People understand them. People learn concepts by thinking, discussing, reading, listening and/or writing about them.
Similarities Between Skills and Concepts
Both can be learned and they are each the point of education.
Both have a natural progression, or order, in which they should be taught.
Both are a huge component of math success.
1. Education
Most of education focuses on skills. Skills are easier to observe and grade because a person can demonstrate skills. Proving that you understand a concept is difficult. Teachers try to measure a student’s understanding by asking them to write about, discuss or draw concepts. Even then, students are still limited in showing their understanding by their language, writing or artistic skills. For example, most adults in the U.S. understand the concept of basic nutrition. How many adults in the U.S. could explain basic nutrition in a foreign language? Our limited skill set in the foreign language would limit how well we could prove our understanding.
Retaining concepts is easier than retaining skills. What happens when we don’t practice a skill? We lose the skill. Most adults can think of a skill that they frequently practiced as child, but don’t practice now (piano for example). Chances are that their younger selves were much better at that skill than their current self.
If you understand a concept, you have that understanding forever. You may need to think about it before you remember all the details, but the underlying concept will always be there. You will always be able to build upon the concepts you understand and your previous understanding makes learning easier and faster.
2. Progression
Skills build on top of each other. When learning to swim, most children learn to float around the same time as learning to flutter kick. They are both beginning level skills. They must master all the beginning level skills before attempting an advanced skill, like swimming in open water or attempting the butterfly stroke.
Concepts are also best taught progressively. Our brains use neural pathways to make connections. Our understanding of underlying concepts pave the way for understanding new concepts. The deeper and broader our knowledge base is, the easier it is for us to connect it to new concepts.
3. Math Success
Skills are the “how-to” parts of math.
Children should master adding and subtracting before starting multiplication. They must know how to multiply and divide before attempting percentages.
Concepts are the underlying ideas of math. Concepts are ideas like equality and symbolic representation. Many math concepts build upon each other. A child who has a solid understanding of the relationship of quantity and numbers, or “number sense”, will find the concept of “wholes and parts”, naturally makes sense.
How Skills and Concepts Work Together
Understanding concepts makes learning skills easier. Mastering skills, especially thinking skills, makes learning concepts easier. Each prepares the brain differently.
People might be able to do a skill without understanding “why” it works. Understanding why a skill works in sports is helpful, but not critical. Can you imagine swim lessons at the neighborhood pool to 5 year-olds including a study of fluid dynamics and propulsion?
People might also have a concept about something, without the skill to execute it.
Many adults understand the concept of bacteria and wound maintenance, but they still go to a skilled professional to get stitches. Some people call this “book smarts” versus “street smarts.” Understanding the why helps you build your knowledge base and your retention of skills.
Most people in life don’t care about what others understand. They care about what others do. A conceptual understanding helps build skill sets faster.
How Skills and Concepts Work Together in Math
Math skills and concepts should be taught simultaneously. Children who learn math skills without learning the underlying concepts, will find math can get very confusing. Their lack of understanding will limit their ability to apply math in a variety of problem solving situations. Without understanding a concept, we are forced to rely on remembering and practicing a skill. For example, let’s say a 5th grader learned how to divide fractions using the "copy, dot, flip" method but never understood the concept behind why that process worked.
Then the 5th grader progresses to 6th grade and stops practicing dividing fractions because they are learning new skills. When that child stops practicing, he will then likely forget how to divide fractions. This will be a problem when dividing fractions comes up again in algebra and advanced math. The child who has both the skills and the concepts will be much better prepared.
Children who learn math concepts without learning the skills, will struggle to apply what they know. Knowing the difference between concepts and skills helps to identify the problems that arise in math.
How we Approach Skills and Concepts at Mathnasium
At Mathnasium of Littleton we focus on teaching foundational math skills like Counting, Numerical Fluency (adding and subtracting and multiplication facts), time and money and the order of operations while also teaching concepts such as Number Sense, Wholes and Parts, and Proportional Thinking. These latter are concepts that also involve skills.
Additionally, thinking is a skill that must be practiced. Thinking skills enable a child to learn the concepts and we never neglect to teach concepts. We encourage our students to ask us questions and we ask them questions to promote deep thinking and conceptual understanding.
The progression of skills and concepts and how they work together is exactly why at Mathnasium of Littleton, we work hard to close math gaps.
For more information about our methods, click here. The result is stronger math skills with a deeper understanding of mathematical concepts. Our motto is: “We Make Math Make Sense!”
Give us a call today! 303-979-9077
Articles referenced in this post:
Practice Makes Perfect so Perfect Practice is Essential
Multiple Practice Sessions Provide Better Learning than Cramming
Where Does your Child Go To Practice Math?
Is Mathematical Understanding Really Necessary?
Worried Your Child has Not Memorized the Multiplication Tables?
4 Tips for Figuring Out Percentages the Easy Way
Learning Math Symbols in Elementary School Takes Time
Prepare Your Child for Calculus Starting in Second Grade
Is Your Child Dependent on Algorithms and is that a Bad Thing?
Why Does Mathnasium of Littleton Focus on Foundational Math Skills?
Counting … Its More Complex Than You Imagine
Teaching Number Sense
Focus on Math: Wholes and Parts
Focus on Math: Proportional Thinking
What is Numerical Fluency?
Multiplication Fluency is Coming to Mathnasium of Littleton
Focus on Math: Learning About Money
Does Your Child Ask Questions in Math Class?
Focus on Math: Order of Operations
Understanding Mathematical Reasoning
Understanding Math Learning Gaps
Math Concepts | HowStuffWorks
""What Is the Formula for Distance?
You can find the distance between two points by using the distance formula.
It's an application of the Pythagorean theorem. Remember that from high school algebra?
By Mark Mancini
""You Know the Kilo. Now Say Hello to the Quetta!
When a peta and a tera won't do, you can now call on the quetta or the ronna prefixes. But just how big are these new metric systems of measurement?
By Alia Hoyt
""What Is the Birthday Paradox?
How large does a random group of people have to be for a 50 percent chance to exist that at least two of the people will share a birthday?
By Laurie L. Dove
Advertisement
""What's an Easy Way to Convert Meters to Feet?
Most of the world uses meters, apart from the U.S. and a few other countries. So what's an easy way to convert from meters to feet and vice versa?
By Mark Mancini
""How to Find Range
Finding the range of a set of numbers is an easy subtraction problem!
By Jesslyn Shields
Advertisement
""How to Convert Kilograms to Pounds
Converting kilogram measurements into pounds is not hard.
We'll show you the textbook way plus two quick-and-dirty shortcuts.
By Mark Mancini
""What Is the Formula for Velocity?
Many people get speed and velocity confused. It's no surprise because the terms are often used interchangeably. But they're not quite the same thing. So how do you find the velocity of an object?
By Mark Mancini
Advertisement
""Math World Egg-static About New Egg-shape Equation
Scientists have come up with a new formula to describe the shape of every egg in the world, which will have applications in fields from art and technology to architecture and agriculture.
By Jesslyn Shields
""What Are Real Numbers?
Real numbers are the opposite of imaginary numbers and include every number you can think of.
By Jesslyn Shields
""What Is a Perfect Square?
A perfect square is a number, but it can also be explained using an actual square.
By Jesslyn Shields
""How to Divide Fractions
Dividing fractions is easy once you learn a couple of rules and remember three words — keep, change and flip.
By Jesslyn Shields
Advertisement
""How to Multiply Fractions
Multiplying fractions is easy — it just takes three simple steps!
By Jesslyn Shields
""What Are Imaginary Numbers?
An imaginary number is a value that's the square root of a negative number. It can't exist on a one-dimensional number line. We'll explain.
By Patrick J. Kiger
""How to Use the Unit Circle in Trig
A unit circle is an important part of trigonometry and can define right angle relationships known as sine, cosine and tangent.
By Nokware Knight
Advertisement
""Bayes' Theorem Helps Us Nail Down Probabilities
Bayes' theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event. Sounds intimidating, but we'll walk you through it.
By Mark Mancini
Advertisement
""What Are Prime Numbers, and Why Do They Matter?
You may remember from math class that a prime number is a number that can only be divided by 1 and itself. But why are they important anyway?
By Patrick J. Kiger
1.
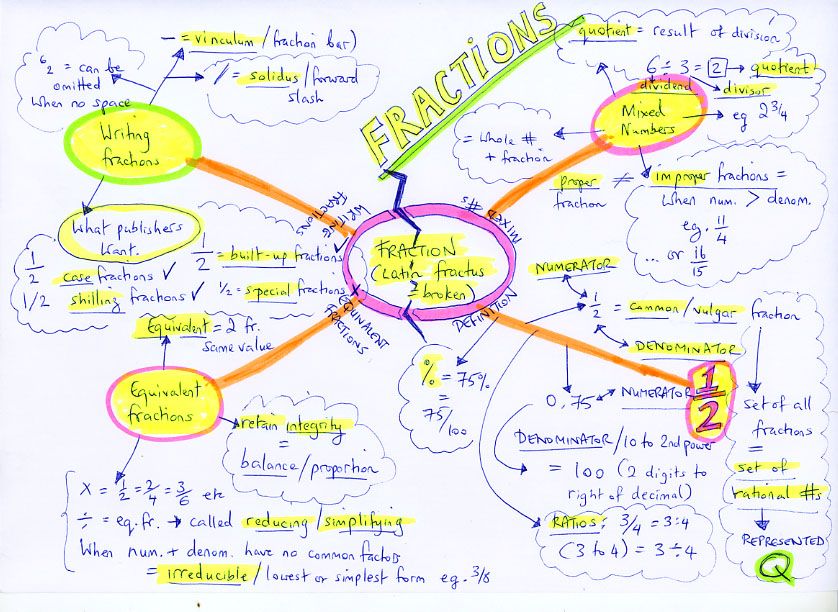Mathematical concepts Lecture #2
in mathematics
Topic: "Mathematical concepts”
Plan:
-
Mathematical concepts
-
Scope and content concepts. Relations between concepts
-
Definition concepts
-
Requirements to definition of concepts
-
Some species definitions
concepts, which are studied in the initial course mathematics is usually represented in the form four groups. The first one includes concepts related to numbers and operations above them: number, addition, term, more, etc. The second includes algebraic concepts: expression, equality, equation and others. The third is geometric concepts: line, segment, triangle etc. The fourth group is formed by the concepts associated with quantities and their measurement. nine0003
How to study such an abundance of different concepts?
Before All you need to do is to understand the concept as a logical category and features mathematical concepts.
AT logic concepts are considered as a form thoughts reflecting objects (objects or phenomena) in their essential and general properties. The language form of the concept is a word or group of words.
Compose the concept of an object means to be able to to distinguish it from others similar to it objects. Mathematical concepts have a number of features. home is that the mathematical objects to be compiled concept does not exist in reality. Mathematical objects are created by the mind person. These are ideal objects reflecting real objects or phenomena. For example, in geometry one studies the shape and size of objects, without taking into account their other properties: color, mass, hardness, etc. From all this distracted, abstracted. therefore in geometry instead of the word "object" say "geometric figure". nine0003
result abstractions are and such mathematical concepts like "number" and "value".
Generally mathematical objects exist only in the thinking of man and in those signs and symbols that form a mathematical language.
To It can be added to what has been said that, by studying spatial forms and quantitative relations of the material world, mathematics not only uses different methods abstraction, but abstraction itself acts as a multi-step process. Mathematics considers not only concepts that emerged in the study real objects, but also concepts arising from the first. For example, the general concept of a function as a correspondence is a generalization of the concepts of specific functions, i.e. abstraction from abstractions. nine0003
To master general approaches to learning concepts in the elementary course of mathematics, The teacher needs knowledge about the volume and the content of the concept, about the relationship between concepts and about the types of definitions of concepts.
Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties.
Among the properties object distinguish between essential and insignificant.
Property feel essential to an object if it inherent in this object and without it, it is not may exist. For example, for square essential are all the properties mentioned above. Not essential for square ABCD property "side AD horizontal." If the square is turned then side AD will be located differently (Fig. 26). nine0003
Therefore, to understand what is given mathematical object know its essential properties.
When talking about a mathematical concept, then usually means a set of objects, denoted by one term (word or group of words). So, speaking of a square, refers to all geometric shapes, which are squares. Think that the set of all squares is the scope of the concept of "square".
Generally volume concepts are the set of all objects, denoted by one term. nine0063
Any concept has not only volume, but also content.
Contents concepts are the set of all essential object properties reflected in this concept .
Consider, For example, the concept of "rectangle".
Volume concepts are many different rectangles, and in its content includes such properties of rectangles, how "to have four right angles", "to have equal opposite sides", "to have equal diagonals”, etc. nine0003
Between scope of the concept and its content there is a relationship: if increases the scope of the concept, then it decreases content and vice versa. For example, the scope of the concept of "square" is part of volume of the concept of "rectangle", and in the content of the concept of "square" contains more properties than in the content of the concept "rectangle" ("all sides are equal", diagonals are mutually perpendicular and etc.).
Any the concept cannot be grasped without realizing it relationships with other concepts. therefore it is important to know in what respects to be concepts, and to be able to establish these connections. nine0003
Relations between concepts are closely related to relationships between their volumes, i.
e. sets.
Let's agree concepts are capitalized Latin alphabet: a, b, c,...,z.
Let two concepts a and b are given. Their volumes will be denoted respectively by A and V.
If AND B (A ≠ B), then they say that the concept of a - specific in relation to the concept b , a concept b - generic in relation to the concept a .
For example, if a is a "rectangle", b - "quadrilateral", then their volumes A and B are in relation to inclusion (A B and A ≠ B), since every rectangle is a quadrilateral. therefore it can be argued that the concept "rectangle" - specific in relation to to the concept of "quadrilateral", and the concept "quadrangle" - generic in relation to the concept of a rectangle. nine0003
If A = B, then they say that concepts a and b are identical.
For example, identical concept of "equilateral triangle" and "equiangular triangle" because their volumes match.
If sets A and B are not related inclusions, then we say that the concepts a and b are not related to genus and species and are not identical.
For example, not related such relations of the concept of "triangle" and "rectangle".
Consider in more detail the relation of genus and species between concepts. First, the concepts of gender and species are relative: the same concept may be generic to one concept and species in relation to another. For example, the concept of "rectangle" - generic in relation to the concept of "square" and specific in relation to the concept "quadrilateral". nine0003
Secondly, for a given concept, one can often specify several generic terms. Yes, for the concepts of "rectangle" are generic are the concepts of "quadrilateral", parallelogram, polygon. Among them, you can specify the nearest. For the concept of "rectangle" to the nearest is the concept of "parallelogram".
Thirdly, the species concept has all the properties generic concept. For example, a square being a species concept in relation to to the concept of "rectangle", has all the properties of a rectangle. nine0003
Since the volume concepts - set, convenient, setting relations between the volumes of concepts, depict them using Euler circles.
Set, for example, relationship between the following couples concepts a and b, if:
1) a - "rectangle", b - "rhombus";
2) a - "polygon", b - "parallelogram";
3) a - "straight", b - "line segment".
AT case 1) the volumes of concepts intersect, but not one set is a subset of another (Fig. 27). nine0003
Consequently, It can be argued that these concepts and b are not related to genus and species.
AT case 2) the data volumes of the concept are regarding inclusion, but do not match - every parallelogram is polygon, but not vice versa (Fig. 28). Therefore, it can be argued that the concept of "parallelogram" - specific in relation to the concept of "polygon", and the concept of "polygon" is generic in relation to the concept of "parallelogram".
nine0003
AT case 3) the volumes of concepts do not intersect, since not a single segment is possible say he is direct, and neither one line cannot be named segment (Fig.
29).
Consequently, these terms are not related genus and species.
O concepts of "line" and "segment" can be say they are for whole and part: A segment is a part of a line, not a type of it. And if the species concept has all the properties generic concept, then the part is not necessarily has all the properties of the whole. For example, a segment does not have such property of the straight line, as its infinity. nine0003
Topic 7. Mathematical concepts Content
-
Mathematical concepts. The scope and content of the concept.
-
Relationship genus and species between concepts.
-
Definition concepts.
-
Requirements to the definition of concepts.
five. Implicit definitions
Main literature 7, 14, 16, 24, 25, 30, 33, 34;
Additional literature 26, 44
studying mathematics at school, college, university, need to learn a certain system concepts, propositions and proofs, but to master this system and then successfully apply acquired knowledge and skills, teaching younger students and solving the problem of their development by means mathematics, one must first understand what features of mathematical concepts, how their definitions, sentences, expressing properties of concepts, and proof.
Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties of the square. nine0003
Among properties of an object distinguish between properties essential and minor to distinguish it from other objects. The property is considered significant for object, if it is inherent in this object and without it it cannot exist. Insignificant properties are those properties, the absence of which does not affect the existence of the object. So, for example, the named properties of a square are essential, and the property "side AB of the square is vertical" insignificant. If the square is turned then side AB will be located differently (Fig. 1). nine0003
AT
AT C
AND C
AND D
D Rice.
1
Therefore, to understand what is given mathematical object is enough know its essential properties. In that case, it is said that there is a concept of this object. nine0003
When talk about a mathematical object, then usually mean the whole objects designated by one term, word, name. So when talking about square, then they mean all geometric shapes that are squares. Aggregate of all squares is the scope of the concept square.
Definition. The scope of a concept is the totality of all objects designated by the same term.
Any concept has not only scope, but also content. nine0003
Definition . The content of the concept is a set all essential properties of the object, reflected in this concept.
T. Well, every concept is characterized by term, volume, content.
Note.
Learn more
