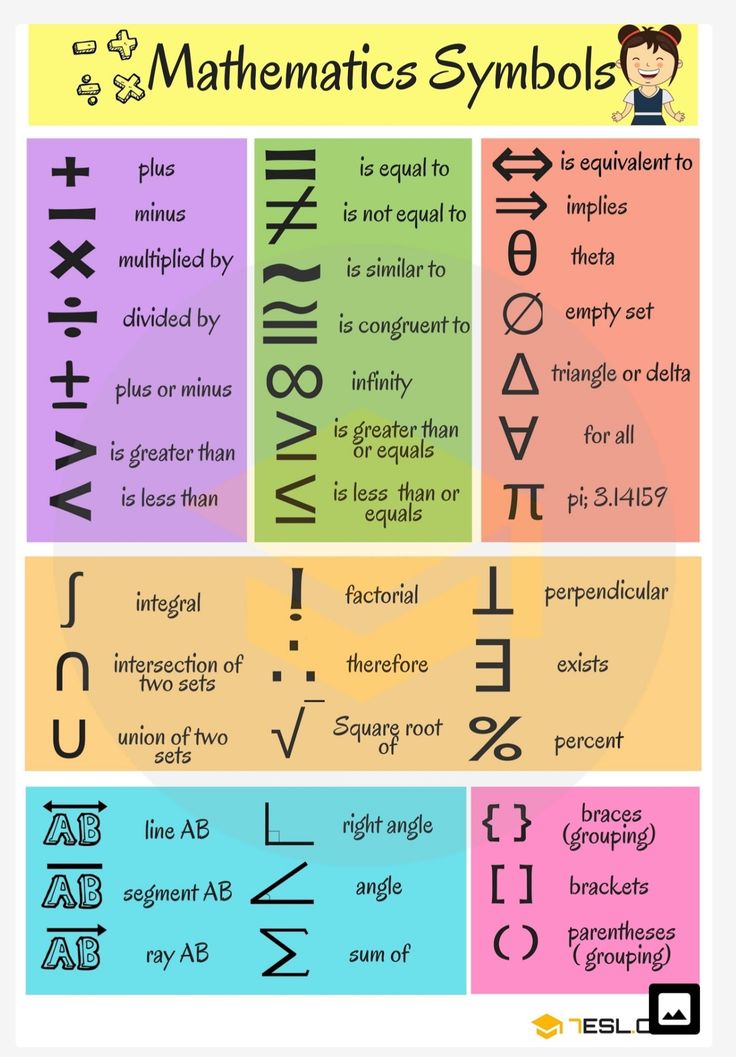
What is k in math

Constant Of Proportionality With Example

When two variables are directly or indirectly proportional to each other, then their relationship can be described as y = kx or y = k/x, where k determines how the two variables are related to one another. This k is known as the constant of proportionality.

1.	What is Constant of Proportionality?
2.	Why Do We Use The Constant of Proportionality?
3.	How to Solve The Constant of Proportionality?
4.	Identifying The Constant of Proportionality
5.	Solved Examples
6.	Practice Questions
7.	FAQs on The Constant of Proportionality

What is Constant of Proportionality?

Constant of proportionality is the constant value of the ratio between two proportional quantities. Two varying quantities are said to be in a relation of proportionality when, either their ratio or their product yields a constant. The value of the constant of proportionality depends on the type of proportion between the two given quantities: Direct Variation and Inverse Variation.

Direct Variation: The equation for direct proportionality is y = kx, which shows as x increases, y also increases at the same rate. Example: The cost per item(y) is directly proportional to the number of items(x) purchased, expressed as y ∝ x
Inverse Variation: The equation for the indirect proportionality is y = k/x, which shows that as y increases, x decreases and vice-versa. Example:The speed of a moving vehicle (y) inversely varies as the time taken (x) to cover a certain distance, expressed as y ∝ 1/x

In both the cases, k is constant. The value of this constant is called the coefficient of proportionality. The constant of proportionality is also known as unit rate.

Why Do We Use The Constant of Proportionality?

We use constant of proportionality in mathematics to calculate the rate of change and at the same time determine if it is direct variation or inverse variation that we are dealing with. Let us assume that the cost of 2 apples = $20. We determine that the cost of 1 apple = $10. We have found the Constant of Proportionality for the cost of an apple is 2.

If we want to draw a picture of the Taj Mahal by sitting in front of it on a piece of paper by looking at the real image in front of us, we should maintain a proportional relationship between the measures of length, height, and width of the building. We need to identify the constant of proportionality to get the desired outcome. Based on this, we can draw the monument with proportional measurements. For instance, if the height of the dome is 2 meters then in our drawing we can represent the same dome with height 2 inches. Similarly, we can draw other parts. In such scenarios, we use constant of proportionality.

Working with proportional relationships allows one to solve many real-life problems such as:

Adjusting a recipe's ratio of ingredients
Quantifying chance like finding odds and probability of events
Scaling a diagram for drafting and architectural uses
Finding percent increase or percent decrease for price mark-ups
Discounts on products based on unit rate

How to Solve The Constant of Proportionality?

We apply our knowledge on the direct and inverse variations, identify them and then determine the constant of proportionality and thereby get the solutions to our problems.

Example 1:Find the constant of proportionality, if y=24 and x=3 and y ∝ x.

Solution: We know that y varies proportionally with x. We can write the equation of the proportional relationship as y = kx. Substitute the given x and y values, and solve for k.

24 = k (3)

k = 24 ÷ 3 = 8

Therefore, the constant of proportionality is 8.

Example 2: 4 workers take 3 hours to finish the desired work. If 2 more workers are hired, in how much time will they complete the work?

Solution: Let x1 = number of workers in case 1 = 4

x2 = Number of workers in case 2 = 6

y1 = number of hours in case 1 = 3

y2 = number of hours in case 2 = To be found

If the number of workers is increased, the time taken to complete will reduce. We find that number of workers is inversely proportional to the time taken, (y1 = k/x1) ⇒ 3 = k / 4⇒ k = 12

Again, to find the number of hours, (y2 = k/x2) ⇒ y2 = 12/6 = 2 hours.

Identifying The Constant of Proportionality

We shall now learn how to identify the constant of proportionality (unit rate) in tables or graphs. Examine the table below and determine if the relationship is proportional and find the constant of proportionality.

Number of Days = x	1	3	5	6
Number of Articles Written = y	3	9	15	18

We infer that as the number of days increases, the ariticles written also increases. Here we identify that it is in direct proportion. We apply the equation y= kx. To find the constant of proportionality we determine the ratio between the number of articles and the number of days. We need to evaluate for k = y/x

y/x = 3/1 = 9/3 = 15/5 = 18/6 = 3

From the result of the ratios of y and x for the given values, we can observe that the same value is obtained for all the instances. The Constant of Proportionality is 3.

If we plot the values from the above table onto a graph, we observe that the straight line that passes through the origin shows a proportional relationship. The constant of proportionality under the direct proportion condition is the slope of the line when plotted for two proportional constants x and y on a graph.

X	Y
5	1
25	5
16	3
35	7

FAQs on Constant of Proportionality

What is the Other Name for the Constant of Proportionality?

Another name for the constant of proportionality in mathematics is the unit rate.

What is the Constant of Proportionality in a Graph?

The straight line that passes through the origin is the constant of proportionality in a graph.

Why do we Use Constant of Proportionality?

We use constant of proportionality in mathematics to determine the nature of proportionality, whether it is direct proportion or indirect proportion. The constant of proportionality helps in solving the equations involving ratios and proportions.

What is the Constant of Proportionality of 12/6?

To find the constant of proportionality, in the case of direct proportionality, we use k=y/x. Let us take y = 12 and x = 6, then k = 12/6 = 2.

What is the Constant of Proportionality?

If the ratio of one variable to the other is constant, then the two variables have a proportional relationship, If x and y have a proportional relationship, the constant of proportionality is the ratio of y to x. Sometimes, we also represent it as x is to y.

Download FREE Study Materials

Commercial Math

Variation Equations | Purplemath

Word ProblemsMore Prob's

Purplemath

Variation problems aren't hard once you get the hang of the lingo. The only real difficulty is learning the somewhat specialized vocabulary and the techniques for this classification of problems.

Variation problems involve fairly simple relationships or formulas, involving one variable being equal to one term. That term might be linear (something with just an "x"), quadratic (something in "x²"), more than one variable (such as "r²h"), a square root (something like "

"), or something else.

But there is always just the one term in the formula; this term will be multiplied by some number and, if you don't yet know what that number is, the number is usually denoted by "k". This number k is called "the constant of variation".

Content Continues Below

MathHelp.com

Direct Variation

So variation equations may have complicated expressions, but they'll only ever have the one term. Their equations will never have two or more terms added together. For instance, y = 3x is a variation equation, but y = 3x + 2 is not.

What are the keywords for variation equations?

The keywords for variation equations are:

directly
inversely
jointly

What do these variation-equation keywords mean?

The keywords' meanings are:

directly: things are working together; you are multiplying everything.
inversely: things working against each other; you are dividing something somewhere.
jointly: many things are working together; you are multiplying lots of stuff.

An example of a variation equation would be the formula for the area of the circle:

A = π r²

In the language of variation, this equation means:

the area A varies directly with the square of the radius r

...and the constant of variation is k = π. This formula is an example of "direct" variation."Direct variation" means that, in the one term of the formula, the variable is "on top".

(By the way, if you see a formula with a "∝" character in it instead of an "equals" sign, that character is pronounced as "is directly proportional to", and indicates that they've given you a direct-variation equation, but without telling you what the variation constant is.)

On the other hand, "inverse variation" means that the variable is underneath, in the bottom of a fraction. Suppose, for instance, that you inherit a money market account containing $100,000, and you wonder how much money your rich uncle initially invested eight years ago. Depending on the average interest rate "r", the formula you would use would be:

...where P is the principal that your uncle invested. (This formula is a variant of the compound-interest formula, by the way.) In the language of variation, this formula reads as:

the principal P varies inversely with

...with the constant of variation being k = 100,000.

The other case of variation is "jointly". "Joint variation" means "directly, but with two or more variables". An example would be the formula for the area of a triangle with base "b" and height "h":

In words:

the area A varies jointly with b and h

The constant of variation for this equation is

k = ¹/₂.

To review:

"F varies as x" means F = kx

"F varies jointly as x and y" means F = kxy

"F varies as x + y" means F = k(x + y)

"F varies inversely as x" means

Be careful with those middle two statements above. Almost always, when you translate word problems from English into math, "and" means "plus" or "added to". But in joint variation, "and" just means "both of these are together on the same side of the fraction" (usually on top), and you multiply. If you are supposed to add two variables, they'll use the format in that third bulleted example above, or they'll say "varies as the sum of x and y.

(If they have you working with something that varies "directly" with one thing and "inversely" with another thing, this may be referred to as a "combined" variation. )

Translating variation problems isn't so bad, once you get the hang of it. But then they want you to move on to setting up and solving word problems. These generally fall into two categories: the ones where they want you to find the value of "k", and the ones where they want you to find some other value, but only after you've found "k" first.

What are some examples of solving variation equations?

Since this is direct variation, the formula is "y = kx²".The reason they've given me the data point (x, y) = (2, 8) is that I have to be able to find the value of "k". So I'll plug in the information they've given me, and solve for k:

y = k x²

8 = k (2²)

8 = 4k

2 = k

Now that I have k, I can rewrite the formula completely:

y = 2x²

With this, I can answer the question they actually asked: "Find y when x = 1. "

y = 2x²

y = 2 (1)²

y = 2 (1)

y = 2

Then the answer is:

y = 2

Translating the formula from English to math, I get:

y = kxz

Plugging in the data point they gave me, and solving for the value of k, I get:

5 = k(3)(4)

5 = 12k

⁵/₁₂ = k

Now that I have the value of k, I can plug in the new values, and solve for the new value of y:

y = (⁵/₁₂)xz

y = (⁵/₁₂)(2)(3)

y = (⁵/₁₂)(6)

y = ⁵/₂

Then the answer is:

y = ⁵/₂

This one is somewhat complex. I'll work in small pieces.

They've told me that y varies inversely with the specified expression, so I know that the form of the expression will have a constant of variation on top of a rational expression (that is, a polynomial fraction), and a variable expression on the bottom of that expression. But what is the variable expression?

"The difference of w and x" means:

w − x

The square of this difference is:

(w − x)²

This expression will go on the bottom of the fraction, and the variation constant k will go on top, so my equation so far is:

y = k/(w − x)²

In order to find the complete equation for y, I'll need to find the value of the constant. To do this, I'll plug in the values they gave me:

6 = k/(3 − 1)²

6 = k/(2)²

6 = k/4

24 = k

Now I have all the parts of my equation, and my answer is:

y = 24/(w − x)²

URL: https://www. purplemath.com/modules/variatn.htm

Page 2Page 3

Coefficients k and b | 7th grade | Algebra

Contents

In the previous lessons we have considered a linear function and learned how to build its graph on the coordinate plane. In this lesson, we will delve into the theory and analyze why the chart looks the way it does.

Recall that the linear function has the form $y = kx+b$, where $x$ is a variable and $k$ and $b$ are some numbers, called coefficients .

For example,

$y = \textcolor{blue}{5}x + \color{green}{10}$ is a linear function
$\color{blue} k = $5
$\color{green} b = $10.

The graph of a linear function is a straight line, and its position on the plane depends on the $k$ and $b$ of the function.

Coefficient k

Coefficient $k$ is called angular , since it shows the slope of the linear function on the graph relative to the $Ox$ axis

For $k > 0$, the angle between the graph and the $Ox$ axis is less than $90 \ degree$ (sharp)

For $k < 0$, the angle between the graph and the $Ox$ axis is greater than $90 \degree$ (stupid)

Coefficient b

Coefficient $b$ is called free . On the graph, it shows the length of the segment that the line of the function cuts off along the ordinate axis relative to the origin.

In other words, the coefficient $b$ shows how much the graph is above or below the $Oy$ axis.

If $b > 0$, the chart is shifted up,
if $b < 0$, then the chart is shifted down.

On our graph of the function from the piggy bank example, it can be seen that the straight line intersects the $Oy$ axis above the origin by $500$ units (this number is equal to the coefficient $b$).

Particular cases. b = 0

If the coefficient $b = 0$, the function becomes $y = kx + 0$, which can be reduced to $y = kx$.

Substitute in the formula $x = 0$, we get: $$y = k \times 0$$

So the graph will pass through the origin $O(0;0)$.

To construct a graph of a function of the form $y = kx$, it is enough to find one point, the second - the origin.

 "questions": [{ "widgets": { graph: { "type": "graph", "func": "line", "settings": { "cells": 12 }, "answer": { "k": 2, "b": 0 } } }, "content": "Plot the function $y=2x$[[graph]]" }, { "widgets": { graph: { "type": "graph", "func": "line", "settings": { "cells": 12 }, "answer": { "k": 1 "b": 0 } } }, "content": "Plot the function $y=x$[[graph]]" }, { "widgets": { graph: { "type": "graph", "func": "line", "settings": { "cells": 12 }, "answer": { "k": 0. 5 "b": 0 } } }, "content": "Plot the function $y=0.5x$[[graph]]" }] }

k = 0

If the coefficient $k = 0$, the slope will also be $0$.

The function then takes the form $y = 0 \times x + b$, i.e. $y = b$.

Where did the variable $x$ go? We no longer need it, because no matter what $x$ we substitute, the value of $y$ will not change.

 { "questions": [{ "widgets": { graph: { "type": "graph", "func": "line", "settings": { "cells": 12 }, "answer": { "k": 0 "b": 2 } } }, "content": "Plot the function $y=2$[[graph]]" }, { "widgets": { graph: { "type": "graph", "func": "line", "settings": { "cells": 12 }, "answer": { "k": 0 "b": 1. 5 } } }, "content": "Plot the function $y=1.5$[[graph]]" }, { "widgets": { graph: { "type": "graph", "func": "line", "settings": { "cells": 12 }, "answer": { "k": 0 "b": 0 } } }, "content": "Plot the function $y=0$[[graph]]" }] }

Table

Rate the lesson

Share the lesson →

What can be improved?

Presentation of the material

Incomprehensible explanation

Lesson incomplete, not enough information

Lesson overloaded, too much information

Tests are of poor quality

Tests are not enough

Tests are too many

Tests are too easy

Tests are too hard

Images

Poor Images

Images are not enough

Images too many

other

Come in to evaluate the lessons

What needs to be fixed?

Thank you for helping us become better!

Comments

Mathematical formulas in algebra and geometry for the exam

How to learn all the formulas in mathematics for the USE

To pass the USE in mathematics, you need to know the mathematical formulas from the school course of algebra and geometry.

In order to memorize the formulas of school mathematics, it is advisable to keep a cheat sheet with beautifully written formulas in a conspicuous place throughout the year. Thus, visual memory is connected and formulas are better remembered.

Test yourself from time to time: try to write all the important mathematical formulas from memory, and then check. In fact, there are not so many formulas that need to be learned by heart. And a whole academic year is enough to learn everything.

Many algebraic, geometric, trigonometric formulas can be quickly deduced right on the exam, if you have forgotten them. But this will take some time. Therefore, the advantage is given to those students who have learned the formulas.
Knowing mathematical formulas by heart, you can solve complex problems in algebra, trigonometry and geometry on the exam much faster.

We have collected the most important formulas from the school mathematics course that you need to learn to successfully pass the exam.