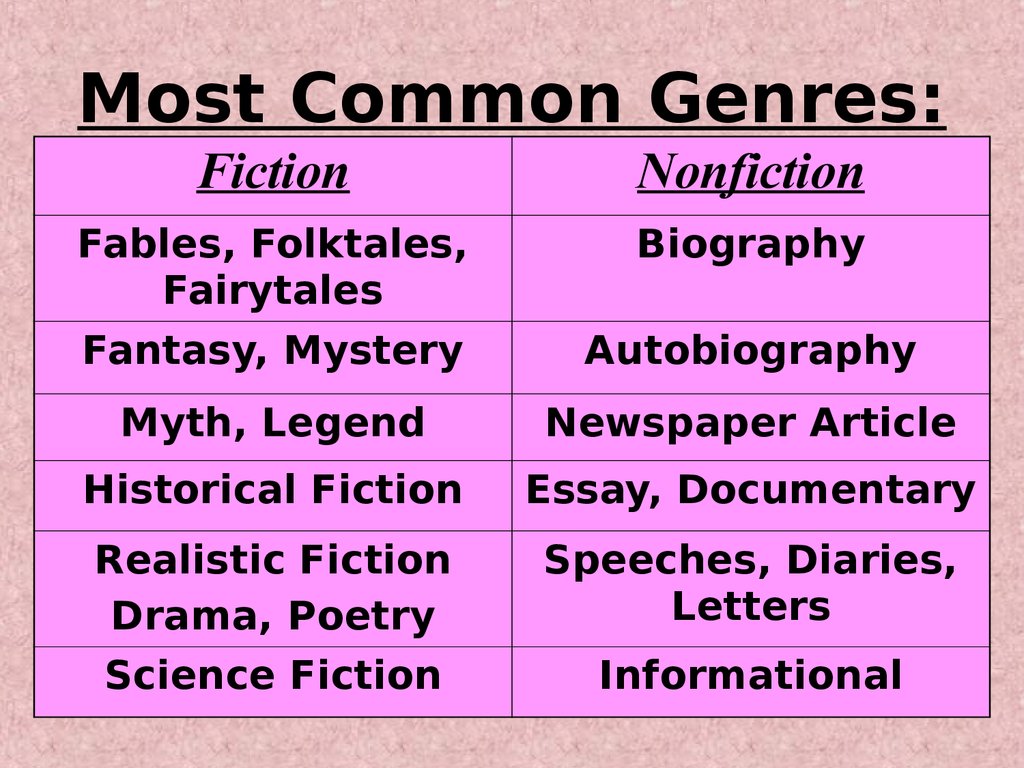
Basic math topics
4 Crucial Basic Math Concepts
Search my site:
Your child's success in learning Math depends on mastering these five crucial concepts. They are essential for building a strong foundation in Math. They help your child understand and make sense of numbers and problem-solving; they strengthen his or her number sense.
The good news is that it is very easy to help your child understand these concepts. The key is to practice a few minutes several times a day. Make it a family affair so your child does not feel overly stressed. Your child or children will remember the lessons better if they had fun with it.
1. Understanding Numbers
The first concept your child must master is knowing how to read, write and understand numbers. Print out 2 sets of the number chart here. Use one set as a reference. Cut out the individual numbers from the second set.
Some ideas for you:
- read and write numbers
- recite a list of numbers forwards and backwards
- what number comes before or next
- arrange numbers in order (start with consecutive numbers)
- even and odd numbers
Print out this set of place numbers for older children.
2. More, Less or Equal
The next important concept in Math is to know how 2 numbers compare; whether one number is more, less or equal to another number.
Numbers represent quantity. Your child must first understand these types of questions.
- Amanda has 12 stickers. Benjamin has 9 stickers. Who has more stickers?
- Jack has 35 stamps. Alan has 19 stamps. Who has fewer stamps?
- Sam has 107 balloons. Jodie has 90 balloons. Who has more balloons? How many more?
- Charlie is 30-years-old. Mary is 17-years-old. Who is younger? How many years younger?
Followed by these types of questions:
- Rodney has $3 more than Janice. How much money does Rodney have if Janice has $26?
- I have 7 fewer pencils than books.
How many books do I have if I have 20 pencils? - John spent $11 less than Mark. How much did they spend altogether if Mark spent $15?
And these types of questions:
- 5 pencils cost the same as 2 books. Which is more expensive, the pen or the book?
- 6 apples cost the same as 10 oranges. What is the cost of 1 apple if 1 orange costs $0.60?
- Mary and James have the same amount of money. Mary spent half of her money. James spent one-third of his money. Who spent more money?
No matter how difficult the questions get, they can all be broken down into simple comparisons of more, less or equal.
3. Knowing Which Operation to Use
In Basic Maths there are actually only 4 operations your child needs to know: addition, subtraction, multiplication and division. Here are some clues to help your child decide which of these to use. Print the following graphic for your child to use as a guide.
4. Different Ways to Get to the Answer
When it comes to Math, many children assume there is only one way or method to use to come up with the correct answer. If your child does not understand the teacher's method, he or she assumes that it is because he or she too stupid to understand.
You must help your child realize that there can be different ways of understanding a problem and different strategies can be used to find the answer. However, though the strategies may differ, the answer to the question must always be the same.
Play this family game: Write out simple word problems on cards. Read out a problem, then each person explains how he or she comes up with the answer.
Example
Mary has 9 sweets. She bought a few more sweets and now she has 13 sweets. How many sweets did Mary buy?
Some methods of solving:
- Say '9' then count '10, 11, 12, 13' on your fingers. Since you used 4 fingers to count, the answer is 4.
- Draw 9 circles in a row. Draw 13 circles in a second row below the first, making sure you line them up exactly. Compare the two rows and point out there are 4 extra circles in the second row. The answer is 4.
- Write the numbers 1 to 13 on a number line. Point out that after the number 9, there are 4 more numbers to reach the number 13. The answer is 4.
Play this game often and your child will become more flexible and logical in his or her thinking. He or she will automatically look for different ways to solve a hard problem. This will surely help in tackling complicated Math problems later on in school. Teach your child to ask "Is there another way of solving?" when he or she cannot understand one explanation.
This will help them realize that failure to understand does not mean they are cannot learn Math.
After your child has mastered this Math concept, introduce deliberate mistakes in your reasoning to see if your child can spot and correct them.
But do this only after your child has thoroughly understood the different strategies or you'll only end up confusing your child.
For older children, you can help them understand the properties of the different operations of addition, subtraction, multiplication and division.
Sometimes the order that these operations are used does not matter. Sometimes it does. Discuss the different strategies to find out when order matters, and when it doesn't.
Example
Max bought 3 boxes of pencils. Each box contains 12 pencils. He gave 5 pencils to his brother and 8 pencils to his sister. How many pencils does Max have left?
Methods of solving:
- To find the total number of pencils at first, you can multiple (3 x 12) or add (12 + 12 + 12).
- To find the number of pencils left, you can add first (5 + 8) and then subtract
(36 - 13). - Or you can subtract only (36 - 5 - 8).
I hope these strategies help your child excel in Maths.
Share them with other parents whose children struggle with Maths.
Branches, Fundamentals, Important Topics, Preparation Tips
Math is the science of quantity, pattern, order, structure and relation that has continuously evolved from basic practices of counting, measurements and symmetric study of shapes. It primarily involves applying logical reasoning and quantitative computation to find optimal solutions to problems. It has been worldwide recognized as an indispensable computational tool in the field of engineering, biology, medicine and natural sciences.
Math As A Subject
Math as a subject is an important part of the curriculum that plays a significant role in shaping a child’s future. It involves studying many useful concepts and topics relevant to practical life. Although math is an interesting subject, students often find it boring and complex due to the way it is taught conventionally. Cuemath helps students to explore and understand fundamental concepts in a fun and intuitive manner.
Fundamentals of Math
Fundamentals of math are the basic building blocks that help students form a solid mathematical foundation. Math learning entirely relies on the understanding of these fundamental concepts. If children lack the basic understanding of division or subtraction, then algebra automatically becomes confusing for them. Therefore, it is imperative that children must have a crystal clear knowledge of all fundamentals of math.
- Addition and Subtraction of Whole Numbers
- Multiplication and Division of Whole Numbers
- Exponents, Roots, and Factorization of Whole Numbers
- Introduction to Fractions and Multiplication and Division of Fractions
- Addition and Subtraction of Fractions, Comparing Fractions, and Complex Fractions
- Decimals and Fractions
- Ratios and Rates
- Techniques of Estimation
- Measurement and Geometry
- Signed Numbers
- Algebraic Expressions and Equations
Branches of Mathematics
Mathematics involves complex studies of interlinked topics and several concepts that overlap each other.
Generally, it can be categorized into the following branches:
Arithmetic
Arithmetic is the most basic branch of mathematics that deals with the elementary aspects of numbers, mensuration and numerical computations. This term is derived from the Greek word ‘arithmos’ which means number. It generally involves studying numbers and their relationships to solve problems that include the operations of addition, multiplication, subtraction, division, extraction of roots and raise to power.
Algebra
Algebra is an important and ancient branch of math that covers basic operations and symbols to represent numbers in formulas and equations. The word Algebra means the science of restoring and balancing. Learning algebra enables students to understand many real-life phenomena around them. It is a symbolic representation of numbers and how they work together to provide structure to equations. It forms the basis for advanced study in many fields like science, medicine, engineering, etc.
It allows mathematicians to write formulas and solve maths problems more efficiently.
Geometry
Geometry is the branch of math which deals with computation of various dimensions of solid shapes including height, width, area, volume, perimeter and angles. It has several useful applications from the construction of homes to interior designs.
Trigonometry
Trigonometry is an important branch of math that involves studying the relationship between angles, lengths, heights and distance. The applications of trigonometry can be found in many spheres including architecture, physics, surveying, electronics, satellite navigation, astronomy and engineering.
List of Branches of Maths
Important Math Topics
A thorough understanding of all important math topics will benefit students throughout their lifetime. Some of the essential math concepts that students must have an in-depth understanding of are based on the topics listed below.
- BODMAS Rule
- Prime and Composite numbers
- HCF and LCM
- Basic Menstruation
- Divisibility Rules
- Decimal and Fractions
- Ratio and Proportion
- Three-dimensional shapes
- Geometry
- Probability
Math Calculators
Students often find math challenging due to complex mathematical calculations. Math Calculators are handy tools to resolve all such problems. It makes calculations simple and quick. With the use of math calculators, calculations ranging from elementary arithmetic operations to complicated equations can be solved within a few seconds.
List of important calculators for students to solve problems quickly and get accurate solutions.
Important Math Formulas
Math formulas are expressions created after several years of research to help solve problems easily. Performing simple numerical operations like addition, subtraction and division are easy.
However, to solve algebraic expressions, and other complex operations we use mathematical formulas. These are quite useful in obtaining the answers precisely. Cuemath provides formulas for each math topic along with the illustrated steps of equations for students to understand them logically.
List of important formulas that students must learn and memorize.
Tips And Tricks To Learn Math Fast
Although math is a vast subject there are some tips and tricks to learn math fast. These tips and tricks will help students improve along their math journey.
Clear All Basic: The first and foremost step in learning mathematics is to clearly understand all basics. It will not only allow you to learn math faster but will also help in establishing links between various math topics.
Set Objectives: After clearing all basics, set goals for what you need to focus on. Once you understand your objective, start working on it. Explore various resources that can help you improve and get well versed in those topics.
Practice Daily: Math requires daily practice, implementing a proper study routine will help in grasping concepts better.
Take Guidance: Heading in the right direction is necessary as it will ensure good results. Consider taking help from your teacher or a math tutor if you feel doubtful about topics and concepts.
FAQs on Math
What Exactly is Math?
Math is the science involving numbers, shapes and patterns which is present in almost everything around us. It helps us to derive analytical solutions to practical problems. It is applied in various fields such as engineering, finance, physical science, etc. It has a great impact in every domain of our life and we can find many mathematics applications around us.
How to Get Better at Math?
Getting better at math requires enforcing a study routine and analyzing mistakes. Students must try to understand and rectify their mistakes through daily practice. Doing so will also help them clear all their doubts.
Students with better mathematical abilities achieve higher academic success. Thus, it is crucial to cultivate math interest in children at an early age. Cuemath’s visually-enriched math concepts enhance a child’s interest in mathematics and make it easier to learn the subject.
Why is Math Important in Our Daily Life?
Math is highly important in our daily life as there are several applications of mathematics in real-world situations. Statistics or probability theory are examples of applied maths.
What are the Fundamentals of Mathematics?
Fundamentals of mathematics are the building blocks for a solid math foundation. Students must possess a clear knowledge of all the fundamentals of mathematics to study advanced mathematical concepts. These fundamentals of mathematics are given below.
- Addition and Subtraction of Whole Numbers
- Multiplication and Division of Whole Numbers
- Exponents, Roots, and Factorization of Whole Numbers
- Introduction to Fractions and Multiplication and Division of Fractions
- Addition and Subtraction of Fractions, Comparing Fractions, and Complex Fractions
- Decimals and Fractions
- Ratios and Rates
- Techniques of Estimation
- Measurement and Geometry
- Signed Numbers
- Algebraic Expressions and Equations
How many Branches of Mathematics do we Have?
The branches of mathematics can be broadly categorized as:
- Arithmetic: Arithmetic involves studying numbers and their relationships to solve problems that include the operations of addition, multiplication, subtraction, division, extraction of roots and raise to power.
- Algebra: Algebra is the symbolic representation of numbers that provides structure to equations. It forms the basis for advanced study in many fields like science, medicine, engineering, etc.
- Geometry: Geometry is the calculation of various dimensions of solids including height, width, areas, volumes, perimeter and angles. It has many practical applications in architecture and other fields.
- Trigonometry: trigonometry deals with the study of the relationship between angles, lengths, and heights. The applications of trigonometry can be found in many spheres including architecture, physics, surveying, electronics, satellite navigation, astronomy and engineering.
What are the Most Important Math Topics?
Some of the most important math topics are prime numbers, composite numbers, BODMAS rule, geometry, probability, divisibility rules, HCF, LCM, three-dimensional shapes, basic menstruation, decimal, fractions, ratio and proportion.
An in-depth understanding of all important math topics will enable students to score well in exams.
How Math is Used in Sports?
Math is used in sports to accumulate data, study conditions and generate performance statistics which are considered for planning and optimizing the training session. The data collected in these mathematical calculations is also helpful for taking strategic decisions based on the team’s performance.
How Maths is Related to Other Subjects?
Math is related to other subjects, especially chemistry, physics, computer science and engineering. In chemistry, mathematics is used to write and balance equations. In physics. It is applied to calculate mass, velocity and acceleration. In computer science, math is used to build algorithms and solve problems.
all classes, all formulas, all topics
Dear schoolchildren, students! On the site you will find topics on mathematics for grades 5-11 and lectures on higher mathematics. We not only study theoretical material, but also solve problems - we analyze them in detail.
We also pay attention to the analysis of interesting USE problems in mathematics. Here you will find all the formulas in mathematics for grades 5-11, learn to reason and solve equations, inequalities, systems of equations and inequalities, analyze functions, take derivatives and integrals. We paid special attention to an important section of mathematics - "Geometry". Solving spatial problems, reasoning, diagrams and much more awaits you in this section.
Trigonometry is another important section in mathematics, it links together both geometry and algebra, helps to comprehend space. Trigonometric equations and inequalities are discussed in detail in this section. All necessary formulas are given.
USE in mathematics profile level
The figure shows parts of the graphs find the ordinate of the intersection point
016
The figure shows parts of the graphs of functions and . Find the ordinate of the point of intersection of the graphs of these functions.
USE in mathematics profile level
Find the smallest value of the function y=x√x-27x+6 on the segment [1; 422]
044
Find the smallest value of the function on the interval [1; 422]. Solution: We know that in order to find
Grade 8 Geometry.
Parallelogram and its properties
059
Definition: A parallelogram is a quadrilateral with opposite sides in pairs
Grade 7. Algebra.
Linear function y=kx+b and its graph
0416
If the function is given by the formula , where and are some numbers, it is called a linear function.
5th grade. Maths.
How to multiply by a column in grade 3 and in grade 4
0497
In this article we will consider how to multiply by a column various
grade 5. Maths.
Numeric expressions and letter expressions - rules
017. 3k.
When solving examples and equations, it is necessary to clearly distinguish between
5th grade. Maths.
5.6.3. Solving problems with percentages. Part B
04.4k.
Problem 1. The first number is 80% of the second.
5th grade. Maths.
5.6.2. Solving problems with percentages. Part A
016.5k.
Problem 1. Water makes up 76% of potatoes. How many kilograms
Grade 5. Maths.
5.5.7. Rounding numbers
011.6k.
To round a number to any digit - underline
5th grade. Maths.
5.5.6. Decimal division
013.3k.
I. To divide a number by a decimal, you need
6th grade. Maths.
Numerical inequality, properties of numerical inequalities and examples of solutions
06.5k.
Consider what is the numerical inequality
Grade 6.
Maths.
6.5.1. Linear equation with one variable
08.5k.
Very many schoolchildren have
6th grade. Maths.
6.4.2. Bracket opening. Reduction of similar terms
024.1k.
1. Opening brackets, before which
6th grade. Maths.
6.9.3. Solving systems of linear equations by the addition method.
023.7k.
To solve a system of linear equations
Grade 6. Maths.
6.9.2. Solving systems of linear equations by the substitution method
011.4k.
For solving a system of linear equations
6th grade. Maths.
6.4.1. Algebraic expression
18.6k.
I. Expressions in which along with
7th class. Algebra.
Linear function y=kx+b and its graph
0416
If the function is given by the formula , where and
7 class.
Algebra.
Identity - what is it in mathematics
09k.
Very often in mathematics there are such words «
Grade 7. Algebra.
7.2.3. Actions with monomials and polynomials
15.2k.
I. To multiply a monomial by a polynomial, you need to multiply
7th grade. Algebra.
7.2.2. Polynomial
03.1k.
I. The sum of monomials is called a polynomial.
Grade 7. Algebra.
7.2.1. Monomial.
02.4k.
I. Expressions that are made up of numbers, variables
Grade 7. Algebra.
7.1.2. Standard form of the number
210.3k.
Very large and very small numbers are usually written
Grade 8. Algebra.
8.2.1. Solving incomplete quadratic equations
07.5k.
I. ax2=0 - incomplete quadratic equation (b=0, c=0).
Grade 8. Algebra.
8.2.5. Decomposition of a square trinomial into linear factors
030.6k.
The square trinomial ax2+bx+c can be decomposed into linear ones
Grade 8. Algebra.
8.2.4. Application of Vieta's theorem
08.2k.
Often you need to find the sum of squares (x12+x22) or
Grade 8 Geometry.
Parallelogram and its properties
059
Definition: parallelogram
Grade 8 Geometry.
8.2.3.1. Rectangle. Problem solving 2
01.7k.
Task 1. Diagonal of a rectangle
Grade 8 Geometry.
8.2.3. Rectangle. Problem solving
08.5k.
Task 1. One side of a rectangle
Grade 8 Geometry.
8.2.5. Basic trigonometric identities. Part 2
01.9k.
Basic trigonometric identities.
Grade 9 Algebra.
9.3.3. Definition of an arithmetic progression. Examples
01.8k.
A numerical sequence, each member of which, starting from the second, is equal to the previous one, added with
9th grade. Algebra.
9.3.1. The numerical sequence is
018.1k.
The function an=f (n) of natural argument n (n=1; 2; 3; 4;...) is called a numeric sequence. Numbers a1;
Grade 9 Algebra.
9.3.2. Arithmetic progression. Theory
05.5k.
A numerical sequence, each member of which, starting from the second, is equal to the previous one, added with
10th class. Algebra.
Reduction formulas
114.2k.
The reduction formulas refer to the trigonometric function
Grade 10. Algebra.
10.3.0. Calculation of derivatives
012.4k.
In this lesson we will learn how to apply formulas
Grade 10. Algebra.
10.2.6. Solution of trigonometric inequalities. Part 6
02.3k.
In the previous lessons we solved trigonometric
Grade 11. Algebra.
11.1.9.3. Areas of curvilinear trapezoids enclosed between two curves
02.1k.
Problems of finding the area are often solved in algebra
Grade 11. Algebra.
11.1.9.2. Area of a curvilinear trapezoid adjacent to the Oy axis
02.4k.
If a curved trapezoid adjacent to the OU axis (Fig.
grade 11. Algebra.
11.1.9.2. The area of a curved trapezoid. Examples
031.2k.
The area of a curved trapezium, limited from the above
grade 11 algebra.
11.1.9.1. Definite integral. Area of a curvilinear trapezoid
02.3k.
Time to get acquainted with the most powerful research tool
Geometry
Rectangle area
211.3k.
The area of a rectangle is often required to find
Geometry
How to calculate the area of a circle - all formulas
114.3k.
The area of a circle is often required to be calculated in various
6th grade. Tests.
Test 6.6.1. Inequalities and their properties
02.5k.
Mathematics. 6th grade. Test 6.
Grade 6. Tests.
Test 6.5.1. Rounding decimals. Infinite periodic fraction
63.5k.
Mathematics. 6th grade. Test 5. Option 1.
Grade 6. Tests.
Test 6.4.1. All actions with rational numbers
02k.
Mathematics. 6th grade. Test 4.
Grade 6. Tests.
Test 6.3.1. Addition, multiplication of rational numbers
01.7k.
Mathematics. 6th grade. Test 3.
Introductory course of elementary mathematics - Mathematics - Theory, tests, formulas and problems
- Some basic information on basic mathematical operations
- Reduced multiplication formulas
- Quadratic equation and factorization formula for a quadratic trinomial
- Parabola
- Basic properties of degrees
- Basic properties of mathematical roots
Some basic information on basic mathematical operations
To contents...
Rules for multiplying and dividing negative and positive numbers:
- When you multiply or divide two positive numbers, the result is a positive number.
- Multiplying or dividing two negative numbers results in a positive number.
- Multiplying or dividing one positive and another negative number (in any order) results in a negative number.
The main property of a fraction: the numerator and denominator of a fraction can be multiplied or divided by the same number, not equal to zero, while the value of the fraction will not change. If we divide the numerator and denominator by some number, then this procedure is called fraction reduction. Multiplying the numerator and denominator by the same number is commonly used to reduce multiple fractions to the same (common) denominator. Note that in the record of an ordinary fraction (i.e., in a fraction with a bar): the numerator is at the top and the denominator is at the bottom.
The smallest (best) common denominator of fractions is the smallest number that is divisible by all the denominators of the original fractions.
When performing addition or subtraction of fractions with the same denominators , it is necessary to add or subtract the numerators of these fractions, and write the result of this operation into the numerator, and rewrite the original denominator.
If necessary add or subtract fractions with different denominators , then they must first be reduced to a common denominator, and then add fractions with the same denominator.
For conversion of a fraction with an integer part to an improper fraction , you can use the following rule: multiply the integer part by the denominator and add the numerator to this product. We write the result in the numerator of the improper fraction, and leave the denominator unchanged.
For the reverse conversion of an improper fraction to a proper fraction with integer part do the following: First divide the numerator by the denominator. When you divide a larger number by a smaller one, you get an integer (whole part) and a remainder. The integer part is written before the fraction, the remainder of the division is written in the numerator, and the denominator is not changed.
For multiplication of fractions , the following rule is applied (the product of numerators is written in the numerator, and denominators in the denominator), while both fractions must be reduced to the wrong form, i.
e. they do not have to have an entire part selected.
Division of fractions is done by replacing division with multiplication. Namely: the fraction by which it is divided (the second fraction), is turned over, changing the numerator and denominator in places, and instead of the division sign, the multiplication sign is put. Then the multiplication is carried out in the usual way. Fractions again must be without an integer part. This rule can be written as a formula:
When dividing a fraction by , you need to represent the number as a fraction with a denominator of 1, and then perform the usual division of fractions using the previous property. This rule can also be represented as a formula:
If the division sign (two dots) is replaced by another fraction bar, then to perform the operation of dividing the fraction by a number, you just need to perform the reverse substitution, and then proceed as usual:
you need to act similarly, i.
e. replace the number with a fraction with a single denominator, and then perform standard actions in the usual way. Let's write the rules for dividing a number by a fraction in the form of formulas:
In order to multiply the number by the sum in brackets or vice versa, you need to multiply this number by each term in brackets and add the results. This rule is true for any number of terms in the bracket. In the form of formulas, this rule can be written as follows:
This rule is also valid for any number of terms in brackets. Let's write an example of such an operation in the form of a formula:
If, when multiplying a bracket by a number or when multiplying a bracket by a bracket, there are minuses in one of the brackets, then you just need to consider each number together with the sign that precedes it, and carefully perform multiplication and further summation according to all the rules.
Performing ordinary calculations with a large number of operations:
- first perform operations in brackets;
- then count products and/or divisions;
- is then summed up or subtracted;
- and lastly, if it was a multi-storey fraction, they divide the already completely simplified numerator by the also completely simplified denominator.
Moreover, when performing operations in brackets in the first place, they also follow the same sequence, first products or divisions inside brackets, then summation or subtraction in brackets, and if there is another bracket inside the bracket, then the actions in it are performed first of all.
The monomial is the product of some negative or positive number by one or more variables in different powers. Polynomial is the sum (or difference) of monomials.
Similar terms in a polynomial are such terms-monomials in which the combination of variables and their degrees is completely repeated, while the numbers of these monomials may be different. Thus, like terms of a polynomial are such monomials that can be added, usually you need to do this, and the procedure for adding all kinds of like terms is called reducing like terms.
The solution to the simplest linear equation is as follows:
Algorithm for solving linear equations:
- Expand all brackets.
- Move all terms with a variable to the left of the equal sign, and all terms without a variable to the right of the equal sign, remembering to change the signs in front of the terms when moving.
- List all similar terms on the left and right. We get an equation of the form: ax = b .
- Find the answer by division like: x = b / a .
When solving linear inequalities there is only one big trick: you need to change the inequality sign when dividing (or multiplying) the inequality by a negative number. To change the inequality sign means to change the sign "less than" to the sign "greater than" or vice versa. At the same time, the plus signs for minus, bypassing the previously studied mathematical rules, do not need to be changed anywhere. If we divide or multiply the inequality by a positive number, the inequality sign does not need to be changed. Otherwise, the solution of linear inequalities is completely identical to the solution of linear equations.
The main property of the proportion:
Reduced multiplication formulas
To the table of contents...
When performing various algebraic transformations, it is often convenient to use the reduced multiplication formulas. Often these formulas are used not so much to shorten the multiplication process, but rather to understand from the result that it can be represented as a product of some factors. Thus, these formulas need to be able to apply not only from left to right, but also from right to left. We list the basic formulas for abbreviated multiplication. Sum squared:
Square of differences:
Square difference:
Cubate difference:
Cuba summation:
Cubes of the sum:
9000 often convenient to use in the form:
Quadratic equation and the formula for factoring a quadratic trinomial
0004
Let the square equation have the form:
Then Discriminant are found according to the formula:
If D > 0, then The square equation has two roots that are found according to formulas :
9000if D = 0, then the quadratic equation has one root (its multiplicity: 2), which is searched for by the formula :
In the case when the quadratic equation has two roots, the corresponding a quadratic trinomial can be factored using the following formula :
Only in the case of if the quadratic equation has two roots (i.
e. the discriminant is strictly greater than zero) is Vieta's theorem true. According to Vieta's Theorem, the sum of the roots of the quadratic equation is:
The product of the roots of a square equation can be calculated by the formula:
Parabola
To be tableties ...
Parabilac schedule is set quadratic function:
A quadratic function, like any other function, crosses the function, crosses it, crosses axis OX at the points that are its roots: ( x 1 ; 0) and ( x 2 ; 0). If there are no roots, then the quadratic function is axis OX does not intersect, if the root is one, then at this point ( x 0 ; 0) the quadratic function only touches the axis OX , but does not intersect it. The quadratic function always intersects the OY axis at the point with coordinates: (0; c ). The graph of a quadratic function (parabola) may look like this (in the figure, examples that far from exhaust all possible types of parabolas):0519 a > 0, in the function y = ax 2 + bx + c , then the branches of the parabola are directed upwards;
Parabola vertex coordinates can be calculated using the following formulas. X of the vertex of the parabola (or the point at which the square trinomial reaches its maximum or minimum value):
Y of the vertex of the parabola or the maximum if the parabola branches are directed downwards ( a < 0), or the minimum if the parabola branches are directed upwards ( a > 0), the value of the square trinomial:
Basic properties of powers
Table of contents...
A formal definition of a natural degree can be given using the following notation:
Mathematical degrees have several important properties, we list them. When multiplying powers with the same base, the exponents add up:
When dividing powers with the same bases, the exponent of the divisor is subtracted from the exponent of the dividend:
multiply the numbers, and then raise the product to that power.
The reverse procedure is also possible, if there is a product in a power, then each of the multiplied ones can be raised to this power separately, and the results can be multiplied:
Also, if you divide numbers with the same power but different base, you can first divide the numbers and then raise the quotient to this power (the reverse procedure is also possible):
a number to the power of zero equals one.
- Zero to any positive ( n > 0) degree is equal to zero. Remember: zero cannot be raised to a negative or zero power.
The main property of a negative degree is written as follows:
The main properties of mathematical roots To represent the mathematical root as a power, use the following formula:
The square root of is the mathematical root of the second degree:
The square root can only be taken from a non-negative number.
Learn more
