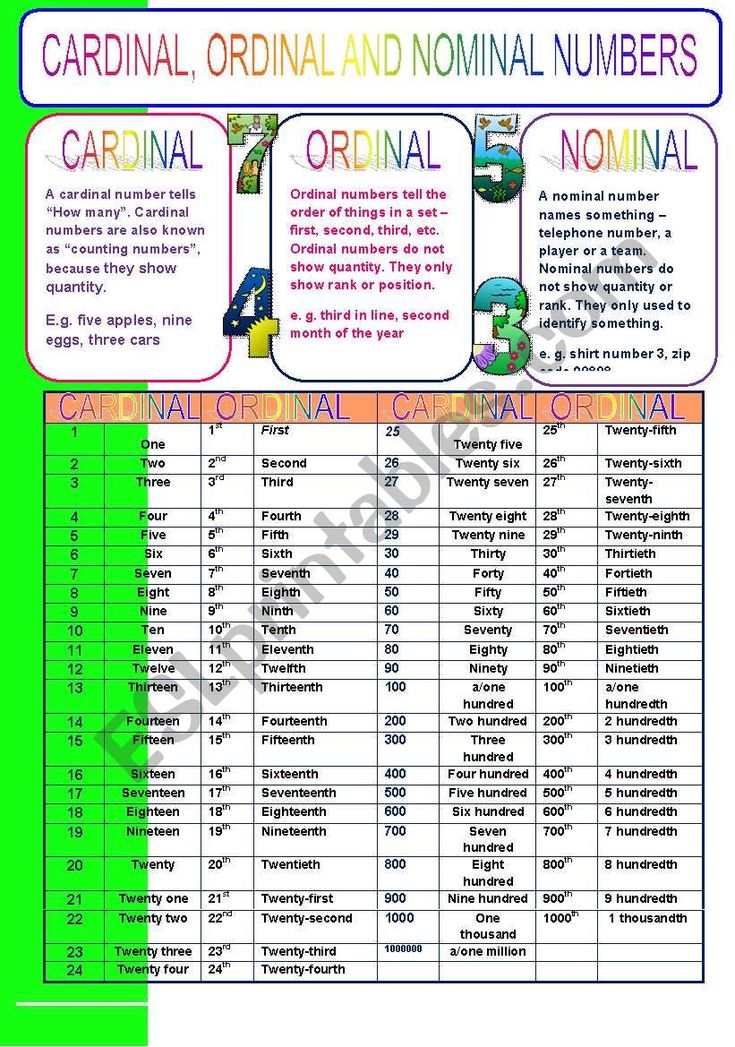
Cardinal numbers math
Cardinal Numbers - Meaning, Examples, Sets
Cardinal numbers are numbers that are used for counting. They are also known as natural numbers or cardinals. A set of cardinal numbers starts from 1 and it goes on up to infinity. We use cardinal numbers to answer the question "how many?". For example, how many students are going to the school picnic? The answer could be any number like 20, 23, 30, etc. So, all these numbers come in the category of cardinal numbers. In this article, we will explore the world of cardinal numbers and understand the difference between cardinal and ordinal numbers.
| 1. | What are Cardinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Cardinal Numbers from 1 to 100 |
| 4. | Cardinal Numbers of a Set |
| 5. | FAQs on Cardinal Numbers |
What are Cardinal Numbers?
A cardinal number describes or represents how many of something are present. Example 2 apples, 5 flowers, etc. It quantifies an object. It does not have values as fractions or decimals. Cardinal numbers are counting numbers, they help to count the number of items. Let's have a look at cardinal numbers examples. Ana wants to count the number of people standing in a queue at a billing counter. Can you help her? Ana started to count using Natural numbers.
Ana counted 1, 2, 3, 4, and 5. There are 5 people standing in a queue at the billing counter. Counting numbers are cardinal numbers! Now, Let's consider another example, Noah kept eight apples in a basket. The number eight denotes how many apples are there in the basket, irrespective of their order.
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on. The smallest cardinal number is 1 as 0 is not used for counting, so it is not a cardinal number.
Difference Between Cardinal and Ordinal Numbers
All the natural numbers are also referred to as cardinal numbers.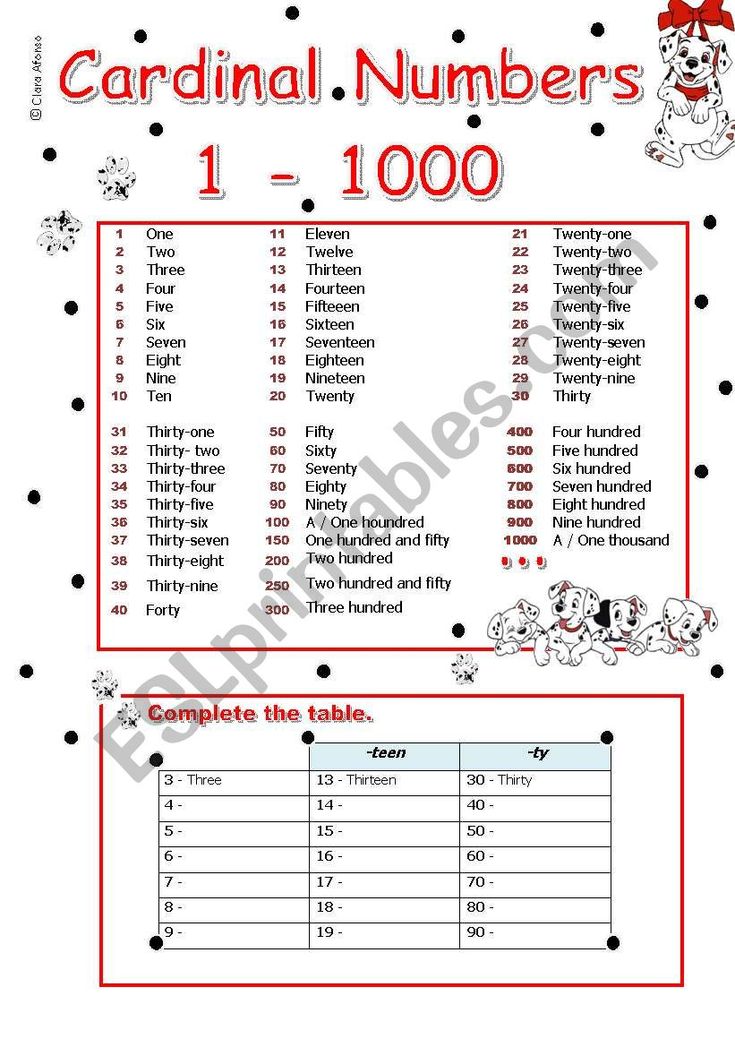
Cardinal numbers are used for counting. While an ordinal number is a number that denotes the position or place of an object. Example: 1st, 2nd, 3rd, 4th, 5th, etc. Ordinal numbers are used for ranking. Here is an example that explains cardinal and ordinal numbers:
In the above image, we can see a team of 4 workers on the construction site. This is an example of cardinal numbers.
In the above image, we can see the position of the runners in the running event. First, second, third, and so on. This is an example of ordinal numbers. Let's discuss ordinal and cardinal number differences in the table below:
| Cardinal Numbers | Ordinal Numbers |
|---|---|
| They are counting numbers that represent quantity. | They are based on the rank or position of an object in a given list or order. |
Cardinal numbers give us the answer of 'how many?'. |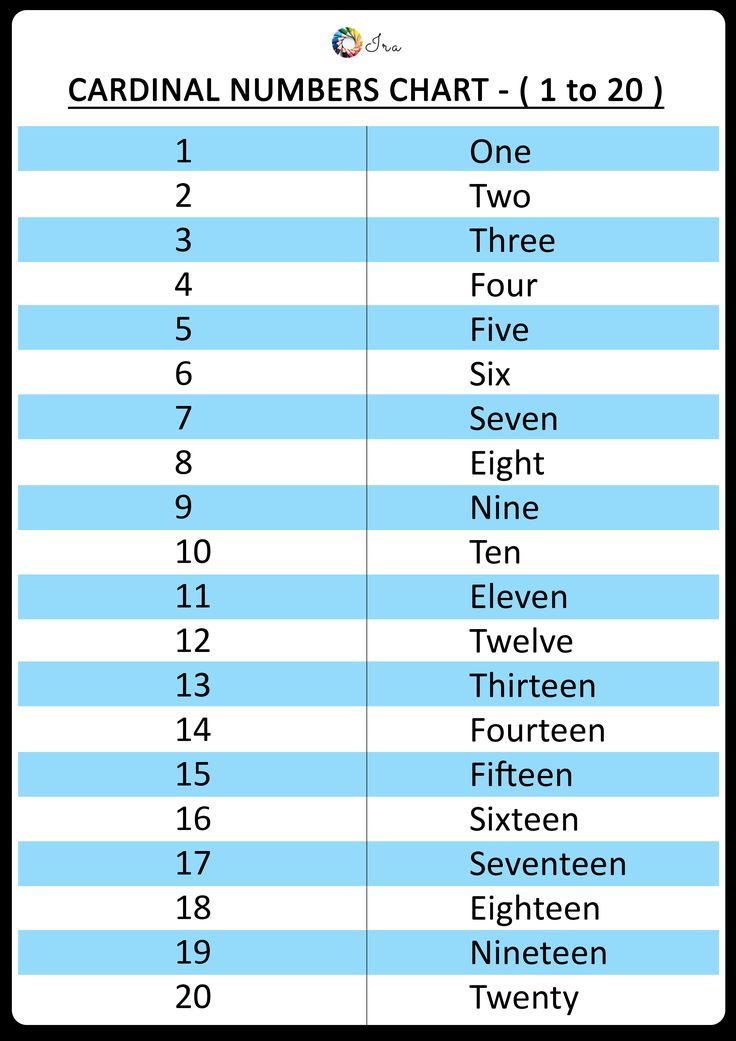
Ordinal numbers give us the answer of 'where'. For instance, where does the object lies in the list? |
| Examples are 1, 2, 3, 4, 5, 10, etc. | Examples are 1st, 2nd, 3rd, 4th, 5th, 10th, etc. |
List of Cardinal Numbers from 1 to 100
Given below are the basic and most important cardinal numbers, which form the base for other counting numbers.
| 1 - One | 6 - Six |
| 2 - Two | 7 - Seven |
| 3 - Three | 8 - Eight |
| 4 - Four | 9 - Nine |
| 5 - Five | 10 - Ten |
| 10 - Ten | 60 - Sixty |
| 20 - Twenty | 70 - Seventy |
| 30 - Thirty | 80 - Eighty |
| 40 - Forty | 90 - Ninety |
| 50 - Fifty | 100 - Hundred |
Given below is the list of all cardinal numbers from 1 to 100.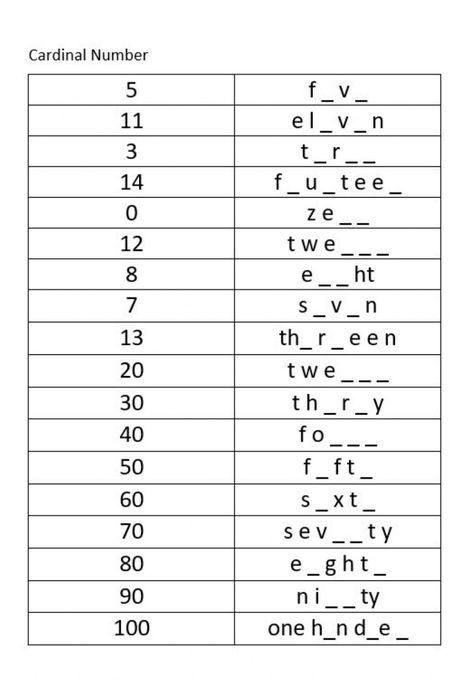
It will also help you to see how we write cardinal numbers in words like 21- twenty-one.
Cardinal Numbers of a Set
In the case of a set, the cardinal number is the total number of elements present in it. In other words, the number of distinct elements present in a set is the cardinal number of the set. The cardinal number of a set A is represented as n(A). For example, the cardinal number of set W = {1, 3, 5, 7, 9} is n(W)=5, as there are 5 elements in it.
Think Tank:
- Maria wrote January 1, 2020, as today’s date in her notebook. Does the number 1 in the date, represent a cardinal number?
- There are _______ people in the line ahead of me. I am the 7th person in the line.
Important Notes:
- Cardinal numbers help us to count the number of things or people in or around a place or a group.
- The collection of all the ordinal numbers can be denoted by the cardinal.
- Cardinal numbers can be written as words such as one, two, three, etc.
- Cardinal numbers tell how many items, whereas ordinal numbers show position or ranking.
Related Articles
Check out these interesting articles to know more about cardinal numbers and its related articles.
- Ordinal Numbers
- Whole Numbers
- Natural Numbers
- Difference Between Natural and Whole Numbers
Cardinal Numbers Examples
-
Example 1: Kate has a list of numbers as shown - 7, 8th, 10, Two, Fourth, 2nd. Identify the cardinal numbers.
Solution:
7, 10 and two help us in counting, whereas 8th, fourth and 2nd helps us in identifying the position. Thus, 7, 10, and two are cardinal numbers.
-
Example 2: Help Ryan, to calculate the number of vowels in "NUMBERS".
Also, identify the number of alphabets used to form this word.Solution:
(i) We know that a, e, i, o, and u are the vowels and in the given word u and e are used. Therefore, 2 vowels are used to form this number (2 is the required cardinal number).
(ii) We start counting from N to S, we see that "Numbers" has 7 alphabets in all. Therefore, a total of 7 alphabets are required to form the given word and here 7 is a cardinal number.
go to slidego to slide
Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations with Cuemath.
Book a Free Trial Class
Practice Questions on Cardinal Numbers
go to slidego to slidego to slide
FAQs on Cardinal Numbers
What is a Cardinal Number Example?
Cardinal numbers are used for counting. Some examples of cardinal numbers are 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 100, etc.
In our daily life, we use cardinal numbers a lot. Even a small child uses this mathematical concept without knowing the term for it. They do count how many toys they have, how many people are there around them, how many friends they have, how many subjects do they study at school, etc.
What is the Smallest Cardinal Number?
The smallest cardinal number is 1 (one) as whenever we count, we always start from 1.
How do you Find Cardinal Numbers?
Cardinal numbers can be found by counting. We start by 1 and then go on as per the number sequence.
How is Cardinal Number Different from the Ordinal Number?
Cardinal numbers are numbers that represent the number of items(quantity) while ordinal numbers represent the rank or position of an item in the given list.
What is a Cardinal Number in Sets?
In set A, if there are a total of 25 elements then 25 is the cardinal number of set A represented by n(A).
Can Cardinal Numbers Negative?
No, cardinal numbers cannot be negative.
They are positive integers or natural numbers, as we always count the number of items starting from number 1, and then it goes up to infinity.
Is Zero a Cardinal Number?
No, 0 is not a cardinal number as cardinal numbers represent quantity, and 0 means nothing or no quantity.
What is the Biggest Cardinal Number?
There are infinite natural numbers. Therefore, there are as many cardinal numbers as natural numbers. There can be no generalization of the biggest natural number and so does for the biggest cardinal number.
Cardinal numbers
A cardinal number is a natural number that is used to represent how many of something there are in a group. Cardinality is studied as a part of set theory.
Given a set of objects, A, the cardinal number of the set, n(A), is the number of elements in the set. Given the set A = {1, 2, 3}, there are 3 elements, so the cardinal number is n(A) = 3. Another way to say this is that the cardinality of the set is 3.
Example
Given the following sets of numbers: {1, 2, 3}, {4, 5, 6}, {7, 8, 9}, {10, 11, 12}, determine the cardinality of each set.
Although the numbers in each set of numbers above are different, they all have the same cardinality: 3.
We can also count that there are 4 sets of 3 numbers; 4 is another cardinal number.
One real life example of a cardinal number is a team. A soccer team has 11 players on the field at any one time, a baseball team has 9, and so on. Players on the team may have the jersey numbers 11 and 9, but those numbers wouldn't be considered cardinal numbers, because they aren't actually counting anything, and are instead used as identification; these types of numbers are known as nominal numbers.
Properties of cardinal numbers
Cardinal numbers are used for counting, so fractions, decimals, negative numbers, etc., are not considered cardinal numbers, only natural numbers. Also, the cardinality of a set can only be determined if the set is finite, since the cardinality is dependent on the number of elements in the set; a set with infinite elements cannot be counted, so we cannot find the cardinality of an infinite set.
0 is also not included in the cardinal numbers. If a given set is empty, or A = {}, the cardinality of the set is 0.
Cardinal arithmetic follows many of the same rules and shares a number of properties of arithmetic operations with natural numbers. For example, cardinal addition is also associative and commutative. Cardinal multiplication also follows the respective rules for associativity and commutativity in ordinary multiplication.
There are various other properties of cardinal numbers, these are just a few.
Cardinal, ordinal, and nominal numbers
These three types of numbers are often discussed together since it is necessary to understand them in order to effectively communicate using numbers. Briefly, a nominal number differs from a cardinal number in that nominal numbers are only used for identification purposes, typically to distinguish elements within a set of similar objects. They do not represent a count of something as cardinal numbers do.
Ordinal numbers, unlike cardinal or nominal numbers, tell us something about order, rank, or position.
They can be identified by using terms such as first, second, third, and fourth to represent the cardinal numbers 1, 2, 3, and 4.
As an example that includes the use of all three types of numbers, imagine that there are 15 people running in a race. 15 is a cardinal number. The participants in the race are assigned the numbers 1-15 depending on when they registered for the race. Their respective numbers are nominal numbers. Only the three people who finish the race fastest get a prize based on whether they ranked first, second, or third. First, second, and third are ordinal numbers.
Ordinal and Quantity of a Number
- Previous
- Back to index
- Next
Main page => library => table of contents
In the older group, children begin to learn for the first time to use ordinal numbers. In everyday life, five-year-old children, although they use ordinal numbers, often use them incorrectly, replacing cardinal numbers with them.
Therefore, it is necessary to reveal the meaning of ordinal numbers. To reveal the ordinal value of a number allows its comparison with a quantitative value. When they want to know how many objects, they count them: one, two, three, four, etc., i.e., counting like this, they find the answer to the question how many? But when you need to find the order, the place of the subject among others, they think differently. Answering questions which? what number?, count: first, second, third, etc.
Children often confuse questions which? and which? The latter requires the selection of the qualitative properties of objects: color, size, etc. How much alternation of questions? which the? what's the score? which? reveals their meaning.
Children have been shown more than once that to answer the question, how much? it doesn't matter what order the items are counted in. Now they will learn that in order to determine the ordinal place of an object among others, the direction of the count is essential.
The teacher demonstrates this by counting the same objects in different directions. He finds out, for example, that among 7 flags, blue is in 5th place, if counted from left to right, and if counted from right to left, then he is in 3rd place. Children try to determine the place of an object among others by counting in different directions. They conclude that when determining in what place the object is, it is necessary to indicate the direction of the account (third from the left, fifth from the right, etc.).
First, homogeneous objects that differ in color or size are used as counting material, for example, multi-colored flags or circles, Christmas trees of different heights, etc. . In ordinal counting, children are also trained on plotless material, for example, on models of geometric figures, stripes of different sizes, etc. place?"), arrange the items in the order indicated.
Some children, when determining the place of an object, replace ordinal numbers with quantitative ones.
The teacher listens to how the children keep score and points out mistakes. The so-called combined exercises are especially effective, in which the ordinal count is combined with the comparison of two or more sets of objects, the grouping of geometric shapes, and the ordering of objects by size.
Teaching ordinal counting is the main task of 3-4 lessons, in the future, ordinal counting skills are consolidated in the course of working on new material.
HP Metlin. Mathematics in kindergarten. Moscow: Education, 1984.
Main page => library => table of contents
L.S. Metlin. Mathematics in kindergarten. M.: Enlightenment, 1984.
Add to bookmarks:
- Previous
- Back to index
- Next
See also:
- ORIENTATION IN SPACE
- SHAPE
- SAMPLE LESSON
- DIVISION OF THE WHOLE INTO PARTS
- COMPOSITION OF A NUMBER OF 2 NUMBERS LESS THAN THIS NUMBER
- EXERCISES IN MEMORIZING NUMBERS
- SHAPE
- QUANTITY
- TIME ORIENTATION
- VALUE
Natural numbers: definition, examples, properties
Definition of a natural number
Natural numbers are numbers that we use to count something specific, tangible.
These are the natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, etc.
ascending order. The first hundred can be viewed in the table.
| Singularities of natural numbers |
|---|
|
What operations are possible on natural numbers
Sign up for math courses for students from grades 1 to 11!
Mathematics Demo Lesson
Find out which topics are “lame” for you, and then analyze them without cramming formulas and boring lectures.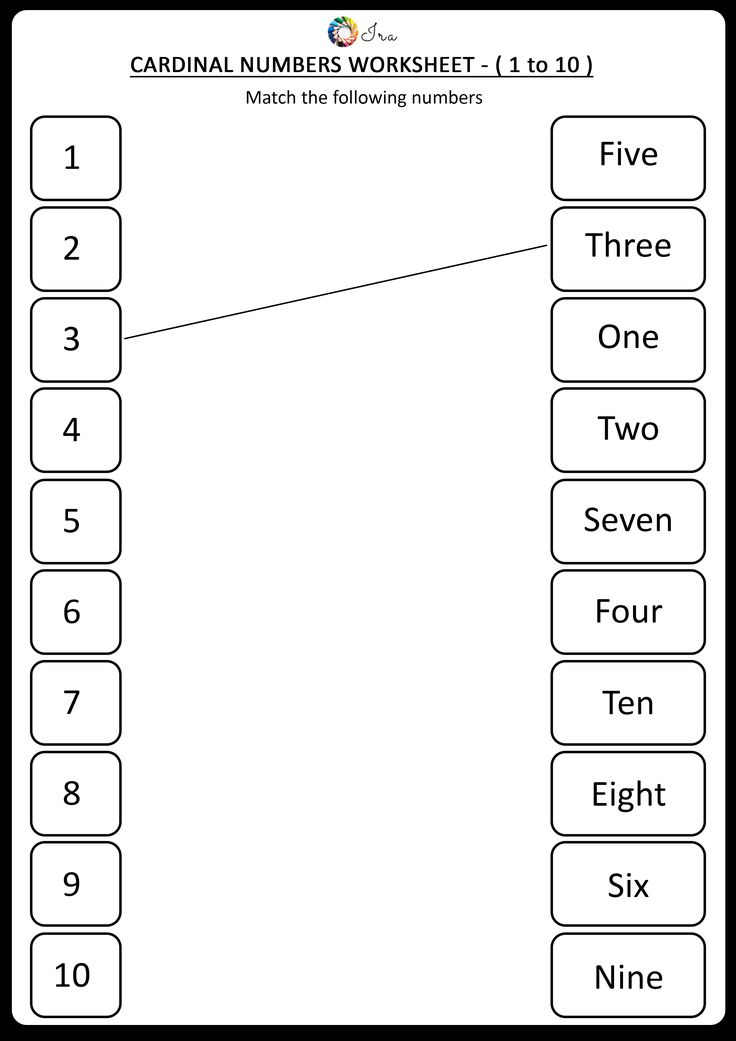
Decimal notation of a natural number
At school we go through the topic of natural numbers in the 5th grade, but in fact, a lot of things can be intuitively clear to us even earlier. Let's talk about important rules.
We regularly use numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. When writing any natural number, you can use only these digits without any other symbols. We write the numbers one by one in a line from left to right, using the same height.
Examples of correct writing of natural numbers: 208, 567, 24, 1467, 899112. These examples show us that the sequence of numbers can be different and some can even be repeated.
077, 0, 004, 0931 are examples of incorrect notation of natural numbers, because zero is on the left. The number cannot start from zero. This is the decimal representation of a natural number.
Quantitative meaning of natural numbers
Natural numbers carry a quantitative meaning, that is, they act as a tool for numbering.
Imagine that we have a banana 🍌 in front of us. We can record that we see 1 banana. In this case, the natural number 1 is read as "one" or "one".
But the term "unit" has another meaning: that which can be considered as a whole. An element of a set can be denoted by a unit. For example, any tree from a set of trees is a unit, any leaf from a set of leaves is a unit.
Imagine that we have 2 bananas 🍌🍌 in front of us. The natural number 2 is read as "two". Further, by analogy:
| 🍌🍌🍌 | 3 items ("three") |
| 🍌🍌🍌🍌 | 4 items (“four”) |
| 🍌🍌🍌🍌🍌 | 5 items ("five") |
| 🍌🍌🍌🍌🍌🍌 | 6 items (“six”) |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 items ("seven") |
| 8 items ("eight") | |
| 9 items ("nine") |
The main function of a natural number is to indicate the number of objects.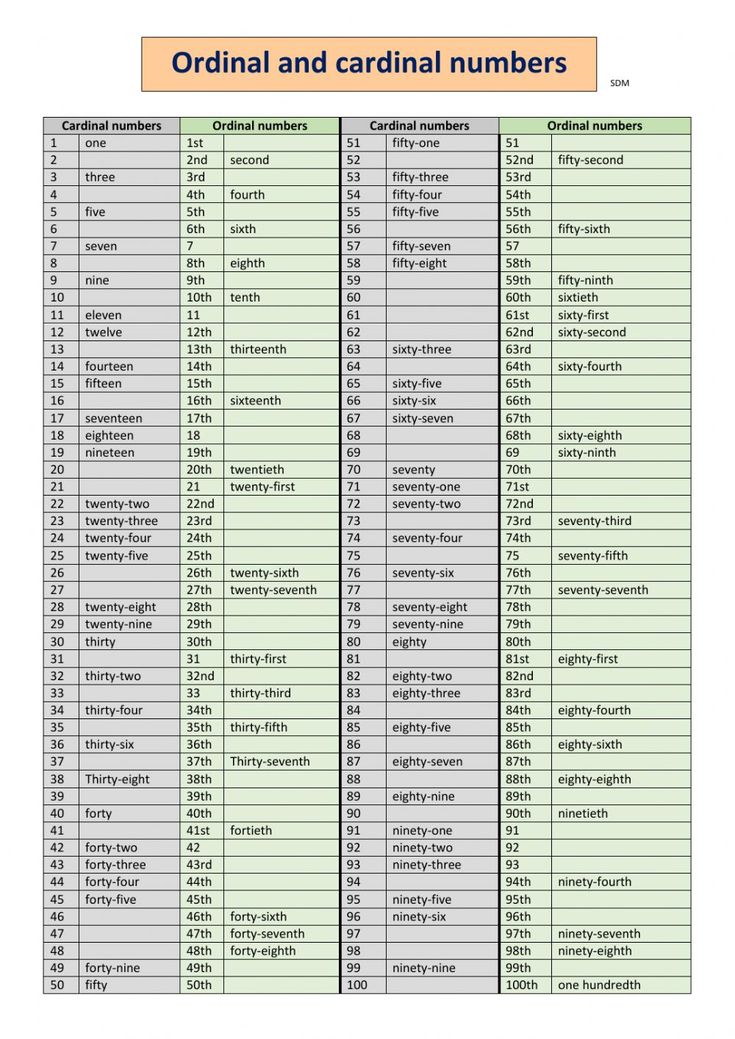
If the entry of a number matches the number 0, then it is called "zero". Recall that zero is not a natural number, but it can mean the absence. Zero items means none.
Free English lessons with native speaker
Practice 15 minutes a day. Learn English grammar and vocabulary. Make language a part of life.
One-digit, two-digit and three-digit natural numbers
One-digit natural number is such a number, which consists of one sign, one digit. Nine single-digit natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Two-digit natural numbers are those that include two signs, two digits. The numbers may be repeated or different. For example: 88, 53, 70.
If the set of objects consists of nine and one more, then we are talking about 1 dozen (“one dozen”) objects. If one ten and one more, then we have 2 dozen (“two tens”) and so on.
Basically, a two-digit number is a set of single-digit numbers, where one is written on the right and the other on the left.
The number on the left shows the number of tens in the natural number, and the number on the right shows the number of ones. There are 90 two-digit natural numbers in total.
Three-digit natural numbers - numbers, which include three characters, three digits. For example: 666, 389, 702.
One hundred is a set of ten tens. One hundred and another hundred - 2 hundreds. Let's add another hundred - 3 hundreds.
This is how a three-digit number is written: natural numbers are written one after the other from left to right.
The rightmost single digit indicates the number of units, the next one indicates the number of tens, the leftmost one indicates the number of hundreds. The number 0 indicates the absence of units or tens. So 506 is 5 hundreds, 0 tens and 6 ones.
Four-digit, five-digit, six-digit and other natural numbers are defined in the same way.
Multi-digit natural numbers
Multi-digit natural numbers consist of two or more characters.
1,000 is a set with ten hundred, 1,000,000 is a thousand thousand, and one billion is a thousand million. A thousand million, just imagine! That is, we can consider any multi-valued natural number as a set of single-valued natural numbers.
For example, 2873206 contains: 6 ones, 0 tens, 2 hundreds, 3 thousand, 7 tens of thousands, 8 hundreds of thousands and 2 millions.
How many natural numbers are there?
One-digit 9, two-digit 90, three-digit 900, etc.
Properties of natural numbers
We already know about the features of natural numbers. And now we will tell you in detail about their properties:
| set of natural numbers | is infinite and starts from one (1) |
| each natural number is followed by another | it is more than the previous one by 1 |
| the result of dividing a natural number by one (1) | is itself a natural number: 5 : 1 = 5 |
| the result of dividing a natural number by itself | units (1): 6 : 6 = 1 |
| commutative law of addition | the sum does not change from the rearrangement of the places of the terms: 4 + 3 = 3 + 4 |
| combination law of addition | the result of adding several terms does not depend on the order of operations: (2 + 3) + 4 = 2 + (3 + 4) |
| commutative law of multiplication | the product will not change from permutation of the places of factors: 4 × 5 = 5 × 4 |
| combination law of multiplication | the result of the product of factors does not depend on the order of operations; you can at least like this, at least like that: (6 × 7) × 8 = 6 × (7 × 8) |
| distributive law of multiplication with respect to addition | to multiply the sum by a number, you need to multiply each term by this number and add the results: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| distributive law of multiplication with respect to subtraction | to multiply the difference by a number, you can multiply by this number separately reduced and subtracted, and then subtract the second from the first product: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| distributive law of division with respect to addition | to divide the sum by a number, you can divide each term by this number and add the results: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| distributive law of division with respect to subtraction | to divide the difference by a number, you can divide by this number first reduced and then subtracted, and subtract the second from the first product: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Digits of a natural number and the value of the digit
Recall that its value depends on the position on which the digit stands in the record of the number.
So, for example, 1123 contains: 3 units, 2 tens, 1 hundred, 1 thousand. At the same time, we can formulate it differently and say that in a given number 1123, the digit 3 is located in the units digit, 2 in the tens digit, 1 in the hundreds digit and 1 serves as the value of the thousands digit.
The digit is the position, the location of the digit in the record of a natural number.
Each digit has its own name. The most significant digits are always on the left, and the least significant ones are on the right. To remember faster, you can use a table.
The number of digits always corresponds to the number of digits in the number. This table contains the names of all digits for a number that consists of 15 characters. The following digits also have names, but they are used extremely rarely.
The lowest (lowest) digit of a multi-digit natural number is the units digit.
The highest (highest) digit of a multi-digit natural number is the digit corresponding to the leftmost digit in the given number.
You must have noticed that textbooks often put small spaces when writing multi-digit numbers. This is done so that natural numbers are easy to read. And also to visually separate different classes of numbers.
Class is a group of digits that contains three digits: units, tens and hundreds.
Decimal
People at different times used different methods of writing numbers. And each number system has its own rules and features.
Decimal number system is the most common number system in which ten digits are used to write numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
In the decimal system, the value of one and of the same digit depends on its position in the number entry.
