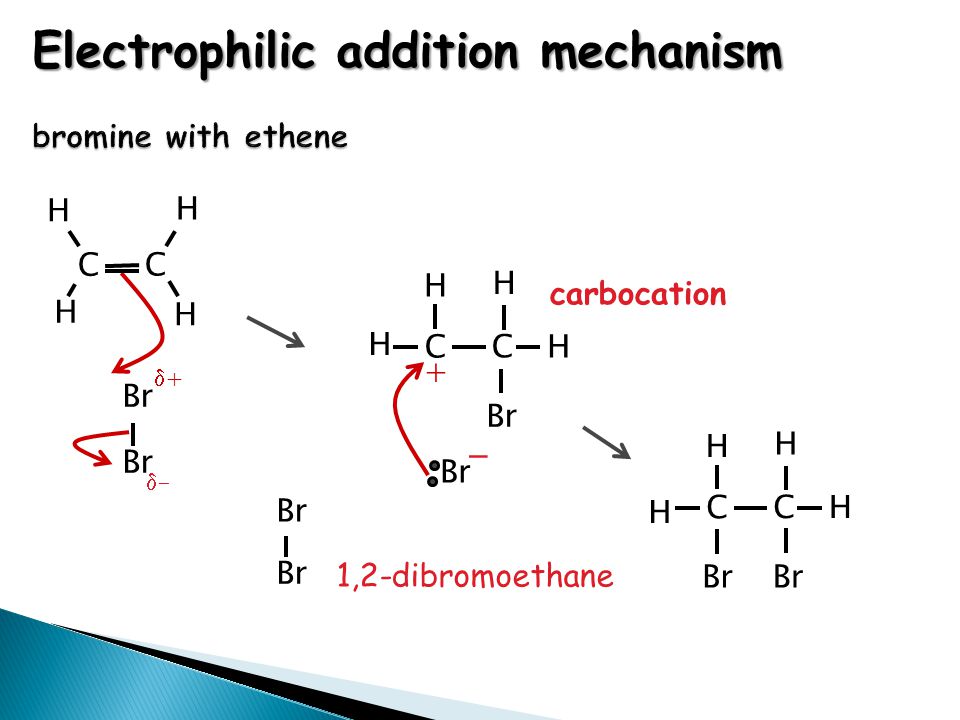
Concept of addition
What is Addition? Definition, Formula, Properties & Examples
What Is Addition?
Addition is a way of combining things and counting them together as one large group.
Addition in math is a process of combining two or more numbers. Addends are the numbers added, and the result or the final answer we get after the process is called the sum. It is one of the essential mathematical functions we use in our everyday activities. There are many situations in which we use to add numbers. One of the most common everyday uses for adding numbers is when we work with time or money—for example, adding up bills and receipts.
The addition symbol used to indicate adding numbers is “+” (also called the plus symbol). For example, we read $5 + 3$ as “5 plus 3”.
An addition sentence is a mathematical expression that shows two or more values added together and their sum. The two or more values that are added are called addends. The parts of an addition sentence are two or more addends, plus symbol(s), equal sign, and the sum.
Solve Addition Problem
To add small numbers can be done using your fingers.
Example:
Using The Number Line
We can use the number line to add. Let us look at the following addition example.
To add 5 and 7, we can count forward 7 steps from 5, as shown below.
Using The Number Grid
Number chart is another way to add numbers.
Example: Add 57 and 16 using a hundred grid.
| Step 1: Locate the bigger number $(57)$. Step 2: If the number to be added $(16)$ is more than 10, break it into tens and ones. $16 = 10 + 6$. Step 3: Jump as many 10s as in the second number. $57 + 10 = 67$ Step 4: Move forward as many ones as in the second number. $67 + 6 = 73$. The number reached is the answer. So, $57 + 16 = 73$ |
Vertical Addition
While solving the problem, we can add the numbers vertically. Here, we arrange the numbers vertically using their respective place values, like ones, tens, hundreds, thousands, etc. We start adding from the right side (or digit at ones or unit place). While solving such problems, we may come across some cases with regrouping and some without regrouping. Let us understand with the help of examples.
Here, we arrange the numbers vertically using their respective place values, like ones, tens, hundreds, thousands, etc. We start adding from the right side (or digit at ones or unit place). While solving such problems, we may come across some cases with regrouping and some without regrouping. Let us understand with the help of examples.
Addition without Regrouping
Example: Add 41 and 26.
| Step 1: Write the numbers one below the other as per the places of the digits. | |
| Step 2: Start adding from the digits in ones place $(1 + 6 = 7)$. Write the sum under the ones digit. | |
| Step 3: Add the tens digits $(4 + 2 = 6)$. |
Addition with Regrouping
Example: Add 57 and 16
| Step 1: Write the numbers below the other as per the places of the digits. | |
Step 2: Start adding from the digits in ones place $(7 + 6 = 13)$. If the sum of the ones digit is greater than 9, write the ones digit of the sum under the ones and carry forward its tens digit to the tens column.
If the sum of the ones digit is greater than 9, write the ones digit of the sum under the ones and carry forward its tens digit to the tens column. | |
| Step 3: Add the tens digits. If there was a carry-forward digit, add it along. $5 + 1 + 1 $(carry$-$over) $= 7$ |
Fun Fact
- Adding zero to a number gives the number itself.
- Adding 1 to a number gives the successor of that number.
- Changing the order of the addends does not change the sum. For example, $5 + 3 + 2 = 5 + 2 + 3 = 10$
Solved Examples
Question 1: What is the sum of the first 10 odd numbers?
Answer:
The first ten odd numbers are $1, 3, 5, 7, 9, 11, 13, 15, 17, 19$.
The sum of the first ten odd numbers
$= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19$
$= 100$
Question 2: If a bag has 5 balls and 4 more balls are added to it, how many balls are there in the bag?
Answer:
Originally, there were 5 balls in the bag. Now 4 more balls have been added.
Now 4 more balls have been added.
The number of balls in this bag is now $5 + 4 = 9$.
Therefore, the bag has 9 balls.
Question 3: The present age of Manny is 7 years. What will be his age after 10 years?
Answer:
Current age of Manny is 7 years.
To find Manny’s age after 10 years, add 10 to his current age.
After 10 years, his age would be $7 + 10$ or 17 years old.
Question 4: Samantha bought a bag for $\$$214 and some books for $\$$149. How much did she spend on both?
Answer:
To find the total cost, add 214 and 149.
Thus, Samantha spent $\$$363 in all.
Conclusion
Adding numbers is a fundamental mathematical process that combines two or more numerical values. We use this operation in our daily lives; some easy examples are calculating money, calculating time, counting students in a class, etc. The symbol of this operation is a ‘+’ (plus sign). Visit SplashLearn to learn more math facts.
Visit SplashLearn to learn more math facts.
Practice Problems
1
Which of the following equations represents the total number of circles in the figure below?
$6 + 7 = 13$
$8 + 6 = 14$
$8 + 7 = 15$
$7 + 5 = 12$
Correct answer is: $8 + 7 = 15$
There are 8 green circles and 7 blue circles, So, there are $8 + 7 = 15$ circles in all.
2
What is the sum of 700 and 136?
636
664
736
836
Correct answer is: 836
Sum of 700 and 136 is $700 + 136$ or 836.
3
Find the value of 4 hundreds $+ 26$ tens?
426
606
660
4026
Correct answer is: 660
4 hundreds $+ 26$ tens $= 400 + 260 = 660$
4
Which of the following is the sum of the smallest and the greatest two-digit numbers?
19
99
100
109
Correct answer is: 109
Which of the following is the sum of the smallest and the greatest two-digit numbers?
Frequently Asked Questions
Why is addition important?
Adding numbers is a fundamental mathematical concept, essential for the simplest problems in our daily activities. One of the most common applications is when we work with money—for example, adding up bills and receipts.
One of the most common applications is when we work with money—for example, adding up bills and receipts.
What is addend?
Addend is the part of the statement where we add two numbers; an addend is defined as the value that is to be added to find a sum.
What is a sum?
A sum is a result when we add two or more numbers.
What is meant by addition with and without regrouping?
Addition without regrouping is when the sum of the digits in each place value column is less than or equal to 9. Addition with regrouping is when the sum of the digits in at least one of the place value columns is greater than 9.
Addition - Formula, Definition, Examples
Addition is the process of adding two or more items together. In math, addition is the method of calculating the sum of two or more numbers. It is a primary arithmetic operation that is used commonly in our day-to-day life. One of the most common uses of addition is when we work with money, calculate our grocery bills, or calculate the time.
One of the most common uses of addition is when we work with money, calculate our grocery bills, or calculate the time.
| 1. | What is Addition? |
| 2. | Parts of Addition |
| 3. | Addition Word Problems |
| 4. | FAQs on Addition |
What is Addition?
Addition is an operation used in math to add numbers. The result that is obtained after addition is known as the sum of the given numbers. For example, if we add 2 and 3, (2 + 3) we get the sum as 5. Here, we performed the addition operation on two numbers 2 and 3 to get the sum, i.e., 5
Addition Symbol
In mathematics, we have different symbols. The addition symbol is one of the widely used math symbols. In the above definition of addition, we read about adding two numbers 2 and 3. If we observe the pattern of addition (2 + 3 = 5) the symbol (+) connects the two numbers and completes the given expression. The addition symbol consists of one horizontal line and one vertical line. It is also known as the addition sign or the plus sign (+)
If we observe the pattern of addition (2 + 3 = 5) the symbol (+) connects the two numbers and completes the given expression. The addition symbol consists of one horizontal line and one vertical line. It is also known as the addition sign or the plus sign (+)
Parts of Addition
An addition statement can be split into the following parts.
- Addend: The numbers that are added are known as the addends.
- Addition Symbol: There is the addition symbol (+) which is placed in between the addends. If the statement is written horizontally as shown below, then we place an equal to sign (=) just before the sum is written.
- Sum: The final result obtained after adding the addends is known as the sum.
Addition Formula
The addition formula is the statement that shows an addition fact and is expressed as, addend + addend = sum.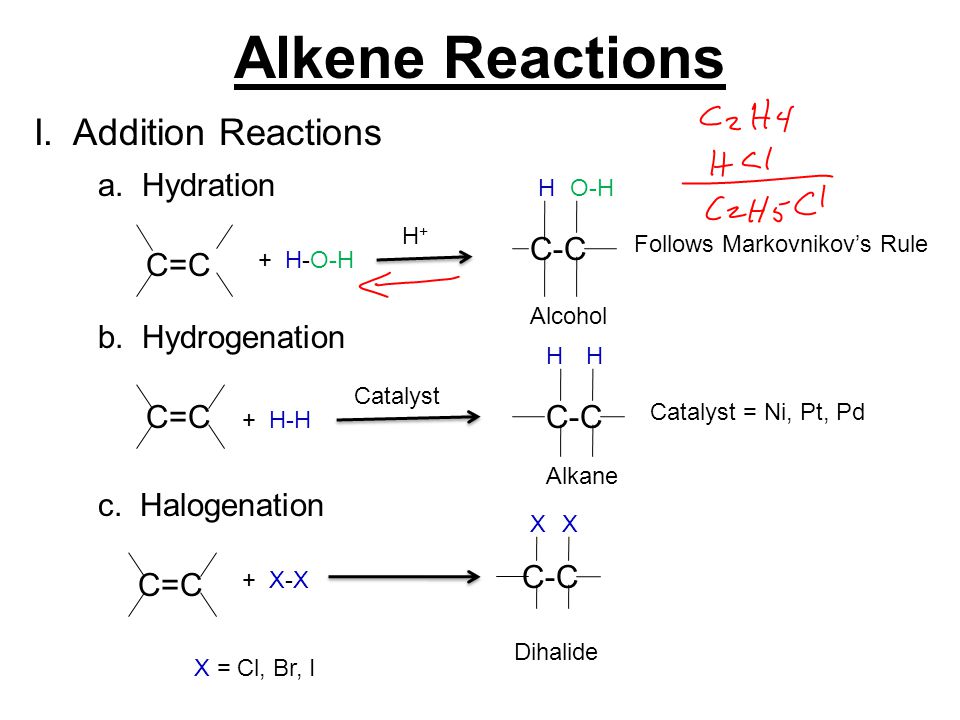 This can be understood with the help of the example shown in the figure given below. The basic addition formula or the mathematical equation of addition can be explained as follows.
This can be understood with the help of the example shown in the figure given below. The basic addition formula or the mathematical equation of addition can be explained as follows.
Here, 5 and 3 are the addends and 8 is the sum. It should be noted that there can be multiple addends in an addition fact. For example, 5 + 7 + 9 + 3 = 24.
How to Solve Addition Problems?
While solving addition problems, one-digit numbers can be added in a simple way, but for larger numbers, we split the numbers into columns using their respective place values, like ones, tens, hundreds, thousands, and so on. We always start doing addition from the right side as per the place value system. This means we start from the ones column, then move on to the tens column, then to the hundreds column and so on. While solving such problems we may come across some cases with carry-overs and some without carry-overs. Let us understand addition with regrouping and addition without regrouping using in the following sections.
Addition Without Regrouping
The addition in which the sum of the digits is less than or equal to 9 in each column is called addition without regrouping. Let us understand how to add two or more numbers without regrouping with the help of an example.
Example: Add 11234 and 21123
Solution: We will use the following given steps and try to relate them with the following figure.
- Step 1: Start with the digits in ones column. (4 + 3 = 7)
- Step 2: Move to the digits in tens column. (3 + 2 = 5)
- Step 3: Now add the digits in hundreds column. (2 + 1 = 3)
- Step 4: After this, add the digits in thousands column. (1 + 1 = 2)
- Step 5: Finally, add the digits in ten thousands column. (1 + 2 = 3)
- Step 6: 11234 + 21123 = 32357.
In addition without regrouping, we simply add the digits in each place value column and combine the respective sums together to get the answer.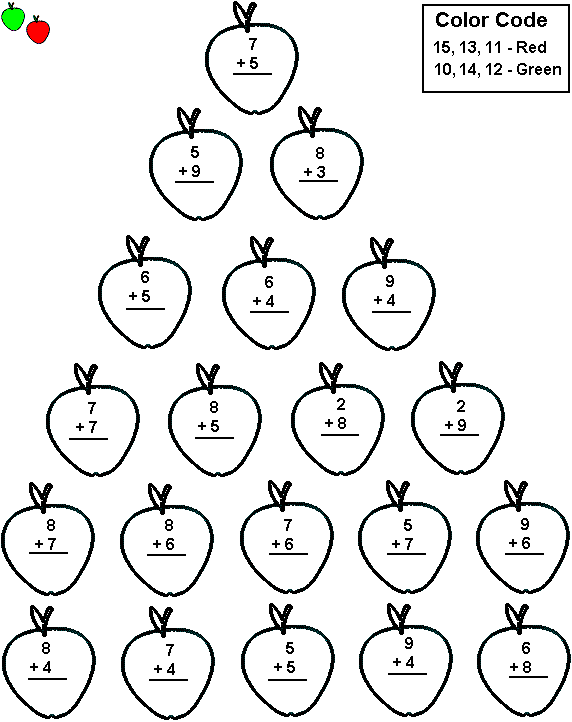 Now, let us understand addition with regrouping.
Now, let us understand addition with regrouping.
Addition With Regrouping
While adding numbers, if the sum of the addends is greater than 9 in any of the columns, we regroup this sum into tens and ones. Then we carry over the tens digit of the sum to the preceding column and write the ones digit of the sum in that particular column. In other words, we write only the number in 'ones place digit' in that particular column, while taking the 'tens place digit' to the column to the immediate left. Let us understand how to add two or more numbers by regrouping with the help of an example.
Example: Add 3475 and 2865.
Solution: Let us follow the given steps and try to relate them with the following figure.
- Step 1: Start with the digits in ones place. (5 + 5 = 10). Here the sum is 10. The tens digit of the sum, that is, 1, will be carried to the preceding column.
- Step 2: Add the digits in the tens column along with the carryover 1.
 This means, 1 (carry-over) + 7 + 6 = 14. Here the sum is 14. The tens digit of the sum, that is, 1, will be carried to the hundreds place.
This means, 1 (carry-over) + 7 + 6 = 14. Here the sum is 14. The tens digit of the sum, that is, 1, will be carried to the hundreds place. - Step 3: Now, add the digits in the hundreds place along with the carryover digit 1. This means, 1 (carry-over) + 4 + 8 = 13. Here the sum is 13. The tens digit of the sum, that is, 1, will be carried to the thousands place.
- Step 4: Now, add the digits in the thousands place along with the carryover digit 1, that is, 1 (carry-over) + 3 + 2 = 6
- Step 5: Therefore, the sum of 3475 + 2865 = 6340
Note: There is an important property of addition which states that changing the order of numbers does not change the answer. For example, if we reverse the addends of the above illustration we will get the same sum as a result (2865 + 3475 = 6340). This is known as the commutative property of addition.
Addition on Number Line
Another way to add numbers is with the help of number lines. Let us understand the addition on a number line with the help of an example and the number line given below. If we need to solve 10 + 3 we start by marking the number 10 on the number line. When we add using a number line, we count by moving one number at a time to the right of the number. Since we are adding 10 and 3, we will move 3 steps to the right. This brings us to 13. Hence, 10 + 3 = 13.
Addition Properties
While performing addition we commonly use the properties listed below:
- Commutative Property: According to this property, the sum of two or more addends remains the same irrespective of the order of the addends. For example, 8 + 7 = 7 + 8 = 15
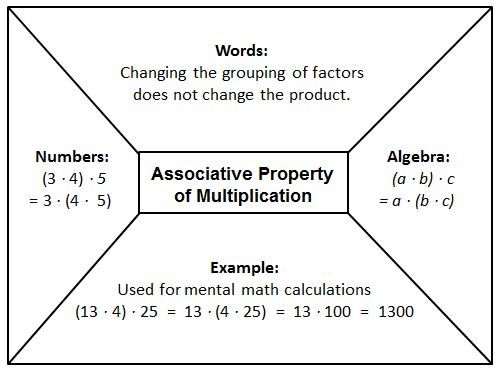
- Associative Property: According to this property, the sum of three or more addends remains the same irrespective of the grouping of the addends. For example, 5 + (7 + 3) = (5 + 7) + 3 = 15
- Additive Identity Property: According to this property of addition, if we add 0 to any number, the resultant sum is always the actual number.
 For example, 0 + 7 = 7.
For example, 0 + 7 = 7.
Addition Word Problems
The concept of the addition operation is used in our day-to-day activities. We should carefully observe the situation and identify the solution using the tips and tricks that follows addition. Let us understand how to solve addition word problems with the help of an interesting example.
Example: A soccer match had 4535 spectators in the first row and 2332 spectators in the second row. Using the concept of addition find the total number of spectators present in the match.
Solution:
The number of spectators in the first row = 4535; the number of spectators in the second row = 2332. We can get the total number of spectators if we add the given number of spectators in the two rows.
Here 4535 and 2332 are the addends. Let us find the total number of spectators by adding these two numbers using the following steps.
- Step 1: Add the digits in the ones place.
 (5 + 2 = 7)
(5 + 2 = 7) - Step 2: Add the digits in the tens place. (3 + 3 = 6)
- Step 3: Add the digits in the hundreds place. (5 + 3 = 8)
- Step 4: Now add digits in the thousands place. (4 + 2 = 6)
- Step 5: 4535 + 2332 = 6867
Therefore, the total number of spectators present in the match = 6867
Here are a few tips and tricks that you can follow while performing addition in your everyday life.
Tips and Tricks on Addition
- Words like 'put together, 'in all', 'altogether', 'total' give a clue that you need to add the given numbers.
- Start with the larger number and add the smaller number to it. For example, adding 12 to 43 is easier than adding 43 to 12.
- Break numbers according to their place values to make addition easier. For example, 22 + 64 can be split as 20 + 2 + 60 + 4. While this looks difficult, it makes mental addition easier.
- When adding different digit numbers, make sure to place the numbers one below the other in the correct column of their place value.
- Adding zero to any number gives the number itself.
- When 1 is added to any number, the sum is the successor of that number.
- The sign used to denote an addition is '+'
- The order in which you add a set of numbers doesn't matter, the sum remains the same. For example, 2 + 5 + 3 = 10; and 5 + 3 + 2 = 10. It is called the associative property of addition.
☛Related Links
- What is regrouping in math addition?
- Addition Calculator
- Addition of Algebraic Expressions
- Addition of Fractions
- Adding Decimals
FAQs on Addition
What is Addition in Math?
Addition is the process of adding two or more numbers together to get their sum. Addition in math is a primary arithmetic operation, used for calculating the total of two or more numbers. For example, 7 + 7 = 14.
Addition in math is a primary arithmetic operation, used for calculating the total of two or more numbers. For example, 7 + 7 = 14.
Where do we use Addition?
We use addition in our everyday situations. For example, if we want to know how much money we spent on the items we bought, or we want to calculate the time we would take to finish a task, or we want to know the number of ingredients used in cooking something, we need to perform the addition operation.
What are the Types of Addition?
The types of addition mean the various methods used in addition. For example, vertical addition, addition using number charts, the addition of small numbers using your fingers, addition using number line, and so on.
What are Addition Strategies?
Addition strategies are the different ways in which addition can be learned. For example, using a number line, with the help of a place value chart, separating the tens and ones and then adding them separately, and many others.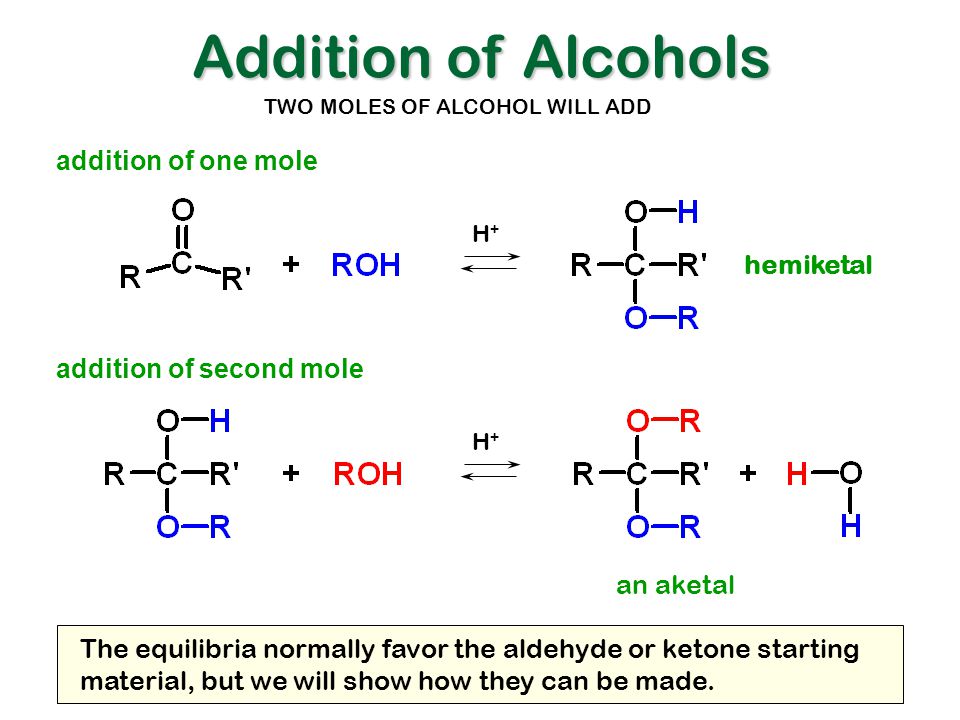
What are the Real-Life Examples of Addition?
There are many addition examples that we come across in our day-to-day lives. Suppose you have 5 apples, and your friend gave you 3 more, after adding 5 + 3, we get 8. So, you have 8 apples altogether. Similarly, suppose there are 16 girls and 13 boys in a class, if we add the numbers 16 + 13, we get the total number of students in the class, which is 29.
What are the Properties of Addition?
The basic properties of addition are given below. Each property has its individual significance based on addition.
- Commutative Property: According to this property, the sum of two or more addends remains the same even if the order of the addends changes. For example, 3 + 7 = 7 + 3 = 10
- Associative Property: According to this property, the sum of three or more addends remains the same irrespective of the grouping of the addends. For example, (8 + 7) + 2 = 8 + (7 + 2) = 17
- Additive Identity Property: According to this property of addition, if we add 0 to any number, the resultant sum is always the actual number.
 For example, 0 + 16 = 16.
For example, 0 + 16 = 16.
What are the Parts of Addition?
The different parts of addition are given below. Let us understand these parts with the help of an example. For example, let us take 4 + 7 + 2 = 13
- Addend: In addition, the numbers or terms that are added together are known as the addends. In this case, 4, 7, and 2 are the addends.
- Addition symbol (+) and the equal-to sign (=): The addition symbol is used in between the addends and the equal-to sign is placed just before the sum.
- Sum: The final result obtained after performing addition is known as the sum. Here, the sum is 13.
What is the Identity Property of Addition?
According to the identity property of addition, if 0 is added to any number, the resultant sum is always the actual number. For example, 0 + 16 = 16.
What is the Difference Between Addition and Subtraction?
Addition is a math operation in which we add the numbers together to get their sum.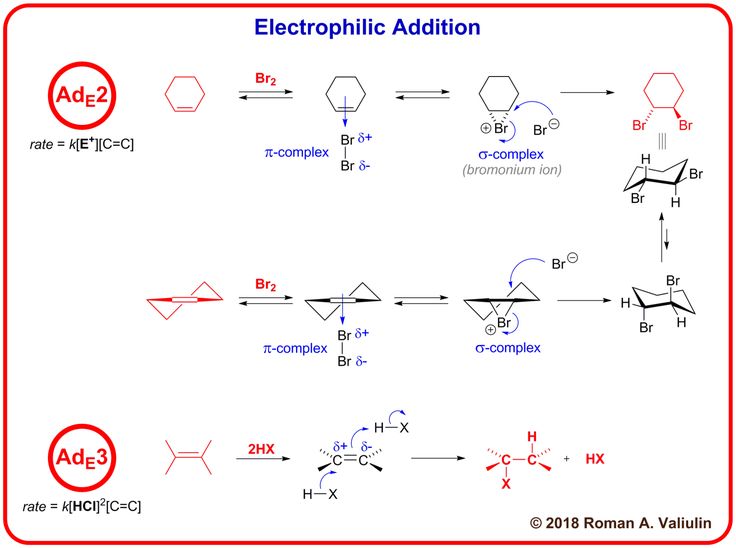 It is denoted by the addition symbol (+). For example, on adding 5 and 7 we get 12. This is represented as, 5 + 7 = 12. Subtraction is the arithmetic operation of calculating the difference between two numbers. It is denoted by the subtraction symbol (-). For example, if we subtract 8 from 19, we get 11. This is represented as 19 - 8 = 11.
It is denoted by the addition symbol (+). For example, on adding 5 and 7 we get 12. This is represented as, 5 + 7 = 12. Subtraction is the arithmetic operation of calculating the difference between two numbers. It is denoted by the subtraction symbol (-). For example, if we subtract 8 from 19, we get 11. This is represented as 19 - 8 = 11.
Textbook. Add parameters to a template - Azure Resource Manager
- Article
- Reading takes 5 minutes
In the previous exercise, you learned how to add an Azure storage account to a template and deploy it. In this tutorial, you'll learn how to enhance your Azure Resource Manager (ARM) template by adding parameters to it. This instruction will take about 14 minutes .
Prerequisites
We recommend that you follow the instructions in the resource tutorial, but this is not required.
You will need to install Visual Studio Code with the Resource Manager Tools extension, and either Azure PowerShell or the Azure Command Line Interface (Azure CLI). For more information, see the template tools section.
Template validation
At the end of the previous exercise, the template contained the following JSON file:
"$schema": "https://schema.management.azure.com/schemas/2019-04-01/deploymentTemplate.json#", "contentVersion": "1.0.0.0", "resources": [ { "type": "Microsoft.Storage/storageAccounts", "apiVersion": "2021-09-01", "name": "{provide-unique-name}", "location": "eastus", "sku": { "name": "Standard_LRS" }, "kind": "StorageV2", properties: { "supportsHttpsTrafficOnly": true } } ] } You may have noticed that there is a problem with this template. The storage account name is hardcoded. This template can only be used to deploy the same storage account each time.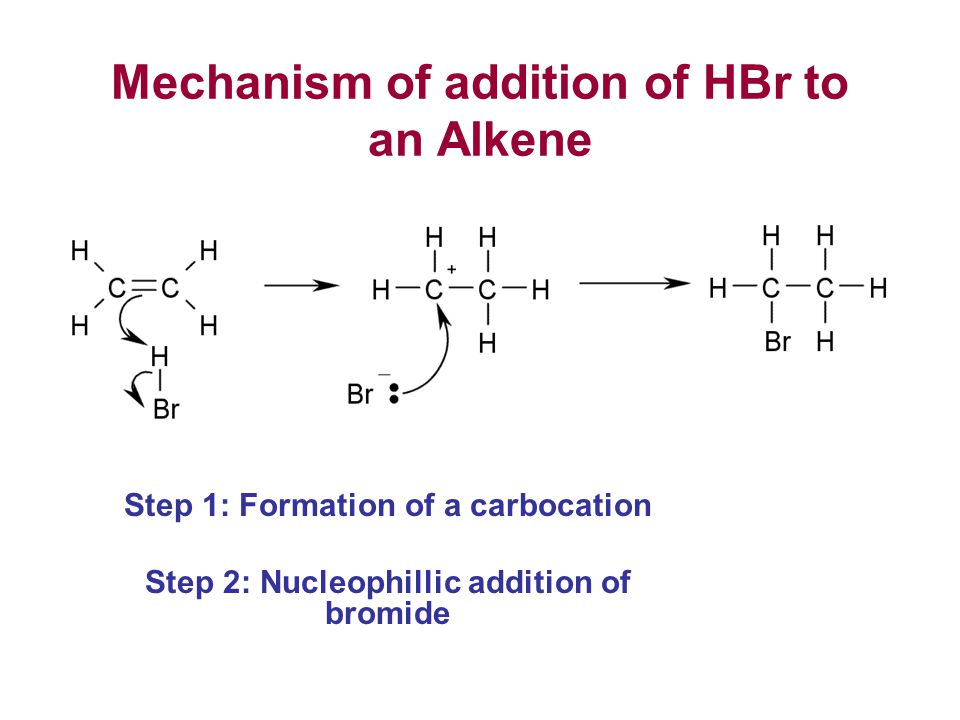 To deploy a storage account with a different name, you will need to create a new template. Obviously, this method is not suitable for automating deployments.
To deploy a storage account with a different name, you will need to create a new template. Obviously, this method is not suitable for automating deployments.
Change template for reuse
To make a template reusable, you need to add a parameter that you can use to pass the name of the storage account. The highlighted JSON file in the following example shows the changes to the template. Parameter storageName is defined as a string. The storage account name must contain only lowercase letters or numbers and is limited to 24 characters.
Copy the entire file and replace the template with its contents.
"$schema": "https://schema.management.azure.com/schemas/2019-04-01/deploymentTemplate.json#", "contentVersion": "1.0.0.0", "parameters": { "storageName": { "type": "string", minLength: 3 "maxLength": 24 } }, "resources": [ { "type": "Microsoft.Storage/storageAccounts", "apiVersion": "2021-09-01", "name": "[parameters('storageName')]", "location": "eastus", "sku": { "name": "Standard_LRS" }, "kind": "StorageV2", properties: { "supportsHttpsTrafficOnly": true } } ] } Deploying the template
Let's deploy the template. The following example deploys a template using the Azure CLI or PowerShell. Note that you specify the storage account name as one of the values in the deployment command. For the storage account name, enter the same name that you used in the previous tutorial.
The following example deploys a template using the Azure CLI or PowerShell. Note that you specify the storage account name as one of the values in the deployment command. For the storage account name, enter the same name that you used in the previous tutorial.
If you have not yet created a resource group, see this section. This example assumes that for variable templateFile is the path to the template file, as shown in the first tutorial.
- PowerShell
- Azure CLI
New-AzResourceGroupDeployment` -Name addnameparameter ` -ResourceGroupName myResourceGroup` -TemplateFile $templateFile` -storageName "{your-unique-name}" Resource refresh concept
After deploying a storage account with the same name as before, you might wonder how redeployment affects the resource.
If the resource already exists and there are no changes to the properties, no further action is required. If the resource exists and the property changes, it is updated. If the resource does not exist, it is created.
If the resource exists and the property changes, it is updated. If the resource does not exist, it is created.
This way of handling updates means that the template can include all the resources required by the Azure solution. You can safely redeploy the template and ensure that resources are only modified or created when necessary. If you have added files to your storage account, you can redeploy the storage account without losing those files.
Environment-specific customization
Parameters allow you to customize your deployment by providing values that are specific to your environment. You can pass different values, for example, depending on whether you are deploying a test/development environment or a production environment.
The previous template always deploys the standard redundant local storage (LRS) account Standard_LRS . You may need to be able to deploy different SKUs depending on your environment. The following example shows the changes to add a parameter for the SKU. Copy the entire file into a template.
Copy the entire file into a template.
"$schema": "https://schema.management.azure.com/schemas/2019-04-01/deploymentTemplate.json#", "contentVersion": "1.0.0.0", "parameters": { "storageName": { "type": "string", minLength: 3 "maxLength": 24 }, "storageSKU": { "type": "string", "defaultValue": "Standard_LRS", "allowedValues": [ "Standard_LRS", "Standard_GRS", "Standard_RAGRS", "Standard_ZRS", "Premium LRS", "Premium_ZRS", "Standard_GZRS", "Standard_RAGZRS" ] } }, "resources": [ { "type": "Microsoft.Storage/storageAccounts", "apiVersion": "2021-09-01", "name": "[parameters('storageName')]", "location": "eastus", "sku": { "name": "[parameters('storageSKU')]" }, "kind": "StorageV2", properties: { "supportsHttpsTrafficOnly": true } } ] } Parameter storageSKU has a default value.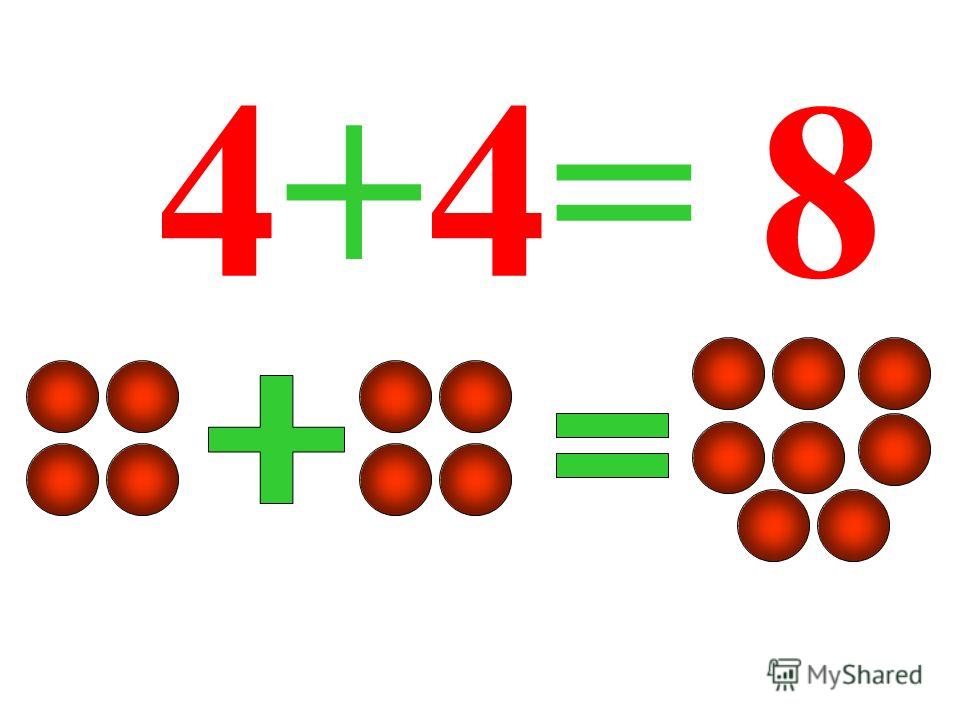 Use this value if it is not specified in the deployment. It also contains a list of valid values. They correspond to the values required to create a storage account. You want template users to pass in SKUs that work.
Use this value if it is not specified in the deployment. It also contains a list of valid values. They correspond to the values required to create a storage account. You want template users to pass in SKUs that work.
Redeploy the template
Now you are ready to redeploy. Because the default SKU is Standard_LRS , you've already provided a value for the parameter.
- PowerShell
- Azure CLI
New-AzResourceGroupDeployment` -Name addskuparameter ` -ResourceGroupName myResourceGroup` -TemplateFile $templateFile` -storageName "{your-unique-name}" Note
If deployment fails, use option verbose for information about the resources being created. Use option debug for more debugging information.
To see how flexible the template is, let's expand it again. This time, set the SKU to Standard Geo-Redundant Storage (GRS) Standard_GRS .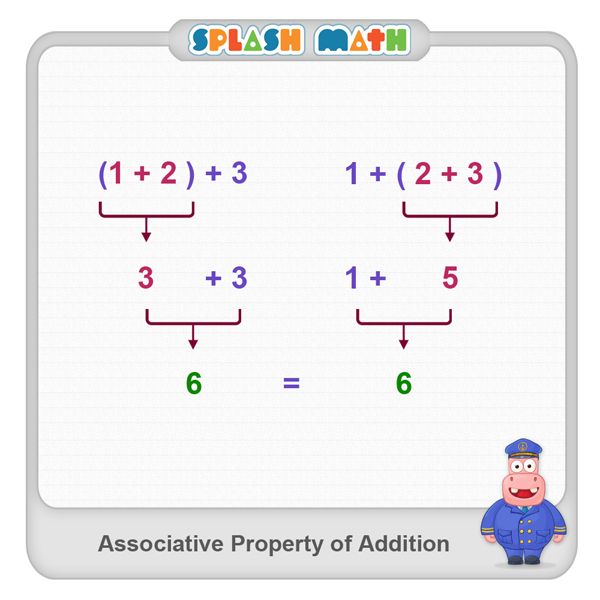 You can pass in a new name to create a different storage account, or use the same name to update an existing storage account. Both options work.
You can pass in a new name to create a different storage account, or use the same name to update an existing storage account. Both options work.
- PowerShell
- Azure CLI
New-AzResourceGroupDeployment` -Name usenondefaultsku ` -ResourceGroupName myResourceGroup` -TemplateFile $templateFile` -storageName "{your-unique-name}" ` -storageSKU Standard_GRS Finally, let's run another test and see what happens if you pass in a SKU that is not in the list of valid values. In this case, we are testing a scenario where the template user thinks that base is one of the SKUs.
- PowerShell
- Azure CLI
New-AzResourceGroupDeployment` -Name testskuparameter ` -ResourceGroupName myResourceGroup` -TemplateFile $templateFile` -storageName "{your-unique-name}" ` -storageSKU basic The command fails and at the same time an error message appears containing a list of valid values. The ARM processor finds the bug before the deployment starts.
The ARM processor finds the bug before the deployment starts.
Cleaning up resources
If you continue to the next tutorial, you do not need to delete the resource group.
If you are stopping work now, you may need to clean up deployed resources by deleting the resource group.
- In the Azure portal, select Resource group from the menu on the left.
- Enter the name of the resource group in the text box Filtering all fields... .
- Check the box next to myResourceGroup and select myResourceGroup or the name of your resource group.
- From the main menu, select Delete resource group .
What to do next
You improved the template created in the first tutorial by adding parameters. In the next tutorial, you will be introduced to the functions of templates.
Tutorial for adding template functionality to an Azure Resource Manager template
Functional food.
 What it is?
What it is? Functional foods are food products that have additional properties, in addition to the traditional nutritional value, due to the addition (enrichment) of additional ingredients, new or existing. Also, specially bred crops rich in certain useful substances are classified as functional foods.
Functional foods are formulated to provide physiological benefits and/or reduce the risk of chronic disease.
- Proponents of functional foods say they promote optimal health and help reduce the risk of disease. The simplest and most familiar example of a functional food is oatmeal, as it contains soluble fiber that can help lower cholesterol levels. Another example of a functional food would be orange juice fortified with calcium for healthy bones and teeth.
- The properties of functional foods or food ingredients must be based on sound scientific evidence, with the "gold standard" being repeated, randomized, placebo-controlled studies in humans.
 However, there are many products on the market today that claim to be functional, but there is no conclusive evidence to support such claims.
However, there are many products on the market today that claim to be functional, but there is no conclusive evidence to support such claims. - Functional foods represent one of the most intensively researched and widely promoted areas in food and nutrition science. However, it should be emphasized that these products and ingredients are not magic “pills” or a panacea for health. Diet is just one aspect of a holistic approach to health and longevity.
That food can be beneficial is not new. However, this "food as medicine" philosophy was not very popular in the 19th century due to the development of the pharmaceutical industry and the advent of modern medicines. In the early 20th century, the important role of proper nutrition in disease prevention and health promotion came to the fore again. During the first 50 years of the 20th century, scientists paid attention to identifying the main elements, in particular vitamins, and their role in the prevention of various diseases associated with nutritional deficiencies. This emphasis on nutritional deficiencies or "malnutrition" has changed dramatically, however, in 1970s, when diseases associated with overnutrition became a new serious public health problem.
This emphasis on nutritional deficiencies or "malnutrition" has changed dramatically, however, in 1970s, when diseases associated with overnutrition became a new serious public health problem.
During this time, attention began to focus on the importance of diets low in saturated fat and high in vegetables, fruits, whole grains, and legumes in reducing the risk of chronic diseases such as heart disease, cancer, osteoporosis, diabetes, and stroke. Scientists have also begun to identify physiologically active compounds in plant and animal foods that could potentially reduce the risk of various chronic diseases. These scientific advances, combined with a growing older population, changing dietary habits, numerous technological advances, and a market ripe for the introduction of health-promoting foods, have formed in 90's. It was then that the first functional foods appeared.
Functional foods do not currently have a generally accepted definition.
All foods are functional to some extent because all foods have a certain nutritional value.
Foods are currently being extensively researched for additional physiological benefits that may reduce the risk of chronic disease or otherwise optimize health. It is research like this that has led to global interest in a growing category of food called "functional foods."
- The concept of "functional nutrition" was first developed in Japan in the 1980s when the Japanese Ministry of Health and Welfare faced rising health care costs. A special system was developed under which certain foods with documented health benefits were registered. Products registered in this way are eligible for a special seal and are now recognized as products for special use (FOSHU) . By July 2002, almost 300 foodstuffs had received the FOSHU status in Japan.
- In 1994, the US National Academy of Sciences Food and Nutrition Board defined functional foods as "any modified food or food ingredient that, in addition to its traditional nutritional value, may provide health benefits.
 " Another definition of functional foods is “foods that, due to the presence of physiologically active components, provide health benefits in addition to basic nutrition.” The American Dietetic Association has defined functional foods as foods that are "whole, fortified, or improved," but more importantly, such foods should be consumed as "...part of a varied diet on a regular basis."
" Another definition of functional foods is “foods that, due to the presence of physiologically active components, provide health benefits in addition to basic nutrition.” The American Dietetic Association has defined functional foods as foods that are "whole, fortified, or improved," but more importantly, such foods should be consumed as "...part of a varied diet on a regular basis."
Another term often used as a synonym for functional foods is "nutraceutical" . The term, coined in 1991 by the Medical Innovation Foundation, refers to almost any biologically active component that provides health benefits.
It is known that diseases, the development of which is associated with malnutrition, account for about 70% of the causes of total mortality.
Dietary patterns associated with leading causes of death across countries are high in total and saturated fat, cholesterol, sodium and refined sugars and low in unsaturated fats, grains, legumes, fruits and vegetables.
An accumulated body of research now suggests that the consumption of certain foods or associated physiologically active components may be associated with a reduced risk of certain diseases. The vast majority of these components come from plants; however, there are several classes of physiologically active functional food ingredients of animal and microbial origin.
Health claims of functional foods should be based on sound scientific evidence, but all too often so-called "new evidence" is the basis for the marketing of certain functional foods or their ingredients.
Functional products of animal origin - the most intensively studied class of physiologically active components at present.
- Of particular interest are the omega-3 fatty acids , which are predominantly found in oily fish such as salmon, tuna, mackerel, sardines and herring. Docosahexaenoic acid (DHA), one of the Omega-3 PUFAs, is an important component of cell membrane phospholipids, especially in the brain and retina, and is essential for their proper functioning.
DHA is especially important for the development of these organs in children, and more recently the FDA approved the use of DHA and arachidonic acid in formulas for term infants. Hundreds of clinical studies support the role of omega-3 PUFAs in cardiovascular health.
- Another class of biologically active components of animal origin, which has received more and more attention in recent years, is probiotics . The health benefits of probiotics have been considered since the turn of the century, when Nobel Prize-winning biobiologist Mechnikov first suggested that lactic acid bacteria contributed to the longevity of Bulgarian peasants. It is believed that a wide variety of living microorganisms can contribute to human health, although most of the research is done on animals. In addition to the numerous strains of Lactobacillus acidophilus, other strains of Lactobacillus that include functional foods are currently on the market, including L. johnsonii La1, L. reuteri, L.
GG and L. casei Shirota. Scientists continue to study the properties of probiotics.
- Recently, research efforts have focused on prebiotics , non-digestible food ingredients that benefit human health by selectively stimulating the growth and/or activity of beneficial bacteria in the colon. Prebiotics include short chain carbohydrates such as fructooligosaccharides and inulin, which enter the colon and serve as substrates for endogenous colon bacteria.
- Concept 9 is even newer0015 "Synbiotics" , which are blends of probiotics and prebiotics that benefit the body by selectively stimulating the growth and/or activating the metabolism of healthy bacteria.
- Another ingredient that has been the focus of research in recent years is Conjugated Linoleic Acid (CLA) . This component, which was first identified as a potent antimutagenic agent in roasted ground beef, is a mixture of structurally similar forms of linoleic acid (cis-9, trans-11-octadecadienoic acid).
CLA is present in almost all foods, but is especially abundant in dairy products and products derived from ruminants. For example, raw beef contains 2.9–4.3 mg CLA/g fat, while lamb, chicken, pork, and salmon contain 5.6, 0.9, 0.6, and 0.3 mg CLA/g fat, respectively, and dairy products contain 3.1–6.1 mg CLA/g fat. The suppression of mammary carcinogenesis in animals is a proven physiological effect of CLA. There is also preliminary evidence that CLA can reduce body fat and increase muscle mass, increase bone density (in animal models).
Plant based functional foods are plant based foods and physiologically active ingredients derived from plants.
Plant foods with health benefits include β-glucan, soy protein, cranberries, garlic, nuts, grapes, chocolate, and others.
- The effectiveness of cranberry in the treatment of urinary tract infections was recognized in the 20s of the last century.
More recent studies have confirmed that the condensed tannins (proanthocyanidins) in cranberries are biologically active and prevent E. coli from adhering to the epithelial cells lining the urinary tract.
- Garlic has been used for thousands of years for a wide range of medicinal purposes; its effects are likely related to the presence of numerous physiologically active organosulfur compounds (eg allicin, allyl sulfides). The most documented clinical effect of garlic concerns its ability to lower blood cholesterol levels.
- There is a growing body of research supporting the health benefits of other functional or plant-based foods, such as tea (contains catechins), tomato lycopene (especially from cooked and/or processed), and the carotenoids lutein and zeaxanthin (from green leafy vegetables).
While there is evidence that certain functional foods or food ingredients may play a role in disease prevention and health promotion, safety should not be overlooked. Thus, more and more attention is being paid to the issues of the interaction of drugs with various plant components. One of the clearest examples of such an interaction can be St. John's wort , the extract of which significantly increases the metabolic activity of liver cytochrome P450, which inactivates or weakens the effect of drugs such as theophylline, cyclosporine, warfarin, oral contraceptives.
Research is currently focused on deepening our understanding of "functional foods". Significant efforts are being made by academic, government and private research institutions around the world to determine how functional foods and nutritional ingredients can help prevent chronic disease or optimize health, thereby reducing healthcare costs and improving the quality of life of the population.
A new discipline that is sure to have a profound impact on future functional food research and development is nutrigenomics , which investigates the interaction between diet and disease development based on an individual's genetic profile. Interest in nutrigenomics has increased significantly since the complete decoding of the human genome. This technological breakthrough may eventually make it possible to tailor a diet to a person's specific genetic profile. Another technology that will greatly influence the future of functional foods is biotechnology. Examples of new crops obtained through biotechnology are golden rice enriched with β-carotene and rice enriched with iron.
Numerous surveys over the past decade have shown that as more and more people take responsibility for their health, more and more people realize the importance of nutrition and changing eating habits to improve the quality of life. Many people today view the “kitchen cabinet as a first aid kit” and understand that healthy eating is the best way to fight disease.
The general age of the population continues to increase, age-related diseases (such as heart disease, cancer, osteoporosis, Alzheimer's disease, age-related macular degeneration) increase healthcare costs worldwide. Preventive health strategies, including nutritional approaches, will significantly reduce these costs.
Functional foods focused on health benefits will be in demand over the next few decades, given the interest of consumers in maintaining health for as long as possible, demographic aging and rising health care costs
In the Russian Federation, one of the main tasks is the development production of food products enriched with irreplaceable components, functional products. In accordance with the Action Plan for the implementation of the Strategy for Improving the Quality of Food Products in the Russian Federation until 2030, approved by the Decree of the Government of the Russian Federation dated 2906.06.2016 No. 1364-r, measures are being taken to support domestic manufacturers of functional food products.
Any health benefits of functional foods must be based on sound and rigorous scientific criteria, including rigorous safety and efficacy studies. Interactions with other dietary components and potential adverse interactions with pharmaceutical agents should be clearly identified.











