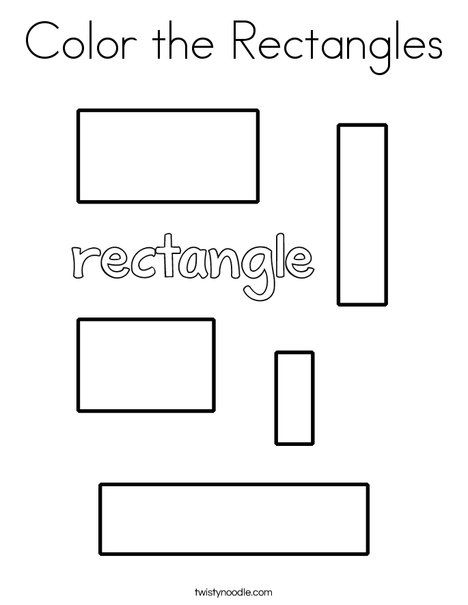
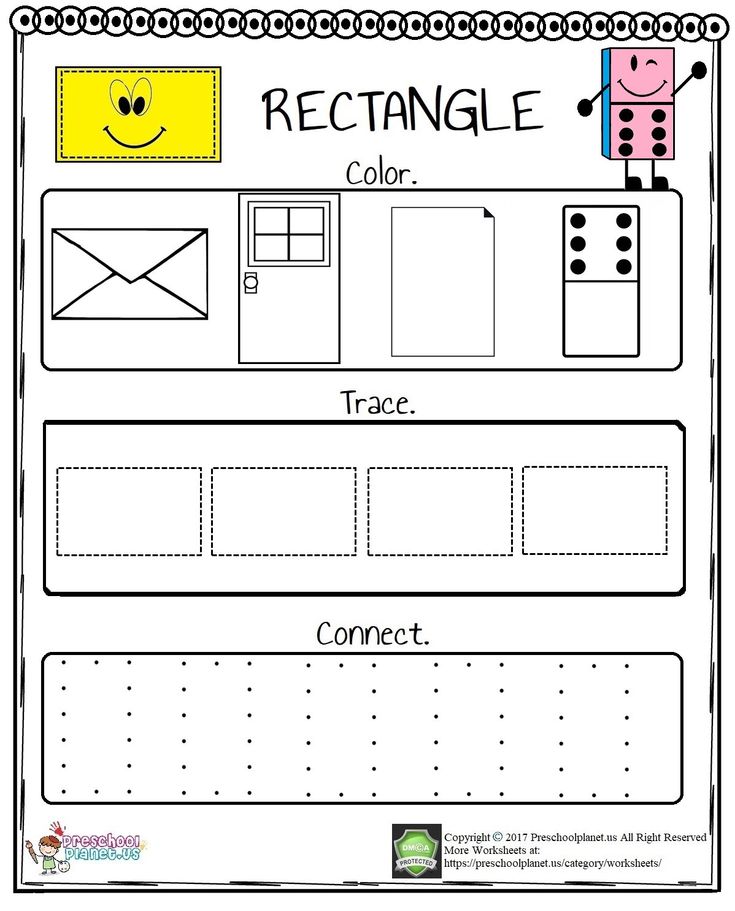
Home » Misc » Definition of a rectangle for kids

Definition of a rectangle for kids


Rectangle Definition & Meaning - Merriam-Webster

rect·​an·​gle ˈrek-ˌtaŋ-gəl 

: a parallelogram all of whose angles are right angles

especially : one with adjacent sides of unequal length

Example Sentences

Recent Examples on the Web What appears to be a rumpled towel is actually a rectangle of creased, folded and painted steel. —Mark Jenkins, Washington Post, 2 Dec. 2022 The eraser is a rectangle, even though the pencil is round. —Diana Budds, Curbed, 9 May 2022 Overhead, every fifty yards or so, a row of flags hung from wires stretched across the street, and at the end of the canyon, where the buildings stopped, was a rectangle of open sky. —Isaac Chotiner, The New Yorker, 4 Aug. 2021 Thus, the optimal value of the ratio, which minimizes the time to scan the entire rectangle, is about 3/2, not far from the golden ratio. —Alan Lightman, The Atlantic, 5 Dec. 2022 That means, for the most part, a new phone today means a big, flat, sleek rectangle prone to falls and being thrown against a wall out of frustration. —Chloe Toscano, WIRED, 3 Dec. 2022 Although a pricer option when compared to our other picks, this rectangle mirror looks super luxurious with its antique bronze finish and gilded ornate detailing. —Alyssa Gautieri, Good Housekeeping, 22 Nov. 2022 Tequila 512 wanted the reality TV star and her business partners to change the company name and logo, which includes black lettering, a vertical yellow rectangle and a reference to a area code in the Los Angeles area. —Timothy Fanning, San Antonio Express-News, 17 Nov. 2022 First, cut a rectangle from the front of the book using an Xacto knife ($4, Walmart). —Emily Vanschmus, Better Homes & Gardens, 9 Nov. 2022 See More

These example sentences are selected automatically from various online news sources to reflect current usage of the word 'rectangle. ' Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.

Word History

Etymology

Medieval Latin rectangulus having a right angle, from Latin rectus right + angulus angle — more at right, angle

First Known Use

circa 1560, in the meaning defined above

Time Traveler

The first known use of rectangle was circa 1560

See more words from the same year

Dictionary Entries Near

rectangle

rectal

rectangle

rectangled

See More Nearby Entries 

Cite this Entry

Style

MLAChicagoAPAMerriam-Webster

“Rectangle. ” Merriam-Webster.com Dictionary , Merriam-Webster, https://www.merriam-webster.com/dictionary/rectangle. Accessed 12 Jan. 2023.

Copy Citation

Kids Definition

rectangle

noun

rect·​an·​gle ˈrek-ˌtaŋ-gəl 

: a four-sided polygon that has four right angles and each pair of opposite sides parallel and of the same length

More from Merriam-Webster on

rectangle

Thesaurus: All synonyms and antonyms for rectangle

Nglish: Translation of rectangle for Spanish Speakers

Britannica English: Translation of rectangle for Arabic Speakers

Britannica. com: Encyclopedia article about rectangle

Last Updated: - Updated example sentences

Subscribe to America's largest dictionary and get thousands more definitions and advanced search—ad free!

Merriam-Webster unabridged

Rectangle Facts for Kids

For the record label, see Rectangle (label).

In Euclidean plane geometry, a rectangle is a shape with for sides and four right angles. A rectangle with four sides of equal length is a square. The term oblong is occasionally used to refer to a non-square rectangle.

The word rectangle comes from the Latin rectangulus, which is a combination of rectus (as an adjective, right, proper) and angulus (angle).

Other geometries, such as spherical, elliptic, and hyperbolic, have so-called rectangles with opposite sides equal in length and equal angles that are not right angles.

Rectangles are involved in many tiling problems, such as tiling the plane by rectangles or tiling a rectangle by polygons.

Contents

  • Classification
    • Traditional hierarchy
  • Properties
    • Symmetry
    • Rectangle-rhombus duality
  • Formulae
  • Theorems
  • Crossed rectangles
  • Other rectangles
  • Squared, perfect, and other tiled rectangles

Classification

A rectangle is a special case of both parallelogram and trapezoid. A square is a special case of a rectangle.

Traditional hierarchy

A rectangle is a special case of a parallelogram in which each pair of adjacent sides is perpendicular.

A parallelogram is a special case of a trapezium (known as a trapezoid in North America) in which both pairs of opposite sides are parallel and equal in length.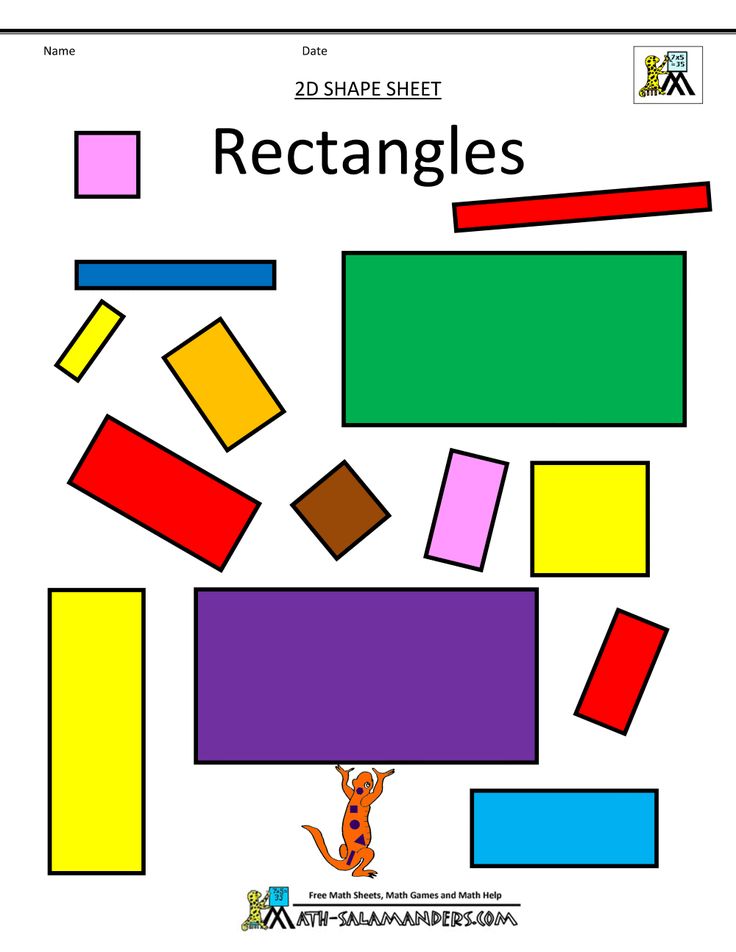

A trapezium is a convex quadrilateral which has at least one pair of parallel opposite sides.

A convex quadrilateral is

  • Simple: The boundary does not cross itself.
  • Star-shaped: The whole interior is visible from a single point, without crossing any edge.

Properties

Symmetry

A rectangle is cyclic: all corners lie on a single circle.

It is equiangular: all its corner angles are equal (each of 90 degrees).

It is isogonal or vertex-transitive: all corners lie within the same symmetry orbit.

It has two lines of reflectional symmetry and rotational symmetry of order 2 (through 180°).

Rectangle-rhombus duality

The dual polygon of a rectangle is a rhombus, as shown in the table below.

Rectangle Rhombus
All angles are equal. All sides are equal.
Alternate sides are equal. Alternate angles are equal.
Its centre is equidistant from its vertices, hence it has a circumcircle. Its centre is equidistant from its sides, hence it has an incircle.
Two axes of symmetry bisect opposite sides. Two axes of symmetry bisect opposite angles.
Diagonals are equal in length. Diagonals intersect at equal angles.
  • The figure formed by joining, in order, the midpoints of the sides of a rectangle is a rhombus and vice versa.

Formulae

The formula for the perimeter of a rectangle

The area of a rectangle is the product of the length and width.

If a rectangle has length and width

  • it has area ,
  • it has perimeter ,
  • each diagonal has length ,
  • and when , the rectangle is a square.

Theorems

The isoperimetric theorem for rectangles states that among all rectangles of a given perimeter, the square has the largest area.

The midpoints of the sides of any quadrilateral with perpendicular diagonals form a rectangle.

A parallelogram with equal diagonals is a rectangle.

The Japanese theorem for cyclic quadrilaterals states that the incentres of the four triangles determined by the vertices of a cyclic quadrilateral taken three at a time form a rectangle.

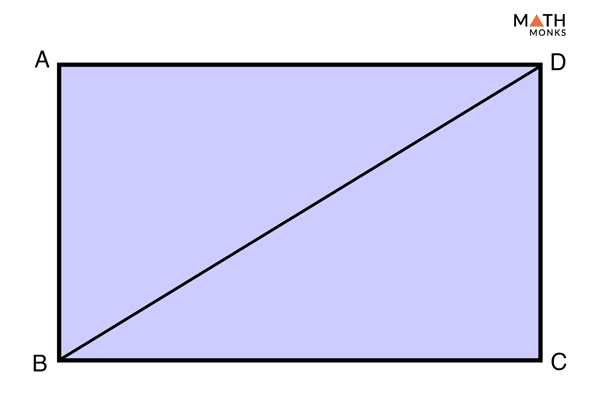
The British flag theorem states that with vertices denoted A, B, C, and D, for any point P on the same plane of a rectangle:

Crossed rectangles

A crossed quadrilateral (self-intersecting) consists of two opposite sides of a non-self-intersecting quadrilateral along with the two diagonals. Similarly, a crossed rectangle is a crossed quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals. It has the same vertex arrangement as the rectangle. It appears as two identical triangles with a common vertex, but the geometric intersection is not considered a vertex.

A crossed quadrilateral is sometimes likened to a bow tie or butterfly, sometimes called an "angular eight". A three-dimensional rectangular wire frame that is twisted can take the shape of a bow tie.

The interior of a crossed rectangle can have a polygon density of ±1 in each triangle, dependent upon the winding orientation as clockwise or counterclockwise.

A crossed rectangle may be considered equiangular if right and left turns are allowed. As with any crossed quadrilateral, the sum of its interior angles is 720°, allowing for internal angles to appear on the outside and exceed 180°.

A rectangle and a crossed rectangle are quadrilaterals with the following properties in common:

  • Opposite sides are equal in length.
  • The two diagonals are equal in length.
  • It has two lines of reflectional symmetry and rotational symmetry of order 2 (through 180°).

Crossed rectangles

Other rectangles

A saddle rectangle has 4 nonplanar vertices, alternated from vertices of a cuboid, with a unique minimal surface interior defined as a linear combination of the four vertices, creating a saddle surface. This example shows 4 blue edges of the rectangle, and two green diagonals, all being diagonal of the cuboid rectangular faces.

In spherical geometry, a spherical rectangle is a figure whose four edges are great circle arcs which meet at equal angles greater than 90°. Opposite arcs are equal in length. The surface of a sphere in Euclidean solid geometry is a non-Euclidean surface in the sense of elliptic geometry. Spherical geometry is the simplest form of elliptic geometry.

In elliptic geometry, an elliptic rectangle is a figure in the elliptic plane whose four edges are elliptic arcs which meet at equal angles greater than 90°. Opposite arcs are equal in length.

In hyperbolic geometry, a hyperbolic rectangle is a figure in the hyperbolic plane whose four edges are hyperbolic arcs which meet at equal angles less than 90°. Opposite arcs are equal in length.

Squared, perfect, and other tiled rectangles

A perfect rectangle of order 9

A rectangle tiled by squares, rectangles, or triangles is said to be a "squared", "rectangled", or "triangulated" (or "triangled") rectangle respectively. The tiled rectangle is perfect if the tiles are similar and finite in number and no two tiles are the same size. If two such tiles are the same size, the tiling is imperfect. In a perfect (or imperfect) triangled rectangle the triangles must be right triangles. A database of all known perfect rectangles, perfect squares and related shapes can be found at squaring.net. The lowest number of squares need for a perfect tiling of a rectangle is 9 and the lowest number needed for a perfect tilling a square is 21, found in 1978 by computer search.

A rectangle has commensurable sides if and only if it is tileable by a finite number of unequal squares. The same is true if the tiles are unequal isosceles right triangles.

The tilings of rectangles by other tiles which have attracted the most attention are those by congruent non-rectangular polyominoes, allowing all rotations and reflections. There are also tilings by congruent polyaboloes.

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:

Rectangle Facts for Kids. Kiddle Encyclopedia.

Mathematics lesson in the 2nd grade on the topic "Rectangle and square" (program of a promising elementary school)

Sections: Primary school

Targets:

  • learn to distinguish geometric shapes: rectangles and squares; nine0006
  • reinforce the skill of constructing geometric figures on checkered paper;
  • develop spatial thinking and Attention.

PROGRESS OF THE LESSON

1. Organizational moment

The long-awaited call is given -
The lesson starts.
Here are ideas and tasks,
Games, jokes, everything for you!
I wish you good luck -
To work in a good hour

nine0039

2. Oral counting

1. Masha and Katya were archery. Which of them turned out to be the winner after three attempts?

Who scored more points and by how much?

2. What is the mass of a watermelon? What is equal to mass of melon?

3. Message of the topic of the lesson. Update basic knowledge

Someone is tired of fairy tales,
And someone is captivated by fairy tales,
And our best lesson
Let's start with familiar names

Place a period at the beginning of the line. Get down down 6 cells down, draw a line, count 8 cells to the right: and draw a line, go up 6 cells and draw line, count 8 cells to the left and draw line. What did we get? Prove it's rectangle. (4 corners are highlighted, colored opposite sides are marked with pencils)

If all corners are right
And there are only four corners,
Well, on both sides
Opposite and equal,
This chegyrekhugopnik
Let's name the rectangle

- Look at the drawing. Find the "extra" figure.

- What is the name of this figure? (Rectangle)
- Today in the lesson we will distinguish geometric shapes and build rectangles.

IV. Work on topic lesson

Frontal conversation on questions:

– What is the smallest number of corners that a figure?
What shapes with angles do you know?
- Define a polygon quadrilateral, rectangle and square.
- Is a square a square?
- A quadrilateral can always be called square?
Can every polygon be named? quadrilateral? Is everyone quadrilateral polygon?

nine0013 He is my friend for a long time
Every angle in it is straight
All four sides
Same length
I am glad to present it to you
And his name is square

Task 1 .

- Name the figures shown in the picture. (This quadrangles.)
Which of them are rectangles? (Rectangle - is a quadrilateral with all corners straight.)
Find the rectangles with a square.
- Draw the rectangles in your notebook.
Are there any among these rectangles that have where all sides are equal
by lenght?
- Check it with a ruler. Colorize such rectangles.
Rectangles with all sides equal are called squares.
How many squares are in the picture? (Two.)

Task 2

- Draw a square on the checkered paper.

Task 3

- Draw a rectangle that is not :square.
- Color in part of this rectangle so that so that the shaded part of this rectangle was a square.

Task 4

- Cut out a square from a piece of paper.
- Cut it into two identical shapes. Make It Different
ways,
- Show how it can be done.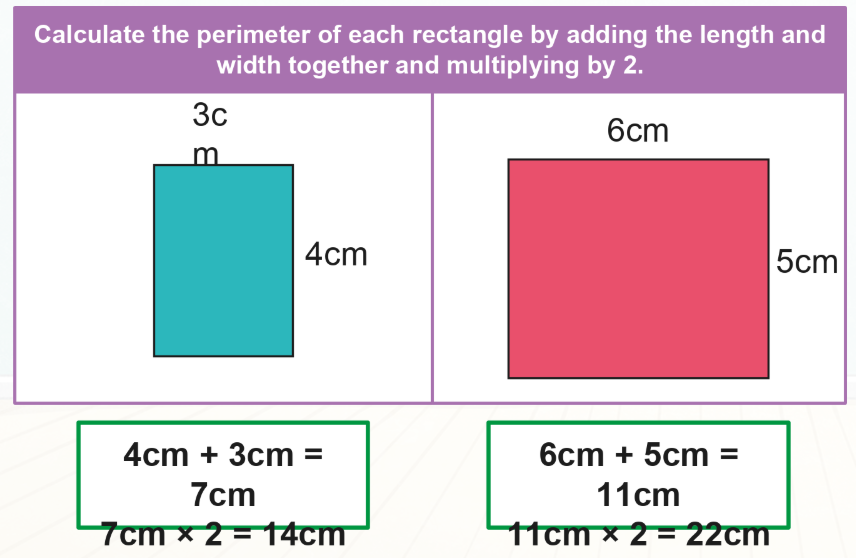

Task 5

- Draw four lines, intersection points which are the vertices of the square.

Task 6

– Count the number of squares on figure.

Answer: 14 squares.

Card work.

- Look at the picture and mark in red pencil all the dots that are vertices of right angles. nine0011

Summary of the lesson. Fairy tale dramatization

– What did you learn new at the lesson?
What shape is called a quadrilateral?
What is the name of the quadrilateral rectangle?
What rectangle is called a square?

Homework: compose and solve expression problem 90 - 9.

Math lesson "Rectangle"

Lesson objectives:

  • introduce students to the definition “rectangle”
  • learn to distinguish a rectangle from others geometric shapes
  • develop spatial and logical thinking by matching geometric figures
  • develop the ability to build a rectangle and distinguish it from a series of quadrilaterals
  • summarize students' knowledge of the geometric concepts
  • expand knowledge about the world around
  • cultivate love for the subject, stimulate active creative work.

Equipment: IPC, right angle model, geometric shapes (square, rectangle), unit plates, drawings of logical tasks.

Lesson progress

1. Organizational moment.

Slide 1.

Long awaited call
Let's start our lesson.

- Let's sit straight, close our eyes and say:

At the lesson, our eyes are attentively watching and everyone ... (see),

Ears listen attentively and that's all ... (hear).

The head works well.

2. Oral calculation.

- When and where can you hear another call? Phone

Slide 2.

– Let's call. You call by choosing an expression, count and name its value. If right, you've called. nine0011

nine0275
17-8 100-60 40+15 18-8 80+20
10+30 40-8 34+4 50-2 73+1
16+4 36-6 5+9 56-50 25-25
65+0 72+6 63-3 68-60 99+1

- Well done, everyone got through!

3.

Message topics and goal setting.

Slide 3.

- We will go to the country "Geometry", where do your mobile phones represent geometric figure, what? (Rectangle).

- Here you have named the topic of our lesson "Rectangle".

- This is familiar to you, but we will give a clear definition of "rectangle", we can distinguish from other geometric shapes.

- I tell you everything about geometry - section mathematics, and what is “Geometry”. In translation from the Greek language "measurement of the Earth", "geo" - Earth, "metria" - measurement.

Slide 4.

- What does Geometry study? Solve riddles! nine0011

This is a strange figure,
Well, quite a miniature!
And on a small piece of paper
We will deliver hundreds….. points.

He flies from the sun,
Breaking through the thick clouds
And it happens in a notebook,
And it is simply called - beam.

No angle, no side,
And relatives - only pancakes! circle

Angry Spadetail Fish
Bit off half a square -
A whole corner, believe it or not!
Who is he, poor thing, now? triangle

Semi Oval Triangle
The circle was teased - "Fat friend."
Circle, upset to tears,
But then he got up and grew up.
Who will guess here,
What is his name now? oval

Here are the four sides.
And all sides are equal.
And the figure is that guys.
Called ….. square

Got a square on the corner,
I poked my nose into the ceiling,
Up he grew for another five days
How to call it now? rhombus

Twin squares,
Half of their father.
Attach sides,
Tell me their father's name! rectangle

- Well done! Know geometric shapes.

– Dimensions also live in the camp of Geometry.

- Name the units of magnitude now in order increase.

Cards are placed on the board - mm cm dm m

4. Work on new material.

Slide 5.

- Look at the geometric shapes.

– What unites them all?

- quadrilaterals

- 4 corners

- 4 sides

- What two groups can these figures be divided into?

- figures with right angles

- figures without right angles. – Display on the board.

- Remember the theme of our lesson. What do we need shapes? square and rectangle

- In geometry they are correctly called (horus) - rectangles.

– Why?

- What is the definition of a rectangle?

- Let's check your statements in the textbook. Mathematics textbook page 12 rule - Rectangle is a quadrilateral with all angles straight. nine0201

- Everything matched! Well done!

- You know even more about these rectangles separately.

Slide 6. Slide 7.
SQUARE RECTANGLE
- 4 corners - 4 corners
- 4 sides - 4 sides
- all sides equal - opposite sides equal

- Find items around you that have rectangle shape and prove. You will need for this what? ( Right Angle Model ). Let's do her from the cloud by bending. Item display students.

- Well done! nine0011

– So, what is a rectangle?

A rectangle is a quadrilateral where all angles are right.

Slide 8.

PHYSMINUTE.

Relieve eye strain.

- Have you noticed what geometric shapes used a pig to build a house? Rectangles.

5. Work in a notebook.

- Let's take drawing tools - a ruler and simple pencil. nine0011

- Draw two segments, the length of the first is 2 cm, the second - 3 cm.

- Using these segments, we will construct geometric figures. First a square and then rectangle.

- Why two squares and one were drawn rectangle? (Knowing that the properties of these figures are square, all sides are equal, then the 1st one has a length sides 2 cm, and the 2nd side length is 3 cm. And rectangles with identical sides length 3 cm and width 2 cm.)

– What other geometric problems can we solve? nine0011

  • compare lengths of segments;
  • find the length of a broken line;
  • find the perimeter of geometric shapes.

– We will solve problems orally, writing down only the answers in a line through a cell with a unit of magnitude:

  1. Dad's step length is 70 cm, and son's step length is 50 cm. see dad's step is longer than son's step?
  2. Mom bought 6 m of red ribbon, and the ribbon blue color is 10m more. How many meters of tape Did your mom buy the blue one? nine0006
  3. Table perimeter 78 dm and chair perimeter 70 dm smaller. What is the perimeter of the chair?
  4. The class is 9 m long and 6 m wide. How many meters Is the width of a class smaller than its length?
  5. Throwing the ball, Katya threw 4 meters and Dima threw 5 meters farther. How far did Dima's ball fly?
  6. Draw a broken line of four links - 2 cm, 1 cm, 5 cm, 3 cm. What is the length of the whole broken line?

- Green paste. Self-test. Correct underline the answer. nine0011

Slide 9.

20 cm 16 m 8 dm 3 m 9 m 11 cm.

– Well done!

PHYSMINUTE.

We correct posture
We bend the backs together.
Right, left we bent
Reached up to the socks.
Straightened up!
Shoulders up, back and down.
Smile and sit down!

- One problem says about the perimeter. What is P the perimeter? (Sum of all sides)

- Find the perimeter of our shapes. Perimeter girls find the first square, and the second - boys. (At the blackboard, 1 student each).

- Write on the right side of the square.

Р=2+2+2+2=8(cm)

Р=3+3+3+3=12(cm)

– We find the perimeter of the rectangle and write together on the right side rectangle.

R= 2+3+2+3=10(cm)

6. Summing up.

- Today we again visited the country of Geometry and summarized your knowledge of geometric shapes.

Learn more