Help with 1st grade math

The Most Important Math Concepts Kids Learn In 1st Grade

Your child has progressed from kindergarten to first grade. That’s exciting news! There is so much learning to come their way, especially from their first grade math class.

Math skills and concepts build on each other from grade to grade, which is why children need to get a firm foundation so they can handle the more complex challenges as they progress in school.

As a concerned parent, you might be wondering what some of these mathematical concepts will be and, more importantly, how you can help your child master them. You don’t have to figure it out on your own.

Here, we will give you a breakdown of what to expect from your child’s math class. We’ll also add a few tips on how to help your young learner thrive through it all.

Let’s get started!

Why Is Math Important?

Math is taught in the classroom, but that doesn’t mean that’s the only place it’s relevant. We use it every day!

From the hexagonal bee combs to the circles, semi-circles, and crescents of the phases of our moon, mathematics is an essential part of the world we live in, and learning it helps us make sense of everything around us.

Did you know that math skills can also be linked to music? Children who play musical instruments use the same part of the brain when doing math. This is why studies have shown that music students do better in mathematics than their non-musical peers.

Sports and mathematics also have an interesting connection. Just think about all the coordination involved in performing well in certain sports. Research has shown that these skills can also be used to learn math.

In addition, mathematics helps us be stronger logical thinkers. Since most young kids tend to enjoy math time, it’s essential to foster this natural love for the subject just as much as we want to encourage children’s love for reading.

Helping children develop a love for mathematics generally works well when approached actively as a problem-solving skill rather than a rote memory task. Math helps children thrive in various aspects of their lives.

So, how do we get there? It all starts with the foundation.

Below are the key first grade math concepts your child will soon learn and some tips on how you can support them on their journey.

8 Important First Grade Math Concepts

1) Numbers And Counting

At first grade level (and for the next few years in school), learning different numbers and counting will form a significant part of your child’s mathematics lessons.

By the end of the first grade, your child will have learned to:

Count and write numbers from 1 to 100
Count by 1s, 2s, 5s, and 10s
Count backward
Count onward from any number
Count backward from any number

There are different ways to help your child grasp numbers and counting at home, and hands-on activities work best.

An effective strategy is to help your child visualize what all these numbers mean. For example, instead of just memorizing the numbers, they can count bears, large dried beans, or even craft sticks.

2) Addition And Subtraction

In first grade math, your young learner will start adding and subtracting numbers up to 30. They will also solve basic word problems with the help of drawings, objects, and equations.

By the end of the first grade, your child will have been shown how to:

Add three one-digit numbers
Write and show an understanding of the mathematical symbols (+, -, =)
Solve problems involving one and two-digit numbers
Solve problems involving an unknown. For example, 1 + _ = 4

Addition and subtraction are two math skills that can be demonstrated in everyday life situations. This makes it relatively easy to practice at home!

For instance, you might ask, “If you have two teddy bears and granny buys you three more, how many teddy bears will you have in total?” Or, “There were six strawberries in the fridge. Daddy ate some strawberries. There are now four left. How many did daddy eat?”

3) 2-D Shapes

During pre-k, children get introduced to different shapes. In first grade, they will continue to extend their understanding of them.

By the end of the first grade, your child may be able to:

Examine the attributes of different shapes (number of sides, faces, etc.)
Name the 2-D shapes

To help your child grasp these shapes at home, continue to point out and name the 2-D shapes in the world around you (circles, triangles, pentagons, etc.).

When doing so, remember to always highlight the attributes (e.g., this book has four equal sides, so it’s a square).

4) Sorting And Patterns

Understanding and sorting patterns also forms a part of first grade math.

Your first grader will learn to:

Sort different objects by attributes such as color, shape, and function. For example, sorting a mixed group of blocks so that the red, blue, green, and yellow blocks are separated.
In addition, if these blocks are placed in a pattern (e.g., green, yellow, green, yellow, etc.), your child should be able to both predict which color will come next and create their own identical pattern. This skill will help develop your child’s logical thinking.

Continue to allow your young learner to play with fun building blocks and create their own patterns to help them master this skill.

5) Fractions

Montessori material. Children’s hands. The study of mathematics School and kindergarten. Whole and part. Fractions

As a first-grader, your child will be introduced to fractions as equal shares and basic fractions such as ½, ⅓, and ¼. For children to fully grasp these concepts, it’s essential to keep things intuitive.

For example, you can start by helping them understand that a half is two equal parts, a third is three equal parts, and so forth. They also need to understand that although three is bigger than two, ⅓ is smaller than ½.

Fractions can be tricky for kids to learn, which is why it’s important to use practical and everyday items.

For example, you can help your young learner examine the fractions of a full pizza. Then, as you divide the pizza into different slices, talk about the parts that you’ve created from the whole.

The concept of equal shares can also be demonstrated from one object and a group. For instance, you can have ½ of a single item (e.g., ½ of a cookie), or you can have ½ of a group of objects (e.g., ½ of four cookies is two cookies).

6) Number Place Values

With all the counting in first grade math, your child will naturally be introduced to the concept of place values. For instance, understanding that in the number 288, the 2 is worth 2 “hundreds” (or 200).

There are various activities you can do at home to help your young learner with this concept, including:

Using number lines
Base ten blocks

For more ideas to help with number place values and other 1st grade math concepts, take a look at the book Games for Math: Playful Ways to Help Your Child Learn Math, From Kindergarten to Third Grade by HOMER’s very own Peggy Kaye.

7) Time

Telling time (both digital and analog) is an important life skill that kids learn from first grade. The concept of elapsed time will also be introduced at this stage.

In first grade math, your child will learn to:

Tell time to the nearest hour, half-hour, and quarter-hour (sometimes even to five minutes)
Make the connection between time and events (e.g., shorter, longer, after, before)

Understanding the analog clock can be tricky for a child who’s only exposed to digital clocks. So help your young learner by buying one (or making one for learning) to hang up at home.

You can then speak to your child about what it means when the hands move. To make things easier, start by helping them tell time to an hour and half-hour before progressing to quarter-hours.

8) Measurements And Comparisons

First grade math also involves some measuring and unit comparisons.

Your child will learn how to measure using a ruler and, after taking measurements, compare and order objects by length. First-graders will also learn how to compare the weights and volumes of different objects.

To help your young learner at home, keep rulers nearby and take measurements together of some of the objects they love (e.g., stuffed toys, cookies, etc.).

Bonus tip: If you’re a regular baker, why not help them see how you use measuring tools to create their favorite treats? Yum!

Helping Your Child With First Grade Math

We’ve already mentioned a few ways in which you can help your first grader with math at home. In addition to the above, playing math games is a fun and easy way to practice math at home!

Here are some examples of more math activities your young learner will enjoy at home:

Fill in a number grid puzzle
Build objects with legos and measure
Number Hunt, Hopscotch, Is It A Number, and Find A Number

Math Is All Around Us

Helping your child grasp first grade math concepts at home is easier when you focus on the fact that mathematics is a part of our everyday lives. It is in the shape of road signs, the parts of sliced pizza, and even the watches on our wrists!

Sometimes kids (and parents) forget that math can be lots of fun. So whenever you can, incorporate games and activities to bring a little excitement to all the learning.

Will this help your child become our next best mathematician? Only time will tell. But one thing is for sure — all of the great mathematicians started somewhere. Even Isaac Newton had to master first grade math!

For more ideas and inspiration, visit the HOMER Learn & Grow app.

Author

First Grade Math Tips

Hoping to help your first-grader with math skills? Here are some basic tips that experts suggest.

Learn math from everyday objects

Your child can build an understanding of addition, subtraction, and the other math concepts they are learning in first grade by playing with everyday objects. Use items that your child enjoys playing with, such as Legos, and place them into two groups of unequal number. Place the larger grouping on the left to develop the habit your child will need later for subtracting from left to right. Next, ask your child to add objects to the smaller group from the larger group until your child counts the same number in both groups. As with all math activities, don't push it if your child resists, since math development varies greatly from child to child and your child may just not be ready for certain concepts.

Count with items

Count using items like blocks, pennies, and candy. Have some items handy for counting by ones and by tens. You can use interlocking blocks that allow students to connect two blocks to three blocks to represent 2 + 3. Use regular household items like pennies for counting by ones, and dimes for counting by tens.

Develop estimation skills

When things are stored or poured into varying size containers you have an opportunity to build your child's concept of estimation and quantity. At breakfast, ask their which bowl has more and which has less cereal. Ask them to compare the different amounts of the same liquid in three clear glasses by lining them up from least to most full. To build your child's vocabulary of comparisons, after successful practice use measuring cups with numbers. Ask their what your child notices about the number each liquid reaches in the measuring cup when they are lined up in sequence from least to most and then from most to least full.

Read math problems aloud

Help your child by reading math problems aloud slowly and carefully, so your child can hear the problem and think about what is being asked. If your child can read, have them read them.

Use real money

Children become so accustomed to seeing their parents pay with credit and debit cards that counting actual money can be an unfamiliar practice. Engage your child in the transaction of buying things at the store, allowing them to pay with cash and to count the change. This will help not only with their math skills but will foster an understanding of the concepts of saving and spending.

Reward effort for math

Speak positively about math and reward effort, rather than grades or ability. Think about how important reading is and how we are told to model this behavior for our children. We need to place math in the same category. Don't discount the importance of math by saying, "I'm not a math person, I was never good at math." Help your child read books that incorporate math, such as "Millions of Cats" by Wanda Gag or "On Beyond a Million'" by David Schwartz.

Use analog clocks

Go pre-digital with time. Reading time on a digital clock is vastly different than on a clock with a face. First grade standards focus on telling time to the hour and half hour, so have some old-fashioned analog clocks around your house as your child is learning to tell time. Consider giving their a wristwatch with a face, rather than a digital display.

Keep a calendar at home

Keep a calendar displayed in your home. Review the days of the week with your child and encourage their to count down the number of days until an event they are anticipating.

Play games with simple math

Play a game in the car using simple addition or subtraction. For example: I'm thinking of a number that equals seven when it is added to three. What number is that? Look for opportunities to play simple addition and subtraction games, for example, while they are eating, with the number of items on their plate.

Play games with math vocabulary

Play a mind-reader game. Think of a number for your child to guess. After each guess respond with the words "higher" or "lower." At different times use the words "more" or "less" so your child learns different arithmetic vocabulary. This game helps their correlate the number words and counting sequence with actual amounts or sizes.

Play family math games

Plenty of family games incorporate math. Tic-tac-toe, Connect Four, and dominoes are just some of the many games that help build math skills.

To find out what your first-grader will be learning in math class, check out our first grade math skills page.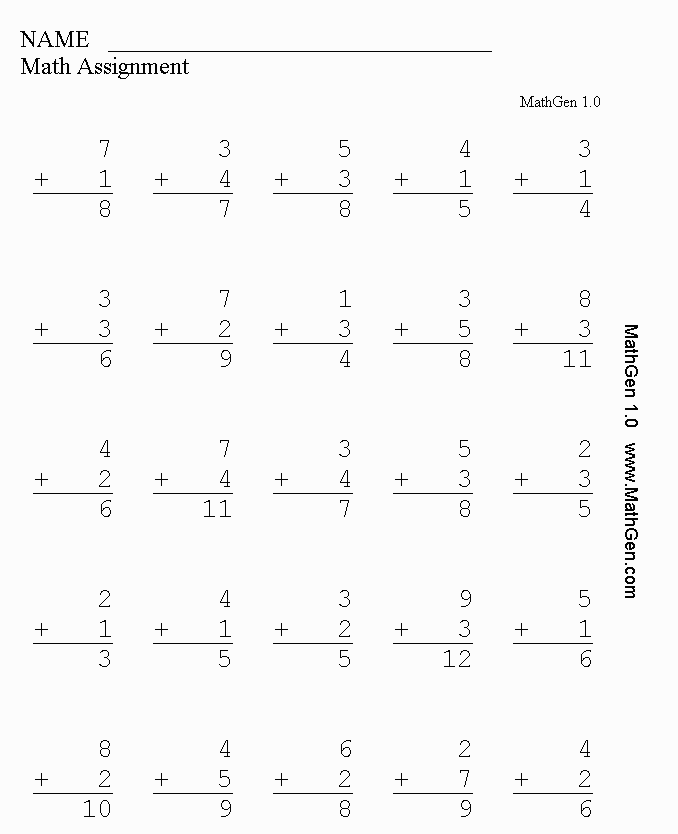

Parent Toolkit resources were developed by NBC News Learn with the help of subject-matter experts, including Joyce Epstein, Director, Center on School, Family and Community Partnerships, Johns Hopkins University; Pamela Mason, Program Director/Lecturer on Education, Harvard Graduate School of Education; Denise Walston, Director of Mathematics, Council of the Great City Schools; Nell Duke, Professor, University of Michigan; Leanna Baker, Retired Math Teacher; Bon Crowder, Math Teacher and Blogger, MathFour.com; and Robin Schwartz, VP, Association of Teachers of Math of NYC, and align with the Common Core State Standards.

7 Ways to Help a Primary School Student with Mathematics

Let's assume that mathematics already in the elementary school of a child is going poorly, with creaking. Difficult and boring to add and subtract, not to mention something more complex. New topics do not want to fit in the head. Writer and mother of three children Ksenia Buksha tells, based on her own experience, how to help a child master mathematics.

Putting difficulties on the shelves

At the level of 1-5 grades, there are no children incapable of mathematics. But there are children with specific difficulties that can and should be overcome. Let's think about why it is difficult for a child with mathematics.

Here are the options or combinations.

Poor counting, no counting skills. Not very familiar with numbers.
Cannot grasp the essence of the task, hardly understands what needs to be done. Tries all options (“So wrong? Then I’ll try to divide”, “Three times more - do you need a plus or a minus here?”).
Assimilates a template solution, but cannot refine it. Faced with the slightest change in conditions, he falls into a stupor.
Cannot read complex texts. As a result, he does not understand either the description of the rules or the text of the task. If you explain on your fingers what needs to be done, he immediately decides normally.
The concepts do not fit in my head. He understands them with difficulty and quickly forgets them. Such a child can hear an explanation of what x (unknown) is a hundred times, but never understand.
Visualization skill not developed. Cannot imagine, draw a schematic picture, "see in the mind".
Short attention: understands everything, but makes a lot of mistakes, especially in long complex examples.

As you can see, mathematics is decomposed into many different skills. When we figured out what the problem is, we can solve it. I apologize in advance to teachers and methodologists: I am just a parent, and my thoughts on this matter are just a private opinion, although I try to substantiate it.

We are waiting for the ability to think abstractly

The brain of a neurotypical child does not mature to abstraction and generalization far from immediately. For some it happens sooner, for others later. For example, not all children can match number and quantity. For very many, even in the 2nd or 3rd grade, there are only "15 apples", but simply "15" is not.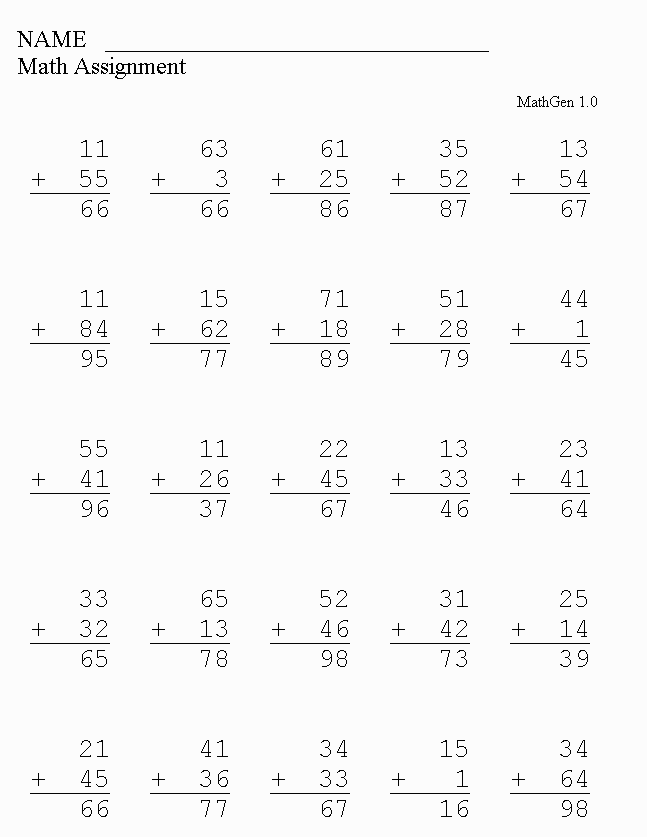

At the same time, they somehow get used to operating with numbers, and the gap in the basic understanding is not very noticeable until it comes to a little more complex things. For example, it is difficult for them to understand why there cannot be “one and a half” in the answer to the question “how many diggers?”. And when percentages or tasks for speed and distance begin, it becomes quite difficult.

It is worth going back to the specifics. Perhaps, in order to understand fractions, for now it is necessary to pronounce “watermelons in the numerator, boys in the denominator; 21 watermelons went to 42 boys, each with half a watermelon.” Even in the fifth grade, almost all concepts can still be grounded to the point.

Developing counting skills

Just learning to count is boring. All sorts of games with numbers will help us. For starters, complicated walkers with 2-3 dice (when in one move the maximum is 18 points, not 6), then various dice games where you need to count points.

The simplest game is known to me as "one": players take turns rolling one die (or two, or three), trying to get to a hundred points. The series is interrupted when the player has at least one one: in this case, the points for this series burn out, and you need to be able to stop on time.

I highly recommend dice poker. In this game, there are a number of combinations, each of which must be thrown in three attempts. These attempts can be saved. Players take turns making moves, the one who completes all the combinations first wins. In addition to the simple skill of adding points, poker gradually develops a fine understanding of randomness and probability, calculated risk and odds. Even a six- or seven-year-old can learn to play such poker.

To practice division and multiplication, my daughter and I talked about numbers as "relatives". For example, the number 72 has a very large "family": he has "children" 24 and 36, there are "grandchildren" - 2, 3, 4, 6, 12, 18. But the number 37 did not get himself any "family", it is simple. But if you "marry" him with another "loner" - 41, they will get 78 together, now you can "have children and grandchildren." This helps a lot to navigate the multiplication table.

Learning to see and visually generalize the problem

In order to schematize well, one must be able to highlight exactly what is important for the condition of the problem and schematically depict it in the picture. First, we learn to highlight the main thing. These are the famous “what is superfluous?” games, in which there may be several answers. Watermelon, stork, apricot, grapes - what is superfluous? Depending on what sign.

Peterson's textbook has wonderful problems cluttered with a bunch of unnecessary data or lacking necessary conditions. In the task, the author asks to find and highlight only those conditions that are needed for the solution, and if they are not there, to indicate what is missing. Having learned to see the task, you can move on to schematization.

Many children do not understand at all why drawing diagrams for tasks and why it is easier. This is because these schemes are ready-made. But on what basis are they built? Why, for example, does it matter how long the train itself is if it travels from A to B? How to draw "3 o'clock"? And "all the pears planted by boys"?

You can draw diagrams of different tasks together, and then invite your child to come up with similar ones. There are such tasks in textbooks, but there are few of them. For some, this difficulty generally determines all relations with mathematics, and indeed with the ordering of data, abstraction, generalization, and the search for a solution.

Sharpening logic

Logic is one of the tools that everyone needs. There are no people who would not be inclined to logic, there are those who have it "not set". It's like the ability to wield a screwdriver: anyone who has hands can learn. You can judge for yourself how iron-clad your logic is. I really love this wonderful test.

A person with logic cannot be confused by any propaganda or advertising, he will not be confused by an unscrupulous bank, he is much better oriented in the world around him.

With children, you can start with simple syllogisms that sometimes sound funny but lead to understanding of very important things. For example, after hearing from someone the maxim “boys don’t cry,” a child may clarify: “some or all?”

If the children do not go through the concept of a set, it is worth at least a little bit to draw "circles" with it (it is not necessary to immediately introduce all the concepts) and solve the corresponding problems: here are the boys, here are the cats, and here are those whose name is Vasya. Where are the boys whose name is not Vasya? And where are the girls? Where is Barsik the cat?

Imagination development

Imagination is necessary for everything related to mathematics and logic. (I don't even write "strange as it may seem" because it's not at all strange. ) Especially the ability to think in images.

I really like the game in which the parent and child take turns asking each other "graphic riddles" that do not have an exact answer. Each draws a series of incomprehensible geometric shapes or combinations thereof (a point in a triangle, a lightning bolt and a circle, several circles, tangents ...), and the other draws them in such a way that a picture is obtained. The smarter the solution, the more fun both players get.

There are many ancient and new games in which you need to add patterns from the details and fragments of an egg (Columbian egg), a square, differently colored faces of a cube (“Fold a pattern”). There are also three-dimensional sets, for example, "Pentamino". It's not about completing tasks, although all these sets can be used that way, but it's about creativity from the available details and the ability to see the image.

And you can also cut out snowflakes, draw symmetrical butterflies and little men, invent ciphers, draw labyrinths and maps.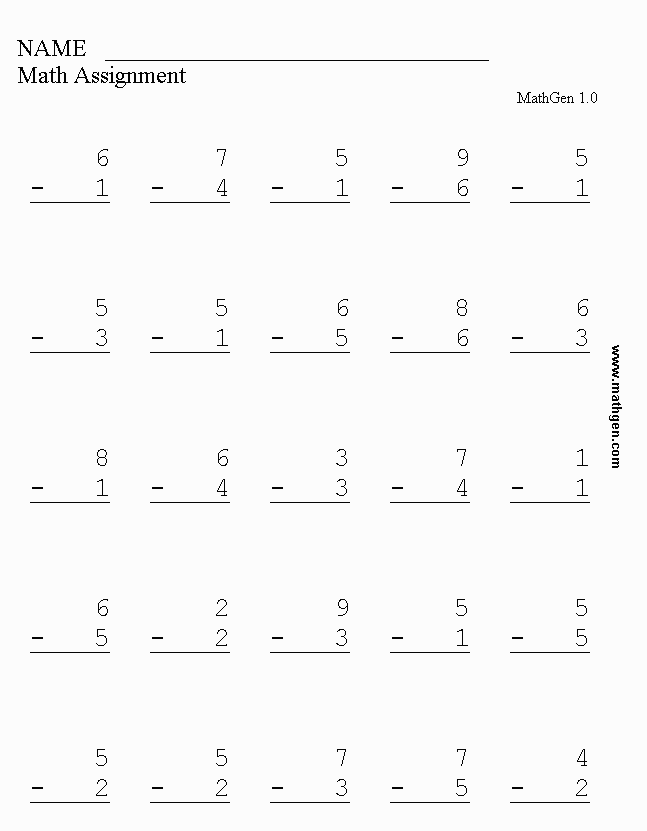 All this is the development of mathematical imagination.

Teaching a child to isolate what specifically he does not understand (metacognition)

I have written about it more than once - both in connection with mathematics and in connection with essays. Briefly, metacognition is the ability to "understand how I think", "know what exactly I do not know", awareness of one's thought process. This is what is almost never taught in school, and sometimes even spoil the already developed ability. After all, it is assumed that there are simple and complex ways to solve a particular problem. Often this is the case, but sometimes it is much more valuable to be able to go on your own and check yourself step by step: “Is it necessary to do this? I'm right?"

Joint reasoning (and I'm not talking about mathematics) is valuable both because it brings the child and the parent closer, and because we show how the thinking process goes. It doesn't have to be smooth and automatic. It has dead ends, unexpected turns. “Our initial assumption is wrong, which means that we need to go not on road 1, but on road 2.” By the way, this will also come in handy in school mathematics, when you need to understand the proofs of theorems. After all, the only thing that is well remembered is what went through with your own mind, when you were able to repeat other people's reasoning and you know every turn in them.

5 problems with learning mathematics due to underdeveloped executive functions

Executive functions play a large role in the successful solution of mathematical problems. They help children put into practice what they know and develop new skills. Therefore, when a child has problems with executive functions, they have a hard time with mathematics, even if they understand it.

Listed below are the problems they usually face.

1. Do homework quickly and incorrectly

Some children with executive function problems may be impulsive or impatient. They do their homework quickly and somehow. When it comes to math, children need to understand the task well, but children with executive function problems will most likely not read the problem and think about what they need to do, they immediately jump into the solution.

For example, a child may assume that the problem is solved by addition, because it was so yesterday. Hurrying to start, he does not notice that in today's problem in all the examples there is a minus sign, not a plus sign. So he gets everything wrong.

2. Having difficulty putting new rules into practice

Learning new things requires finding new solutions to new problems. This requires a flexible mind, as well as stopping and thinking before acting. But children with executive function problems often get stuck on what they already know. As a result, they find it hard to step back to come up with a different solution to a problem.

For example, when a child is learning about fractions, he will insist that ¼ is greater than ½ because he knows that 4 is greater than 2. However, in this case, the larger the denominator, the smaller the fraction. To find out which fraction is larger, he needs to understand this system, learn a new rule.

3. Answer without thinking

Some children with executive function problems solve problems based on experience. Instead of assessing each situation consciously, they give the answer automatically. When it comes to math, they may ignore key information in a problem and have difficulty writing equations because of this.

Suppose a child solves addition problems. 3 + 3 is 6, so he answers. Then he sees 3 - 3 and also writes 6 in the answer. It's not that he doesn't know how to subtract, but he sees 3 and 3 and answers the first thing that comes to his mind.

4. Getting lost in the middle of complex math problems

Working memory plays an important role in solving complex math problems. Known information learned earlier (for example, a formula, an answer from a previous problem, an example of an exercise from a textbook) can help solve a new problem, but children with poor working memory are easily lost in building the right actions.

Here is an example. Dividing in a column, the child forgets that he must lower the remainder after subtraction. He can't remember what to do next and gives up or comes up with the wrong answer.

Also, students often have to show how they solve problems. To do this, they use a draft, which shows step by step how they came to this decision. But children with executive function problems are disorganized. They paint the information on a piece of paper randomly, which confuses not only the teacher, but also themselves.

5. Not aware of their mistakes

Children need to be aware of their development and their achievements. Children with executive function problems cannot analyze their work. It simply cannot occur to them that the answer does not make sense and they need to find their mistake or ask for help.

Suppose such a child finishes his math test early. Despite the fact that he has extra time, he does not check the work for errors - he does not see the point in this, as he is sure that he did everything right.

How can you help?

If your child's math problems are getting in the way, there are a variety of ways to help them overcome them.

Start by teaching him to read the problem before you start solving it. Have him underline questions and highlight important points (including plus and minus signs). He must evaluate whether he knows how to solve the problem and whether he needs help. Let him ask himself questions like “how is this task similar and how is it different from the previous one?”.

Help your child create their own list of things to look out for before submitting work for review. Teach him to independently check his work and identify errors.

One of the most effective tools for developing executive functions is the Fast ForWord online methodology. This technique works at the root of the problems associated with impaired development of the executive and cognitive functions, and thanks to this, quickly and permanently eliminates them.

Help your child with difficult math homework:

Here's what to remember when helping your child with difficult math homework:

For starters, not understanding something is very nerve-wracking. Support the child and stop all the negativity that arises in the process of work.
Ask the child to show examples of the problem. For example, a similar problem they solved in class, or an example from a textbook that comes with the correct answer.
If your child has not found an example problem, try to find help on the Internet. Your child's textbook has headings or some keywords that can be used to find articles or examples of problems on the Internet. Try several sites, they probably describe in detail how to solve such problems.
After you find an example of a problem, ask the child how the teacher solved it. Having a solved example before their eyes, the child can remember how the teacher solved the problem.
Use the sample problem to see how to solve it step by step. Write down each step that your child remembers while doing the first task together. This will remind your child that math is a process. By writing down your child's reasoning, you'll create a list that the child can give to the teacher to show that they tried even if they didn't succeed. Using this list, the teacher can explain exactly where the child went wrong so that in the future he can solve this problem.

What should you avoid when helping your child with math homework?

Here's what not to do if your child asks you for help with math homework:

Don't start with questions like "What did your teacher tell you to do?" If your child remembered what the teacher told him, he probably would not ask you for help.
Don't contact the teacher right away. Children who have difficulty learning or concentrating easily give up and get angry when things don't work out, but it's important to show them to try to find a way out of a situation before asking a teacher for help.
Learn more