Interesting concepts in maths
List of "Cool Things" | Discovering the Art of Mathematics
How do you find "Cool Things" to share in your own classes? In this list, we are sharing a few of our ideas, with hopefully a few pointers so you can start creating your own list:
Share what is interesting and exciting to you about the world and mathematics
- Tell stories! The students love to hear stories; stories about you, or your kids, etc., or stories about mathematics and mathematicians.
- Read them cool things that you have recently read, e.g. from:
- Notices AMS
- Monthly, Math. Mag., CMJ
- Scientific American
- New York Times
Using Ideas from our Books for "Cool Things"
- 4 dimensions and the hypercube using soap bubbles Geometry
- 0.99999... = 1, The Infinite and Patterns
- Gabriel's Wedding Cake, The Infinite
- Surreal Numbers, The Infinite
- Goldbach's Conjecture, Number Theory
- Fractals and Chaos, Geometry and Proof
- Grandi series, The Infinite
- Tangles, Knot Theory
- Polyominoes, Knot Theory
- Butterfly effect, Proof
- Bees as mathematicians, Student toolbox
- Millinillitrillion, Patterns
- Flexagons and Feynman stories, Art and Sculpture
- Perspective drawing, Geometry
Connections with Nature
- The 4 dimensional torus and how the universe might be finite (Jeff Weeks: The shape of Space)
- Dance of the planets Dance of the planets and how it connects to star polygons and salsa rueda ( Dance )
- Fibonacci
- Number of Trees (NPR story)
Connections with Society
- Arithmetic is not equal to mathematics.
- Voting and voter registration
- Share some news from the math education world (K-12 teaching, testing,...).
- Talk about the mathematics behind fingerprinting and how fingerprinting is not always correct.
Being a Mathematician
- What does it mean to you to be a mathematician?
- Colbert clip about Perlman and the Poincaré Conjecture.
- Dance my phd example
- Stories about how you learned mathematics and why you fell in love with it.
- Mathematical Reviews (With Stewart quote about more mathematics in the past 50 years)
- Fields Medal
- Women in mathematics
- Ask students if they know the name of a famous mathematician. They probably don't know anyone! Tell lots of stories about mathematicians, e.g.
- Alan Turing – Enigma and leopard spots
- Code Talkers
- Wiles
- Lewis Carroll was a mathematician
Games
- Jeff Week’s geometry games
- Straight cut origami ( Art and Sculpture ) and Erik Demaine
- The game nim ( Games and Puzzles -- play 3 piles against them and win all the time sorting piles using base 2)
- Show a maypole pattern and think about the math involved
- Math magic – Mathematical magic tricks -
- Domino Artwork and Obaminoes -
- Peg Solitaire using group theory
Cool student work
- Show slice forms created by students
- Show string art created by students
- Read a math poem or a poem a student wrote
- 8 graders found Rascal’s Theorem
- 13 year old invents solar tree
Connection with the Arts
- Play math inspired music that a student composed
- Look at math and art exhibit in the department hallway
- Show Dmitri Tymoczko's space of musical chords
- Show the space of salsa dancing – paper by Volker Ecke and Christine von Renesse
Other Cool Mathematics
- Milennium Prize Problems
- Minimal surfaces
- Tessellations
- Euler characteristic
- Dragon curves
- Kaleidoscopes
- Soap bubbles and paths
- M.
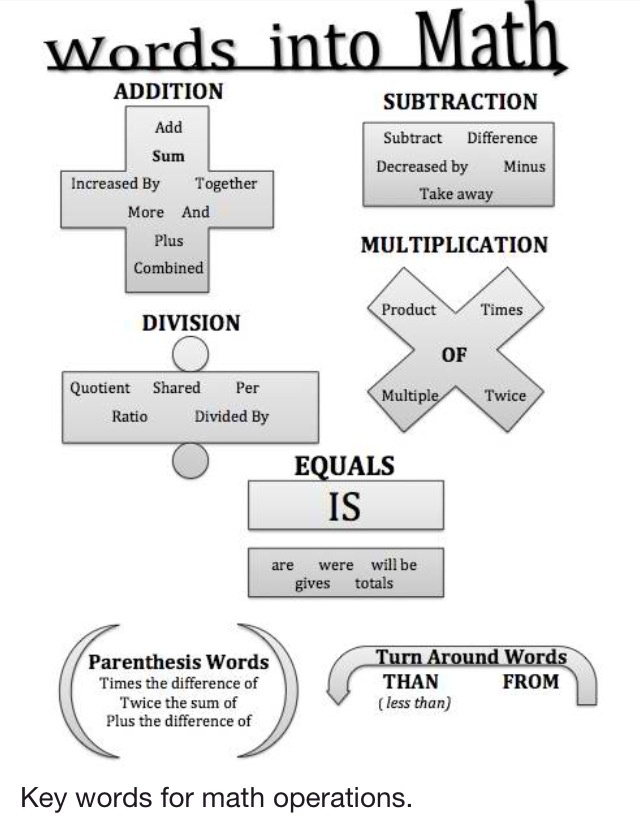 {i \pi}+1=0$
{i \pi}+1=0$ - Mersenne Prime Search – GIMPS and the reward, Number Theory
- Why $\pi$? Why does it go on forever? How do we know?
- Penrose tilings and inflation and the fractal nature of the proof.
- SETI at home
- Daniel Tammet: the boy with the incredible brain
The mystique of mathematics: 5 beautiful math phenomena
Fractals - patterns that repeat themselves on smaller scales - can be seen frequently in nature, like in snowflakes. Credit: Unsplash.Mathematics is visible everywhere in nature, even where we are not expecting it. It can help explain the way galaxies spiral, a seashell curves, patterns replicate, and rivers bend.
Even subjective emotions, like what we find beautiful, can have mathematic explanations.
"Maths is not only seen as beautiful—beauty is also mathematical," says Dr. Thomas Britz, a lecturer in UNSW Science's School of Mathematics & Statistics. "The two are intertwined."
"The two are intertwined."
Dr. Britz works in combinatorics, a field focused on complex counting and puzzle solving. While combinatorics sits within pure mathematics, Dr. Britz has always been drawn to the philosophical questions about mathematics.
He also finds beauty in the mathematical process.
"From a personal point of view, maths is just really fun to do. I've loved it ever since I was a little kid.
"Sometimes, the beauty and enjoyment of maths is in the concepts, or in the results, or in the explanations. Other times, it's the thought processes that make your mind turn in nice ways, the emotions that you get, or just working in the flow—like getting lost in a good book."
Here, Dr. Britz shares some of his favorite connections between maths and beauty.
1. Symmetry—but with a touch of surprise
Symmetry is everywhere you look. Credit: UnsplashIn 2018, Dr. Britz gave a TEDx talk on the Mathematics of Emotion, where he used recent studies on maths and emotions to touch on how maths might help explain emotions, like beauty.
"Our brains reward us when we recognize patterns, whether this is seeing symmetry, organising parts of a whole, or puzzle-solving," he says.
"When we spot something deviating from a pattern—when there's a touch of the unexpected—our brains reward us once again. We feel delight and excitement."
For example, humans perceive symmetrical faces as beautiful. However, a feature that breaks up the symmetry in a small, interesting or surprising way—such as a beauty spot—adds to the beauty.
"This same idea can be seen in music," says Dr. Britz. "Patterned and ordered sounds with a touch of the unexpected can have added personality, charm and depth."
Many mathematical concepts exhibit a similar harmony between pattern and surprise, elegance and chaos, truth and mystery.
"The interwovenness of maths and beauty is itself beautiful to me," says Dr. Britz.
Each frond of a fern shoots off smaller versions of themselves. Sometimes, the frond pattern can even be seen in the leaves as well. Credit: Shutterstock
Credit: Shutterstock 2. Fractals: infinite and ghostly
Fractals are self-referential patterns that repeat themselves, to some degree, on smaller scales. The closer you look, the more repetitions you will see—like the fronds and leaves of a fern.
"These repeating patterns are everywhere in nature," says Dr. Britz. "In snowflakes, river networks, flowers, trees, lightning strikes—even in our blood vessels."
Fractals in nature can often only replicate by several layers, but theoretic fractals can be infinite. Many computer-generated simulations have been created as models of infinite fractals.
"You can keep focusing on a fractal, but you'll never get to the end of it," says Dr. Britz.
"Fractals are infinitely deep. They are also infinitely ghostly.
"You might have a whole page full of fractals, but the total area that you've drawn is still zero, because it's just a bunch of infinite lines."
The Mandelbrot Set is arguably the most famous computer-generated fractal.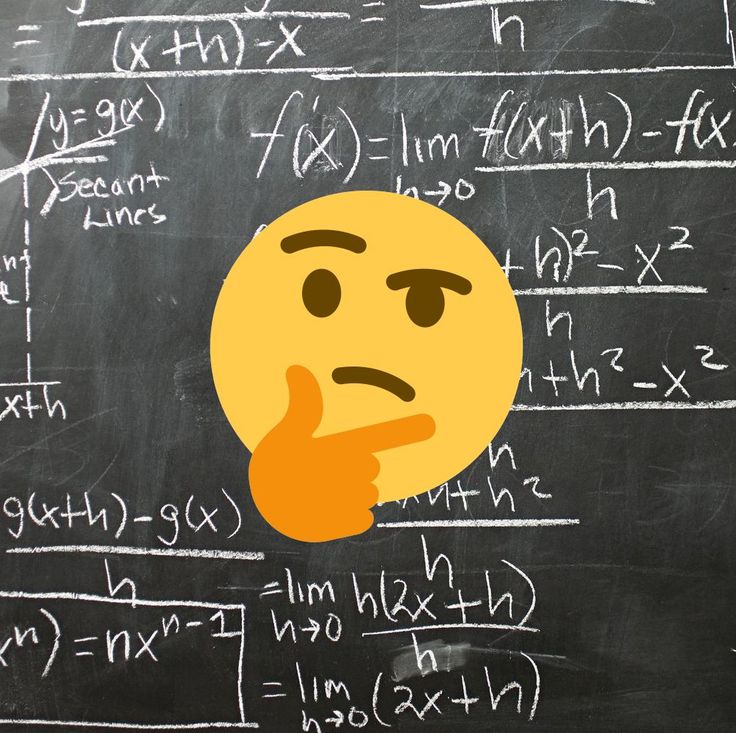 Zooming in will reveal the exact same image on a smaller scale – a dizzying and hypnotic endless loop. Credit: Shutterstock
Zooming in will reveal the exact same image on a smaller scale – a dizzying and hypnotic endless loop. Credit: Shutterstock 3. Pi: an unknowable truth
Pi (or 'π') is a number often first learned in high school geometry. In simplest terms, it is a number slightly more than 3.
Pi is mostly used when dealing with circles, such as calculating the circumference of a circle using only its diameter. The rule is that, for any circle, the distance around the edge is roughly 3.14 times the distance across the center of the circle.
But Pi is a lot more than this.
"When you look into other aspects of nature, you will suddenly find Pi everywhere," says Dr. Britz. "Not only is it linked to every circle, but Pi sometimes pops up in formulas that have nothing to do with circles, like in probability and calculus."
Despite being the most famous number (International Pi Day is held annually on 14 March, 3.14 in American dating), there is a lot of mystery around it.
"We know a lot about Pi, but we really don't know anything about Pi," says Dr. Britz.
"There's a beauty about it—a beautiful dichotomy or tension."
Pi is tied to ocean and sound waves through the Fourier series, a formula used in rhythms and cycles. Credit: UnsplashPi is infinite and, by definition, unknowable. No pattern has yet been identified in its decimal points. It's understood that any combination of numbers, like your phone number or birthday, will appear in Pi somewhere (you can search this via an online lookup tool of the first 200 million digits).
We currently know 50 trillion digits of Pi, a record broken earlier this year. But, as we cannot calculate the exact value of Pi, we can never completely calculate the circumference or area of a circle—although we can get close.
"What's going on here?" says Dr. Britz. "What is it about this strange number that somehow ties all the circles of the world together?
"There's some underlying truth to Pi, but we don't understand it. This mystique makes it all the more beautiful."
This mystique makes it all the more beautiful."
4. A golden and ancient ratio
The Golden Ratio (or 'ϕ') is perhaps the most popular mathematical theorem for beauty. It's considered the most aesthetically pleasing way to proportion an object.
The ratio can be shortened, roughly, to 1.618. When presented geometrically, the ratio creates the Golden Rectangle or the Golden Spiral.
"Throughout history, the ratio was treated as a benchmark for the ideal form, whether in architecture, artwork, or the human body," says Dr. Britz. "It was called the "Divine Proportion."
The Golden Spiral is often used in photography to help photographers frame the image in an aesthetically pleasing way. Credit: Shutterstock"Many famous artworks, including those by Leonardo da Vinci, were based on this ratio."
The Golden Spiral is frequently used today, especially in art, design and photography. The center of the spiral can help artists frame image focal points in aesthetically pleasing ways.
5. A paradox closer to magic
The unknowable nature of maths can make it seem closer to magic.
A famous geometrical theorem called the Banach-Tarski paradox says that if you have a ball in 3-D space and split it into a few specific pieces, there is a way to reassemble the parts so that you create two balls.
"This is already interesting, but it gets even weirder," says Dr. Britz.
"When the two new balls are created, they will both be the same size as the first ball."
Mathematically speaking, this theorem works—it is possible to reassemble the pieces in a way that doubles the balls.
Duplicating balls is impossible - right? Credit: Unsplash"You can't do this in real life," says Dr. Britz. "But you can do it mathematically.
"That's sort of magic. That is magic."
Fractals, the Banach-Tarski paradox and Pi are just the surface of the mathematical concepts he finds beauty in.
"To experience many beautiful parts of maths, you need a lot of background knowledge," says Dr. Britz. "You need a lot of basic—and often very boring—training. It's a bit like doing a million push ups before playing a sport.
Britz. "You need a lot of basic—and often very boring—training. It's a bit like doing a million push ups before playing a sport.
"But it is worth it. I hope that more people get to the fun bit of maths. There is so much more beauty to uncover."
Provided by University of New South Wales
Citation: The mystique of mathematics: 5 beautiful math phenomena (2020, May 20) retrieved 22 March 2023 from https://phys.org/news/2020-05-mystique-mathematics-beautiful-math-phenomena.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without the written permission. The content is provided for information purposes only.
Dictionary of terms in mathematics from A to Z - POCHEMUKHA.
 RU answers to questions.
RU answers to questions. Axiom is a statement accepted without proof.
The algebraic expression is a number of numbers, denoted by letters or numbers, and connected using the operations of addition, subtraction, multiplication, division, raising to a power, and extracting a root.
Abcissa (French word). One of the Cartesian coordinate points. Is the first. It is usually denoted by the symbol "X". First used by G. Leibniz in 1675 (German scientist).
Additivity. Some property of quantities. He speaks about the following: the value of a certain quantity corresponding to a full-fledged object is equal to the sum of the values of such a quantity that correspond to its parts in any division of a full-fledged object into parts.
Adjunct. Fully corresponds to algebraic addition.
Axonometric. One of the ways to represent spatial figures on a plane.
Algebra. Part of mathematics that studies problems and solutions of algebraic equations. The term was first seen in the 11th century. Applied Muhammed ben-Musa al-Khwarizmi (mathematician and astronomer).
Argument (function). Variable value (independent) with which the value of the function is determined.
Arithmetic. The science that studies operations on numbers. Originated in Babylon, India, China, Egypt.
Asymmetric. Absence or violation of symmetry (inverse of symmetry).
Infinitely large value is greater than any given number.
An infinitely small value is less than any finite value.
Billion. One thousand million (one followed by nine zeros).
Bisector. A ray starting at the corner vertex (divides the corner into two parts).
Vector. Directed straight line segment. One end is the beginning of the vector; the other is the end of the vector. For the first time the term was used by W. Hamilton (an Irish scientist).
Directed straight line segment. One end is the beginning of the vector; the other is the end of the vector. For the first time the term was used by W. Hamilton (an Irish scientist).
Vertical corners. A pair of corners that has a common vertex (formed by the intersection of two lines in such a way that the side of one corner is a direct continuation of the second).
Vector is a quantity characterized not only by its numerical value, but also by its direction.
Graph - a drawing that clearly depicts the dependence of one value on another, a line that gives a visual representation of the nature of the change in the function.
Hexahedron. Hexagon. The term was first used by Pappus of Alexandria (Ancient Greek scholar).
Geometry. Part of mathematics that studies spatial forms and relationships. The term was first used in Babylon/Egypt (5th century BC).
Hyperbole. Open curve (consists of two unrestricted branches). The term appeared thanks to Apollonius of Perm (ancient Greek scientist).
Hypocycloid. This is the curve that the point of the circle describes.
Homothety. An arrangement between figures (similar), in which the lines connecting the points of these figures intersect at the same point (this is called the center of the homothety).
Degree. Unit for flat corner. Equal to 1/90 of a right angle. Measuring angles in degrees began more than 3 centuries ago. For the first time such measurements were used in Babylon.
Deduction. Form of thinking. With its help, any statement is deduced logically (based on the rules of the modern science of "logic").
Diagonal. A line segment that connects the vertices of a triangle (they do not lie on the same side). First used the term Euclid (3rd century BC).
Discriminant. An expression made up of the values that define the function.
Fraction is a number made up of a whole number of fractions of one. It is expressed as the ratio of two integers m/n, where m is the numerator showing how many parts of the unit are in the fraction, and n is the denominator showing how many parts the unit is divided into.
Denominator. Numbers that make up a fraction.
The golden ratio is the division of a segment into two parts so that the larger part is related to the smaller one, as the entire segment is to the larger part. Approximately equal to 1.618. The criterion of beauty, used in architecture, etc. The term was introduced by Leonardo da Vinci.
Index. Alphabetic or numeric index. With its help, mathematical expressions are supplied (this is done in order to distinguish from each other).
Induction. Method for proving a mathematical equation.
Int. Basic concept of mathematical analysis. It arose due to the fact that it took to measure volumes and areas.
Irrational number. A number that is not rational.
Leg. One of the sides of a right triangle that is adjacent to a right angle.
Square Regular quadrilateral (or rhombus). Each corner of the square is a straight line. All angles in a square are equal (by 90 degrees).
Mathematical constant. A value that never changes in its value. A constant is the opposite of a variable.
Cone. A body that is bounded by a single cavity by means of a conical surface. It intersects a plane (the plane is perpendicular to its axis).
Cosine. Is one of the trigonometric functions. The designation in mathematics/higher mathematics is cos.
Equation root - solution, the value of the unknown, found through known coefficients.
The constant is a constant value.
Coordinates are numbers that define the position of a point on a plane, surface, or in space.
Logarithm. Exponent "m". It must be raised to the "a" power in order to get some NT. For the first time, the logarithm was proposed by J. Napier.
Line is the common part of two adjacent surface areas.
Max. Highest value of the function.
Scale. The ratio of two linear dimensions to each other. Used in many modern industries. The main - cartography, geodesy.
Matrix. Rectangular table. It is formed using the set of a number (definite). Includes columns and rows (matrix structure). For the first time, the term "matrix" appeared with the scientist J. Sylvester.
Median. A segment that connects the vertex of a triangle and its midpoint on the opposite side.
Minimum. Smallest value of the function.
Polygon. Geometric figure. The definition is a closed broken line.
Module. Absolute value (real number).
The set is a collection of elements united by some attribute.
Norm. The absolute value of the number.
The inequality is two numbers or expressions connected by signs (greater than) or (less than).
Oval. Convex, closed figure (flat).
Circle. Numerous points located on a plane.
Ordinate. One of the Cartesian coordinates. It is usually designated as the second.
Octahedron. Geometric figure. One of the five polyhedra (regular). The octahedron includes 8 faces (regular), 6 vertices and 12 edges.
Parallelepiped. Prism. The base is a parallelogram or a polyhedron (equivalent concepts). Has 6 edges. Each face is a parallelogram.
Has 6 edges. Each face is a parallelogram.
Parallelogram. Quadrilateral. Its opposite sides are parallel (in pairs). At the moment, there are 2 special cases of a parallelogram: a rhombus and a square. The main property of this geometric figure:
• Opposite sides are equal;
• Opposite angles are equal.
Perimeter. The sum of all sides of a geometric figure. For the first time it was possible to meet at Archimedes and Heron (ancient Greek scientists).
Perpendicular. A straight line that intersects a plane (any) at a right angle.
Pyramid. Polyhedron. Its base is a polygon. Any other face is a triangle (these faces have a common vertex). At the moment, pyramids can be of various types: triangular, quadrangular, and so on (they are distinguished by determining the number of corners).
Planimetry. One of the most important parts of elementary (simple) geometry. Planimetry studies the properties of figures that are on a plane. For the first time, the term was designated by Eculid (an ancient Greek scientist).
Planimetry studies the properties of figures that are on a plane. For the first time, the term was designated by Eculid (an ancient Greek scientist).
Plus. A sign that denotes a mathematical operation - addition. In addition, positive numbers are denoted with a plus. For the first time, the sign was introduced by J. Vidman (a famous Czech scientist).
Limit. The basic concept of mathematics. Denotes: a variable value approaches a constant value (defined) indefinitely. The term was first used by the famous scientist Newton.
Prism. Polyhedron. The first 2 faces are equal angles (these are the bases of the prism). The rest is the side faces.
Projection. One of the ways to depict spatial and flat figures.
Variable is a value whose numerical value changes according to a certain, known or unknown law.
Plane is the simplest surface. Any line connecting two of its points belongs entirely to it.
Any line connecting two of its points belongs entirely to it.
Line is a set of points common to two intersecting planes.
Percentage is a hundredth of a number.
Radian. Angle unit.
Rhombus. Parallelogram. All sides of this figure are equal. A rhombus having right angles has the term "square".
Segment. Part of a circle (limited by a chord that connects the ends of the arc).
Secant. Trigonometric function. The designation in mathematics/higher mathematics is sec.
Sector. Part of a circle. Constrained by a circle + two radii (connects the ends of one arc to the center of the circle).
Symmetry - match.
Sinus. Trigonometric function. The designation in mathematics / higher mathematics is sin.
Stereometry. Part of elementary geometry. Engaged in the study of full-fledged spatial figures.
Part of elementary geometry. Engaged in the study of full-fledged spatial figures.
Tangent. Trigonometric function. The designation in mathematics/higher mathematics is tg.
Tetrahedron. Polyhedron, includes 4 triangular faces. Each vertex has 3 faces (converge at the vertices). A tetrahedron has 4 faces + 6 edges + 4 vertices.
Dot. Has no definite and final concept. Any point is denoted by letters A, B, C.
Triangle. Polygon (simple). Includes 3 tops + 3 sides;
Theorem is a statement to be proved based on axioms and previously proven theorems.
Identity is an equality valid for all values of the coefficients included in it.
Topology is a branch of mathematics that studies the properties of figures that do not change under any deformations carried out without ruptures and gluing.
An equation is a mathematical notation of the problem of finding the values of unknowns under which the values of two given functions are equal.
Angle. Geometric figure (flat). It is formed by two rays that come out of one point (the points are the corner vertices).
Factorial is the product of natural numbers from 1 to any given natural number n. Denoted n!. Factorial of zero o! = 1.
The formula is a combination of mathematical symbols that expresses a sentence.
Function is a numerical relationship between elements of two sets, in which one element of one set corresponds to a certain element of another set. Can be given by formula or graph.
Chord. A segment that connects 2 points on a circle.
Digits are symbols for numbers.
Central The middle of something (for example: a circle).
Cyl. A body bounded by a cylindrical surface + parallel planes (two). For the first time, the concept of "cylinder" could be found in Euclid and Aristarchus.
Compass. Special instrument designed for drawing arcs, linear measurements and circles.
Numerator. A specific number with which a fraction is composed. The term was first used by Maxim Planuda (Byzantine scholar).
The number is one of the basic concepts of mathematics that arose in connection with the counting of individual objects.
Ball. Geometric body. It is the total set of all points in a certain space.
Exhibitor. Same as exponential function. The term was first introduced by G. Leibniz (a German scientist).
Ellipse. Oval curve. For the first time this term was introduced by Apollonius of Perga (an ancient Greek scientist).
How to Invent a Mathematical Concept
If math is not good for you, it may not be about you, but how it is presented to you. Jason Wilks in his book Math on Fire. Non-boring non-textbook" turns the usual idea of mathematics as a boring and abstract discipline that only remains to memorize, and invites you to invent your own mathematics.
 Yes, yes, you read that right - invent.
Yes, yes, you read that right - invent.
Jason Wilkes
Mann, Ivanov & Ferber, 2020
Before we create an analysis, we need to learn how to create things. More precisely, we need to understand how to develop mathematical concepts. Let's illustrate the process with two simple examples: the area of a rectangle and the steepness of a line. We will see later that these two concepts form the backbone of the analysis. The first is the basis for the "integral", the second is for the "derivative". These concepts are opposite, and the exact meaning in which they are opposite is described by the so-called fundamental theorem of analysis (the Newton-Leibniz formula).
Don't worry if you already know how to calculate them. Anyone will gain something from discussing these issues - either in their understanding or in teaching them, since the process of invention is rarely discussed.
When we invent mathematics from scratch, we always start with an intuitively clear everyday concept. The invention process contains an attempt to translate a fuzzy qualitative idea into a precise quantitative one. No one can truly represent an object in five, seventeen, or an infinite number of dimensions. How are mathematicians going to define something like "curvature" in a way that allows them to talk about the curvature of high-dimensional objects? How did a person come to the necessary definitions, when they are often so abstract that one seems to need to have superhuman abilities for multidimensional intuition in order to “see” the truth?
The invention process contains an attempt to translate a fuzzy qualitative idea into a precise quantitative one. No one can truly represent an object in five, seventeen, or an infinite number of dimensions. How are mathematicians going to define something like "curvature" in a way that allows them to talk about the curvature of high-dimensional objects? How did a person come to the necessary definitions, when they are often so abstract that one seems to need to have superhuman abilities for multidimensional intuition in order to “see” the truth?
This process is not as mysterious as it seems. Creation is just a transition from qualitative to quantitative
I hope that explicit teaching of the process of creation at all levels of mathematics will one day find its rightful place in the curriculum, along with less important issues like addition, multiplication, lines, planes, circles, logarithms, groups Syulov, fractals and chaos, […] and everything else that we teach mathematics students from elementary school to doctoral studies. But this is much more important than .
But this is much more important than .
Mining in our brains: the invention of the area
[…] The fact that a rectangle with a length of l and a width w has an area of lw is simple, and you almost certainly know it. Try to forget it. Let's imagine that we have no idea that the area of a rectangle is the product of its length and width.
Suppose we know roughly what we mean by "area" in the non-mathematical sense. In other words, we know it's a word that describes how big a two-dimensional thing is, but we don't know how to relate this concept to something mathematical. At this stage, we can use the abbreviation A (area) for area and write a useless phrase like A = ? , but no more. However, based on our everyday non-mathematical representation, we know the following for certain.
The first consideration of our everyday conception. Whatever we mean by the area of a rectangle, it somehow depends on its length and width. If someone has a definition of area that doesn't include length and width, that's nice, but that's not what we mean by area.
If someone has a definition of area that doesn't include length and width, that's nice, but that's not what we mean by area.
Think of an abbreviation for these words. We can express the above in an extremely condensed form by writing:
A (l, w) = ?
instead of A = ? as above. The new something inside the brackets says: “This is somehow dependent on the length and width, and we will reduce them to l and w . I don't know anything else."
[…]
Since we are building the exact mathematical concept of area, starting with an intuitive everyday representation, we have no numbers to start from. If we don't have anything quantitative to start with, we have to start with a qualitative one. Since there are no laws to tell us what to do, we want to ensure that our precise concept matches our everyday one. Let's see what else our everyday mathematical representation says.
The second consideration of our everyday representation. Whatever we mean by the area of a rectangle, if we double the width without changing the length, we will have two copies of the original rectangle and the area will double. If someone has a definition of area that doesn't behave like this, that's nice, of course, but that's not what we mean by area.
Whatever we mean by the area of a rectangle, if we double the width without changing the length, we will have two copies of the original rectangle and the area will double. If someone has a definition of area that doesn't behave like this, that's nice, of course, but that's not what we mean by area.
Whatever we mean by area, if we double the width of a rectangle without changing the length, the area must double. show: if we double the width, the area will double (leave the length unchanged for now). We can write this idea like this:
A (l, 2w) = 2A (l, w).
For the same reasons, if we double the length without changing the width, the area will also double. We can shorten it like this:
A (2l, w) = 2A (l, w).
It is not necessary to use doubling in this sentence. If we triple the width, then we get three copies of the original piece and the area triples. The same can be said about length, quadrupling, or multiplying by any other whole number. What about non-integer numbers? Let's say if we change the length from l to "one and a half l " (without changing the width), then we get one and a half copies of the original figure; accordingly, the area should be one and a half times larger than the original. It turns out that whatever we mean by area, sentences of this kind reflect our intuition that the amount of increase is not important. We can write this whole infinite set of sentences at once like this:
What about non-integer numbers? Let's say if we change the length from l to "one and a half l " (without changing the width), then we get one and a half copies of the original figure; accordingly, the area should be one and a half times larger than the original. It turns out that whatever we mean by area, sentences of this kind reflect our intuition that the amount of increase is not important. We can write this whole infinite set of sentences at once like this:
A (#l, w) = #A (l, w) (1.1)
and
A (l, #w) = #A ( l, w) (1.2)
[…]
Equations 1.1 and 1.2 tell us that we can pull numbers from the Area Calculation Machine regardless of their value. But if this is true, nothing prevents us from being dexterous and pulling out the length and width ourselves! After all, they are just numbers. Since l is the same as l ⋅ 1, and w is the same as w ⋅ 1, we can quietly use both facts from Equations 1. 1 and 1.2 for the numbers themselves l and 0 w It turns out like this:
1 and 1.2 for the numbers themselves l and 0 w It turns out like this:
A (l,w)= lA (1,w)= lwA (1,1). (1.3)
And this shows that the area of the rectangle is the length times the width... and something else. What is this A (1, 1) doing here?!
It turns out that equation 1.3 shows us the concept of units of measure. It says that we can find the area of any rectangle, but only after we set the area of a single rectangle - with length 1 and width 1 (or whatever). If we measured lengths in light years, we would like A (1, 1) would be the area of one square light year. If we measured lengths in nanometers, we would like A (1, 1) to be the area of one square nanometer.
We usually get out of this situation by assuming that A (1, 1) should be 1. But this is just for convenience. We could choose to have A (1, 1) represent the number 27 if we wanted, and then we would have the formula A (l, w) = 27lw . It looks strange, but there is no error here. Instead of being forced to count A (1, 1) as a unit or some other number, we can interpret equation 1.3 differently:
It looks strange, but there is no error here. Instead of being forced to count A (1, 1) as a unit or some other number, we can interpret equation 1.3 differently:
This shows that we do not need to talk about units (in other words, decide what A (1, 1) should be at our request), but we can no longer talk about the squares themselves. This interpretation says that something equals the length times the width, but it is not the area. This is the "ratio" of areas, or how many times can you fit A (1, 1) into A (l, w) .
[…]
It is easy to see that the same argument will work in any number of dimensions. Imagine that we have a three-dimensional thing like a box, and let's denote its length, width and height as l, w and h . For the same reasons as for a rectangle, if we double, for example, the height without changing the length and width, we get two original boxes, and the volume should double. As before, it is not necessary to double exactly, you can increase it any number of times. The same for length and width. Accordingly, in three dimensions, such statements are true for any number #, which is not necessarily the same in the following three sentences:
The same for length and width. Accordingly, in three dimensions, such statements are true for any number #, which is not necessarily the same in the following three sentences:
V (#l, w, h) = #V (l, w, h),
V (l, #w, h) = #V (l, w, h),
V(l, w, #h) = #V(l, w, h).
As before, we can use these ideas for the numbers l, w and h themselves and write:
V (l, w, h) = lwh⋅V (1, 1, 1).
Now you can do something weirder and more interesting: start talking about higher-dimensional spaces. If n is some big number, we can't draw anything in n-dimensional space. Nobody is actually can't. At this stage, we are not even quite sure that we mean by the expression " n -dimensional space". Great! Nobody bothers to say: “Whatever I mean by n -dimensional space and n -dimensional version of a rectangular thing like a box, they should behave similarly enough to their “relatives” in two and three dimensions, and we can apply the same arguments as just used.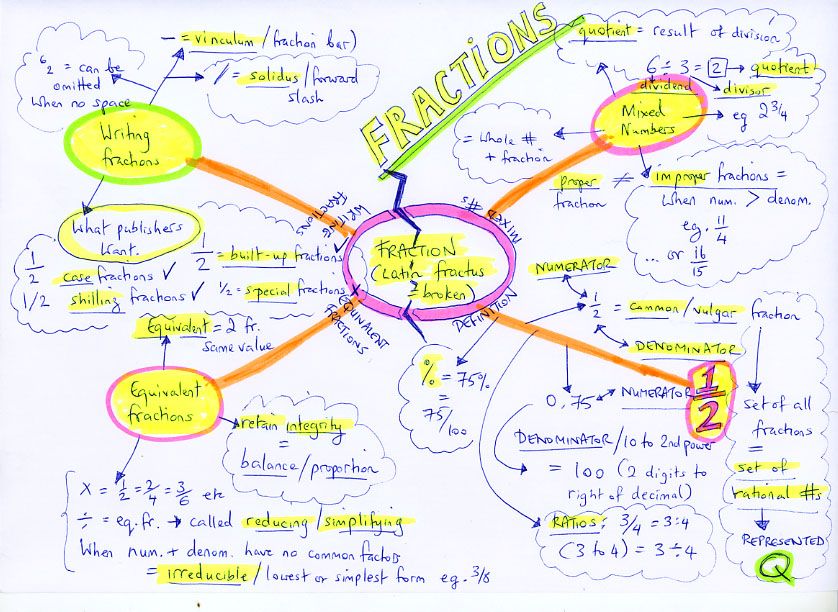 And if they don't behave like that, that's just not what I mean by now n -dimensional space". Then we can emphatically write:
And if they don't behave like that, that's just not what I mean by now n -dimensional space". Then we can emphatically write:
V (l1, l2,… , ln) = l1l2⋅⋅⋅ln⋅V (1, 1,… , 1),
where V stands for "what we wish to call volume in n -dimensional space". Moreover, we decided not to give all directions their own strange names, as for two and three dimensions. It's easier to shorten them to the letter l , and then attach different numbers to each to call them separately (l1, l2, ..., ln).
[…]
So we see that in the process of thinking about our everyday concept of area while reducing our thoughts in a way that reduces infinitely many sentences into one, our vague ideas led to the fact that the area of the rectangle should be lw A ( eleven). So we discovered not only the familiar formula "length times width", but also one more thing that we forgot to consider: the concept of units of measurement. However, mathematics kindly reminded us of this.
[…]
1.2.2. How to Do It Wrong: Instruction on the Foolishness of Memory
But it took several years before I realized that teaching science is really hard work. The goal should not be to implant in the student's head the facts that the teacher knows; it is necessary to introduce a way of thinking that will allow in the future to master in one year what the teacher studied for two years. Only in this way can we move from one generation to the next. And when I realized this, my teaching style changed: not to give a bunch of fragments, but to analyze only a few problems, but with real depth.
Edwin Jaynes, Jaynes E. T. A Backward Look to the Future. http://bayes.wustl.edu/etj/articles/ backward.look.pdf.
One of the worst things about many elementary math courses (at least the ones I have) is that the instructors somehow become staunch believers that the purpose of the course is to tell you facts. I can no longer agree with this. You will be surprised: what can the course be about, in my opinion, if not about mathematics? This is important, let's say it once and for all and put it in a frame. ❓Why write it in a frame with such a pretentious name? Good question! Full disclosure: when you're writing a book (as I've learned since I started writing), it's fun to show respect for something you love sometimes. This box is a tribute to my favorite textbook, published after the death of the author, the main work of Edwin Jaynes, The Theory of Probability. The logic of science. Perhaps because he died before completing the book, but also because Jaynes was a fiery man and this work is full of his wonderfully soulful personal witticisms and much more that is rarely found in textbooks. For example, "Declaration of Emancipation" in Appendix B. I've always liked this section. Now I am writing my book in tribute to Jaynes. He deserved it.
You will be surprised: what can the course be about, in my opinion, if not about mathematics? This is important, let's say it once and for all and put it in a frame. ❓Why write it in a frame with such a pretentious name? Good question! Full disclosure: when you're writing a book (as I've learned since I started writing), it's fun to show respect for something you love sometimes. This box is a tribute to my favorite textbook, published after the death of the author, the main work of Edwin Jaynes, The Theory of Probability. The logic of science. Perhaps because he died before completing the book, but also because Jaynes was a fiery man and this work is full of his wonderfully soulful personal witticisms and much more that is rarely found in textbooks. For example, "Declaration of Emancipation" in Appendix B. I've always liked this section. Now I am writing my book in tribute to Jaynes. He deserved it.
[…]
Mathematics is a whole world in which there is nothing accidental and where the mind can educate itself in such an intense and clear way that it cannot come out with another discipline. What's more, as you train your mind, you'll learn along the way a subject that happens to describe everything in the world. This is incredibly useful, but such practicality is a side effect of mind training. If we talk about what is useful and worth putting in a frame, here's something else that you will never be told.
What's more, as you train your mind, you'll learn along the way a subject that happens to describe everything in the world. This is incredibly useful, but such practicality is a side effect of mind training. If we talk about what is useful and worth putting in a frame, here's something else that you will never be told.
Once we understand this, we immediately notice two things. First, it's obvious why training the mind in this way is beneficial, no matter what you do. Secondly, it is obvious that mathematics courses focus on exactly the wrong things.
Let's study a specific example. In algebra classes, class-filled sleepy students are taught about something called the FOIL method. This stands for First, Outer, Inner, Last - "first, outer, inner, last." transl.
This is a rule for remembering sentences like:
(a + b)2 = a2 + 2ab + b2
or more generally
(a + b) (c + d) = ac + ad + bc + bd.
We already see that FOIL is a way to help you remember a fact about math, rather than rediscovering it every time you need it. What is the point here? Most students can see her better than teachers: she's not here. Let's invent both facts so that we never have to remember them again.
What is the point here? Most students can see her better than teachers: she's not here. Let's invent both facts so that we never have to remember them again.
Fig. 1.4. Here, in fact, everything that the FOIL 9 rule says0005
If we take a sheet of paper and draw a picture on it, it will not change the area of the sheet. It doesn't matter what we depict: a house, a dragon or something else. Let's say we're experimenting with the ideas we've found and stumble upon what looks like (a + b)2. We can think of this as the area of a square.
If a square has side length tili-tili , its area is ( tili-tili ) · ( tili-tili ), or ( tili-tili )2. So we can think about ( a + b )2 as for the area of a square with a side ( a + b ). Let's draw this square, and then add a picture to it, as in Fig. 1.4. It looks like something lopsided with signatures, but these are just two straight lines that divide the sides into parts with lengths a and b . This makes it possible to talk about the same thing in two ways. Since drawing lines on a square does not change its area, we see that:
This makes it possible to talk about the same thing in two ways. Since drawing lines on a square does not change its area, we see that:
(a + b)2 = a2 + 2ab + b2.
Now you don't need to remember this formula. Let's see if we can invent a more complex one in the same way:
(a + b) (c + d) = ac + ad + bc + bd.
Fig. 1.5. Here, really, everything that the FOIL rule says
Any two multiplied numbers, that is, in general form ( tili-tili ) ⋅ ( trali-vali ), can be represented as the area of a rectangle with sides of length tili-tili and trali - Vali. Draw a picture where ( tili-tili ) is ( a + b ) and ( trali-wali ) is ( c + d ). Look at fig. 1.5. It shows that the area of the large rectangle is the sum of the areas of all the small ones. The essence of the picture can be expressed in a compressed form:
(a + b) (c + d) = ac + ad + bc + bd.
Now you don't need to remember this formula. If you forget it, you can reinvent it. You don't even have to try to memorize these formulas. Better even try to forget them immediately! In each math classroom, an inscription should be posted above the board:
If you forget it, you can reinvent it. You don't even have to try to memorize these formulas. Better even try to forget them immediately! In each math classroom, an inscription should be posted above the board:
Since your goal is to follow the path of reasoning on your own, you should not memorize the steps in this derivation, it is better to understand its essence well so that if you forget any formula (which should do ), you can immediately reinvent it in a few seconds . When you do this, you find yourself "remembering" things inadvertently, simply because you understand them well. To test if this Zen process of "learning without memorization" has been successful for you, you can test whether you can apply this line of reasoning to something new ?
The logic is that if you can apply the same reasoning to new areas you've never seen, you won't just memorize facts. Unfortunately, in an environment that punishes experimentation and failure (such as in school), testing things in new contexts becomes more of a source of anxiety rather than the intellectually satisfying game it should be.
Let's forget all this and just play.
Inventing something
Above, we discussed the silly acronym FOIL for the First, Outer, Inner, Last construct. This method of remembering the fact rather than understanding the process leads us to create numerous "methods" and we will have to remember them. For example, it is true:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac.
This is an ugly sentence and no one in their right mind would want to memorize it. If our goal was just to capture this, rather than understand general reasoning strategies, we could take the same approach as the guy who invented the FOIL acronym and call it the LT.MT.RT.15.16.24.26.34.355 method. Let's not do that. Instead, use the same strategy as above (drawing a picture and looking at it carefully) to invent this ugly expression for yourself. Hint: draw a square and divide each side into three parts instead of two as before.
Now it's time to play around in three dimensions and see if the same reasoning doesn't work here.
We really don't want to remember an ugly sentence like this:
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Instead of memorizing this, let's invent it in the same way as before: draw a picture and look at it carefully. Hint: draw a cube and divide each side into two parts. Study fig. 1.6. Try the first example first: it's harder to visualize in this case, and if you get stuck, it's easy to get discouraged and think you don't get the idea when you really do.
Fig. 1.6. This picture may help in inventing the formula in 2
Although this method of reasoning allows us to invent things that others have asked us to remember, there are two unfortunate circumstances. First, it's not that easy (I'll explain why shortly). Secondly, it's basically useless for things like (a + b)4 or (a + b)100 , because it's hard for the human mind to visually represent objects if there are more than three dimensions. It turns out that there is a remedy for both problems.
[…]
Suppose we have a sheet of paper. Imagine that it is torn into two arbitrary parts. Even if we do not know anything about areas numerically, it is clear that the area of the original sheet is equal to the sum of the areas of the two scraps. We can rediscover the FOIL method and all its more complex variants in any number of dimensions (regardless of whether we are able to draw a suitable picture or not) simply by applying the idea of tearing over and over again. Let's write it in an abbreviated form.
Fig. 1.7. The obvious law of tearing: if you tear something into two parts, the area of the original object will be equal to the sum of the areas of these two fragments. We can say it in short: (a + b) ⋅ (something) = a ⋅ (something) + b ⋅ (something). Textbooks usually call this "distributive law"
Let's say we're inventing something and we get to the point where we write something like (something) ⋅ (a + b) or perhaps (a + b) ⋅ (something) .
It's the same thing, the reasoning works for both cases. Let, as before, we can represent this as the area of a rectangle, two sides of which are (something) , and the other two are (a + b) . If we tear it exactly along the line, as shown in fig. 1.7, we get one piece with an area of a ⋅ (something) and the second square b ⋅ (something) . This doesn't change the total area (we don't throw away any parts), so the following should be true:
(a + b) ⋅ (something) = a ⋅ (something) + b ⋅ (something).
I will call this the obvious law of tearing things apart, but the name is not important here. Call it whatever you want. Textbooks use the term "distributive law". It sounds pretentious, but such a name also makes sense. […]
Now, if we want everything to look like in a textbook, we can write the letter c instead of 9 in the obvious law0430 (something) . This is fine too, I wrote (something) to remind you that the law is true no matter what (something) looks like.
If it turned out to be the sum of two things (or if we wanted to put it that way), we could replace (something) with something like (c + d) and rewrite the obvious law:
(a + b) ⋅ (c + d) = a ⋅ (c + d) + b ⋅ (c + d).
However, using the obvious law again (for each of the parts on the right), we get:
(a + b) ⋅ (c + d) = ac + ad + bc + bd,
that is exactly the expression that we invented earlier when drawing pictures. The above sentence is also a FOIL method. But since we invented it by means of an obvious law, we don't need to memorize it. Ready, attention, forget it forever!
The obvious law looks ordinary. In addition, it turns out that he offers us a window into higher dimensions. The visual way of thinking about (a + b)3 requires drawing a 3D object (a cube), and we quickly notice that the method doesn't help us much for (a + b)4 or any higher degrees, because we cannot imagine four-dimensional objects.
But even if we are not interested in algebraic tediousness like decomposing (a + b)4 for our own benefit, we may be interested in deeper questions, such as how to cut a four-dimensional cube along each of the three-dimensional "surfaces", none of which we can represent due to the limitations of the human brain. But it is we primates who are faced with the problems of the visual method, and the obvious law has no such limitation. Therefore, if desired, we could apply the obvious law to something like a decomposition (a + b)4 several times, and once we have completely unraveled it, the resulting (very long) expression would provide us with a little insight into four-dimensional geometry. For example, the number of terms in the final expression would be the number of pieces into which a four-dimensional cube can be cut along three-dimensional planes. I have no idea how to portray what I just said, but it's true! So should be . Just by using the everyday fact of tearing a rectangle in two, we can coax a mathematician into telling us something that is far beyond the imaging capabilities of the human brain.