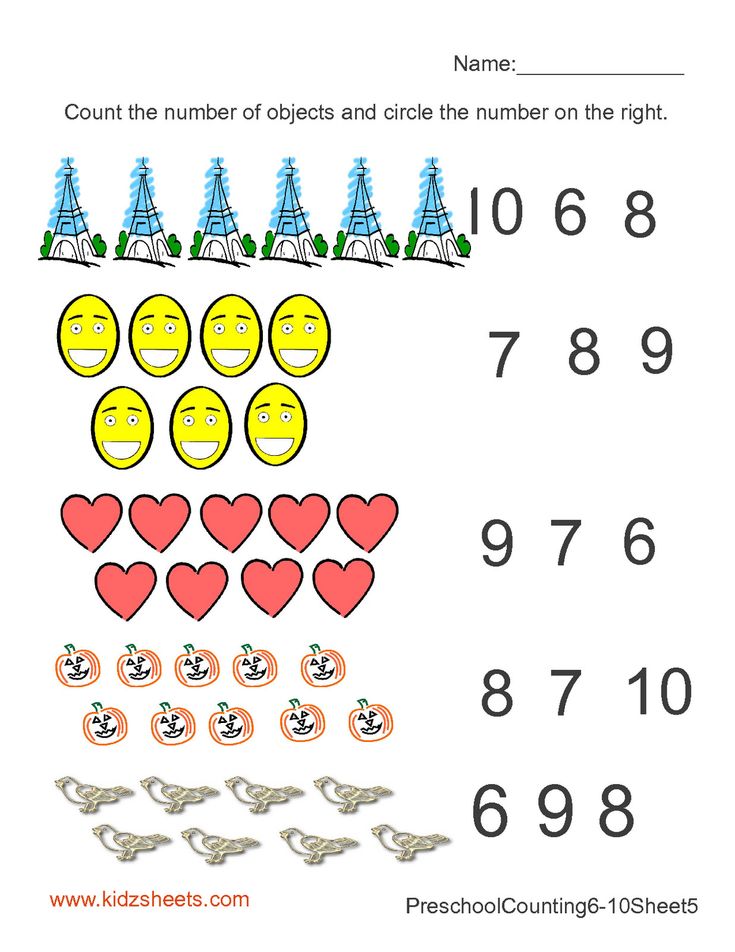
Learning how to count

How Children Learn to Count

• Education
• Maths Tips
• 5 and under

Counting is easily taken for granted but there's a lot of fascinating research into how we learn to count - and there's more to it than you may think.

The mathematical brain

It’s first worth considering where our capacity to do mathematics comes from.

Neuropsychologist Brian Butterworth in his book “The Mathematical Brain” suggests we’re born with an innate sense of number hard-wired into our brain and he attributes this to a small region of the brain behind the left ear he calls "the number module". He compares this idea to colour – in the same way we perceive the “greenness” of a leaf we can also perceive the “twoness” or “threeness” of a group of objects.

Take counting. Like times tables and algebra, we tend to think it's something kids have to be taught. Wrong, says Butterworth - it's an instinct. Sure, we have to learn the names and symbols of numbers to develop that instinct, but, because the number module is hardwired into the brain, basic counting comes naturally.

Remote tribes can count even when they have no words for numbers. In maths as in language he believes, "kids start off with little starter kits" And their maths starter kit is the number module.

There are other theories too - such as maths being an extension of our spatial awareness – but there’s something nice in the idea of a “little maths starter kit”.  

A Word of warning - All this doesn't mean a child is predestined to be either good at maths or not. Far from it, we’re all born ready to learn maths – and it’s what happens in the first 10 years or so that sets us up.

Counting with toddlers

Research suggest that toddlers - even as young as 12 months - have a sense of how many there are in a set - up to around three objects. This comes from their innate sense of number.

Counting is learned when the toddler starts making the connection between this innate sense of "how many there are" and the language we use to count "one, two, buckle my shoe". This is the first stage in learning maths and it's the building block for many early concepts.

Should parents count with their toddlers? Absolutely, using a variety of real objects. And since counting and language are interlinked reading to your toddlers is equally, if not more, important.

Counting - early learning milestones

Here are some stages of learning to count that you may notice your child going through at ages 3 to 5:

• Recognising how many objects are in a small set without counting. So if you show your child four apples they won't have to count them to tell you there's four.
• Knowing the "number words" from one to ten and their order.
• Know the sequence regardless of which number they start on. So if you say "start counting at four" they will count "four, five . ." as opposed to always counting from one.
• Conservation of quantity - This is where children realise that the number of objects in a set stays the same unless any are added or removed. So if they count six cans of beans in a straight line, then you rearrange the beans ( in front of their eyes ) into say two stacks of three - they will realise there's still six without recounting.
• Counting non-visible objects - your child will realise they can count things they can't touch or even see - such as sounds, members of someone else's family, or even ideas.
• Cardinality, not to be confused with carnality - This is knowing that the last number counted is equal to the quantity of the set. If your child counts six oranges 1,2,3,4,5,6 and then you ask "how many oranges are there"? and they count them again then they haven't grasped "cardinality".

Counting on - as a step towards adding

Learning to add comes as an extension of counting. Here are some stages a child goes through to make this connection:

• Counting all - For 3 + 5, children will count "one, two, three" and then "one, two, three, four, five"  to establish the quantity of the sets to be added – for example, three fingers on one hand and five fingers on the other. The child will then count all the objects "one, two, three, four, five, six, seven, eight"
• Counting on from the first number - Some children come to realise that it is not necessary to count the first number to add. They can start with three, and then count on another five to get the solution. Using finger counting, the child will no longer count out the first set, but start with the word ‘Three’, and then use a hand to count on the second added: ‘Four, five, six, seven, eight’.
• Counting on from the larger number -  It's more efficient when the smaller of the two numbers is counted. The child now selects the biggest number to start with which is "five", and then counts on "six, seven, eight".
• The final stage isn't really counting - it's where learners know their number facts and skip the time-consuming counting altogether.

Number lines are great visual tools for making this connection between "counting on" and addition or subtraction - we use them in Komodo a lot. Here's an earlier blog article all about number lines.

Beyond basic counting

Counting is the first mathematical pattern learners encounter. From here they soon begin to count backwards which is a step towards subtraction and they'll also count in twos, fives and tens which are a foundation for multiplication.

The next big step is the idea of place value and counting to base 10. Learners often make this leap simply because it's an obvious and efficient way to count large numbers. In Komodo, we use practice examples like this to help learners make the connection to counting in tens and ones.

It's easy to forget that counting is a key concept in maths with many stages before it's mastered. There's certainly a lot more to it than one, two, three!

I'm Ged, Co-founder of Komodo, ex-maths teacher and dad. If you have any questions please get in touch.

About Komodo - Komodo is a fun and effective way to boost primary maths skills. Designed for 5 to 11 year olds to use in the home, Komodo uses a little and often approach to learning maths (15 minutes, three to five times per week) that fits into the busy routine. Komodo users develop fluency and confidence in maths - without keeping them at the screen for long.

Find out more about Komodo and how it helps thousands of children each year do better at maths - you can even try Komodo for free.

Related Posts

Mindset - the path to mastery

People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.

Top tips to de-stress homework time

Homework can be a trigger for some of the worst fights and arguments that we have with our children. Here are some solutions that can help reduce tensions and get homework done without arguments.

Learning to Count: 9 Ways to Help Your Child

• Home
• >
• Blog
• >
• How to Teach Counting: All You Need to Know

Jessica Kaminski

14 minutes read

March 8, 2022

Counting is a fundamental skill alongside reading, and kids should start learning to count much earlier than in pre-K. While counting seems simple, it’s a more complicated process under close consideration, especially when you explain it to kids.

From this article, you will learn about stages of counting, its components, as well as strategies and fun ways to teach this topic. Keep reading to learn about counting stages.

Developmental Stages of Counting

We perceive counting as a uniform process, but only because we count automatically without even thinking about it. In reality, counting consists of several stages. Let’s describe them in detail and explain how children learn counting below:

Count All

There is a group of items – five apples on the table. If you ask your kid to tell you how many apples there are, they will count them one by one. One, two, three, four, five.

It is the first stage of counting, and it’s called count all – children have to count all items one by one to tell how many of them there are.

Count on

Let’s say you put three oranges on the table next to the five apples we mentioned previously. Afterward, you ask a student to tell you how many fruits there are on the table in total.

At this point, a student will start counting from five: five, six, seven, eight – there are eight fruits on the table.

This counting stage is called count on because kids can perceive previously counted objects as a single entity and start counting from the previous result.

Maintain Cardinality

Let’s say you add five more apples to the table again and ask a student to tell you how many there are in total.

At this point, a student keeps in mind two groups of objects, five apples and three oranges, and considers them one entity – eight fruits.

Then, they start counting new apples from eight – nine, ten, eleven, twelve, thirteen. There are thirteen fruits on the table. Such an approach means maintaining cardinality.

What Are Different Components of Counting?

Before children begin learning counting stages, they have to learn the numbers. Consequently, parents should introduce kids to numbers and numerals in the first place. Once kids learn to pronounce numbers and write associated symbols (five is the same as 5), you can proceed to different counting components.

Rote Counting

Rote counting is counting in sequence up to a certain point – one, two, three, four, five. For instance, you ask a student to count to eight. They start – one, two, three, four, five, six, seven, eight. They count numbers without violating a sequence and up to a certain point, which is eight in our case. If students perform this task without mistakes, you can proceed to other counting components.

One-to-one Correspondence

Understanding one-to-one correspondence is key to counting. It’s the ability to associate an item with a number word. Let’s recall apples once again to illustrate how one-to-one correspondence works:

1. A kid sees five apples on the table.
2. They point at an apple and pronounce “one.”
3. They point at another apple and pronounce “two.”
4. They repeat the same pattern until they pair all the available apples with numbers according to the number sequence “five apples – five numbers”: one, two, three, four, five.

Once children pair items with numbers, they consider them “counted” and leave them behind, switching to other objects. They realize that one item equals one particular number, hence one-to-one correspondence.

Cardinality

Cardinality is the understanding of the last number in a sequence as the property of a group of items. Thus, in a set of five apples, the number five is the group’s property, which means this quantity includes five objects. Consequently, children can perceive it as a single entity labeled “five,” with five being a quantitative property of this entity.

When to Teach Counting to Your Kid

Children start learning how to count numbers as early as they begin to recognize letters. By the age of five, kids fully realize one-to-one correspondence, count by ten, understand cardinality, and count items in the groups. It means parents should start working on their kid’s counting skills as early as the age of three and four.

How to Teach Counting to 100: Top Strategies

Teaching counting to 100 requires continuous practice and teaching strategies:

#1 How to Teach Counting by 10s Using Coloring Books

You can incorporate math coloring and drawing books where children draw pictures by connecting the numbered dots. It’s one of the best tools to practice number order with fun.

#2 Teaching the Concepts of Fewer and More

You have to introduce children to the concepts of fewer, less, more, or many using illustrative examples:

• Place four red candies on the table.
• Place two blue candies on the table separately.
• Count red sweets – one, two, three, four.
• Count blue treats – one, two.
• A kid will observe that there are visually more red candies than blue sweets on the table.
• Explain to them that we use the word “more” when we speak about a greater amount when comparing something. Plus, you will illustrate why 4 is bigger than 2 – it’s visually clear.
• Do the same with the concept of “fewer.” There are fewer blue candies than red ones.

#3 How to Teach Counting to Kindergartners Using Fruits

It’s so much easier to teach kindergartners to count using fruits. You can incorporate the following fun counting activities:

Pick Fruits

Fruits are not only healthier than sweets but also good for counting drills. Imagine your kid is going to play outdoors. Let them prepare snacks on their own; take fruits and sandwiches. Let them count apples/oranges or whatever fruit they take. This drill develops decision-making and counting skills at the same time.

Cook Together

Cooking provides endless counting opportunities since each recipe requires calculations. So grab your child and prepare fruit salads together.

How many bananas do you need? Ask your child to bring the required number. How many times do you need to cut a pomegranate to extract its seeds easily? These activities involve a lot of counting.

#4 Using Toys to Teach Counting

Children and toys are inseparable. 84% of American kids play with toys for up to six hours a day. Why not dedicate at least half an hour to counting? Using LEGO is the easiest way to teach counting to preschoolers. This method also helps with teaching counting on as long as you group bricks by color, shape, etc.

Encourage your child to count LEGO parts they use for creations – you can do it naturally by playing with your kid, not just commanding them to count LEGO bricks.

How to Teach Counting and Increase Counting Skills with Fun

You can come up with a lot more ways to teach counting to kids with fun – games, toys, and songs. Let’s get into this in detail.

#5 Counting Games

Check out a few fun counting games below:

Draw Whatever You Imagine Game

Children love to draw, and it’s an excellent chance to develop imagination and strengthen counting skills at the same time. Play an awesome drawing game and note its rules:

• Ask your kid to draw animals, let them be frogs – two, three, four frogs – you name the number.
• Ask your kid to draw an imaginary animal with eight eyes, four wings, five legs, three tails, etc. It’s up to you and your kid to decide.

Outdoor Hunting Counting Game

You can count objects and items while walking and make it a fun game. Here is the concept:

Your kid notices particular items, cars, or animals within your walking route and counts them. Once they count by a particular number, they get a reward.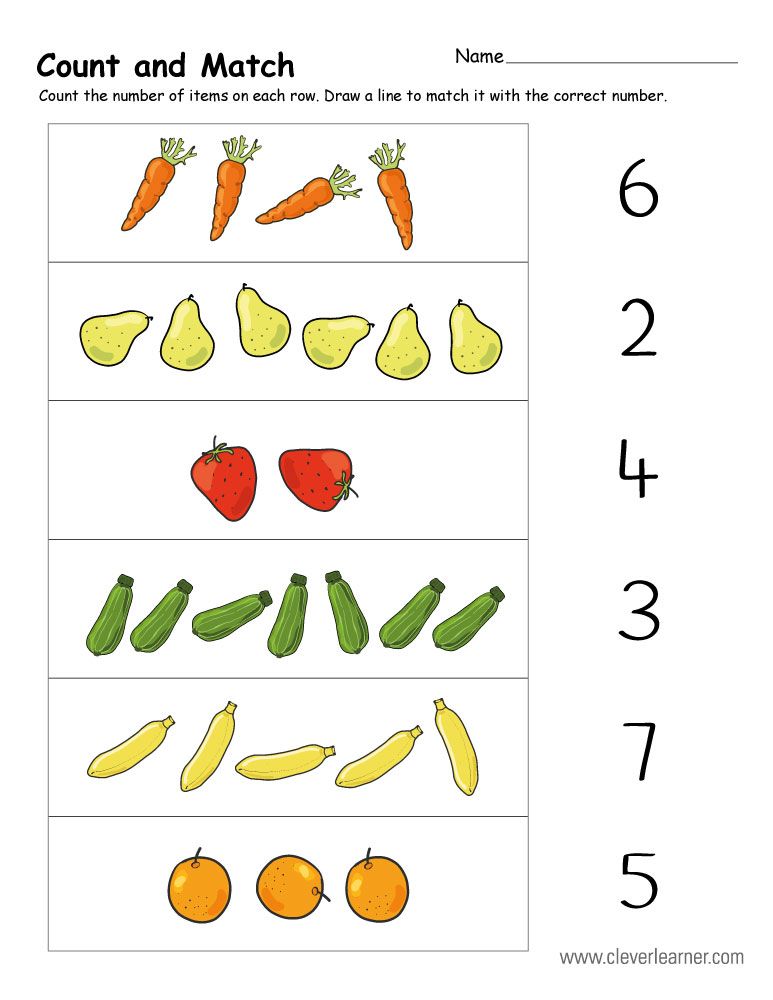 Thus, ask your kid to find or “hunt” ten yellow cars along the streets.

Decide on the reward – it’s up to your imagination. But keep in mind that rewards are crucial – think of something to motivate your child. Otherwise, this game will bring nothing but disappointment.

Digital Counting Games

Over 90% of American children play video games. The good news is that you can make this screen time much more efficient with counting games.

Well-made counting games offer engaging counting drills embedded into the gameplay so that your child will have fun while enhancing their math skills.

#6 How to Teach a Toddler to Count Using Toys?

Kids learn to count through play, and this approach yields the best results. No wonder there are so many counting toys on the market. Check out some inexpensive toy ideas you can implement right now:

Wooden Counting Puzzles

You can buy simple wooden puzzles that consist of numbered ring stacking and colored rings that match the numbers on the labels. Such toys teach toddlers to count numbers and promote counting skills in the most effective way as children can touch, pick, and play around with the rings.

Abacus

Abacus is an ancient calculation tool and a counting toy to help toddlers with learning to count. Your child will touch and slide the beads, counting them in the process. While Abacus doesn’t grip children’s attention on its own, you can come up with many fun activities to use this toy.

#7 Teaching Counting by 10s with Awesome Books

Help your kids with learning to count using these gripping books:

Goodnight, Numbers

This New York Times bestseller by Danica McKellar will lead your kid through a warm, soft bedtime story. As your kid will wish goodnight to items mentioned in the book, they will recall numbers and strengthen their counting skills.

Counting with a Ladybug

Counting with a Ladybug offers a captivating adventure to the world of garden animals – bees, dragonflies, ducks, butterflies, and so on. Its pages reveal many animals to count as well as bright gripping artwork and high-definition pictures to examine.

Count Your Chickens

Count Your Chickens contains numerous math challenges throughout its pages, encouraging kids to reread the book and count chickens once again. It’s an excellent choice to practice counting skills and develop attention to detail.

#8 Best Counting Songs and Rhymes

At this point, you can use seven methods to teach counting to your child, but you can go the extra mile with these catchy counting songs:

Here Is the Beehive

Lyrics:

Here is the beehive (make a fist)

Where are the bees?

Hiding inside where nobody sees

Watch them come creeping out of the hive

One, two, three, four, five (release one finger at a time from the fist/hive)

…BUZZ-ZZZ (wiggle fingers)

Why Use This Song

This simple, easy-to-remember rhyme teaches rote counting – one, two, three, four, five bees. Plus, you can modify it to teach counting by 10s. Just add more bees!

One, Two, Three, Four, Five

Lyrics:

One, two, three, four, five,

Once I caught a fish alive,

Six, seven, eight, nine, ten,

Then I let it go again.

Why did you let it go?

Because it bit my finger so.

Which finger did it bite?

This little finger on my right.

Why Take This Song?

This catchy verse teaches counting by 10. You can also extend the counting sequence however you want. Just add the same verse starting with eleven, twelve, thirteen, and so on.

There Were Ten in The Bed

Lyrics:

There were ten in the bed,

And the little one said, “Roll over, roll over”,

So they all rolled over, and one fell out.

There were nine in the bed…

Why Pick This Song?

This gripping song teaches counting backward, and it’s also highly customizable – you may say there are twenty, thirty, etc. in the bed.

Brighterly’s Tutors Help with Counting

All parents are homeschoolers to some extent, and teaching your kid counting can be mentally exhausting due to a lack of time and resources. After all, learning to count takes hundreds of hours that you might not always repel from home chores, job duties, and so on.

The good news is that you can enroll your child in comprehensive math courses where dedicated personal tutors will care about your kid’s math knowledge. Brighterly offers full-fledged math courses to children where they learn deeply about all math topics, counting included.

Bottom Line

While counting seems intuitive to adults, it’s a complex skill and all children go through several development stages of counting. You have to ensure that your kid goes through them smoothly because counting is the foundation of mathematics.

You can use toys, development games, and interactive activities to teach counting to your children. Plus, you can enhance and solidify your kid’s counting skills with professional math tutors.

Jessica Kaminski

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master's degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

How to learn to quickly count in your mind? - Meduza

1

Why in the mind when you can on a calculator or in a column?

Minimum counting skills, a sense of numbers are the same element of human culture as literate writing and speech, knowledge of a foreign language, a basic understanding of art and the world around.

In addition, when you easily count without improvised means, you feel a completely different level of reality control - you know in advance how much change you will be given in the store or whether it is worth cramming seven into an elevator with a carrying capacity of 400 kilograms.

Think about the fact that the calculator and the actions in a column are a kind of magic. Most likely, you do not understand how it works, and you are forced to simply trust them. And when you have a good understanding of how mathematical operations work and can reproduce them "by hand", your sense of control (and self-confidence) gets a serious bonus.

And finally, mental counting develops your mental abilities: attention, memory, concentration, switching between several streams of thought, and can also serve as a means for meditation or distraction from sad thoughts.

2

But where can I get tasks for training? Think of examples for yourself?

Of course not. The network is full of mobile applications that will offer you the training of math skills for every taste.

When choosing, keep in mind that a good application, at least, must have sufficiently flexible difficulty settings and keep statistics of the tasks you have solved.

Try these apps for iOS and Android, or look for alternatives on the App Store and Google Play.

3

How exactly should you train?

There are only four basic mathematical operations - addition, subtraction, multiplication and division. Each action has its own characteristics, but they are not complex. You need to figure it out once, and then train for 5-10 minutes a day, and very soon you will feel that you think better. Most likely, in two or three months you will reach a fairly decent level that can be maintained by episodic training.

4

Where do you start?

Start with the easiest level, single digit addition, and work it up to perfection: 99% correct, 1-2 seconds for each answer. For solving "with the transition through 10" examples, try using the following technique - "Reliance on the ten".

Let's say you need to add 8 and 7.

1) Ask yourself how much 8 is missing from 10 (that's 2).

2) Imagine 7 as the sum of 2 and some second piece (that's 5).

3) First add to 8 that part of the number 7, which was missing to 10, and then that second piece - you get 10 and 5, and this, of course, is 15.

5

How to add multi-digit numbers?

Here the most important principle is the addition of identical digits to each other. Having broken both numbers into "bit parts", start adding from the highest digits - thousands with thousands, hundreds with hundreds, tens with tens, ones with ones. If necessary, enlarge what happens and count everything together again.

For example, how do you add 456 and 789?

1) 456 consists of three bit parts - 400, 50 and 6.

789 is also divided into three bit parts - these are 700, 80 and 9.

2) Add hundreds with hundreds: 400 + 700 = 1100, tens with tens: 50 + 80 = 130, ones with units: 6 + 9 = 15.

10+5, that is, 1200+40+5 = 1245.

Amendment . When adding the digits, we mixed up the units and added 8 instead of 9 to 6. As a result, the sum also turned out to be incorrect - 1244 instead of 1245. We apologize for the mistake, and do not repeat it - carefully follow the numbers, especially in the mental account!

6

What about subtraction?

And here you need to start from the basic level - subtracting a single digit from the numbers of the first and second ten - and bring this skill to perfection. As with addition, problems usually arise with "going through 10" subtraction. And here a similar method of "reliance on a dozen" will help.

Let's say we need to subtract 8 from 12.

1) Let's ask ourselves how much we need to subtract from 12 to get 10 (that's 2).

2) We will subtract 8 from 12 in parts - first we subtract this 2, and then everything else. And the rest is how much? (that's 6).

3) After subtracting 2 from 12, we got 10, and we need to subtract 6 more, we get 4. Done!

7

What about multi-digit numbers? Is everything difficult with them?

Not particularly. It is only important not to confuse the technique of subtraction with the technique of addition. When adding, it was convenient for us to break each of the numbers into digit parts, and here we break only the number that we subtract.

So let's say we need to subtract 512−259.

1) The number 259, which we subtract, consists of three digit parts - 200, 50 and 9. We will subtract them in turn.

2) 512−200 - subtracting hundreds does not affect the tens and units of the number 512 in any way, it only affects hundreds, so the result will be this - 312.

3) From what happened after subtracting hundreds, now subtract tens, 312 -50.

This is similar to subtracting by ten. First subtract 10 from 312 to whole hundreds (units will not be affected), we get 302. And then subtract everything else (50 had to be subtracted in total, 10 has already been subtracted, it remains to subtract 40), we get 262.

4) It remains to subtract the units: 262−9.

Clean transition through ten - first subtract 2, we get 260, and then subtract the rest, 7, we get 260−7 = 253. Here is the answer.

8

How does multiplication work?

Let's start with single-digit multiplication. First you need to remember that multiplication is when you add the same thing several times. For example, multiplying 4 by 7 means adding four sevens. Using the addition technique, we can easily calculate - two sevens, 7 and 7, will be 14, if we add the third 7, we get 21, and adding the last, fourth seven, we get 28 as a result.0003

Gradually, as a result of training, you will remember the reference multiplication values ​​that are convenient for you and with their help you will be able to quickly calculate neighboring ones. For example, if you need to multiply 6 by 7 (that is, add six sevens), and you remember that 5 times 7 (that is, add five sevens) will be 35, then to get the final result, you just need to add the sixth seven - you get 42.

The most difficult example in the multiplication table is 7∙8. To remember it, there is a good mnemonic rule “five six seven eight”, which means 56 = 7∙8.

9

How to multiply a multi-digit number by a single-digit number?

Let's look at an example. Let's say we need to multiply 468 by 6.

1) 468 consists of 400, 60 and 8, and all this needs to be multiplied by 6. Well, taken separately, these problems are no more difficult than multiplying single-digit numbers.

2) Going from the most significant digit to the least significant: 400∙6 = 2400 (since 400 is 100 times greater than 4, then the result of 400∙6 will be 100 times greater than the result of 4∙6).

Accordingly, 60∙6 = 360, and 8∙6 = 48.

3) And now, as in addition, we add it all together, grouping the same digits: 400+300)+(60+40)+8 = [add the same digits] =

= 2000+700+100+8 = [group and add the same digits] =

= 2000+800+8 = [further enlarge nothing, we get the answer] = 2808.

10

How to multiply two-digit numbers?

For an ordinary person, this is already aerobatics! If you have mastered double-digit multiplication, consider that you have been accepted into the world of the mental counting elite. But in fact, there is nothing fundamentally complicated here, just a higher load on short-term memory (at the same time we will train it).

So, for example, let's multiply 78 by 56. This means that we need to add (take) the number 78 56 times.

1) These 56 times can be divided into stages - first add 78 50 times, then 6 times, and then combine the results.

2) Adding the number 78 50 times is not difficult - it is 10 times more than adding it 5 times. 78∙5 = 70∙5+8∙5 = 350+40 = 390. So, 78∙50 = 3900, remember this number.

3) Now let's calculate 78∙6 = 70∙6+8∙6 = 420+48 = 468.

4) Now let's add both results together: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Voila!

Amendment . At the final stage, when adding 3900 and 468, we incorrectly split the second number into digits - we forgot about 60. As a result, the total turned out to be 4308. We apologize for the mistake, and do not repeat it - you cannot lose terms in the mental calculation.

11

Wow, the last thing left is action, division?

Yes, we are at the finish line. And again, let's start from the simplest level: dividing by a single-digit number of those numbers that are familiar to us from multiplying single-digit numbers.

So what is division? In fact, this is the "reverse" operation to multiplication.

For example, dividing 56 by 7 means picking up such a number that if you multiply it by 7, you get 56. Since you are already well versed in the multiplication table by this point, you will surely remember that exactly 8 times 7 gives 56. So, the desired number is 8, 56:7 = 8.

And so always - remember which number, when multiplied, gives the desired result - this is the number that you need.

12

How do you divide multi-digit numbers by single-digit numbers?

Let's divide 6144 by 8. Our way is to "cut off" the maximum "round" parts from the original number, each of which is guaranteed to be divisible by 8 according to the multiplication table.

1) Select from 6144 as large a part as possible, which is divisible by 8 according to the multiplication table. This will be 5600, because 56 is divisible by 8, and the next number that is divisible by 8 is already 64, which does not suit us, since 6400 is greater than 6144. Great, 6144 is 5600 and 544 (here we needed the subtraction skill ).

We will divide along the way:

6144:8 = [select the maximum convenient round part] =

= (5600+544):8 = [divide the selected part by 8, and work on the second part in the next step] =

= 700+544:8. We will remember

700 as a partial result, and we ourselves will deal with the division 544:8.

2) Similarly, out of 544, the largest part that can be conveniently divided by 8 according to the multiplication table is 480 (after all, 48 is divisible by 8, and the next number - 56 - does not suit us, because 560\u003e 544) .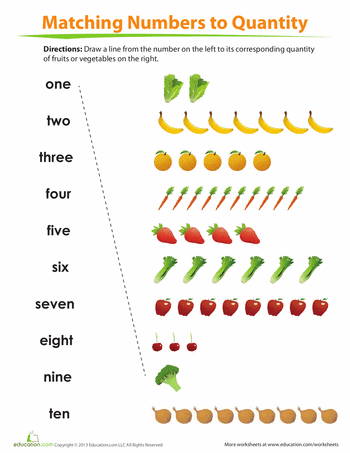 So 544 = 480+64.

We continue the division:

544:8 = [select the maximum convenient round part] =

= (480+64):8 = [divide the selected part by 8, and work on the second part in the next step] =

= 60 +64:8.

60 add to 700, 700+60 = 760 - remember this as the second part of the result and move on to the last division, 64:8.

3) The remaining piece, 64, is also divisible by 8 according to the multiplication table, 64:8 = 8.

Accordingly, the total result of division is 760+8=768. All!

13

How do you divide by a two-digit number?

The technique of dividing by a two-digit number is the most diverse, unlike anything, exquisite. Let's get acquainted with it on the example of 5148:66.

1) Guess what ten is our result. Recall that 5148:66 means: we are looking for a number that, when multiplied by 66, will give 5148. We will use the "shooting" technique.

Just randomly try the number 20 as a possible candidate. 20∙66 = 1320, which is 4 times less than 5148, which we need.

4 times more than 20 is 80, let's try it. 80∙66 = 5280, it turned out more than the desired 5148, but a little, most likely, this is the “top” ten.

Let's check for reliability 70, the previous before 80 tens. 70∙66 = 4620, which is just less than 5148, great! This means that the number we are looking for lies between 70 and 80.

2) Let's use the mathematical law about the last digit of the result of multiplying two numbers.

It turns out that it always coincides with the last digit of the result of multiplying the last digits of these numbers (try to think why this is so). For example, what number will 123 9 end with0061 4 ∙567 8 ? To the same as 4 ∙ 8 , that is, to 2 (4∙8 = 3 2 ).

Therefore, if we are looking for a number that, when multiplied by 6 6 , will give 5148, then to guarantee this 8 in last place, the desired number can only end in either 3 or 8 (3∙ 6 = 18, 8 6 = 48).

3) With these endings between 70 and 80, we have two total candidates - 73 and 78.

5148 is clearly closer to 5280, so let's check 78 first.

78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, hooray!

(Well, if the result did not converge, then we would check the second number, and it would already fit exactly).

14

What are some final recommendations?

Here, in general, and all the methods that are enough to know to train confident counting within 10,000 (and the ability to work mentally with large numbers, perhaps, is already beyond the scope of the necessary general development).

Surely you will also come across other techniques, the so-called. "tricks" of quick counting, but do not rush to get carried away with them. In addition, remember that regularity is more important than intensity - try to exercise on the simulator every day for 5-10 minutes, no more is needed, otherwise there is a high risk of "burning out" and giving up.

Don't rush anywhere in the process - catch your rhythm, focus on correct answers, not speed, speed will come later.

Be sure to try to pronounce your actions out loud, especially at first - you will have a chance to feel how everything is like poetry, and it will be easier to decide this way.

And don't be upset if something doesn't work out - the walker will master the road, and sooner or later you will definitely succeed.

How to learn to quickly count any numbers in your head: mental counting techniques

Mental arithmetic is an activity that fewer and fewer people are bothering with nowadays. It is much easier to get a calculator on your phone and calculate any example.

But is it really so? In this article, we will present math hacks that will help you learn how to quickly add, subtract, multiply and divide numbers in your mind. Moreover, operating not with units and tens, but with at least two-digit and three-digit numbers.

After mastering the methods in this article, the idea of ​​reaching for a calculator on your phone doesn't seem so good anymore. After all, you can not waste time and calculate everything in your mind much faster, but at the same time stretch your brains and impress others (of the opposite sex).

So, welcome to the exciting world of computing! We have collected tips from our authors on how to improve mental arithmetic and become a math hero and genius. By the way, if you are interested in mathematics, you can read the article "Limits for dummies" in our blog.

Warning! If you are an ordinary person and not a child prodigy, then it will take training and practice, concentration and patience to develop mental numeracy. At first, everything can turn out slowly, but then things will go smoothly, and you can quickly count any numbers in your head.

Gauss and mental counting

One of the mathematicians with a phenomenal speed of mental counting was the famous Carl Friedrich Gauss (1777-1855). Yes, yes, the same Gauss who came up with the normal distribution.

In his own words, he learned to count before he could speak. When Gauss was 3 years old, the boy looked at his father's payroll and declared, "The calculations are wrong." After the adults checked everything, it turned out that little Gauss was right.

In the future, this mathematician reached considerable heights, and his works are still actively used in theoretical and applied sciences. Until his death, Gauss did most of his calculations in his head.

Here we will not deal with complex calculations, but start with the simplest.

Adding numbers in your head

To learn how to add large numbers in your head, you need to be able to accurately add numbers up to 10 . Ultimately, any complex task comes down to performing a few trivial actions.

Most often, problems and errors occur when adding numbers with "going through 10 ". When adding (and even when subtracting), it is convenient to use the technique of “reliance on a dozen”. What is this? First, we mentally ask ourselves how much one of the terms is missing up to 10 , and then we add to 10 the difference remaining to the second term.

For example, add the numbers 8 and 6 . To get 8 from 8 , 2 is missing. Then to 10 it remains to add 4=6-2 . As a result, we get: 8+6=(8+2)+4=10+4=14

The main trick with adding large numbers is to break them into bit parts, and then add these parts together.

Let's add two numbers: 356 and 728 . The number 356 can be represented as 300+50+6 . Similarly, 728 would be 700+20+8 . Now add up:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

come easy. But unlike addition, where each number is divided into bit parts, when subtracting, you only need to “break” the number that we subtract.

For example, how much is 528-321 ? We split the number 321 into bit parts and get: 321=300+20+1 .

Now we calculate: 528-300-20-1=228-20-1=208-1=207

Try to visualize the processes of addition and subtraction. At school, everyone was taught to count in a column, that is, from top to bottom. One way to restructure thinking and speed up counting is not to count from top to bottom, but from left to right, breaking numbers into place parts.

Mental multiplication

Multiplication is the repeated repetition of a number. If you need to multiply 8 by 4 , this means that the number 8 needs to be repeated 4 times.

8*4=8+8+8+8=32

Since all complex problems are reduced to simpler ones, you need to be able to multiply all single-digit numbers. There is a great tool for this - multiplication table . If you do not know this table by heart, then we strongly recommend that you first learn it and only then take up the practice of mental counting. In addition, there is, in fact, nothing to learn there.

Multiplication of multi-digit numbers by single digits

First, practice multiplying multi-digit numbers by single-digit numbers. Let's multiply 528 by 6 . Breaking down the number 528 into digits and go from oldest to youngest. We multiply first and then add the results.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

4 9002, by the way! For our readers, there is now a 10% discount on any kind of work