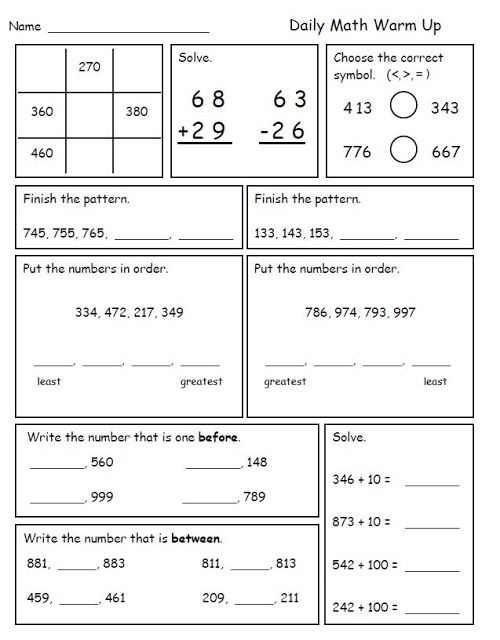
Learning math for children
Help Your Child Develop Early Math Skills
Before they start school, most children develop an understanding of addition and subtraction through everyday interactions. Learn what informal activities give children a head start on early math skills when they start school.
Children are using early math skills throughout their daily routines and activities. This is good news as these skills are important for being ready for school. But early math doesn’t mean taking out the calculator during playtime. Even before they start school, most children develop an understanding of addition and subtraction through everyday interactions. For example, Thomas has two cars; Joseph wants one. After Thomas shares one, he sees that he has one car left (Bowman, Donovan, & Burns, 2001, p. 201). Other math skills are introduced through daily routines you share with your child—counting steps as you go up or down, for example. Informal activities like this one give children a jumpstart on the formal math instruction that starts in school.
What math knowledge will your child need later on in elementary school? Early mathematical concepts and skills that first-grade mathematics curriculum builds on include: (Bowman et al., 2001, p. 76).
- Understanding size, shape, and patterns
- Ability to count verbally (first forward, then backward)
- Recognizing numerals
- Identifying more and less of a quantity
- Understanding one-to-one correspondence (i.e., matching sets, or knowing which group has four and which has five)
Key Math Skills for School
More advanced mathematical skills are based on an early math “foundation”—just like a house is built on a strong foundation. In the toddler years, you can help your child begin to develop early math skills by introducing ideas like: (From Diezmann & Yelland, 2000, and Fromboluti & Rinck, 1999.)
Number Sense
This is the ability to count accurately—first forward. Then, later in school, children will learn to count backwards.
A more complex skill related to number sense is the ability to see relationships between numbers—like adding and subtracting. Ben (age 2) saw the cupcakes on the plate. He counted with his dad: “One, two, three, four, five, six…”
Representation
Making mathematical ideas “real” by using words, pictures, symbols, and objects (like blocks). Casey (aged 3) was setting out a pretend picnic. He carefully laid out four plastic plates and four plastic cups: “So our whole family can come to the picnic!” There were four members in his family; he was able to apply this information to the number of plates and cups he chose.
Spatial sense
Later in school, children will call this “geometry.” But for toddlers it is introducing the ideas of shape, size, space, position, direction and movement. Aziz (28 months) was giggling at the bottom of the slide. “What’s so funny?” his Auntie wondered. “I comed up,” said Aziz, “Then I comed down!”
Measurement
Technically, this is finding the length, height, and weight of an object using units like inches, feet or pounds.
Measurement of time (in minutes, for example) also falls under this skill area. Gabriella (36 months) asked her Abuela again and again: “Make cookies? Me do it!” Her Abuela showed her how to fill the measuring cup with sugar. “We need two cups, Gabi. Fill it up once and put it in the bowl, then fill it up again.”
Estimation
This is the ability to make a good guess about the amount or size of something. This is very difficult for young children to do. You can help them by showing them the meaning of words like more, less, bigger, smaller, more than, less than. Nolan (30 months) looked at the two bagels: one was a regular bagel, one was a mini-bagel. His dad asked: “Which one would you like?” Nolan pointed to the regular bagel. His dad said, “You must be hungry! That bagel is bigger. That bagel is smaller. Okay, I’ll give you the bigger one. Breakfast is coming up!”
Patterns
Patterns are things—numbers, shapes, images—that repeat in a logical way.
Patterns help children learn to make predictions, to understand what comes next, to make logical connections, and to use reasoning skills. Ava (27 months) pointed to the moon: “Moon. Sun go night-night.” Her grandfather picked her up, “Yes, little Ava. In the morning, the sun comes out and the moon goes away. At night, the sun goes to sleep and the moon comes out to play. But it’s time for Ava to go to sleep now, just like the sun.”
Problem-solving
The ability to think through a problem, to recognize there is more than one path to the answer. It means using past knowledge and logical thinking skills to find an answer. Carl (15 months old) looked at the shape-sorter—a plastic drum with 3 holes in the top. The holes were in the shape of a triangle, a circle and a square. Carl looked at the chunky shapes on the floor. He picked up a triangle. He put it in his month, then banged it on the floor. He touched the edges with his fingers. Then he tried to stuff it in each of the holes of the new toy.
Surprise! It fell inside the triangle hole! Carl reached for another block, a circular one this time…
Math: One Part of the Whole
Math skills are just one part of a larger web of skills that children are developing in the early years—including language skills, physical skills, and social skills. Each of these skill areas is dependent on and influences the others.
Trina (18 months old) was stacking blocks. She had put two square blocks on top of one another, then a triangle block on top of that. She discovered that no more blocks would balance on top of the triangle-shaped block. She looked up at her dad and showed him the block she couldn’t get to stay on top, essentially telling him with her gesture, “Dad, I need help figuring this out.” Her father showed her that if she took the triangle block off and used a square one instead, she could stack more on top. She then added two more blocks to her tower before proudly showing her creation to her dad: “Dada, Ook! Ook!”
You can see in this ordinary interaction how all areas of Trina’s development are working together.
Her physical ability allows her to manipulate the blocks and use her thinking skills to execute her plan to make a tower. She uses her language and social skills as she asks her father for help. Her effective communication allows Dad to respond and provide the helps she needs (further enhancing her social skills as she sees herself as important and a good communicator). This then further builds her thinking skills as she learns how to solve the problem of making the tower taller.
What You Can Do
The tips below highlight ways that you can help your child learn early math skills by building on their natural curiosity and having fun together. (Note: Most of these tips are designed for older children—ages 2–3. Younger children can be exposed to stories and songs using repetition, rhymes and numbers.)
Shape up.
Play with shape-sorters. Talk with your child about each shape—count the sides, describe the colors. Make your own shapes by cutting large shapes out of colored construction paper.
Ask your child to “hop on the circle” or “jump on the red shape.”
Count and sort.
Gather together a basket of small toys, shells, pebbles or buttons. Count them with your child. Sort them based on size, color, or what they do (i.e., all the cars in one pile, all the animals in another).
Place the call.
With your 3-year-old, begin teaching her the address and phone number of your home. Talk with your child about how each house has a number, and how their house or apartment is one of a series, each with its own number.
What size is it?
Notice the sizes of objects in the world around you: That pink pocketbook is the biggest. The blue pocketbook is the smallest. Ask your child to think about his own size relative to other objects (“Do you fit under the table? Under the chair?”).
You’re cookin’ now!
Even young children can help fill, stir, and pour. Through these activities, children learn, quite naturally, to count, measure, add, and estimate.
Walk it off.
Taking a walk gives children many opportunities to compare (which stone is bigger?), assess (how many acorns did we find?), note similarities and differences (does the duck have fur like the bunny does?) and categorize (see if you can find some red leaves). You can also talk about size (by taking big and little steps), estimate distance (is the park close to our house or far away?), and practice counting (let’s count how many steps until we get to the corner).
Picture time.
Use an hourglass, stopwatch, or timer to time short (1–3 minute) activities. This helps children develop a sense of time and to understand that some things take longer than others.
Shape up.
Point out the different shapes and colors you see during the day. On a walk, you may see a triangle-shaped sign that’s yellow. Inside a store you may see a rectangle-shaped sign that’s red.
Read and sing your numbers.
Sing songs that rhyme, repeat, or have numbers in them.
Songs reinforce patterns (which is a math skill as well). They also are fun ways to practice language and foster social skills like cooperation.
Start today.
Use a calendar to talk about the date, the day of the week, and the weather. Calendars reinforce counting, sequences, and patterns. Build logical thinking skills by talking about cold weather and asking your child: What do we wear when it’s cold? This encourages your child to make the link between cold weather and warm clothing.
Pass it around.
Ask for your child’s help in distributing items like snacks or in laying napkins out on the dinner table. Help him give one cracker to each child. This helps children understand one-to-one correspondence. When you are distributing items, emphasize the number concept: “One for you, one for me, one for Daddy.” Or, “We are putting on our shoes: One, two.”
Big on blocks.
Give your child the chance to play with wooden blocks, plastic interlocking blocks, empty boxes, milk cartons, etc.
Stacking and manipulating these toys help children learn about shapes and the relationships between shapes (e.g., two triangles make a square). Nesting boxes and cups for younger children help them understand the relationship between different sized objects.
Tunnel time.
Open a large cardboard box at each end to turn it into a tunnel. This helps children understand where their body is in space and in relation to other objects.
The long and the short of it.
Cut a few (3–5) pieces of ribbon, yarn or paper in different lengths. Talk about ideas like long and short. With your child, put in order of longest to shortest.
Learn through touch.
Cut shapes—circle, square, triangle—out of sturdy cardboard. Let your child touch the shape with her eyes open and then closed.
Pattern play.
Have fun with patterns by letting children arrange dry macaroni, chunky beads, different types of dry cereal, or pieces of paper in different patterns or designs.
Supervise your child carefully during this activity to prevent choking, and put away all items when you are done.
Laundry learning.
Make household jobs fun. As you sort the laundry, ask your child to make a pile of shirts and a pile of socks. Ask him which pile is the bigger (estimation). Together, count how many shirts. See if he can make pairs of socks: Can you take two socks out and put them in their own pile? (Don’t worry if they don’t match! This activity is more about counting than matching.)
Playground math.
As your child plays, make comparisons based on height (high/low), position (over/under), or size (big/little).
Dress for math success.
Ask your child to pick out a shirt for the day. Ask: What color is your shirt? Yes, yellow. Can you find something in your room that is also yellow? As your child nears three and beyond, notice patterns in his clothing—like stripes, colors, shapes, or pictures: I see a pattern on your shirt. There are stripes that go red, blue, red, blue.
Or, Your shirt is covered with ponies—a big pony next to a little pony, all over your shirt!
Graphing games.
As your child nears three and beyond, make a chart where your child can put a sticker each time it rains or each time it is sunny. At the end of a week, you can estimate together which column has more or less stickers, and count how many to be sure.
References
Bowman, B.T., Donovan, M.S., & Burns, M.S., (Eds.). (2001). Eager to learn: Educating our preschoolers. Washington, DC: National Academy of Sciences.
Diezmann, C., & Yelland, N. J. (2000). Developing mathematical literacy in the early childhood years. In Yelland, N.J. (Ed.), Promoting meaningful learning: Innovations in educating early childhood professionals. (pp.47–58). Washington, DC: National Association for the Education of Young Children.
Fromboluti, C. S., & Rinck, N. (1999 June). Early childhood: Where learning begins. U.S. Department of Education, Office of Educational Research and Improvement, National Institute on Early Childhood Development and Education.
Retrieved on May 11, 2018 from https://www2.ed.gov/pubs/EarlyMath/title.html
Are We Teaching the Math Kids Need?
Jo Boaler has spent a lot of time thinking and writing about anxiety—math anxiety, in particular—and its impact on kids’ learning trajectories.
Mathematics, she writes in her 2019 book, Limitless Mind: Learn, Lead, and Live Without Barriers, is the subject “with the most damaging ideas held by teachers, students, and parents.” It’s one of the few academic subjects in which multitudes of students, early on, decide they’re not cut out for it: We’re either a “math person” or we’re not. That notion tends to stick well into adulthood. “It is difficult to know how many people walk around in society harboring damaging ideas about their math ability, but I estimate it to be at least half of the population,” she writes.
Boaler, a professor of mathematics education at Stanford University, a best-selling author, and the cofounder of the math education site youcubed.
org, has spent decades thinking about how to undo the damage. Her work, closely aligned with Stanford psychology professor Carol Dweck’s research on growth mindset, explores what Boaler calls “our most harmful and persistent ideas about innate ability.” She’s a vocal proponent of changing the way we assess mathematics and modernizing the math curriculum—especially in high school—so that it’s more engaging, more inclusive, and more likely to prepare kids for the modern workforce.
Critics argue that by insisting on math as a joyful, creative exploration, we’re doing kids a disservice, and that by reducing or eliminating memorization and math drills, for example, we’re setting kids up for a lack of mathematical fluency. But Boaler says that she’s got no quarrel with things like math facts and that teachers should help kids develop these—not by “emphasizing facts for the sake of facts, or using timed tests, but by encouraging students to use, work with, and explore numbers,” a process that ultimately builds critical number sense and reinforces math facts in a more organic way.
I sat down with Boaler recently for a Zoom discussion about mathematical freedom, anxiety-producing teaching practices, and the systemic changes she says are critical for modernizing math curricula.
Sarah Gonser: In your book Limitless Mind, you say that learning is about identity. Can you explain?
Jo Boaler: Well, we know that when people learn, it’s not just about an accumulation of knowledge; it’s really about changing who they are as people.
And we’ve found over the years that the traditional approach to teaching maths—I’m just going to show you methods; you’re going to accept them and use them—is incompatible with the identities kids want, particularly around adolescence. Kids want to have their own ideas; they want to be respected as thinkers; they don’t want to just be given information that they simply reproduce.
They see it as a subject area where they can’t be their full selves, and it’s a large part of why people drop out of maths.
Gonser: It’s also a subject that causes a lot of very real anxiety. Why is that?
Boaler: I would say it comes from a few different things: It’s a subject that is heavily tested; it’s a subject that’s often taught as right and wrong answers; and there are these widespread myths that you’re either born as a math person or you’re not. Somehow, you have the right brain, or you don’t.
There’s lots of micromessaging in classrooms that might get kids to think they can’t be successful. Speed is very much at the heart of it. If you ask the class a question and then take the answer from the first kid who raises their hand, you’re sending the message that you value speed. And we know that professional mathematicians are not fast; they’re some of the slowest thinkers.
Finally, we have stereotyped ideas about who can be good at maths. So if you’re a woman or a person of color, you’re dealing with that pressure. If you have fixed ideas about who can do maths, a fixed mindset, then that stereotype can really take root.
Gonser: So how can we slow it all down and avoid making math class a place of stress and anxiety?
Boaler: I think a big part of it is A for L—Assessment for Learning—I just think that’s so critical. It changes the whole culture of classrooms for kids.
If we assess kids by giving them diagnostic feedback, not grades, and ask them to do their own reflection so that they’re able to see themselves progress on this journey—everything changes when assessment is like that in classrooms.
But we also want to change the way content is taught. Kids don’t need lots of short questions with one method and one answer. It can be open questions that students think about creatively and visually.
Gonser: You’re also an advocate of encouraging struggle and mistakes in classrooms. In Limitless Mind, you describe high achievers who work “at the edge of their understanding, making mistake after mistake in difficult circumstances, correcting mistakes, moving on and making more mistakes.
” In the classroom, why is that important?
Boaler: The best times for learning are when you’re struggling and finding things difficult; that’s when your brain is on fire with activity. I think it’s really important to share the value of struggle with students. When I teach, I say to students, “I want you to struggle, because that’s really good for you.” I think it’s freeing for students when they know that’s a goal. And I think you should keep sharing that, reinforce it during every lesson.
It’s really going to involve changing how we assess kids. If kids take a test and they’re penalized for making mistakes, that’s a counter message—and studies have shown that this mixed message is worse than no message at all. Don’t tell them that struggle is good if you’re going to mark them wrong when they struggle.
I think it’s important that we always let kids resubmit work. And if you’re using grading—I’m not a fan of grading myself—but if students don’t do well the first time, to allow them to work on it again sends a great message that learning and struggle are valued.
Gonser: Let’s talk about broader, more systemic curricular changes. You’re a prominent voice in the conversation about re-sequencing math curricula so that it’s more than a gateway to higher-level mathematics. What’s changed in our world to make this so urgent?
Boaler: Well, we need to modernize not just how we teach it, but the actual content we’re teaching in classrooms. The content we teach in maths was created around the 1800s and really hasn’t changed since then. It was created at a time when we needed kids to be calculators. And so learning arithmetic, calculating things quickly—that was important.
But the world has changed dramatically. In high school, in particular, we’re teaching a wide array of methods for kids to do by hand that they’ll never use in their lives again. You will never go into a workplace and have people, by hand, go through synthetic division. So we’re spending too many hours giving kids this outdated content that they’re so turned off by.
For what reason?
Gonser: What should we be teaching instead?
Boaler: So I’m very excited about bringing data science into mathematics. I am one of the five writers of a new framework in California where we are highlighting data science as a really important part of maths.
Now, it’s hard to do that because the Common Core Standards really didn’t include data science, and they need to be updated. But what we’ve done is try and bring a data science perspective to the current standards. This data science initiative is very exciting, not only because it gives teachers of all grades interesting content to work with, but it also helps kids become data literate, which is something they really need in this world.
There are more data points in the world than there are stars in the galaxies right now; the world is filled with data. So even little kids need to prepare to become data literate.
Gonser: You’re also leading the charge on changing the high school math sequence, streamlining the algebra-geometry-algebra sandwich so there’s room for a data science class—can you tell me more about that?
Boaler: In the high school years, something very exciting is happening.
For generations, really, there’s been this race to get to calculus because it can get you into college.
It’s built on a very inequitable system. Because there are so many courses before calculus in middle school and high school, it’s effectively meant we’re pushing kids out of the calculus track in sixth grade, which is awful. The content is also not very up-to-date and not very engaging.
There’s recently been a dramatic change in California: The UC and Cal State systems will now accept data science as a third-year course instead of Algebra 2. This is amazing and important because Algebra 2 is a course that is the end of the road for most kids, and now they can take data science instead.
Gonser: Why is Algebra 2 the end of the road for so many kids?
Boaler: Because it’s so procedural and uninteresting that the vast majority of kids, after they’ve done Algebra 2, don’t take any more maths. Data science is completely different. As we’re rolling it out, we’re communicating: This can be a course in high school that any student can take.
You don’t have to be advanced in middle school, and yet it can lead to a high-level STEM career. I see that completely changing who ends up going into STEM.
Gonser: What do you say to critics who argue this is a change that will water down the curriculum, make it less rigorous?
Boaler: It’s totally rigorous, actually. Mathematics is a very broad subject. There’s no reason that we should say, “Let’s just value this part, which is calculus.” The mathematics of data science involves matrices and probability and statistics and linear algebra—which is beyond what’s often taught in calculus.
Gonser: My last question comes from an Edutopia reader, a teacher, who asks: “What’s your greatest piece of advice for early math educators?”
Boaler: My biggest piece of advice is to really spend time trying to change kids’ mindsets and ideas about themselves, because that will pay huge dividends. If you encourage struggle, if you remind kids that they can learn anything, we now know there are no limits to what people can learn.
Kids should know that if the kid next to them is solving something more quickly, it doesn’t matter. We know that kids enter school with a growth mindset, and that drops with each passing year. And part of that is kids looking at other kids and thinking, “Oh, they can do it better than me.” We have to counter those ideas and couple that with math that’s open and creative. When you do that, things change.
Entertaining math for preschoolers, online math games and tasks
HomeExerciseMath
Math
Learning shapes course
View all
What is symmetry?
Part of the whole
We study the figures (1)
We study the figures (2)
Study the figures (3)
We study the figures (4)
Posal Line
polygon
polygons (1)
View all
Course Learn numbers
View all
Number 1 (1)
Distinguish numbers from 0 to 9 (1)
Distinguish numbers from 0 to 9 (2)
Distinguish numbers from 0 to 9 (3) 9000
Distinguish numbers from 0 to 9 (4)
Number line up to 10 (1)
Digit 1 (2)
Digit 2 (1)
Digit 2 (2)
See all
View all
Funny numbers (1)
Funny numbers (2)
Cheerful count up to 3
Cheerful count up to 5
Where else? (1)
Where is more? (2)
Let's count!
Remove the numbers up to 3
We play and consider
View all
Consider up to 10
View all
Funny account up to 10 (1)
Funny score up to 10 (2)
Tasks for up to 10 up to 10 (1)
Number line problems up to 10 (2)
Play and count (1)
Play and count (2)
Which is in order up to 10?
Count down from 10 to 1 (1)
Count down from 10 to 1 (2)
View all
Count up to 20
View all order up to 20 (1)
Correlating objects and numbers up to 20 (1)
Composition of the number 12
Counting in pairs up to 20
Counting objects up to 20
Counting objects up to 20 (2)
Count items up to 20 (3)
Count items up to 20 (4)
View all
Count up to 100
View all
Approximate count (2)
Millimeter
Approximate count (1)
Arrange in order to 100 (1)
Count to one hundred
View all
Number composition
View all
Number composition 3 20 90Ol000 Learning to solve problems up to 10 (1)
Learning to solve problems up to 10 (2)
Examples in pictures
Subtract and add
Subtraction with the transition through a dozen (2)
Subtraction through ten (3)
Drag answer
Addition.
Terms. Sum. (1)
Addition. Terms. Sum. (2)
View all
Compare numbers
View all
Longer, shorter, equal in length
Comparing numbers in pictures up to 10
Odd or even
Comparing expressions. Equalities and inequalities
Comparison of numbers within a million
Comparison of numbers in pictures up to 20
Comparison of numbers within 20
Compare the numbers
View all
We multiply and divide
View all
Remember the multiplication table
Division by 10 and 100
Division with a remainder of
The division of a three -digit number by a single -digit
Multiplication and division problems
Do you know the multiplication table? (1)
Do you know the multiplication table? (2)
Written division with remainder
Written multiplication by a two -digit number
View all
We solve problems and examples
View all
Learning to solve problems up to 10 (1)
Money LOVE
diagrams
Subtraction checks for multiplication tasks and tasks for multiplication and division
Examples with brackets
Add and subtract
Composition of the number
Composition of the number
View all
Determine the time
View all
days of the week (1)
days of the week (2)
Memorial months (2)
Distinguish the seasons
We remember months (1)
Determine the time by shooters
hours with arrows
Autumn riddles (1)
Seasons - spring (2)
View all
Why do we need mathematics?
Mathematics is a fundamental science that appeared at the moment when a person needed to calculate something.
We can say that her age is not much different from the age of mankind. Mathematics helps, on the one hand, to develop abstract thinking, on the other hand, to solve applied problems in everyday life.
Mathematical thinking, or mathematical mindset, is based on logic, the ability to build cause-and-effect relationships, critical thinking, the desire to get to the bottom of a question or problem.
Mathematics forms skills that are relevant for any historical period, especially for the present.
What is entertaining mathematics?
Undoubtedly, mathematical abilities are developed by special efforts.
One option is to study mathematics by solving mathematical problems. For an easier and more exciting learning process, a special section is used - entertaining mathematics. In thoughtful game tasks, interesting plots, using humor, the science of mathematics appears in the most attractive form, which is especially important when teaching children.
Children's curiosity and excitement allow you to get involved in the world of abstract calculations and go from entertaining puzzles to real complex mathematics.
Why does the child not understand mathematics?
There is no definite answer to this question. Perhaps the child has not yet fully mastered the skills of counting. Here, counting games from very simple to complicated options, for example, with dice (as an option, rpg board games) will help.
Very young children may still have unformed abstract thinking: it is easier for them to operate with visual objects. A parent or teacher always shows the application of mathematics, explaining why mathematics is needed in life.
If we are talking about an older age, then it is possible to structure abstract thinking in the form of diagrams on paper, helping not to keep all the data in mind, but to see the full picture visually.
If mathematics is difficult for a child, it may be worth paying additional attention to the development of imagination.
It is not necessary to use the detailed solution of math problems; you can go through mazes, cut out patterns, collect various crafts according to the schemes. Creativity is welcome, because mathematics is not always about dry numbers.
Math in pictures for preschoolers online is now available to every child. The section includes tasks and games in arithmetic for children, exciting tasks that develop addition and subtraction lessons for children. The exercises in this section will help develop attention and concentration, form elementary mathematical concepts in children.
Playful activities
Your child will have a fun and productive time.
Children are engaged with pleasure, are completely immersed in the learning process and achieve results. For children under 6 who have not yet learned to read, we voiced each task.
Cups and medals for children
Awards that motivate children to achieve success.
Each child has his own “hall of awards and achievements”. If the tasks are completed correctly, children receive cups, medals and nominal diplomas. The awards can be shared on social networks, and the diploma can be printed.
Personal training
Fully controlled development of the child.
We save all the successes of the child and show you what you should pay special attention to. Make up your own training programs so that the child develops harmoniously in all the right directions.
Start studying with your child
today - it's free
Register and get 20 tasks for free. To remove restrictions and achieve great results in your studies - choose and pay for the tariff plan that suits you.
Register orSelect tariff
How to captivate a child with mathematics. Advises Lyudmila Peterson
Mathematics "according to Peterson" is widely known not only in Russia.
In December 2018, Lyudmila Georgievna's textbook for elementary and basic schools successfully passed all the necessary examinations and, at the numerous requests of teachers and parents, returned to the federal list again. At the beginning of the school year, we asked her to tell us how to help a child with mathematics, how to get adults interested in it, and why it is important for children to feel their success.
How to get a child interested in mathematics if teaching at school is mediocre?
First, let's make a reservation that "mediocre teaching" is a very conditional term. All parents and teachers have a different idea of what it should be. But in general, I understand what you mean: let's say a child comes from school with dull eyes, and at the very word "mathematics" he develops a persistent disgust.
Let's try to understand why children cannot be torn away, for example, from computers, in contrast to the study of mathematics. What attracts them so much in computer games? It seems to me that several factors are at work:
- they are not forced to play;
- do not scold in case of failure;
- children understand the goal (to score a goal, overcome an obstacle), it is significant for them, and they achieve it themselves;
- they are interested in content, design;
- achievements are necessarily recorded (points, levels), which feeds the feeling of victory;
- the results of the game are significant for peers, and thus the child's need for recognition is satisfied.
This set of factors sufficiently provides the mechanism of motivation “must” – “want” – “can”. To interest a child in mathematics, you can act by analogy.
Ludmila Peterson1. The main thing is not to force, but to inspire
The desire to engage in any business arises only in an atmosphere of mutual respect, trust and goodwill. Without close relationships with children, parents can do little to help them other than buying food, clothes, and stationery.
It is very important to understand what exactly makes a child unwilling to study. This requires a calm, nonjudgmental conversation. The child must be sure that you are asking him not to evaluate or give instruction, but to help him cope with what is not working yet.
Give him a chance to talk. Think together about the reasons why math has become an unloved subject. It is always easier to attribute everything to “mediocre teaching” or to something else external that does not require work on oneself.
But this will not help solve the problem, rather the opposite. To inspire a child to work on himself, you need to sincerely believe in him and not get tired of repeating that he will succeed.
2. Do not scold your child for mistakes and poor grades
This does not mean remaining indifferent to its results. On the contrary, an adequate reaction of parents to failure is empathy and complicity: "Let's figure out what has not worked out so far." It is not notation that helps to move forward, but awareness of one's problems.
Each child develops at an individual pace, so it is not the result that matters, but the dynamics relative to oneself.
Any effort is already a small victory. A job well done is one more step. It turned out that it didn’t work before - the next
It is very important to notice and fix any forward movement, even the smallest one. Then the child will feel that he is not accused, his parents are on the same side with him, they are his friends and support.
3. Help to achieve the goal
The child's awareness of what is not yet achieved will help lead him to a new goal. In studies, it is always to find out what he “does not know” yet, to learn what he “does not know” yet. That is why it is so important to understand what specifically causes difficulties. Let me give you an example of an introductory dialogue. Suppose he says that he understands nothing about mathematics.
— Nothing at all? Let's look through the textbook, notebook.
— Are you able to do such tasks? What about those?
When examining a textbook together with a child, you need to show the simplest tasks first, then the more difficult ones. And so on until the really incomprehensible comes across. Next, we need to think together how to carry out such tasks.
— Excellent! You figured out what you need to learn (goal). Now let's think about how this can be done?
It is important to let the child speak out, to listen to his options, to suggest the possibilities that he did not name.
There may be many of them. For example, approach a teacher, ask a friend or older sister, figure it out from a textbook on your own or with you.
The main thing is to outline an action plan and bring it to a successful result. Let the child believe in himself, be sure to pay attention to what happened: “That’s cool, but you said you don’t know how!”
4. Maintain interest
Of course, it is useful to involve a child of any age and any level of training in solving game and non-standard tasks. It's always better to start small. Throw up a problem that he will definitely cope with, and then another one, more difficult.
Now on the Internet you can find a huge number of interesting tasks of any complexity, not limited, of course, only to our textbook. For example, the wonderful books by Y. Perelman "Entertaining Mathematics", "Funny Problems", "Quick Counting", "Live Mathematics"; B. Kordemsky "Mathematical ingenuity"; A. Kalinina, E. Katz, A. Tilipman "Mathematics is in your hands", cartoon problems from TED and many others.
Don't rush, don't chuckle if he gives a wrong answer. Admire his achievements: “Wow, but I didn’t guess! Great!"
If a child's eyes light up when he talks about a problem that he could solve, then he is ready to set higher goals - first participation, and then victory in various mathematical Olympiads. Now, in addition to the All-Russian Olympiad for schoolchildren, there are many, full-time and online. The main thing is to make sure that interest does not disappear, and that the level and pace are feasible for him.
5. Notice and fix the situation of success
A child will always strive only for what he succeeds. We all, like water for life, need a situation of success. The teacher Vasily Sukhomlinsky wrote: "The child draws moral strength to overcome his weaknesses in his successes."
At the same time, success is not directly related to grades. For example, you can get an A for writing off work. There is nothing to rejoice. And you can, with effort, reach the top three - this is a real victory! Her formula: "difficulty - effort in overcoming it - success.
" The greater the effort, the happier the victory.
Adults often praise a child only for grades. It seems to me that it is much more important to observe his efforts, dynamics, achievement of goals and share the joy of victories with him.
6. Make victories meaningful family events
The need for recognition and respect from others is one of the basic needs of any person. Recognition gives rise to self-confidence, the desire to achieve a result that is significant for others.
That is why the family's attention to success is so important. Tell your grandparents about your child's victories. Remember and rejoice during a family dinner or on a walk. By doing this, you will not only support the desire to do mathematics, but also help your child develop self-respect.
These simple rules are just some model that does no harm to follow. Of course, it is important that mathematics be interesting to the parent himself: the more useful it will be, the more he is passionate about it.
After all, you can hardly be carried away by something that you yourself are not interested in.
What should adults do who did not like mathematics at school, but now they understand that they missed something important? Where to begin?
Now there are more and more such adults. Recently, I came across a book by Nelly Litvak, professor of mathematics at the University of Twente in Holland, in collaboration with Alla Kechedzhan, "Mathematics for Hopeless Humanities", which was born as a response to this request from adults. The authors, having learned how many readers the book has, created a Facebook group for them called "Mathematics - Great and Terrible". Now it has tens of thousands of members and is constantly growing.
Nelly Litvak and Alla Kechedzhan’s book “Mathematics for Hopeless Humanities” was published by the AST publishing house in 2019 This is just one example, but many other excellent books can be recommended. For example, “The Great Novel about Mathematics.
The history of the world through the prism of mathematics" Mikael Lone. This book is part of the "Pleasure of Science" series and helps to understand how interesting and exciting mathematics is. The author tells about the history of this science from antiquity to the present day and about what it will become in tens, hundreds of years.
There are also many fascinating videos and films of various genres that inspire the study of mathematics. For example, the videos "We and Math", "Nature in Numbers", the films "The Great Secret of Mathematics", "Proof", "Good Will Hunting", "Sensual Math", "X + Y", "Professor's Favorite Equation", " The Man Who Knew Infinity", "Secret Sign", "Sofya Kovalevskaya", "Twenty One", "The Big Short Game", "Stephen Hawking's Universe", "Infinity", "Agora", "Pi", "Math and the Devil ”,“ I.
Q. ”,“ Mind Games ”.
There are many lectures and comprehensive math courses for adults on the Internet, including free ones. In a couple of hours, everyone can build their own trajectory of mathematical development. The best scenario is to study it together with children, discover new mathematical concepts and formulas with them, solve interesting problems, joke and enjoy success. And the main thing is to communicate with them and do a common thing, for which parents often do not have enough time today and what children need so much.
In 2019year, your benefits returned to the federal list of textbooks. What has changed for you since that moment and what are your plans for the new academic year?
The return of the textbooks to the FPU, no doubt, removed the gigantic problem that prevented the work of thousands of schools and kindergartens. Not only because teachers can use textbooks again without any problems. The main thing is that justice has been restored in relation to brilliant teachers who have prepared more than one generation of successful and talented children over the years.
As always, we have a lot of plans. For all teachers working on our continuous mathematics course "Learning to Learn", there will be free monthly online consultations for all classes.
Methodological webinar by Lyudmila PetersonIn September, we are planning to launch the Smart Solver project. This is an online educational platform where children and parents can not only find ready-made solutions to the tasks of our course, but also independently understand the causes of difficulties associated with solving certain problems.
We continue the work of the Federal Innovation Platform and the All-Russian Research Project, which today brings together more than four thousand leaders in their regions. This year, the All-Russian project became international. Within these platforms, we develop and test new directions for solving problems that concern everyone today: how to systematically and effectively form the ability to learn, how to measure and evaluate meta-subject results of education, how to transfer schools with so-called low learning outcomes for children, the system of Olympiad training in mathematics from 1st to 9thth class.
We are looking for answers to these and other questions: we create educational programs and technologies, test them in schools and kindergartens.
Each student in our "Children's Academy" undergoes a comprehensive monitoring of aptitudes, according to the results of which our specialists, together with the child himself and his parents, draw up an individual route of his education. Classes at the "Children's Academy" are more like exciting quests, where everyone can move at their own pace along the chosen route.
Children work in groups of different ages - they play, experiment, build mathematical models, solve design problems in teams. For each group, the lesson is assembled with the help of a special "constructor" that takes into account the age, interests, and characteristics of the children of this group.
Thus, we implement the ideas of personalized learning (including within the framework of online education).
Last time you said that education should result not only in knowledge, but also in the development of certain qualities in children. Can we say that modern education is moving in this direction?
Yes, this is the key question. From his decision, in my opinion, the competitiveness of the school in the future will depend. More and more parents are waiting for their children to be interested in learning, so that their faith in their own strengths grows, experience of personal and collective victories accumulates, so that they are ready for self-development and consciously choose their path - along with the acquisition of new knowledge. All this is achieved by the meta-subject results of education, the skills of the 21st century.
This requires new teaching methods.
However, in practice, educators often prefer to simply explain topics to children. The reason is clear. Any structure, achieving efficiency, focuses on the result for which it reports. In our case, these are mainly administrative tests, the average score of the VPR, the OGE and the Unified State Examination. These results are achieved to some extent by habitual training.
Why should teachers change something? After all, explaining the material to children is much easier than leading them to discover it on their own
A real transition to a new school requires new measures of educational outcomes. Now many people are engaged in this area, including us, both in theoretical research and applied development within the framework of the over-subject course "The World of Activity".
Already today there are different options for criteria and monitoring of meta-subject skills, but so far they are all in the testing stage. There is still a lot of work ahead to refine and improve them.
How significant is the USE in this sense? Or is it just about knowledge?
The exam, like any exam, of course, is not only about knowledge, but also about diligence, responsibility, the ability to build a strategy for one's preparation, cope with excitement, focus and much more. However, the final result of the USE, from my point of view, does not provide sufficient information about the quality of education.
What was the initial level of the child and what is the dynamics of his growth? What can he do on his own - without tutors and mentors? Does he know how to work in a team? What are his interests and hobbies? How stress-resistant is he if something goes wrong? What are his goals and plans and how does he set and describe them?
The answers to these and many other questions, it seems to me, are no less important for evaluating the results than the score received on the USE. Moreover, it is these questions that will primarily be of interest to future employers of our graduates.
Therefore, it is obvious to me that the USE will change and be supplemented over time in order to meet the requirements of our life.
You have been studying mathematics for many years, and you do not seem to get bored at all. Tell us why it might be of interest to everyone?
The most precise definition of mathematics was given, in my opinion, by the great Henri Poincaré: "Mathematics is the art of calling different things by the same name." This definition combines the essence of the mathematical language - a generalized description of the patterns of the surrounding world - and the magic and beauty that mathematical laws carry. Albert Einstein was always surprised and admired by how easily and clearly mathematics describes the Universe.
Let's take a simple series of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… In it, each number, starting from the third, is equal to the sum of the previous two. This sequence was built by Leonardo Fibonacci over seven centuries ago.
And it turned out that it is these numbers that, as a rule, express the number of petals on flowers. How can it be?
But that's not all. The sequence of Fibonacci numbers can be visually depicted using a spiral. We will unexpectedly find this form in nature on completely unrelated objects: snail spirals, Galaxy spirals, spirals on a cut of a head of cabbage, in a sunflower inflorescence, whirlwinds and cyclones have the same form.
Fibonacci sequenceWhy is that? Why is the ratio of numbers in the golden ratio, which simultaneously describes the proportions of the human body, and the arrangement of leaves on the stem of a flower, and the rules of harmony in painting, architecture, design, which are already more than 4000 years old, all this is directly related to the ratio of neighboring numbers of the Fibonacci series? Is it really possible not to be surprised?
For me, the beauty of mathematics is associated primarily with the depth and universality of its laws
If, for example, we randomly select 1000 people and plot their distribution by height, then we get a Gaussian curve, where the top point of the graph will correspond to the average height in the group.
The more people in the sample, the more aesthetically perfect the line will be. The famous English scientist Francis Galton said: "If the ancient Greeks knew the Gaussian law of normal distribution, they would have deified it."
Mathematics is a living, developing science. Today, of course, it does not describe all the phenomena of the world, and this means that amazing mathematical discoveries await us ahead. We want children to master this science as part of culture, so the main task is to help them see mathematics in its development, to feel the beauty and depth of its laws.
To do this, it is important to create an environment in which children can make discoveries for themselves - face the unknown, experience inspiration, put forward their ideas, experience victories and failures, be surprised and admire the logic of mathematics and the beauty of mathematical laws. We see our task in creating pedagogical tools for this - technologies, methods, new content of mathematical education.
