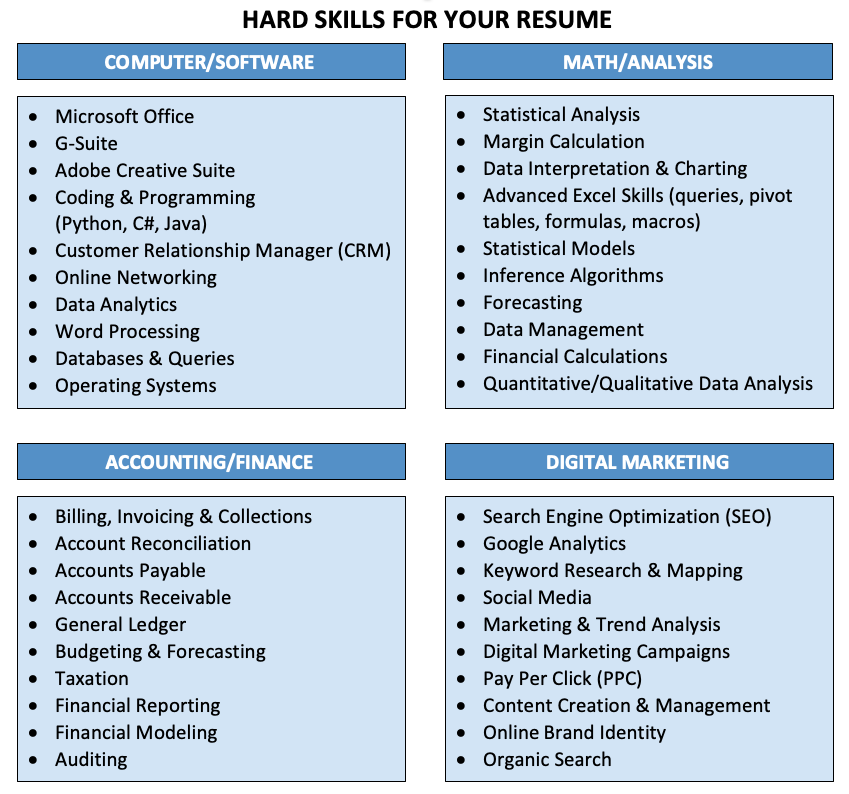
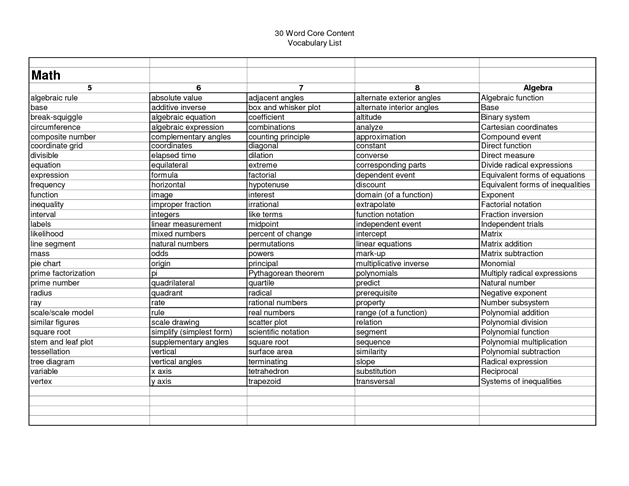
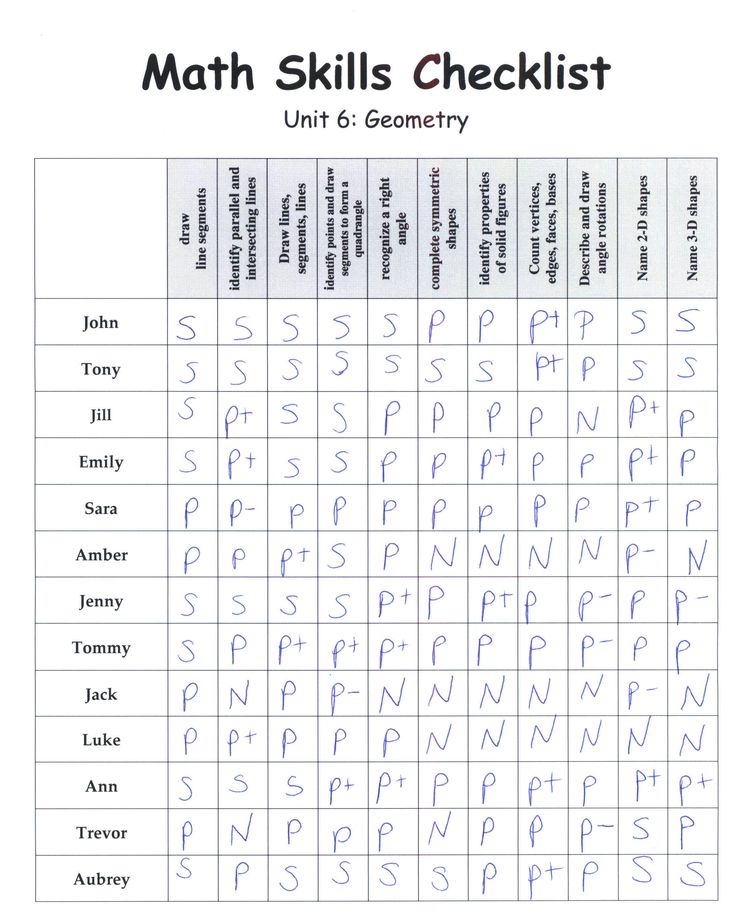
Home » Misc » List of mathematical skills

List of mathematical skills


Help Your Child Develop Early Math Skills

Before they start school, most children develop an understanding of addition and subtraction through everyday interactions. Learn what informal activities give children a head start on early math skills when they start school.

Children are using early math skills throughout their daily routines and activities. This is good news as these skills are important for being ready for school. But early math doesn’t mean taking out the calculator during playtime. Even before they start school, most children develop an understanding of addition and subtraction through everyday interactions. For example, Thomas has two cars; Joseph wants one. After Thomas shares one, he sees that he has one car left (Bowman, Donovan, & Burns, 2001, p. 201). Other math skills are introduced through daily routines you share with your child—counting steps as you go up or down, for example. Informal activities like this one give children a jumpstart on the formal math instruction that starts in school.

What math knowledge will your child need later on in elementary school? Early mathematical concepts and skills that first-grade mathematics curriculum builds on include: (Bowman et al., 2001, p. 76).

  • Understanding size, shape, and patterns
  • Ability to count verbally (first forward, then backward)
  • Recognizing numerals
  • Identifying more and less of a quantity
  • Understanding one-to-one correspondence (i.e., matching sets, or knowing which group has four and which has five)

Key Math Skills for School

More advanced mathematical skills are based on an early math “foundation”—just like a house is built on a strong foundation. In the toddler years, you can help your child begin to develop early math skills by introducing ideas like: (From Diezmann & Yelland, 2000, and Fromboluti & Rinck, 1999.)

Number Sense

This is the ability to count accurately—first forward. Then, later in school, children will learn to count backwards. A more complex skill related to number sense is the ability to see relationships between numbers—like adding and subtracting. Ben (age 2) saw the cupcakes on the plate. He counted with his dad: “One, two, three, four, five, six…”

Representation

Making mathematical ideas “real” by using words, pictures, symbols, and objects (like blocks). Casey (aged 3) was setting out a pretend picnic. He carefully laid out four plastic plates and four plastic cups: “So our whole family can come to the picnic!” There were four members in his family; he was able to apply this information to the number of plates and cups he chose.

Spatial sense

Later in school, children will call this “geometry.” But for toddlers it is introducing the ideas of shape, size, space, position, direction and movement. Aziz (28 months) was giggling at the bottom of the slide. “What’s so funny?” his Auntie wondered. “I comed up,” said Aziz, “Then I comed down!”

Measurement

Technically, this is finding the length, height, and weight of an object using units like inches, feet or pounds.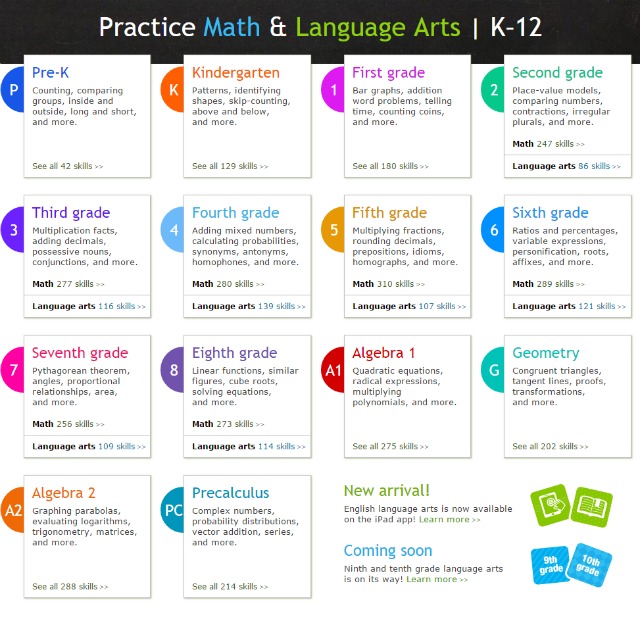 Measurement of time (in minutes, for example) also falls under this skill area. Gabriella (36 months) asked her Abuela again and again: “Make cookies? Me do it!” Her Abuela showed her how to fill the measuring cup with sugar. “We need two cups, Gabi. Fill it up once and put it in the bowl, then fill it up again.”

Estimation

This is the ability to make a good guess about the amount or size of something. This is very difficult for young children to do. You can help them by showing them the meaning of words like more, less, bigger, smaller, more than, less than. Nolan (30 months) looked at the two bagels: one was a regular bagel, one was a mini-bagel. His dad asked: “Which one would you like?” Nolan pointed to the regular bagel. His dad said, “You must be hungry! That bagel is bigger. That bagel is smaller. Okay, I’ll give you the bigger one. Breakfast is coming up!”

Patterns

Patterns are things—numbers, shapes, images—that repeat in a logical way. Patterns help children learn to make predictions, to understand what comes next, to make logical connections, and to use reasoning skills. Ava (27 months) pointed to the moon: “Moon. Sun go night-night.” Her grandfather picked her up, “Yes, little Ava. In the morning, the sun comes out and the moon goes away. At night, the sun goes to sleep and the moon comes out to play. But it’s time for Ava to go to sleep now, just like the sun.”

Problem-solving

The ability to think through a problem, to recognize there is more than one path to the answer. It means using past knowledge and logical thinking skills to find an answer. Carl (15 months old) looked at the shape-sorter—a plastic drum with 3 holes in the top. The holes were in the shape of a triangle, a circle and a square. Carl looked at the chunky shapes on the floor. He picked up a triangle. He put it in his month, then banged it on the floor. He touched the edges with his fingers. Then he tried to stuff it in each of the holes of the new toy. Surprise! It fell inside the triangle hole! Carl reached for another block, a circular one this time…

Math: One Part of the Whole

Math skills are just one part of a larger web of skills that children are developing in the early years—including language skills, physical skills, and social skills. Each of these skill areas is dependent on and influences the others.

Trina (18 months old) was stacking blocks. She had put two square blocks on top of one another, then a triangle block on top of that. She discovered that no more blocks would balance on top of the triangle-shaped block. She looked up at her dad and showed him the block she couldn’t get to stay on top, essentially telling him with her gesture, “Dad, I need help figuring this out.” Her father showed her that if she took the triangle block off and used a square one instead, she could stack more on top. She then added two more blocks to her tower before proudly showing her creation to her dad: “Dada, Ook! Ook!”

You can see in this ordinary interaction how all areas of Trina’s development are working together. Her physical ability allows her to manipulate the blocks and use her thinking skills to execute her plan to make a tower. She uses her language and social skills as she asks her father for help. Her effective communication allows Dad to respond and provide the helps she needs (further enhancing her social skills as she sees herself as important and a good communicator). This then further builds her thinking skills as she learns how to solve the problem of making the tower taller.

What You Can Do

The tips below highlight ways that you can help your child learn early math skills by building on their natural curiosity and having fun together. (Note: Most of these tips are designed for older children—ages 2–3. Younger children can be exposed to stories and songs using repetition, rhymes and numbers.)

Shape up.

Play with shape-sorters. Talk with your child about each shape—count the sides, describe the colors. Make your own shapes by cutting large shapes out of colored construction paper. Ask your child to “hop on the circle” or “jump on the red shape.”

Count and sort.

Gather together a basket of small toys, shells, pebbles or buttons. Count them with your child. Sort them based on size, color, or what they do (i.e., all the cars in one pile, all the animals in another).

Place the call.

With your 3-year-old, begin teaching her the address and phone number of your home. Talk with your child about how each house has a number, and how their house or apartment is one of a series, each with its own number.

What size is it?

Notice the sizes of objects in the world around you: That pink pocketbook is the biggest. The blue pocketbook is the smallest. Ask your child to think about his own size relative to other objects (“Do you fit under the table? Under the chair?”).

You’re cookin’ now!

Even young children can help fill, stir, and pour. Through these activities, children learn, quite naturally, to count, measure, add, and estimate.

Walk it off.

Taking a walk gives children many opportunities to compare (which stone is bigger?), assess (how many acorns did we find?), note similarities and differences (does the duck have fur like the bunny does?) and categorize (see if you can find some red leaves). You can also talk about size (by taking big and little steps), estimate distance (is the park close to our house or far away?), and practice counting (let’s count how many steps until we get to the corner).

Picture time.

Use an hourglass, stopwatch, or timer to time short (1–3 minute) activities. This helps children develop a sense of time and to understand that some things take longer than others.

Shape up.

Point out the different shapes and colors you see during the day. On a walk, you may see a triangle-shaped sign that’s yellow. Inside a store you may see a rectangle-shaped sign that’s red.

Read and sing your numbers.

Sing songs that rhyme, repeat, or have numbers in them. Songs reinforce patterns (which is a math skill as well). They also are fun ways to practice language and foster social skills like cooperation.

Start today.

Use a calendar to talk about the date, the day of the week, and the weather. Calendars reinforce counting, sequences, and patterns. Build logical thinking skills by talking about cold weather and asking your child: What do we wear when it’s cold? This encourages your child to make the link between cold weather and warm clothing.

Pass it around.

Ask for your child’s help in distributing items like snacks or in laying napkins out on the dinner table. Help him give one cracker to each child. This helps children understand one-to-one correspondence. When you are distributing items, emphasize the number concept: “One for you, one for me, one for Daddy.” Or, “We are putting on our shoes: One, two.”

Big on blocks.

Give your child the chance to play with wooden blocks, plastic interlocking blocks, empty boxes, milk cartons, etc. Stacking and manipulating these toys help children learn about shapes and the relationships between shapes (e.g., two triangles make a square). Nesting boxes and cups for younger children help them understand the relationship between different sized objects.

Tunnel time.

Open a large cardboard box at each end to turn it into a tunnel. This helps children understand where their body is in space and in relation to other objects.

The long and the short of it.

Cut a few (3–5) pieces of ribbon, yarn or paper in different lengths. Talk about ideas like long and short. With your child, put in order of longest to shortest.

Learn through touch.

Cut shapes—circle, square, triangle—out of sturdy cardboard. Let your child touch the shape with her eyes open and then closed.

Pattern play.

Have fun with patterns by letting children arrange dry macaroni, chunky beads, different types of dry cereal, or pieces of paper in different patterns or designs. Supervise your child carefully during this activity to prevent choking, and put away all items when you are done.

Laundry learning.

Make household jobs fun. As you sort the laundry, ask your child to make a pile of shirts and a pile of socks. Ask him which pile is the bigger (estimation). Together, count how many shirts. See if he can make pairs of socks: Can you take two socks out and put them in their own pile? (Don’t worry if they don’t match! This activity is more about counting than matching.)

Playground math.

As your child plays, make comparisons based on height (high/low), position (over/under), or size (big/little).

Dress for math success.

Ask your child to pick out a shirt for the day. Ask: What color is your shirt? Yes, yellow. Can you find something in your room that is also yellow? As your child nears three and beyond, notice patterns in his clothing—like stripes, colors, shapes, or pictures: I see a pattern on your shirt. There are stripes that go red, blue, red, blue. Or, Your shirt is covered with ponies—a big pony next to a little pony, all over your shirt!

Graphing games.

As your child nears three and beyond, make a chart where your child can put a sticker each time it rains or each time it is sunny. At the end of a week, you can estimate together which column has more or less stickers, and count how many to be sure.

References

Bowman, B.T., Donovan, M.S., & Burns, M.S., (Eds.). (2001). Eager to learn: Educating our preschoolers. Washington, DC: National Academy of Sciences.

Diezmann, C., & Yelland, N. J. (2000). Developing mathematical literacy in the early childhood years. In Yelland, N.J. (Ed.), Promoting meaningful learning: Innovations in educating early childhood professionals. (pp.47–58). Washington, DC: National Association for the Education of Young Children.

Fromboluti, C. S., & Rinck, N. (1999 June). Early childhood: Where learning begins. U.S. Department of Education, Office of Educational Research and Improvement, National Institute on Early Childhood Development and Education. Retrieved on May 11, 2018 from https://www2.ed.gov/pubs/EarlyMath/title.html

 

What They Are And Examples – Zippia

  • What Are Mathematical Skills?
  • How to Improve Your Mathematical Skills
  • How to Highlight Mathematical Skills on a Resume
  • Improving Your Mathematical Skills Is Worth the Effort
  • Frequently Asked Questions
  • Sign Up For More Advice and Jobs

Show More

Improving your mathematical skills will increase your chances for professional success, no matter what career path you pursue.

Many professionals use mathematical skills directly in their day-to-day duties without realizing it.

Even for the rare jobs that never directly deal with numbers and figures, you’ll often need the same problem-solving and critical thinking abilities used in math to succeed.

In this article, we’ll cover the most important mathematical skills to master for the workplace. You’ll also learn how to improve your math skills and highlight them during the job-search process.

Key Takeaways:

  • 10 mathematical skills that are useful in the workplace are time management, mental arithmetic, constructing logical arguments, abstract thinking, data analysis, research, visualization, creativity, forecasting, and attention to detail.

  • Improve your mathematical skills by acquiring conceptual understandings of the skills and solving practice problems.

  • A mathematical skill should be listed on a resume when the job listing states the skill as a requirement.

  • Most mathematical skills are transferable and help you stand out in a crowd of applicants.

What Are Mathematical Skills?

The term “mathematical skills” doesn’t just refer to nebulous topics taught in school, such as calculus. They’re the practical abilities that are useful no matter the industry or size of business you work in.

This includes skills such as:

  1. Time management. Being able to manage your time efficiently is critical for your day-to-day activities, in addition to long-term planning success.

    The average person wastes three entire hours each day due to inefficient time management.

    Not only does that immediately translate to wasted money, but to wasted time that could be devoted to your non-work passions and activities.

    The inability to manage time over the long-term could also lead to underperformance and missed deadlines that could harm or even destroy your career.

  2. Mental arithmetic. Being able to do mental math quickly will serve you well in a variety of professions.

    Retail workers may need to quickly and accurately figure out a customer’s change when given a large sum of money.

    If a business client suggests an order or asks about certain specifications, you might need to quickly determine the mathematical viability of whatever their request is.

  3. Constructing logical arguments. Many careers demand the same precise, logical reasoning that’s used to solve math problems.

    An attorney needs to ensure that their legal argument logically follows from the facts and evidence provided.

    A sales representative must present relevant reasons to clients in order to convince them to purchase a product.

  4. Abstract thinking. Abstract thinking is the ability to understand and compare non-physical concepts, such as freedom or honesty.

    Improving your abstract thinking skills is useful for any career that involves creativity or navigating through complex rules.

    For example, programmers and physicists use abstract thinking when learning how a program or system functions.

  5. Data analysis. A large variety of professions will require you to interpret and analyze data at some point.

    Any scientific career will involve heavy interpretation of complex sets of data.

    Jobs in business-related fields will likewise require you to understand charts and figures in order to extract meaningful patterns.

  6. Research. Knowing how to effectively research information is crucial for developing solutions for the many problems you’ll face in your career.

    In the age of the internet, there is a nearly infinite wealth of information about any topic you could wish to learn about.

    The downside is that much of that information is misleading or false, making it critical that you develop the ability to fact-check and distinguish reputable sources from untrustworthy ones.

  7. Visualization. The same ability to visualize problems and outcomes is critical for finding solutions in the workplace.

    Any problem you face during your career will present a variety of possible solutions with which to tackle it.

    Visualization skills allow you to weigh the available data and tools, the target goal, and other factors to solve the challenge.

  8. Creativity. Improving your creativity skills allows you to come up with new ideas and innovations.

    Presenting fresh ideas and solutions will also help you stand out among the competition in the workplace.

    This makes the skill applicable to almost every possible career, not just those commonly considered “creative.”

  9. Forecasting. Forecasting is the ability to extrapolate events into the future based on available data and knowledge.

    This skill is critical for any job that involves planning for the future.

    For example, a manager needs to be able to forecast details such as revenue and budget into the future to make effective decisions in the present.

  10. Attention to detail. Some jobs require more attention to small details than others.

    An athlete may be mostly unaffected by miscalculating some small aspect of their daily fitness regimen, but a software developer that misses a single piece of syntax could crash an entire program.

How to Improve Your Mathematical Skills

You can improve your mathematical skills in the same way that you would improve any other skill – through consistent practice.

More specifically, there are two key actions you should follow:

  • Acquire conceptual understanding. You can’t improve a mathematical skill if you don’t even know what that math skill entails.

    For example, suppose that you wish to improve your data analysis skills.

    A quick Google search reveals that the main elements of data analysis include understanding statistics, visuals such as charts and graphs, and how to apply the data to practical problems.

    You could then look up those specific elements and further branch down to fill any gaps in your knowledge. Use the internet and it’s nearly infinite examples and descriptions to help you learn.

  • Solve practice problems. It’s not enough to understand a concept to master it; you must practice practically applying it.

    This piece of advice applies to certain math skills more than others. You can find plenty of online games to help you improve your hard skills, such as mental arithmetic, but maybe not your creativity.

    You’ll have to use your own creativity to find ways to target those skills and challenge yourself in the same way that you would target a specific muscle group when working out.

How to Highlight Mathematical Skills on a Resume

Improving your mathematical skills positively affects your work performance.

However, we still want to find a way to highlight them to recruiters, so they know that we’ve mastered them.

There are a few important guidelines to follow:

  • List or prove on your resume. The skills section of your resume can be an okay place to mention your math skills.

    1. The job listing states the skill as a requirement. If your resume doesn’t contain the specific term, some companies’ applicant tracking systems (ATS) may automatically filter you out.

    2. Not significant enough to waste additional resume space. Despite being required, some skills may not be essential enough to waste more than a single bullet point talking about.

      For example, a job may require basic clerical skills such as multiplying and dividing small figures.

      Once you meet this baseline requirement, however, companies would rather read more about your other qualifications than your ability to multiply well.

    “Critical-thinking skills” and “problem-solving skills” are generically added to so many resumes that the terms often become meaningless.

    A better way to highlight your math skills on a resume is to prove it through the results you’ve achieved. Use numbers to emphasize the positive value you created for a past employer.

    For example, “Developed a new marketing strategy by analyzing millions of data points that improved customer conversion rates by 23%” proves to recruiters that you possess strong data-analysis abilities.

  • Prove them in your cover letter. You want to give examples of when you used mathematical skills to create value for a past employer.

    This differs from the resume strategy in that cover letters are narrower in scope.

    Your resume needs to fit many examples on a single page, while your cover letter can target a few key skills to demonstrate with greater detail.

    To figure out which math skills to focus on, pay attention to the essential requirements and duties listed in the job listing. Make your best judgment on the most important skills to highlight.

    Unlike on your resume, where simply listing a mathematical skill without examples to back it up can sometimes make sense, never do this on your cover letter.

  • Explain in-depth during your job interview. Job interviews allow you the time to dive much deeper into examples of how you’ve utilized mathematical skills.

    Consider the previous resume example about developing a new marketing strategy using data-analysis skills.

    During the interview, you could expand on the specific technical skills and tools you used. Explain the initial problem and the thought process you employed to tackle it.

    Of course, the type of job interview does affect the content of your answer. If the job isn’t directly related to marketing or data-analysis, then expand only on your transferable skills and the more generally applicable aspects of your thought-process.

Improving Your Mathematical Skills Is Worth the Effort

Many professionals neglect to train their mathematical skills in favor of skills that are more directly relevant to their jobs. While direct skills are important, you should improve both categories of skills to help you stand out from the crowd.

Most mathematical skills are transferable, meaning they’ll remain useful throughout your entire career rather than just at your current job. From researcher to nurse, designer to manager; mathematical skills such as data analysis and problem-solving will serve you well.

Frequently Asked Questions

  1. What are the most important math skills?

    2. The most important math skills in the workplace depend on your needs.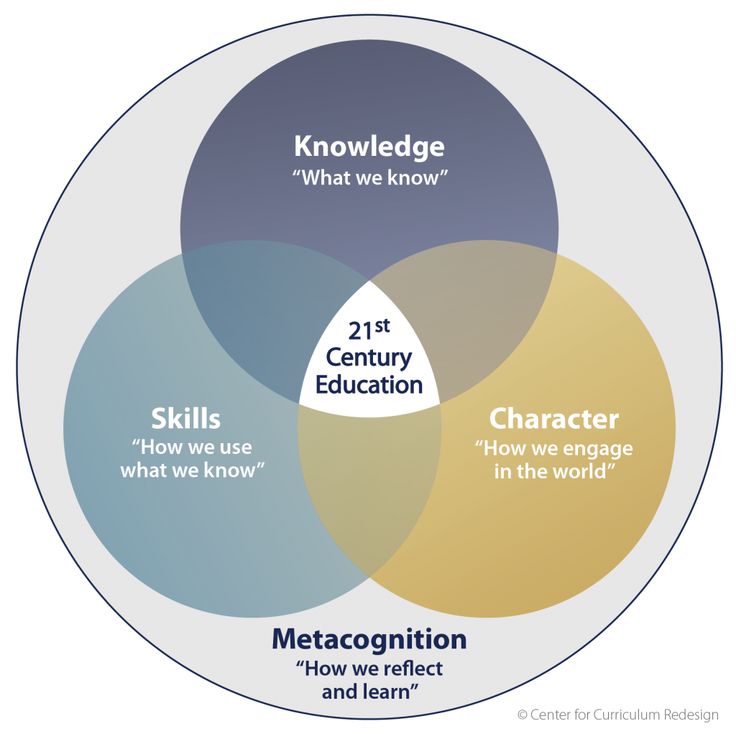 The four fundamental arithmetic operations of adding, subtracting, multiplying and dividing are very important for all adults to have a basic understanding because they appear in many of our lives daily.

    Time management, logic, and abstract thinking are also very important for most adults to know, regardless of profession, because they help provide structure to your life and prepare you for critical thinking.

  2. Why are mathematical skills important?

    3. Mathematical skills are important because they provide structure to solving problems rationally. Mathematical skills can be used everyday to make sense of a chaotic world. Recognizing patterns, using logic, building on abstract concepts all are what help keep society moving.

  3. How do you list math skills on a resume?

    4. List math skills under the skills section of a resume. In order to be efficient with space, make sure to only list relevant skills that are found in the job description and avoid general terms.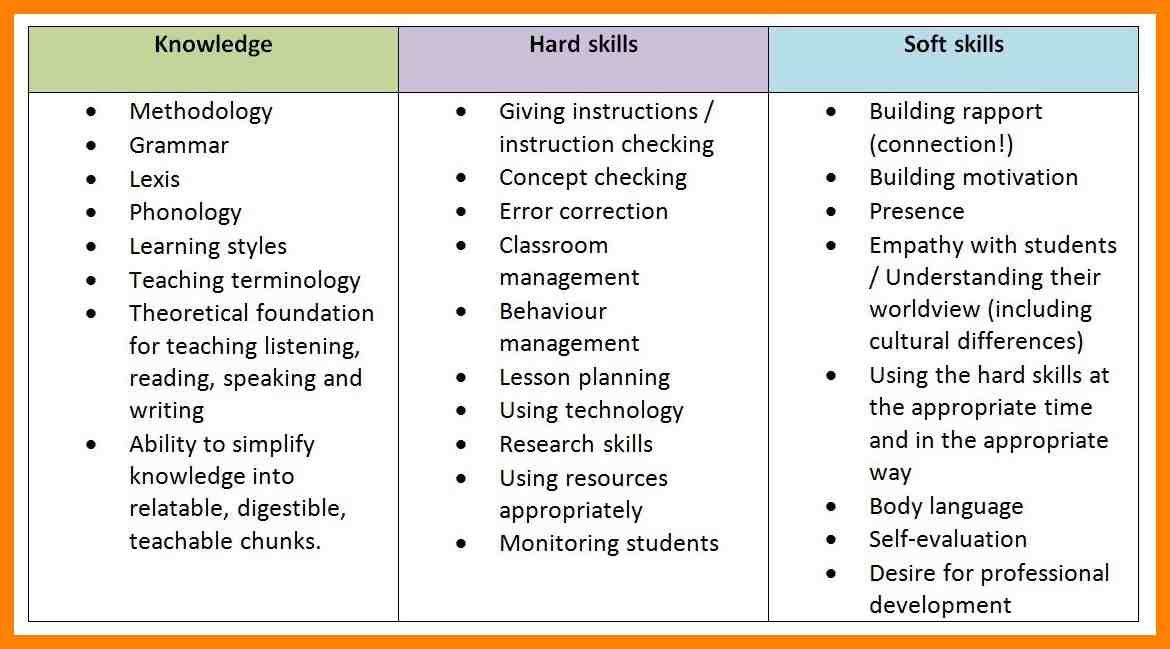

How useful was this post?

Click on a star to rate it!

Average rating / 5. Vote count:

No votes so far! Be the first to rate this post.

Never miss an opportunity that’s right for you.

Theory in Mathematics | Basic and profile level of the USE in mathematics

The USE in mathematics is one of the most difficult subjects for graduates. USE levels in mathematics - basic and profile. And if everyone can cope with basic mathematics, although difficulties arise here, then not everyone can cope with profile mathematics.

USE levels in mathematics and types of tasks

The basic level of the USE in mathematics does not pass anyone by. Even a born humanist will have to pass it, albeit in the basic version. The base is mandatory for all graduates. 20 tasks, three hours. In the tasks themselves there are graphs, charts, tables, tasks. The student must show that he can count the change in the store, the days of the week in the calendar. They are not complicated, it is important to carefully read the condition and thoughtfully write the solution. A graduate should be able to calculate and transform, solve inequalities, navigate in logarithms, equations, know mathematical models. The tasks are easy and a student with good academic performance does not have difficulties with them.

The profile level of the USE in mathematics is a completely different matter. It is much more difficult than the basic one. At the same time, profile mathematics is one of the leaders of elective subjects for passing the exam. In 2019, half of all graduates took it. Profile mathematics enables graduates to associate themselves with technical, economic specialties. The core exam includes the same topics as the core exam.

Where to find out what will be on the exam

The list of skills to be tested and the list of topics are posted in the public domain on the FIPI website. In the "Demos, Specifications, Codifiers" section, you can see the structure of the profile level, topics, skills being tested. In any case, at the profile level, the USE in mathematics will not be those that would not be studied at school. According to the codifier, all topics can be divided into 12. They look like this.

USE topics in mathematics

A graduate should practice:

  • the basics of algebra;
  • logarithms and powers;
  • derivative and function analysis;
  • probability theory;
  • trigonometry;
  • simple geometry;
  • text tasks for movement, mixtures, teamwork;
  • inequalities;
  • solving an economic problem;
  • complex geometry;
  • tasks with parameters;
  • number theory and olympiad tasks.

If you work out:

  • six topics, you can score 60 points.
  • nine topics already give 80 points.
  • 12 topics give 100 points.

USE tasks in mathematics require both short and detailed answers. The exam itself consists of 19 tasks and four hours to complete.

There are 12 test items in the first part. Most of the guys solve them without errors. They give a total of 62 points.

But then the problems begin. Graduates experience difficulties in solving problems in geometry, both in planimetry and stereometry. In the rating of "bad" tasks - tasks with a parameter. The theory of mathematics for the exam is in the program, but the difficulty is that tasks of this type are not considered at school. In the exam, they are and these are high-level tasks that give four primary points at once. Gaps can arise when solving tasks for logarithms, trigonometry and an economic problem. These are 13, 14, 17 tasks.

It is naive to hope, having decided to go to the profile level of the Unified State Examination in mathematics, that you will just be “lucky”. Luck factor, of course. But it will work up to a maximum of 70 points. Those who need good results - 80 or more points, must prepare for the exam and work throughout the school year.

Preparing for the Unified State Examination in Mathematics profile level is based primarily on understanding and systematic preparation. Before completing the task, you first need to understand it, then apply the formulas and solution schemes. The mere solution of problems and options and coaching according to the template does not give the desired result. You can solve 120 options for 17 tasks, and the 121st option will fall on the exam. Tasks, especially in the second part, can be formulated from the “other end” and if there is no understanding, then you can simply lose points. And every point counts!

What mathematical skills will be tested

The required list of skills to be tested is described in detail in the KIM USE specification for mathematics profile level. It is posted on the FIPI website. According to this document, a graduate must apply knowledge and skills in mathematics in his daily life, calculate and transform, solve equations and inequalities, build mathematical models, perform actions with functions, coordinates, vectors. Mastering these skills guarantees high scores on the exam. And for this you need:

  • throw away the calculator and learn to count without it;
  • repeat the whole theory, learn the formulas. This is the base that will help solve problems.
  • identify your weak points. Work them out.
  • keep track of the time. If the solution of one problem takes you one hour, then it will be problematic to pass the exam for high scores and enter the university of your dreams.

It is important to properly allocate time for the exam itself. The first part of tasks (1-12) can be solved in 30 minutes. Then you can proceed to tasks 13, 14, 17. And if you have not made a mistake even once, then this will give 80 points. The solution of these 3 tasks can be postponed for an hour and a half. Then you can proceed to the most difficult ones - 14,16,18,19.

Options for preparing for the Unified State Exam

There are several options for organizing preparation for the Unified State Examination in mathematics at the specialized level.

  • School

Mathematics lessons are held and, in principle, teachers are preparing for the USE. But the teacher builds his preparation with an eye on the average student. The average student doesn't need high scores. Therefore, the effect of preparation at school will not be very high. If you need good results from 75 points, the school alone will not be enough.

  • Self-training

Suitable for motivated and disciplined students. Not everyone has these qualities. It is difficult to prescribe an individual preparation plan and stick to it, and we still do not mention the difficulties that arise with non-standard USE tasks.

  • Tutor

More common variant. It is important that the tutor really understands not only the tasks, but also has an idea about the structure of the exam, the design of tasks. The price of a mistake will be high both literally and figuratively. Because you can lose time and money.

  • USE preparation courses

Preferred preparation option. Classes are held in mini-groups, each student sees himself from the outside and compares himself with others, learns from the mistakes of others. This creates an atmosphere of healthy competition. Classes are taught by teachers who work for the result. Therefore, they also know the teaching methods, and are interested in their students passing as well as possible. The USE course in mathematics from the Unicum RUDN University is one of those. Here they do not train for an exam, but teach them to understand and apply the laws of mathematics. The results of Unicum compared to other courses are 30-40% higher than the average.

How exactly one prepares is the decision of the graduate. The most effective solution would be preparatory courses. The USE profile exam in mathematics is too difficult and serious to let it take its course. It requires a systematic approach and organization of the process. The sooner you start preparing, the better you will pass the exam!

Key disciplines - Educational program "Applied Mathematics" - National Research University "Higher School of Economics"

Undergraduate studies at the Higher School of Economics are built from 5 main elements:

1. General cycle of disciplines , including for the bachelor's program "Applied Mathematics":

  • History - 1 course
  • Law – 1 course
  • BZD - the beginning of the first course
  • Physical culture

2. Professional cycle of disciplines, or "Major" . This cycle forms the basis of the bachelor's program and accounts for two-thirds of all credits. Some of the disciplines of the cycle are basic (compulsory), some are chosen by the student himself. Compulsory subjects for a student of the bachelor's program "Applied Mathematics" are:

1 course

  • Calculus
  • Linear Algebra and Analytic Geometry
  • Physics
  • Algorithmization and programming

2 course

  • Mathematical analysis
  • Discrete Mathematics
  • Algorithmization and programming
  • Differential Equations
  • Probability and mathematical statistics
  • Theory of functions of a complex variable
  • Algebra
  • Theoretical mechanics
  • Functional analysis

At the end of the 2nd year, each student chooses a "specialization" in which he will study in the 3rd-4th year.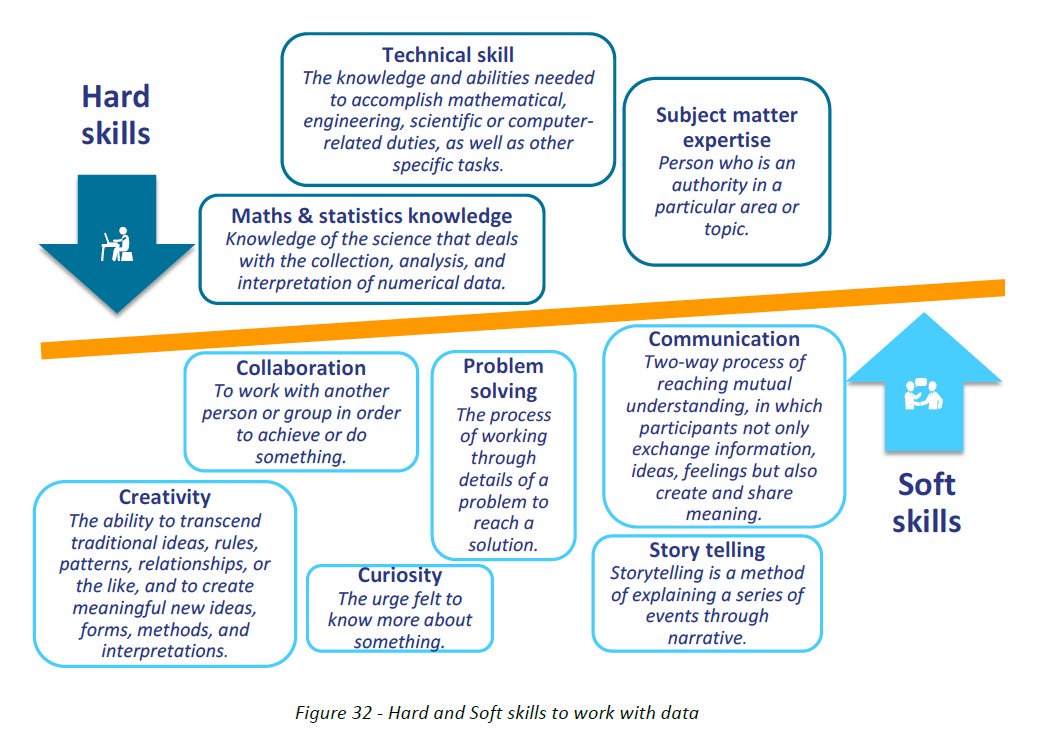 Each specialization consists of a set of compulsory disciplines and a research seminar. Read more...

3. Additional profile, or "Minor" . The disciplines of this profile allow students to gain knowledge and competencies in areas other than their main field of study. A minor is chosen by the student himself at the end of the first year, and his specialization can be any, nothing prevents a student-philosopher from choosing a minor in programming and vice versa. Students study minor disciplines on specially allocated days in the second and third years. The list of minors available to students of previous years is available at the link.

4. Project and research work includes the preparation of term papers and graduation papers, computer workshops, industrial practice, the implementation of projects (educational, scientific), as well as the participation of students in project and research seminars.

For 1-2 courses, the curriculum includes computer workshops, career guidance seminar, project seminar.

Main objectives of computer workshops

  • to teach how to use software tools (MatLab, Mathematica) to solve the set mathematical problems and visualize the results;
  • to develop the skills of designing and programming computer applications that will be used in the performance of various tasks and work in the disciplines studied in subsequent courses;
  • formation of practical skills of low-level programming in assembly language;
  • formation of practical skills in using the basic principles of object-oriented programming used in the development and implementation of algorithms, creation and debugging of computer programs.

The main objectives of the career guidance seminar:

  • formation of students' understanding of new modern concepts and technologies in the field of applied mathematics;
  • students' choice of a profile (specialization) of education, determination of professional inclination and ways of further development in the chosen profession.

The main objectives of the project seminars:

  • formation of practical skills for students to apply knowledge in the field of applied mathematics and computer technology necessary for the implementation of research projects.

In the 3rd year, students implement an educational project within the framework of the project seminar "International Scientific and Technical Projects" with a mandatory defense of it in English; perform interdisciplinary course work and undergo mandatory internships.

On the 4th year, it is planned to carry out another educational and research project, as well as a research seminar within each of the specializations.

Projects, term papers and graduation papers of our students are led by MIEM teachers, employees of laboratories: Space research in the field of technologies, systems and processes, Mathematical methods of natural science, Simulation modeling, employees of the base department "Applied information and communication tools and systems" of the Computing Center of the Russian Academy of Sciences, scientific employees from external employers: Scientific Center of the Russian Academy of Sciences in Chernogolovka, Institute of Applied Mathematics.

Learn more