Math 1 class
Integrated Math 1 - Course
Integrated 1 is year one of a three-year high school mathematics sequence. The program is designed to use patterns, modeling, and conjectures to build student understanding and competency in mathematics. The expectation is to develop and maintain a students growth mindset and teach students how to learn math in a collaborative process where multiple methods and representations are celebrated. Students will be expected to learn through collaboration, collection of data, experimentation, and conjectures. The course aligns with the five goals of the UC mathematics requirement. The students will learn mathematical sense-making, make and test conjectures and justify conclusions, use mathematical models to represent real-world data, be able to provide clear and concise answers, and have computational and symbolic fluency. All five of these goals are embedded in the curriculum and core pedagogical beliefs.
RECOMMENDED PREREQUISITE: Mathematics competency through 7th grade
Register for Integrated Math 1
Basic and On Demand are always open for registration.
Plus courses are created upon request.
SEMESTER 1Unit 1: Solving Equations and Inequalities
- The Distributive Property
- Solving Multi-Step Equations Part 1
- Solving Multi-Step Equations Part 2
- Solving Equations with Variables on Both Sides
- Literal Equations and Formulas
- Ratios, Rates, and Conversions
- Solving Proportions
- Solving Multi-Step Inequalities
- Compound Inequalities
- Absolute Value Equations
- Absolute Value Inequalities
Unit 2: An Introduction to Functions
- Using Graphs to Relate Two Quantities
- Patterns and Linear Functions
- Patterns and Nonlinear Functions
- Graphing a Function Rule
- Writing a Function Rule
- Formalizing Relations and Functions
- Arithmetic Sequences
Unit 3: Linear Functions
- Rate of Change and Slope
- Slope and Graphs
- Slope-Intercept Form
- Point-Slope Form
- Standard Form
- Slopes of Parallel and Perpendicular Lines
- Graphing Absolute Value Functions
Unit 4: Systems of Equations and Inequalities
- Solving Systems by Graphing
- Solving Systems Using Substitution
- Solving Systems Using Elimination
- Applications of Linear Systems
- Linear Inequalities
- Systems of Linear Inequalities
Unit 5: Exponential and Radical Functions
- Zero and Negative Exponents
- Exponential Functions
- Comparing Linear and Exponential Functions
- Exponential Growth and Decay
- Solving Exponential Equations
- Geometric Sequences
- Combining Functions
- Simplifying Radicals
Unit 6: Data Analysis
- Frequency and Histograms
- Measures of Central Tendency and Dispersion
- Box-and-Whisker Plots
- Scatter Plots and Trend Lines
- Two-Way Frequency Tables
Unit 7: Tools of Geometry
- Nets and Drawings for Visualizing Geometry
- Points, Lines, and Planes
- Measuring Segments
- Measuring Angles
- Exploring Angle Pairs
- Midpoint and Distance in the Coordinate Plane
Unit 8: Transformations
- Translations
- Reflections
- Rotations
- Compositions of Isometries
Unit 9: Congruent Triangles
- Congruent Figures
- Triangle Congruence by SSS and SAS
- Triangle Congruence by ASA and AAS
- Using Corresponding Parts of Congruent Triangles
- Isosceles and Equilateral Triangles
- Congruence in Right Triangles
- Congruence in Overlapping Triangles
- Congruence Transformations
Unit 10: Connecting Algebra and Geometry
- Perimeter and Area in the Coordinate Plane
- Areas of Parallelograms and Triangles
- Areas of Trapezoids, Rhombuses, and Kites
- Polygons in the Coordinate Plane
Unit 11: Reasoning and Proof
- Basic Constructions
- Patterns and Inductive Reasoning
- Conditional Statements
- Biconditionals and Definitions
- Deductive Reasoning
- Reasoning in Algebra and Geometry
- Proving Angles Congruent
"SCOUT" is a trademark of the Boy Scouts of America, and is used under license.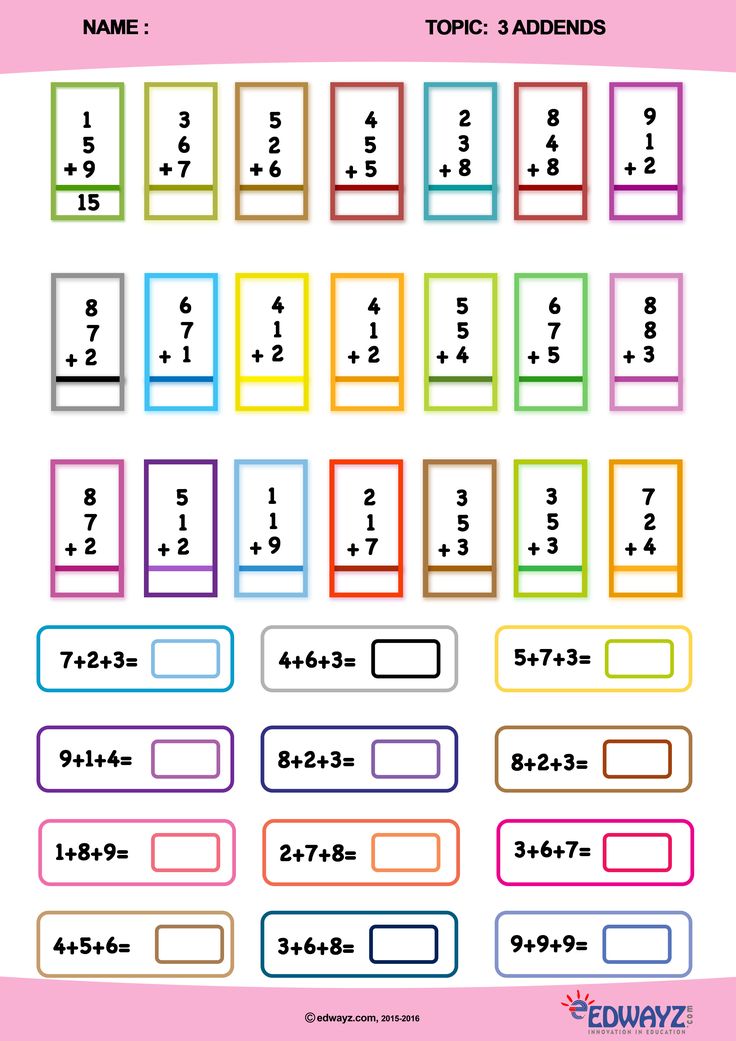
All Rights Reserved.
Integrated Math 1, Part 1
Add to Cart
This course is the first part of Integrated Math 1 and covers the topics of solving linear equations, both simple and multi-step, as well as absolute value equations and literal equations. It also covers linear inequalities, both their graphs and solutions, and goes on to explain solving compound inequalities and absolute value inequalities. The graphing of linear functions are also covered, inlcuding function notation, transformations and shifts. From there, the course covers the writing of linear functions, scatter plots and lines of best fit, systems of linear equations, and exponential and radical functions, including exponential growth and decay. Finally, the course covers both arithmetic and geometric sequences, including finding the nth term, the sum of n terms, and the sum of infinite geometric series’. Integrated Math 1 is approved by the University of California A-G as mathematics (category C).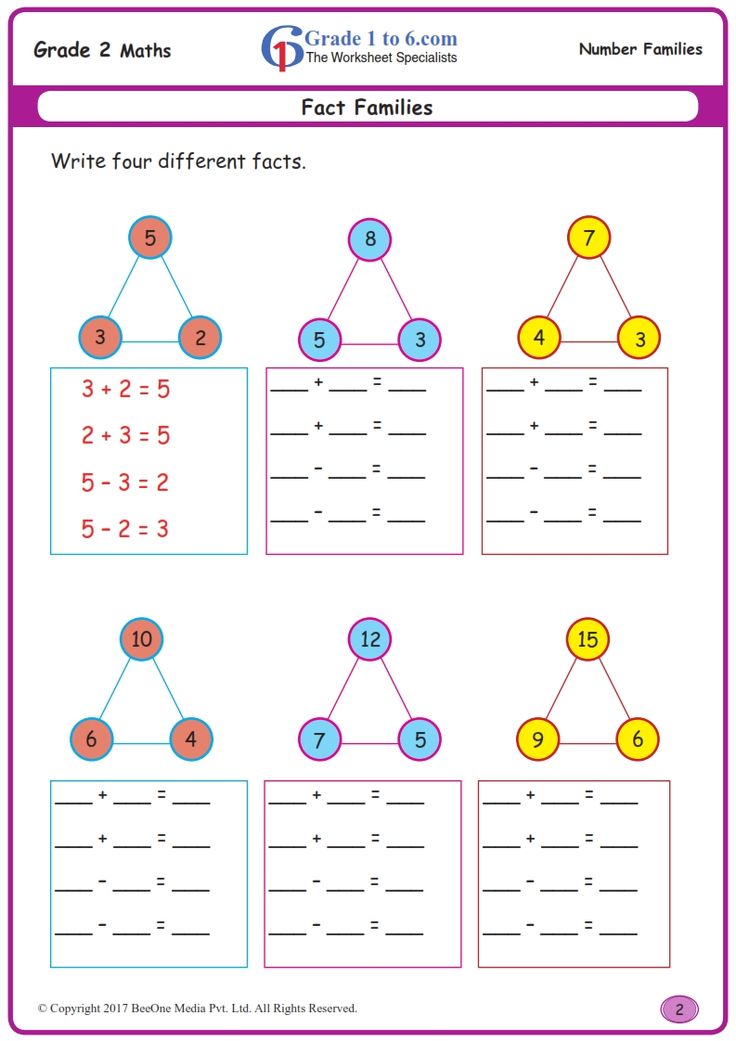
Upon completion of this course, the student is awarded 5 credits. Each credit corresponds to 15 hours of study. Of course, some students work more quickly than others, and some can devote more hours to study, so some students are able to complete the course in an accelerated rate.
LEARNING OBJECTIVES
In this module, students gain a comprehension of the following:
- How to solve linear equations, including multistep and Absolute value equations, as well as proportions.
- To solve linear inequalities, compound inequalities, and absolute value inequalities.
- How to graph linear functions, as well as how transformations and shifts affect graphs.
- To write linear functions in: slope intercept, point slope, and standard forms, as well as how to derive lines of best fit from scatter plots.
- How to solve systems of linear equations using the three methods: graphing, substitution, and the elimination method.
- To solve exponential and radical functions, and to graph growth and decay functions, along with simplifying radicals and zero and negative exponents.
- How to find the nth term and the sum of n terms for arithmetic, geometric, and infinte geometric sequences.
TOPICS COVERED
This course covers the following topics:
- Simple ( One Step ) Equations
- Multi-Step Equations
- Equations with Variables on Both Sides
- Solving Ratios & Proportions
- Absolute Value Equations
- Solving Literal Equations
- Writing Inequalities
- Graphing Inequalities ( on a number line )
- Solving Simple Inequalities
- Solving Multi-Step Inequalities
- Solving Compound Inequalities
- Absolute Value Inequalities
- Functions
- Linear Functions
- Function Notation
- Graphing Linear Equations
- Transformations and Shifts in Linear Graphs
- Graphing Absolute Value Functions
- Slopes and Graphs
- Writing Linear Equations- Slope-Intercept Form
- Writing Linear Equations – Point-Slope Form
- Writing Linear Equations – Standard Form
- Scatter Plots and Lines of Best Fit
- Solving Systems of Equations- Graphing Method
- Solving Systems of Equations- The Substitution Method
- Solving Systems of Equations- The Elimination (aka Addition) Method
- Special Systems of Linear Equations
- Graphing Linear Inequalities (2 Variables)
- Systems of Linear Inequalities
- Zero and Negative Exponents
- Exponential Functions
- Exponential Growth vs.
Decay - Solving Exponential Equations
- Simplifying Radicals
- Arithmetic Sequences
- Geometric Sequences
- Infinite Geometric Series
Add to Cart
Course Details:
• One Semester Credit: $125
• First Semester of Int. Math 1
Approvals
• University of California A-G:
Yes• NCAA:
YesCourse Syllabus
Course Screenshot
Course Instructions
GDZ in mathematics Grade 1 Moro textbook 1, part 2
Part 1. Pages
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
Part 2.
Pages - 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
Additional GDZ Moro
- Mathematics workbook Grade 1 Moro, Volkova
- Testing work in mathematics Grade 1 Volkova
See also
- Workbook on the world around 1st grade Pleshakov
- Russian language textbook Grade 1 Kanakina, Goretsky
- Russian language workbook Grade 1 Kanakina, Goretsky
Description
Collection of ready-made homework according to M.
I. Moro, S.I. Volkova, S. V. Stepanova "Mathematics Grade 1" demonstrates the principles for performing basic numbers.
For convenience, the material is divided into two parts. GDZ pages strictly correspond to the textbook. There are necessary explanations for analytical tasks, brief notes of tasks for addition, subtraction, drawings, inequalities.
The advantage of the manual is that it presents solutions to exercises under the line, which is not always found in the authors of other GDZ.
High-quality illustrations look crisp and legible. A visual explanation of the algorithms helps to understand the principles of solution, step-by-step recording, final design. This allows you to quickly transfer the skills of work to children.
Your message has been sent!
+
GDZ in mathematics grade 1 textbook Moro, Volkova part 1
- Type: GDZ, Reshebnik.
- Author: Moro M. I., Volkova S.
I., Stepanova S. V. - Year: 2020.
- Series: School of Russia (FSES).
- Publisher: Enlightenment.
Reshebnik - page 69 Finished homework
Anya washed 3 large plates and 3 small ones. How many dishes did Ann wash in total?
Answer:
3 + 3 \u003d 6 (t.) - total. Answer: 6 bowls.
Vitya brought 4 packets of yogurt. We drank 3 packs of kefir per day. How many packets of yogurt are left?
Answer:
4 − 3 \u003d 1 (p.) - remained. Answer: 1 pack.
Say the numbers first in increasing order and then in decreasing order.
Answer:
In increasing order: 1, 2, 4, 5, 7, 8, 9, 10. In decreasing order: 10, 9, 8, 7, 5, 4, 2, 1.
Sasha drew a segment 6 cm long. Anya continued this segment by 1 cm.
