Math concepts first grade
The Most Important Math Concepts Kids Learn In 1st Grade
Your child has progressed from kindergarten to first grade. That’s exciting news! There is so much learning to come their way, especially from their first grade math class.
Math skills and concepts build on each other from grade to grade, which is why children need to get a firm foundation so they can handle the more complex challenges as they progress in school.
As a concerned parent, you might be wondering what some of these mathematical concepts will be and, more importantly, how you can help your child master them. You don’t have to figure it out on your own.
Here, we will give you a breakdown of what to expect from your child’s math class. We’ll also add a few tips on how to help your young learner thrive through it all.
Let’s get started!
Why Is Math Important?
Math is taught in the classroom, but that doesn’t mean that’s the only place it’s relevant. We use it every day!
From the hexagonal bee combs to the circles, semi-circles, and crescents of the phases of our moon, mathematics is an essential part of the world we live in, and learning it helps us make sense of everything around us.
Did you know that math skills can also be linked to music? Children who play musical instruments use the same part of the brain when doing math. This is why studies have shown that music students do better in mathematics than their non-musical peers.
Sports and mathematics also have an interesting connection. Just think about all the coordination involved in performing well in certain sports. Research has shown that these skills can also be used to learn math.
In addition, mathematics helps us be stronger logical thinkers. Since most young kids tend to enjoy math time, it’s essential to foster this natural love for the subject just as much as we want to encourage children’s love for reading.
Helping children develop a love for mathematics generally works well when approached actively as a problem-solving skill rather than a rote memory task. Math helps children thrive in various aspects of their lives.
So, how do we get there? It all starts with the foundation.
Below are the key first grade math concepts your child will soon learn and some tips on how you can support them on their journey.
8 Important First Grade Math Concepts
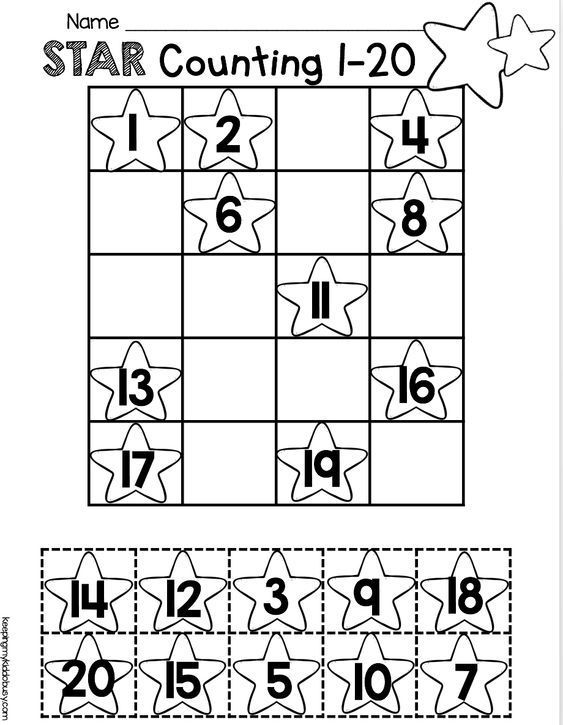
1) Numbers And Counting
At first grade level (and for the next few years in school), learning different numbers and counting will form a significant part of your child’s mathematics lessons.
By the end of the first grade, your child will have learned to:
- Count and write numbers from 1 to 100
- Count by 1s, 2s, 5s, and 10s
- Count backward
- Count onward from any number
- Count backward from any number
There are different ways to help your child grasp numbers and counting at home, and hands-on activities work best.
An effective strategy is to help your child visualize what all these numbers mean. For example, instead of just memorizing the numbers, they can count bears, large dried beans, or even craft sticks.
2) Addition And Subtraction
In first grade math, your young learner will start adding and subtracting numbers up to 30. They will also solve basic word problems with the help of drawings, objects, and equations.
They will also solve basic word problems with the help of drawings, objects, and equations.
By the end of the first grade, your child will have been shown how to:
- Add three one-digit numbers
- Write and show an understanding of the mathematical symbols (+, -, =)
- Solve problems involving one and two-digit numbers
- Solve problems involving an unknown. For example, 1 + _ = 4
Addition and subtraction are two math skills that can be demonstrated in everyday life situations. This makes it relatively easy to practice at home!
For instance, you might ask, “If you have two teddy bears and granny buys you three more, how many teddy bears will you have in total?” Or, “There were six strawberries in the fridge. Daddy ate some strawberries. There are now four left. How many did daddy eat?”
3) 2-D Shapes
During pre-k, children get introduced to different shapes. In first grade, they will continue to extend their understanding of them.
By the end of the first grade, your child may be able to:
- Examine the attributes of different shapes (number of sides, faces, etc.)
- Name the 2-D shapes
To help your child grasp these shapes at home, continue to point out and name the 2-D shapes in the world around you (circles, triangles, pentagons, etc.).
When doing so, remember to always highlight the attributes (e.g., this book has four equal sides, so it’s a square).
4) Sorting And Patterns
Understanding and sorting patterns also forms a part of first grade math.
Your first grader will learn to:
- Sort different objects by attributes such as color, shape, and function. For example, sorting a mixed group of blocks so that the red, blue, green, and yellow blocks are separated.
- In addition, if these blocks are placed in a pattern (e.g., green, yellow, green, yellow, etc.), your child should be able to both predict which color will come next and create their own identical pattern.
 This skill will help develop your child’s logical thinking.
This skill will help develop your child’s logical thinking.
Continue to allow your young learner to play with fun building blocks and create their own patterns to help them master this skill.
5) Fractions
Montessori material. Children’s hands. The study of mathematics School and kindergarten. Whole and part. FractionsAs a first-grader, your child will be introduced to fractions as equal shares and basic fractions such as ½, ⅓, and ¼. For children to fully grasp these concepts, it’s essential to keep things intuitive.
For example, you can start by helping them understand that a half is two equal parts, a third is three equal parts, and so forth. They also need to understand that although three is bigger than two, ⅓ is smaller than ½.
Fractions can be tricky for kids to learn, which is why it’s important to use practical and everyday items.
For example, you can help your young learner examine the fractions of a full pizza. Then, as you divide the pizza into different slices, talk about the parts that you’ve created from the whole.
The concept of equal shares can also be demonstrated from one object and a group. For instance, you can have ½ of a single item (e.g., ½ of a cookie), or you can have ½ of a group of objects (e.g., ½ of four cookies is two cookies).
6) Number Place Values
With all the counting in first grade math, your child will naturally be introduced to the concept of place values. For instance, understanding that in the number 288, the 2 is worth 2 “hundreds” (or 200).
There are various activities you can do at home to help your young learner with this concept, including:
- Using number lines
- Base ten blocks
For more ideas to help with number place values and other 1st grade math concepts, take a look at the book Games for Math: Playful Ways to Help Your Child Learn Math, From Kindergarten to Third Grade by HOMER’s very own Peggy Kaye.
7) Time
Telling time (both digital and analog) is an important life skill that kids learn from first grade. The concept of elapsed time will also be introduced at this stage.
The concept of elapsed time will also be introduced at this stage.
In first grade math, your child will learn to:
- Tell time to the nearest hour, half-hour, and quarter-hour (sometimes even to five minutes)
- Make the connection between time and events (e.g., shorter, longer, after, before)
Understanding the analog clock can be tricky for a child who’s only exposed to digital clocks. So help your young learner by buying one (or making one for learning) to hang up at home.
You can then speak to your child about what it means when the hands move. To make things easier, start by helping them tell time to an hour and half-hour before progressing to quarter-hours.
8) Measurements And Comparisons
First grade math also involves some measuring and unit comparisons.
Your child will learn how to measure using a ruler and, after taking measurements, compare and order objects by length. First-graders will also learn how to compare the weights and volumes of different objects.
To help your young learner at home, keep rulers nearby and take measurements together of some of the objects they love (e.g., stuffed toys, cookies, etc.).
Bonus tip: If you’re a regular baker, why not help them see how you use measuring tools to create their favorite treats? Yum!
Helping Your Child With First Grade Math
We’ve already mentioned a few ways in which you can help your first grader with math at home. In addition to the above, playing math games is a fun and easy way to practice math at home!
Here are some examples of more math activities your young learner will enjoy at home:
- Fill in a number grid puzzle
- Build objects with legos and measure
- Number Hunt, Hopscotch, Is It A Number, and Find A Number
Math Is All Around Us
Helping your child grasp first grade math concepts at home is easier when you focus on the fact that mathematics is a part of our everyday lives. It is in the shape of road signs, the parts of sliced pizza, and even the watches on our wrists!
Sometimes kids (and parents) forget that math can be lots of fun. So whenever you can, incorporate games and activities to bring a little excitement to all the learning.
So whenever you can, incorporate games and activities to bring a little excitement to all the learning.
Will this help your child become our next best mathematician? Only time will tell. But one thing is for sure — all of the great mathematicians started somewhere. Even Isaac Newton had to master first grade math!
For more ideas and inspiration, visit the HOMER Learn & Grow app.
Author
1st Grade Math Skills, What Your Child Will Learn, Komodo Math
- Math Tips
- Education
- 1st
Your child is heading to first grade! After the year in kindergarten, your first grader will be ready for some amazing growth. For many children, first grade is the year that they bloom as readers and mathematicians. Get ready to support your child’s mathematical growth by learning about first grade math skills.
In first grade, you can expect your child to learn about:
1. Addition and subtraction facts to 20
Now that your child has mastered the idea of adding and subtracting, they’re ready to practice math facts. This means getting faster when answering addition and subtraction problems to 20.
Help your child develop fluency by asking basic addition and subtraction problems - we find that using treats can help keep kids interested! If your first grader needs support, encourage the use of physical objects or fingers as problem-solving tools.
2. Addition and subtraction as inverse operations
Your child probably understands the concept of addition as “putting together” and subtraction as “taking apart.” In first grade, children are encouraged to see the connections between addition and subtraction. Your child will learn how addition and subtraction are inverse operations, or that one is the opposite of the other, and create “fact families” of related addition and subtraction problems.
When working with addition and subtraction, ask your child to see connections. For example, if your child has four dolls and three cars, ask how many toys there are in all. Then ask how many toys there would be if the four dolls are taken away.
3. Count and write within 120
Your child has probably mastered counting to 20. But in first grade kids will learn to count all the way up to 120! That’s not all. Kids will be expected to not only count, but write, the numbers. This is great practice for understanding multi-digit numbers.
At home: Encourage your child to write numbers whenever possible. Talk about how two-digit numbers are made up of tens and ones and how three-digit numbers are made up of hundreds, tens, and ones. Just looking closely at multi-digit numbers together can be a great learning opportunity.
4. Add within 100
Now that your child has an understanding of numbers past 100 as well as basic addition and subtraction facts, it’s time to practice adding within 100. Children will practice adding one-digit numbers to two-digit numbers using strategies like counting on and number charts. Children can practice adding larger numbers with the help of a 1-100 chart.
Children will practice adding one-digit numbers to two-digit numbers using strategies like counting on and number charts. Children can practice adding larger numbers with the help of a 1-100 chart.
First graders are also ready to practice adding and subtracting 10s to and from two digit numbers.
At home: Help your child see patterns when adding and subtracting 10s. For example, after solving a problem like 59 - 10 = 49, point out to your child that 49 has one less 10 than 59. This is another great way to learn about place value.
5. Measure objects
In first grade, kids learn how to measure using rulers and more unusual things like paper clips. After taking measurements, children compare and order objects by length.
At home: Kids love measuring things around the house, so keep a couple of rulers handy. Pay attention to how your child is using a ruler and taking measurements. Sometimes kids don’t quite measure from end to end, so they might need a bit of help...
Pay attention to how your child is using a ruler and taking measurements. Sometimes kids don’t quite measure from end to end, so they might need a bit of help...
6. Tell time to hour and half hour
One of the trickiest concepts first graders will learn is to tell time. Using analog clocks is confusing, especially when kids are more used to seeing digital clocks. In first grade, your child will learn about the big and little hands of a clock and will practice telling time to the hour and half hour.
At home: Get hold of an analog clock for your home (either a real one or one made just for learning). Talk with your child about the time and how the hands move around the clock. Remember to just focus on telling time to the hour and half hour to start!
7. Understand basic fractions
First graders also get an introduction to fractions as equal shares. They will learn how to divide into equal groups and learn basic fractions like ½, ⅓, and ¼. First graders usually have a good understanding of fairness, so practicing making equal shares should be a relatively easy task for them!
First graders usually have a good understanding of fairness, so practicing making equal shares should be a relatively easy task for them!
At home: Help your child to divide pizzas, pies, and sandwiches into equal shares. As you do, talk about the fractions of the whole that you created.
First graders are ready to dive deep into mathematical concepts. Find time to connect with your child about classroom learning and get ready to have some fun!
Found this useful? Check out our grade by grade math guides from Kindergarten to 5th grade
Written by Lily Jones, Lily loves all things learning. She has been a kindergarten & first grade teacher, instructional coach, curriculum developer, and teacher trainer. She loves to look at the world with curiosity and inspire people of all ages to love learning. She lives in California with her husband, two kids, and a little dog.
About Komodo – Komodo is a fun and effective way to boost K-5 math skills. Designed for 5 to 11-year-olds to use in the home, Komodo uses a little and often approach to learning math (15 minutes, three to five times per week) that fits into the busy family routine. Komodo helps users develop fluency and confidence in math – without keeping them at the screen for long.
Designed for 5 to 11-year-olds to use in the home, Komodo uses a little and often approach to learning math (15 minutes, three to five times per week) that fits into the busy family routine. Komodo helps users develop fluency and confidence in math – without keeping them at the screen for long.
Find out more about Komodo and how it helps thousands of children each year do better at maths – you can even try Komodo for free.
Back to School - 5 Tips to Help you Ease Back into the Routine
Here are some steps you can take to ease children back from full vacation mode so that the first week of school doesn't knock you sideways.
Mindset - The Path to Mastery
People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.
| Mathematical definitions and concepts | |||||||||||||
| | | Geometric figures. Point and straight line are basic geometric figures. The simplest geometric shapes are a segment, a ray, a broken line. Geometric figures are flat and voluminous. Flat geometric figures are a quadrilateral, triangle, polygon, square, rectangle, circle, oval, rhombus, trapezium, etc. other | |||||||||||
| | Point. Lines. A point is the smallest geometric figure. Lines are straight, curved, broken. A straight line is a geometric figure that has neither beginning nor end, it is endless. |
A segment is a part of a straight line that has a beginning and an end. Length can be measured. | 3 cm
| ||||||||||
| |
A ray is a part of a straight line that has a beginning but no end. Corners |
| |||||||||||
| | Angle is a geometric figure formed by two rays from one point. |
| |||||||||||
| | Rectangle. A rectangle is a quadrilateral in which all angles are right and opposite sides are equal. The larger side is called the length, the smaller side is called the width. |
| |||||||||||
| | square. A square is a quadrilateral with all sides and angles equal. 9Expressions. 0007 |
| |||||||||||
| Expressions are records of numbers and letters connected by arithmetic signs. Expressions are literal - they contain letters (a + 3), numeric - are composed of numbers (5 - 2). | |||||||||||||
| | Statements. Propositions are true and false sentences about which the question makes sense: is it true or false. | ||||||||||||
| | Equality. Equality are statements written with the sign =. An inequality is two numbers or expressions connected by one of their signs: >, To put one of these signs between numbers or expressions means to compare them. | ||||||||||||
| | Increase and decrease by.
| ||||||||||||
| | Components when added. 1 term 2 term Sum 4 4 2 2 6
sum | To find the unknown term, subtract the known term from the sum. | |||||||||||
| | Subtraction components. reduced deductible difference 8- 3 = 5 difference | To find an unknown subtract, it is necessary to subtract the difference 9 from a reduced deduction0007 To find the unknown minuend, add the subtrahend and the difference. | |||||||||||
| | Equation. An equation is an equality with a variable whose value is to be found. To solve an equation means to find all its roots. Algorithm: 1. Select components. 2. Apply the rule. 3. Find the root of the equation. 4. Check. | 1C 2C with x + 2 = 6 x = 6 - 2 x = 4 4 + 2 = 6 6 = 6 | |||||||||||
| | .
| To solve problems, you can use - drawing - diagram - short note Tanya has 4 mushrooms, and Sasha has 2 mushrooms. How many mushrooms do Tanya and Sasha have?
| |||||||||||
| | Whole and parts. ?
Looking for the whole. To find the whole, the parts must be added together. |
Looking for a part. To find a part, you must subtract the other part from the whole. | |||||||||||
| | Comparison task. Tanya has 4 mushrooms, and Sasha has 2 mushrooms. | ||||||||||||
| Scheme
T. 4 gr. 2 gr.
> | ||||||||||||
|
| |||||||||||||
| |
| ||||||||||||
Mathematics lesson Grade 1 Perspective "Introduction of the concept of "task""
Summary of the lesson in mathematics.
Place of work: MAOU secondary school No. 31, Tambov city
Teacher: Dubinina Irina Valerievna - primary school teacher
Subject and teaching materials: Mathematics. 1 class. "Perspective".
Theme of the lesson: "Task"
Place of the lesson in the topic: No. 1
1
Type of lesson: Discovery of new knowledge
Objectives:
Educational:
To form an idea of the structure of the task. To form the ability to distinguish the condition of the problem, the question.
Developing:
To promote the development of mathematical speech, working memory, voluntary attention, visual and effective thinking.
Foster:
Foster culture of behavior in frontal, individual, group work.
Formation of UUD
the ability to distinguish the structure of a text task; the ability to distinguish the condition of the problem, the question.
Metasubject :
Regulatory: the ability to accept and save a learning task corresponding to the stage of learning; the ability to plan their action in accordance with the task; the ability to determine the sequence of actions; the ability to follow the points of the algorithm, the implementation of step-by-step control of one's actions with a focus on the teacher's action; the ability to distinguish a correctly completed task from an incorrect one; the ability to evaluate together with the teacher or classmates the result of their actions;
Cognitive: ability to navigate in one's knowledge system; to distinguish the new from the already known with the help of a teacher; the ability to acquire new knowledge: find answers to questions using a textbook, your life experience and information obtained in the lesson; the ability to analyze, compare the object; the ability under the guidance of a teacher to carry out generalization, conclusions;
Communication skills: ability to work in pairs and groups; the ability to understand the questions asked; the ability to listen and enter into a dialogue, participate in a collective discussion; the ability to express one's point of view; ability to adequately perceive other opinions and positions.
Personal: positive attitude towards studying the subject of mathematics; interest in new experiences.
Course of the lesson:
Organizational moment
Here the bell rings again,
Invites you to the lesson.
We will count together,
Add and subtract.
Guys, today we have guests at our math lesson. Let's turn to them and give them our smiles.
The motto of our lesson will be the words of the remarkable Russian scientist M.V. Lomonosov:
“Mathematics should be taught later, that it puts the mind in order.”
How do you understand these words?
How do we usually start a math lesson? (from the oral account)
2. Oral account
Oral account
A) On the screen examples (fans of numbers):
4+1 4) 6-0
3+2 5) 5-1
3) 8+0 6) 5-2
In which examples can the answer be given immediately without performing calculations? (in examples with 0)
Read these examples. (8+0, 6-0)
What rule did you use when calculating with zero? (If you add 0 to a number, or subtract 0 from a number, you get the same number) Solve examples with zero (8+0=8, 6-0=6)
Which rule will you use when calculating with one? (If you add one to a number, you get the next number. If you subtract one, you get the previous number) Solve these examples (4+1=5, 5-1=4)
What rule would you use when adding the number 2? subtracting the number 2? (To add 2 to a number, you must first add 1, and then another 1. To subtract 2 from a number, you must first subtract 1, and then another 1) Solve these examples (3 + 2 \u003d 5, 5-2 \u003d 3)
To subtract 2 from a number, you must first subtract 1, and then another 1) Solve these examples (3 + 2 \u003d 5, 5-2 \u003d 3)
B) Logical warm-up
- The task is on the screen.
Giraffe, rhinoceros and hippopotamus lived in different houses. The giraffe did not live in a red or blue house. The hippo lived neither in green nor in red. What houses did the animals live in? (The giraffe lived in the green house. The hippo lived in the blue house. The rhinoceros lived in the red house.)
C) And now let's try to solve some puzzles from the field of mathematics. (R 1 A (homeland), PO2L (basement), 3BUNA (tribune), YOU3 (wipe), 7I (family), R1KA (mole), AK3CA (actress), S3ZH (swift)).
3. Motivational-target stage
Can you solve the puzzle on my board? (task)
How many of you know what a task is, guess? Want to know what a task is?
4. Work on the topic of the lesson
Work on the topic of the lesson
Now I will tell you a very short story about Dunno picking mushrooms. Listen carefully.
First Dunno found 4 mushrooms (the teacher shows mushrooms, puts them in a basket and attaches a card with number 4 to the board), and then 2 more mushrooms (shows mushrooms, puts them in a basket and attaches a card with number 2 to the board).
- How many mushrooms did Dunno find in total? (The answer is hidden, and under the numbers 4 and 2 the teacher attaches a card with a sign?)
-Such stories in mathematics are called TASKS. (Teacher pins up the “Problem” sign)
- Who guessed what the topic of today's lesson is? What will we be learning? What goals will we set? (Let's find out how the problem is built, we will solve problems, write down the solution of the problem and the answer)
And now let's continue working on the problem. Repeat the task. What do we know? (Dunno first found 4 mushrooms, and then 2 more mushrooms)
Repeat the task. What do we know? (Dunno first found 4 mushrooms, and then 2 more mushrooms)
This is the condition of the problem. (Next to the numbers 4 and 2 I attach the “Condition” card) How can I say in other words what the condition of the problem is? (what is known)
-What is asked in the problem? (How many mushrooms did
Dunno find in total?)
This is a question of the problem. (A sign "Question" appears on the board.) How in other words to say what is the question of the task? (what is asked in the problem)
- So, guys, we have a condition and a question. (The teacher draws connecting lines with chalk from the “Task” plate to the “Condition” and “Question” plates.)
-When we talked about the objectives of the lesson, you said that we would solve problems. Let's try to solve the problem. How to find out how many mushrooms Dunno found in total? (On the board: 4+2) Why did you choose the action of addition? (more mushrooms)
-This is the solution to the problem. (There is a sign “Decision” on the board)
(There is a sign “Decision” on the board)
-How much did we get?
Six mushrooms is the answer to the problem. (There are 6 mushrooms on the blackboard, and next to it is the “Answer” sign.)
- How can I find out the problem? What parts does it consist of? Let's recap the parts of the problem. Any problem should have these parts. (condition, question, decision, answer)
Physical education
Continuation of work on the topic.
Listen to 2 stories and compare them.
1. Bought 2 pears and 1 apple at the market. How many fruits did you buy?
2. Bought 2 pears and 1 apple at the market. Fruits are very healthy.
- What do you think, which of these stories can be placed in the textbook "mathematics", and which - in the textbook "world around"? (The first story is in a mathematics textbook. The second is in the surrounding world)
The second is in the surrounding world)
-Who will tell you the name of the first story in the language of mathematics? (task)
- Let's try to prove it.
- What is the condition in the problem? (Bought 2 pears and 1 apple at the market)
- What do you need to know? (How many fruits did you buy in total?)
- Count how many fruits did you buy? (2+1=3)
Read the question again and answer it.
- Let's go back to the second story and find out: is this a task? (No, there is no question in it)
5. Fixing.
A) And now we will try to make a task together (cards: condition, question, solution, answer) Write a problem that would be solved by the action of addition. (There were 5 cars in the parking lot, 2 more arrived. How many cars were in the parking lot? 5 + 2 = 7) Make up a problem that would be solved by a subtraction action. (There were 7 flowers on the window, one flower broke? How many flowers are left on the window? 7-1 = 6)
(There were 7 flowers on the window, one flower broke? How many flowers are left on the window? 7-1 = 6)
B ) Work in pairs. Game yes no. One head is good, but two is better
Determine where the task is written. Next to the task put +, and if it is not a task - -.
1. “Misha has 4 pears” (no)
2. “Misha has 4 pears, and Masha has 3 pears.” (no).
3. “Misha has 4 pears, and Masha has 3 pears. How many pears do Misha and Masha have together? (Yes).
4. “How many more tangerines than pears?” (no).
5. Misha has 4 pears, he ate one. How many pears does he have left? (yes)
Assess your work in pairs. If you did everything right, put a red flag, a little mistake - green, failed - blue.
B) Work in the workbook (p. 90, No. 1)
Fill in the gaps with the correct numbers. Draw the lines you need.
Draw the lines you need.
- Reading the task.
-Where is the condition of the problem?
-Where is the question?
-How will we solve the problem? What action will we choose?
-How much will it be?
-Write the answer to the problem.
D) Group task. Take it together, it won't be heavy.
1 row - the first team, 2 row - the second team, 3 row - the third team.
Solve the examples one by one. The result of the calculation becomes the first number in the following example. The first team to complete the calculation correctly wins. And after successfully solving the examples, you can color the pictures at recess.
6. Summary of the lesson
Share your impressions of the lesson.
I liked ...
I remember .
Learn more



 Inequality.
Inequality. 

 How many more mushrooms does Tanya have than Sasha?
How many more mushrooms does Tanya have than Sasha?