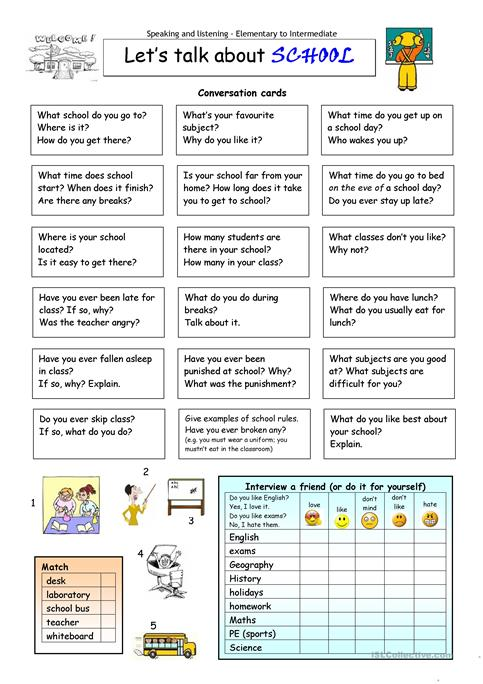
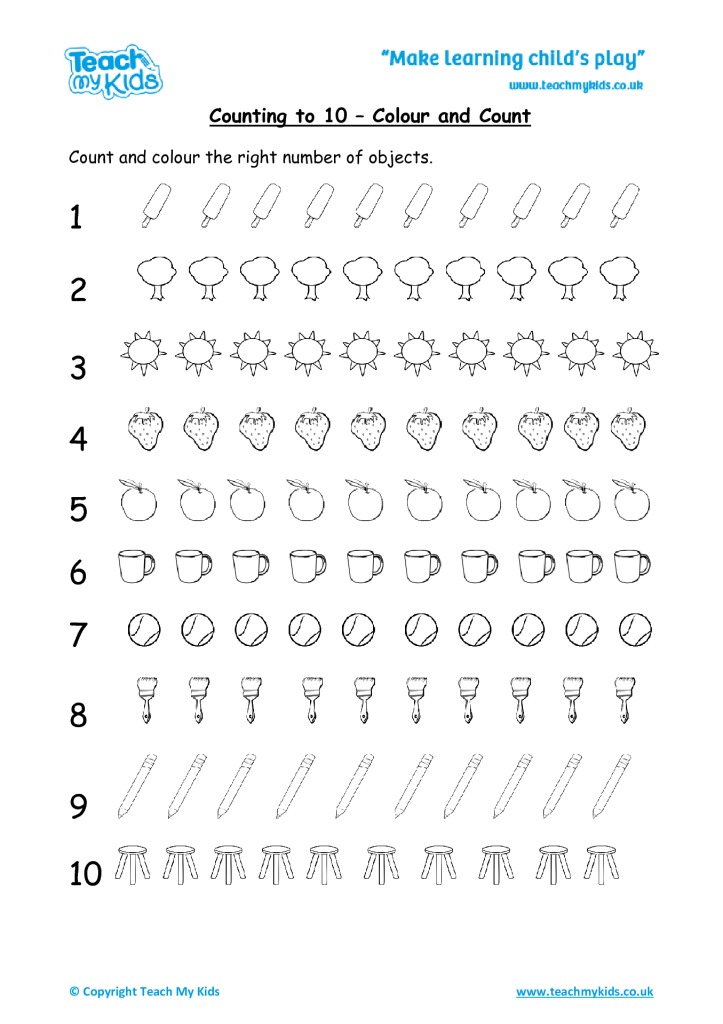
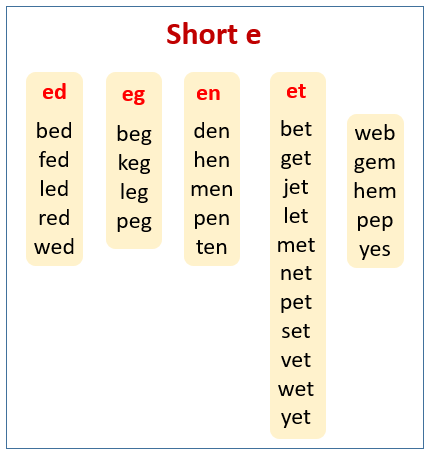
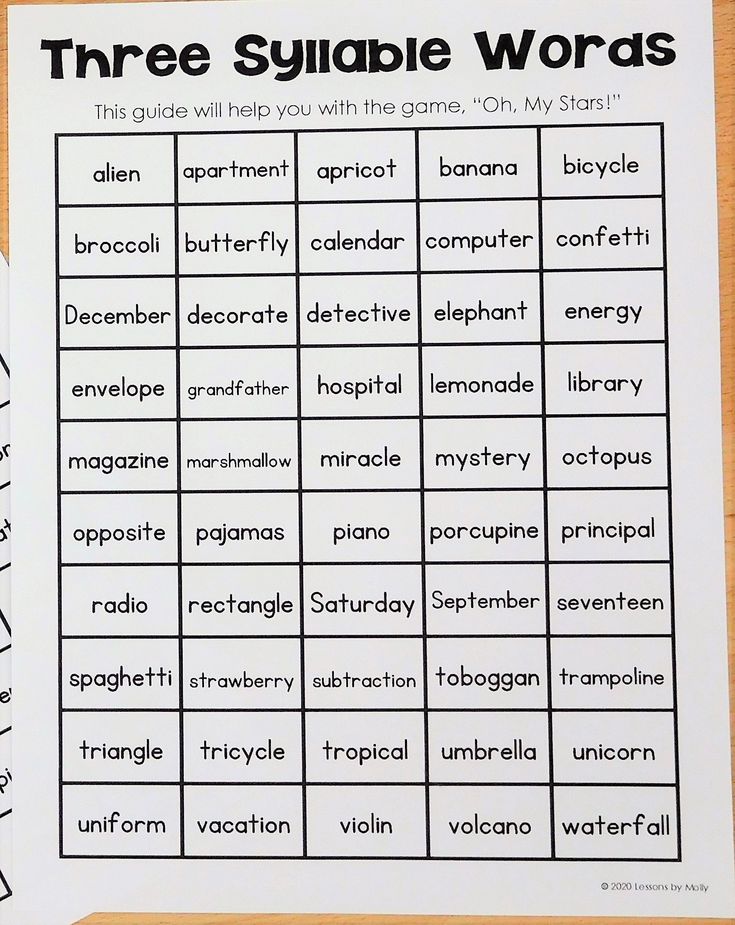
Math concepts for elementary
The 4 Major Math Concepts Your Kids Learn in Grades 1-2
So many fun and important ideas are being introduced in first and second grade! I love when I get to work with this age group because they get excited trying new things and are open to new ways of learning. Below are some of the major concepts taught in first and second grade math, as well as tips on how you can support your child(ren) at home.
1. Addition & Subtraction. 1st and 2nd graders extend their previous understanding from kindergarten with adding and subtracting. They begin to memorize their addition and subtraction facts up to 20, as well as solve word problems using objects, drawings, and equations. Children also begin to solve problems with more than two numbers and determine if a number is even or odd.
Encourage your child to:
- Create and draw stories about adding and subtracting. For example:
Addition: Some bunnies were sitting on the grass. Three more bunnies hopped over to sit with them.Then there were five bunnies. How many bunnies were on the grass before? ? + 3 = 5
Subtraction: Five apples were on the table. I ate some apples. Then only three apples were left. How many apples did I eat? 5 – ? = 3
- Practice their addition and subtraction facts by playing games with numbers, dice, online, etc.
- Decide if numbers they see in the real world are even or odd.
2. Number Sense. Your 1st and 2nd grader is also beginning to understand the concept of place value. Your child is learning about each place — ones, tens, and hundreds — by drawing pictures, counting in groups, and using base ten blocks. They are writing numbers up to 1,000 and comparing numbers. They are also building their mental math skills by solving problems mentally.
Encourage your child to:
- Read numbers out loud and record numbers you say verbally.
- Practice understating place value by deciding what the value of a digit is in a specific number.
For example: How much is the digit 7 worth in the number 379? 70 because the 7 is in the tens place.
- Compare numbers using symbols: > (greater than), < (less than), or = (equal to). Play a game where you give them two numbers: 14 and 40. They can answer 14 < 40. Or 40 is > 14.
- Solve problems mentally. For example: What is 75 + 20? 95
3. Measurement & Data. 1st and 2nd graders are beginning to understand measurement by estimating and measuring using rulers to the nearest inch, foot, yard, etc. They are beginning to count and use money to solve problems. Children are also figuring out how to tell time using both analog and digital clocks, as well as describing and creating different graphs.
Encourage your child to:
- Estimate how long they think different objects are around the house and use rulers or tape measures to determine the actual size.
- Read different looking clocks and use appropriate language describing the time using a.
m. and p.m. - Collect and organize different data.
- Find graphs in newspapers, magazines, online and compare them.
4. Geometry. In 1st and 2nd grade, children extend their previous understanding from kindergarten with 2-D and 3-D shapes. They examine the attributes of these shapes and are looking at the number of sides, angles, faces, etc. Children also beginning to partition shapes into equal pieces and use appropriate language.
Encourage your child to:
- Identify 2-D shapes in the world: triangles, quadrilaterals, pentagons, hexagons, and octagons.
- Identify 3-D shapes in the world: cubes, cones, cylinders, spheres, and triangular and rectangular prisms.
- Count and find the number of sides or faces and angles each shape has.
- Cut (partition) circles and rectangles into equal size pieces and use language such as halves, thirds, half of, a third of, etc.
Featured Photo Credit: Ableimages/Thinkstock
Have questions about your child’s math? Submit them to Jennifer here so she can consider answering in an upcoming blog.
Or Share them with us on the Scholastic Parents Facebook Page.
Key Concepts in Elementary Math
CHRISTI O'DONNELL
26 SEP 2017
CLASS
... Hemera Technologies/AbleStock.com/Getty Images
The Common Core State Standards Initiative, adopted by 45 out of 50 states by July 2013, details the key concepts taught in elementary schools nationwide. The Common Core, as it is usually called, identifies five domains for elementary mathematics. These domains are Counting & Cardinality, Operations & Algebraic Thinking, Number & Operations, Measurement & Data and Geometry. Key skills and concepts within these domains are introduced and reinforced as students move through the grades. It is common for teachers to revisit lessons from previous grades at the reintroduction of each topic, reviewing and reinforcing the basic information that students should have already mastered before moving on to new details and skills.
Explore this article
- Counting & Cardinality
- Operations & Algebraic Thinking
- Number & Operations
- Measurement & Data
- Geometry
1 Counting & Cardinality
.
.. BananaStock/BananaStock/Getty Images
Counting & Cardinality primarily applies to children in kindergarten. Within this domain, young students learn the names of whole numbers and the correct sequencing of these numbers. Once children are able to recognize and identify numbers, they move on to counting groups of objects, applying the concept of one-to-one correspondence. Finally, kindergarten students learn to compare numbers and identify which number in a pair is larger or smaller. By the end of kindergarten, children should be able to count to 100 by ones and tens, write numbers up to 20 and count to identify how many objects are in a group (up to 20).
2 Operations & Algebraic Thinking
... Creatas/Creatas/Getty Images
Operations & Algebraic thinking begins with simple addition and subtraction skills. Children in kindergarten learn to represent addition and subtraction equations with objects, to count to solve problems and to puzzle out simple word problems.
These skills are then carried through the higher elementary grades as multiplication and division are added for an understanding of the four basic operations. The focus remains on whole numbers through the elementary years. In third and fourth grades, students become familiar with factors and multiples, and by the end of fourth grade they begin generating and analyzing algebraic patterns.
3 Number & Operations
... Jupiterimages/Comstock/Getty Images
There are two Number & Operations domains -- Number & Operations in Base 10 and Number & Operations with Fractions. Children in kindergarten through second grade focus solely on Number & Operations in Base 10. In these grades, students begin with an understanding of place value and numbers 11 through 19 and move through an understanding of place value in three-digit numbers. Students finishing second grade should be able to add and subtract numbers within the thousands, add up to four two-digit numbers, and mentally add with tens and hundreds.
Third- and fourth-grade students continue to work with these skills. In addition to base 10, older students also gain an understanding of fraction equivalencies and ordering. They are also introduced to decimals and begin comparing decimal quantities.
4 Measurement & Data
... Thinkstock/Comstock/Getty Images
The Measurement & Data domain incorporates a large number of crucial elementary-school concepts. Children in kindergarten begin learning how to describe and compare measurable attributes and spend a great deal of time classifying objects by size, shape, color and texture. They also begin working with time, money and standard units. As they move through elementary school, children gain the ability solve problems that involve measurement, to convert larger units to smaller units and to represent data in a variety of ways. Creating and interpreting graphs is practiced at all levels.
5 Geometry
... Hemera Technologies/PhotoObjects.
net/Getty Images
Elementary geometry begins with students' ability to identify, describe and create basic two-dimensional shapes -- circle, square, rectangle, triangle, rhombus, trapezoid and hexagon. Students then move on to partition shapes into equal parts and to describe these parts using fraction words -- half, third, quarter or fourth. By the time they are ready to leave elementary school, students should be able to draw and identify shapes based on the properties of their lines, angles and points of symmetry.
references
- 1 Common Core State Standards Initiative: Mathematics
About the Author
A lifetime resident of New York, Christi O'Donnell has been writing about education since 2003. O'Donnell is a dual-certified educator with experience writing curriculum and teaching grades preK through 12. She holds a Bachelors Degree from Sarah Lawrence College and a Masters Degree in education from Mercy College.
Related Articles
Encyclopedia of elementary mathematics. Book 1 (arithmetic)
Pavel Sergeevich Aleksandrov, Alexey Ivanovich Markushevich, Alexander Yakovlevich Khinchin
M.-L., GTTI, 1951. 448 p.
Circulation 50,000 copies.
| |||||||||||
The publication of the "Encyclopedia of Elementary Mathematics" was conceived by the Academy of Pedagogical Sciences of the RSFSR as a manual for secondary school mathematics teachers and students of physical and mathematical faculties of pedagogical and teacher's institutes. Its purpose is to give a systematic exposition of the scientific foundations of the school subject of mathematics.
The book cannot serve as an initial study of the subject. It is intended for people who have studied elementary mathematics and who have already become or are preparing to become a teacher of elementary mathematics. It does not, as a rule, follow either the order or the way of presenting mathematics in high school, since both are determined by the age characteristics of students and the educational goals of high school, i.e. considerations that do not play a role in relation to the trained professional reader. The logic of the publication is the logic of a systematic, as simple and accessible as possible, presentation of those questions of mathematical science from which the school course is built, as well as those that, although they do not find direct expression in this course, are nevertheless necessary for its correct and conscious understanding and create prospects for further development of the content and methods of the school course.
The book begins with an article on number and numbering systems.
Next comes an article on the construction of the theoretical foundations of arithmetic - very general mathematical concepts (sets, groups, rings and fields) are considered, as well as an axiomatic presentation of the theory of natural numbers, on the basis of which the theory of integers, rational, real and complex numbers is introduced. The next article is devoted to issues related to the theory of divisibility, in particular, the theory of continued fractions. The last article is devoted to the issues of rounding numbers, the rules of approximate calculations, the calculation of errors and auxiliary means of calculation.
Contents
Foreword.
Origin of number systems.
(I.G. Bashmakova and A.P. Yushkevich)
Introduction.
§ 1. The initial stage of development of the account.
§ 2. Non-positional number systems.
§ 3. Alphabetical numbering systems.
§ 4.
Local or positional number systems.
§ 5. Distribution of the positional principle of writing numbers in Western Europe and in Russia.
§ 6. Fractions.
Conclusion.
Concept of set, group, ring and field. Theoretical foundations of arithmetic.
(I.V. Proskuryakov)
Introduction.
Chapter I. Sets.
§ 1. The concept of a set.
§ 2. Operations on sets.
§ 3. Function, mapping, power.
§ 4. Finite and infinite sets.
§ 5. Ordered sets.
Chapter II. Groups, rings and fields.
§ 6. Group.
§ 7. Ring.
§ 8. Field.
§ 9. Axiomatic construction of mathematics. Isomorphism.
§ 10. Located rings and fields.
Chapter III. Integers.
§ 11. Axioms of natural numbers.
§ 12. Addition.
§ 13. Multiplication.
§ 14. Order.
§ 15. Inductive definitions. The sum and product of several numbers.
§ 16. Subtraction and division.
§ 17. Remarks on the system of axioms of natural numbers.
Chapter IV. Ring of integers.
§ 18. The extension principle in arithmetic and algebra.
§ 19. Equivalence and division into classes.
§ 20. Definition of the ring of integers.
§ 21. Properties of integers.
Chapter V. The field of rational numbers.
§ 22. Definition of the field of rational numbers.
§ 23. Properties of rational numbers.
Chapter VI. Field of real numbers.
§ 24. Complete and continuous fields.
§ 25. Definition of the field of real numbers.
§ 26. Properties of real numbers.
§ 27. Axiomatic definition of real numbers.
Chapter VII. The field of complex numbers.
§ 28. Definition of the field of complex numbers.
§ 29. Properties of complex numbers.
§ 30. Hypercomplex numbers, quaternions.
Literature.
Elements of number theory.
(A.Ya. Khinchin)
Chapter I. Divisibility and prime numbers.
§ 1. Introduction.
§ 2. Single-valued decomposition of numbers into prime factors.
§ 3. On prime numbers.
Chapter II. comparison method.
§ 4. Introduction.
§ 5. Comparisons and their main properties.
§ 6. Classification of numbers modulo given.
§ 7. Comparisons containing unknowns.
Chapter III. Euclid's algorithm and continued fractions.
§ 8. Euclid's algorithm.
§ 9. Elementary theory of continued fractions.
Chapter IV. Representation of numbers by systematic and continued fractions.
§ 10. Introduction.
§ 11. Systematic fractions.
§ 12. Continued fractions.
Chapter V. Continued fractions and Diophantine approximations.
§ 13. Suitable fractions as best approximations.
§ 14.
Diophantine approximations.
Chapter VI. Algebraic and transcendental numbers.
§ 15. Liouville's theorem and the first occurrence of transcendental numbers.
§ 16. Cantor's method.
§ 17. Arithmetic nature of the classical constants.
Literature.
Oral and written account. Auxiliary means of calculations.
(V.M. Bradis)
Chapter I. General information about the account and approximate calculations.
§ 1. General considerations about the study of counting at school.
§ 2. Oral account.
§ 3. Written account.
§ 4. Computing aids.
§ 5. Approximate values.
§ 6. Various ways of estimating the accuracy of approximate values.
§ 7. Processing of measurement results.
Chapter II. Accounting for errors.
§ 8. Calculations with strict allowance for errors by the method of boundaries.
§ 9. Calculations with strict allowance for errors by the method of error limits.
§ 10. Limiting errors of the results of operations on approximate values. Rules for counting numbers.
§ 11. Root-mean-square errors of the results of operations on approximate numbers. The principle of academician A.N. Krylov.
§ 12. Distribution of errors in the results of calculations.
§ 13. Practical applications of the rules for counting numbers. Summary of these rules.
Chapter III. Various questions.
§ 14. Approximate formulas. Abbreviated steps.
§ 15. Mathematical tables.
§ 16. Graphic calculations.
§ 17. Counting slide rule.
§ 18. Computational work in different years of study.
Literature.
Alphabetical index.
References
- Book 1. Arithmetic. (1951, 448 pp.)
- Book 2. Algebra. (1951, 424 pp.)
- Book 3. Functions and limits, fundamentals of analysis. (1952, 559 pp.)
- Book 4.
Geometry. (1963, 568 pp.) - Book 5. Geometry. (1966, 624 pp.)
| |||||||||||
Permanent address of this page: http://math.ru/lib/57
Educational and methodical complex “Ulya. Elementary Mathematics»
Hands-on learning with a range of organized play to help children master basic math concepts. Classes with the complex promote a positive mood and can ensure that each child remains involved in the learning process at all times. The technology is based on the well-being of children and flexible learning methods.
Who is this complex for?
Pre-school children:
• Age appropriate for 4-7 year olds
• Game forms of lessons
are used • There is a friendly character
• Based on project activity
• Work in groups (up to 24 people)
Teachers of preschool educational organizations:
• Convenient for the teacher, both when conducting GCD and when planning additional classes and games with children
Tasks of the complex
• Formation of elementary mathematical concepts and development of mathematical competencies.
• Improving the ability to form coherent structures in speech.
• Mastering the sign system, learning the basics of mathematics.
• Development of mathematical activities.
• Development of logical thinking, memory, ingenuity, systemic and algorithmic thinking.
• Formation of skills in design and project activities.
• Socio-communicative and emotional development.
• Development of creative thinking.
Method of work with the complex
Forms of work: The lesson takes the form of an educational board or role-playing game using cards, chips, a mini-robot or objects assembled from a constructor.
Composition of the complex: All components of the complex, including distribution cards for children, complement each other and make the work of the educator methodically meaningful and systematic, without holding back his initiative and creativity.
Ways of presenting material: The child gains knowledge in communication with a teacher, including through oral instructions and graphic presentation of material, notes, diagrams, abstract signs, images based on specific objects.
Problems to be solved: The complex contains a comprehensive case of subject-practical classes for children of senior preschool age.
How does it work? The complex develops the intellect, reveals the child's abilities, helps to find new information, teaches to formulate thoughts, draw conclusions.
Advantages of the proposed method
For teachers:
• Simple and clear lesson plans
• Methodological support
• Constantly updated teaching aids
• Diagnostic cards
• Demo
• Cards for children
• Full set of necessary equipment
For parents:
• Activity cards can be used to easily track the content of the program and the child's progress
• Filling out diagnostic cards will allow you to see the level of development of the child and will provide an opportunity for correction
• Interaction during the execution of tasks will lead to building a trusting parent-child relationship
Kit benefits
• A comprehensive solution for preschool educational institutions, designed for the initial study of mathematics in a group of up to 24 children;
• A complete set of materials for the organization of work on the development of mathematical abilities in preschoolers in all sections of the beginnings of mathematics;
• Promotes the formation of elementary mathematical concepts and the development of children's understanding of numbers, counting, the relationship between number and quantity, the development of spatial concepts, the difference in shapes and the search for patterns.
With the help of counters, playing fields, dice and other materials, children will get their first ideas about probability, demonstration and handouts will reinforce their understanding of the concepts of the number line and the passage of time;
• Teaching technology, uses innovative pedagogical forms of work based on information, project, problem-oriented educational technologies and team games. Classes are organized in the form of an educational board or role-playing game using cards, chips, a programmable mini-robot or objects assembled from a constructor.
Composition of the complex
The complex includes an educational and methodological kit for a teacher and children, which is a set of printed materials supplied in a separate box, including:
1. Guidelines for the teacher;
2. Diagnostic materials;
3. Lesson scenarios.
Ready-made lesson scenarios provide an opportunity to achieve the planned results of the development of basic educational programs in accordance with the Federal State Educational Standard.
