Math concepts for kindergarten

The 4 Major Math Concepts Your Kids Learn in PreK & Kindergarten

There are so many different topics our children learn throughout the year, just keeping up with each night’s new piece of homework and its latest ideas can feel very overwhelming. As parents, we don’t get to see the major idea behind the “everyday” work and it can be frustrating to understand where each skill is going. In this first blog post of a continuing series, I will be highlighting the major math concepts that are taught at the different grade levels so we, as parents, can help to build and support these ideas at home.

Here are the four major math concepts taught in pre-kindergarten and kindergarten, along with exercises you can practice with your children to help reinforce their learning.

1. Counting. Students are beginning their experience with numbers through counting, number names and written numerals. Students are learning to count objects and understand a one-to-one correspondence. They are also starting to compare different sets of objects and use appropriate language.

Encourage your child to:

• Touch different objects and count out loud.
• Move objects from one group to another.
• Count a set of objects and “see” or “write” that corresponding number.
• Start to use comparing words: more than, less than, the same as.

2. Addition & Subtraction. This is the very early stage of adding and subtracting. The focus should be on developing an understanding of addition as “putting together and adding to,” and subtracting as “taking apart and taking from.” Students do not need to write equations at this young an age, but are encouraged to begin using them.

Encourage your child to:

• Tell stories about adding and subtracting. For example, for addition: Two bunnies sat on the grass. Three more bunnies hopped there. How many bunnies are on the grass now? For subtraction: Five apples were on the table. I ate two apples. How many apples are on the table now? Draw pictures about putting together and taking apart.
• Count to 10 and break apart numbers (decompose – math’s fancy word for “breaking apart”) into different combinations. For example, 5 can be seen as:

Image Credit: http://kindercraze.com

3. Measurement & Data. Young children are beginning to describe and compare their physical world. They are starting to classify, sort and group objects into categories.

Encourage your children to:

• Compare two different objects using appropriate language. For example:
  “John is taller than Sarah.”
  “This tree is shorter than that tree.”
  “My bag is heavier than your bag.”
• Sort objects by color, size, material, etc.
• Describe their physical world with directional words: in front of, behind, on top of, next to, below, etc.

4. Geometry. Students are starting to look at and compare two-dimensional (flat) and three-dimensional (solid) shapes. They are using appropriate language to recognize different shapes and talk about their attributes.

Encourage your child to:

• Find 2-D shapes in the world: squares, circles, triangles, rectangles, and hexagons.
• Find 3-D shapes in the world: cubes, cones, cylinders, and spheres.
• Count the different number of sides, vertices, angles, etc.Model different shapes using clay, sticks, pipe-cleaners, etc.

See all blog posts in this series for information on what your child will learn in math class from preschool all the up through 8th grade. 

Kindergarten Math | Kindergarten Math Skills

While every state and school district differs slightly, below you will find useful detail surrounding some of the Math concepts children will likely be covering in Kindergarten: Counting and Number Sense, Beginning Addition and Subtraction, Money, Place Value, Basic Patterns, Picture Graphs (pictographs), Telling Time, Measurement, Shapes and Solids, Symmetry, and Fractions. The Giggle Facts Math Program will not only help Kindergarten Students master their Addition and Subtraction Facts, but will also help kids with many other math concepts they will encounter in Kindergarten.

You may notice that many math concepts and math skills repeat over these four grade levels. This is due to the fact that math concepts build on each other grade by grade. Giggle Facts is designed for kids aged 4 to 8 and supports math learning, skills and concepts in Kindergarten, First Grade, 2nd Grade and 3rd Grade. It is a complete math program including Kindergarten math games and should also be played with children older than 8 if they need help “catching up” or mastering Math Facts.

Counting & Number Sense

Kindergarten students will work on one-to-one correspondence (see Glossary), learn about ordinal numbers (First, Second, Third, Fourth, etc.), learn to count by 1s, and may even begin learning to skip count by numbers like 2s, 5s, and 10s (ex: 2,4, 6, 8, or 5, 10, 15, 20).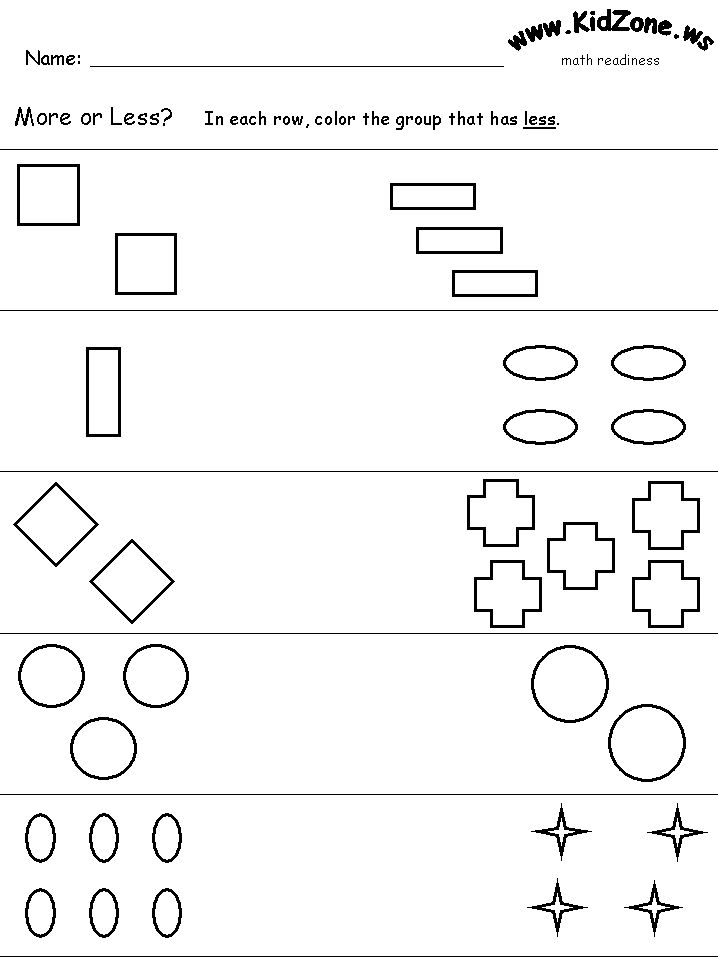 Frequently, a Hundreds Board and/or number line is used to visually represent these Kindergarten math concepts, and to assist students in learning these math skills. Read our blog for advice on how to teach your child skip counting by 5’s. Giggle Facts teaches children the relationship between numbers (Number Sense), which in turn helps with math concepts such as skip counting, greater than / less than, before / after, odd and even numbers, etc.

Beginning Addition and Subtraction

Addition and Subtraction Math Facts may be introduced in Kindergarten. Students may be introduced to Addition as the concept of “adding on” to another number, and they may even encounter Addition strategies such as “Doubles” (6+6 or 4+4) and “Turnarounds” (2+1 = 3, so 1+2 = 3). They may also be introduced to Subtraction, learning the concept of Subtraction as “taking away”. Students will likely begin inventing simple number stories using Addition and Subtraction (ex: Tom has 4 apples. He picks 2 more from the tree. How many apples does Tom have now?).

Children may begin to practice some simple Math Facts in the classroom, however, children will certainly benefit from practicing more at home, to begin learning and retaining Math Facts at this earlier stage. The Giggle Facts^TM program begins at this early stage of math learning. Since instant recall of Math Facts is imperative to learning higher-level math concepts (see Research), it is beneficial to begin practicing and learning Math Facts in Kindergarten. Giggle Facts^TM is a perfect way to play while learning Addition and Subtraction Facts, without relying solely on tedious flashcards. The Math Program includes the frequent use of playing cards, dominoes, and multi-sided dice to make learning fun and to make the math games engaging for children.

Money

Kindergarteners will identify the names and values of pennies, nickels, and dimes, and perhaps begin counting small numbers of coins. Children who have begun learning Addition and Subtraction Facts will, overall, have an easier time adding / counting money. Giggle Facts^TM allows children to develop their number sense that will help them make connections between Math Facts and skip counting with money.

Place Value

Each digit in larger numbers has a value, depending on its position in the number. For example, in the number 78, the 7 is worth 7 “tens” (or 70), and the 8 is worth 8 “ones”, or simply 8. Kindergarteners will begin breaking numbers from 10 to 20 into “tens” and “ones” as an introduction to Place Value.

Giggle Facts^TM teaches students to break down larger numbers into their smaller components (tens and ones) through 2 different strategies. There is an Addition strategy named “Teens”, and a Subtraction strategy named “More Teens” in the Giggle Facts^TM program that supports the concept of Place Value.

Basic Patterns

Students will identify basic patterns using colors, shapes and numbers (ex: red, blue, red, blue or 2,4,2,4) in kindergarden.

Picture Graphs (Pictographs)

Children in Kindergarten may do simple surveys such as finding out their classmates’ “Favorite Season”. This information might be represented using a Pictograph, where each season would have a different picture representing it (ex: Spring: umbrella, Summer: sunshine, Fall: leaves, Winter: snowflake). The kindergarten students would place a picture of their favorite season on a graph, creating a giant picture graph or pictograph of the class data.

Telling Time

Learning to tell time is an important math skill that students begin to work on in Kindergarten. Children will learn about the concept of time (morning, afternoon, days, weeks, years), and they may learn to tell time to the hour and half-hour.

Measurement

Kindergarteners will have many opportunities to measure in a variety of ways. Kindergarten students will compare various lengths, weights and temperatures. The children may also have the opportunity to do some measuring using non-standard units (ex: hand spans), and using calendars, etc.

Shapes and Solids

Kindergarden students will learn to identify and describe 2-dimensional shapes such as circles, triangles, squares, and rectangles. They may look at simple 3-D solids such as cubes.

Symmetry

Kindergarten students may have opportunities to look for symmetry in everyday objects. An image that is symmetrical is something that has two sides that are identical. One side could be seen as a “mirror image” of the other side.

Fractions

Kindergarten students will possibly investigate fractional parts of a whole as part of the math curriculum (ex: the child will divide shapes into equal parts like halves, thirds, or fourths).

Mathematics and its importance in the development of preschool children

Even in early childhood, babies are faced with objects that differ in shape, color and quantity. At this age, the basic elementary ideas and abilities of the child begin to form. The first toys resemble geometric shapes: cubes, constructors, pyramids. The count begins with mom's questions: "Tell me, how old are you?". Parents of children are taught to name the shapes of toys, their size, quantity.

Through play activities, the ability to distinguish different properties and features of objects is formed. The baby is forming the first concept of mathematics, although he still does not know and is not aware of this. The consciousness of a child in early childhood is chaotic. Parents teach children to compare, group objects, call them by their proper names.

Through visual-objective actions - they help the child to remember what he heard on the basis of objective images. Before the age of three, the child already knows how to group objects according to their external features, color, shape. So, for example, a child can put green toys away from red ones, choose pencils from a pile of other objects and put them together, can add pyramids in size, in order of the pyramid rings.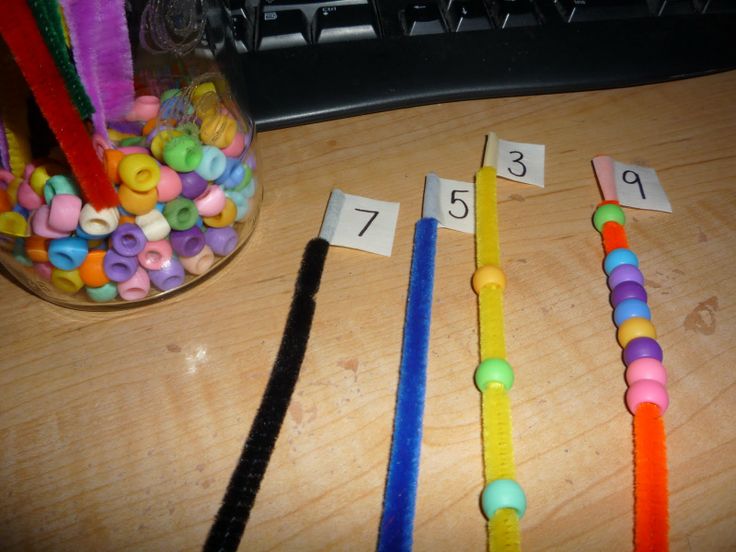
Being engaged with objects through game activity, the child compares them. This is where the first acquaintance with mathematics begins.

By the age of four, children can easily count up to five, and a little older up to ten, but they can also make mistakes in counting.

By the age of six, children already begin to understand when the numbers increase and when they decrease. That is why it is important to start systematic classes from kindergarten in order to increase the mental perception of the child.

In today's modern society, one of the requirements for preschool education is that children receive mathematical knowledge and elementary ideas in kindergarten.
Preschoolers in the course of their development receive the first elementary ideas about mathematics. The available methods and means of forming elementary mathematical representations are developed specifically for age categories, taking into account the gradual development of skills and abilities in preschoolers in this direction.

Mathematics is an independent educational subject and is designed to develop intellectual abilities depending on the natural potential of preschoolers. Its role in the development of elementary ideas in preschoolers is very great. In the course of such activities, the child develops and develops cognitive and personal abilities.
In the process of learning, through the means of mathematical classes, the child receives the first ideas about mathematical concepts.

Mathematics is one of the few disciplines that covers different aspects of the personality of children. In the process of forming elementary mathematical concepts and learning, preschoolers actively develop all cognitive processes: speech, thinking, memory, perception, and representation. This becomes effective if, when setting up classes, the frequency and sequence of the development of cognitive processes in a child are taken into account, depending on the psychophysical development of each child.

If a child has not reached the age at which he is able to understand mathematical processes, then classes will not play any role for his consciousness.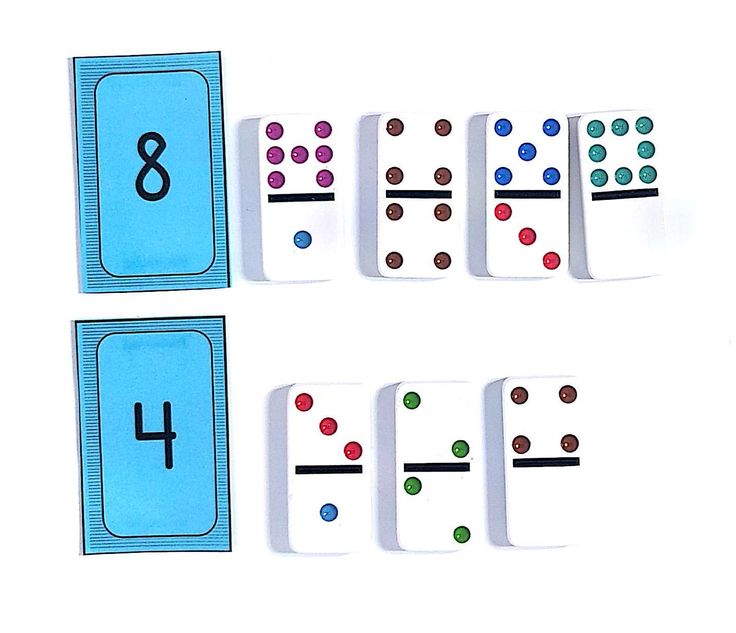 The possibilities of the child are determined by his psychology. In the modern world, innovative methods and means are increasingly included in the educational programs for preschoolers.

The abilities of each child depend on his individual psychological characteristics. Mathematical abilities cannot be innate, since only anatomical and physiological features of a person are innate. Mathematical is a special kind of abilities, they depend on the integral quality of the mind and develop in the process of mathematical activity.

A person's abilities can manifest themselves in various areas, and here, like everything else, mathematical abilities are revealed in the course of a preschooler's activities. The preschool age is considered the most favorable period for the development of abilities.
An analysis of scientific research (A.M. Leushina, N.I. Nepomnyashchaya, A.A. Stolyar, etc.), pedagogical experience convinces us that rationally organized teaching of mathematics to preschool children ensures the overall mental development of children. (Rationally organized education is timely, appropriate for the age and interests of children.) At the same time, pedagogical guidance from an adult is important. Children acquire elementary knowledge about the multitude, number, size and shape of objects, learn to navigate in time and space. They master the account and measurements of linear and volumetric objects with the help of conditional and generally accepted measures, establish quantitative relationships between quantities, the whole and parts.

In recent years, such a concept as pre-mathematical preparation has been introduced into practice. Preparing the child and his cognitive world for the mathematical way of thinking. A variety of ways of forming the cognitive sphere allow you to prepare the child for the study of the subject - mathematics. When organizing classes, there is an impact on visual and logical thinking, memory, creative imagination, perception, voluntary attention of a preschooler.

Children at preschool age observe and imitate adults, they observe every action and listen carefully to what the teacher says and this is an important property. Children should be taught to act independently, show and tell about their actions. Preschoolers should be encouraged to repeat after the teacher about the properties and qualities of objects. Games with children should contain mathematical actions.

Mathematics classes in kindergarten form the simplest types of practical and mental activities of children. Under the types of activity - in this case, methods of examination, counting, measurement - they understand the objective sequential actions that the child must perform in order to assimilate knowledge: element-by-element comparison of two sets, imposing measures, etc. Mastering these actions, the child learns the purpose and methods of activity, as well as rules that ensure the formation of knowledge.

As a rule, educational tasks in the classroom are solved in combination with educational ones. So, the educator teaches children to be organized, independent, listen carefully, do the work efficiently and on time. This disciplines children, contributes to the formation of their focus, organization, responsibility. Thus, teaching children mathematics from an early age ensures their comprehensive development.

Naturally, the basis of knowledge is sensory development, acquired through experience and observation. In the process of sensory cognition, representations are formed - images of objects, their properties, relationships. So, operating with a variety of sets (objects, toys, pictures, geometric shapes), children learn to establish equality and inequality of sets, to call the number of words: “more”, “less”, “equally”.

Comparison of specific sets prepares children for the subsequent assimilation of the concept of number. It is operations with sets that are the basis that children turn to not only in kindergarten, but also throughout the subsequent years of schooling. The idea of ​​a set forms in children the basis for understanding an abstract number, the laws of a natural series of numbers. Although the concepts of a natural number, as well as a geometric figure, magnitude, part and whole are abstract, nevertheless they reflect the connections and relationships of objects in the surrounding reality.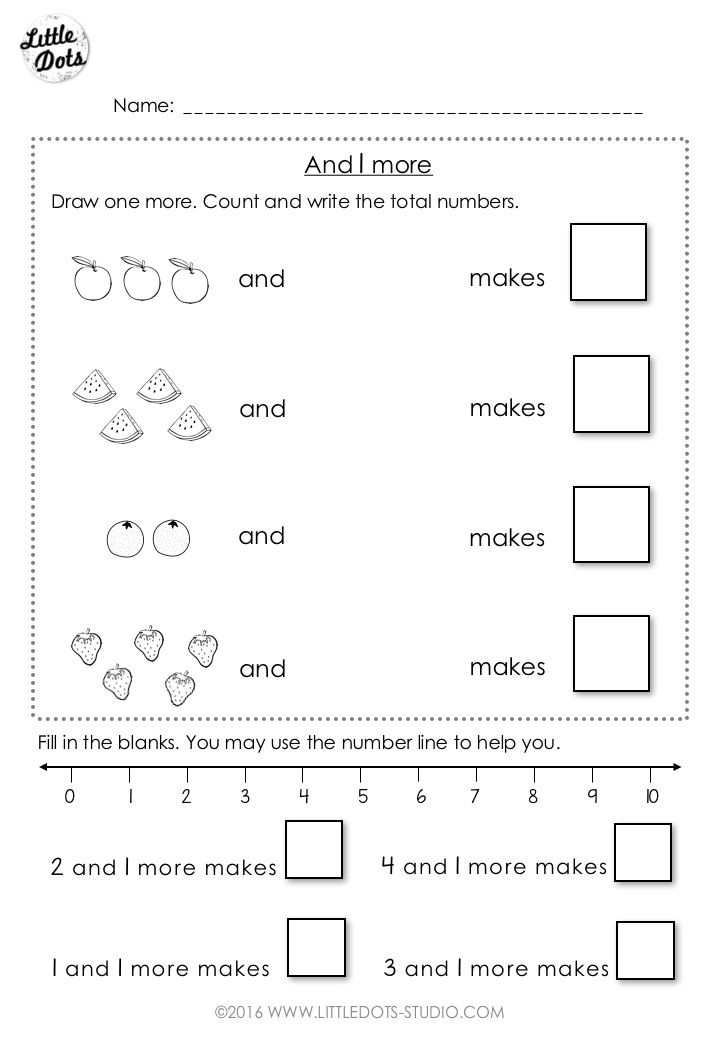

At the same time, preschoolers are taught to compare objects by size (size) and designate the results of the comparison with the corresponding words-concepts (“more - less”, “narrow - wide”, etc.), build rows of objects according to their size in ascending or decreasing order (large , small, even smaller, smallest). However, in order for the child to learn these concepts, it is necessary to form specific ideas in him, teach him to compare objects with each other, first directly - by superimposing, and then indirectly - with the help of measurement.

The central task of the mathematical development of children in kindergarten is learning to count. The main methods in this case are imposition and application, the mastery of which anticipates learning to count with the help of numeral words.

Preschool children are able to divide objects and name their parts, such as dividing an apple into slices or a pie. Preschoolers need to understand that a whole apple is bigger than a slice or half of an apple. Senior students must learn and understand that the number 7 is greater than six, but less than eight. By the end of the training period, preschoolers should be able to perform simple mathematical operations.

In the mathematical preparation of children, the development of elementary mathematical concepts, an important role is played by the teaching of measurement, as the initial way of knowing the quantitative characteristics of the environment. This makes it possible for preschoolers, first of all, to use not generally accepted, but conditional measures when measuring bulk, liquid substances and lengths. At the same time, children develop an eye, which is very important for their sensory development.

Kindergarten math program provides for the development of children's eye in determining the size of objects. To do this, they are trained to evaluate the size (size of objects) as a whole or by individual parameters, comparing with the size of known objects. Attention is drawn to the formation of the ability to check the correctness of the assessment in their practical activities, using additions, reductions, etc. Each practical action replenishes the knowledge of children with new content. It is proved that the formation of elementary mathematical knowledge occurs simultaneously with the development of their practical skills and abilities

Practical actions, while playing a certain role in the mathematical development of children, do not themselves remain unchanged. Thus, the activity associated with the account is changed. At first, it relies on a practical element-by-element comparison of two concrete sets, and later, a number as an indicator of the power of a set and a natural series of numbers acquires special significance, which subsequently replaces one of the concrete sets.
First, children take objects with their hands, shift them, and then count the objects without touching them, or perceive them only by touch.

On the basis of practical actions, children develop such mental operations as analysis, synthesis, comparison, generalization. The teacher should be guided in evaluating the results of his work, first of all, on these indicators, on how children are able to compare, analyze, generalize, and draw conclusions.

In the process of systematic teaching of mathematics, children master special terminology - the names of numbers, geometric shapes (circle, square, triangle, rhombus, etc.), elements of figures (side, top, base), etc. However, it is not recommended when working with children to use such words-terms as “natural rad”, “set”, “structure”, “elements of the set”, etc. Children should also master measured values: meter, centimeter, kilogram, gram, etc. At the same time, work is not limited to classes. They learn to find and compare objects in everyday life, on the street and in nature. For example: three birch trees under the window.

Shcherbakova E.I. among the tasks for the formation of elementary mathematical knowledge and the subsequent mathematical development of children, he singles out the main ones:

- the acquisition of knowledge about the set, number, size, shape, space and time as the foundations of mathematical development;

– formation of a broad initial orientation in the quantitative, spatial and temporal relations of the surrounding reality;

- formation of skills and abilities in counting, calculations, measurement, modeling, general educational skills;

- mastery of mathematical terminology;

- development of cognitive interests and abilities, logical thinking, general intellectual development of the child.

These tasks are most often solved by the teacher at the same time in each lesson in mathematics, as well as in the process of organizing various types of independent children's activities. Numerous psychological and pedagogical studies and advanced pedagogical experience in preschool institutions show that only properly organized children's activities and systematic training ensure the timely mathematical development of a preschooler.

Goals and objectives of the mathematical development of preschoolers. The value of teaching children mathematics

Purpose:

To formulate the main goals and objectives of the mathematical development of preschoolers.

Show the role of teaching mathematics for the comprehensive development of the child's personality.

The problem of teaching mathematics in modern life is becoming increasingly important. This is explained, first of all, by the rapid development of mathematical science and its penetration into various fields of knowledge.

Increasing the level of creative activity, problems of production automation, modeling on electronic computers and much more presupposes that specialists in most modern professions have a sufficiently developed ability to clearly and consistently analyze the processes being studied. Therefore, training in kindergarten is aimed primarily at educating children in the habit of full-fledged logical argumentation of the environment. Learning experience indicates that the development of logical thinking in preschoolers is most facilitated by the study of elementary mathematics. The mathematical style of thinking is characterized by clarity, brevity, dismemberment, accuracy and logic of thought, the ability to use symbolism. In this regard, the content of teaching mathematics at school and kindergarten is being systematically restructured.

Naturally, the basis of knowledge is sensory development, acquired through experience and observation. In the process of sensory cognition, representations are formed - images of objects, their properties, relationships. So, operating with a variety of sets (objects, toys, pictures, geometric shapes), children learn to establish equality and inequality of sets, to call the number of words: “more”, “less”, “equally”. Comparison of specific sets prepares children for the subsequent assimilation of the concept of number. It is operations with sets that are the basis that children turn to not only in kindergarten, but also throughout the subsequent years of schooling. The idea of ​​a set forms in children the basis for understanding an abstract number, the laws of a natural series of numbers. Although the concepts of a natural number, as well as a geometric figure, magnitude, part and whole are abstract, nevertheless they reflect the connections and relationships of objects in the surrounding reality.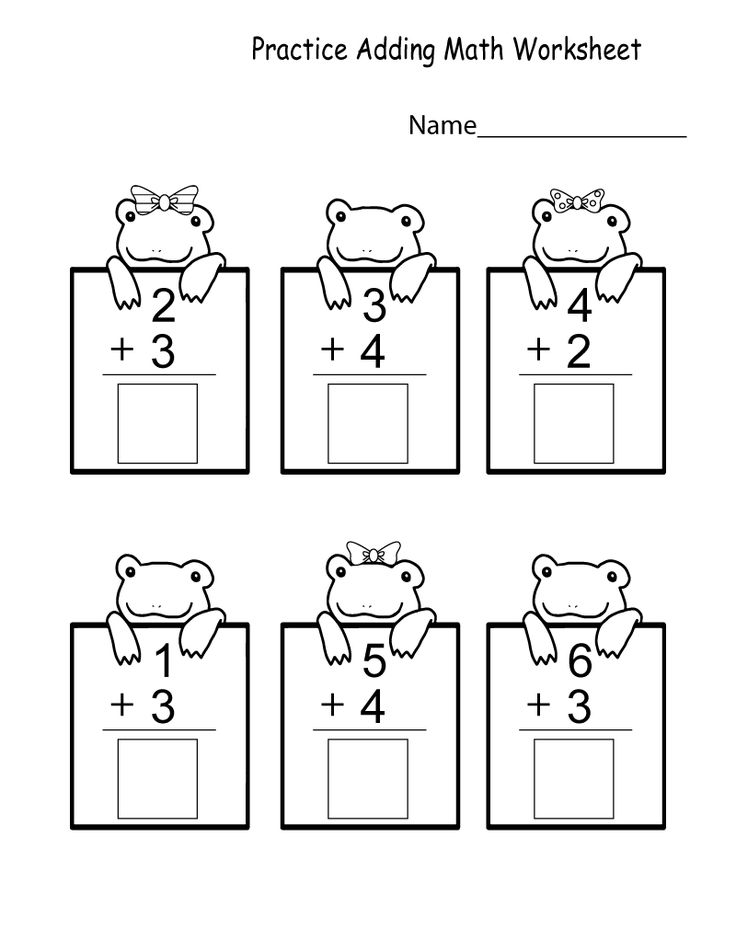

It has been proven that familiarizing children with different types of mathematical activities in the process of purposeful learning orients them to understanding connections and relationships. The formation of initial mathematical knowledge and skills in preschool children should be carried out in such a way that training gives not only an immediate practical result (counting skills, performing elementary mathematical operations), but also a broad developmental effect. As a rule, the mathematical development of preschoolers is understood as qualitative changes in the forms of cognitive activity of the child, which occur as a result of the formation of elementary mathematical representations and the logical operations associated with them. An analysis of scientific research (A.M. Leushina, N.I. Nepomnyashchaya, A.A. Stolyar, etc.), pedagogical experience convinces us that rationally organized teaching of mathematics to preschool children ensures the overall mental development of children.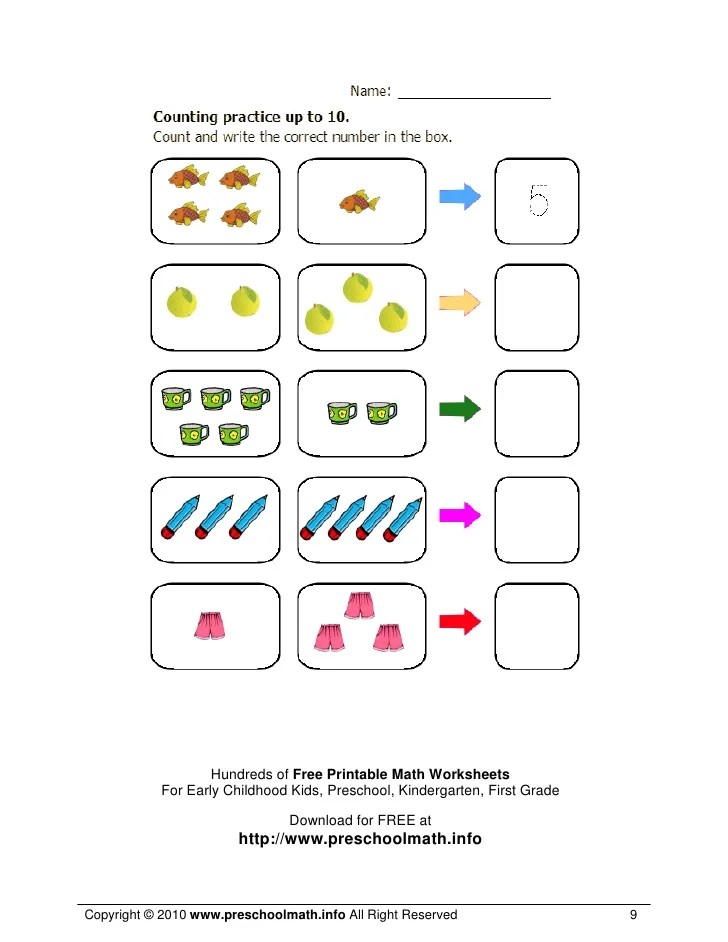 (Rationally organized education is timely, appropriate for the age and interests of children.) At the same time, pedagogical guidance from an adult (educator or parents) is important. Children acquire elementary knowledge about the multitude, number, size and shape of objects, learn to navigate in time and space. They master the account and measurements of linear and volumetric objects with the help of conditional and generally accepted measures, establish quantitative relationships between quantities, the whole and parts.

In the mathematical preparation of children, the development of elementary mathematical concepts, an important role is played by the teaching of measurement as the initial way of knowing the quantitative characteristics of the environment. This makes it possible for preschoolers, first of all, to use not generally accepted, but conditional measures when measuring bulk, liquid substances and lengths. At the same time, children develop an eye, which is very important for their sensory development.

In the process of systematic teaching of mathematics, children master special terminology - the names of numbers, geometric shapes (circle, square, triangle, rhombus, etc.), elements of figures (side, top, base), etc. However, it is not recommended when working with children to use such words-terms as “natural glad”, “set”, “structure”, “elements of the set”, etc. At the same time, work is not limited only to classes. It should be borne in mind the use of the entire didactic space in an educational situation.

Mathematics classes are of particular importance in connection with the development of children's cognitive interests, the ability to show strong-willed efforts in the process of solving mathematical problems.

As a rule, educational tasks in the classroom are solved in combination with educational ones. So, the educator teaches children to be organized, independent, listen carefully, do the work efficiently and on time. This disciplines children, contributes to the formation of their focus, organization, responsibility. Thus, teaching children mathematics from an early age ensures their comprehensive development.

Among the tasks for the formation of elementary mathematical knowledge and the subsequent mathematical development of children, the main ones should be distinguished, namely:

• acquisition of knowledge about set, number, size, form, space and time as the foundations of mathematical development;

• formation of a broad initial orientation in the quantitative, spatial and temporal relations of the surrounding reality;

• formation of skills and abilities in counting, calculations, measurement, modeling, general educational skills;

• mastery of mathematical terminology;

• development of cognitive interests and abilities, logical thinking, general intellectual development of the child.

These tasks are most often solved by the teacher at the same time in each lesson in mathematics, as well as in the process of organizing various types of independent children's activities. Numerous psychological and pedagogical studies and advanced pedagogical experience in preschool institutions show that only properly organized children's activities and systematic training ensure the timely mathematical development of a preschooler.

Numerous studies (A.M. Leushina, N.A. Menchinskaya, G.S. Kostyuk and others) have proved that the age capabilities of preschool children allow them to form scientific, albeit elementary, initial mathematical knowledge. More precisely, children acquire elements of mathematical knowledge. At the same time, it is emphasized that in accordance with the age of the child, it is necessary to select the forms and method of education. In this regard, at specific age stages, the most favorable conditions for the formation of certain knowledge and skills are created.

So, in the second junior group of the kindergarten (the fourth year of life), the main attention is paid to the formation of knowledge about the multitude. The concept of a set is one of the basic and most general, it runs through all of mathematics. The concept of a set is so broad that it is not defined even at the modern level of development of science, but is introduced as the original one and explained with specific examples. In the middle group, in the process of studying the basic properties of a set, the concept of a number is formed, and in the older group, the first ideas about the natural series of numbers are formed. At preschool age, the understanding of the basic properties of the set is limited. However, awareness of its individual properties (equality and inequality, independence of the power of a set from its qualitative features) is possible already at a younger preschool age.

Along with the formation of initial mathematical concepts and concepts, the kindergarten education program provides for familiarization of preschool children with a number of mathematical dependencies and relationships. So, children are aware of some relationships between sets (equal power - uneven power; order relations in a series of quantities, natural numbers; spatial and temporal relations, etc.). At the same time, all mathematical knowledge is presented in interconnection. For example, the formation of ideas about quantity is associated with the formation of ideas about the multitude and size of objects with the development of the ability to see, conditionally determine the size, parameters, as well as the assimilation of relationships between objects. It must be borne in mind that, while acquiring knowledge about number, children learn to abstract quantitative estimates from all others (color, shape, size).

The formation of initial mathematical knowledge in interconnection allows you to gradually and purposefully concretize and refine each of the selected properties. Familiarization of children with the measure and measurements contributes to the formation of a more accurate understanding of the number, and above all the unit. It is the connection of counting and measurement that helps the child to realize the dependence of the result of counting (measurement) on the unit of counting (conditional measure).

Mathematics classes in kindergarten form the simplest types of practical and mental activities of children. Under the types of activity - in this case, methods of examination, counting, measurement - they understand the objective sequential actions that the child must perform in order to assimilate knowledge: element-by-element comparison of two sets, imposing measures, etc. Mastering these actions, the child learns the purpose and methods of activity, as well as rules that ensure the formation of knowledge. For example, comparing equal and unequal sets, superimposing or applying elements, the child is aware of the concept of quantity. Therefore, special attention is paid to the development of practical actions of children with objects.

The central task of the mathematical development of children in kindergarten is learning to count. The main methods in this case are imposition and application, the mastery of which anticipates learning to count with the help of numeral words.

At the same time, preschoolers are taught to compare objects by size (size) and designate the results of the comparison with the corresponding words-concepts (“more - less”, “narrow - wide”, etc.), build rows of objects according to their size in ascending or decreasing order (large , small, even smaller, smallest). However, in order for the child to learn these concepts, it is necessary to form specific ideas in him, teach him to compare objects with each other, first directly - by superimposing, and then indirectly - with the help of measurement.

The kindergarten math program provides for the development of children's eye in determining the size of objects. To do this, they are trained to evaluate the size (size of objects) as a whole or by individual parameters, comparing with the size of known objects. Attention is drawn to the formation of the ability to check the correctness of the assessment in their practical activities, using additions, reductions, etc. Each practical action replenishes the knowledge of children with new content. It is proved that the formation of elementary mathematical knowledge occurs simultaneously with the development of their practical skills and abilities.

Practical actions, while playing a certain role in the mathematical development of children, do not remain unchanged. Thus, the activity associated with the account is changed. At first, it relies on a practical element-by-element comparison of two concrete sets, and later, a number as an indicator of the power of a set and a natural series of numbers acquires special significance, which subsequently replaces one of the concrete sets.

First, children take objects with their hands, shift them, and then count the objects without touching them, or perceive them only by touch.

On the basis of practical actions, children develop such mental operations as analysis, synthesis, comparison, generalization. The teacher should be guided in evaluating the results of his work primarily on these indicators, on how children are able to compare, analyze, generalize, and draw conclusions. The level of children's mastery of mental operations depends on the use of special methodological techniques that allow children to exercise in comparison, generalization. So, children learn to compare sets by quantity, while carrying out a structural and quantitative analysis of the set. Comparing objects by shape, children identify the size of individual elements, comparing them with each other.

An important task is the development of thinking and speech in children (mastery of mathematical terminology). Much more attention should be paid to the development of the initial skills of inductive and deductive thinking, the formation of children's cognitive interests and abilities. It should be noted that general methods of cognition form the basis of any scientific thinking, including mathematical. Naturally, the latter has its own special significance.

In practice, there is often a one-sided understanding of abilities as highly specialized, which borders on giftedness. In this regard, educators sometimes underestimate the formation of general cognitive abilities in all children. Any activity is impossible if a person does not have the ability to do it. In psychology, abilities are designated as personality traits necessary for the successful performance of an activity. The educator needs to know what exactly these abilities are, what mental properties the chosen activity will require and without which it is generally impossible.

Abilities should be considered not only in connection with a certain type of children's activity, but also in connection with its general structure, in which, first of all, orienting and performing actions are distinguished. And when we talk about general abilities for activity, we mean how much a child is able to use his knowledge, skills, and what level of cognitive independence he has. All this determines the effectiveness of the performing part of the general abilities. Along with this, it is necessary to form in children the ability to abstract, to highlight the main thing.

So, the mathematical development of children involves a broad program of introducing them to activities, in this case, mathematical, which is led by an adult (teacher, parents).

Tasks of the methodology of mathematical development as a scientific field:

1. Scientific substantiation of program requirements for the level of

formation of mathematical representations in preschoolers in each age group

.

2. Determination of the content of mathematical material for

teaching children in preschool.

3. Development and introduction into practice of effective didactic tools, methods and various forms of organization of work on the mathematical development of children.

4. Implementation of continuity in the formation of mathematical representations in preschool educational institutions and at school.

5. Development of the content of the training of highly specialized personnel capable of carrying out work on the mathematical development of preschoolers.

6. Development of guidelines for parents on the mathematical development of children in a family.

The purpose of the mathematical development of preschoolers

• Comprehensive development of the child's personality.

• Prepare for success in school.

• Correctional and educational work.

Problems of mathematical development of preschoolers

1. Formation of a system of elementary mathematical representations.

2. Formation of prerequisites for mathematical thinking.

3. Formation of sensory processes and abilities.

4. Expanding and enriching the vocabulary and improving

related speech.

5. Formation of initial forms of educational activity.

Education leads development, is the source of development.

Learning must go ahead of development. It is necessary to focus not on what the child himself is already capable of doing, but on what he can do with the help and under the guidance of an adult. L. S. Vygodsky emphasized that it is necessary to focus on the “zone of proximal development”.

Well-ordered ideas, well-formed first concepts, well-timed mental abilities are the key to further successful education of children at school.

Psychological research proves that in the process of learning there are qualitative changes in the mental development of the child.

From an early age, it is important not only to communicate ready-made knowledge to children, but also to develop the mental abilities of children, teach them to independently, consciously acquire knowledge and use it in life.

Learning in everyday life is episodic. For mathematical development, it is important that all knowledge is given systematically and consistently. Knowledge in the field of mathematics should become more complicated gradually, taking into account the age and level of development of children.

It is important to organize the accumulation of the child's experience, to teach him to use standards (forms, sizes, etc.), rational methods of action (counting, measurements, calculations, etc.).

Taking into account the little experience of children, learning proceeds mainly inductively: first, concrete knowledge is accumulated with the help of an adult, then they are generalized into rules and patterns. It is also necessary to use the deductive method: first, the assimilation of the rule, then its application, concretization and analysis.

For the implementation of competent teaching of preschoolers, their mathematical development, the educator himself must know the subject of the science of mathematics, the psychological characteristics of the development of mathematical representations of children and the methodology of work.

The role of teaching mathematics for the comprehensive development of the child's personality:0003

Physical