Home » Misc » Math strategies 1st grade

Math strategies 1st grade


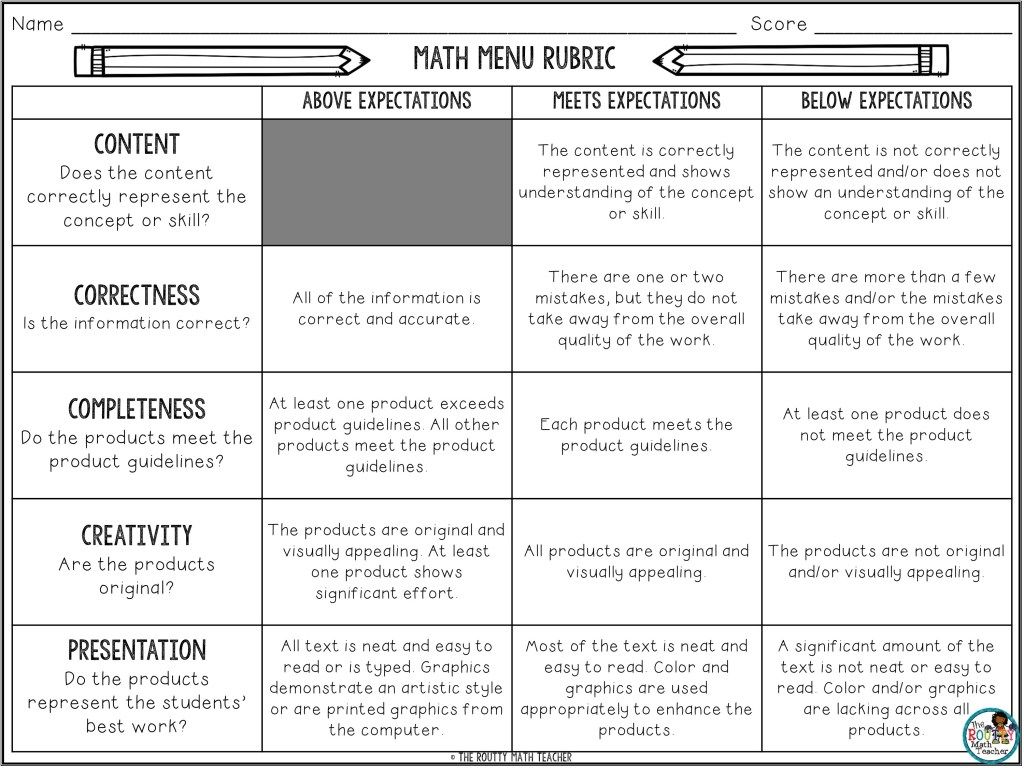
Addition Strategies for First Graders

Home » Blog » Operations » Addition » Addition Strategies for First Graders

Written by: Angie Olson

365 shares

  • Share194
  • Tweet

First grade is the year that students are developing their foundational mathematical skills.  It is critical that when learning how to add numbers, our students are learning and understanding HOW to use a math algorithm to find an answer and also able to explain WHY they are doing so.  When I teach my students addition, they have a solid understanding of numbers and place value first.  Then I introduce different addition strategies.  After some practice with these strategies, the focus can shift to memorization of facts.  This, of course, comes later.

Some strategies that I like to use when teaching addition are:

(these are all covered in the First Grade Addition Interactive Notebook)
1.  Zero Facts
2.  Turn-Around Facts
3.  Counting On
4.  Doubles Facts
5.  Using Fingers
6.  Using Manipulatives
7.  Near Doubles
8.  Make a Ten
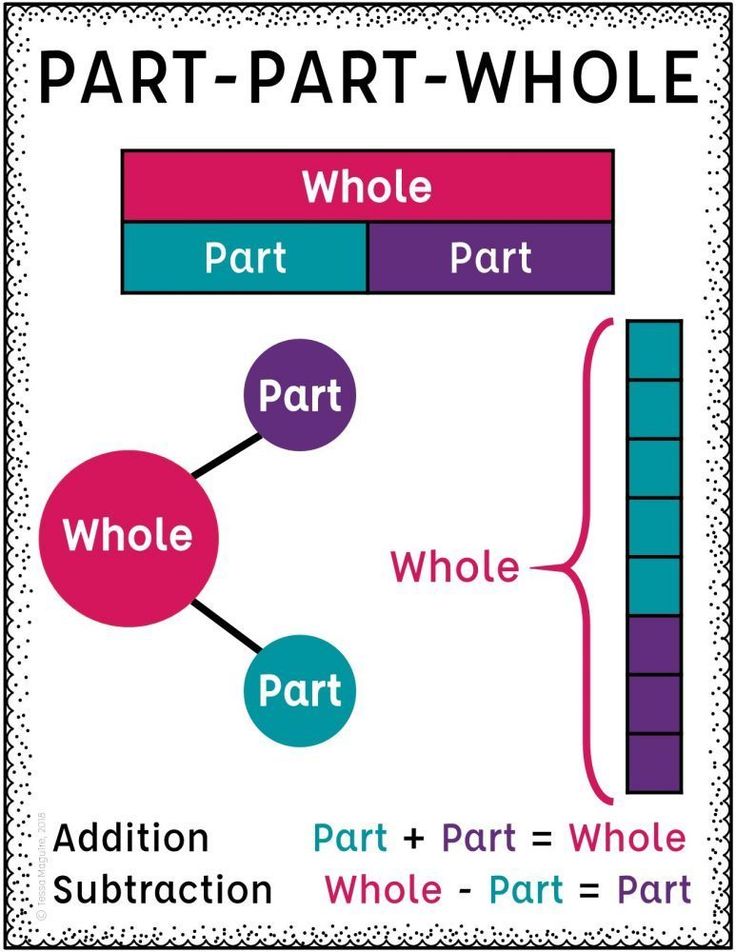
9.  Part Part Whole
10.  Combining Numbers
11.  Tally Marks
12.  Ten Frames
13.  Fingers

Download Addition Strategies Flip Flaps HERE

Another important component to teaching any new unit in math is to teach the vocabulary words that go with the concept.  This particular interactive math notebook activity includes 10 vocabulary words with definitions.  You could have your students glue their definitions under the vocabulary word or write the definition themselves.

Download Addition Vocabulary Flaps HERE

This First Grade Addition Strategies Notebook includes all of the strategies you read from above along with activities for practice of these addition strategies.  I believe most first graders benefit from using manipulatives when learning a math skill so these interactive notebook activities were designed to accompany some of the most basic math manipulatives such as dice, counters, dominoes, etc.

Download All Things 1st Grade Interactive Notebooks HERE

My favorite part about this First Grade Addition Strategies Notebook is the word problem story mats.  Word problems seem to always be a trickier concept for students to master so I knew that I wanted to find a way for students to practice this skill in a practical way.  That’s when these word problem story mats came to life!

I love that there are pictures provided for each story or I can use any math manipulative that I have laying around my classroom.  These word problem story mats can also be easily differentiated.  For the struggling student, I would use these as a part of their math center.  I would provide the story prompt and a limited number of counters.  I can also see this being used with at grade level students by having them work with a partner to determine a story, place counters on the story mat, and write the addition sentence to go with the word problem.  For the advanced first graders, I would provide the story mats and an increased number of counters.  Then they would work independently or with a partner to write a word problem of their own along with the addition sentence to go with the word problem.  The First Grade Addition Notebook includes 5 different stories with counters.

Download Word Problem Story Mats HERE

Feel free to use the image below to save this post to your Pinterest board.  Happy Teaching!  🙂

365 shares

  • Share194
  • Tweet

First Grade Math Strategies | 1st Grade Math Concepts

While every state and school district differs slightly, below you will find many of the Math concepts children will likely be covering in 1st Grade Math such as Skip Counting and Using a Hundreds Board, Math Facts, Money, Place Value, Telling Time, Measurement, Shapes and Solids, Symmetry, Fractions, Patterns, and Graphs. The Giggle Facts Math Program will not only help students master their Addition and Subtraction Facts, but will also help kids with many other math concepts they will encounter in First Grade.

You may notice that many concepts and skills repeat over these four grade levels. This is due to the fact that math concepts build on each other grade by grade. Giggle Facts is designed for kids aged 4 to 8 and supports math learning, skills and concepts in Kindergarten, First Grade, 2nd Grade and 3rd Grade. It is a complete math program and is great for First Grade Math Games.

Skip Counting & Using a Hundreds Board

Students in First Grade will learn to count by 1s, and skip count by numbers like 2s, 5s, and 10s (ex: 2,4, 6, 8, or 5, 10, 15, 20). Frequently, a Hundreds Board is used to visually represent these concepts, and to assist students in learning them.

Giggle Facts teaches children the relationship between numbers (Number Sense), which in turn helps with concepts such as skip counting, greater than / less than, before / after, odd and even numbers, etc.

Math Facts – Addition and Subtraction

Addition and Subtraction Math Facts will be introduced in First Grade (if they weren’t already introduced in Kindergarten). Students will learn Math Fact Addition strategies such as “Doubles” (6+6 or 4+4), “Turnarounds” (2+7 = 7+2), “Near Doubles”, “Almost Doubles” or “Doubles Plus 1” (6+6+12, so 6+7= one more, or 13). They will also be introduced to the concept of Subtraction, and will learn the “easier” Subtraction Facts.

Students will likely have opportunities to practice Math Facts in the classroom, however, most children need to spend more time at home practicing them. Giggle Facts (see Giggle Facts Homepage) reinforces the strategies above, and incorporates many others as well. Since instant recall of Math Facts is imperative to learning higher-level math concepts (see Research), it is very important to practice Math Facts often. Giggle Facts (see Sample Games) is a perfect way to play while learning Addition and Subtraction Facts, without relying solely on tedious flashcards. The Math program includes the frequent use of playing cards, dominoes, and multi-sided dice (see Program Components) to make learning fun and to make the math games engaging for children.

Money

First Graders will count / add pennies, nickels, dimes, quarters, and perhaps dollar bills. The concept of making change will be introduced. Children who know their Addition and Subtraction Facts will, overall, have an easier time adding / counting money. Students who have an understanding of Subtraction will have an easier time with making change. Giggle Facts allows children to develop their number sense that will help them make connections between Math Facts and skip counting with money.

Place Value

Each digit in larger numbers has a value, depending on its position in the number. For example, in the number 478, the 4 is worth 4 “hundreds” (or 400), the 7 is worth 7 “tens” (or 70), and the 8 is worth 8 “ones”, or simply 8.

Giggle Facts teaches students to break down larger numbers into their smaller components (tens and ones) through 2 different strategies. There is an Addition strategy named “Teens”, and a Subtraction strategy named “More Teens” in the Giggle Facts program that supports the concept of Place Value.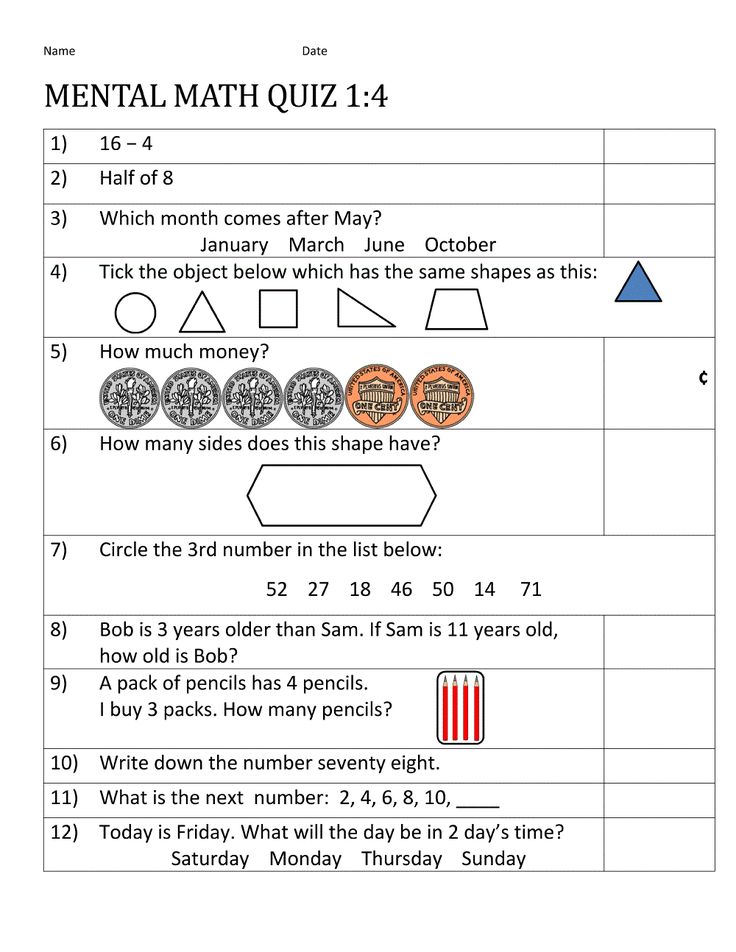

Telling Time

Learning to tell time is an important skill that students work on in First Grade. They will likely tell time to the hour, half-hour, quarter-hour, and perhaps even to 5 minutes using both digital and analog clocks.

The concept of elapsed time may also be introduced, and once again, the keen number sense that students will develop through the Giggle Facts program will aid them in understanding this tricky concept.

Measurement

First Graders will have many opportunities to measure in a variety of ways. Grade One students will learn linear measurement with non-standard units (ex: hand spans) and standard units (ex: inches or centimeters), as well as temperature using a thermometer, time using calendars, etc.

Shapes and Solids

Students will learn to classify 2-dimensional shapes by shape, color and size. They will also look at various attributes of shapes (ex: number of sides, corners, etc. ). Solids (3-D) such as cones, cylinders, prisms, pyramids and spheres will also be introduced.

Symmetry

An image that is symmetrical is something that has two sides that are identical. One side could be seen as a “mirror image” of the other side. Students will have opportunities to look for symmetry in everyday objects, as well as create symmetrical patterns of their own.

Fractions

Fractional parts of a whole will be investigated (ex: the child will see a circle, and will divide it into several equal parts like halves, thirds, fourths, sixths, etc.). Fractions of a group might also be introduced (ex: how to divide a class of 24 children into 6 equal groups).

Patterns

First Grade students have done some work with Color, Shape and Number Patterns, and they will continue to discover ways to create new patterns. This skill incorporates some adding and subtracting, logical thinking, etc.

Graphs

First Graders will have many opportunities to measure in a variety of ways. Grade One students will learn linear measurement with non-standard units (ex: hand spans) and standard units (ex: inches or centimeters), as well as temperature using a thermometer, time using calendars, etc.

Games and strategies. Problems for symmetry. Number Complement Problems. - Mathematics

Games and strategies.

Games and strategies are a separate class of mathematical problems. Most of the time two people play. At the same time, the rules of the game are stipulated in the condition. It is necessary to show which of the players has the opportunity to win regardless of the moves of the opponent.

When solving a game problem, write down:

I) the move of the first player;

II) the algorithm of moves in response to each move of the opponent, i.e. the winning strategy;

III) to show that regardless of the opponent's move there is an opportunity to make a move, i. e. his last move will be victorious.

The main (but not the only) ideas of strategies:

  • Joking games.

  • Games that use symmetry.

  • Games in which the strategy is complement to a fixed number.

  • Games using the winning position method

Today in class we will go over each idea in detail.

1. Joking games.

Games - jokes - these are games where you don't need to know anything to build a winning algorithm, since the result in them will depend not on the game of partners, but on the initial conditions. However, in order to do this, it should be noted in the solution that this is a joke game, and not some other game in which you need to look for a winning strategy. In fact, there is no strategy (and they want to deceive us that it allegedly exists!) It's just .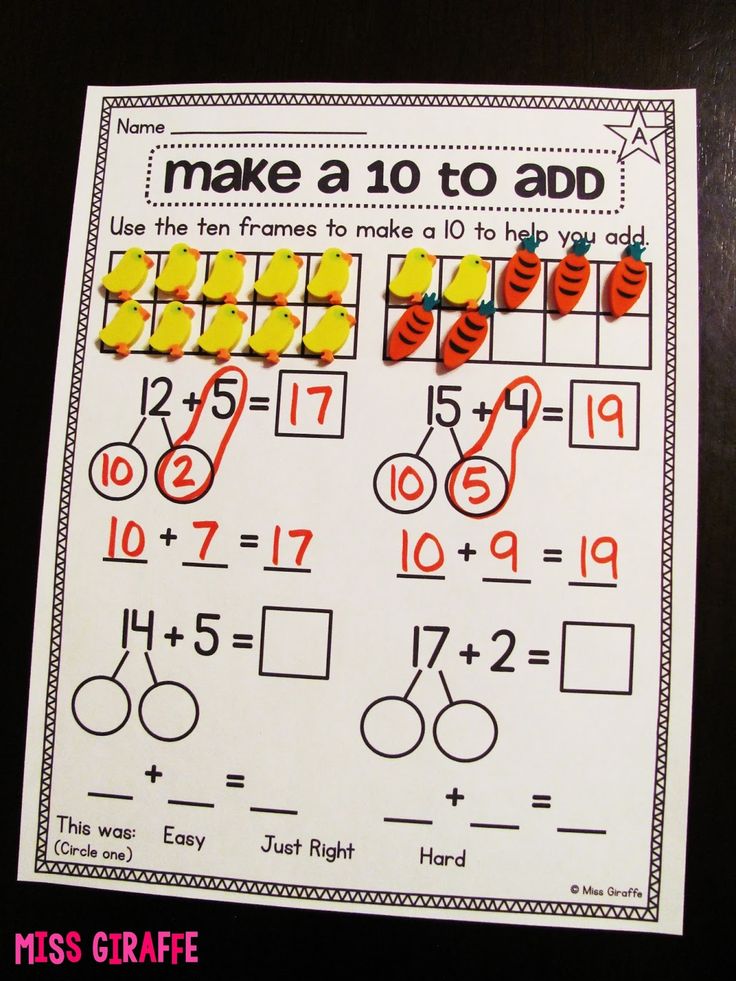 .. no matter how anyone moves, either the first player (the one who starts the game) always wins, or always the second one. The task is to mathematically prove such a pattern. For proof, there is usually some value that is clear what it is equal to at the beginning and end and it is clear how it changes on each move - here you can even unambiguously calculate the number of moves to the end. This quantity is called an invariant (parity is the most famous invariant in mathematics).

Invariant (from Latin invarians - unchanged), in mathematics - a value that remains unchanged under certain transformations.

1. The following situation occurs in a number of problems. Some system sequentially changes its state, and it is required to find out something about its final state. It can be difficult to follow all the transitions completely, but sometimes it helps to answer the required question by calculating a certain quantity that characterizes the state of the system and is preserved during all transitions (such a quantity is called invariant for the considered system). It is clear that then in the final state the value of the invariant will be the same as in the initial state, i.e. the system cannot be in a state with a different value of the invariant.

2. In practice, this method comes down to the fact that a certain value is calculated in two ways: first, it is simply calculated in the initial and final states, and then its change is traced during successive small transitions.

3. The simplest and most common invariant is the parity of a number; the invariant can also be the remainder of division not only by 2, but also by some other number. Auxiliary colorings are sometimes useful for constructing invariants, i.e., dividing the objects under consideration into several groups (each group consists of objects of the same color).

Many problems are easily solved if you notice that some quantity has a certain parity. It follows from this that situations in which this quantity has a different parity are impossible. Sometimes this value (function) needs to be constructed, for example, consider the parity of a sum or product, divide objects into pairs, notice the alternation of states, color objects in 2 colors.

Note that often to find the idea of ​​solving a problem, you can use the "method of small numbers", that is, start the search for a solution with small numbers.

Problems:

  1. Two people take turns breaking a 5x8 chocolate bar. In a turn, you can break any piece in a straight line between the slices. The one who cannot make a move loses. Who wins with the right play?

Solve the same problem in general terms, about the MxN chocolate bar.

  1. There are three piles of stones: in the first - 10, in the second - 15, in the third - 20. In a move, you can split any pile into two smaller ones. The one who cannot make a move loses. Who won?

  2. Numbers are written on the board: 10 zeros and 10 ones. During a move, you can erase any two numbers and write 0 instead of them if they were the same or 1 if they were different. If 1 remains on the board, the first one wins. If 0 - second.

  3. 2007 ones and 2008 zeros are written on the board. Each of the two players chooses two random numbers, erases them, and replaces them with 0 if they were equal, and 1 if they weren't. At the end, only one number remains on the board. If this number is 1, then the first player wins, if 0, then the second one. Who won?

2. Symmetry.

A very simple, but powerful and beautiful method of solving game problems - a symmetrical strategy. Its essence is to make each time a move that is symmetrical to the opponent's move or complements it to something. The proof of the correctness of our strategy will be based on the fact that after each of our moves the position is symmetrical: if so, then if the opponent managed to make his move, then we can also make a move symmetrical to him.

Problems for the topic:

  1. Two people take turns placing nickels on a round table so that they do not overlap and do not protrude beyond the edge of the table. The one who cannot make a move loses. Who won?

  2. Two people play by placing crosses and tac-toes in turn on a 9x9 square field. At the end, everyone gets a point for each row and column in which they have more characters. Can the first player win?

  3. There are two piles of stones, 7 in each. You can take any number of stones per turn, but only from one pile. The one who cannot make a move loses. Who won?

3. Games in which the strategy is complement to a fixed number.

Another idea of ​​a winning strategy in games is to complement the opponent's move to some fixed number, reducing the total number of elements by some constant number with each "joint" move (i. e., the move of the first and second players), which reduces the game to a game with less number of elements, i.e. more simple. It is clear that the victory in this strategy depends on the total amount of data on the condition of the elements.

Consider an example of such a strategy for specific problems.

  1. Two people are playing a game. The moves, which are made in turn, consist in the fact that any number of stones from 1 to 5 is removed from a pile of 26 stones. The one who takes the last stone wins. Who will win in this game?

  2. Two people play a game which consists in adding to zero any natural number not exceeding seven. The one who says the number 50 wins. Who will win in this game?

5. The method of winning positions

This method is based on considering each position in terms of benefit to the player who has to move. We begin to consider from the end - from the last move, then the penultimate one, etc.

  1. The Lame Rook can move in a straight line to the right or up. Initially, it stands in the lower left corner of the chessboard. Two are playing. The one who places the rook in the upper right corner wins.

  2. There are two piles of sweets: one contains 20, the other contains 21. In a move, you need to eat all the candies in one of the piles, and divide the second into two not necessarily equal piles. The one who cannot make a move loses. Who won?

Games and strategies. Tasks.

  1. At the ends of the checkered strip 1 x 20 there is a checker. During a move, it is allowed to move any checker in the direction of another one or two cells. You can't jump over the checker. The one who cannot make a move loses. Who wins with the right play?

  2. There are 25 matches on the table. Two people take turns taking from 1 to 4 matches. The one who has no matches left loses. Who wins when played correctly? What if there are 24 matches?

  3. There are 25 matches on the table. Two people take turns taking 1, 2 or 4 matches. The one who has no matches left loses. Who wins when played correctly?

  4. There are 2 piles of matches on the table, 7 in one and 10 in the other. In one move, it is allowed to take 1 match from one (any) pile or a match from two piles at once. Whoever cannot make a move (no matches left) loses. Who wins with the right play?

Try to look at that problem on the chessboard.

Extra:

  1. There is a pile of stones. Two players take turns taking 1, 2 or 3 stones. The one who takes the last stone loses. Stones can be pre-counted. How to win A if he starts the game?

  2. There are 2 piles of stones m and n. Each player takes as many stones as they want, but from one pile. The one who takes the last stone wins. For what m and n does the first win, for what does the second win, and what strategy will be winning?

  3. There are 25 stones in a pile. Two players take turns taking either 2, or 4, or 7 stones. The one who has no move loses. Who will win with the right play?

Mathematical games and strategies. - Mathematics

Games and strategies.

Math games are very popular, as are all games. And not always a more difficult game is more interesting. Often millions of people play the simplest games with unquenchable interest, and it is these games that are most valued, they enter the history of mathematics and glorify their creators.

The simplest mathematical games are often used as problems in which you need to find a winning strategy, or translate one position into another.

Sometimes problems are very simple when they are solved by known methods, such as invariant and coloring, but there are also very simple, but still unsolved problems associated with mathematical games.

What is a game, strategic task? This is not an ordinary mathematical problem, since, firstly, there is often nothing numerical in it, that is, it is not clear, but what, in fact, needs to be solved, or more precisely, what should be written in solving such problems?

Secondly, sometimes in games it is impossible to come up with an algorithm for winning or, as they say, a strategy for winning, that is, to be able to act in a certain algorithmic way in response to each move of the opponent, in other words, it is possible to win in a game without a strategy, as well as a draw .

Thirdly, in order to solve a game problem, you need to be able to write it down correctly. And this entry depends, for example, on who wins in a given game.

So, games and strategies are a separate class of mathematical problems. Most of the time two people play. At the same time, the rules of the game are stipulated in the condition. It is necessary to show which of the players has the opportunity to win regardless of the moves of the opponent.

When solving a game problem, write down:

I) the move of the first player;

II) the algorithm of moves in response to each move of the opponent, i.e. the winning strategy;

III) show that regardless of the opponent's move there is an opportunity to make a move, i.e. his last move will be victorious.

The main (but not the only) ideas of strategies:

  • Joking games.

  • Games that use symmetry.

  • Games in which the strategy is complement to a fixed number.

  • Winning Position Games

Today in class we will go over each idea in detail.

1. Joking games.

Joking games are games where you don't have to know anything to build a winning algorithm, since the result in them will depend not on the partners' game, but on the initial conditions. However, in order to do this, it should be noted in the solution that this is a joke game, and not some other game in which you need to look for a winning strategy. In fact, there is no strategy (and they want to deceive us that it allegedly exists!) It's just ... no matter how anyone moves, either the first player (the one who starts the game) always wins, or always the second one. The task is to mathematically prove such a pattern. For proof, there is usually some value that is clear what it is equal to at the beginning and end and it is clear how it changes on each move - here you can even unambiguously calculate the number of moves to the end. This quantity is called an invariant (parity is the most famous invariant in mathematics).

Invariant (from Latin invarians - unchanged), in mathematics - a value that remains unchanged under certain transformations.

1. The following situation occurs in a number of problems. Some system sequentially changes its state, and it is required to find out something about its final state. It can be difficult to follow all the transitions completely, but sometimes it helps to answer the required question by calculating a certain quantity that characterizes the state of the system and is preserved during all transitions (such a quantity is called invariant for the considered system). It is clear that then in the final state the value of the invariant will be the same as in the initial state, i.e. the system cannot be in a state with a different value of the invariant.

2. In practice, this method comes down to the fact that a certain value is calculated in two ways: first, it is simply calculated in the initial and final states, and then its change is traced during successive small transitions.

3. The simplest and most common invariant is the parity of a number; the invariant can also be the remainder of division not only by 2, but also by some other number. Auxiliary colorings are sometimes useful for constructing invariants, i.e., dividing the objects under consideration into several groups (each group consists of objects of the same color).

Many problems are easily solved if you notice that some quantity has a certain parity. It follows from this that situations in which this quantity has a different parity are impossible. Sometimes this value (function) needs to be constructed, for example, consider the parity of a sum or product, divide objects into pairs, notice the alternation of states, color objects in 2 colors.

Note that often to find the idea of ​​solving a problem, you can use the "method of small numbers", that is, start the search for a solution with small numbers.

Problems:

  1. Two people take turns breaking a 5x8 chocolate bar. In a turn, you can break any piece in a straight line between the slices. The one who cannot make a move loses. Who wins with the right play?

Solve the same problem in general terms, about the MxN chocolate bar.

  1. There are three piles of stones: in the first - 10, in the second - 15, in the third - 20. In a move, you can split any pile into two smaller ones. The one who cannot make a move loses. Who won?

  2. Numbers are written on the board: 10 zeros and 10 ones. During a move, you can erase any two numbers and write 0 instead of them if they were the same or 1 if they were different. If 1 remains on the board, the first one wins. If 0 - second.

  3. 2007 ones and 2008 zeros are written on the board. Each of the two players chooses two random numbers, erases them, and replaces them with 0 if they were equal, and 1 if they weren't. At the end, only one number remains on the board. If this number is 1, then the first player wins, if 0, then the second one. Who won?

2. Symmetry.

A very simple, but powerful and beautiful method of solving game problems - a symmetrical strategy. Its essence is to make each time a move that is symmetrical to the opponent's move or complements it to something. The proof of the correctness of our strategy will be based on the fact that after each of our moves the position is symmetrical: if so, then if the opponent managed to make his move, then we can also make a move symmetrical to him.

Problems for the topic:

  1. Two people take turns placing nickels on a round table so that they do not overlap and do not protrude beyond the edge of the table. The one who cannot make a move loses. Who won?

  2. Two people play by placing crosses and tac-toes in turn on a 9x9 square field. At the end, everyone gets a point for each row and column in which they have more characters. Can the first player win?

  3. There are two piles of stones, 7 in each. You can take any number of stones per turn, but only from one pile. The one who cannot make a move loses. Who won?

3. Games in which the strategy is complement to a fixed number.

Another idea of ​​a winning strategy in games is to complement the opponent's move to some fixed number, reducing the total number of elements by some constant number with each "joint" move (i.e., the move of the first and second players), which reduces the game to a game with less number of elements, i.e. more simple. It is clear that the victory in this strategy depends on the total amount of data on the condition of the elements.

Consider an example of such a strategy for specific problems.

  1. Two people are playing a game. The moves, which are made in turn, consist in the fact that any number of stones from 1 to 4 is removed from a pile of 26 stones. The one who takes the last stone wins. Who will win in this game?

  2. Two people play a game which consists in adding to zero any natural number not exceeding seven. The one who says the number 50 wins. Who will win in this game?

4. The method of winning positions

This method is based on considering each position in terms of benefit to the player who has to move. We begin to consider from the end - from the last move, then the penultimate one, etc.

  1. The Lame Rook can move in a straight line to the right or up. Initially, it stands in the lower left corner of the chessboard. Two are playing. The one who places the rook in the upper right corner wins.

  2. There are two piles of sweets: one contains 20, the other contains 21. In a move, you need to eat all the candies in one of the piles, and divide the second into two not necessarily equal piles. The one who cannot make a move loses. Who won?

Games and strategies. Tasks.

  1. At the ends of the checkered strip 1 x 20 there is a checker. During a move, it is allowed to move any checker in the direction of another one or two cells. You can't jump over the checker. The one who cannot make a move loses. Who wins with the right play?

  2. There are 25 matches on the table. Two people take turns taking from 1 to 4 matches. The one who has no matches left loses. Who wins when played correctly? What if there are 24 matches?

  3. There are 25 matches on the table. Two people take turns taking 1, 2 or 4 matches. The one who has no matches left loses. Who wins when played correctly?

  4. There are 2 piles of matches on the table, 7 in one and 10 in the other. In one move, it is allowed to take 1 match from one (any) pile or a match from two piles at once. Whoever cannot make a move (no matches left) loses. Who wins with the right play?

Try to look at that problem on the chessboard.

  1. There is a pile of stones. Two players take turns taking 1, 2 or 3 stones. The one who takes the last stone loses. Stones can be pre-counted. How to win A if he starts the game?

  2. There are 2 piles of stones m and n. Each player takes as many stones as they want, but from one pile. The one who takes the last stone wins. For what m and n does the first win, for what does the second win, and what strategy will be winning?

  3. There are 25 stones in a pile. Two players take turns taking either 2, or 4, or 7 stones. The one who has no move loses. Who will win with the right play?

  4. Two numbers are written on the board: 2014 and 2015.

    Learn more