Maths concepts for preschoolers
The Most Important Math Concepts Kids Learn in Pre-K
Although there’s a lot of emphasis placed on emergent reading, experts show that pre-k math skills are just as important for your child’s learning development.
Understanding what skills your child will be exposed to as a math beginner will give you an idea of what concepts you can emphasize in fun, easy ways at home!
Fortunately, kids are exposed to many math concepts from a very young age — putting puzzles together, sorting objects, and even playing with building blocks. These activities all help build a good foundation for math.
In this article, we’ll take you through the most important pre-k math concepts so you can encourage and motivate your budding mathematician!
Table Of Contents
- What Are The Components Of Pre-K Math?
- Basic Pre-K Math Checklist
- Pre-K Math Development
- 9 Fun Pre-K Math Activities
What Are The Components Of Pre-K Math?
There are five basic components of pre-k math. They act like umbrella terms, each with many different elements hidden inside their broad concepts.
Your child will become acquainted with all of these essential concepts when they begin learning pre-k math.
1) Numbers And Counting
Children typically start with the bedrock of math — numbers! They’ll learn number names and how to write numbers, typically beginning with 1-10.
Counting is not easy business! While your child learns how to count — first with physical objects, then conceptually — they are bound to make mistakes here and there. This is perfectly all right. Counting will take time to master.
Most of kids’ initial exposure will be through representational counting. This could mean counting the number of strawberries in their lunch box, how many blocks are on the floor, and so on. These counting activities will set the stage for a strong foundation in counting.
By understanding that numbers represent objects, your child will begin to understand one-to-one correspondence (each object counted gets its own number and only that number) as well as the counting principle that when counting the number of objects, the last number counted equals the amount present.
Over time, a child’s reliance on physical objects for counting will decrease. They’ll depend more on conceptual counting as their skills develop.
This conceptual counting is called “number sense.” They’ll understand that quantities, whether tangible or theoretical, are countable. They’ll also learn that numbers can be compared: two or more numbers can have a more-than, less-than, or same-as number relationship.
There are many fun ways to get your child comfortable with numbers and counting at home without making it feel burdensome.
Here are a few simple yet effective strategies you can try:
- Encourage your child to touch and count objects they see in everyday life — for example, a bunch of bananas or a stack of books.
- After they count a set of objects, help them write down the corresponding number on a piece of paper.
- Have your child compare different items using the appropriate language. For example, “Let’s count the number of blueberries and strawberries on the plate.
 Are there more strawberries than blueberries?”
Are there more strawberries than blueberries?” - Hang a simple number line on the wall or tape one to your refrigerator. Throughout the day, point to each number with your child and count from 1-10 together.
- Ask your child to help set the table by counting out the right number of forks and spoons. Once they have collected them, they can count them again as they put one at each place setting.
These simple activities allow children to make sense of numbers. And the more they practice counting principles outside of the classroom, the more they’ll realize how relevant they are to everyday life.
2) Addition And Subtraction
Once your child has a firm grasp on counting and is developing number sense, they’ll explore the relationships between numbers more often. Describing how numbers are the same or different will lead into learning how to combine two numbers to make a new number!
Similar to the last concept, children will typically learn how to add and subtract by relying on counting activities with tangible objects. For example, you could set up two separate groups of apples and ask how many you will have if you join them together.
For example, you could set up two separate groups of apples and ask how many you will have if you join them together.
The first group may have three apples, while the second group has two apples. At first, many children will count one group and then start over to count the second group. It is a good idea to count both groups individually and then bring them together and count the total amount.
This is their first introduction to addition! The same idea works for subtracting. What happens when you begin with five apples and then take away two of them?
“Taking away” objects may be a little harder for your child to master at first. This is why many children will remove apples first and then count the remaining apples rather than counting backward.
To help, practice counting backward together. Pretend to be a rocket ship, and start counting down from five to one, gradually increasing the beginning number each time. After you get to one, shout, “Blastoff!” and jump into the air as high as you can. This fun game can help your child become more comfortable with counting down.
This fun game can help your child become more comfortable with counting down.
Pictures can also help your child master addition and subtraction concepts. For addition practice, present one sheet of paper with three apples and another with two. Then say, “Count the apples on both pieces of paper. How many apples do you have total?”
For subtraction problems, present this scenario: “On our paper, we have five apples total. How many apples will you see if I cover up two of them?” Then, count the remaining apples together.
Pictures are an effective way for your child to visualize mathematical problems. But, if you prefer not to draw, you can also use real objects instead. You could get out several apples (stuffed animals, cups, or whatever) and count them. Then, use those items for math practice.
Remember that adding and subtracting are basically making comparisons between numbers or establishing relationships between them. There are many strategies a child might use to solve a problem, which is a good thing since our main goal is to help children think mathematically.
3) Geometry And Spatial Reasoning
Shapes are everywhere in our world, which will be one of your greatest assets when it comes to teaching your child about shapes and spatial reasoning.
They’ll start out by learning about the basic 2-D shapes that are used in math: squares, triangles, circles, rectangles, rhombuses, and ovals. Learning how to draw these basic shape illustrations can be helpful for their learning process.
Some of these shapes you’ll be able to reference easily in your day-to-day life. This will help reinforce your child’s understanding of the shapes after their initial introduction.
For example, when making breakfast with your child, you could hold up a plate and ask them, “What shape is this? Do you think it’s a square or a circle?”
Other shapes, like triangles or rhombuses, may be a little harder to find hanging around. Challenge your child to find these shapes in nature. Are there any flower petals in your garden that are shaped like triangles (or an aloe vera plant hanging in their windowsill)?
Encourage your child to be creative with identifying shapes! It will help them with learning geometry in the long run.
Next, learning 3-D shapes will come after learning 2-D shapes. Like their flatter cousins, 3-D shapes are all around the world, too! Your child’s soccer ball is a sphere; the paper towel roll in the kitchen is a cylinder.
We recommend learning the basic form of these shapes and how they appear first. Then, you can use the natural 3-D shapes in your child’s environment to reinforce their learning!
Point out shapes when you see them and play a shape version of “I Spy” to practice. If your child has a set of blocks, talk about the different shapes of the blocks. Challenge them to use only one shape to build something. Then, see what they can make by using all of the shapes.
Kids also learn about spatial reasoning by discovering how to describe the shapes they see and play with. They can compare them with dimensional adjectives like “big” and “small,” or characteristics of their shape like “straight” and “curvy.”
This includes the spatial relationship between different objects, too. Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.
Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.
4) Sorting And Patterns
We categorize things in our daily lives without even realizing it. Your child probably already does this, too — they may arrange their stuffed animals or toys in a certain way. For example, they may keep farm animals separated from dinosaurs.
Sorting and patterns are related to categorical reasoning. In the same way grocery stores sort out items by their parallel uses, your child will learn how to sort things based on their characteristics and how they are the same or different from other objects.
They’ll sort objects by weight, shape, quantity, texture, color, and other traits, often without even realizing it!
It’s important to note here that sorting and counting aren’t sequential. Your child might begin sorting before they begin counting, in fact.
For instance, if you want your child to sort a bowl of fruit, you can ask them to count all of the strawberries. They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.
They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.
Once a child has learned to isolate characteristics, they can begin to identify, extend, and even create patterns. Your child will learn how to:
- Copy a pattern
- Identify the parts that repeat and continue a pattern
- Correct a mistake in a pattern
- Explain a pattern
- Create their own patterns
To encourage your child to explore patterns, take a few moments to build a pattern for them when you play together. Use whatever materials you have available and create a simple AB pattern, such as truck, car, truck, car.
Next, point to each object. Say its name aloud. Then, when you get to the end of the row, ask them what comes next. If they aren’t sure, grab the next object and put it down. Once you’ve completed one round, start at the beginning and repeat each item to reinforce the pattern.
5) The Language Of Math
Part of learning how to do math means learning how to “speak” math. We don’t mean your child will turn into C-3PO — just that they will learn how to use mathematically correct language, or how to tell a story with math terms.
This can happen in daily life. While picking at an afternoon snack, your younger child may say, “Hey! My brother has more crackers than me!” Then you might agree to “add” to the cookies on the younger child’s plate so that both plates are “equal.”
These skills may be naturally exciting for your child — they’ll feel like they’re learning how to speak “grown up!” Show them how fun it is to incorporate mathematically appropriate language into their daily speech and use it to tell stories about what’s going on around them.
Using words to describe things in their lives will help them give ownership over ideas and observations. Motivate them to think about the order of the world around them and use different words to describe them, such as:
- More than
- Less than
- Shape names
- Light or heavy
- Small or big
Mastering math language will help them in their quest to become robust mathematicians! It’ll also help them develop a strong vocabulary so they’re better prepared for kindergarten.
Basic Pre-K Math Checklist
Now that you know some of the concepts your child will be learning in pre-k math, let’s look at some of the skills they’ll build during this time.
- Rote count to 10
- Use one-to-one correspondence to count up to 10 objects and tell how many there are altogether
- Recognize basic shapes (circle, triangle, square)
- Understand the concept of quantity (more/less)
- Sort objects by one characteristic
- Understand and use directional terms, such as up, down, in, out
- Pick what object goes next in a simple pattern
While these aren’t all of the math skills your child might learn in pre-k, they will give your child a solid mathematical foundation to build on in kindergarten. And they’re all skills you can practice in fun ways!
Pre-K Math Development
As your child grows and learns, they’ll work through three phases of mathematical development: concrete, representational, and abstract. They’ll likely be in the concrete stage at the beginning of pre-k.
They’ll likely be in the concrete stage at the beginning of pre-k.
During this phase, students need hands-on activities and real-world examples to help them understand mathematical concepts. This is why math manipulatives are so crucial in the early years. It’s also essential to present math concepts in a very concrete way during this stage.
For example, if you’re teaching your child about numbers, don’t just tell them that five is more than three. Instead, show them five objects and three objects, and let them count for themselves. This will help them understand the concept of more and less.
As your child continues to learn and practice a mathematical concept, they can move into the representational phase. Here, students can count pictures or images instead of actual objects. For example, they realize that numbers can be represented by lines or drawings.
Then, they’ll be ready to try the abstract stage. At this point, children understand that numbers can be represented by symbols. They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.
They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.
The activities above will help your child to build their understanding of mathematical concepts so they can move through the different stages.
But, in pre-k, it’s important to focus on the process, not the answer. So don’t worry if your child doesn’t get the solution right away. Let them work through the problem and try to figure it out for themselves.
A strong foundation in pre-k math sets children up for success when they start kindergarten. By providing opportunities for them to explore and experiment with math, you can help them develop the skills they need to be successful in school and beyond.
9 Fun Pre-K Math Activities
Now that you’re clear on all of the exciting new math concepts your pre-kindergartener will be exposed to and what skills they’ll practice, let’s talk about some games and activities you can play at home to help your child hone them.
We’ve already discussed some math activities you can incorporate into everyday life. Now, we’re sharing our list of fun games to encourage your young learner to love math even more.
1) What Did I Do?
This game helps reinforce counting, adding, and subtracting. It’s quick to play, so it’s perfect for when you have a few extra minutes.
What You’ll Need
- Small objects (e.g., paper clips)
What To Do
Place some paper clips (or any other small objects) in your hand, and let your child count how many you have. After they’ve done this, put your hands behind your back and either add or remove some.
Next, show your child the new quantity and ask them to count how many there are now. You can ask your child questions, such as, “Did I add or take away some paper clips?” or “How many did I add or take away?”
For even more fun and learning opportunities, take turns playing the game. And when it’s your turn to guess, it’s OK to guess wrong — “I think you took away 10!… No! I added two!” This back and forth offers lots of laughs and critical thinking for your little mathematician.
Remember that because your child is in pre-k, the concepts of addition and subtraction are still new. Therefore, it’s best to keep the number of objects used in this game low (e.g., 1-10 clips) so they aren’t confused or overwhelmed.
2) Math Tic-Tac-Toe
Add a mathematical twist to the classic game of Tic-Tac-Toe!
What You’ll Need
- Paper
- Pencil
- Ruler
- Markers (or colored pencils)
What To Do
Start by dividing your sheet of paper into squares by drawing lines (three horizontal by three vertical). In traditional tic-tac-toe, you’d leave these squares blank until the game starts. Not this time.
For this version of the game, you’ll need to fill each box with dots and have your child tell you how many dots are in a box before placing their X or O in it. The first player to get three Xs or Os wins!
The Xs or Os don’t have to be in order at this point, but you can add that requirement as a challenge once your child gets the hang of playing the game.
This activity helps kids work on their counting skills while also incorporating lots of fun.
3) NumberBow
Your child will add numbers to create a beautiful rainbow in this game.
What You’ll Need
- Two dice
- Two sheets of paper
- Colored pencils (or crayons)
- Pencil
What To Do
Draw two identical rainbow-shaped boards (one on each sheet of paper) with numbered boxes on the rainbows. (You can check out this link for reference.). The aim of the game is to color the numbered boxes in.
To play, each player throws two dice, then adds the numbers from the throw together and colors in the corresponding box on their rainbow.
For example, if your child throws a three and a one, they’d need to add 3+1 and color in the “4” box. If they’ve already colored that box in, they’d have to wait for their next turn. Each player gets 10 turns to have the most colorful rainbow at the end!
While this is an effective game to help your child work on their addition skills, some children might experience difficulty adding larger numbers together (e. g., 5 and 6). If you need to help them, that’s OK!
g., 5 and 6). If you need to help them, that’s OK!
Remember that exposure and repetition are very beneficial for young learners.
4) Fill The Cup
This game can be challenging for younger children, so if it causes frustration, play other math games until your child is more comfortable with adding and counting.
What You’ll Need
- Dice
- Plastic cup
- Small objects that are easy to count (e.g., paper clips, dried beans, pebbles, etc.)
What To Do
To begin the game, players roll the dice at the same time. The number rolled indicates the number of items you can add to your cup. For example, if you roll a five, you add five dried beans. The goal for your child is to be the first one to fill their cup.
At the pre-kindergarten stage, some children might not be comfortable with the steps needed to play this game (rolling the dice, reading the number aloud, adding the items to the cup). So, before starting, take a few minutes to get them used to the process.
If you notice that it’s still too challenging, you can make it easier by choosing to roll the dice for each other. In this option, you can roll the dice and then help your child read the number and add the right amount of items to their cup.
Whichever variation you choose, this is a fun and engaging way to help children learn numbers and practice counting.
5) Stand Up, Sit Down
Kids enjoy playing this active game where they get to use their bodies and their brains! (Note: This game requires more than one child player, so it’s a great activity for siblings or to do when your child has a friend over.)
What You’ll Need
- Index cards
- Marker
What To Do
Write the numbers 1-10 on the index cards (one number per card) and hand three to each participant. Then, say a math equation (or word problem) out loud.
If the answer matches a number they’re holding, the child will stand. If they don’t have the answer, they remain seated.
For example, if the question is, “If I have three dried beans and I throw away one, how many do I have left?”, the child with “2” would then need to stand up and show their card.
The player who has the least number of cards left at the end of five rounds wins. Note: To make it easier, you can give children small items (e.g., blocks, dried beans, paper clips, etc.) to help them count.
Stand Up, Sit Down is also helpful for children learning shapes. Instead of writing numbers on the cards and handing them out, you can draw different 2-D and 3-D shapes that children learn in pre-k (as discussed above) and hand those out.
To play, someone describes a shape and the player who has that shape stands up and says what it is. For example, “If you are holding a shape that has three sides, stand up right now!”
When the child stands up, they’ll need to say that their shape is a triangle, and they get the point. In this version of the game, the player with the most points at the end wins.
Using this game allows children to learn the names and attributes of the different 2-D and 3-D shapes they get exposed to in pre-kindergarten.
6) Who Has More?
This game is perfect for helping kids understand the concepts of more and less, which are critical in early math development.
What You’ll Need
- A small bowl or container
- A teaspoon
- A handful of objects (e.g., buttons, pennies, cereal pieces, etc.)
What To Do
Place the objects in one bowl. Have your child scoop a teaspoon of them out and count them. Then, you do the same and see who got the most. That person’s the winner!
Note: Counting past 10 is difficult at this age, so you’ll want to use big enough items (such as large kidney beans) and stick to a teaspoon for scooping so your child doesn’t end up with more than 10 per spoonful.
7) Read Math Books
Help your child develop a love for math by reading math-related books together.
What You’ll Need
- A mathematical-themed book to read together (see some recommendations below)
What To Do
Grab one of the following books and snuggle up with your little one for a math-themed storytime. As you read, point out any mathematical concepts in the book.
As you read, point out any mathematical concepts in the book.
- From the Garden by Michael Dahl
- The Shape of Me and Other Stuff by Dr. Seuss
- The Button Box by Margarette S. Reid
- A Pair of Socks by Stuart J. Murphy
- The Berenstain Bears and the Spooky Old Tree by Stan and Jan Berenstain
- Pattern Fish by Trudy Harris
When you finish reading, discuss any new math concepts your child learned. You could even do a related activity or two to reinforce what they’ve learned.
8) In The Box
This game helps your child practice prepositions or direction words, like “under,” “behind,” and “in front of.” These concepts are essential for mathematical development as well as reading comprehension.
What You’ll Need
- A stuffed animal
- An empty box large enough for the animal to fit inside
What To Do
Ask your child to put the animal inside the box. If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”
If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”
Once the animal is in the box, ask them to describe where it is using prepositions. So, they might say, “The animal is in the box.”
Then, take the animal out and place it behind the box. Ask your child to describe its location again. For example, they might say, “The animal is behind the box.”
Next, let them take a turn placing the animal in, on, under, next to, etc. the box. When they’re done, you describe where it is. Continue taking turns as you practice different prepositions.
9) Number Line Race
This game helps kids with number recognition as well as one-to-one correspondence.
What You’ll Need
- Number cards (we recommend the ones from the HOMER Explore Numbers Kit)
- A die
What To Do:
Spread the cards out in numerical order, with a bit of space between each one. They should form a line on the floor, though it doesn’t need to be perfectly straight.
They should form a line on the floor, though it doesn’t need to be perfectly straight.
Have your child stand on the card with the number one on it. Hand them the die and let them roll it. Call out the number they rolled. Next, ask them to move that many numbers forward, moving from one index card to the next as they count aloud.
If they land on a number that would take them off the end of the line, they start from the beginning for their next throw (each player gets five throws). Then, it’s your turn! Start on one and see how far you can get, too.
The person to end on the card with the highest number is the winner!
Encouraging A Love Of Pre-K Math At Home
Pre-k math isn’t just reserved for pre-k classes. You can help your child explore the exciting world of pre-k math right from your home!
HOMER is always here to help and happy to be your at-home learning partner. Our Learn & Grow app offers tons of opportunities for your child to develop their pre-k math skills from conception to execution.
Our games are personalized to accommodate your child’s specific interests. They include pattern-identification games like Ribbons or shape-building games like the Castle Creator.
Your child can also explore the Shapery Bakery, where they help the cute, cuddly Tisa the Cat by sorting treats based on their shape. All that and so much more can help your child develop their pre-k math skills!
Author
How to Teach Maths to Preschoolers
- Share
Children start developing their mathematical skills while they are still babies exploring their environment and continue into their preschool years.
By the time they are learning formal mathematical concepts in the first grade, the foundation for success is already set.
Here are some tips for how to teach maths to preschoolers at school or at home by using hands-on activities and following a concrete-pictorial-abstract approach.
Early maths refers to the mathematical concepts and skills a child builds informally during the first few years. These are also called pre-maths skills or early numeracy skills.
It is essential to first develop these before trying to introduce concepts that are too advanced.
When wanting to introduce your child to maths, you may immediately think of numbers and try to teach your preschooler how to count, recognize the numbers and add or subtract them, but these are really some of the more advanced early mathematical skills.
It’s important to first understand how children learn mathematical concepts.
How Children Learn Maths: The Concrete Pictorial Abstract ApproachThe three stages of learning any mathematical concept are concrete, pictorial and abstract.
The Concrete StageIn the concrete stage, children need to physically experience a concept. They need to develop an understanding of one item by holding one block.
They need to develop an understanding of one item by holding one block.
By playing with concrete objects, children form the concept that there can be one object, multiple objects, less objects, more objects, etc.
Many mathematical processes are going on while a child is building a tower of blocks next to his friend. Concepts such as more, less, one more, not enough, how many, plenty, fewer, take away and add on are picked up.
Children compare objects and learn that a value can be attached to objects.
The Pictorial StageIn the pictorial stage, which follows the concrete stage, children are able to see a picture of objects and understand that it represents real objects.
For example, a child can look at a picture and understand that the 4 leaves represent 4 actual leaves.
Later on, a child can see a dice with 4 dots on it and assign the value 4, knowing that the dots could hypothetically represent any object.
They would then be able to add the 4 dots on one dice to the 3 dots on another and say there are 7 dots altogether.
The Abstract StageThis is the final stage of understanding a mathematical concept. It means that a child can look at a sum, e.g. 4 + 3, written in number symbols, and add them without concrete objects or pictures.
The child has matured enough to understand that the symbols 4 and 3 represent a number of objects to be added.
This post contains affiliate links for educational products that I personally recommend. If you purchase through one of them, I earn a commission at no extra cost to you. Read the terms and conditions for more details.
Are Preschoolers In the Concrete, Pictorial or Abstract Stage?Preschoolers are mostly in the concrete stage.
In fact, up until the third or fourth grade, any teacher worth their salt will still introduce a new concept in a concrete way before moving onto books or worksheets with examples to solve.
When children understand a concept concretely, it is then much easier to solve abstract problems.
This means that in the preschool years, trying to push a child to count pictures of objects or understand the value of the number symbols is premature and will cause frustration.
You may want to expose your child to numbers (e.g. playing with wooden numbers like these or magnetic number tiles) or rhymes that teach counting, but do not expect your child to understand the value of these numbers yet.
How to Teach Maths to Your Preschooler: 15 Simple ActivitiesThe best way to teach preschoolers mathematical skills is through their main medium of learning – play!
This means that during these early years children don’t need formal lessons, activity sheets and workbooks, or anything that looks more like “real work.”
Here is a list of just a few basic everyday opportunities that double up as the perfect preschool maths activities.
1.
 Play With Shapes
Play With ShapesPlaying with foam or wooden shapes familiarises your child with basic geometric shapes, as well as their properties. It teaches shape recognition.
2.
Make Shape PicturesCut basic shapes out of colored paper and make a picture out of them. Children learn to join 2D shapes together to make different forms.
Tangrams (like these) are great for making pictures with shapes.
3.
Build PuzzlesPuzzles are excellent for developing visual perception and will build a child’s understanding of geometry.
Choose good quality wooden puzzles with a wooden tray.
4.
Play With PegboardsPegboards are another great activity for building mathematical skills. They develop number concept and geometrical knowledge.
5.
Build FortsThis may not seem like a math activity, but building forts and other structures and climbing inside them is the first step in a child learning about space and shape. These early play sessions are a must!
These early play sessions are a must!
6.
Use ManipulativesThere are so many benefits of playing with blocks and that children should have opportunities to play with manipulatives daily. Also offer beads, counters or other construction toys. (read about the benefits of Lego too).
Playing with blocks is the first step in building a number concept and every child should have a good set of wooden blocks at home. This set is perfect for the classroom or home.
7.
Make Mud PiesWhen children play in the sandpit and make mud pies and other structures, they begin to use terms such as “I need to make another one,” “There are 3 cakes” or “I made one for each of us.”
8.
Learn Counting SongsCounting songs are a fun way for a young child to learn to count forwards and backwards. This is known as rote counting. They also learn about increasing and decreasing quantity in songs such as “5 Green Bottles. ”
”
9.
Play With NumbersLet your child play with foam, rubber, wooden or plastic numbers in the bath or on a magnetic board. Because they are physical objects, your child can touch them and feel their shapes.
This is far more meaningful to a young child than looking at numbers on an activity page. With time, they will naturally learn to recognize them and know how they are formed.
10.
Make Playdough NumbersPlaydough is one of the best substances out there, with some amazing benefits. Take the previous activity a step further and mould the numbers out of playdough.
This sensory activity will imprint the numbers in your child’s mind far quicker than trying to write the numbers on paper.
11.
Play With ContainersProvide containers of different sizes and shapes and let your child discover the basics of capacity while having fun in the bath or sandpit.
Baking is a great mathematical experience.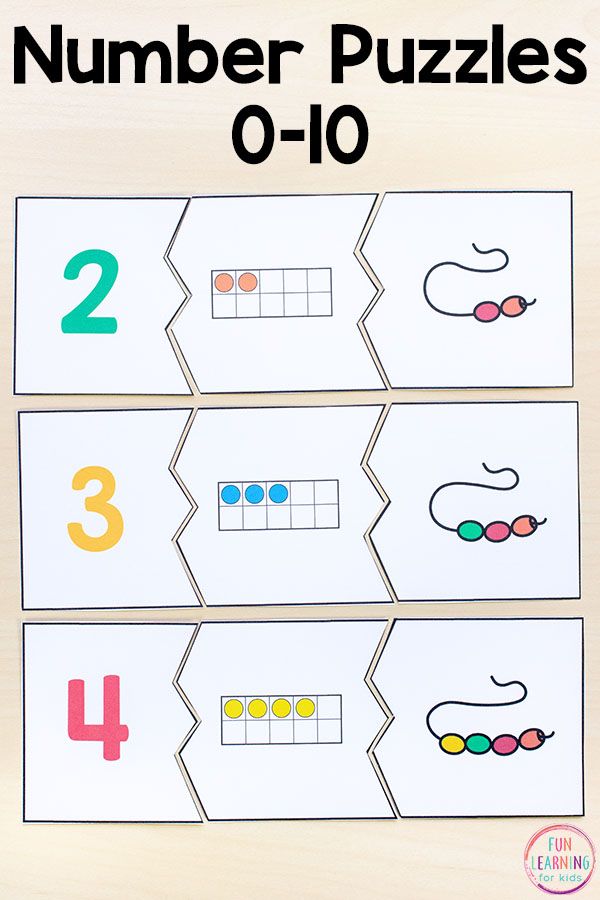 Let your child be involved in measuring the ingredients to introduce them to units of measurement and quantities.
Let your child be involved in measuring the ingredients to introduce them to units of measurement and quantities.
12.
Measure ObjectsAsk your child to measure certain objects – such as a book, table or room – using body parts such as hands or feet, and later objects, such as a block or book. Children must first learn to measure length using non-standard items before they can be introduced to standard measurements.
13.
Talk About TimeFind opportunities daily to talk about time. Use the daily routine as a starting point. Discuss concepts such as the time of day (morning, afternoon) as well as clock time (“I’ll pick you up at 12 ‘o clock when the school bell goes”).
14.
Play With ObjectsGive your child different objects and ask him to feel which are heavy or light and to compare the weight of different objects. Use a balancing scale (or make one) and place various household items on it.
15.
 Problem Solve
Problem SolveProblem solving can be the most, um… problematic, of all the maths tasks! Children in the grades often struggle to visualize problems and what they actually mean.
They often resort to guessing operations (e.g. it says more so I should add) without having any idea what the problem is actually about and how, when visualized, the solution is usually so logical.
The best way to prepare your child for problem solving is to give non-stop opportunities to actually solve real problems!
You need to train your child to develop their critical thinking skills.
You don’t necessarily need to be giving mathematical problems, just general problems that require training the brain to think, and think outside the box!
Allow many opportunities to:
- Build puzzles
- Solve brainteasers such as tangram puzzles
- Solve riddles
- Play games that require thinking
- Play with construction toys (e.
 g. figuring out how to make a bridge that doesn’t fall)
g. figuring out how to make a bridge that doesn’t fall) - Discuss problems and solutions during storytime
- Ask your child for solutions to everyday problems
As you can see, most play experiences have hidden opportunities for learning maths.
Learn to recognize them and use them to consciously teach certain skills. Remember to introduce new vocabulary and ask questions constantly during play.
Introduce words such as: heavier, lighter, longer, shorter, earlier, later, more, less, more than, less than, fewer, extra, not enough, altogether, left, another, full, empty, matching, same, different.
I hope you’ve enjoyed reading this article and have some new ideas to try!
Get FREE access to Printable Puzzles, Stories, Activity Packs and more!
Join Empowered Parents + and you’ll receive a downloadable set of printable puzzles, games and short stories, as well as the Learning Through Play Activity Pack which includes an entire year of activities for 3 to 6-year-olds.
Access is free forever.
Signing up for a free Grow account is fast and easy and will allow you to bookmark articles to read later, on this website as well as many websites worldwide that use Grow.
- Share
Basic mathematical concepts
The FEMP methodology in the system of pedagogical sciences is designed to help prepare preschool children for the perception and assimilation of mathematics - one of the most important subjects in school and the comprehensive development of the child.
The FEMP technique has a specific, purely mathematical terminology .
This is:
- set;
- number;
- counting and computing activities;
- value;
- geometric figures;
- time;
- space.
SET is a collection of objects that are considered as a single whole . The world in which a person lives is represented by a variety of sets: a lot of stars in the sky, plants, animals around him, a lot of different sounds, parts of his own body.
Sets consist of elements. The elements of the set are the objects that make up the set. It could be real objects (things, toys, drawings), as well as sounds, movements, numbers, etc. .
The elements of a set can be not only individual objects, but also their combinations . For example, when counting in pairs, triplets, tens. In these cases, the elements of the set are not one object, but two, three, ten - a set.
Thus, the set is considered as a set, a set , a collection of any objects and objects, united by a common, for all characteristic property .
Any property can be considered as belonging to some objects.
Attention!
If you need help writing a paper, we recommend that you contact professionals. Over 70,000 authors are ready to help you right now. Free corrections and improvements. Find out the value of your work.
Calculation CostGuaranteesReviews
For example, has the property of being red for some flowers, berries, cars and other objects. The property of being round is possessed by the moon, the ball, the wheels of bicycles and cars, parts of various machines and machine tools, etc.
Thus, each property is associated with a set (objects) that have this property. It is also said that the set is characterized by the given property - or the set is given by specifying the characteristic property.
Under the characteristic property of a set is meant such a property, which all objects belonging to a given set (elements of this set) have, and not a single object that does not belong to it, i.e. this item is not its element.
If some set A is specified by specifying the characteristic property P , then this is written as follows:
A = { x | P ( x )}
and reads like this: “ A is the set of all x such that x has the property P ”, or, in short, “A is the set of all 9003 having property P ". When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property.
When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property.
Thus, if the set A is given by the characteristic property P , this means that it consists of all objects that have this property, and only of them. If some a has the property P , then it belongs to the set A , and vice versa, if the object a belongs to the set A , then it has the property P .
An infinite set of objects can have some property, only a finite set can have another. Therefore, the sets are subdivided into end and end .
A finite set can be specified by direct enumeration of all its elements in an arbitrary order. For example, the set of children of a given group living on Sadovaya Street can be described using a characteristic property: { x | x - lives on Sadovaya Street) or listing all its elements in an arbitrary order: {Lena, Sasha, Vitya, Ira, Kolya}.
It is quite clear that an infinite set cannot be defined by listing all of its elements .
Mathematics mostly deals with infinite sets (numbers, points, figures and other objects), but basic mathematical ideas and logical structures can be modeled on finite sets.
Naturally, in pre-mathematical preparation usually deals with finite sets .
COUNT - first and main mathematical activity based on element-by-element comparison of finite sets.
NUMBER is the general invariable category of the set , which is an indicator of the cardinality of the set. This is just a sound designation.
Theoretical foundations for the formation of elementary mathematical concepts in preschoolers include a detailed study of only the system of natural numbers . Therefore, when we say "numbers", we mean natural numbers.
NUMBERS - a system of characters (“letters”) for writing numbers (“words”) (numerical characters). The word “digit” without qualification usually means one of the following ten characters: 0 1 2 3 4 5 6 7 8 9 (so-called “Arabic numerals”). Combinations of these numbers generate two (or more) digit numbers.
The word “digit” without qualification usually means one of the following ten characters: 0 1 2 3 4 5 6 7 8 9 (so-called “Arabic numerals”). Combinations of these numbers generate two (or more) digit numbers.
The number has 2 values : number and ordinal.
With a quantitative value of , we are interested in the number of elements in the set. We use the question HOW MUCH? and we start counting with the cardinal number ONE.
When the ordinal value is , we are interested in the place of the number among others or the ordinal number of the element in the set. The question is WHICH COUNTS? and set the direction of the account. Ordinal numbers are used, counting begins with the word FIRST.
When we talk about quantity, it does not matter the direction of the count, the object from which the count started. The final number does not change. With an ordinal count, the final number may change.
COUNTING is considered as an activity with specific elements of the set, in which a relationship is established between objects and numerals. The study of numerals and sets of objects leads to the assimilation of counting activities.
The study of numerals and sets of objects leads to the assimilation of counting activities.
CALCULATION ACTIVITY - is an activity with abstract numbers, carried out through addition and subtraction. The simple naming of numerals will not be called counting activity. The system of computational actions is formed on the basis of quantitative knowledge.
VALUE is the quality and property of an object, with the help of which we compare objects with each other and establish a quantitative characteristic of the compared objects.
The concept , the value in mathematics is considered as the main one.
A direct answer to the question “what is a quantity?” no, since the general concept of magnitude is a direct generalization of more specific concepts: length, area, volume, mass, speed, etc.
The size of an object is its relative characteristic , emphasizing the length of individual parts and determining its place among homogeneous ones. The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.
The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.
Item size, i.e. item size , determined by only based on comparison . It is impossible to say whether it is a large or a small object, it can only be compared with another.
The perception of magnitude depends on the distance from which the object is perceived, and also on the magnitude of the object with which it is compared . The farther an object is from the one who perceives it, the smaller it seems, and vice versa, the closer it is, the larger it seems.
The characteristic of the size of an object also depends on its location in space . The same object can be characterized either as high (low), or as long (short). This depends on whether it is in a horizontal or vertical position. So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short.
So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short.
The value of an item is always relative to , it is dependent on which item it is compared to . Comparing an object with a smaller one, we characterize it as a larger one, and comparing the same object with a larger one, we call it a smaller one.
So, the magnitude of a particular object is characterized by the following features : comparability, variability and relativity.
1) comparability carried out:
- overlay,
- application,
- measurement using a conditional measure,
- comparison by eye.
2) relativity - depends on the object with which we are comparing, on the distance at which we are comparing, on the location in space.
3) variability . Size is closely related to size. And size is a property of magnitude variability. Each item has its own generic purpose. It can change its dimensions without changing its essence.
GEOMETRIC FIGURE is an abstract concept with the help of which we personify all the objects around us in form.
A geometric figure is the presence of points on a plane, limited by space.
Figures are flat (circle, square, triangle, polygon…) and spatial (ball, cube, parallelepiped, cone...), which are also called geometric bodies.
GEOMETRIC BODY is a closed part of space, limited by flat and curved surfaces.
If the surface bounding the body consists of planes, then the body is called a polyhedron . These planes intersect along straight lines, which are called edges, and form the faces of the body. Each of the faces is a polygon whose sides are the edges of the polyhedron; the vertices of this polygon are called the vertices of the polyhedron.
Some polyhedra with a certain number of faces have special names : tetrahedron - tetrahedron, hexahedron - exahedron, octahedron - octahedron, dodecahedron - dodecahedron, twenty-sided - icosahedron.
What is a geometric FORM?
SHAPE is the outline, the outer appearance of the object.
Form (lat. forma - shape, appearance) – the mutual arrangement of the boundaries (contours) of the subject, object, as well as the relative position of the points of the line.
TIME is a philosophical concept that is characterized by the change of events and phenomena and the duration of their existence.
Time has properties :
- fluidity (time cannot be stopped)
- irreversibility and uniqueness
- duration .
SPACE is the quality by which relationships such as neighborhoods and distances are established.
Orientation in space implies orientation towards oneself, away from oneself, from other objects, orientation on the plane and orientation on the ground.
We will help you write any work for a similar one subject
-
Abstract
Basic mathematical concepts
From 250 rubles
-
Control job
Basic mathematical concepts
From 250 rubles
-
Coursework
Basic mathematical concepts
From 700 rubles
Get a job done or expert advice on your educational project
Find out the cost
| Lyudmila Pavlova Theory and methodology for the development of mathematical representations among preschoolers: a training manual for students of pedagogical universities Ministry of Education and Science of the Russian Federation Federal higher education 9000 " Moscow State Pedagogical University Reviewers: 9 Т. The academic discipline "Theory and Methods of Development of Mathematical Concepts in Preschool Children" occupies one of the important places in the professional training of teachers for the system of preschool education. The manual was compiled in accordance with the new Federal State Educational Standards for Higher Education of the Russian Federation. The content of the manual is based on the work program of the academic discipline, modern normative documents of higher and preschool education, on research in the field of methodological and psychological and pedagogical sciences. In the course of studying the academic discipline, students are expected to master the theoretical and didactic foundations for the development of mathematical concepts in children. Students analyze the issues of the formation of the methodology for teaching children mathematics, modern problems and concepts of mathematical education for preschoolers. They get acquainted with the content, forms and methods of forming mathematical knowledge, didactic teaching aids. Part I Content of practical classes Section 1 Theoretical and didactic foundations of the discipline “Theory and methodology for the development of mathematical representations in preschool children” Topic 1 The main mathematical concepts of discipline issues for discussion 1. 2. The concept of number, its types and functions. 3. Natural number, natural series of numbers and its properties. 4. Essence of counting and computational activity. Guidelines for the study of the topic The concepts of "set", "number", "count" are central in teaching mathematics to preschoolers. This knowledge will form the theoretical basis for understanding the content and methodology for the development of the initial mathematical concept in children. When studying the topic, G. Kantor's main provisions about the set are considered. The basic concepts of set theory are studied: a set, an element of a set, a subset, an empty set, a characteristic property or a condition for setting a set. The main types and operations on sets, etc. are considered. Then it is necessary to dwell on the main method of comparing sets - establishing a one-to-one correspondence, the concept of equivalence. When preparing for the third question, you should know that the natural number has several functions, and some of them are already familiar to children at preschool age. The question of the essence of counting and computational activity is considered, their distinctive features are specified. Assignments for independent work 1. Give 1 example for each operation on sets, drawing them with Euler-Venn circles. 2. Give examples of how children use the properties of symmetry and transitivity of equivalent sets in life situations to determine the equality of objects. 3. Give 2 examples of sets that are identical and that are equivalent but not identical. 4. Give 2 examples each of discrete, infinite, continuous, finite sets. Basic literature 1. Vereshchagin N. K., Shen A. Lectures on mathematical logic and theory of algorithms. Part 1. The Beginning of Set Theory. - 4th ed., add. - M.: MTSNMO, 2012. - 112 p. 2. Encyclopedia "Circumnavigation". – www.krugosvet.ru (Set Theory). Additional reading 1. Vilenkin N. Ya. Stories about sets. - M., 2005. 2. Kozhukhov I. B., Prokofiev A. A. Handbook of mathematics. - M., 1999. - S. 5-8, 16-24, 30-54. 3. Popov Yu. P., Pukhnachev Yu. V. Mathematics without formulas. Book. 1. -M.: KomKniga, 2010. -232 p. 4. Popov Yu. P., Pukhnachev Yu. V. Mathematics without formulas. Book. 2. -M.: Librokom, 2011. -242 p. 5. Rybnikov KK Introduction to discrete mathematics and the theory of solving extremal problems on finite sets: Textbook. 6. Stoilova LP, Freilakh NI Theoretical foundations for the formation of elementary mathematical concepts in preschoolers. - M., 1997. 7. Sporer 3. Oh, this mathematics! - M.: Pedagogy, 1985. 8. Encyclopedia for children. Maths. T. 11 / Ed. M. D. Aksenova. – M.: Avanta+, 2000. Topic 2 The development of mathematical concepts in the history of mankind Questions for discussion 1. Stages of development of ideas about number and counting in the history of mankind. 2. The history of the emergence of number systems and types of written numbering. Characteristics of the decimal number system. 3. Stages of development of the system for measuring the length of objects, mass and volume of substances. 4. The genesis of geometric representations in the history of mankind. 5. History of time measures. Guidelines for the study of the topic The practical lesson is devoted to the study of the history of the emergence and development of the basic concepts of mathematics. Numbers arose from the need to count and measure and have undergone a long path of historical development. Knowing the ways of development in human society of the activity of counting and measurement, one can more clearly imagine the significance of the knowledge that children have to master. Analyzing this historical material, it is necessary to single out the stages of development of the concept of number and counting in the history of mankind. When analyzing the issue of written numbering, one should characterize the different types of notation of numbers (hieroglyphs, cuneiform, alphabetic systems of notation of numbers, Roman and Arabic numerals), show the essence of positional (additive) and non-positional (multiplicative) number systems, get acquainted with the rules of translation from one number system to another. It is necessary to determine the advantages and distinctive features of the positional decimal number system, the concept of category, class, and the relationship between them. |


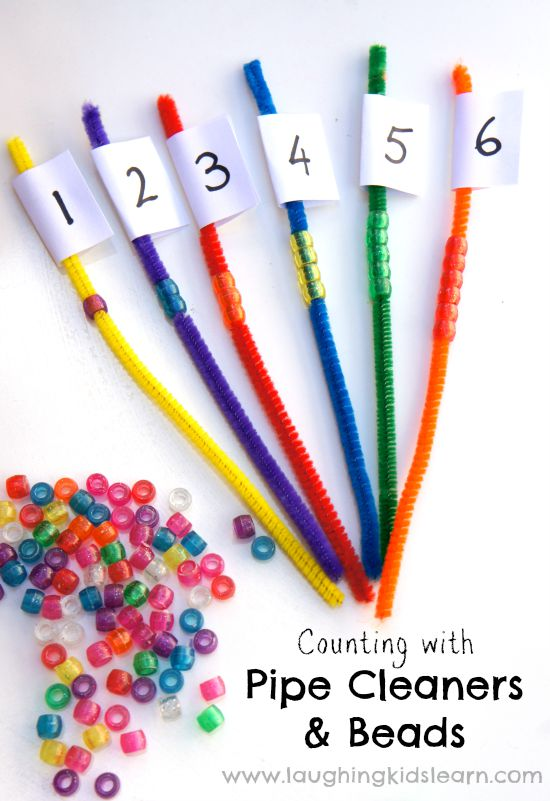 In the process of studying the discipline, independent activity of students is assumed, during which they study and analyze scientific and methodological literature, write abstracts, class notes, exercise in the development of didactic games and exercises, perform creative tasks, develop diagnostic methods, prepare consultations for educators and parents. For self-preparation for control measures, a list of exemplary questions for the test and exam, verification test tasks is proposed. Subjects of abstracts, term papers, final qualifying works are presented. Recommendations are given for their writing with approximate plans and lists of references. The implementation of practical tasks should show the level of understanding and comprehension of the studied material.
In the process of studying the discipline, independent activity of students is assumed, during which they study and analyze scientific and methodological literature, write abstracts, class notes, exercise in the development of didactic games and exercises, perform creative tasks, develop diagnostic methods, prepare consultations for educators and parents. For self-preparation for control measures, a list of exemplary questions for the test and exam, verification test tasks is proposed. Subjects of abstracts, term papers, final qualifying works are presented. Recommendations are given for their writing with approximate plans and lists of references. The implementation of practical tasks should show the level of understanding and comprehension of the studied material.  Characteristics of the concept of "set".
Characteristics of the concept of "set".  From the standpoint of the set-theoretic approach, it is necessary to give a definition of a natural number. The role of set theory for understanding how children master the idea of number and counting is analyzed. The axiomatic definition of the system of natural numbers is analyzed. To do this, it is necessary to study the system of axioms for determining the natural number of J. Peano.
From the standpoint of the set-theoretic approach, it is necessary to give a definition of a natural number. The role of set theory for understanding how children master the idea of number and counting is analyzed. The axiomatic definition of the system of natural numbers is analyzed. To do this, it is necessary to study the system of axioms for determining the natural number of J. Peano. 
 - M.: Helios ARV, 2010. - 320 p.
- M.: Helios ARV, 2010. - 320 p.