Home » Misc » Number recognition activities preschool

Number recognition activities preschool


15 Number Recognition and Counting Activities for Preschoolers

As a parent or a pre-school teacher, one of the most important skills that you would want to impart to preschool kids is to make them understand numbers and how to count. Learning numbers for toddlers can be a fun activity using games rather than something that is taught by means of rote learning.

Here are some fun and engaging number games for preschoolers that can be easily played and does a great work at making kids grasp numbers.

1. Connect the Dots

Connect the dots is one of the most fun and fastest ways of helping toddlers understand how numbers are sequenced. Connect the dots is an interesting puzzle where kids can connect dots which are numbered in ascending fashion (dot numbered 1 to 2, 2 to 3, and so on). Once completed, the dots create a picture which kids can colour later.

What you need:

You can get connect the dots puzzles in daily newspapers. There is also an option of downloading existing templates from the internet and getting them printed or you can make your own puzzle using some pen and paper.

How to do:

Mark the dots with the numbers marked over them sequentially, which forms an outline of a simple shape or a closed figure when completed. Ask the kid to connect the dots using a pencil starting sequentially from the dot numbered 1 and moving ahead to bigger numbers to complete the figure using lines to join the dots between two numbers.

2. Painting Using Numbers

In this fun and informative game, preschoolers are made to colour according to colour schemes that are coded with fixed numbers. Children are supposed to colour the picture according to the colouring code that they receive with the sketch. This game not only teaches the child to understand numbers but also to associate them with a specific colour.

What you need:

You can easily get online templates for colouring which can be directly printed out to use for this activity. You can also create your own sketches by creating a colour code using a sheet of paper, a black sketch pen, or a marker, and a box of colouring pens, pencils or crayons.

How to do:

Make your own sketch with colouring scheme made on top as to what number should be coloured with which colour. Add numbers accordingly to the sketch that you made. Ask the kid to paint the sketch according to the colours corresponding to the numbers in the figure. This activity not only helps the child with understanding numerals but also in relating to corresponding colours.

3. Abacus

An abacus is an educational toy that has been in use for thousands of years and was a predecessor to out modern-day calculator for counting things. It consists of movable beads on wires fixed to a stationary wooden or bamboo frame. An abacus can be used for learning higher arithmetic operations and it also strengthens the child’s counting skills.

What you need:

An abacus can be bought online or picked up at any educational or recreational toy store.

How to use it:

Ask the child to count the number of things in the house, like windows or chairs by recording it on the abacus. The child can do this by moving the number of beads on the abacus corresponding to the number of things being counted in the exercise. This strengthens a child’s number recognition ability and improves his counting skills.

4. Number Treasure Hunt

Children love treasure hunts! This is one of those number games for children that satiates their inquisitive and adventurous spirit and helps them learn as well. Creating a treasure hunt with numbers, where the kids have to collect numbers by exploring different places ensures that the children recognize numbers and do it in an engaging and enjoyable way.

What you need:

You will need sheets of paper that can be cut into small cards, a pair of scissors, a double-sided tape, a pen or pencil, a marker and a place to carry out the treasure hunt.

How to do:

You can cut the sheets of paper into smaller cards, on which numbers need to be written down and stuck in different places at the location where the activity is being carried out. Ask the child to explore the place and find as many numbers as possible in the time allotted.

5.Tracing Numbers Using Terracotta

This activity focuses on using the clay to trace numbers on paper. This is educational as well as recreational for the children. They learn how to write numbers, apart from reading and recognizing numbers in a fun and easy way.

What you need:

A standard packet of play dough or clay, sheets of paper, and a pencil or pen.

How to do:

Trace the outline of the numbers on the sheets of paper. Now hand out the sheets of paper to the children along with instructions to fill the outlines with clay and recite the number that was traced along with the activity.

6. Counting Cars of Different Colours

A road-trip is incomplete without car games, be it I-spy or just singing songs. Make your road-trip with children fun and informative with counting game. The objective of the game is to count the number of cars of a specific colour that you pass by.

What you need:

All you need is time and will to play the game during the journey.

How to do:

You can do this activity by choosing an uncommon colour for cars, like green or sky blue, or red. Then you can tell the child to keep his eyes out on the road for counting the number of cars of the same colour you pass by. This activity will boost colour as well as number recognition in your child and prepare him well for preschool.

7. Maze of Numbers

Create a puzzle in the form of a maze of numbers. It will help children in understanding the sequence of progression of numbers effectively. While doing this activity, children can start from the point numbered as 1 and keep following the numbers in sequence to complete the maze.

What you need:

A place to create the maze, some sheets of paper and a marker.

How to do:

Mark the different checkpoints in the maze with numbers starting from 1. Ask the kid to start at point number 1 and move ahead in sequence to reach the end of the maze by sticking to the sequence. This helps the child understand the sequence of numbers and effectively comprehend and apply it in a real-life situation.

8. Counting Using Styrofoam Cups

This activity can be carried out using multiple styrofoam cups wherein the kids can be asked to count and sort different varieties of products. This activity can improve a child’s counting as well as shape recognition and sorting skills.

What you need:

4 to 5 Styrofoam cups and different items like toffees, erasers, blocks and marbles in different quantities. You would also need a pen or a sketch pen to mark the cups as well.

How to do:

Mark the cups starting from 1 to 5. Arrange items in quantity as per to the numbers on the cups, for example, 1 toffee, 2 blocks, 3 erasers, 4 marbles and so on. Give the mixture to the child and ask them to sort the different items first. Then ask them to count the different items separately and drop them in the styrofoam cups with the numbers as per the quantity of the respective item. This is one of the most powerful counting activities for preschoolers as it teaches them to count and recognize the number corresponding to the counted quantity, apart from also teaching them effective sorting skills.

9. Counting Dice

Dice are very simple toys used in board games for children. A die has six faces, each with a different number of dots from 1 to 6. Dice can be used as powerful educational tools to teach kids how to count and recognize numbers effectively.

What you need:

You can carry out this activity with children using just a pair of dice.

How to do:

Roll a pair of dice on a table with kids and ask them to count the number of dots on both the dice separately and cumulatively to make the child adept at counting and adding numbers.

10. Matching Playing Cards

This is a fun exercise where you can ask kids to match the face value of one card with the face value of another card. This can help the child in relating and equating same numbers by counting as well as by understanding the way of writing the numerals.

What you need:

You can carry out this activity with a standard deck of playing cards.

How to do:

Ask the child to pick a card from the deck (make sure that it is a number card and not a face card). Next, you can ask her or him to find the cards equal in face value to the card selected by the child. You can repeat the same with other numerals.

11. Counting Flower Petals

This activity makes the kids go out into nature and enjoy its beauty in addition to teaching them how to count effectively in a fun manner.

What you need:

A flower with many petals.

How to do:

Take the children to a nice blossoming garden with multiple blooming flower beds. Ask them to collect a specific number of flowers. Once they collect the number of flowers allotted to them, ask them to count the total number of petals on the flowers they have collected.

12. Making Number Tower using Numeral Blocks

This exercise involves forming a tower of numerals using blocks with numbers on them in ascending order.

What you need:

You need a toy with blocks having numerals printed on them from 1 to 9.

How to do:

This exercise involves guiding the kids to build a tower made of blocks with numerals printed on each one of them. This helps the children to understand number sequencing and recognizing numerals through a classic method.

13. Chores List using Dominoes

This can be an interesting activity in kindergarten, wherein the children are asked to pick up a domino and asked to count the number of dots on it and list down chores equal to the number of dots selected for the day.

What you need:

A set of dominoes, a sheet of paper, and a pencil.

How to do:

Get a set of dominoes and ask the children to pick a domino. Next, ask them to count the number of dots on the selected domino. Once they successfully count the number of dots, ask them to list down the chores for the day on the sheet of paper, equal to the number of dots counted on the domino and complete them throughout the day. This activity imbibes basic planning skills in addition to counting skills in a preschooler’s mind.

14. Hopscotch

Hopscotch is a fun game which has squares which are numbered in ascending order and the kids playing it hop one-legged to the square on which they are supposed to land. This can be a fun way to make the kids understand numbers as well as promote outdoor activity.

What you need:

This exercise would require a space to make the hopscotch tiles and a chalk to mark the squares.

How to play:

Make the hopscotch tiles according to the usual standards with numbers marked in the ascending order on them. Call out a number and ask the kids to jump to reach the square with the number called out to them. In this way, the children learn to recognize numerals along with getting an enjoyable playing session.

15. Bowling with Numbered Plastic Bottles

This is an interesting and extremely fun activity with plastic bottles which are numbered from 1 to 10 arranged in the form of bowling pins. Kids can bowl the pins over with a softball and count the pins accordingly.

What you need:

10 empty plastic bottles, a softball, a permanent marker, a whiteboard marker, and a whiteboard.

How to do:

Mark the empty plastic bottles with numbers from 1 to 10 using the permanent marker. Arrange them in a formation similar to bowling pins. Ask the child to bowl with the softball on the marked plastic bottles. After bowling, ask the child to count and record the number of bottles that are up and the number of bottles that are down.

These were a few of the fun activities that can be carried out to creatively engage preschoolers and make them learn about numbers and reinforce number recognition in their impressionable minds.

Also Read: 15 Fun Learning Activities for Kids

23 SIMPLE Number Recognition Activities

Let’s talk about some SIMPLE ways you can teach your children about the numbers.

 

I always appreciate it when things are easy to set up, teach, and implement to my kids! I am a working mom, so I try to plan fun and simple activities, so my kids can learn!

 

Number recognition and counting in numerical order are essential skills that all of our kids need to know! It’s one of the first skills preschool work on to get them ready for kindergarten!

 

So, let’s dive into my 23 SIMPLE Number Recognition Activities For Kids to help you learn how to teach numbers to your kids!

 

Activity #1: DIY Number Cards

 

Do you order from Amazon a lot?

 

I know I do! Don’t recycle those boxes just yet! You can use them for some activities.

 

 

 

How to do this activity:

 

1. Materials you need- medium/large-sized cardboard box, sharpie, clothespins, and stickers/mini erasers.

 

2. Cut the cardboard box into a square shape, big enough to write a few numbers on it, and place the stickers or mini-erasers.

 

3. On the bottom part of the square, write 3 different numbers in sharpie and give your child a clothespin!

 

4. Put a specific amount of stickers or mini erasers on the large part of the square and have your child place the clothespin the correct amount number of corresponding items.

 

5. Got an older child? Instead of writing numbers, write tally marks or dots, so they have to use higher-level thinking skills to answer the questions.

 

Activity #2: Swat the Number

 

Wait, your kids can actually hit something, and it’s okay?

 

Yes! They will be so excited. Swat the number is an activity where your kids can use fly swatters to smack the correct number.

 

 

How to do this activity:

 

1. Materials you need- fly swatters and numbers 0-20.

 

View/ Check Amazon's Price

 

2. Set out the numbers on the floor and ask your kids to find a specific number and swat it with the fly swatter!

 

3. Another way to play is to have the kids swat a number and tell you what number they hit.

 

Simple as that!

 

Activity #3: Stamping Numbers

 

You can use letter stamps in several different ways. I have used them on paper, and I also have used it in Play-Doh.

 

 

How to do this activity:

 

1. Materials you need- art tray, Melissa and Doug alphabet+number stamps, Play-Doh and paper

 

View/Check Amazon's Price

 

2. Flatten out Play-Doh on a tray and stamp numbers on the Doh! You can put numbers in number order, practice teen numbers, and even practice some math facts since there are math symbols included in this pack.

 

3. Another way to talk about number recognition is to stamp numbers on the play-doh and ask your child to find specific numbers!

 

Activity #4: 1:1 Correspondence

 

The best thing about 1:1 correspondence is that you can use any object that you have lying around the house to do activity!

 

I do like to have a specific theme, but you don’t have to do that.

 

 

All 1:1 correspondence means is that you have a number out for your child to see, and they have to match the amount of objects to the number.

 

How to do this activity:

 

1. Materials you need- an object that you want to use as the manipulative (eggs, cars, bows, pom-poms, etc.), a marker, stamper, or moveable numbers like magnetic numbers.

 

2. Place or write the number down on a sheet of paper or the floor, depending on what you are using!

 

3. Have your child count out for each number how many objects they need to place next to each number, as you see above.

 

4. For younger kids, start with numbers 1-5. For older kids, you can do as many as you’d like!

 

Activity #5: Number Search

 

Bringing in some number play while doing a sensory activity? OH YA! Your kids will love it.

 

Many sensory bin fillers can be used for number searches, but this is the one that worked well for us!

 

 

In this bin, are colored chic peas! I made them green and red to go along with an apple tree theme from the book Chicka Chicka 1, 2, 3.

 

How to do this activity:

 

1. Materials you need-  tray, 2 bags of chic peas, liquid watercolors, FREE APPLE NUMBERS WORKSHEET, and numbers.

 

View/Check Amazon's Price

 

2. In a ziplock bag, dump a bag of chickpeas and squirt a bunch of liquid watercolor into the bag.

 

3. Zip it up and shake, shake, shake! Make sure to cover as much of the chickpeas in the color as you can.

 

4. Repeat this step if you want to do another color in a separate bag.

 

5. Line a baking sheet with parchment paper and dump the colored peas out to dry. Let them dry for at least a half-hour before play. The liquid watercolors dry pretty quickly!

 

6. Once dry, dump them into a medium-sized container and hide numbers throughout the chic peas.

 

7. Download my Apple Numbers for the kids to match up numbers when they find them!

 

Don’t have the book? You don’t have to go out and buy it, have your little one listen to it online! 

RELATED: THE BEST 22 SENSORY BIN IDEAS FOR KIDS

 

Activity #6: Geoboard Number Building

 

Does anyone remember using these boards when you were younger? I remember teachers busting these out every now and then for us to use!

 

You can create numbers, letters, make sight words with multiple boards, or just have fun and create whatever design you want!

 

 

Plus, this is a fine motor activity, so it works on increasing those little muscles to be able to do critical everyday tasks like zipping up their coats or buttoning their shirts.

 

How to do this activity:

 

1. Materials you need- geoboards (they come with the rubber bands)

 

View/ Check Amazon's Price

 

2. Encourage your child to try to make specific numbers; some will be easier than others due to the curves. However, you can still create those numbers; they just will look more box-like.

 

3. If your child can’t do it on their own, you can create the number and work on number recognition skills by asking what number it is.

 

4. For older kids, you can even create addition and subtraction problems using these boards!

 

 

Activity #7: Number Line

 

Kids LOVE sticky notes. I know, right? Sometimes, it’s the simplest things.

 

While I was setting this activity up, my oldest was making letters to all of us on sticky notes and hiding them! I’m telling you, they love these things.

 

How to do this activity:

 

1. Materials you need- post-it and sharpie

 

View/Check Amazon's Price

 

2. On the post-its, write as many numbers as you want to practice with your kids. My recommendation would be to first start by writing numbers 1-10. For older kids, you can write 1-20.

 

3. Place the post-it’s on the wall in a mixed-up order. Have your child place them in numerical order on a different wall, so they don’t get confused by all the different sticky notes!

 

4. For older children, make this more challenging by placing some numbers on the wall and ask them to find the missing numbers and fill them in!

 

Activity #8: Egg Carton Counting

 

It’s actually near Easter time while I’m writing this, but this activity can be done at any time!

 

 

My kids are obsessed with plastic eggs. They love putting things inside them, even when it’s not Easter time, especially if candy is involved.

 

How to do this activity:

 

1. Materials you need- egg carton, plastic eggs and candy (jelly beans/M&M’s)

 

2. Write the numbers on the plastic egg with a sharpie- if you use a dry erase marker, it will come off when your child touches it!

 

3. You can write the numbers on the bottom of the carton as well so they can match it up or you don’t have to! Have your child match up the number egg to the place it should go in the egg carton in numerical order.

 

4. To extend this activity, you can have your child place the correct amount of candies to match the number in the egg! They will enjoy this part; sometimes we need to bring in a little something extra, don’t we?

 

Activity #9: Tactile Sticks 

 

The possibilities are endless here! I love doing holiday-themed things, and my favorite one that I have done recently is my Halloween themed tactile sticks.

 

 

These sticks can be done with googly eyes, small pom poms, glitter glue dots, or even small hair ties!

 

View/ Check Amazons Price

 

How to do this activity:

 

1. Materials you need- popsicle sticks, glue, and whatever object of your choice listed above!

 

2. On each popsicle stick, write a number 1-10.

 

3. Have your little one say what number is on the stick, then count out how many pieces of supplies that they need to glue on each stick.  This works on number recognition and numerical counting.

 

4. Remember, a little dot does a lot 🙂 So, a small amount of glue for each object is perfect!

 

Activity #10: Bath Number Puzzle

 

Bath crayons are the BEST!

 

It’s a way for the kids to draw on the walls of your house and not ruin anything! If I could insert an emoji here, the double high five’s would be right here!

 

 

For most kids, bath time is a lot of fun, but sometimes kids don’t like it. This could be a way to help excite your kids at bath time while learning.

 

How to do this activity:

 

1. Materials you need- bath crayons and bath foam numbers

 

View/Check Amazons Price

 

2. With a bath crayon, trace the numbers you want to teach/ review on the bath wall.

 

3. Have your child say the number if they can before they match up the foam number or just attempt to match the correct number with the shape that’s on the wall!

 

4. With an older child, have them trace the numbers to get some handwriting practice! Or, you can even write a few numbers on the wall and have them find the missing numbers to challenge them.

 

Activity #11: LEGO Block Count

 

Your kids will be so excited to count when LEGO blocks are involved! The best thing about this activity is that it can be toddlers and for early elementary-aged students!

 

 

How to do this activity:

 

1. Materials you need- LEGO blocks and a dry erase marker

 

View/Check Amazons Price

 

2. With toddlers, I would write numbers 1-10 on the blocks and have them stack them in order. For preschoolers, you can do 1-20.

 

3. To challenge early elementary students, you can practice skip counting by 2’s, 5’s, or 10’s!

 

Activity #12: Pipe Cleaner Count

 

I started doing some fine motor activities with my son, he’s 2, and he just fell in LOVE with doing these sorts of activities.

 

I swear this kid is going to be some sort of engineer or something.  Your kids will enjoy this learning challenge.

 

 

How to do this activity:

 

1. Materials you need- pipe cleaners, beads, paper, marker, and a flat surface like an art tray!

 

(Picture of tray)

 

2. On small pieces of paper, write how many numbers that you can fit on your flat surface that you want your child to practice.

 

3. Tape down a pipe cleaner underneath each number and have a bowl of beads ready for your child. (Choking hazard: make sure your child is old enough to do this activity so that they won’t put the beads into their mouth).

 

4. Have your child string the amount of beads associated with the number above the pipe cleaner. Little ones will need help counting out the correct number, but they can try to string the beads on their own!

 

5. Have the older kids try to do this on their own without assistance! You can even have them make a specific pattern with colors to make this a bit more challenging for them.

 

Activity #13: Do-A-Dot Number Painting

 

Do-A-Dots are one of our favorite supplies around here!

 

If you haven’t used them, you are missing out! It’s a way to paint with your kids that they won’t get messy.

 

 

GRAB YOU FREE Do-A-Dot Numbers 1-10 WORKSHEET HERE!

 

How to do this activity:

 

1. Materials you need- My Do-A-Dot Numbers 1-10 FREE Worksheet and Do-A-Dot painters

 

View/Check Amazons Price

 

2. Download and print my number printable and ask your child to name the specific number that you are focusing on. If they don’t know it, that’s okay! Tell them the number and have them try to use the painters to fill in the dot.

 

3. The numbers around the dot are there to help your child differentiate between numbers. They should focus on painting the number in the circles that go along with the big number on the page.

 

Activity #14: Pom Pom Number Matching

 

It’s always nice to have an activity that you know you can pull off using what you have at home!

 

It always makes things more complicated if you have to order something or run out to the store. I always tend to put those activities on the back burner, which sometimes means I even forget about them.

 

 

This is a fine motor activity that builds up small muscles in your children’s hands so they can do daily activities like write their name, tie their shoes, and zip their jackets!

 

How to do this activity:

 

1. Materials you need- cupcake tin, 12 cupcake holders, a marker, pom-poms, and kid-friendly tweezers.

 

View/ Check Amazon's Price

 

2. On the bottom of 12 cupcake liners, write the numbers 1-12 and place them inside the circles in numerical order.

 

3. In a bowl, place the pom-poms in and show your child how to use the kid-friendly tweezers. Have them pick up a pom-pom and place it in the first liner. Explain that depending on what number is on the bottom of the liner, that’s how many they should put in.

 

Activity #15: Sensory Bag Game

 

If you have read some of my other content, you know how much I enjoy a good sensory activity.

 

This sensory game is so much fun, plus it’s a great way to work on number recognition!

 

 

How to do this activity:

 

1. Materials you need- 2 bottles of hair gel, a large ziplock bag, sharpie, food coloring, and plastic coin.

 

2. On the bag, write whatever numbers you want to practice with your kids (1-10, 11-20, 100’s, 1,000’s).

 

3. In the ziplock bag, squirt both hair gels packs inside, drop several drops of food coloring in, place the coin in, and zip the bag shut.

 

4. Massage the bag, so the food coloring and hair gel get all over the bag!

 

5. Ask your child to find a specific number. They should move to the coin through the bag over to that number! Repeat this until you have gone through all the numbers!

Activity #16: Giant Number Matching Game

 

I did this game with the alphabet, and it was such a hit I decided to try it with numbers!

 

This is such an easy set-up, and I always have paper plates on hand, which makes things easier since it’s already at home!

 

 

How to do this activity:

 

1. Materials you need- paper plates and marker

 

2. On paper plates, write which numbers you want to work on with your kids. Make sure you write 2 of the same number since it’s a match game.

 

3. Spread them out all around the ground, making sure that the pairs aren’t right next to each other!

 

4. Have your kids flip one plate over, look at the number, they should say it then flip another plate over to see the number. If it’s a match, they can leave both plates flipped over. If it wasn’t a match, they need to turn it back to its original side and try again.

 

5. Play until all the plates are flipped over, and all the matches are found!

 

Activity #17: Tray Number Writing

 

Did someone say sprinkles!?

 

Any child will be engaged in an activity where sprinkles are involved. We used confetti sprinkles, which is great because they are a little larger.

 

 

This is an excellent pre-writing activity! Especially if your little one struggles with handwriting with a pencil, this is a great alternative to get some practice in to give them confidence!

 

How to do this activity:

 

1.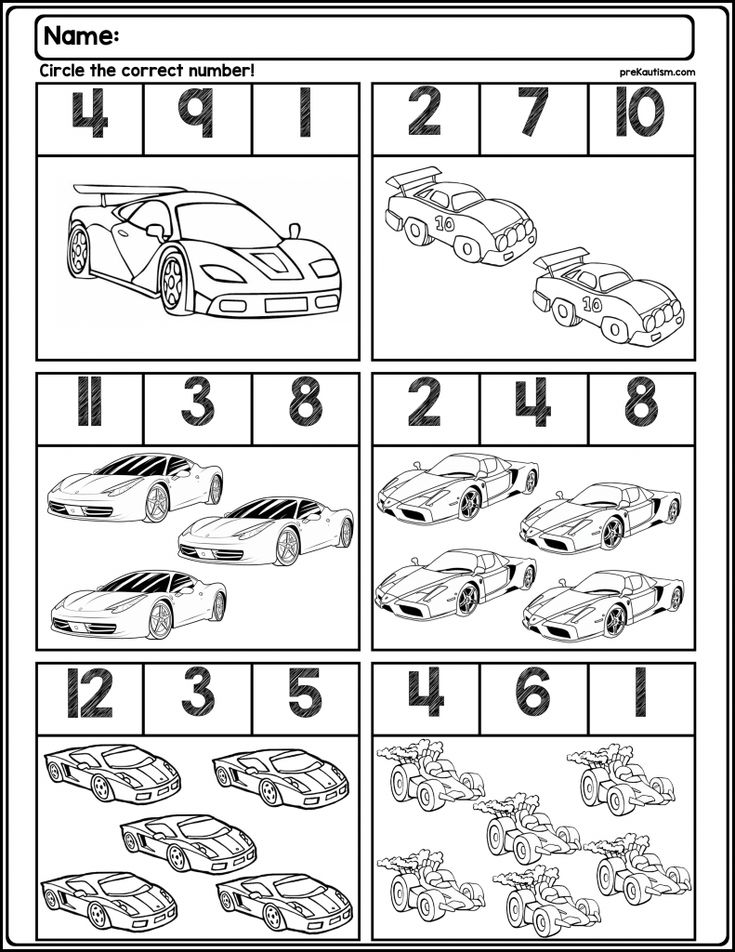 Materials you need-  MY FREE TRACIBLE NUMBER CARDS DOWNLOAD HERE, a flat tray, sprinkles, and a paintbrush

 

2. On a tray, dump out the container of sprinkles. Then, place the tracing card of your choice on the front of the tray.

 

3. Before your child attempts to write the number with their paintbrush, they can use their finger to trace the number, so they get the hang of the shape of the number.

 

4. Then they can use the paintbrush to copy the number shape on the sprinkles!

 

RELATED: 15 FUN HANDWRITING ACTIVITIES FOR PRESCHOOLERS

 

Activity #18: Ice Cream Counting Sensory Bin

 

This is one of my FAVORITE sensory bins that I have ever done.

 

The ice cream bin can be used as an educational bin because you can ask your child to put a specific amount of cotton balls+ sprinkles into a bowl.

 

 

How to do this activity:

 

1. Materials you need- medium-sized container, cotton balls, small colored pom-poms, ice cream bowls/plastic cones, and scoops! We also have ice cream set from Melissa and Doug, that’s where I got the little menu and the 4 scoops that you see in front of the bin.

 

View/Check Price

 

2. In the medium-sized bin, cover the entire tray in cotton balls! Add in some of the small pom poms to be the sprinkles for the ice cream! Add in all of the other little things like the bowls and scoops.

 

3. Help your child learn with this bin by asking them to put a certain number of cotton balls and sprinkles into the bowls, work on addition skills by getting two bowls out to add small amounts together and work on color recognition by asking for specific colors of sprinkles!

 

4. Have an older child at home? Challenge them by doing my FREE ICE CREAM ADDITION WORKSHEET!

 

Kids can work on adding small numbers together to see how many scoops of ice cream need to end up on the last cone! You can even make the worksheet come to life by adding in colored pom-poms to the bin instead of cotton balls! 

 

Activity #19: Puzzle Work

 

The reason why my children were able to learn their numbers was because of our daily practice with the Melissa and Doug number puzzle.

 

Seriously, all it takes is 5 minutes each day, and you will see considerable improvements in their number recognition.

 

View/ Check Amazon's Price

 

Being able to manipulate the number and have a place for it to go helps your child remember the number better than doing other activities, in my opinion.

 

How to do this activity:

 

1. Materials you need- Number puzzle (I recommend the one above because it has numbers 1-20, it can be used for longer and is only a few more bucks than 0-10).

 

2. Focus on one or two numbers a day; once they have mastered those, you can move on to another few.

 

3. I would recommend starting with numbers 1-10 and moving onto the teens when they comprehend the first 10.

 

4. Every day for at least 5 minutes, practice the dew numbers that you are focusing on. Ask them several times to point to the numbers you are saying and place it in the spot where it should go.

 

5. Tip: If your child gets distracted with all the other pieces, hide them so they aren’t a distraction, and they can focus on the few they need to learn.

 

RELATED: HOW TO TEACH YOU TODDLER NUMBERS (9 SIMPLE STRATEGIES)

 

Activity #20: Cupcake Play-Doh Counting

 

Play-Doh cupcakes?! This is sure to excite your kiddos in wanting to play with numbers.

 

 

How to do this activity:

 

1. Materials you need- Play-Doh, silicone cupcake holders, magnetic/ play numbers, + candles

 

View/Check Amazon's Price

 

2. Have your child roll up as many Play-Doh balls as you have silicone holders out for. I used 6 just because that’s what fit on my tray, but feel free to use more or less!

 

3. You can also work on color matching by using the corresponding color Doh with the holders!

 

4. In numerical order, place numbers by the silicone holders, and your little one can start placing the corresponding number of candles in the Play-Doh.

 

Activity #21: Egg Matching Activity

 

Yes, there are several plastic egg activities on this list, they can be used for so many educational activities, it’s fantastic!

 

This is a subitizing activity, so if you have older ones, this is GREAT for them.

 

 

FACT: Everything always looks more enticing when it’s placed in a sensory bin :).

 

How to do this activity:

 

1. Materials you need- medium-sized container, Easter grass, and plastic eggs

 

View/Check Amazon's Price

 

2. In the container, put the Easter grass inside.

 

3. On the plastic Easter eggs, write a number on the top half and on the bottom half write either tally marks or dots that correspond to the number you wrote on the top half.

 

4. I would suggest doing numbers that your child knows since this is a subitizing activity and is a bit more challenging.

 

5. Break the eggs apart and hide them throughout the Easter grass in the bin.

 

6. Have your child try to connect the right egg pieces together! Help them if they are having a hard time with this by showing them how to count using tally marks or dots!

 

Activity #22: Dot Sticker Numbers

 

Dot stickers are one of my MUST-HAVE supplies to have on hand at home.

 

Why? Because they are so versatile! I have an endless amount of activity that they can be used for, which is nice.

 

 

Anyone’s mind go to garage sale stickers when they see these? My family always had garage sales growing up, and that’s all I can think of when we use these stickers!

 

How to do this activity:

 

1. Materials you need- butcher paper, dot stickers, painter’s tape, and a marker

 

View/ Check Amazons Price

 

2. On a piece of butcher paper, write the numbers that you want, so it covers most of the paper.

 

3. Have your children peel off the stickers if they can and place them on the lines of the letters. Try to encourage them to put the stickers on the lines of the letter right next to each other.

 

4. Make sure to talk about each number as you get to it, and when the stickers are all placed on, you can repeat the numbers.

 

5. Challenge older children by having them count how many stickers that it took for them to cover up each number!

 

This is an excellent fine motor activity as well!

 

RELATED: My 10 FAVORITE Learning Supplies For Kid’s Activities

 

Activity #23: Number Hopscotch

 

Active learning is my favorite kind of learning!

 

I am a physical education teacher, and it just makes me so happy to see my kids working on some gross motor or locomotor activities while learning.

 

 

This activity can be used as a hopscotch game or a throwing game! Win, win, right? 

 

How to do this activity:

 

1. Materials you need- painter’s tape and bean bags

 

View/ Check Amazons Price

 

2. With painter’s tape, make a hopscotch set-up as you see above. I wrote the numbers 1-10 in each of the squares, but you can also practice even numbers, odd numbers, or larger numbers!

 

3. You can have your kids play with the hopscotch course, and they can say the numbers that they land on when they get to them!

 

4. Make this into a learning game by getting out some beanbags and work on some throwing! Have your kids try to throw a beanbag and have it land on one of the numbers. Have them say the number it lands on!

 

5. Got older ones? Work on addition by having them throw two beanbags and add the numbers that they landed on together!

 

Final Thoughts and Conclusions

 

Teaching your kids at home can be simple with these 23 number activities! Making learning fun makes it more memorable for your kids, which will help them understand the content better.

 

These activities are great for toddlers, preschoolers, and can even be modified to challenge early elementary students! Make sure to read through my post thoroughly to see how you can challenge each age level!

 

I’d love to hear about some activities that you do at home or school with your kids! Please leave a comment below to share them with our community!

 

Happy Learning!

Counting in Grade 1

Number assignments for preschoolers don't have to be boring and just worksheets, make them fun so your preschooler loves math!

I love math. I'm a nerd, yes. But I love everything that has to do with numbers.

I really hope that I can pass this on to my children by studying numbers and finding them interesting and not a chore.

When I show the numbers, the kids scream excitedly, counting how many things.

Since I am a great mathematician, I was looking for simple and fun activities for preschoolers.

Number recognition for preschoolers

ID numbers can be a learning experience for preschoolers (and younger!). Many of the ABC recognition operations can also be adjusted for numbers.

My kids love these 12 numbers for preschoolers to learn numbers.

  1. Turn your number into sensory art - perfect for the 100th day of school!
  2. Go hunting for numbers and match it with the same number!
  3. Follow the number from start to finish in the maze.
  4. Trace numbers, really big!
  5. A small family task created a parking lot with numbers.
  6. Clap! Find the number and reveal it!
  7. Find and match playing cards.
  8. Have a practice goal with water balloons and numbers
  9. Make art! Make this paint according to the canvas number.
  10. Use stickers and printed number cards to play hide-and-seek from dad's teacher.
  11. Draw and color numbers with q-cues, such as "Toddler in play"!
  12. Clip and match with giant numbers!
NUMBER RECOGNIZATION ACTIVITIES

Sensory Sand

Numbered Heart Hunt
HANDS AS WE GROW

Follow the Labyrinth number
Hands, as we grow

trace of giant numbers
Room parking
Small family mission
9000 9000 9005, 4005 Clopes with accounts and REC

Matching playing cards

How many colors
Hide and look for numbers
LEARN MOM AND DAD

BABY AT THE PLAY

Number Recognition
YOU GOT THIS MATH

Activity counting for preschoolers

Learning that there is a sequence of numbers and what will happen next. Try these 18 numbers to help preschoolers learn to count.

  1. Connect the dots! A simple occupation of the past that reinforces the order of numbers.
  2. Turn the box into a number puzzle!
  3. Create a maze of numbers to drive through. Can they calculate their way to the end?
  4. Stacking boxes and counting how high you can go!
  5. Make a craft out of several pieces. Let your child do the math!
  6. Count cars of a certain color while on the road, floor or van, depending on their interests!
  7. Create an educational game with ABC swearing and number blocks. Select the block number and hammer the corresponding time with a hammer on the corresponding number mat!
  8. Have your child experiment and measure how much something holds! How many cups fit?
  9. Make puzzles with a picture. Label the puzzle sections in numerical order.
  10. Use friendly animal crackers to practice counting and number recognition, how can I teach my child
  11. Measure objects (or yourself!) and count how big they are from the Imagination Tree
  12. Count the objects around the house. "No time for flash cards" wants to know "How many doors do you have?"
  13. Play any board game or make your own!
  14. Count with Legos! Pencil PLAY likes to mark paper with numbers and count legosuckles next to it.
  15. Snack time! Use cube and fruit snacks and play until you've eaten them all, just like on the Kids Activity Blog.
  16. Bring a bag of beans up the stairs, number them!
PRESCHOOL ACTIVITY COUNTER
Connect the dots

Complicated box add the score correctly in order
Hands, how we grow

Calculation of cars
Hands, how we grow

numbers + letters of the game
Hands, as we grow

Measurement and training
hands, as WE GROW

Number Puzzles
GROW IN PREC

Animal Burglar Counting
I CAN TEACH MY CHILD

Hand Measurement50053

Imagination tree

Counts around the house
Small Family Fun Fish

Counting with LEGO
Fresh pencil
9000 9000
Calculate and study mathematical snacks
9006 on the Stairs
HANDS AS WE GROW

Make pizza Count

HANDS AS WE GROW

Individual lessons for preschoolers

Knowing your numbers is one thing, but knowing how to count is another. But being able to put them in the context that each one has meaning is done with a one-to-one correspondence.

I love these 12 exercises that help preschoolers with one-on-one correspondence.

  1. Go to nature and explore flowers. Count and compare flower petals!
  2. Hunt for the number and match it with the corresponding dots.
  3. Build block towers on the mat with the correct number of blocks!
  4. Ignite your child's interest with their interests! An agricultural approach to loading grain bins with the appropriate amount of "grain" pieces.
  5. Have a game of newspaper throwing and count newspaper balls, or how much you earn or miss!
  6. Do something in the kitchen together or do an experiment and have your child measure and count.
  7. Sort objects by color and count how many of each you have!
  8. Fill the dump truck with objects (like dominoes!) and count how many you can fit in them, like the Inspiration Lab.
  9. Rate first for fun, then count the item.
  10. Run a backyard counting race and collect dandelions along the way!
  11. Roll a die (or two!) and practice one-on-one correspondence while the kids build block towers.
  12. Use bones and small items (such as pompoms or corn kernels), count them and fill the tray.
PRIVATE EDUCATION
Count and after another
HANDS AS WE GROW

Measure, count and experiment in the kitchen
HANDS AS WE GROW

Toy sorting and counting color
Hands, how we grow

dump truck
of inspiration laboratories

Assess and consider

calculation and counting

There are also ready-made kits for learning numbers in the game, we advise you to look at:

You can also look at other kits with learning to count other numbers in the game.

Learn number 1 Learn number 2

Learning the number 3

Learning the number 4

Learning the number 5

Learning the number 6

Learning the number 7

Learning the number 8

Learning the number 9

Are you actively working on numbers and counting with your child? Share your favorite activities!

A visual introduction to neural networks using the example of digit recognition

With the help of many animations, a visual introduction to the learning process of a neural network is given using the example of a digit recognition task and a perceptron model.

Articles on the topic of what artificial intelligence is have been written for a long time. And here is the mathematical side of the coin :)

We continue the series of first-class illustrative courses 3Blue1Brown (see our previous reviews on linear algebra and mathematical analysis) with a course on neural networks.

The first video is devoted to the structure of the components of the neural network, the second - to its training, the third - to the algorithm of this process. As a task for training, the classical task of recognizing numbers written by hand was taken.

A multilayer perceptron is considered in detail - a basic (but already quite complex) model for understanding any more modern versions of neural networks.

The purpose of the first video is to show what a neural network is. Using the example of the problem of digit recognition, the structure of the components of the neural network is visualized. The video has Russian subtitles.

Statement of the problem of digit recognition

Imagine you have the number 3, depicted in an extremely low resolution of 28x28 pixels. Your brain can easily recognize this number.

From a computational standpoint, it's amazing how easy the brain is to do this, given that the exact arrangement of the pixels varies greatly from one image to the next. Something in our visual cortex decides that all threes, no matter how they are depicted, represent the same entity. Therefore, the task of recognizing numbers in this context is perceived as simple.

But if you were asked to write a program that takes as input an image of any number in the form of an array of 28x28 pixels and outputs the "entity" itself - a number from 0 to 9, then this task would no longer seem simple.

As the name suggests, the device of the neural network is somewhat close to the device of the neural network of the brain. For now, for simplicity, we will imagine that in the mathematical sense, in neural networks, neurons are understood as a certain container containing a number from zero to one.

Activation of neurons. Neural network layers

Since our grid consists of 28x28=784 pixels, let there be 784 neurons containing different numbers from 0 to 1: the closer the pixel is to white, the closer the corresponding number is to one. These numbers filling the grid will be called activations of neurons. You can imagine this as if the neuron lights up like a light bulb when it contains a number near 1 and goes out when the number is close to 0.

The described 784 neurons form the first layer of the neural network. The last layer contains 10 neurons, each corresponding to one of the ten digits. In these numbers, activation is also a number from zero to one, reflecting how confident the system is that the input image contains the corresponding digit.

There are also a couple of middle layers, called hidden layers, which we'll get to shortly. The choice of the number of hidden layers and the neurons they contain is arbitrary (we chose 2 layers of 16 neurons each), but usually they are chosen from certain ideas about the task being solved by the neural network.

The principle of the neural network is that the activation in one layer determines the activation in the next. Being excited, a certain group of neurons causes the excitation of another group. If we pass the trained neural network to the first layer the activation values ​​according to the brightness of each pixel of the image, the chain of activations from one layer of the neural network to the next will lead to the preferential activation of one of the neurons of the last layer corresponding to the recognized digit - the choice of the neural network.

Purpose of hidden layers

Before delving into the mathematics of how one layer affects the next, how learning occurs and how the neural network solves the problem of recognizing numbers, we will discuss why such a layered structure can act intelligently at all. What do intermediate layers do between input and output layers?

Figure Image Layer

In the process of digit recognition, we bring the various components together. For example, a nine consists of a circle on top and a line on the right. The figure eight also has a circle at the top, but instead of a line on the right, it has a paired circle at the bottom. The four can be represented as three lines connected in a certain way. And so on.

In the idealized case, one would expect each neuron from the second layer to correspond to one of these components. And, for example, when you feed an image with a circle at the top to the neural network, there is a certain neuron whose activation will become closer to one. Thus, the transition from the second hidden layer to the output corresponds to the knowledge of which set of components corresponds to which digit.

Layer of images of structural units

The circle recognition task can also be divided into subtasks. For example, to recognize various small faces from which it is formed. Likewise, a long vertical line can be thought of as a pattern connecting several smaller pieces. Thus, it can be hoped that each neuron from the first hidden layer of the neural network performs the operation of recognizing these small edges.

Thus entered image leads to the activation of certain neurons of the first hidden layer, defining characteristic small pieces, these neurons in turn activate larger shapes, as a result activating the neuron of the output layer associated with a certain number.

Whether or not the neural network will act this way is another matter, which you will return to when discussing the learning process of the network. However, this can serve as a guide for us, a kind of goal of such a layered structure.

On the other hand, such determination of edges and patterns is useful not only in the problem of digit recognition, but also in the problem of pattern detection in general.

And not only for recognition of numbers and images, but also for other intellectual tasks that can be divided into layers of abstraction. For example, for speech recognition, individual sounds, syllables, words, then phrases, more abstract thoughts, etc. are extracted from raw audio.

Determining the recognition area

To be specific, let's now imagine that the goal of a single neuron in the first hidden layer is to determine whether the picture contains a face in the area marked in the figure.

The first question is: what settings should the neural network have in order to be able to detect this pattern or any other pixel pattern.

Let's assign a numerical weight w i to each connection between our neuron and the neuron from the input layer. Then we take all the activations from the first layer and calculate their weighted sum according to these weights.

Since the number of weights is the same as the number of activations, they can also be mapped to a similar grid. We will denote positive weights with green pixels, and negative weights with red pixels. The brightness of the pixel will correspond to the absolute value of the weight.

Now, if we set all weights to zero except for the pixels that match our pattern, then the weighted sum is the sum of the activation values ​​of the pixels in the region of interest.

If you want to determine if there is an edge, you can add red weight faces around the green weight rectangle, corresponding to negative weights. Then the weighted sum for this area will be maximum when the average pixels of the image in this area are brighter, and the surrounding pixels are darker.

Activation scaling up to the interval [0, 1]

By calculating such a weighted sum, you can get any number in a wide range of values. In order for it to fall within the required range of activations from 0 to 1, it is reasonable to use a function that would “compress” the entire range to the interval [0, 1].

The sigmoid logistic function is often used for this scaling. The greater the absolute value of the negative input number, the closer the sigmoid output value is to zero. The larger the value of the positive input number, the closer the value of the function is to one.

Thus, neuron activation is essentially a measure of how positive the corresponding weighted sum is. To prevent the neuron from firing at small positive numbers, you can add a negative number to the weighted sum - a bias, which determines how large the weighted sum should be in order to activate the neuron.

So far we've only talked about one neuron. Each neuron from the first hidden layer is connected to all 784 pixel neurons of the first layer. And each of these 784 compounds will have a weight associated with it. Also, each of the neurons in the first hidden layer has a shift associated with it, which is added to the weighted sum before this value is "compressed" by the sigmoid. Thus, for the first hidden layer, there are 784x16 weights and 16 shifts.

Connections between other layers also contain the weights and offsets associated with them. Thus, for the given example, about 13 thousand weights and shifts that determine the behavior of the neural network act as adjustable parameters.

To train a neural network to recognize numbers means to force the computer to find the correct values ​​for all these numbers in such a way that it solves the problem. Imagine adjusting all those weights and manually shifting. This is one of the most effective arguments to interpret the neural network as a black box - it is almost impossible to mentally track the joint behavior of all parameters.

Description of a neural network in terms of linear algebra

Let's discuss a compact way of mathematical representation of neural network connections. Combine all activations of the first layer into a column vector. We combine all the weights into a matrix, each row of which describes the connections between the neurons of one layer with a specific neuron of the next (in case of difficulty, see the linear algebra course we described). As a result of multiplying the matrix by the vector, we obtain a vector corresponding to the weighted sums of activations of the first layer. We add the matrix product with the shift vector and wrap the sigmoid function to scale the ranges of values. As a result, we get a column of corresponding activations.

Obviously, instead of columns and matrices, as is customary in linear algebra, one can use their short notation. This makes the corresponding code both simpler and faster, since the machine learning libraries are optimized for vector computing.

Neuronal activation clarification

It's time to refine the simplification we started with. Neurons correspond not just to numbers - activations, but to activation functions that take values ​​from all neurons of the previous layer and calculate output values ​​in the range from 0 to 1.

In fact, the entire neural network is one large learning-adjustable function with 13,000 parameters that takes 784 input values ​​and gives the probability that the image corresponds to one of the ten digits intended for recognition. However, despite its complexity, this is just a function, and in a sense it is logical that it looks complicated, because if it were simpler, this function would not be able to solve the problem of recognizing digits.

As a supplement, let's discuss which activation functions are currently used to program neural networks.

Addition: a little about the activation functions. Comparison of the sigmoid and ReLU

Let us briefly touch on the topic of functions used to "compress" the interval of activation values. The sigmoid function is an example that emulates biological neurons and was used in early work on neural networks, but the simpler ReLU function is now more commonly used to facilitate neural network training.

The ReLU function corresponds to the biological analogy that neurons may or may not be active. If a certain threshold is passed, then the function is triggered, and if it is not passed, then the neuron simply remains inactive, with an activation equal to zero.

It turned out that for deep multilayer networks, the ReLU function works very well and it often makes no sense to use the more complex sigmoid function to calculate.

The question arises: how does the network described in the first lesson find the appropriate weights and shifts only from the received data? This is what the second lesson is about.

In general, the algorithm is to show the neural network a set of training data representing pairs of images of handwritten numbers and their abstract mathematical representations.

In general terms

As a result of training, the neural network should correctly distinguish numbers from previously unrepresented test data. Accordingly, the ratio of the number of acts of correct recognition of digits to the number of elements of the test sample can be used as a test for training the neural network.

Where does training data come from? The problem under consideration is very common, and to solve it, a large MNIST database was created, consisting of 60 thousand labeled data and 10 thousand test images.

Cost function

Conceptually, the task of training a neural network is reduced to finding the minimum of a certain function - the cost function. Let's describe what it is.

As you remember, each neuron of the next layer is connected to the neuron of the previous layer, while the weights of these connections and the total shift determine its activation function. In order to start somewhere, we can initialize all these weights and shifts with random numbers.

Accordingly, at the initial moment, an untrained neural network in response to an image of a given number, for example, an image of a triple, the output layer gives a completely random answer.

To train the neural network, we will introduce a cost function, which will, as it were, tell the computer in the event of a similar result: “No, bad computer! The activation value must be zero for all neurons except for the one that is correct. ”

Set cost function for digit recognition

Mathematically, this function represents the sum of the squared differences between the actual activation values ​​of the output layer and their ideal values. For example, in the case of a triple, the activation must be zero for all neurons, except for the one corresponding to the triple, for which it is equal to one.

It turns out that for one image we can determine one current value of the cost function. If the neural network is trained, this value will be small, ideally tending to zero, and vice versa: the larger the value of the cost function, the worse the neural network is trained.

Thus, in order to subsequently determine how well the neural network was trained, it is necessary to determine the average value of the cost function for all images of the training set.

This is a rather difficult task. If our neural network has 784 pixels at the input, 10 values ​​at the output and requires 13 thousand parameters to calculate them, then the cost function is a function of these 13 thousand parameters, it produces one single cost value that we want to minimize, and at the same time in the entire training set serves as parameters.

How to change all these weights and shifts so that the neural network is trained?

Gradient Descent

First, instead of representing a function with 13k inputs, let's start with a function of one variable, C(w). As you probably remember from the course of mathematical analysis, in order to find the minimum of a function, you need to take the derivative.

However, the shape of a function can be very complex, and one flexible strategy is to start at some arbitrary point and step down the value of the function. By repeating this procedure at each subsequent point, one can gradually come to a local minimum of the function, as does a ball rolling down a hill.

As shown in the figure above, a function can have many local minima, and which local minimum the algorithm ends up in depends on the choice of starting point, and there is no guarantee that the minimum found is the minimum possible value of the cost function. This must be kept in mind. In addition, in order not to "slip" the value of the local minimum, you need to change the step size in proportion to the slope of the function.

To slightly complicate this task, instead of a function of one variable, you can represent a function of two variables with one output value. The corresponding function for finding the direction of the fastest descent is the negative gradient -∇С. The gradient is calculated, a step is taken in the direction of -∇С, the procedure is repeated until we are at the minimum.

The described idea is called gradient descent and can be applied to find the minimum of not only a function of two variables, but also 13 thousand, and any other number of variables. Imagine that all weights and shifts form one large column vector w. For this vector, you can calculate the same cost function gradient vector and move in the appropriate direction by adding the resulting vector to the w vector. And so repeat this procedure until the function С(w) comes to a minimum.

Gradient Descent Components

For our neural network, steps towards a lower cost function value will mean less random behavior of the neural network in response to training data. The algorithm for efficiently calculating this gradient is called backpropagation and will be discussed in detail in the next section.

For gradient descent, it is important that the output values ​​of the cost function change smoothly. That is why activation values ​​are not just binary values ​​of 0 and 1, but represent real numbers and are in the interval between these values.

Each gradient component tells us two things. The sign of a component indicates the direction of change, and the absolute value indicates the effect of this component on the final result: some weights contribute more to the cost function than others.

Checking the assumption about the assignment of hidden layers

Let's discuss the question of how the layers of the neural network correspond to our expectations from the first lesson. If we visualize the weights of the neurons of the first hidden layer of the trained neural network, we will not see the expected figures that would correspond to the small constituent elements of the numbers. We will see much less clear patterns corresponding to how the neural network has minimized the cost function.

On the other hand, the question arises, what to expect if we pass an image of white noise to the neural network? It could be assumed that the neural network should not produce any specific number and the neurons of the output layer should not be activated or, if they are activated, then in a uniform way. Instead, the neural network will respond to a random image with a well-defined number.

Although the neural network performs digit recognition operations, it has no idea how they are written. In fact, such neural networks are a rather old technology developed in the 80s-90 years. However, it is very useful to understand how this type of neural network works before understanding modern options that can solve various interesting problems. But the more you dig into what the hidden layers of a neural network are doing, the less intelligent the neural network seems to be.

Learning on structured and random data

Consider an example of a modern neural network for recognizing various objects in the real world.

What happens if you shuffle the database so that the object names and images no longer match? Obviously, since the data is labeled randomly, the recognition accuracy on the test set will be useless. However, at the same time, on the training sample, you will receive recognition accuracy at the same level as if the data were labeled in the right way.

Millions of weights on this particular modern neural network will be fine-tuned to exactly match the data and its markers. Does the minimization of the cost function correspond to some image patterns, and does learning on randomly labeled data differ from training on incorrectly labeled data?

If you train a neural network for the recognition process on randomly labeled data, then training is very slow, the cost curve from the number of steps taken behaves almost linearly. If training takes place on structured data, the value of the cost function decreases in a much smaller number of iterations.

Backpropagation is a key neural network training algorithm. Let us first discuss in general terms what the method consists of.

Neuron activation control

Each step of the algorithm uses in theory all examples of the training set. Let us have an image of a 2 and we are at the very beginning of training: weights and shifts are set randomly, and some random pattern of output layer activations corresponds to the image.

We cannot directly change the activations of the final layer, but we can influence the weights and shifts to change the activation pattern of the output layer: decrease the activation values ​​of all neurons except the corresponding 2, and increase the activation value of the required neuron. In this case, the increase and decrease is required the stronger, the farther the current value is from the desired one.

Neural network configuration options

Let's focus on one neuron corresponding to the activation of neuron 2 on the output layer. As we remember, its value is the weighted sum of the activations of the neurons of the previous layer plus the shift, wrapped in a scaling function (sigmoid or ReLU).

So to increase the value of this activation, we can:

  1. Increase shift b.
  2. Increase weights w i .
  3. Swap previous layer activations a i .

From the weighted sum formula, it can be seen that the weights corresponding to connections with the most activated neurons make the greatest contribution to neuron activation. A strategy similar to biological neural networks is to increase the weights w i in proportion to the activation value a i of the corresponding neurons of the previous layer. It turns out that the most activated neurons are connected to the neuron that we only want to activate with the most "strong" connections.

Another close approach is to change the activations of neurons of the previous layer a i in proportion to the weights w i . We cannot change the activation of neurons, but we can change the corresponding weights and shifts and thus affect the activation of neurons.

Backpropagation

The penultimate layer of neurons can be considered similarly to the output layer. You collect information about how the activations of neurons in this layer would have to change in order for the activations of the output layer to change.

It is important to understand that all these actions occur not only with the neuron corresponding to the two, but also with all the neurons of the output layer, since each neuron of the current layer is connected to all the neurons of the previous one.

Having summed up all these necessary changes for the penultimate layer, you understand how the second layer from the end should change. Then, recursively, you repeat the same process to determine the weight and shift properties of all layers.

Classic Gradient Descent

As a result, the entire operation on one image leads to finding the necessary changes of 13 thousand weights and shifts. By repeating the operation on all examples of the training sample, you get the change values ​​for each example, which you can then average for each parameter separately.

The result of this averaging is the negative gradient column vector of the cost function.

Stochastic Gradient Descent

Considering the entire training set to calculate a single step slows down the gradient descent process. So the following is usually done.

The data of the training sample are randomly mixed and divided into subgroups, for example, 100 labeled images. Next, the algorithm calculates the gradient descent step for one subgroup.

This is not exactly a true gradient for the cost function, which requires all the training data, but since the data is randomly selected, it gives a good approximation, and, importantly, allows you to significantly increase the speed of calculations.

If you build the learning curve of such a modernized gradient descent, it will not look like a steady, purposeful descent from a hill, but like a winding trajectory of a drunk, but taking faster steps and also coming to a function minimum.

This approach is called stochastic gradient descent.

Supplement. Backpropagation Math

Now let's look a little more formally at the mathematical background of the backpropagation algorithm.

Primitive neural network model

Let's start with an extremely simple neural network consisting of four layers, where each layer has only one neuron. Accordingly, the network has three weights and three shifts. Consider how sensitive the function is to these variables.

Let's start with the connection between the last two neurons. Let's denote the last layer L, the penultimate layer L-1, and the activations of the considered neurons lying in them a (L) , a (L-1) .

Cost function

Imagine that the desired activation value of the last neuron given to the training examples is y, equal to, for example, 0 or 1. Thus, the cost function is defined for this example as

C 0 = (a ( L) - y) 2 .

Recall that the activation of this last neuron is given by the weighted sum, or rather the scaling function of the weighted sum: (L) ).

For brevity, the weighted sum can be denoted by a letter with the appropriate index, for example z (L) :

a (L) = σ (z (L) ).

Consider how small changes in weight w affect the value of the cost function (L) . Or in mathematical terms, what is the derivative of the cost function with respect to weight ∂C 0 /∂w (L) ?

It can be seen that the change in C 0 depends on the change in a (L) , which in turn depends on the change in z (L) , which depends on w (L) . According to the rule of taking similar derivatives, the desired value is determined by the product of the following partial derivatives:

∂C 0 /∂w (L) 9069.

Definition of derivatives

Calculate the corresponding derivatives: and desired.

The average derivative in the chain is simply the derivative of the scaling function:

∂a (L) /∂z (L) = σ'(z (L) )

/∂w (L) = a (L-1)

Thus, the corresponding change is determined by how activated the previous neuron is. This is consistent with the idea mentioned above that a stronger connection is formed between neurons that light up together.

Final expression:

∂C 0 /∂w (L) = 2(a (L) - y) σ'(z (L) ) a (L-1)

Backpropagation

Recall that a certain derivative is only for the cost of a single example of the training sample C 0 . For the cost function C, as we remember, it is necessary to average over all examples of the training sample: The resulting average value for a specific w (L) is one of the components of the cost function gradient. The consideration for shifts is identical to the above consideration for weights.

Having obtained the corresponding derivatives, we can continue the consideration for the previous layers.

Model with many neurons in the layer

However, how to make the transition from layers containing one neuron to the initially considered neural network. Everything will look similar, just an additional subscript will be added, reflecting the number of the neuron within the layer, and the weights will have double subscripts, for example, jk, reflecting the connection of neuron j from one layer L with another neuron k in layer L-1.

The final derivatives give the necessary components to determine the components of the ∇C gradient.

You can practice the described digit recognition task using the training repository on GitHub and the mentioned MNIST digit recognition dataset.

Learn more