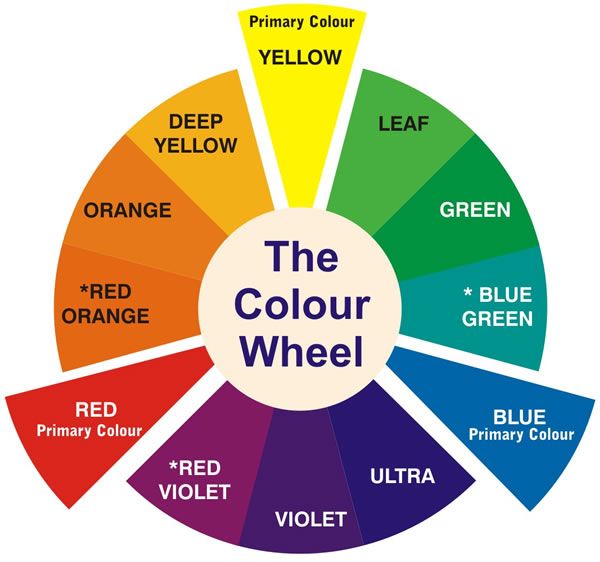
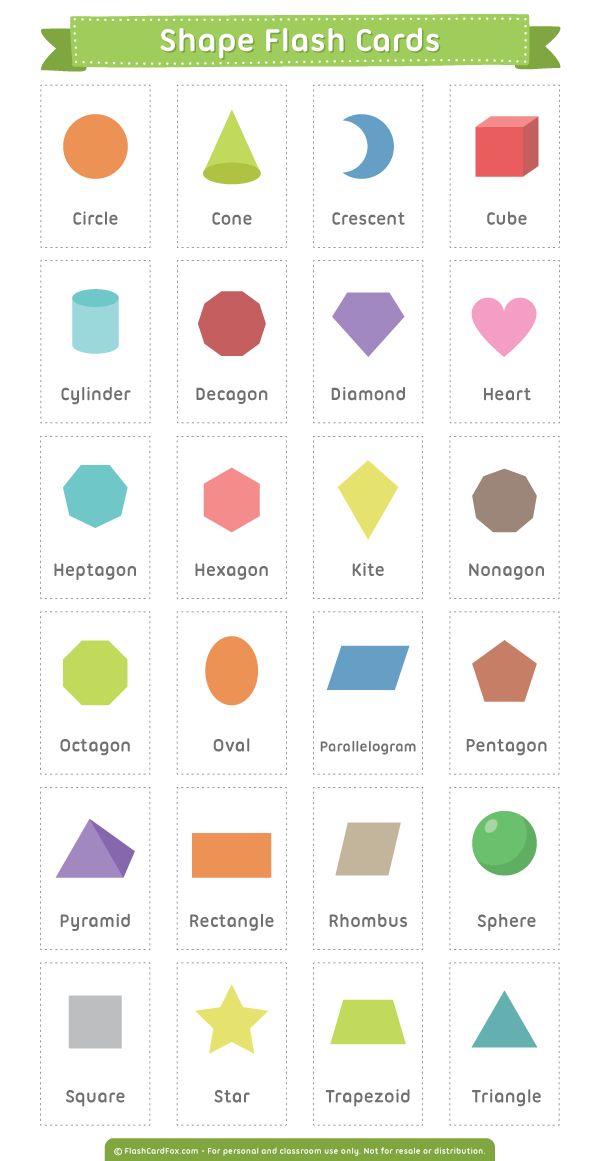
Study of shapes

What is Geometry? - Definition Facts and Examples

What is Geometry

Geometry is a branch of mathematics that studies the sizes, shapes, positions, angles, and dimensions of things. 

2D Shapes in Geometry

Flat shapes like squares, circles, and triangles are a part of flat geometry and are called 2D shapes. These shapes have only 2 dimensions, the length and the width.

Examples of 2D shapes in flat geometry are as shown below. 

2D shapes can be further classified as open and closed shapes. Open shapes can be defined as a shape or figure whose line segments and/or curves do not meet. They do not start and end at the same point. Closed shapes are geometric shapes that begin and end at the same point.

3D Shapes in Geometry

In geometry, a three-dimensional shape can be defined as a solid figure or an object or shape that has three dimensions – length, width, and height. Unlike two-dimensional shapes, three-dimensional shapes have thickness or depth.

The attributes of a three-dimensional figure are faces, edges, and vertices. The three dimensions compose the edges of a 3D geometric shape.

A cube, rectangular prism, sphere, cone and cylinder are the basic 3-dimensional shapes we see around us. 

Angle

In geometry, an angle can be defined as the figure formed by two rays meeting at a common endpoint. An angle is represented by the symbol ∠. Angles are measured in degrees (°) using a protractor. For example, 45 degrees is represented as 45°. 

The angles are classified based on their measurements as:

1. An acute angle measures less than 90°.
2. An obtuse angle is between 90° and 180°.
3. A right angle precisely measures 90°.
4. An angle measuring exactly 180° is a straight angle.
5. A reflex angle measures between 180°- 360°.
6. A complete angle measures 360°.

The vertex of a shape where two edges meet form an angle. Different shapes in geometry have different angle measures.

For example:

• A triangle is a 3 sided shape, and the sum of its 3 interior angles is 180˚
• A square, rectangle or quadrilateral are 4 sided shapes, and the sum of their 4 interior angles is 360˚
• Other polygons like the pentagon, hexagon, heptagon, octagon have 5, 6, 7, 8 sides respectively and varying angles.

Examples of different Polygons with their angles and sides are as shown below.

We learn various aspects of shapes, like the measurement of angles, length of sides, area, volume, etc in geometry. Similarity and congruence are two important aspects of geometry.

Similarity: Similarity is when two shapes are the same but their sizes may vary.

Congruence: Congruence is when two shapes are exactly the same in shape and size.

Coordinate Plane:

• A coordinate plane is a 2D surface formed by using two number lines that intersect each other at the right angle.
• The horizontal number line is the x-axis, and the vertical number line is the y-axis.
• The intersection of the two axes is the (0,0) coordinate.
• Using the coordinate plane, we plot points, lines, etc. By joining various points on the coordinate plane, we can create shapes.

We use Formula and Theorems to solve the geometry problems.

A formula is a mathematical equation to solve a geometry problem while a theorem is a statement that is proved using previously known facts.

For example, the “Pythagoras Theorem” proved that a2+b2=c2 for a right-angled triangle, where a and b are the sides of the right-angled triangle, and c is the hypotenuse.

However, a2+b2=c2 is the formula for finding the hypotenuse of a right-angled triangle.

Fun Facts

– The word geometry is made from the Greek words “Geo” meaning “earth” and “metry” meaning “measurement”.

Solved Examples

1. Is the given shape an example of a simple closed curve that is also a polygon?

Solution:

A closed shape that does not cross itself is a simple closed curve. Polygons are closed shapes formed of only straight lines like triangles, rectangles, pentagons and so on.

The given figure is curved and is not made of only straight lines, this is not a polygon.

2. In a triangle ABC, right angled at B, if ∠C=45° what is the measure of ∠A? 

Solution: △ ABC is the given right triangle with ∠B=90°.

Sum of the angles of a triangle = 180°

∠A+∠B+∠C=180°

∠A+∠C=180°-90°=90°

But, ∠C=45° hence ∠A=90°-45°=45°

3. Identify the flat surfaces in the given prism. 

Solution:

The flat surfaces in the prism are as given below:

Rectangle AECB, Rectangle DCEF, Rectangle ABDF form the rectangular faces of the prism.

△ BCD and △ AEF form the triangular faces of the prism.

Practice Problems

A

B

C

D

Correct answer is: B
A closed shape that does not cross itself is a simple closed curve. It has the same start and end points.

A

B

C

D

Correct answer is: D
The given shape is a 3d shape and is called a cube.

10 sides and 10 corners

12 sides and 10 corners

5 sides and 5 corners

18 sides and 5 corners

Correct answer is: 10 sides and 10 corners
The star shaped figure is made of 10 straight lines. Thus, it has 10 sides and 10 corners.

Frequently Asked Questions

What is the relationship between mathematics and geometry?

Mathematics is an umbrella term for various disciplines that focus on logic and abstract concepts. Geometry is one of the branches of mathematics that deals with shapes and sizes of figures and their properties. 

What are some applications of geometry?

Geometry can be applied to many areas such as architecture, electronics, engineering, and construction. It can also be used in fields like science to develop projects or programs for space exploration. 

What is the main difference between 2D and 3D shapes?

The main difference between 2D and 3D shapes is the absence of depth or height in 2D shapes. They are flat figures. 3D shapes exist in three dimensions with length, breadth, and height and do not appear flat.

What is the difference between algebra and geometry?

Algebra is a branch of mathematics that uses variables, in the form of letters, to act as numbers or quantities in equations and formulas. Geometry is a branch of mathematics that studies the sizes, shapes, positions, angles, and dimensions of things.

What Children Know and Need to Learn about Shape and Space

Geometry encompasses two major components. One is reasoning about shape. We learn, for example, that triangles must have three straight sides and three angles, but the angles may be narrow or wide, and the triangles may be tall or short, red or blue, or tilted in any number of ways.  The second component is thinking about space. We learn how objects relate to one another and to us in space: the ball is on top of the sofa, the sofa is under the ball, and we are in front of both. 

Although children accurately perceive shape and space in their everyday environments, preschool children from about three to five years of age need to learn to think about these topics. Our main educational goal should be to promote understanding of basic geometry.

Context and overview

Perception of objects begins soon after birth. From their earliest days to about 18 months, babies can easily see the differences between common objects: they see that mother is different from father and that dog is different from cat. Babies can differentiate types of objects: they see that this is the plate and this is the cup, even if they don’t know the name for each and cannot articulate the key differences between them.  Further, babies can identify objects even when they change location: this is mother regardless of whether we see her from one side or another, or whether she is close or far, lying down or standing up, or partially or fully visible.

By the end of infancy, object perception is relatively well developed, and children navigate the everyday world with relative ease. At the same time, they still have a great deal to learn, particularly the analysis of shapes, that is, understanding their essential features. Learning the shape names is easy. But analyzing them is much harder. Hence, the focus of early geometry education should be on analysis and understanding. 

Early perceptions and ideas of shape

At roughly three and four years of age, children learn several aspects of shapes, both two-dimensional (2-D) and solid (3-D). The illustrations that follow mostly involve 2-D shapes, but the same points can be made about solids as well. 

Perception of difference and sameness  

Young children can easily discriminate (see or perceive the differences) between various shapes.  For example, asked whether the 2-D shapes in Figure 1 are different, children will quickly agree that they are. 

They can also easily discriminate between 3-D shapes, for example, between a rectangular prism (like a book) and a sphere (like a ball), or between a sphere and a cube (like a block with six square faces). 

Clearly young children can see differences between triangles and rectangles, and between books and balls. They may even know the names triangle and rectangle. But at the same time, they may not be able to analyze the basis for their discriminations. They may have no knowledge about the properties of triangles and rectangles. They may not understand, for example, that a triangle must have three sides, that it is a closed figure, or that both figures are polygons.

In brief, the ability to discriminate means only that the children see that the shapes look different. At the same time, the children may not know anything important about them.  We need to distinguish between seeing and thinking, perception and thought. 

What about the idea of same? Young children can see that two rectangles are perceptually the same or identical (congruent). They might even see the congruence if one of the rectangles were tilted a little to the side (but not too much!). Figure 2 shows an example.

Identifying sameness, in the sense of congruent shape, is not very difficult for young children, who are expert perceivers, at least of what is on the surface. Their perception is largely non-verbal and direct. Note that language is not essential for any of these judgments: children (or animals) can see that shapes are identical without being able to name them. Children can also give the shapes incorrect names but still accurately perceive sameness (and difference). For example, you can say that a pack of “dogs” are the same when you should have called them “elephants.” The objects are seen as the same, whatever you call them.  

Figure 3 illustrates an interesting complication. Sometimes children seem not to recognize a clear difference. For example, a three-year-old might say that the shapes in Figure 3 are the same because they both have “pointy tops.”

Does this mean that the child cannot see the difference between the shapes? Not necessarily. The child probably sees the differences, but thinks that the shapes are nevertheless the same. If the adult asks whether the shapes are at all different, the child might say that one has three sides and the other four, but they are the same because they each have that “pointy top.” So the child sees a perceptual difference, but thinks the shapes are the same because they each share a vertex on top. Actually, the child is quite right: even though the shapes are different, they are the same in the property the child describes. This is one reason to interview children in an attempt to uncover the thinking that underlies their overt responses.  The child may say “same” but also understand that the shapes are different in another respect.

Classification. Young children need to go beyond perceiving sameness and difference. They must learn to classify objects that are similar (as opposed to congruent) in key respects. They need to learn that three-sided figures of different sizes are all triangles; that non-congruent but similar four-sided figures with equal length and right angles are all squares; that basketballs and globes are spheres; and that blocks varying in color can be cubes. 

Some classifications are easier for young children than others. For example, they can see that squares of different sizes all go together. They can identify prototypical, that is standard common triangles, like those in Figure 4, regardless of size. Again, this can be done without knowing the names. Whatever the figures are called, some go together and others do not.

Names. Of course, children need to learn the correct names.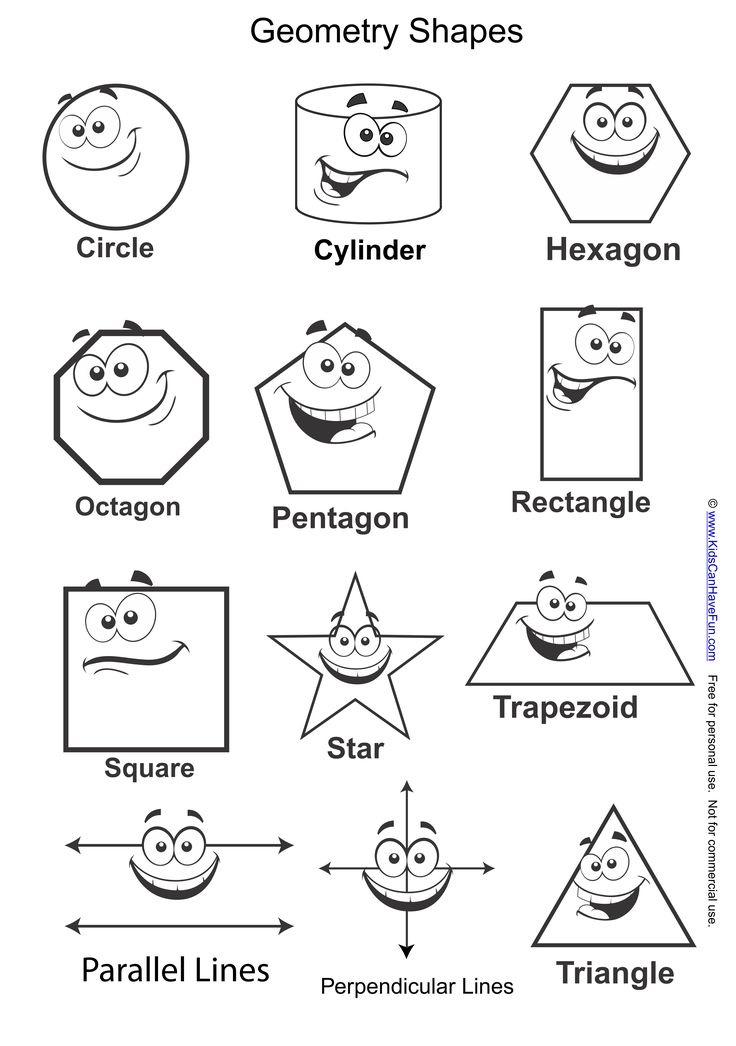  Names are useful in several ways: they allow you to communicate to others (“This is a triangle.”) and they also refer you to a category to analyze (“This is called a triangle and so are these. I wonder how they are the same.”). The English shape names are a bit odd, because many derive from Greek or Latin. For example, the word triangle derives from the Greek for “three angles.” By contrast, the Chinese shape names are transparent. In Chinese, the name for rectangle translates as "four-sided shape." Despite this, geometric names are not difficult for children to learn. Preschool children know thousands of names, including special names like Brontosaurus or esoteric names of cartoon characters or toys or action figures. Given their ability to absorb language, young children should experience little difficulty in learning names like rectangular prism or pentagon. But the adult should always keep in mind that names, while necessary, are superficial. Children need to learn to understand the properties of shapes, not just how to sort or name them.

Understanding. Understanding is multifaceted. Children need to learn to analyze shapes, identify their defining properties, and talk about them. They need to learn what makes a triangle a triangle and how a triangle is different from a square. They need to learn that a square is a sub-class of rectangles.

As mentioned above, children can easily learn to categorize prototypical shapes. They learn that equilateral, isosceles, and right triangles are all triangles. At the same time, children may not know that a long, thin, scalene triangle, like that in Figure 5, is also a legitimate member of the triangle family, and that all triangles of any color can be small or large, tipped to the side or lying on a horizontal base. Size, color and orientation do not matter when the goal is to identify shapes that are the same type.

The child's main challenge is to acquire explicit knowledge of the defining properties of shapes.  Children need to understand that a triangle has certain defining properties and a square has others and that these forms are invariant over changes in size, orientation, and color. They also need to be able talk about the shapes; to explain why the triangle is a triangle even if it is not prototypical.

Children’s limited understanding of essential and non-essential properties may stem in part from the limited array of shapes that they see. Children are often exposed to prototypical shapes in books and toys. If a picture book introduces a triangle, it is likely to be equilateral or isosceles, and rarely scalene. Shape sorting toys also involve prototypes, in this case three dimensional, like an equilateral triangular prism.

Given that children are seldom presented with non-prototypical shapes, adults need to expose children to them and teach the basic properties of shapes, making explicit the reasons why one shape is a triangle and the other is a pentagon. As in other areas, adults need to help children mathematize their knowledge of shapes, that is, develop an explicit awareness of the formal mathematics. Children need to learn how to think and talk explicitly about mathematical properties such as the number of vertices and sides that define a figure.

Composing and decomposing shapes. Children also need to explore and learn about taking shapes apart and using shapes to construct other shapes. For example, if the goal is to create a square from two triangles, the child must pay attention to the interior angles and the lengths of the sides of the triangles. Composition and decomposition foster analysis.

Children can explore shapes using several activities of this type. As shown in Figure 6, children can compose shapes. When a child puts two squares of the same size together by aligning their widths, the result is a long rectangle. When  a child places two identical semicircles together by aligning their diameters, the result is a full circle.

Children can also decompose shapes. As shown in Figure 7, when a child divides a rectangle along its diagonal or cuts an equilateral triangle down the middle, the child gets two right triangles.

Composing and decomposing can be a lot of fun, whether the shapes are physical forms or computer graphics, and whether the child is engaged in exploration or solving a problem created by the adult.   

Context and overview

Humans (and animals too) require basic concepts of space if they are to function adequately in the everyday world. For this reason, often on their own, young children (even infants) begin to use or develop basic spatial concepts, including ideas about location, relative position, symmetry, and direction. Some spatial skills and ideas are built into the human perceptual system: even babies demonstrate that they can distinguish between near and far when they attempt to reach for the closer of two toys. Babies and toddlers further develop these abilities as they crawl or walk around, become aware of their surroundings, and think about where they are going. They know where they are in space and how to move from one location to another. In familiar places such as homes and schools, they generally know where things are and how to get to the things they want. They learn that the ball is close to the chair, that the doll is under the chair, and that the fastest route to the chair involves going under the table. They learn to use words to describe positions, locations, and directions. When they get older they use blocks and other objects to create symmetries that are sometimes beautiful, such as the creation shown in Figure 8.                                                                

Although their everyday spatial ideas are often useful (as in the case of moving around familiar surroundings) and sometimes surprisingly powerful (as in the case of complex symmetries), young children still have a great deal to learn and need adults to help them move forward. Teachers and parents can build upon and extend what young children already know about space. Adults can help young children mathematize their everyday ideas of space.  This involves using language and various representations to describe and understand spatial ideas.

The Importance of a Mathematical Understanding of Space

There are many reasons for learning about space, just as there are for shape and number.

Space is interesting in itself. Spatial ideas include the following:

• Simple location and position: the dog is on top of the elephant and at the same time the elephant is under the dog.
• Perspective: from where I sit I see the cat on the left and the whale on the right, but from where you sit, opposite me, you see the cat on the right and the whale on the left.
• The coordinates on the Cartesian plane: the poodle is in the fourth row and the fifth column.
• Directions: the child can get to the treasure chest by walking two steps forward, turning right, and then moving four steps forward, whereupon the child makes a half turn leftward and follows the diagonal for five paces.
• The aesthetic qualities of reflectional symmetry: this symmetrical design is really beautiful but this asymmetrical mess is not.

Each of these topics presents challenges: if the mouse is on top of the cat that is on top of the dog, then the cat is both on top of and underneath something else at the same time. Children find it difficult to coordinate the two different relations (such as on top of and underneath), but adults can help.

Spatial ideas underlie much of our mathematical understanding. To understand addition, a child might use ideas of merging two separate groups of objects or jumping to the right on a standard number line. To understand subtraction the child might think of monkeys jumping off a bed. To understand equivalence, the child might imagine balancing objects on a scale. To understand multiplication, the child might refer to areas or arrays of dots. Indeed, spatial metaphors and ideas permeate children’s and adults’ understanding of number.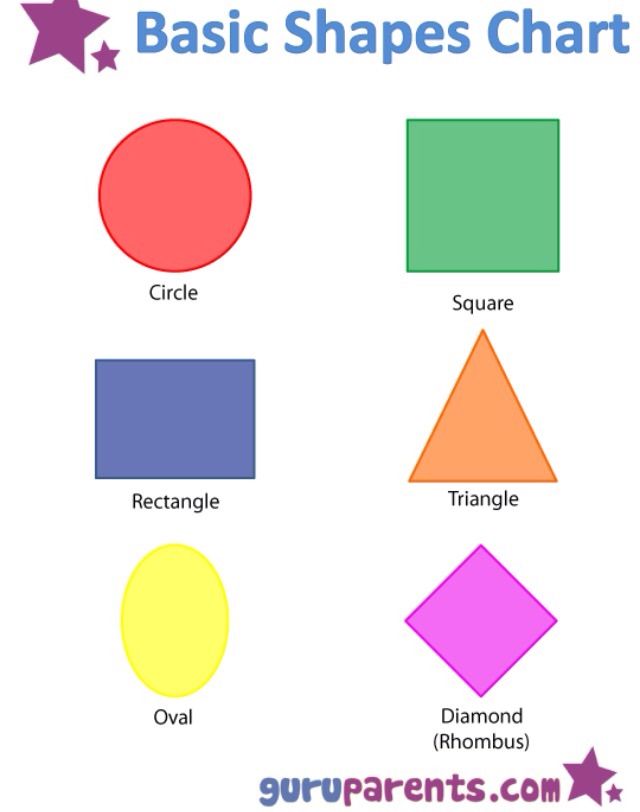

Spatial understanding, language, and symbolism are of practical value. Children (and adults) live in space. Moving purposefully in it requires first an understanding of spatial relations in the everyday environment, as when the baby learns that the stuffed cow is behind the sofa. Later, the child learns and uses appropriate spatial language to get around in the world (for example, when mother says, “Go to the living room and look under the sofa for your toy raccoon.”). Later still, reading a highway map is necessary for getting to a destination. The adult uses ideas of space to build a bookcase or carpet a room. Language and symbolism allow us to surpass the everyday spatial knowledge of animals.

Spatial knowledge and language predict future academic performance. Those children who acquire a solid understanding of space and spatial language tend to demonstrate higher math achievement than students who do not achieve such mastery. 

What Children Need To Learn About Space

Children have an informal knowledge about space on which early math education can build.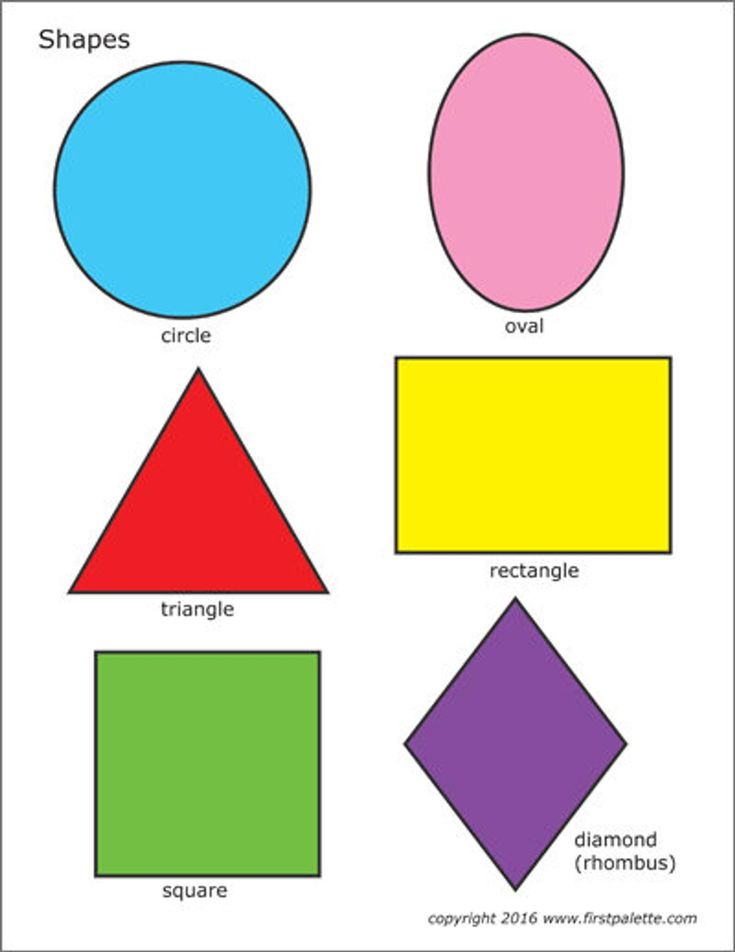  They are quite capable of learning more about the following important topics.

Basic position. Children are skilled at locating things in their environments. They often use informal or vague language to describe where things are in relation to other things, including themselves. But they need to deepen their understanding of position and learn correct mathematical words for talking about it.

Consider how a child might specify the locations of objects and people in a room. 

• I am standing on top of the desk.
• I put my gooey candy on the white sheet.
• I threw the apple core behind the tree.
• I put my underwear under the bed.
• I put the pickle in the middle of the sandwich.
• My chair is below the window.
• There is a spider in the bottom of the cup.
• I put the coin in my piggy bank.

All of the nouns in the examples refer to things, classes of objects that the child can easily identify.  For example, there are many kinds of apples and the child can easily learn to identify them all as apples. But positions and locations are abstract ideas, and all are relative. For example, the pickle in the middle of the sandwich touches the bread immediately on top of and below it. The underwear underneath is relative to the bed above it.

Another way of thinking about spatial relations is that objects serve as landmarks for the location in question. Landmark means to mark the land, or to specify an object that helps define the location. Even young infants can use landmarks to find the location of a hidden object. For example, if you place a toy behind a sofa as a child watches, she can locate the toy later: she knows that the toy is behind the sofa. In this case, the toy is the object, the sofa is a landmark, and the relation between the landmark and object is behind or in back of. 

In all of these cases, children need to learn two things: the words and the concepts.  They need to learn positional words such as above or next to and they need to know the concepts to which these words refer. For example, the words next to refer to a concept specifying that an object is adjacent to another in a variety of ways, either on its right or its left. You can help children learn to develop these words and concepts by modeling. For example, if a preschooler is asked, "Where are the picture books?" she may reply by saying, "Over there" and gesturing. You can reply, "You're right. They are on the shelf next to the coat closet."          

Complex positions. Left and right are notoriously difficult for young children to learn, and they need a lot of practice with these ideas. First, children need to remember that one hand is on the right and the other is on the left. This idea is reinforced when children put a sticker on their right hand and then shake hands properly. Then children must apply the idea of right and left to external objects. This is especially difficult because these concepts are always relative to the direction the child is facing. For example, if Mario is looking at a table from one direction, he sees a book on his right and a block on his left. When he moves to the opposite side of the table, he sees the reverse. Children are not likely to master left and right until they are older, perhaps in early elementary school. Don’t obsess about their initial failure. 

Understanding dual relations, taking different perspectives at the same time, is very difficult for preschoolers. In our previous example, the pickle in the sandwich is at the same time above the bottom piece of bread and below the top piece. How can a pickle endure the ambiguity—the dual identity or split personality—of being simultaneously above and below? Because children tend to be egocentric, that is, to see things and their relations only from one point of view, they find it difficult to deal with dual, or more generally, multiple relations.  In this way, children are similar to the pickle.

Another task, locating objects in two dimensions, involves simple dual relations between height and width. Suppose the child sees a grid of unit squares that goes up five spaces and sideways five spaces (and of course has all the appropriate squares in the middle).

Someone has placed an object on the grid, as shown in Figure 9. I ask the child to describe where it is because I can’t see it. She can say it is over there, but that does not help. She can say it’s above that square, but that doesn’t help either. What she has to say is something like this: “Go to the bottom square on the left. Then go four squares up and two squares to the right.” 

In everyday life children engage in locating or directional activities. Hopscotch, for example, is about jumping to different squares according to a series of numbers. Another example is board games such as Sorry, in which they may go forward a designated number of spaces and later must go backwards.  

At the preschool level, teachers can help children become increasingly skilled at following location directions and understanding them. At snack time, for example, the teacher can say, “When we set the table for snack, we put the cups next to the plates, and we put the juice in the middle of the table where you can all reach it. And remember to put a napkin on this side of each plate.” 

Complex relations also include another important mathematical topic, symmetry, which is ubiquitous in nature. The butterfly’s left wing is the mirror image of the other. The human body embodies symmetries: the left hand is a mirror image of the right hand.

Mathematics defines many different kinds of symmetries. Consider the mirror image idea, namely that symmetry bisects a figure in such a way that one side is in the opposite orientation from the other. Imagine that you have some figure on a flat surface. You hold a mirror vertically next to the figure. You then have the figure and the mirror image of the figure.  The figure and mirror image are symmetrical. Using a mirror in this way can help children to explore and to understand what line symmetry means. For example, in Figure 10, each shape is symmetrical and each line is a line of symmetry.

Children create both two-dimensional and three-dimensional symmetries all the time when they play with blocks. Figure 11 shows an example of how a child can explore symmetries using pattern blocks. Notice that in order to make this figure, the child had to manually rotate some of the blocks, such as the red trapezoids, to produce the mirror image. Young children may need to physically manipulate objects to correctly show the reflection. Further, these experiences can help a child later to develop the ability to see how shapes can be mentally turned or flipped without having to construct them.

Maps. Maps involve a special kind of symbolism showing where things are in relation to one another. You can represent a classroom in many different ways.  You can describe it in words. You can take a picture of it. You can do a realistic drawing of it. You can create a smaller three-dimensional model of it. You can create a two-dimensional map of it from a bird’s eye view, above. You can create a topographical map of it. You can create something like a subway map that shows relative position but does not accurately capture distances.

Before children can understand how their classroom looks in all these different ways, they must understand point of view or perspective. Infants' and young children's early spatial thinking is often from their own perspective. A child thinks of an object's location in relation to his own location in space. Later, when children realize that they have a distinct point of view, they can begin to imagine how space looks from other perspectives. For example, the child may come to see that the way the classroom looks from her chair is different from the way the classroom looks from a friend's chair, or the way the classroom looks from her spot on the rug differs from the way the classroom looks from the chair the teacher sits on during rug time. It is not easy for young children to de-center and visualize how spaces look from other points of view. Working with maps and models can provide children with experiences that will help them see space from other perspectives.

Standard maps (though maybe not topographical) are hard for children to understand because they represent a three-dimensional reality on a two-dimensional space and also because the map is proportionally smaller than the reality. Preschoolers need to learn first how to read simple maps, such as a map of the classroom, and then to create them. Map activities can take place at circle time, where the teacher can use a map to show children where they should sit, or at line-up, when a map can show who goes first, second and so on, so that the child can identify both her own position and her friend’s.

Conclusions for Shape and Space

Shape and space are fundamental mathematical topics that children need to explore.  They need to grasp the basic concepts, mathematize and elaborate on their everyday knowledge, and learn to communicate what they have learned. The study of geometry can be deeper than many adults imagine and can provide young children with enjoyable intellectual challenges.

Background Reading

Clements, D. H.  Geometric and spatial thinking in young children. In Copley, J. V. (Ed.). (1999). Mathematics in the early years. Reston, VA: National Council of Teachers of Mathematics.

Dehaene, S. (2011). The number sense: How the mind creates mathematics (Rev. and updat ed.). New York: Oxford University Press.

Early Math Collaborative at Erikson Institute. (2014). Big ideas of early mathematics: What teachers of young children need to know (First ed.). Boston: Pearson.

Hawes, Z., Tepylo, D., & Moss, J. (2015). Developing spatial thinking: Implications for early mathematics education In B. Davis and Spatial Reasoning Study Group (Eds. ). Spatial reasoning in the early years: Principles, assertions and speculations (pp. 29-44). New York, NY: Routledge. 

Lehrer, R., Jacobson, C., Kemeny, V., & Strom, D. (1999). Building on children's intuitions to develop mathematical understanding of space. In E. Fennema & T. A. Romberg (Eds.), Mathematics classrooms that promote understanding. Mahwah, NJ: Lawrence Erlbaum Associates, Publishers.

National Research Council. (2009). Mathematics learning in early childhood: Paths toward excellence and equity. Committee on Early Childhood Mathematics, Christopher T. Cross, Taniesha A. Woods, Heidi Schweingruber, Editors. Center for Education Division of Behavioral and Social Sciences and Education, Washington DC: The National Academies Press.

Nora S. Newcombe & Mike Stieff (2012): Six Myths About Spatial Thinking, International Journal of Science Education, 34:6, 955-971

Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research: Learning trajectories for young children. New York: Routledge.

Learning geometric shapes with kids from 1 year old

In today's article I would like to talk about how easy and fun it is to learn geometric shapes with a baby, and why bother with geometry at such an early age. What games will be interesting for a baby from 1 year old, and what materials you will need for classes - read about all this in the article. In addition, here you will find some useful materials for download.

1. We see geometric shapes everywhere, they can be seen in most of the objects around us: a round ball, a rectangular table, etc. Analyzing the similarity of surrounding objects with geometric shapes, the child wonderfully trains associative and spatial thinking.

2. The study of geometric shapes is useful for the overall development of the baby, expanding his knowledge about the world around him. If you introduce a child to forms at an early age, it will be much easier for him at school.

3. Many interesting educational games are based on the ability to distinguish geometric shapes. These are construction, games with a sorter, a mosaic, a mathematical tablet, Gyenesh blocks, etc. Therefore, the study of forms at such an early age will contribute to the further successful development of the child.

So, games for learning and strengthening knowledge about geometric shapes :

If you come across a figure while playing games or reading books, be sure to draw your child's attention to it and name it (“Look, the ball looks like a circle, and the cube looks like a square”). Even if it seems to you that the child is still unlikely to remember the names of the figures, pronounce them anyway, and they will certainly be deposited in his head. You can do this for up to a year. At first, point only to the main shapes (square, circle, triangle), then, when you realize that the baby has mastered them, start studying other shapes.

You can learn anything with lotto: colors, geometric shapes, vegetables, animals, etc. And geometric lotto is also quite easy to do on your own: on a sheet of paper or cardboard, draw or print two identical sets of figures, one of which is cut into cards. Everything is ready, you can play. Our lotto templates for learning geometric shapes can be DOWNLOADED HERE.

For the first lessons with the baby, it is better to use loto, where there are only 3-4 figures. When the baby has mastered such a game well, gradually complicate the task. It is also useful for the first time to make all the pieces on the playing field of the same color and size. In this case, the child will focus on only one sign - the form, while other characteristics will neither distract nor prompt him.

Both cards with the image of figures and three-dimensional figures can be placed on the playing field. Good for this purpose are Gyenesh blocks (Ozon, KoroBoom), figures from a sorter, an insert frame.

Well, the most troublesome option is to buy a ready-made loto with geometric shapes.

Approximately at the age of 1 year, the child begins to notice that the figure of the sorter chosen by him (Ozone, Labyrinth, My-shop) can not be pushed into every hole. Therefore, during the game, it is necessary to focus on this: “So, here we have a circle - it doesn’t fit here, it doesn’t fit here, but where does it fit?”. At first, turning the figure at the right angle can be difficult for the baby, but it's not scary, it's a matter of practice. Most importantly, do not forget to pronounce the names of the figures all the time during the exciting process of “pushing through”, and the child will quietly remember them all.

Important! When choosing a sorter, pay attention to the fact that all the main geometric shapes are presented there, and not just hearts and crescents.

You will need an insert frame that contains all the main figures. At its core, the game is similar to a sorter.

The process of sorting objects began to interest my daughter at the age of 1 year 4 months. We sorted the items by color, size and, of course, shape. I think Taisiya really liked this game, because we often involved her toy friends in it. As soon as, for example, the Masha doll was called into the game, she immediately reported that she liked to play only with triangles, and the bear said that he only liked rectangles. So we had to carefully select the figures so as not to offend anyone :)

When drawing together with your child, do not forget to say the names of the shapes. "So, let's draw a square, now a triangle - we got a house", "Let's draw a circle, an oval, a stick, a stick - we get a little man."

From about 1.5 years old, the baby can already be offered to trace shapes using stencils. You can make the first stencils with geometric shapes yourself from thick cardboard, because.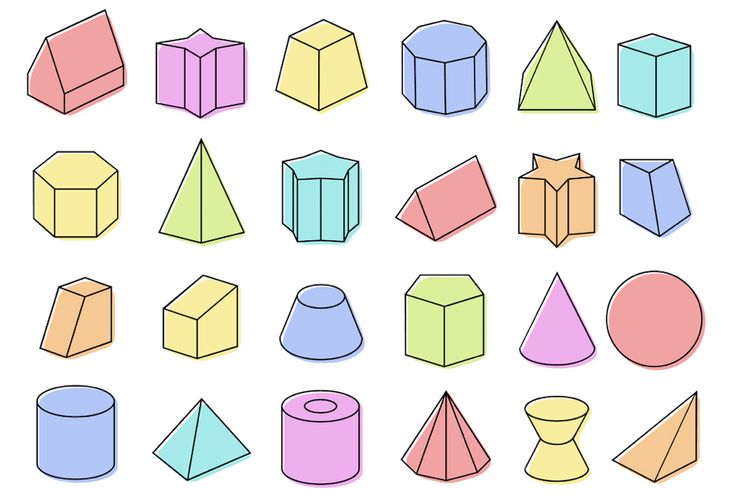 ready-made stencils are usually very small for the very first drawing experiences. I made the first stencils for Taisiya from a not very successful set of cards (the pictures were not very good, but the cardboard is excellent), four main figures were enough for us (the size of our stencils is 8 × 8 cm).

At the age of 2, Taisiya fell in love with drawing on small stencils (another option), and also at this age we started tracing Gyenes blocks from the outside, it was no less interesting, although more difficult.

You can use geometric shapes in appliqué lessons even from the very first lesson. When a baby is just getting acquainted with glue (in my opinion, acquaintance goes well at the age of 1 year 2-3 months), he is more interested in the process of gluing than in creating some kind of composition. Therefore, it is not necessary to create complex pictures in the first applications with the baby, start simply by chaotically gluing pieces of paper on a piece of paper, or even better, by chaotically gluing geometric shapes! While the kid enthusiastically smears the figure with glue (with your help) and puts it on a piece of paper, you tell him what it is called. With such a game, all the names fit very well in the baby’s head, one might say, firmly “stick”

When the baby already succeeds in sticking appliqué elements to the specified places (from about 1.5 years old), you can try to create a simple composition.

You can also use various ready-made manuals in your lessons, for example:

• School of the Seven Dwarfs 1+. Form, color (Ozon, My-shop)

• Educational stickers for babies. Form (Ozon, My-shop)

• Wonderful stickers. Cheerful geometry (Ozon, My-shop)

For little ones a little older (from 1 year 6–9 months) it is very useful to draw analogies between geometric shapes and surrounding objects. While reading and playing, on a walk, draw your baby's attention to the fact that a plate is a circle, a window is a rectangle, and a sandbox is a square, etc. Thus, you will contribute to the development of the child's spatial and associative thinking.

You can also perform tasks to find objects in the picture that match the given figure, for example, "Find all the round objects." Several tasks can be DOWNLOAD HERE .

Here is another interesting shape recognition game - "Find a similar shape" (Maze, My-shop). Despite the fact that the age on it is 3-5 years old, it will be of interest to a child of 2 years old and even a little earlier.

In fact, I find this method of studying forms to be the most effective. If you study with Doman's cards, the child will remember all the figures very quickly, and you will spend a minimum of effort on this. However, it should be noted that in order for the knowledge gained from Doman's cards to be deposited in the baby's head, they must be consolidated through other games (see above). Otherwise, the child will quickly forget everything that you showed him. Therefore, I recommend starting to look at Doman's cards with geometric shapes at about the age of 1 year, since at this time the baby becomes interested in sorters, insert frames, drawing, appliqué, etc. And, having studied the forms from the pictures, he will be able to use the knowledge gained in these games. By the way, cards "Geometric shapes" can be DOWNLOAD HERE and buy HERE.

You can read about our experience in studying figures using Doman's cards here.

Well, of course, it doesn't hurt to watch cartoons on the theme "Geometric shapes", now you can find a lot of them on the Internet. Here are some of them: they show the child a couple of times, for example, a square, and in the future, the training comes down to the question “Tell me, what kind of figure is this?”. This approach is extremely wrong. Firstly, because, like any person, a child does not like it too much when they arrange a knowledge test for him, and this only discourages him from studying.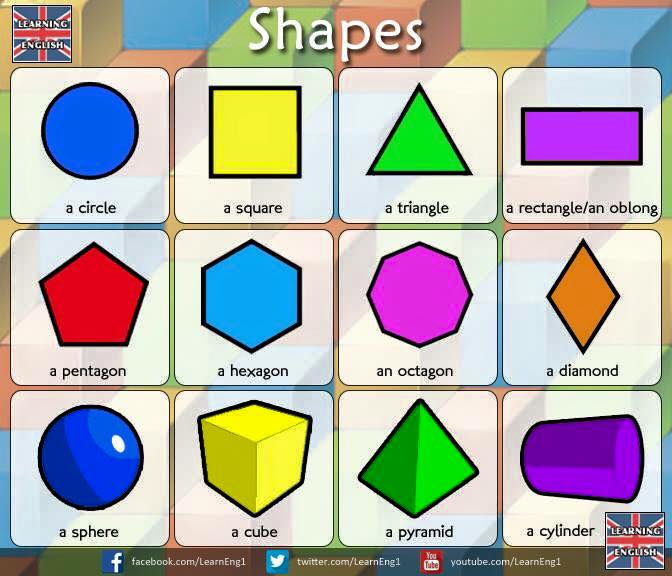 Secondly, before asking a kid about something, he needs to explain and show it a lot of times!

Therefore, try to keep screening questions to a minimum. Just repeat and repeat the information you are learning, be it the names of shapes or something else. Do this while playing and talking with your baby. And the fact that the child has learned everything, you will soon see for yourself without unnecessary checks.

That's all for me, thank you for your attention! I will be very glad if you share with us your ideas of games for the study of shapes.

Sincerely yours, Yana Raznachenko

I also recommend to see articles:

Ready-made games and classes for children from 1 year old to 1 year 3 months 9,0006