Teaching kindergarten maths

6 Tips to Teach Kindergarten Math Without Curriculum

This year, I’m teaching my daughter kindergarten math without curriculum. Kindergarten is the perfect time to “play” school, and kindergarten mathematics is the best place to start with making learning fun.

When my oldest was beginning kindergarten, I excitedly bought a variety of curriculum for him so I could find the best. I had more teacher’s manuals than I could count on one hand. As a result, there were many tears. I persevered. He loved learning (especially math), so he survived the year of double math (among other things).

But each child is different. I knew that if I forced a the same methods and curricula on second child, it would only cause her to hate school time. I needed a new solution. To my surprise, our best result has been to completely drop the kindergarten math curriculum. Here are some tips to make sure your kindergarten math time nurtures your five- or six-year-old child’s natural love for learning.

Use games. Playing card games and board games helps my daughter gain basic number recognition as we count around a board, recognize doubles, and recognize common number pairs. Our current favorite game to play during math time is Skip-Bo, which builds on number sense in great ways!

Read great books. I love reading with my kids. Much of the time, a great picture book can introduce a mathematical concept to a kindergarten-age child in a way that is more memorable than any worksheet-based curriculum could do so. You could even make up your own stories as you go about your days.

Make it real. My daughter loves her analog watch. It helps that it is Minnie Mouse that shows her the time! As we make a schedule and set timers, she learns about passing time, time in general, and reading the time (very generally, at least, in terms of hours). She also loves getting money and shopping at a garage sale with me. Since garage sales deal with small amounts of money (and we can usually find something for a quarter), this is great practical experience. Consider having your child help cook to learn fractions, and counting the bottles of tomato sauce on a grocery run. Even things as simple as helping set the table (How many plates? How many knives?) can count as kindergarten math.

Get moving. My daughter loves anything involving running or jumping around! Use your trampoline to practice counting by tens, or make your math practice a dance party.

Play with toys. In teacher talk, a “manipulative” is something that a child can hold (or manipulate) to help solidify a concept. In your home classroom, anything can be a manipulative! We play with beads, marshmallows, paperclips, pom-poms, mini-erasers, stuffed animals, snap cubes, small plastic jumping frogs. Anything goes! If you can count it, it can be used for math learning. I love the math curriculum-provided manipulatives too, like Cuisenaire rods (also called centimeter rods).

After Planning. As a new homeschool mom, I know would have panicked if someone had suggested ditching the curriculum. Kindergarten is the best place to do so, though, as many states do not require it anyway. In addition, kindergarten concepts are basic enough that you probably cover them on a daily basis. Any gaps that remain are certain to be reviewed in first grade mathematics. To keep track of what you’ve done, sit down after the day is over and write down in your planner what you did. I call this my “after planing” method. I don’t usually plan out our day before we start: I let her choose what we do and we live life. Chances are you can find some way those things relate to math!

Here are the basic concepts commonly addressed in kindergarten math curricula for a whole year. I hope as you read through this list, you’ll think of more ways you can play games, read great books, get moving, make it real, play, and after plan to do your kindergarten math without a curriculum together. It’s more fun than you’ll believe!

Count to 20. (Start with counting to 5, then go from there).
Understand how to count to 100.
Add and subtract within 10 (using manipulatives or images).
Add and subtract within 5 (fluently).
Compare numbers (greater than and less than) under 20.
Count on from a number (…5, ___, 7, 8 ….) rather than starting at the beginning (up to 20)
Identify missing numbers in a sequence (up to 20)
Draw pictures or use manipulatives to show addition (5+2=7)
Find a number to make ten when given a number between 1 and 9 (number ten bonds)
Understand that teen numbers are 10 + a number between 1 and 9.
Compare sizes, such as length and weight, in general using words such as taller, bigger, or shorter.
Identify, compare, sort, and create basic shapes and make new shapes from them.
Recognize the hour and half hour on the clock.
Identify values of pennies, nickles, and dimes.

Rebecca

About the author

Rebecca is a homeschooling mother of three, “Raisin” born in 2007, “Strawberry” born in 2012, and “Kitty” born in 2015.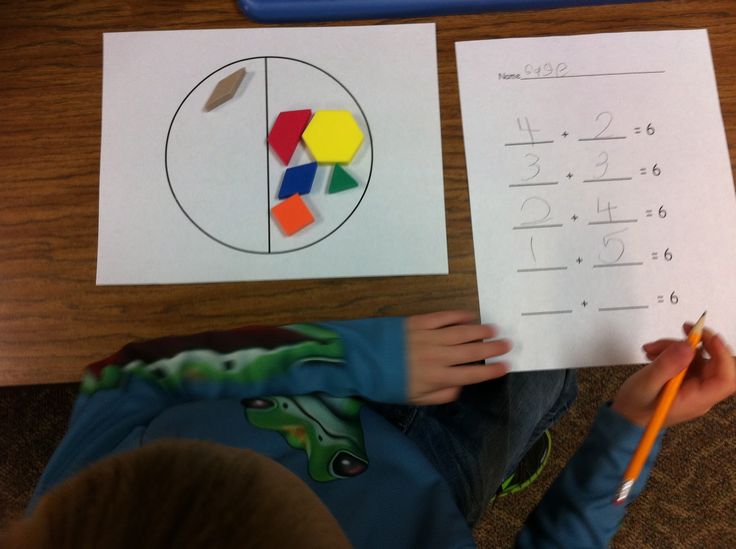 Before she stayed home with her children, she was a professional proofreader. Now that she is home with her kids, she seeks to make learning fun! She loves to incorporate literature, games, and interactive learning in to the homeschooling day. When she's not homeschooling, she loves reading, especially classical literature and history.

Visit My Site

Math in the kitchen – you’ve probably heard about it before. But if you’re like me, you won’t really know where to start.

Building number sense in our homeschooled children is incredibly important, but do you know why? Check out three of the many reasons why!

Rachel Capes

Each night at dinner, our family takes turns sharing our “highs” and “lows” for the day. One night, my daughter said that the best part of her day was finishing her homeschool math lesson. She definitely had struggled a bit through the lesson that day. I figured she was just happy to be done with it, but

Sara Radginski

Kindergarten Math Lessons and Activities for the First 20 Days!

Kindergarten math lesson plans for teaching numbers to 5, 2D shapes, and 3D shapes. This resource provides detailed instruction for your first 4 weeks of math!

Kindergarten Math: The First 20 Days

The first few weeks of school are a hectic time for kindergarten teachers! You are making sure to cover all procedures and routines, all while beginning to teach the kindergarten math curriculum. Many teachers get started with academics right away in order to stay on track for the expected curriculum for the year. Wouldn’t it be nice to have planned out lessons to save you time and stress? You’re in luck! That is just what I have for you – detailed lesson plans and printable resources such as practice sheets to teach all about shapes and numbers to 5.

The First 10 Days…

The lessons start out with students comparing shapes and objects that are the same and different. We like to tie in literature whenever possible to help teach young children academic skills and guide students to make real-life connections. For the first few lessons, you can use this National Geographic Kids book to identify objects that are the same and objects that are different.

On Day 1, students identify shoes that are the same and different. You can create meaningful learning and complete this activity in your classroom as an interactive lesson with real shoes. Your kindergarten students will think it is the “best day ever” when they get to take off their shoes!

In addition to everyday objects, students learn different ways that they can compare shapes. They practice sorting by shape, size, and color.

While making comparisons, students are also counting up to 5 and practicing correct number order on math worksheets.

Days 11-20

Now, you are ready to teach shapes. A great way to read while teaching about 2D shapes is The Greedy Triangle by Marilyn Burns.

We start by introducing 2D shapes and identifying sides and corners.

Then, students have a great time with this color, cut, and paste activity to practice identifying shapes with curves and no curves.

These kindergarten sweeties did a shape sort on the SmartBoard.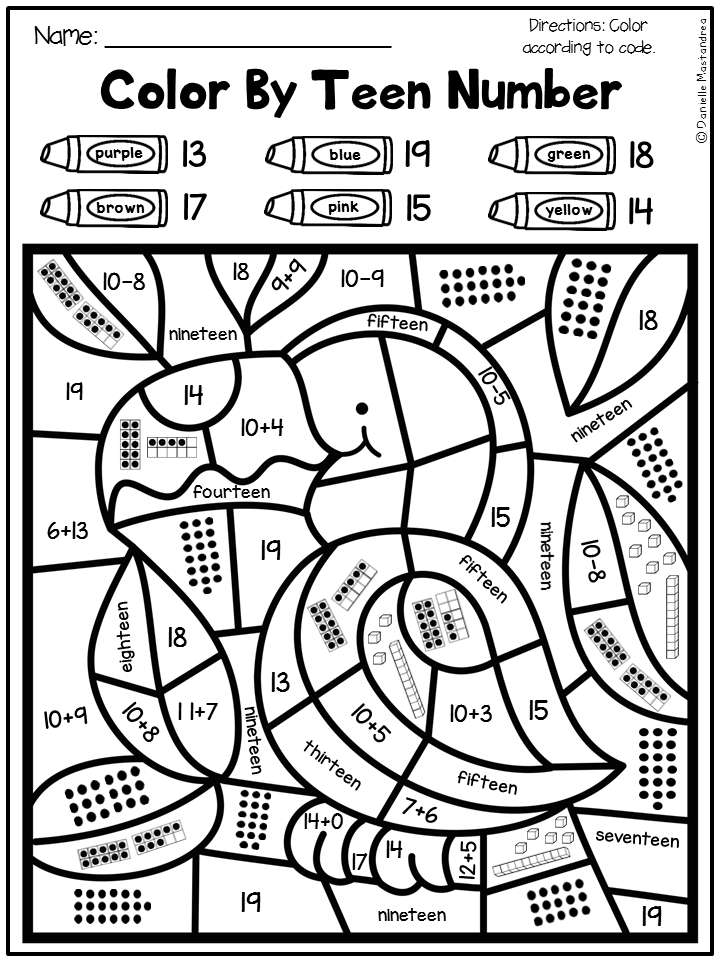

Students explore 3D shapes using interactive kindergarten math games

The mathematical practices for shapes and numbers to 5 are provided in unit 1 of our Guiding Math curriculum. Click here:

Kindergarten Math: Unit 1

We have center activities and journal prompts to provide additional practice for unit 1.

You can find this resource here:

Kindergarten Math Printables Unit 1

Math Assessments

Of course, when you start thinking about instruction, you also start thinking about assessments. ESGI is the best platform for completing assessments. It is so easy! Plus, we’ve added assessments specifically for our Guiding Math Units… making it so simple for you!

Administering these assessments is quick and easy! Do they answer it correctly – simply yes or no.

With assessment trackers ESGI, you can quickly review student progress.

And print off parent letters to send home with students.

ESGI – FREE TRIAL!

There are so many great features with ESGI! If you are not using this amazing assessment tool, give it a try! I know you will love it! You can access a free trial here:

ESGI | Deanna Jump Promo Code

You are covered with math resources for the beginning of the year. Do you need ideas for literacy? Check out this post with alphabet activities for kindergarten:

Fun and Engaging Alphabet Activities for Kindergarten plus a FREE FILE!

"Methods and techniques for the formation of elementary mathematical representations among preschoolers" - JV "Kindergarten No. 2, secondary school No. 30, Syzran" in preschoolers”

Mathematical knowledge of a preschooler is a directly important basis in the mental development of a child. Thanks to mathematical knowledge, children learn to: analyze, compare, synthesize, perform computational operations, think logically, distinguish between geometric shapes, name their features, navigate in space. Preschool children develop memory, attention, thinking. The knowledge gained in kindergarten, children apply in everyday life. Therefore, the task of the teacher: to arouse children's interest in educational activities, to give the necessary elementary mathematical knowledge, to lead children to independent answers, search for solutions. The teacher must find an approach to each child and give this knowledge to all children.

Methods and techniques for the formation of mathematical representations in preschoolers.

In the process of forming elementary mathematical concepts in preschool children, the teacher uses a variety of teaching methods:

practical,
visual,
verbal,
gaming.

When choosing a method, a number of factors are taken into account:

program tasks to be solved at this stage;

age and individual characteristics of children;

availability of the necessary teaching aids, etc. ;

The teacher's constant attention to a reasonable choice of methods and techniques, their rational use in each specific case ensures:

— successful formation of elementary mathematical concepts and their reflection in speech;

- the ability to perceive and highlight relations of equality and inequality (by number, size, shape), sequential dependence (decrease or increase in size, number), highlight quantity, shape, size as a common feature of the analyzed objects, determine relationships and dependencies;

- orientation of children to the application of the mastered methods of practical actions (for example, comparison by comparison, counting, measurement) in new conditions and an independent search for practical ways to identify, detect signs, properties, and connections that are significant in a given situation. For example, in the conditions of the game, to identify the sequence, the pattern of alternation of features, the commonality of properties.

In the formation of elementary mathematical representations, the leading method is a practical method.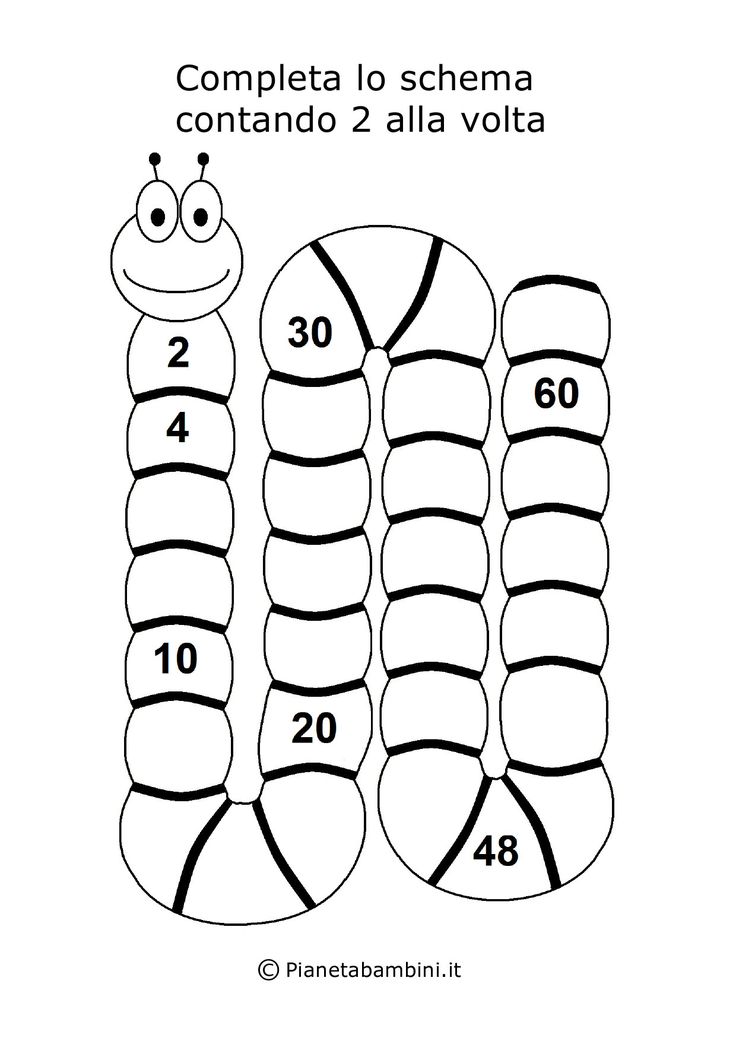

Its essence lies in the organization of children's practical activities aimed at mastering strictly defined methods of action with objects or their substitutes (images, graphic drawings, models, etc.).

Characteristic features of the practical method in the formation of elementary mathematical representations:

— performance of various practical actions;

— wide use of didactic material;

- the emergence of ideas as a result of practical actions with didactic material:

- development of counting skills, measurement and calculation in the most elementary form;

- wide use of formed ideas and mastered actions in everyday life, play, work, i.e. in various types of activity.

This method involves the organization of special exercises that can be offered in the form of an assignment, organized as actions with demonstration material, or proceed in the form of independent work with handout didactic material.

Exercises can be collective - they are performed by all children at the same time, and individual - they are carried out by an individual child at the teacher's board or table. Collective exercises, in addition to mastering and consolidating knowledge, can be used for control.

Individual, performing the same functions, also serve as a model for which children are guided in collective activities.

Game elements are included in the exercises in all age groups: in the younger ones - in the form of a surprise moment, imitation movements, a fairy-tale character, etc.; in seniors, they acquire the character of a search, a competition.

From the point of view of children's manifestation of activity, independence, creativity in the process of performance, reproductive (imitative) and productive exercises can be distinguished.

The game as a method of teaching and the formation of elementary mathematical representations involves the use in the classroom of individual elements of different types of games (plot, mobile, etc.), game techniques (surprise moment, competition, search, etc. Currently a system of so-called learning games has been developed. 0005

All didactic games on the formation of elementary mathematical representations are divided into several groups:

Games with numbers and numbers
Time travel games
Orientation games in space
Games with geometric shapes
Logic games

Visual and verbal methods in the formation of "elementary" mathematical representations are not independent, they accompany practical and game methods.

Techniques for the formation of mathematical representations.

Kindergarten widely uses methods related to visual, verbal and practical methods and applied in close unity with each other: This is the main method of teaching, it has a visual-practical-effective nature, is performed using a variety of didactic means, makes it possible to form skills and abilities in children. It has the following requirements:

- clarity, dissection of the display of methods of action;

- coordination of actions with verbal explanations;

- accuracy, brevity and expressiveness of speech accompanying the show:

- activation of perception, thinking and speech of children.

Manual for self-exercises. This technique is connected with showing the educator methods of action and follows from it. The instruction reflects what and how to do in order to get the desired result. In the older groups, the instruction is given in full before the start of the task, in the younger ones it precedes each new action.
Explanations, explanations, instructions. These verbal devices are used by the educator when demonstrating a method of action or in the course of performing a task by children in order to prevent errors, overcome difficulties, etc. They should be specific, short and figurative.

Demonstration is appropriate in all age groups when getting acquainted with new actions (application, measurement), but it requires activation of mental activity, excluding direct imitation. During the development of a new action, the formation of the ability to count, measure, it is desirable to avoid repeated display.

Mastering the action and improving it is carried out under the influence of verbal techniques: explanations, instructions, questions. At the same time, the speech expression of the mode of action is being mastered.

Questions for children.

Questions activate the perception, memory, thinking, speech of children, provide comprehension and assimilation of the material. When forming elementary mathematical representations, a series of questions is most significant: from simpler ones aimed at describing specific features, properties of an object, the results of practical actions, i.e., ascertaining, to more complex ones that require establishing connections, relationships, dependencies, their justification and explanation, use the simplest proofs.

Most often, such questions are asked after the educator demonstrates the sample or the children complete the exercises. For example, after the children have divided the paper rectangle into two equal parts, the teacher asks: “What did you do? What are these parts called? Why can each of these two parts be called a half? What shape are the parts? How to prove that the squares are obtained? What should be done to divide the rectangle into four equal parts?

Basic requirements for questions as a methodological device:

- accuracy, concreteness, conciseness:

- logical sequence;

— variety of formulations, i. e. the same question should be asked differently

- give children time to think;

- the number of questions should be small, but sufficient to achieve the didactic goal;

- prompting questions should be avoided.

The teacher usually asks the whole group a question, and the called child answers it. In some cases, choral responses are possible, especially in younger groups. Children need to be given the opportunity to think about the answer.

Children's answers should be:

- short or complete, depending on the nature of the question;

- independent, conscious;

- accurate, clear, loud enough;

- grammatically correct (observance of the order of words, the rules for their agreement, the use of special terminology).

In working with preschoolers, an adult often has to resort to the method of reformulating the answer, giving it the correct sample and offering to repeat it. For example: “There are four mushrooms on the shelf,” says the baby. “There are four mushrooms on the shelf,” the teacher clarifies.

During the formation of elementary mathematical concepts in preschoolers comparison, analysis, synthesis, generalization are not only

as cognitive processes (operations), but also as methodological techniques that determine the path along which the child's thought moves in the process of learning.

Comparison is based on establishing similarities and differences between objects. Children compare objects by quantity, shape, size, spatial arrangement, time intervals by duration, and so on. An example of their use is the formation in children of ideas about "many" and "one", which arise under the influence of observation and practical actions with objects.

Modeling is a visual and practical technique that includes the creation of models and their use in order to form elementary mathematical concepts in children. The reception is extremely promising due to the following factors:

- the use of models and modeling puts the child in an active position, stimulates his cognitive activity;

- the preschooler has some psychological prerequisites for the introduction of individual models and elements of modeling: the development of visual-effective and visual-figurative thinking.

Models can perform different roles: some reproduce external connections, help the child to see those that he does not notice on his own, others reproduce sought-after, but hidden connections, not directly perceived properties of things.

Models are widely used in the formation of time representations

: model of parts of the day, week, year, calendar;
quantitative; numerical ladder, numerical figure, etc.), spatial: (models of geometric shapes), etc.
when forming elementary mathematical representations, subject, subject-schematic, graphic models are used.

Experimentation is a method of mental education that provides the child with self-identification through trial and error of connections and dependencies hidden from direct observation. For example, experimentation in measurement (size, measurement, volume).
Monitoring and evaluation .

These techniques are interrelated. Control is exercised through monitoring the process of children performing tasks, the results of their actions, and responses. These techniques are combined with instructions, explanations, explanations, demonstration of methods of action for adults as a model, direct assistance, and include the correction of errors.

Methods and results of actions, behavior of children are subject to evaluation. The assessment of an adult who teaches to be guided by a model begins to be combined with the assessment of comrades and self-esteem. This technique is used during and at the end of the exercise, game, class.

These techniques, in addition to teaching, also perform an educational function: they help to cultivate a benevolent attitude towards comrades, the desire and ability to help them, form emotional responsiveness.

Goals and objectives of the mathematical development of preschoolers. The value of teaching children mathematics

Purpose:

To formulate the main goals and objectives of the mathematical development of preschoolers.

Show the role of teaching mathematics for the comprehensive development of the child's personality.

The problem of teaching mathematics in modern life is becoming increasingly important. This is explained, first of all, by the rapid development of mathematical science and its penetration into various fields of knowledge.

Increasing the level of creative activity, problems of production automation, modeling on electronic computers and much more presupposes that specialists in most modern professions have a sufficiently developed ability to clearly and consistently analyze the processes being studied. Therefore, training in kindergarten is aimed primarily at educating children in the habit of full-fledged logical argumentation of the environment. Learning experience indicates that the development of logical thinking in preschoolers is most facilitated by the study of elementary mathematics. The mathematical style of thinking is characterized by clarity, brevity, dismemberment, accuracy and logic of thought, the ability to use symbolism. In this regard, the content of teaching mathematics at school and kindergarten is being systematically restructured.

Naturally, the basis of knowledge is sensory development, acquired through experience and observation. In the process of sensory cognition, representations are formed - images of objects, their properties, relations. So, operating with a variety of sets (objects, toys, pictures, geometric shapes), children learn to establish equality and inequality of sets, to call the number of words: “more”, “less”, “equally”. Comparison of specific sets prepares children for the subsequent assimilation of the concept of number. It is operations with sets that are the basis that children turn to not only in kindergarten, but also throughout the subsequent years of schooling. The idea of a set forms in children the basis for understanding an abstract number, the laws of a natural series of numbers. Although the concepts of a natural number, as well as a geometric figure, magnitude, part and whole are abstract, nevertheless they reflect the connections and relationships of objects in the surrounding reality.

It has been proven that familiarizing children with different types of mathematical activities in the process of purposeful learning orients them to understanding connections and relationships. The formation of initial mathematical knowledge and skills in preschool children should be carried out in such a way that training gives not only an immediate practical result (counting skills, performing elementary mathematical operations), but also a broad developmental effect. As a rule, the mathematical development of preschoolers is understood as qualitative changes in the forms of cognitive activity of the child, which occur as a result of the formation of elementary mathematical representations and the logical operations associated with them. An analysis of scientific research (A.M. Leushina, N.I. Nepomnyashchaya, A.A. Stolyar, etc.), pedagogical experience convinces us that rationally organized teaching of mathematics to preschool children ensures the overall mental development of children. (Rationally organized education is timely, appropriate for the age and interests of children.) At the same time, pedagogical guidance from an adult (educator or parents) is important. Children acquire elementary knowledge about the multitude, number, size and shape of objects, learn to navigate in time and space. They master the account and measurements of linear and volumetric objects with the help of conditional and generally accepted measures, establish quantitative relationships between quantities, the whole and parts.

In the mathematical training of children, the development of elementary mathematical concepts, an important role is played by teaching measurement as the initial way of knowing the quantitative characteristics of the environment. This makes it possible for preschoolers, first of all, to use not generally accepted, but conditional measures when measuring bulk, liquid substances and lengths. At the same time, children develop an eye, which is very important for their sensory development.

In the process of systematic teaching of mathematics, children master special terminology - the names of numbers, geometric shapes (circle, square, triangle, rhombus, etc.), elements of figures (side, top, base), etc. However, it is not recommended when working with children to use such words-terms as “natural glad”, “set”, “structure”, “elements of the set”, etc. At the same time, work is not limited only to classes. It should be borne in mind the use of the entire didactic space in an educational situation.

Mathematics classes are of particular importance in connection with the development of children's cognitive interests, the ability to show strong-willed efforts in the process of solving mathematical problems.

As a rule, educational tasks in the classroom are solved in combination with educational ones. So, the educator teaches children to be organized, independent, listen carefully, do the work efficiently and on time. This disciplines children, contributes to the formation of their focus, organization, responsibility. Thus, teaching children mathematics from an early age ensures their comprehensive development.

Among the tasks for the formation of elementary mathematical knowledge and the subsequent mathematical development of children, the main ones should be distinguished, namely:

acquisition of knowledge about set, number, size, form, space and time as the foundations of mathematical development;
formation of a broad initial orientation in the quantitative, spatial and temporal relations of the surrounding reality;
formation of skills and abilities in counting, calculations, measurement, modeling, general educational skills;
mastery of mathematical terminology;
development of cognitive interests and abilities, logical thinking, general intellectual development of the child.

These tasks are most often solved by the teacher at the same time at each lesson in mathematics, as well as in the process of organizing various types of independent children's activities. Numerous psychological and pedagogical studies and advanced pedagogical experience in preschool institutions show that only properly organized children's activities and systematic training ensure the timely mathematical development of a preschooler.

Numerous studies (A.M. Leushina, N.A. Menchinskaya, G.S. Kostyuk and others) have proved that the age capabilities of preschool children allow them to form scientific, albeit elementary, initial mathematical knowledge. More precisely, children acquire elements of mathematical knowledge. At the same time, it is emphasized that in accordance with the age of the child, it is necessary to select the forms and method of education. In this regard, at specific age stages, the most favorable conditions for the formation of certain knowledge and skills are created.

So, in the second junior group of the kindergarten (the fourth year of life), the main attention is paid to the formation of knowledge about the multitude. The concept of a set is one of the basic and most general, it runs through all of mathematics. The concept of a set is so broad that it is not defined even at the modern level of development of science, but is introduced as the original one and explained with specific examples. In the middle group, in the process of studying the basic properties of a set, the concept of a number is formed, and in the older group, the first ideas about the natural series of numbers are formed. At preschool age, the understanding of the basic properties of the set is limited. However, awareness of its individual properties (equality and inequality, independence of the power of a set from its qualitative features) is possible already at a younger preschool age.

Along with the formation of initial mathematical concepts and concepts, the program of education in kindergarten provides for familiarization of preschool children with a number of mathematical dependencies and relationships. So, children are aware of some relationships between sets (equal power - uneven power; order relations in a series of quantities, natural numbers; spatial and temporal relations, etc.). At the same time, all mathematical knowledge is presented in interconnection. For example, the formation of ideas about quantity is associated with the formation of ideas about the multitude and size of objects with the development of the ability to see, conditionally determine the size, parameters, as well as the assimilation of relationships between objects. It must be borne in mind that, while acquiring knowledge about number, children learn to abstract quantitative estimates from all others (color, shape, size).

The formation of initial mathematical knowledge in interconnection allows you to gradually and purposefully concretize and refine each of the selected properties. Familiarization of children with the measure and measurements contributes to the formation of a more accurate understanding of the number, and above all the unit. It is the connection of counting and measurement that helps the child to realize the dependence of the result of counting (measurement) on the unit of counting (conditional measure).

Mathematics classes in kindergarten form the simplest types of practical and mental activities of children. Under the types of activity - in this case, methods of examination, counting, measurement - they understand the objective sequential actions that the child must perform in order to assimilate knowledge: element-by-element comparison of two sets, imposing measures, etc. Mastering these actions, the child learns the purpose and methods of activity, as well as rules that ensure the formation of knowledge. For example, comparing equal and unequal sets, superimposing or applying elements, the child is aware of the concept of quantity. Therefore, special attention is paid to the development of practical actions of children with objects.

The central task of the mathematical development of children in kindergarten is learning to count. The main methods in this case are imposition and application, the mastery of which anticipates learning to count with the help of numeral words.

At the same time, preschoolers are taught to compare objects by size (size) and designate the results of the comparison with the corresponding words-concepts (“more - less”, “narrow - wide”, etc.), build rows of objects according to their size in ascending or decreasing order (large , small, even smaller, smallest). However, in order for the child to learn these concepts, it is necessary to form specific ideas in him, teach him to compare objects with each other, first directly - by superimposing, and then indirectly - with the help of measurement.

The math program in kindergarten provides for the development of children's eye in determining the size of objects. To do this, they are trained to evaluate the size (size of objects) as a whole or by individual parameters, comparing with the size of known objects. Attention is drawn to the formation of the ability to check the correctness of the assessment in their practical activities, using additions, reductions, etc. Each practical action replenishes the knowledge of children with new content. It is proved that the formation of elementary mathematical knowledge occurs simultaneously with the development of their practical skills and abilities.

Practical actions, while playing a certain role in the mathematical development of children, do not themselves remain unchanged. Thus, the activity associated with the account is changed. At first, it relies on a practical element-by-element comparison of two concrete sets, and later, a number as an indicator of the power of a set and a natural series of numbers acquires special significance, which subsequently replaces one of the concrete sets.

First, children take objects with their hands, shift them, and then count the objects without touching them, or perceive them only by touch.

On the basis of practical actions, children develop such mental operations as analysis, synthesis, comparison, generalization. The teacher should be guided in evaluating the results of his work primarily on these indicators, on how children are able to compare, analyze, generalize, and draw conclusions. The level of children's mastery of mental operations depends on the use of special methodological techniques that allow children to exercise in comparison, generalization. So, children learn to compare sets by quantity, while carrying out a structural and quantitative analysis of the set. Comparing objects by shape, children identify the size of individual elements, comparing them with each other.

An important task is the development of thinking and speech in children (mastery of mathematical terminology). Much more attention should be paid to the development of the initial skills of inductive and deductive thinking, the formation of children's cognitive interests and abilities. It should be noted that general methods of cognition form the basis of any scientific thinking, including mathematical. Naturally, the latter has its own special significance.

In practice, there is often a one-sided understanding of abilities as highly specialized, which borders on giftedness. In this regard, educators sometimes underestimate the formation of general cognitive abilities in all children. Any activity is impossible if a person does not have the ability to do it. In psychology, abilities are designated as personality traits necessary for the successful performance of an activity. The educator needs to know what exactly these abilities are, what mental properties the chosen activity will require and without which it is generally impossible.

Abilities should be considered not only in connection with a certain type of children's activity, but also in connection with its general structure, in which, first of all, orienting and performing actions are distinguished. And when we talk about general abilities for activity, we mean how much a child is able to use his knowledge, skills, and what level of cognitive independence he has. All this determines the effectiveness of the performing part of the general abilities. Along with this, it is necessary to form in children the ability to abstract, to highlight the main thing.

So, the mathematical development of children involves a broad program of introducing them to activities, in this case, mathematical, which is led by an adult (teacher, parents).

Tasks of the methodology of mathematical development as a scientific field:

1. Scientific substantiation of program requirements for the level

of the formation of mathematical representations in preschoolers in

each age group.

2. Determination of the content of mathematical material for

teaching children in preschool.

3. Development and introduction into practice of effective didactic tools, methods and various forms of organization of work on the mathematical development of children.

4. Implementation of continuity in the formation of mathematical representations in preschool educational institutions and at school.

5. Development of the content of the training of highly specialized personnel capable of carrying out work on the mathematical development of preschoolers.

6. Development of guidelines for parents on the mathematical development of children in a family.

The purpose of the mathematical development of preschoolers

• Comprehensive development of the child's personality.

• Preparing for success in school.

• Correctional and educational work.

Problems of mathematical development of preschoolers

1. Formation of a system of elementary mathematical representations.

2. Formation of prerequisites for mathematical thinking.

3. Formation of sensory processes and abilities.

4. Expanding and enriching the vocabulary and improving

related speech.

5. Formation of initial forms of educational activity.

Education leads development, is a source of development.

Learning must go ahead of development. It is necessary to focus not on what the child himself is already capable of doing, but on what he can do with the help and under the guidance of an adult. L. S. Vygodsky emphasized that it is necessary to focus on the “zone of proximal development”.

Ordered representations, correctly formed first concepts, timely developed mental abilities serve as a guarantee of further successful education of children at school.

Psychological research proves that in the process of learning there are qualitative changes in the mental development of the child.

From an early age, it is important not only to communicate ready-made knowledge to children, but also to develop the mental abilities of children, teach them to independently, consciously acquire knowledge and use it in life.

Learning in everyday life is episodic. For mathematical development, it is important that all knowledge is given systematically and consistently. Knowledge in the field of mathematics should become more complicated gradually, taking into account the age and level of development of children.

It is important to organize the accumulation of the child's experience, to teach him to use standards (forms, sizes, etc.), rational methods of action (counting, measurements, calculations, etc.).

Given the little experience of children, learning proceeds predominantly inductively: first, concrete knowledge is accumulated with the help of an adult, then they are generalized into rules and patterns.