Things that rhyme with math

238 best rhymes for 'math'

1 syllable

Bath

Path

Wrath

Dash

Hash

Stash

Slash

Bash

Flash

Cash

Trash

Crash

Have

Smash

Clash

Splash

Rash

Bass

Glass

Class

Pass

Grass

Last

Mass

Hath

Jazz

Mash

Lash

Fath

Plath

Nath

Spaz

Gash

Thrash

Nash

Brash

Mans

Plans

Dan's

Bags

Grams

Hands

Benz

Fags

Fans

Brass

Dads

Tash

Sash

Pash

Chazz

Mraz

Paths

Gangs

Blacks

Raps

Cracks

Racks

Rats

Backs

Cats

Caps

Acts

Packs

Facts

Tracks

That's

Dance

Stacks

Chance

Glance

Dats

Bands

Stands

Rags

Crass

Sass

Laughs

Cans

Trance

Thanks

Pants

Half

Laugh

Yass

Chasse

Hass

Grabs

Nass

Plass

Fass

Tass

Laps

Tags

Fangs

Stance

Traps

Sans

Vans

Lacks

Pads

Hats

Lands

Tabs

Flags

Jams

Bats

Hangs

Stabs

Adds

Straps

Stats

Sacks

France

Jabs

Asks

Mags

Pans

Lambs

Drags

Lads

Bangs

Crabs

Snacks

Scraps

Snaps

Clans

Trans

Slams

Stan's

Gals

Zags

Yams

Pals

Jacks

Fads

Ganz

Scams

Halves

Claps

Slabs

Scabs

Brags

Sags

Spans

Clams

Labs

Valve

Cabs

Tans

2 syllables

Bloodbath

Warpath

Footpath

Empath

Whiplash

Whereas

Dumbass

Badass

Surpass

Mustache

Backlash

Diaz

Pizzazz

Newsflash

Rehash

Eyelash

Abash

Pizazz

Backslash

Topaz

Boaz

Spetsnaz

Relax

Collapse

Attacks

Perhaps

Harass

Jackass

Relapse

Advance

Bypass

Alas

Amass

Smartass

Trespass

Outclass

Bluegrass

Impasse

Crevasse

Eyeglass

Repass

Morass

Spyglass

Romance

Exams

Xanax

Climax

Comrades

Programs

Demands

Flashbacks

Canals

3 syllables

Aftermath

Psychopath

Telepath

Alcatraz

Razzmatazz

Hourglass

Overpass

Plexiglass

Underclass

Fiberglass

Upperclass

Underpass

Biomass

Sassafras

Understands

4 syllables

Sociopath

Want to find rhymes for another word? Try our amazing rhyming dictionary.

If you write lyrics you should definitely check out RapPad. It has tons of useful features for songwriters, lyricists, and rappers.

Words That Rhyme With "Math"

Rhymes | Synonyms

include near rhymes

Filter Results

show rare words
show proper nouns
show consonances

All|Nouns|Verbs|Adjectives|Adverbs

1 syllable:

ass, baff, barf, bass, bath, blas, bras, caff, calf, Cass, chaff, chasse, class, crass, daff, das, draff, gaff, gaffe, gas, Gath, glass, Graf, graff, graph, grass, Grasse, haff, half, hath, jass, kaph, kas, kras, kvass, lass, lath, laugh, naff, pass, path, Plath, raf, raff, ras, rath, Sas, sasse, sclaff, snath, spath, staff, staph, strass, strath, swath, swathe, tass, tasse, trass, vas, wrasse, wrath, yaff

2 syllables:

agrafe, agraffe, alas, bagasse, behalf, birdbath, bloodbath, carafe, crevasse, cuirass, declass, depass, empath, filasse, footpath, giraffe, harass, impasse, Laplace, megass, morass, paillasse, palliasse, Patras, piaffe, pilaff, rascasse, repass, rubasse, smartass, sunbath, surpass, tarras, towpath, vinasse, warpath

3 syllables:

aftermath, allopath, interclass, isobath, monobath, naprapath, neuropath, plectognath, polymath, psychopath, telepath

4 syllables:

homeopath, homoeopath, naturopath, osteopath, sociopath

5 syllables:

endocrinopath, isothermobath

Mathematics at school: 9 things that infuriate

Mathematics textbooks are written in an incomprehensible language, a rare example from a problem is comparable to real life, and multiplication and division in a column for modern children is tantamount to making fire by rubbing two stones. As a result, schoolchildren get bored in math classes, and parents have to hire tutors. What needs to be changed in mathematics lessons in order to captivate students with it, - figured out Alexander Shklover, a participant in the Teacher for Russia program.

1. A linear rather than a concentric curriculum has been adopted in school mathematics education . The topics covered are again encountered by schoolchildren only if they suddenly turned out to be part of the new material. So, with the dead-end branch of mathematical evolution - percentages - children say goodbye in the sixth grade. Then the crown of the program is to find out the cost of goods at a discount. But then the interest is returned in the 17th task of the Unified State Examination: in it you need to calculate payments on a loan with complex interest calculation.

2. Calculations by hands in a column are put at the forefront , while in real life there are only two kinds of examples: verbal and on a calculator. Well, the truth is, you will count 17 + 21 in your mind, and to multiply 9317 by 319, you will rather climb for a phone than for a piece of paper.

3. Tasks on applied topics are separated from the area where they can be applied. The very first problem in the fifth grade textbook reports that Vasya bought 1% of all cucumbers in the tent. Indeed, the classic way to measure the amount of vegetables. This is not to mention the tasks about the Stakhanovites who overfulfilled the norm.

4. Teaching is dominated by dogmas, not explanations . Mathematics for most schoolchildren remains a set of abstract algorithms and “do it once!” commands. Although it is so easy to explain to a student that he divides 0.6 by 0.2 every day when he pours a jug of water into portions in glasses. But no, first you need to write down the rule about the transfer of a comma in the dividend and divisor.

5. A normal student is not able to extract information from the text of the textbook . Remember yourself: you are rereading the paragraph for the third time, but it has not become clearer one iota. And that's not your problem. In the textbook paragraph on measuring angles, there is no answer to the question of what angles are measured in, and the paragraph on multiplying fractions made me doubt whether I know everything about this magical skill.

6. The student in the lesson receives knowledge, not skills . A rare fifth grader will not reproduce the "speed-time-distance" formula. But the task to measure my speed by running 10 meters put a good half of my class into a stupor. “Ah,” they say, “here you need to divide 4.2 seconds by 10 meters?” It is understandable, it is more convenient to divide by ten.

7. The program is overloaded with higher mathematics, and the entire applied part goes under the knife . A good student at the exit from the 11th grade is able to integrate an exponential function. But to calculate the amount of material needed for repairs, to estimate its cost, the error of this estimate is unlikely.

8. That part of higher mathematics, which has a transparent applied meaning, is for some reason separated from it . The square trinomial describes the trajectory of the ball, the current in the socket changes along a sinusoid, and the logarithm allows you to continuously calculate bank interest. These are things that, it seems to me, it is simply criminal to keep silent in a conversation with schoolchildren.

9. The program is not in the nearest student development zone . Mastering the topic "Decimals" for a fifth grader is an incredible challenge. Almost half of them make a mistake in the 2 + 1.5 example, getting 1.7. However, you will probably have to look for an adult who does not understand what will happen if you add two and one and a half. And this is the leitmotif of the entire school curriculum: everything is very difficult, out of time, early, difficult and it is not clear why. And the result is a dead motivation, crushed self-esteem and a blazing hatred for mathematics.

“Aesthetics in mathematics is a very important thing” - Ogonyok No. 4 (5450) of 01/30/2017

38K 2 15 minutes. ...

"Ogonyok" completes the series "Mathematical walks", which he published throughout the year. In parting, one of the most quoted Russian scientists Anatoly Vershik told why mathematics should be beautiful

Previous photo

A photo: Kommersant / Evgeny Gurko / buy photo

Next photo

one / 3

A photo: Kommersant / Evgeny Gurko / buy photo

- Anatoly Moiseevich, during the year we talked with mathematicians about the most interesting things in their science. And to what extent, in your opinion, does mathematics need it today?

— You know, mathematics is a difficult science to popularize. Unlike the same biology and physics, which, by and large, are engaged in the study of nature, that is, the observable world, mathematics is engaged in a world that is unobservable even for mathematicians themselves. Therefore, it is almost impossible to popularize mathematics for the general public, but for young people it is another matter. There are many beautiful elementary problems in our science that can be explained to schoolchildren and people with little training. Before the war, there were famous books by Yakov Perelman "Entertaining Arithmetic", "Entertaining Mechanics", which perfectly satisfied the first interest in science and infected with enthusiasm. Today, of course, they are outdated, and new tasks have appeared.

— How can mathematics become obsolete?

— Before the war, the theory of information in the form in which we know it today was not yet created. It brought with it elementary problems of a special information-theoretic nature, which did not exist before. For example, you have some coins, some of which are counterfeit. They are slightly lighter than regular ones. You need to do a minimum of weighing to determine how many fake coins you have and how many are real. There were no such tasks in Perelman's time. Today, a good Olympiad problem for a schoolchild can be a simplified result of an article from a recent scientific journal. Often, if a mathematician writes a paper, he is asked to simplify some new elementary consideration to olympiad tasks. I sometimes carried out such orders, this is useful, as it attracts the attention of young people to mathematics. But now, unfortunately, scientists are doing much less.

— Why then can't mathematics be popularized for the general public? Moreover, after the reform of the Russian Academy of Sciences, scientists, in essence, were ordered to do this in order to receive funding . ..

— Now, indeed, even in a number of scientific reports it is supposed to give a popular presentation of the results obtained. But for officials, popularization is sometimes enough to imitate. Another thing is that a specialist, listening to this, can sometimes blush ... If we talk about popularization for the general public, then compared to representatives of other sciences, mathematicians are doing very badly here. A very indicative example is the famous century-old Poincare conjecture, brilliantly proven by Grigory Perelman (famous geometer, namesake of the popularizer of exact sciences Yakov Perelman.—0005 "O" ). Many publications have appeared on this topic that it is impossible to read mathematics either from laughter or from tears. It turned out that some not the most complex things, in principle, cannot be explained to people who do not have a certain set of knowledge. A constant mistake of journalists is that they understood the case of dimension two. But, alas, it was not possible to understand the meaning of the actual hypothesis for dimension three!

- What are you talking about!

- Nevertheless, understanding is accessible to a good student of the second or third year of mathematics or physics. Well, what is the solution itself - this is how the most qualified scientists understood it. This is a real challenge for mathematicians themselves. In fact, the world of mathematics exists separately, this is its strength and weakness.

- After Perelman refused the Clay Mathematical Institute prize, which promised a million dollars for solving the "seven millennium problems", fundamental for the development of mathematics and humanity, you wrote that in principle you are against such prizes. Why?

— Yes, from the very beginning I was very critical of the very idea of these awards. Scientists who are able to solve such problems of the "millennium" will do them without money. In this case, a million is an element of show business, a carrot on a string that was hung in front of the nose. Still, in science they usually give awards after you have done something, and this is natural. I must say that my position has always had many critics, mainly among Americans, but much more scientists in the States, Europe, and Japan supported me. I cited all these arguments to my friend Arthur Jaffe, a remarkable mathematician who was the chairman of the Clay Prize, which was established shortly before 2000. He explained to me that I do not understand anything in American life: if some mother hears that mathematicians are given a million dollars for solving a problem, she will immediately send her son to study mathematics at the university. I do not know how convincing this is, but in general my opinion has not changed. However, quite unexpectedly, Grisha's refusal to receive this and other prizes (and he refused many prizes, except for the award of our St. Petersburg Mathematical Society) had a positive effect. The general public understood: there are mathematicians who separate science from money. This is much more useful for modern society to know than the Poincaré hypothesis.

You need to trust reputable scientists, from beginning to end. Today this approach is distorted: the government's trust in science is based on personal acquaintances. I'm talking about trust based on the opinion of the professional community

Photo: Evgeny Gurko, Kommersant

— And how do you personally choose tasks for yourself? If I am not mistaken, you own the words that only a beautiful task is suitable for work. What does it mean?

— To solve a problem, it is necessary, at least for me, that it attracts aesthetically. Aesthetics in mathematics is a very important thing. Everything else - relevance, importance for applications, production necessity and sports moment - in second place. Personally, I have several topics in mathematics that I deal with alternately, and there are problems that I want to have time to solve, but it makes no sense to explain them. You can only name the areas to which they belong. For example, in my third year, on the advice of my first supervisor Gleb Pavlovich Akilov, I read the works of Gelfand and his co-authors, which by that time were little known here in Leningrad. They struck me with their beauty. Gelfand's ideas made a real revolution in functional analysis. In fact, he is the main creator of modern representation theory. The study of these works largely determined my choice. Since then, I have been fortunate to collaborate with him and with his colleague Mark Iosifovich Graev, who is still working in his 94 years. He once said that the mathematics of the 21st century is combinatorics. Combinatorics, according to many, is something from the program of the 10th or even 9th grade of the school. In fact, this is a fundamental part of mathematics, because every major advance in any field contains a combinatorial kernel. Here I collaborated a lot with my teacher, Nobel laureate Leonid Kantorovich, one of the founders of mathematical economics. Finally, I studied topology and the theory of dynamical systems with my main teacher, Vladimir Abramovich Rokhlin. It is this fusion of combinatorics, representation theory and dynamics that makes up my studies and the studies of my laboratory. It turned out to be quite a successful combination, in any case, our works are very well cited, they are very well known.

— How do you feel about the fact that today citations in scientific journals have become one of the main criteria for a scientist's success? And can anything replace this criterion?

- Citation is a criterion that is easy to test, and that's all its attraction for bureaucrats. And so this, of course, is an important criterion, but it is very limited for application. But, in my opinion, to evaluate scientific work, it is important to take into account a completely different aspect. I would express it in one word - trust. It is necessary to trust the assessments of reputable scientists and put their opinion at the forefront. It is the actively working scientists who should decide which direction to develop, who to hire, and who to give a grant. At the same time, a person, of course, must be responsible for the case in which he understands. Today this approach exists, but in a distorted form. The government's trust in science is based on personal acquaintances. I'm talking about trust based on the opinion of the professional community. The lack of trust of the authorities in scientists is exhaustively illustrated by the reform of the Academy - both by its very content, and by the fact that it was prepared and carried out secretly.

— How realistic is it today in Russia for "pure mathematicians" who do not have a bias in applied sciences to receive a grant for the development of their science?

— The time for foreign grants in Russia is over. I sometimes repeat the phrase, which now looks seditious, that in 2000 I received a NATO grant. Then they decided to support conferences on purely scientific mathematical topics in Russia too, which was very cool. There was also a program of the American Mathematical Society. Its members gathered at the beginning of the 19In the 1990s, a million dollars in grants to Russian mathematicians, and this helped many at that difficult time not to leave science. As for domestic grants, I consider one of the few positive achievements of the post-perestroika era to be the creation of the RFBR, the Russian Foundation for Basic Research. It is modeled after the famous National Science Foundation in America. Three years ago, after the defeat of the Russian Academy of Sciences, the Russian Science Foundation was established, much richer, but also much more severe. My group received a grant from this foundation for three years, but did not receive it for the next two, although we even exceeded the plan in terms of the number of publications. It turned out that the Foundation does not take into account all recognized reputable Russian journals. This is an example of formalism and pathological love for scientometrics. In general, it has become much more difficult to receive grants: of those, for example, who apply to the same RFBR, about a quarter receive funding.

— We are walking along the coast of the Gulf of Finland in Repino. An international mathematical conference was held here 40 years ago, and you were not allowed to read a paper at it. Do you remember what you wanted to talk about then?

— It probably makes no sense to recall the topic now, but the case itself was quite indicative. The fact is that at that time all scientists were divided into two unequal parts: visiting and not traveling abroad. There were people who, although not systematically, were able to travel abroad. And there were a huge number of people who could not even claim it. For a number of reasons, I was just in this part. Therefore, international conferences in our country have always attracted special attention. One such was held here, in Repino, at 1976th. I submitted an application for the report because it was supposed to be a serious mathematical part, which was organized by a wonderful mathematician from the Institute for Information Transmission Problems of the Russian Academy of Sciences Roland Lvovich Dobrushin. But since the conference was connected with coding theory, it was, as they say, restricted access, as it turned out, it was possible to get there only with special permissions.

In general, any participation in an international conference, especially a trip somewhere, began with the fact that the competent authorities gave a reference, which was signed in our case by the dean, the secretary of the party bureau and the secretary of the trade union committee. Later, I found out the wording with which they didn’t sign such a characterization for me - one of my colleagues asked the official why I couldn’t read the report there. They answered him: "He does not conduct social work." My colleague objected - by that time I had been directing the work of the Leningrad Mathematical Society for many years. The answer was: "What is this community service, since he likes it?" In general, they didn’t let me in, but I was relatively young, but for many prominent scientists, the inability to go to an international conference and report there on their achievements was a monstrous injustice. Often refusals were accompanied by promises that soon all documents would be checked and then it would be possible to go. When Western colleagues came to meet the delegation at the airport, they were told that so-and-so "fell ill" or "takes exams"...

— And how did your Western colleagues perceive this state of affairs?

— Oh, that's very interesting! Do you know that the term russian time even appeared then? In 1974, my report was included in one of the sections of the International Congress of Mathematicians in Vancouver. They generally then selected a lot of reports by Russian mathematicians, including David Kazhdan, Sergei Bernstein, Mikhail Birman and others. These reports were included in the schedule, and they could not be replaced by anything. But no one was released. As a result, the reports were announced, followed by silence. This was called "Russian time".

By the way, this story had a sequel. Not so long ago, the International Mathematical Union published on the Internet the names of all speakers of all congresses in different years. I wrote to them that we were not allowed to speak through no fault of ours, and asked them to include names in the general list. As a result, they wrote to me that this would entail great difficulties, because then you need to include the names of Chinese mathematicians who had similar problems. But in the end, to their credit, all the names were named.

— Nevertheless, now you can hear that it was then, in spite of everything, that science flourished, and after the collapse of the USSR, everything withered...

— I treat such conversations, to put it mildly, with distrust. We somehow quickly forgot that the glory of science of that time was largely given by that part of mathematicians who were not officially recognized, they did not work at universities, but in various organizations far from high science. They were not allowed to defend dissertations, publish papers, etc. And against all odds, they became remarkable mathematicians. To speak of them as Soviet scientists is like counting Akhmatova and Bulgakov among the achievements of Soviet literature. The same fake. Everyone says that mathematicians left because of the collapse of the country in perestroika. But this is a lie! Mass migration began as soon as it became possible. Scientists were traveling just as far away from the Soviet system itself. For example, under various pretexts, my most talented students were not taken to graduate school, and I actively helped those who wanted to leave at 1970-1980s. Today they work at the best universities in the world. But maybe they wouldn't have gone if their own country hadn't pushed them away like that. This is one of the reasons for the current crisis in science. Therefore, we no longer have many schools, say, in functional analysis, in algebraic geometry, and so on. Responsibility for the current state of personnel in science lies to a large extent with various representatives of the Soviet government.

I will say one heretical thing: after 19On the 91st, liberal scientists had a chance to take the initiative in scientific leadership into their own hands. Those administrators from science who pushed unwanted people out of science, threw down dissertations on a national basis, calmed down in fear, because they suddenly found themselves out of work - they were no longer invited to meetings, and it became clear who was who. But there was no one to take the initiative, because the liberal scientists somehow also disappeared. And gradually the hushed ones came to life again.

Since 2014, since the beginning of the defeat of the Russian Academy of Sciences, there has been a very fast process of bureaucratization, which threatens to surpass what was in the USSR. That is, the very system of the Soviet organization of science was destroyed, but this process of bureaucratization remained, it seems to live on its own

Photo: Evgeny Gurko, Kommersant

— In other words, you want to say that mathematics was formed in spite of the existing system, and not because of it?

— Difficult to answer unambiguously. Let's tell a telling story about St. Petersburg. This is actually a parody of the relationship between the then American and Soviet science. As you know, there was such a mantra that the Soviet Union at first succeeded in cosmonautics, in launching satellites, because we had a very good mathematical education. This is true: mathematical education was and to some extent remains good, but its role in this matter, of course, is greatly exaggerated. Nevertheless, the Americans allocated large funds for the stimulation and development of mathematical departments. Already at 19In the 80s, specialists at US universities made a whole series of good popular articles on how mathematics helps in various areas of life. And it took effect. Congress increased investment, and so on.

After this outburst in the USA, our Politburo, frightened by the activity of the Americans, also adopted a resolution to increase student scholarships in mathematics departments and to open nothing less than the International Mathematical Institute of the Advanced Study type in Princeton. For some reason, Moscow refused this idea, then it was decided to open it in Kyiv. But at that time, disaster struck.86 years in Chernobyl. So the idea was picked up by the authorities in Leningrad, and we organized the International Institute, which in 1991 received the name of Leonhard Euler. In general, the story is interesting, it is about both sides raising the stakes. But now it is no longer possible.

Why? Is the race for leadership in science over?

— We live in a completely different world! I think the role of fundamental science will weaken. When it comes to applications and technologies, politicians want instant breakthroughs and therefore require minute-by-minute reporting. This impatience is the reason for the attack on the Russian Academy of Sciences, although it, of course, needed a complete reorganization. But, by and large, today no one understands how science works. And there is a very fast process of bureaucratization that threatens to surpass what was in the USSR. That is, the very system of the Soviet organization of science was destroyed, but this process of bureaucratization remained, as if it lives on its own. There is virtually no authority of the Academy anymore. And I don't think there is a clear vision for the future. But in the last few decades, Russian scientists for the first time truly began to enter the international community of scientists, despite political upheavals.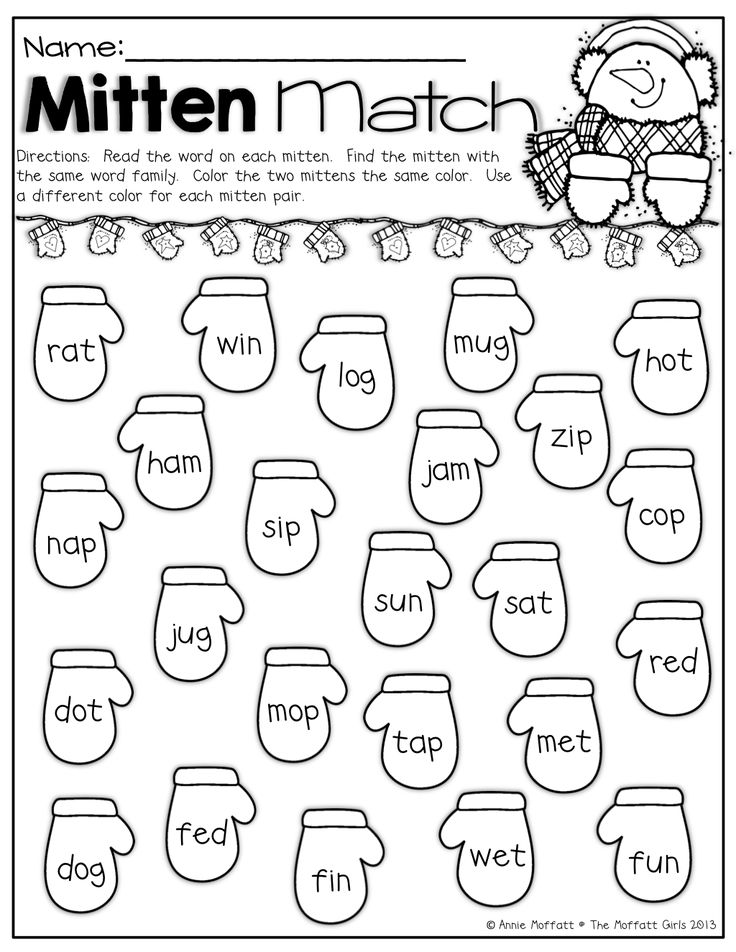 It is very important.

— This year, our magazine opened a column dedicated to understanding the events of a hundred years ago — the 1917 revolution. To what extent do you think it influenced the development of mathematics?

- That's a huge question! The year 1917 laid down the basic principle of a totalitarian state, which is based on inattention to the individual, to the individual human life. In general, the revolution, and especially the time that followed it, became crushing for the mass of talented scientists. Under 19In 1917, the Russian mathematical school was quite strong. Suffice it to mention the names of Alexander Fridman, who died in his youth in 1924 from typhus. The famous Alexander Lyapunov, who committed suicide in 1918. Dmitry Egorov, president of the Moscow Mathematical Society, who was accused of monarchism and convicted of religious beliefs, along with the famous philologist Alexei Fedorovich Losev. He was sent into exile in Kazan, where he died in a prison hospital.

On the whole, the Academy of Sciences tried for quite a long time to maintain relative independence, because it retained many academicians who, although they did not advertise, were clearly skeptical of the Soviet government. It ended after the mass attack on the Academy at 1928th. After that, it was already, so to speak, inlaid with people of a new type.

- Did you find someone from the pre-revolutionary professorship?

- Very few, but it was very important, because these people were the bridge between pre-revolutionary and post-revolutionary mathematics. These acquaintances made it possible to absorb a special tradition of treating science as something valuable in itself. In Leningrad, Vladimir Ivanovich Smirnov was such a link. In Moscow, the same role was played by Yegorov, whom I spoke about, and Nikolai Nikolaevich Luzin, whose students were such famous scientists as A. Kolmogorov, P. Uryson, L. Lyusternik, D. Novikov, and others.

— Anatoly Moiseevich, is it possible today to guess in which direction mathematics will develop, what areas will be in demand?

- Mathematics is a living organism, so it is difficult to predict in which direction it will develop.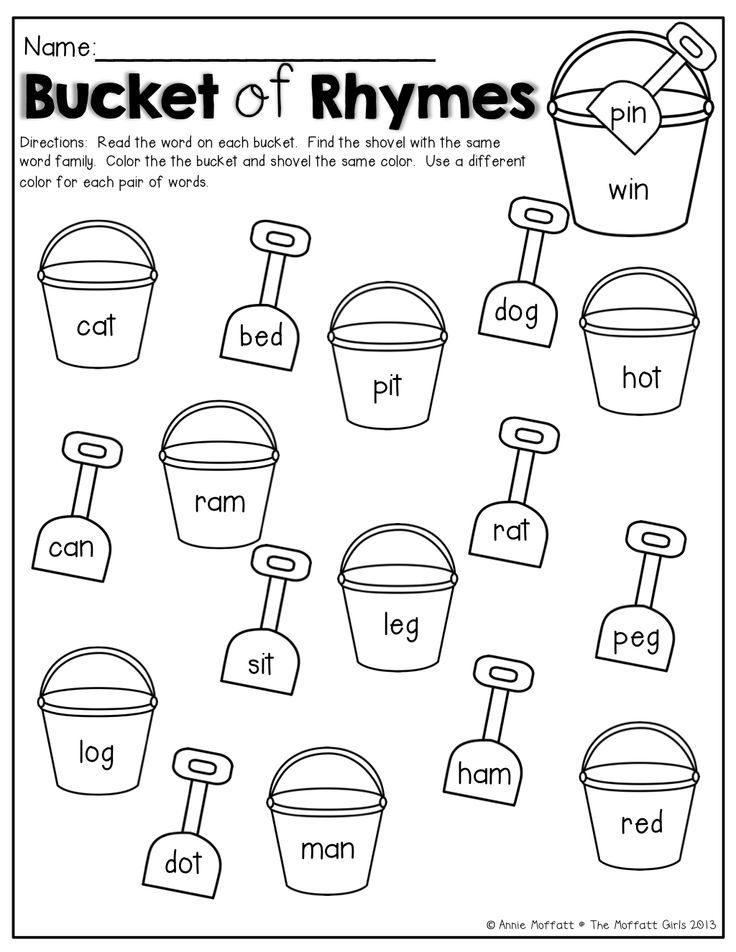 Today in mathematics, of course, the role of applied areas is exaggerated. Mathematics is always open to any intrusions of biology, physics and other sciences, but the main thing in it, as the famous mathematician David Hilbert said, is its internal unity, the deep meaning of its own changing constructions. In a sense, mathematics will always exist, because it is part of the structure of the human mind, and it can be destroyed only by destroying humanity itself.

Visiting card

Anatoly Vershik is one of the most prominent mathematicians in the northern capital of Russia

He was born in 1933, in 1956 he graduated with honors from the Faculty of Mathematics and Mechanics of Leningrad University. Today - Doctor of Physical and Mathematical Sciences, Chief Researcher of the St. Petersburg Department of the Mathematical Institute. V.A. Steklova, professor at St. Petersburg State University, member of the European Academy of Sciences.

He has always taken an active civic position, referring to himself as a special type of liberal professor, who was widely known in Russia before the 1917 revolution.