What does level e mean in iready math
i-Ready Central Resources | Family Center – FAQs
The Diagnostic covers these Reading domains:
Phonological Awareness is the understanding that a spoken word is made up of different parts and that each of these parts makes a sound. For example, the word bat includes the sounds /b/, /a/, and /t/, and the word batter can be broken into two syllables that make the sounds /bat/ and /ter/. Phonological Awareness is an important building block for Phonics. Readers need to be able to distinguish, or make out, the individual sounds in spoken words before they can fully master matching sounds to letters.
Phonics instruction teaches students how to connect the sounds they hear in spoken words to the letters they see in written words. For example, a student who can connect sounds to letters knows to read “th” in
then as a single sound /th/, rather than the sound /t/ and the sound /h/. Students have to learn many different connections between sounds and spelling patterns. In fact, there are so many connections that learning Phonics can feel like learning the rules to understand a hidden code. But this skill is mastered by taking one step at a time, learning one rule and then another, and so on. Once students can make these connections quickly and easily, they can really start to read for meaning.
High-Frequency Words are the words that appear most often in what students read. Words such as the, and, and it are high-frequency words. Because these words appear so often, readers must learn to recognize them automatically. Also, these words are often spelled in ways that can be confusing. Words such as could and there do not follow the rules that connect sounds to letters in most words. Learning to recognize these words automatically helps students read more quickly and easily, which gives them a better opportunity to understand what they are reading.
Vocabulary is the name for the words a student knows. The more words a student knows, the easier it is to understand what they read. Good readers know the meanings of many words. Students grow their vocabularies by hearing and reading new words, talking about words, and being taught specific words.
The more words a student knows, the easier it is to understand what they read. Good readers know the meanings of many words. Students grow their vocabularies by hearing and reading new words, talking about words, and being taught specific words.
Comprehension: Literature describes a student’s ability to understand types of writing that are usually made up, or fictional. Stories are the literary texts that students read most often, but plays and poems are also examples of literary texts. A student who understands literature might identify the sequence of events in a story, discuss the meaning of a poem, or explain the lines a character speaks in a play. As a student develops as a reader, the student is able to understand stories, plays, and poems that are increasingly complicated.
Comprehension: Informational Text describes a student’s ability to understand types of writing that are usually true. Books about science or history are examples of informational text, as are newspaper articles or magazine articles. This kind of writing is often structured differently than literary texts. Informational text often does not tell a story, and it is usually organized into sections with headings. Additionally, it might contain charts, diagrams, and graphs that are important to understanding. A student who understands informational text might identify the main idea and supporting details, describe the way the writing is organized, or draw information out of a photograph or diagram.
This kind of writing is often structured differently than literary texts. Informational text often does not tell a story, and it is usually organized into sections with headings. Additionally, it might contain charts, diagrams, and graphs that are important to understanding. A student who understands informational text might identify the main idea and supporting details, describe the way the writing is organized, or draw information out of a photograph or diagram.
The Diagnostic covers these Mathematics domains:
Number and Operations in Grades K–8 refers to the mathematics skills often thought of as arithmetic, from reading and writing numbers to adding, subtracting, multiplying, and dividing different types of numbers. This includes whole numbers, decimals, fractions, integers, and irrational numbers.
Algebra and Algebraic Thinking
in Grades K–8 refers to mathematics skills related to seeing number patterns, understanding the meaning of addition, subtraction, multiplication, and division, and using symbols to write and solve equations including those used to solve word problems. In the high school grades, this domain covers the Algebra topics related to using functions, equations, and inequalities to model mathematical situations and solve problems by reasoning quantitatively and extending the understanding of operations beyond the real number system.
In the high school grades, this domain covers the Algebra topics related to using functions, equations, and inequalities to model mathematical situations and solve problems by reasoning quantitatively and extending the understanding of operations beyond the real number system.
Measurement and Data in Grades K–8 is a wide range of mathematics skills related to collecting, organizing, and interpreting numerical information, from telling time or using a ruler to measure the length of an object to using formulas to find volume or surface area. It also includes understanding tables and graphs, and in later grades, statistics and probability.
Geometry in Grades K–8 refers to a variety of skills related to analyzing two- and three-dimensional shapes. These include naming and classifying shapes using characteristics such as symmetry, number of sides, and angle measures, and in later grades, using congruence and similarity. In the high school grades, this domain covers Geometry and Measurement topics related to developing spatial geometric reasoning, connecting geometric properties and equations, writing proofs, and using statistics and probability concepts to analyze data.
These summaries of the domains found in the i‑Ready Diagnostic can be downloaded and shared using this PDF resource.
Understanding i-Ready Scores - Issaquah School District 411
- Understanding the 4-Point Scale
- How can I use these scores to help my student?
- Using i-Ready at Home
- Understanding the topics tested and how to support learning in each topic.
- How do I access i-Ready Scores?
- Talking to your student about their score.
- How to use the Lexile Score to find a good-fit book for your student.
- i-Ready Scale Score Charts
This 4-point scale is used with i-Ready and the state assessment, the SBA. We can now provide scores with decimal points so you can see how close your student was to the next or previous level. Remember: Scores are based on the expectation at the time the test was taken, not in comparison to the end-of-year expectation.
We can now provide scores with decimal points so you can see how close your student was to the next or previous level. Remember: Scores are based on the expectation at the time the test was taken, not in comparison to the end-of-year expectation.
4 Exceeding ExpectationScores of 4.00 - 4.99 mean the student scored at advanced levels on the assessment, on track to be well above standard by the end of the year | |
3 Meeting ExpectationScores of 3.00-3.99 mean the student scored at a level at the level expected for a student on track to meet standard by the end of the year. | |
2 Approaching ExpectationScores of 2.00-2.99 mean the student was approaching the score expected for a student on track to meet standard by the end of the year. Students at this level show some strengths and some gaps or difficulties with grade level content. IMPORTANT NOTE: i-Ready tends to be somewhat more challenging than the state assessment, meaning that students at this level may meet standard on state assessments as they continue to build their skills. | |
1 Below ExpectationScores of 1.00-1.99 mean the student scored below the level expected of a student on track to meet standard by the end of the year. |
What if there is no score for one of the topics assessed?
For Phonological Awareness, Phonics and High Frequency words, a missing score indicates that i-Ready determined your student no longer needs to be assessed in that area or topic.
Using the Detail Level
Using the Detail Level, you can quickly understand where your student scored in comparison to expectation on this test for the overall areas of Reading and Math, and for the topics assessed. For example:
For example:
- If a student scores a 3.12 on a test or topic, that means the student scored just above expectation and is on track to meet standard.
- If a student scores 2.75 on a test or topic, that means the student scored 75% of the way between a 2.00 and a 3.00.
Seeing the detail level for each topic tested allows you, like the teacher, to see areas of relative strength and areas for improvement for your student.
If your student scored significantly below 3.00, that may mean that your student has a skill gap needing support. Here are ways you can support your student. You can learn more about the score for each topic assessed in the panel below.
Communicate with your student's teacher
Your student's teacher uses i-Ready AND classroom tests, assignments, and observations to get a clear understanding of your student's skills. Your teacher will have insights and ideas for how you can help your student at home, if it is needed.
Use i-Ready at home
i-Ready creates a custom learning experience for your student called MyPath. The i-Ready system uses your student's answers to the test questions to identify next steps for learning and automatically assign lessons. When your student logs into i-Ready through Clever, at school or at home, there is a next-step lesson for Reading and Math ready to go.
Click here to learn more about using i-Ready at home.
See the panel below on Understanding the topics tested and how to support learning in each topic or visit our Helping your student at home page for more ideas on supporting your student in areas tested by i-Ready.
Your teacher may suggest your student complete i-Ready lessons at school or at home or both. Here are some tips for using i-Ready.
1. access i-Ready through Clever.
IMPORTANT for iPad users: if using an iPad at home, download both the Clever app and the i-Ready app THEN access i-Ready through the Clever app.
2. Review your student's i-Ready Dashboard with your students to see their progress and what they are working on.
Directions:
CLICK HERE to view a video for directions for accessing the dashboard. Or visit the i-Ready Family Center for more information.
This video for directions is available in the following languages: Click on the language to access the video. Arabic, Bengali, Cambodian (Khmer), Chinese (Mandarin), Haitian Creole, Hmong, Korean, Portuguese, Russian, Samoan, Somali, Spanish, Tagalog, Yupik
3. If your student isn't already completing 30-49 minutes per week of i-Ready MyPath lessons at school, you may want to have your student complete i-Ready lessons at home.
Your student will learn how to access lessons at school in the fall. MyPath provides lessons that are assigned to students based on how they answered questions on the i-Ready assessments. Then i-Ready assigned lessons it determined to be most important in developing their skills in reading and math. Their next lesson is always ready for them.
Their next lesson is always ready for them.
Please note: Our focus is for students to complete MyPath lessons IF we identify a skill gap. We don't expect all students to complete MyPath lessons, though some may find it beneficial or even a fun way to extend learning even in areas of strength. Keep in mind, your student may already be doing the suggested amount of i-Ready lessons at school (30-49 minutes per week in each subject where there is need.) We want to be careful not to exhaust our students on i-Ready by spending too much time in it.
Finally, students should complete i-Ready lessons independently. If a student doesn't pass the lesson the first time, that is when they should ask for help from an adult on the learning portion of the lesson, then complete the practice independently.
i-Ready tests 3-6 domains, or topics, in reading and 4 topics in math. Teachers can use scores by topic to further understand your student's learning needs. The tables below is designed to help you understand each topic and suggest ways could support your student at home.
The tables below is designed to help you understand each topic and suggest ways could support your student at home.
Math Topics
Please see our Elementary Learning page to see what specific content is taught at each grade.
| Numbers & Operations | Number and Operations in K-5 includes the following:
| You can help your student in numbers and operation by...
Click here for more. |
|---|---|---|
| Algebra & Algebraic Thinking | Algebra and Algebraic Thinking in Grades K–5 includes the following:
| You can support your student in algebraic thinking by...
Click here for more. |
| Measurement and Data | Measurement and Data in Grades K–5 includes the following:
| You can support measurement and data by.
Click here for more. |
| Geometry | Geometry in Grades K–5 includes to the following:
| You can support your student in geometry by...
Click here for more. |
Reading Topics
Please see our Elementary Learning page to see what specific content is taught at each grade.
| Reading Foundational Skills: Phonological Awareness Phonics High Frequency Words | These topics test how well students understand and can decode words. Phonological Awareness is the understanding of sounds that make up words. This building block of language includes standards for Kindergarten and 1st grade. Phonics is the connection between the sounds of a word and the letters in the written word. There are phonics standards in Kindergarten through 3rd grade. High Frequency Words test the ability to quickly identify words that appear most often in what children read. High frequency words include standards for Kindergarten through 2nd grade. |
|---|---|
| Vocabulary | Vocabulary assess the words a student knows. The more words students know, the easier it is to understand what they read. You can help your student build vocabulary by.
|
| Comprehension of Literary or Informational Text | Comprehension tests whether students understand what they read - for both stories and informational text. The following are comprehension ideas and skills, and questions you can use to talk with your student about what they are reading. Character & Setting: Who is in this book? How did the character change in this book or what did the character learn? What is the book about? Where does it take place? What is the place like? Retelling: What did that page / chapter, say? Summarizing: Tell me about that chapter in a few sentences? What happened first? What is the problem in the story? What was the solution? Inferring: What do you think ____ means? What do you think the character is thinking at that moment? Predicting: What do you think will happen next? How do you think this story will end? Connecting: How is that (idea, experience, story line. |
Directions for Accessing i-Ready Scores
Note: If using a smart phone, please use a web browser on your phone and follow the instructions, as test scores are not available through the app.
1. Log into Family Access. Click here to learn how to use Family Access.
2. Scores are found under Test Scores.
3. Look for the test date for the most recent score, and under test name, look for i-Ready Reading or i-Ready Math
We recommend talking to your student about a few subjects connected to scores:
1. Celebrate achievement and growth! Looking at scale scores; some will have jumps from Fall to Winter, others from Fall to Spring. Focus on the increases. Remember that students who started at a level and ended at the same level had to grow in order to stay at that level over the course of the year!
2. Ask about their experience. How students are engaging with i-Ready can impact scores and how well it supports learning. Some students have shared that they like the lessons and learning games, while others report getting tired of doing i-Ready over time. You can ask your student whether they felt they were able to show their best effort on the last i-Ready assessment.
Ask about their experience. How students are engaging with i-Ready can impact scores and how well it supports learning. Some students have shared that they like the lessons and learning games, while others report getting tired of doing i-Ready over time. You can ask your student whether they felt they were able to show their best effort on the last i-Ready assessment.
In the How do I support my student's learning? panel, you will find there are options for using i-Ready at home, even into the summer. It is important, though, to hear from our students as to whether they need an i-Ready break or whether doing a little more here and there would help them achieve their learning goals.
i-Ready does not test all aspects of reading and math, so please remember that the report cards from your classroom teacher are more comprehensive. They will use observations, tests, and daily work to determine how students are growing and achieving in reading and math. It is possible for a student to meet expectation on i-Ready, and have growth needs. It is also possible for a student to be at score below a 3.00 in i-Ready while showing stronger reading and math skills in class. That is why your teacher provides a report on overall achievement with teacher-parent conferences and the report card.
It is possible for a student to meet expectation on i-Ready, and have growth needs. It is also possible for a student to be at score below a 3.00 in i-Ready while showing stronger reading and math skills in class. That is why your teacher provides a report on overall achievement with teacher-parent conferences and the report card.
Your student's teacher may have already shared a reading level using F&P's letter scale (A-Z). Below is how you can use the Lexile score provided by i-Ready to select books for independent reading.
Always keep in mind that every student has a reading RANGE, not a single level. When reading text that is of high interest, students can read at the high end of their range or even above their range. It is also okay for students to sometimes choose books toward the low end of the range when they want and easier reader or because they have interest in the book. All reading provides benefits.
So how do I use the Lexile Score?
Step 1. Note your student's Lexile Score
Note your student's Lexile Score You can access your student's Lexile Score in Family Access. In family access, under test scores, open your students most recent i-Ready Reading assessment results and take note of the Lexile Score on the far right.
NOTE: Scores that start with BR indicate a "beginning reader score". BR400 is a lower reading level than BR100.
Step 2. Calculate the Lexile RANGE.
The Lexile RANGE is the Lexile score + or - 75. So if a student receives a Lexile score of 500, the student's Lexile range is 425 - 575.
Books have a Lexile Level, so books with levels that fall in this range, are books that match to your student's reading level. Remember, student may want to read books above or below this range based on interest. That is okay too!
Step 3. Use the book finder.Book Finder is an online tool to help parent find books. CLICK HERE to find books by Lexile, Lexile Range or Grade Level.
CLICK HERE to find books by Lexile, Lexile Range or Grade Level.
Other ways to use Lexile:
Your local librarian likely understands Lexile and can help you find books using Lexile.
OR
You can match your student's Lexile Range to an A-Z reading range by using the chart below to estimate F&P reading range from your Lexile range.
Note: Lexile and F&P are two different ways to match a student's reading level to a book. Both are guides, not perfect measures, meaning any given book may match to a higher Lexile and lower A-Z level or lower Lexile and higher A-Z level.
| If the Lexile Score is in this range... | My F&P Reading Level range is likely to be... | Which is at this Grade Level range. |
|---|---|---|
| BR400-BR151 | Pre-A | Pre-Kindergarten - Kindergarten |
| BR150-99 | A-D | Kindergarten - 1st grade |
| 100-199 | D-G | 1st grade |
| 200-299 | G-I | 1st grade - 2nd grade |
| 300-499 | I-M | 2nd grade |
| 500-699 | M-Q | 2nd - 3rd grade |
| 700-849 | P-S | 3rd - 4th grade |
| 850-999 | S-U | 4th - 5th grade |
| 1000+ | W-Y | 5th grade & beyond |
Below are the i-Ready Scale Score charts that show the scale score of a student who is on track to meet standard, based on when the test is given. i-Ready tests are given as follows:
i-Ready tests are given as follows:
- Fall: September (1st-8th Reading, 1st-5th Math)
- Winter: January-February (K-5th Reading and Math)
- Spring: April (K-2nd Reading)
- End-of-Year: late May/June (K-2 Math)
Overall Reading Expected Scale Scores
| Fall | Winter | Spring | End-of-Year | |
| Kindergarten | 346 | 366 | 384 | 396 |
| 1st grade | 396 | 421 | 443 | 458 |
| 2nd grade | 458 | 480 | 500 | 513 |
| 3rd grade | 513 | 526 | 537 | 545 |
| 4th grade | 545 | 559 | 571 | 579 |
| 5th grade | 579 | 591 | 602 | 609 |
| 6th grade | 609 | 612 | 615 | 616 |
| 7th grade | 616 | 622 | 628 | 632 |
| 8th grade | 632 | 636 | 640 | 642 |
| 9th grade | 642 | 650 | 657 | 661 |
Overall Math Expected Scale Scores
| Fall | Winter | Spring | End-of-Year | |
| Kindergarten | 346 | 357 | 367 | 373 |
| 1st grade | 373 | 389 | 403 | 413 |
| 2nd grade | 413 | 424 | 434 | 441 |
| 3rd grade | 441 | 450 | 459 | 464 |
| 4th grade | 464 | 471 | 478 | 482 |
| 5th grade | 482 | 488 | 494 | 498 |
| 6th grade | 498 | 504 | 510 | 514 |
| 7th grade | 514 | 521 | 527 | 531 |
| 8th grade | 531 | 535 | 539 | 541 |
| 9th grade | 541 | 547 | 553 | 556 |
Number e | Materials for preparing for the exam in mathematics USE-Studio
We first meet with a wonderful number e , starting to study the exponential function, logarithms and derivatives. Therefore, for a better understanding, we recommend that you read our articles "Exponential Function" and "Geometric Meaning of the Derivative".
Therefore, for a better understanding, we recommend that you read our articles "Exponential Function" and "Geometric Meaning of the Derivative".
In the article "Exponential Function" we talked about the most important property of a function - for this function grows very quickly. And not just "growing fast" - the more x , the higher its growth rate, the steeper the graph goes. We can say that with an increase of x both the values of the exponential function and its derivative grow. And if the argument of the exponential function is time, then for such a function is a mathematical expression of a rapidly developing process.
Among the exponential functions there is a special one. It is called the exponent, its formula. Its peculiarity is that at each point the growth rate of this function is equal to the value of the function itself at this point. In other words, , that is, the derivative of a function is equal to itself.
Draw several function graphs for and also for . Among these graphs there is such that the tangent to it, drawn at the point, goes exactly at an angle to the positive direction of the OX axis.
Among these graphs there is such that the tangent to it, drawn at the point, goes exactly at an angle to the positive direction of the OX axis.
This is the graph of the function. The number e itself is irrational, that is, it is expressed as an infinite non-periodic decimal fraction. Approximately it is equal to 2.718.
The logarithm to the base e is called natural and is denoted . If you encounter such logarithms in an equation or inequality, you work with them in the same way as with any others that have a base greater than 1.
The function also has an interesting property:
This means that as x grows, the graph of the logarithmic function goes more and more gently, its growth rate decreases, which is what we see.
Formulas for derivative functions and contain the expression:
The number e , like the number , is one of the world's constants. This is the name of the numbers that can be found in mathematical formulas that express the fundamental laws of nature - in physics, statistics, biology or economics.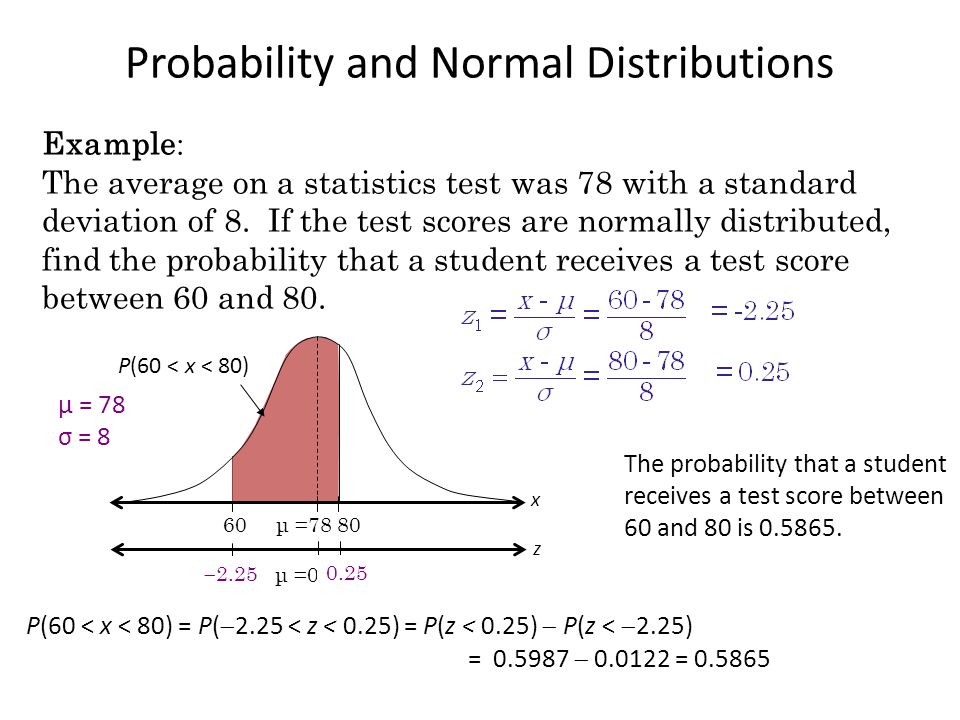
The number has been known to people since ancient times. It is equal to the ratio of the circumference of a circle to its diameter. But with the number e (named after the great mathematician Leonard Euler), mankind met much later. It was first calculated by the mathematician Jacob Bernoulli at the beginning of the 18th century, and he did this by solving a purely practical problem of calculating interest on a bank deposit.
In the tasks of the USE variants, you met tasks where a deposit of x is placed in a bank under p % per annum. It was necessary to find, for example, what the contribution would be in two years. Talking about solving such problems, we have derived convenient formulas:
So, if a bank deposit is placed at 10% per annum, it will grow 1. 1 times in a year, 1.21 times in two years, and approximately 2.6 times in ten. This means that the growth of the deposit depends on how long it lies in the bank, that is, how many times the interest is calculated. And what will happen in a hundred years? And if you find a bank where interest is calculated not once a year, but once a day? And even if every day a very small percentage is charged, but there are a lot of days! Is it true that you can put one dollar in such a bank at one hundredth of a percent a day, and in a couple of decades take a million from the bank?
1 times in a year, 1.21 times in two years, and approximately 2.6 times in ten. This means that the growth of the deposit depends on how long it lies in the bank, that is, how many times the interest is calculated. And what will happen in a hundred years? And if you find a bank where interest is calculated not once a year, but once a day? And even if every day a very small percentage is charged, but there are a lot of days! Is it true that you can put one dollar in such a bank at one hundredth of a percent a day, and in a couple of decades take a million from the bank?
Let's formulate the problem like this. Let the bank charge every day one hundredth of a percent. How many times will the deposit increase in 10,000 days (that's twenty-seven plus years)? In other words, what is the approximate value of ? And what will the value tend to if n tends to infinity?
This is the problem that Bernoulli solved. If n is very large, or, as mathematicians say, infinitely large, tends to infinity (that is, more than a million, more than a billion, more than two billion . ..), then the value will, on the contrary, be very small. We can say that it will tend to zero.
..), then the value will, on the contrary, be very small. We can say that it will tend to zero.
It turns out that in this case the value will tend to the number e . If the bank accrues 1% every year, after 100 years the deposit will increase by about e times (recall that e ≈ 2.718). Even greater accuracy will be achieved if the bank charges 0.01 percent every day. After 10,000 days, the contribution will increase by about 90,003 e 90,004 times. So, if n tends to infinity, then the value tends to the number e .
This unexpected fact is called second remarkable limit. You will meet him in a course on calculus.
Troika in Mathematics — Tatyana's Day
Valentin Fedorovich Butuzov every Thursday participates in meetings of the dean's office of the Faculty of Physics. Today he was also there and even a little late for the interview.
Case studies
- What questions do you discuss at the dean's meeting?
- You know, the lion's share of discussions concerns losers. We have a head for each course, because the courses are large - more than four hundred people each, each head of the course comes with the files of students who are presented for expulsion, or they raise the question of allowing another retake. There is an order of the rector, according to which those who have not liquidated their debts for the past semester by February 21 are subject to deduction. Here we sit and discuss all of them, delve into all sorts of circumstances that allow us to allow another retake. Someone, of course, has to be expelled, someone to give another try.
We have a head for each course, because the courses are large - more than four hundred people each, each head of the course comes with the files of students who are presented for expulsion, or they raise the question of allowing another retake. There is an order of the rector, according to which those who have not liquidated their debts for the past semester by February 21 are subject to deduction. Here we sit and discuss all of them, delve into all sorts of circumstances that allow us to allow another retake. Someone, of course, has to be expelled, someone to give another try.
- And how many of those who do not have time? And what is the percentage of excellent students and those who are so-so?
- I can give some examples. Let's say, in the first year now, after the first session, about 10% of excellent students, only ten, that's about 50 people. Our course is large, 450 people. About half of them manage to get 4 and 5. The other half with triplets. And, I think, after the first course, 25 people will be expelled.
And, I think, after the first course, 25 people will be expelled.
- What was the situation at the physics department 20 years ago? Has something changed?
- Oh sure. Over the years, evolution, unfortunately, is not going in a positive direction. The average level of applicants is getting lower and lower. Although, it would seem, Moscow University selects the most cream, but nevertheless this cream is becoming more and more liquid. Moreover, I can also judge by the fact that I have been teaching at our SUNTS for six years now. SUNC is a specialized educational and scientific center, and its old and current name is the Kolmogorov School. School for the most gifted children from all over Russia. It was organized by Academician Andrey Nikolaevich Kolmogorov at 1963 year. A number of well-known scientists have already come out of this school. I was invited to teach geometry there, since I am one of the authors of a school textbook on geometry. Even in these six years that I have been teaching there, I see that the level of those who come to the SOSC is getting lower and lower.
- What do you think is the reason?
- First of all, the reason is that the level of secondary school graduates is decreasing. But not only the school is to blame, but also many other things that happen in our lives, education becomes less prestigious. The fact that weaker guys come to us than it used to be, this is some kind of pattern. One of the troubles, it seems to me, is that there used to be an exam in geometry at school, and now not for 9th grade, not for the 11th grade. But geometry occupies a special place. This is a subject that teaches logic. Because theorems are proved here, in other courses there are practically no theorems. Geometry produces spatial representations. And when you don't have to take exams... I know that in schools in many cases proofs of theorems are not even taught. For example, they formulate the Pythagorean theorem: "The sum of the squares of the legs is equal to the square of the hypotenuse" - and use it when solving problems. And how to prove it? Many students don't even know. Of course, a lot here depends on the teacher. The role of geometry and the role of mathematics in general in school education has been largely weakened in recent years. And this, it seems to me, is very wrong. Therefore, probably, even in our Kolmogorov school, where children from all over Russia are selected, a generation that is less prepared has already begun to come. I teach grades 10-11 there. My first two-year cycle was four years ago. In general, the system there is as follows: I have two classes, in each class there are three hours of geometry a week, one hour of lectures and two lessons of seminars where we solve problems. So, four years ago, in my two classes of five people each, there were brilliant guys. They participated in various international competitions, were part of the Russian national teams, some in mathematics, some in computer science. The next two classes (two years later) were already weaker, maybe one or two very strong people.
And how to prove it? Many students don't even know. Of course, a lot here depends on the teacher. The role of geometry and the role of mathematics in general in school education has been largely weakened in recent years. And this, it seems to me, is very wrong. Therefore, probably, even in our Kolmogorov school, where children from all over Russia are selected, a generation that is less prepared has already begun to come. I teach grades 10-11 there. My first two-year cycle was four years ago. In general, the system there is as follows: I have two classes, in each class there are three hours of geometry a week, one hour of lectures and two lessons of seminars where we solve problems. So, four years ago, in my two classes of five people each, there were brilliant guys. They participated in various international competitions, were part of the Russian national teams, some in mathematics, some in computer science. The next two classes (two years later) were already weaker, maybe one or two very strong people. And now there is practically no one. Basically, the guys in SUNC are decent, of course. In general, the level here is higher than in ordinary schools, but there is a downward trend in the level.
And now there is practically no one. Basically, the guys in SUNC are decent, of course. In general, the level here is higher than in ordinary schools, but there is a downward trend in the level.
- Are the guys who do not enter the physics department interested in science, theory or entrepreneurship?
- Of course, now, after graduating from the physics department, not everyone, unlike how it was 20-30 years ago, goes to science or to some design bureaus. As you know, now there is no state distribution, before everyone was sent somewhere without fail, or you remained in graduate school or to work at the faculty, and a significant part was distributed among scientific institutions. Now this is not the case, and many are looking for work themselves. And they find her. Generally speaking, our graduates are accepted with pleasure, because these people know how to think, how to compare, establish cause-and-effect relationships, and so on. We have a good computer training, already in the first or second year there is a special block of disciplines in programming, solving problems on a computer, computer modeling. Therefore, many find a place for themselves in some firms where such computer work is performed.
Therefore, many find a place for themselves in some firms where such computer work is performed.
- Has the student changed morally since you started teaching?
- Probably, a student is always a student. But what I don't like, and it seems to be increasing, is that young girls smoke. And yet, before this could not be, so that beer cans and bottles were lying everywhere. In this regard, there has been more licentiousness. You go in the morning and you see, although it is forbidden to smoke here, they are standing on the stairwell and smoking. Naturally, you make a remark. In front of the entrance to the faculty, too, everything is in cigarette butts, chewing gum. This is unfortunate, because the faculty is our home.
It's all about lecturers
- Why did you decide to teach? What is it for you?
- Now it is difficult to say whether I decided or did not decide, somehow everything went by itself. He graduated from the faculty, entered graduate school immediately after graduation. After I graduated from graduate school, I was left to work here. Well, to work at the faculty means to necessarily engage in teaching, especially in our department. The Department of Mathematics is a general department that teaches all mathematics in the first three years, one of the largest departments in the faculty. So I stayed to work, taught, then began to lecture, so everything went by itself.
He graduated from the faculty, entered graduate school immediately after graduation. After I graduated from graduate school, I was left to work here. Well, to work at the faculty means to necessarily engage in teaching, especially in our department. The Department of Mathematics is a general department that teaches all mathematics in the first three years, one of the largest departments in the faculty. So I stayed to work, taught, then began to lecture, so everything went by itself.
- Why did you decide to go to the physics department, and not to the mekhmat?
- There were some hesitations about where to go. We arrived together with my friend, who was very determined to go to the physics department, and, perhaps, under his influence, we applied for the physics department. But I do not regret in any way, moreover, I think that a person who specializes in our department of mathematics and is fundamentally trained in the field of physics has certain advantages over pure mathematicians. Of course, first of all in the setting of tasks, in the search for these tasks. A person who does not know much about physics is often in a difficult position as to what tasks he should do. And mathematics is simply a necessary apparatus of physics, the language of physics, therefore, when a person knows physics well, he has almost no problems what mathematical problems to deal with. So I entered the physics department, and then began to specialize in the department of mathematics, because somehow I liked the mathematics lecturers more. We have always had outstanding lecturers at the department. And this played a role.
Of course, first of all in the setting of tasks, in the search for these tasks. A person who does not know much about physics is often in a difficult position as to what tasks he should do. And mathematics is simply a necessary apparatus of physics, the language of physics, therefore, when a person knows physics well, he has almost no problems what mathematical problems to deal with. So I entered the physics department, and then began to specialize in the department of mathematics, because somehow I liked the mathematics lecturers more. We have always had outstanding lecturers at the department. And this played a role.
Simple about complex
- You deal with singular perturbations, can this be somehow understood by a person who has nothing to do with mathematics?
- (Laughter) You can. It's very simple. I will explain this to you with a simple example. In general, what does the word indignation mean? There is some equation or some task, some mathematical model that describes this or that phenomenon, let's say you can write an equation that describes the oscillations of a pendulum, an equation that describes the movement of a point. But no mathematical model is absolutely accurate, adequate to a physical phenomenon, because some factors are not taken into account. For example, friction is often neglected in mechanics if it is small, and if it is taken into account, then the friction force must somehow be introduced into the problem. So, some factors inevitably have to be neglected, and thus any model is approximate. But if we still want to somehow take into account these factors, we must take a more accurate model. So, there is a certain basic model, and that additional thing that we want to bring into it is called perturbation. Now about what a singular perturbation is. It may be that a seemingly small addition (small perturbation) leads to a strong change in the solution of the problem. Let's consider the simplest equation x - 1 = 0. Its solution: x = 1. Let's add a small term to this equation, denote it by the letter e . Consider the equation x - 1 + e = 0 .
But no mathematical model is absolutely accurate, adequate to a physical phenomenon, because some factors are not taken into account. For example, friction is often neglected in mechanics if it is small, and if it is taken into account, then the friction force must somehow be introduced into the problem. So, some factors inevitably have to be neglected, and thus any model is approximate. But if we still want to somehow take into account these factors, we must take a more accurate model. So, there is a certain basic model, and that additional thing that we want to bring into it is called perturbation. Now about what a singular perturbation is. It may be that a seemingly small addition (small perturbation) leads to a strong change in the solution of the problem. Let's consider the simplest equation x - 1 = 0. Its solution: x = 1. Let's add a small term to this equation, denote it by the letter e . Consider the equation x - 1 + e = 0 .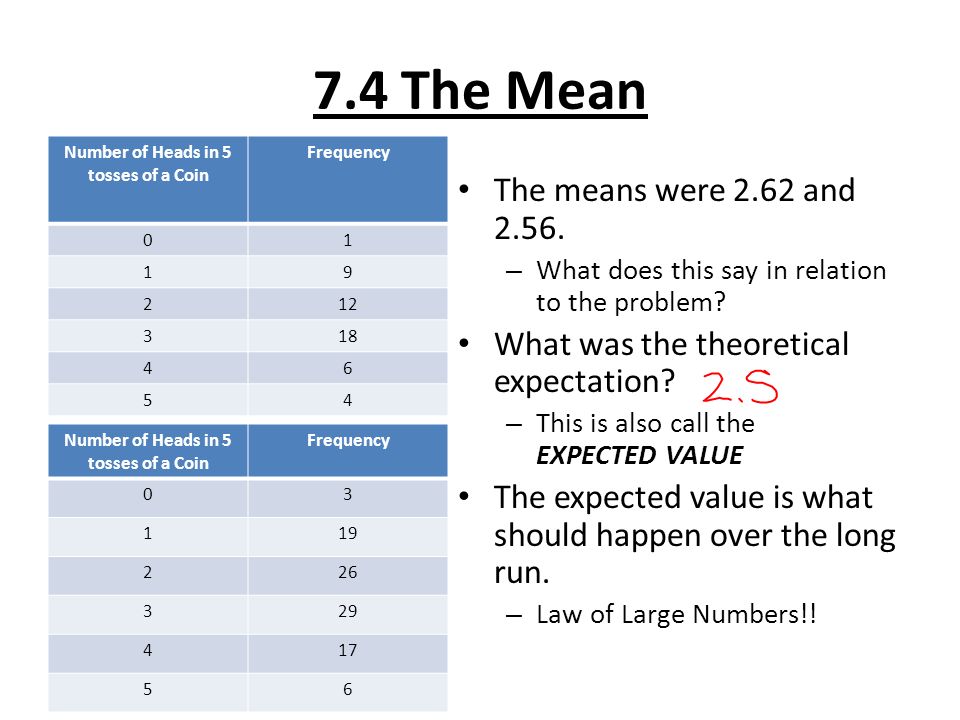 His solution is x = 1 - e . The solution has changed to this e . If e is equal to one hundredth, then the solution has changed by one hundredth. You can add this e with a factor of x, we get equation x - 1 + ex = 0 . Hence, if we bring like terms, x = 1/(1 + e). This solution also differs little from the previous one. Thus, we introduced a small perturbation into the equation, which led to a small change in the solution. Small perturbation - small change. And now I'll add the same e with a factor of x² . We get the equation ex² + x - 1 = 0 . The equation has become square. And he already has two solutions, the picture has changed qualitatively. Further, if we calculate these two roots according to the formula of the roots of the quadratic equation known to schoolchildren and look closely at them, we can see that one of the roots differs little from unity, and the other is very strong.
His solution is x = 1 - e . The solution has changed to this e . If e is equal to one hundredth, then the solution has changed by one hundredth. You can add this e with a factor of x, we get equation x - 1 + ex = 0 . Hence, if we bring like terms, x = 1/(1 + e). This solution also differs little from the previous one. Thus, we introduced a small perturbation into the equation, which led to a small change in the solution. Small perturbation - small change. And now I'll add the same e with a factor of x² . We get the equation ex² + x - 1 = 0 . The equation has become square. And he already has two solutions, the picture has changed qualitatively. Further, if we calculate these two roots according to the formula of the roots of the quadratic equation known to schoolchildren and look closely at them, we can see that one of the roots differs little from unity, and the other is very strong. It would seem a small addition, let's say we added x² with a multiplier of one millionth, and the change that has happened is very significant. Firstly, there are two roots, and secondly, one of the roots is very far from what was in the original equation. Such a perturbation is called singular... Any perturbation theory studies how small perturbing terms affect the behavior of the solution. The theory of singular perturbations deals with those problems in which small perturbations lead to a strong change in the solution.
It would seem a small addition, let's say we added x² with a multiplier of one millionth, and the change that has happened is very significant. Firstly, there are two roots, and secondly, one of the roots is very far from what was in the original equation. Such a perturbation is called singular... Any perturbation theory studies how small perturbing terms affect the behavior of the solution. The theory of singular perturbations deals with those problems in which small perturbations lead to a strong change in the solution.
- Can this be applied in life somehow?
- It finds application both in mathematics and in physics, biology, chemistry. After all, what does the word mathematics mean? It is from the Greek matem , which translates as knowledge . Mathematics is knowledge. How does mathematics know the world? Mathematics, unlike physics, chemistry and other natural sciences, does not deal directly with animate or inanimate nature. It deals with mathematical models of physical, biological, chemical phenomena. For any physical phenomenon, you can write the corresponding equation, or, as they say, a mathematical model. And for a number of problems in physics, chemistry, and biology, these models are singularly perturbed differential equations. There are a lot of such problems in chemical kinetics, in biology, in various fields of physics, in hydrodynamics, in synergetics, which is quite fashionable now - the theory of self-organization. So this is a whole class of equations that arise in a wide variety of applied problems.
It deals with mathematical models of physical, biological, chemical phenomena. For any physical phenomenon, you can write the corresponding equation, or, as they say, a mathematical model. And for a number of problems in physics, chemistry, and biology, these models are singularly perturbed differential equations. There are a lot of such problems in chemical kinetics, in biology, in various fields of physics, in hydrodynamics, in synergetics, which is quite fashionable now - the theory of self-organization. So this is a whole class of equations that arise in a wide variety of applied problems.
- What tasks do you personally deal with?
- I and my colleagues in the scientific group are developing asymptotic methods for singularly perturbed problems. The word asymptotic means approximate , asymptote - approximation. The essence of the asymptotic method is as follows. Most of the problems that arise in practice when describing real phenomena are very complex problems.



 ..
.. Please see this page to learn more about helping your student with Reading Foundational Skills. You can learn more about grade-specific reading foundational skills here.
Please see this page to learn more about helping your student with Reading Foundational Skills. You can learn more about grade-specific reading foundational skills here. ..
.. ..) like something in your life, your personal experience or something you already know?
..) like something in your life, your personal experience or something you already know?