What is a math concept

10 Math Concepts You Can't Ignore

Sets and set theory

A set is a collection of objects. The objects, called elements of the set, can be tangible (shoes, bobcats, people, jellybeans, and so forth) or intangible (fictional characters, ideas, numbers, and the like). Sets are such a simple and flexible way of organizing the world that you can define all of math in terms of them.

Mathematicians first define sets very carefully to avoid weird problems — for example, a set can include another set, but it can't include itself. After the whole concept of a set is well-defined, sets are used to define numbers and operations, such as addition and subtraction, which is the starting point for the math you already know and love.

Prime numbers go forever

A prime number is any counting number that has exactly two divisors (numbers that divide into it evenly) — 1 and the number itself. Prime numbers go on forever — that is, the list is infinite — but here are the first ten: 2 3 5 7 11 13 17 19 23 29 . . .

It may seem like nothing, but . . .

Zero may look like a big nothing, but it's actually one of the greatest inventions of all time. Like all inventions, it didn't exist until someone thought of it. (The Greeks and Romans, who knew so much about math and logic, knew nothing about zero.)

The concept of zero as a number arose independently in several different places. In South America, the number system that the Mayans used included a symbol for zero. And the Hindu-Arabic system used throughout most of the world today developed from an earlier Arabic system that used zero as a placeholder. In fact, zero isn't really nothing — it's simply a way to express nothing mathematically. And that's really something.

Have a big piece of pi

Pi (π): The symbol π (pronounced pie) is a Greek letter that stands for the ratio of the circumference of a circle to its diameter. Here's the approximate value of π:

π ≈ 3.1415926535…

Although π is just a number — or, in algebraic terms, a constant — it's important for several reasons:

Geometry just wouldn't be the same without it. Circles are one of the most basic shapes in geometry, and you need π to measure the area and the circumference of a circle.

Pi is an irrational number, which means that no fraction that equals it exactly exists. Beyond this, π is a transcendental number, which means that it's never the value of x in a polynomial equation (the most basic type of algebraic equation).

Pi is everywhere in math. It shows up constantly (no pun intended) where you least expect it. One example is trigonometry, the study of triangles. Triangles obviously aren't circles, but trig uses circles to measure the size of angles, and you can't swing a compass without hitting π.

Equality in mathematics

The humble equals sign (=) is so common in math that it goes virtually unnoticed. But it represents the concept of equality — when one thing is mathematically the same as another — which is one of the most important math concepts ever created. A mathematical statement with an equals sign is an equation. The equals sign links two mathematical expressions that have the same value and provides a powerful way to connect expressions.

Bringing algebra and geometry together

Before the xy-graph (also called the Cartesian coordinate system) was invented, algebra and geometry were studied for centuries as two separate and unrelated areas of math. Algebra was exclusively the study of equations, and geometry was solely the study of figures on the plane or in space.

The graph, invented by French philosopher and mathematician René Descartes, brought algebra and geometry together, enabling you to draw solutions to equations that include the variables x and y as points, lines, circles, and other geometric shapes on a graph.

The function: a mathematical machine

A function is a mathematical machine that takes in one number (called the input) and gives back exactly one other number (called the output). It's kind of like a blender because what you get out of it depends on what you put into it. Suppose you invent a function called PlusOne that adds 1 to any number. So when you input the number 2, the number that gets outputted is 3:

PlusOne(2) = 3

Similarly, when you input the number 100, the number that gets outputted is 101:

PlusOne(100) = 101

It goes on, and on, and on . . .

The very word infinity commands great power. So does the symbol for infinity (∞). Infinity is the very quality of endlessness. And yet mathematicians have tamed infinity to a great extent. In his invention of calculus, Sir Isaac Newton introduced the concept of a limit, which allows you to calculate what happens to numbers as they get very large and approach infinity.

Putting it all on the line

This pattern continues forever, with each value being halved, which means you can never get to the other side of the room. Obviously, in the real world, you can and do walk across rooms all the time. But from the standpoint of math, Zeno's Paradox and other similar paradoxes remained unanswered for about 2,000 years.

The basic problem was this one: All the fractions listed in the preceding sequence are between 0 and 1 on the number line. And there are an infinite number of them. But how can you have an infinite number of numbers in a finite space? Mathematicians of the 19th century — Augustin Cauchy, Richard Dedekind, Karl Weierstrass, and Georg Cantor foremost among them — solved this paradox. The result was real analysis, the advanced mathematics of the real number line.

Numbers for your imagination

The imaginary numbers (numbers that include the value i = √ - 1) are a set of numbers not found on the real number line. If that idea sounds unbelievable — where else would they be? — don't worry: For thousands of years, mathematicians didn't believe in them, either. But real-world applications in electronics, particle physics, and many other areas of science have turned skeptics into believers.

So, if your summer plans include wiring your secret underground lab or building a flux capacitor for your time machine — or maybe just studying to get a degree in electrical engineering — you'll find that imaginary numbers are too useful to be ignored.

4 Crucial Basic Math Concepts

Search my site:

Your child's success in learning Math depends on mastering these five crucial concepts. They are essential for building a strong foundation in Math. They help your child understand and make sense of numbers and problem-solving; they strengthen his or her number sense.

The good news is that it is very easy to help your child understand these concepts. The key is to practice a few minutes several times a day. Make it a family affair so your child does not feel overly stressed. Your child or children will remember the lessons better if they had fun with it.

1.   Understanding Numbers

The first concept your child must master is knowing how to read, write and understand numbers. Print out 2 sets of the number chart here.  Use one set as a reference.  Cut out the individual numbers from the second set.

Some ideas for you:

-  read and write numbers

-  recite a list of numbers forwards and backwards

-  what number comes before or next

-  arrange numbers in order (start with consecutive numbers)

-  even and odd numbers

Print out this set of place numbers for older children.

2.   More, Less or Equal

The next important concept in Math is to know how 2 numbers compare; whether one  number is more, less or equal to another number.

Numbers represent quantity. Your child must first understand these types of questions.

1. Amanda has 12 stickers.  Benjamin has 9 stickers.  Who has more stickers?
2. Jack has 35 stamps.  Alan has 19 stamps.  Who has fewer stamps?
3. Sam has 107 balloons.  Jodie has 90 balloons.  Who has more balloons?  How many more?
4. Charlie is 30-years-old. Mary is 17-years-old.  Who is younger?  How many years younger?
   

Followed by these types of questions:

1. Rodney has $3 more than Janice. How much money does Rodney have if Janice has $26?
2. I have 7 fewer pencils than books. 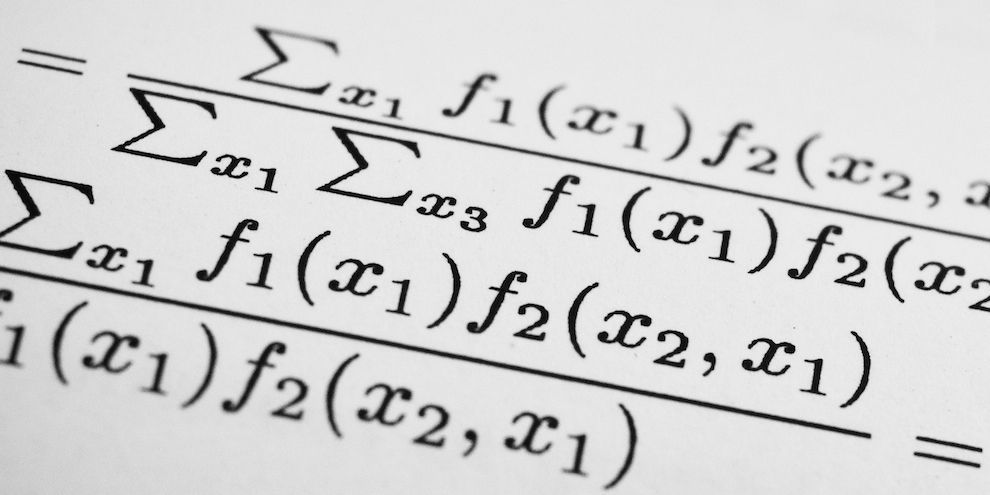  How many books do I have if I have 20 pencils?
3. John spent $11 less than Mark.  How much did they spend altogether if Mark spent $15?
   

And these types of questions:

1. 5 pencils cost the same as 2 books.  Which is more expensive, the pen or the book?
2. 6 apples cost the same as 10 oranges.  What is the cost of 1 apple if 1 orange costs $0.60?
3. Mary and James have the same amount of money.  Mary spent half of her money.  James spent one-third of his money.  Who spent more money?
   

No matter how difficult the questions get, they can all be broken down into simple comparisons of more, less or equal.

3.  Knowing Which Operation to Use

In Basic Maths there are actually only 4 operations your child needs to know: addition, subtraction, multiplication and division.  Here are some clues to help your child decide which of these to use.  Print the following graphic for your child to use as a guide.

4.   Different Ways to Get to the Answer

When it comes to Math, many children assume there is only one way or method to use to come up with the correct answer. If your child does not understand the teacher's method, he or she assumes that it is because he or she too stupid to understand.

You must help your child realize that there can be different ways of understanding a problem and different strategies can be used to find the answer. However, though the strategies may differ, the answer to the question must always be the same.

Play this family game: Write out simple word problems on cards. Read out a problem, then each person explains how he or she comes up with the answer.

Example

Mary has 9 sweets. She bought a few more sweets and now she has 13 sweets. How many sweets did Mary buy?

Some methods of solving:

1. Say '9' then count '10, 11, 12, 13' on your fingers. Since you used 4 fingers to count, the answer is 4.
2. Draw 9 circles in a row. Draw 13 circles in a second row below the first, making sure you line them up exactly. Compare the two rows and point out there are 4 extra circles in the second row. The answer is 4.
3. Write the numbers 1 to 13 on a number line. Point out that after the number 9, there are 4 more numbers to reach the number 13.  The answer is 4.
   

Play this game often and your child will become more flexible and logical in his or her thinking. He or she will automatically look for different ways to solve a hard problem. This will surely help in tackling complicated Math problems later on in school. Teach your child to ask "Is there another way of solving?" when he or she cannot understand one explanation.

This will help them realize that failure to understand does not mean they are cannot learn Math.

After your child has mastered this Math concept, introduce deliberate mistakes in your reasoning to see if your child can spot and correct them.

But do this only after your child has thoroughly understood the different strategies or you'll only end up confusing your child.

For older children, you can help them understand the properties of the different operations of addition, subtraction, multiplication and division.

Sometimes the order that these operations are used does not matter.  Sometimes it does.  Discuss the different strategies to find out when order matters, and when it doesn't.

Example

Max bought 3 boxes of pencils.  Each box contains 12 pencils.  He gave 5 pencils to his brother and 8 pencils to his sister.  How many pencils does Max have left?

Methods of solving:

1. To find the total number of pencils at first, you can multiple (3 x 12) or add (12 + 12 + 12).
2. To find the number of pencils left, you can add first (5 + 8) and then subtract
   (36 - 13).
3. Or you can subtract only (36 - 5 - 8).

I hope these strategies help your child excel in Maths.   Share them with other parents whose children struggle with Maths.

1. Mathematical concepts

Lecture #2

in mathematics

Topic: "Mathematical concepts”

Plan:

1. Mathematical concepts

2. Scope and content concepts. Relations between concepts

3. Definition concepts

4. Requirements to definition of concepts

5. Some species definitions

concepts, which are studied in the initial course mathematics is usually represented in the form four groups. The first one includes concepts related to numbers and operations above them: number, addition, term, more, etc. The second includes algebraic concepts: expression, equality, equation and others. The third is geometric concepts: line, segment, triangle etc. The fourth group is formed by the concepts associated with quantities and their measurement. nine0003

How to study such an abundance of different concepts?

Before All you need to do is to understand the concept as a logical category and features mathematical concepts.

AT logic concepts are considered as a form thoughts reflecting objects (objects or phenomena) in their essential and general properties. The language form of the concept is a word or group of words.

Compose the concept of an object means to be able to to distinguish it from others similar to it objects. Mathematical concepts have a number of features. home is that the mathematical objects to be compiled concept does not exist in reality. Mathematical objects are created by the mind person. These are ideal objects reflecting real objects or phenomena. For example, in geometry one studies the shape and size of objects, without taking into account their other properties: color, mass, hardness, etc. From all this distracted, abstracted. therefore in geometry instead of the word "object" say "geometric figure". nine0003

result abstractions are and such mathematical concepts like "number" and "value".

Generally mathematical objects exist only in the thinking of man and in those signs and symbols that form a mathematical language.

To It can be added to what has been said that, by studying spatial forms and quantitative relations of the material world, mathematics not only uses different methods abstraction, but abstraction itself acts as a multi-step process. Mathematics considers not only concepts that emerged in the study real objects, but also concepts arising from the first. For example, the general concept of a function as a correspondence is a generalization of the concepts of specific functions, i.e. abstraction from abstractions. nine0003

To master general approaches to learning concepts in the elementary course of mathematics, The teacher needs knowledge about the volume and the content of the concept, about the relationship between concepts and about the types of definitions of concepts.

Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties.

Among the properties object distinguish between essential and insignificant. Property feel essential to an object if it inherent in this object and without it, it is not may exist. For example, for square essential are all the properties mentioned above. Not essential for square ABCD property "side AD horizontal." If the square is turned then side AD will be located differently (Fig. 26). nine0003

Therefore, to understand what is given mathematical object know its essential properties.

When talking about a mathematical concept, then usually means a set of objects, denoted by one term (word or group of words). So, speaking of a square, refers to all geometric shapes, which are squares. Think that the set of all squares is the scope of the concept of "square".

Generally volume concepts are the set of all objects, denoted by one term. nine0063