What is ordinal numbers
What are Ordinal Numbers? Definition, List, Examples, Facts
What are Ordinal Numbers?
Numbers that are used to represent the rank or position of an object or a person are known as ordinal numbers. They are also referred to as positioning or ranking numbers.The sequence of ordinal numbers vary on the parameters that are based on the positions that are defined, such as weight, height, marks, size, etc. Such numbers are also known as ordinals.
Recommended Worksheets:
How to Write Ordinal Numbers?
Ordinal numbers or ordinals are written using numerals as prefixes and adjectives as suffixes.
For example, 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 8th and so on. We can easily identify an ordinal number: it talks about positioning.
So, if we were to say, “Bring me the bottle of jam that is lying on the 4th shelf.”, one would know that the ordinal number here is 4, which informs us about the position of the jam bottle.
The above picture shows different floors of a building. Here, we can use ordinal numbers to define the position of the floors.
The numbers 1st (first), 2nd (second), 3rd (third), 4th (fourth), 5th (fifth), 6th (sixth), 7th (seventh), 8th (eighth), 9th (ninth) and 10th (tenth) tell us about the positions of various floors in the building. Therefore, all of them are the ordinal numbers.
Recommended Games:
Applications of Ordinal Numbers
Ordinal numbers are a great way to talk about the order of something. For example, the order of dates. These numbers are only used when data is provided and the data is to be arranged in order.
For example: Someone who has performed well throughout the year may get the chance to be valedictorian. They would be first in line. But someone who performed well, but was unable to score as much as the person before in various tests and exams, may be second in line to be valedictorian. The person who has not performed well at all, has the least amount of chance.
The picture given below shows some athletes competing in a 500-m race. We can also use ordinal numbers to define their positions in order to see who the winner and runners-up of the race are.
Other examples of ordinal numbers are as follows:
- Jennifer always ranks 2nd in the class.
Here 2nd is the ordinal number that tells you about the position that Jennifer has secured.
- Jane is standing at the 5th place in the queue.
Hereby the ordinal number is 5th, we understand Jane’s position in the queue.
- Jenny came 3rd in the race.
Here, 3rd is the ordinal number which tells you about the place that Jenny has secured in the race.
- The 10th table is reserved.
Here, the ordinal number 10th refers to the number of table reservations made.
Ordinal Numbers 1
– 50 listOrdinal Numbers 51
–100 listOrdinal Numbers v.
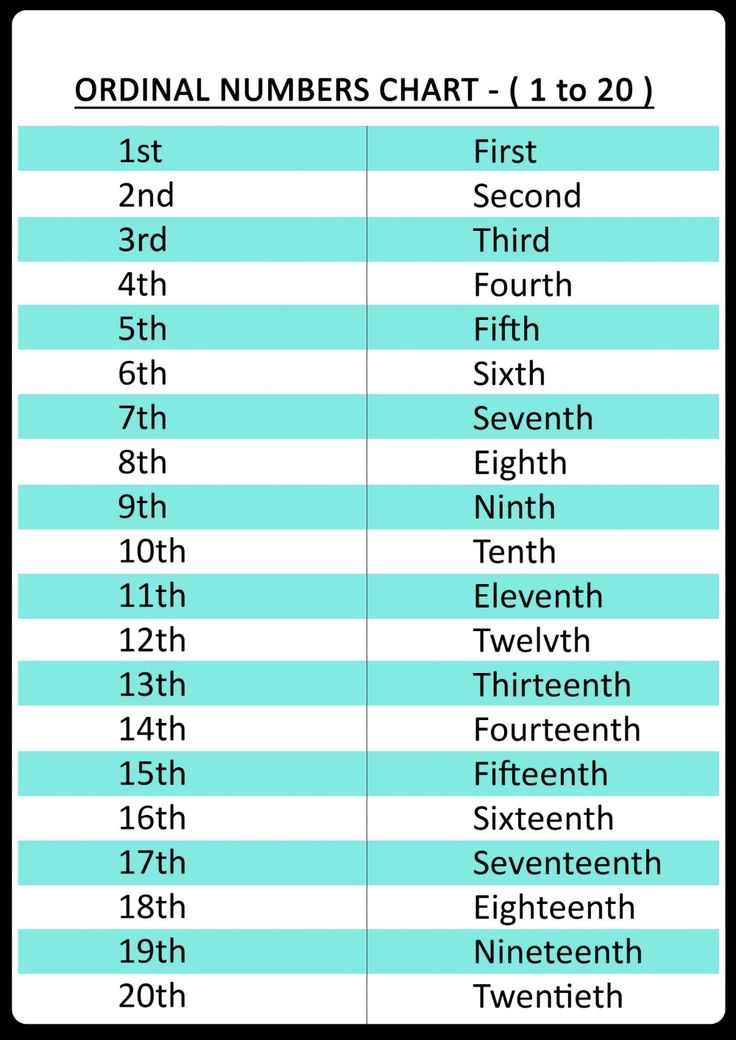 Cardinal Numbers
Cardinal NumbersThe type of numbers that are used for counting the number of objects or persons are known as cardinal numbers. This type of numbers are used for representing the cardinality of the number of elements in a set.
Cardinality means to know about the number of elements in a set.
Cardinal numbers can be the natural numbers that we use while we are counting like one, two, three, four, five and so on.
On the other hand, ordinal numbers are used to determine the rank or position of any object or person. We write ordinal numbers using numbers as prefixes and adjectives as suffixes.
Let us understand the difference with the help of an example.
Some students were asked to collect marbles.
Tom collected 1, Jane collected 2, and Clove collected 3 marbles.
Here the numbers 1, 2, 3 are cardinal numbers as they represent the quantity of marbles.
Now, the one who scores maximum wins. So, Clove stands 1st, Jane stands 2nd and Tom stands 3rd.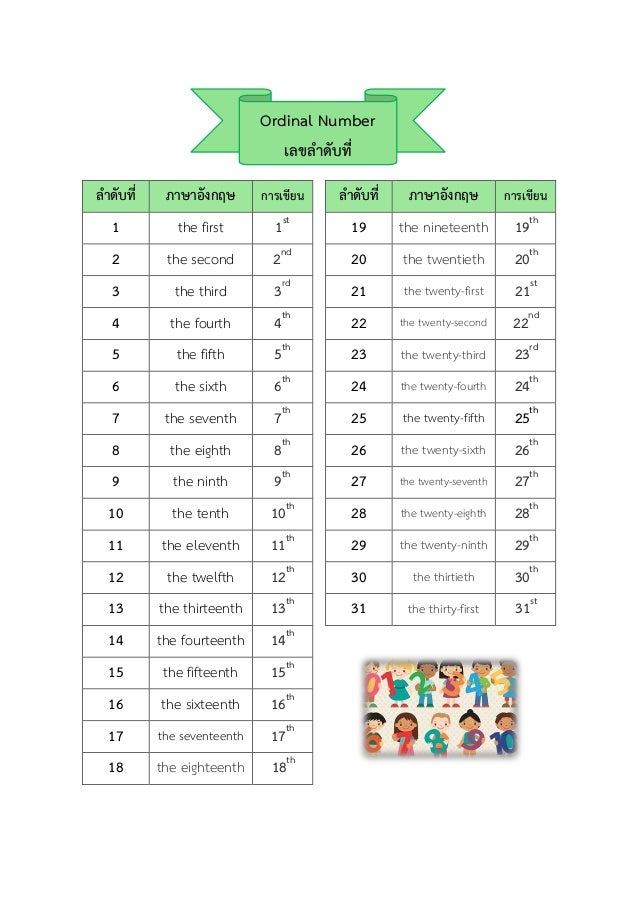
Here the numbers 1st, 2nd and 3rd are ordinal numbers as they represent the position of the students.
Ordinal Numbers v. Nominal Numbers
A set of numbers that are used for labeling certain items or places so that they can be identified easily are known as nominal numbers. Whenever we have to identify an object uniquely, we use nominal numbers. These numbers are not of much use because they are just going to give information about location and not about its quantity, quality, etc. Nominal numbers can be used as area codes, on number plates of vehicles, etc. Operations such as addition, subtraction, multiplication and division are meaningless on nominal numbers.
For example: In a phone number like 202 588-6500, the number is a nominal number. Even if we apply an operation, it will not give us anything meaningful.
On the order hand, the ordinal numbers tell us about the rank or position of any object or person.
For example: Sophia lives in the 34th house on San Pablo Avenue, California.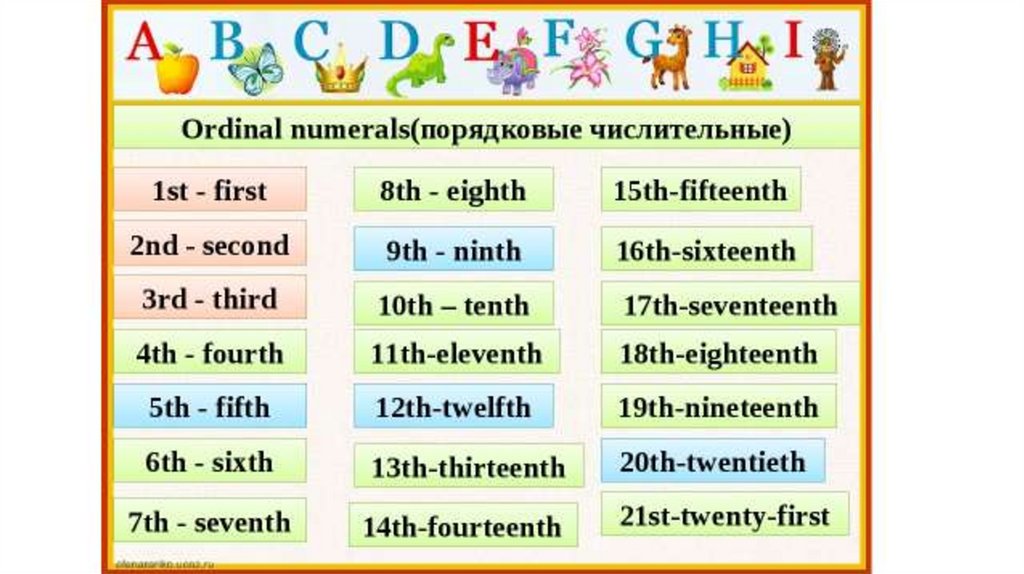
Fun Fact!
11, 12 and 13 are the only numbers to use a suffix ‘–th’ but all other numbers ending with 1 use ‘–st’, those ending with 2 use ‘–nd’ and those ending with 3 use ‘–rd’.
Solved Examples
Example 1: Which English alphabet is 12th from the beginning?
Solution: The alphabet that is 12th from the beginning is L.
Example 2: Kim, Kethy, Kiah and Kaina are sitting in the line in alphabetical order. What is the position of Kiah from the beginning?
Solution: According to alphabetical order, the order in which they’re sitting would be: Kaina, Kethy, Kiah, Kim. So, Kiah is at the 3rd position.
3. Christmas lies on the _____ of December. Solution: Christmas lies on the 25th of December.
Practice Problems
1
Which one of the following denotes an ordinal number?
The vehicle number of Sarah is KL23AB89.
There are 9 apples on the tree.
Catheline came 4th in the drawing competition.
None of these
Correct answer is: Catheline came 4th in the drawing competition.
In the option C, the number 4th is telling about the position of Catheline in the drawing competition.
2
How do you write 51 in ordinal numbers?
51
51st
51th
51rd
Correct answer is: 51st
The ordinal number for 51 for 51st.
3
In the word, “COMPENSATION”, which are the fourth and tenth letters?
M and O
M and N
P and I
E and O
Correct answer is: P and I
The fourth letter is P and the tenth letter is I.
Frequently Asked Questions
Is 0 an ordinal number?
No, we cannot write 0 as an ordinal number.
What are exceptional ordinal numbers?
Exceptional ordinal numbers are the ordinal numbers that do not end with -th. For example: 1st (first), 2nd (second), 3rd (third), etc.
For example: 1st (first), 2nd (second), 3rd (third), etc.
Who invented ordinal numbers?
Ordinal numbers were invented by Georg Cantor in 1883.
Ordinal Numbers - Meaning, Examples
Ordinal numbers are the numbers that talk about the position of objects. For example, 'The cookies are kept in the 3rd drawer from the top', 'The orange dress is the 7th one from the right', 'The soccer ball is kept in the 3rd carton from the left'. All these sentences have one thing in common - they talk about the positions of the objects. This is the main element in the discussion of ordinal numbers.
| 1. | What are Ordinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Ordinal Numbers from 1 to 100 |
| 4. | FAQs on Ordinal Numbers |
What are Ordinal Numbers?
An ordinal number is a number that indicates the position or order of something in relation to other numbers, like, first, second, third, and so on. This order or sequence may be according to the size, importance, or any chronology. Let us understand the ordinal numbers with an example. Ten students participated in a contest. Out of them, the top winners were given medals and were ranked as 1st, 2nd, and 3rd. In this case, the positions: 1st, 2nd, and 3rd are ordinal numbers.
This order or sequence may be according to the size, importance, or any chronology. Let us understand the ordinal numbers with an example. Ten students participated in a contest. Out of them, the top winners were given medals and were ranked as 1st, 2nd, and 3rd. In this case, the positions: 1st, 2nd, and 3rd are ordinal numbers.
Difference Between Cardinal and Ordinal Numbers
A cardinal number is a number that denotes the count of any object. Any natural number such as 1, 2, 3, etc., is referred to as a cardinal number, whereas, an ordinal number is a number that denotes the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, etc. Now, if we say, 'There are 3 ants and 5 bears'. This is an example of cardinal numbers. However, if we say, 'The position of the runners in the running event is first, second, third, and so on', this represents ordinal numbers. Observe the table given below to note the difference between cardinal numbers and ordinal numbers.
Observe the table given below to note the difference between cardinal numbers and ordinal numbers.
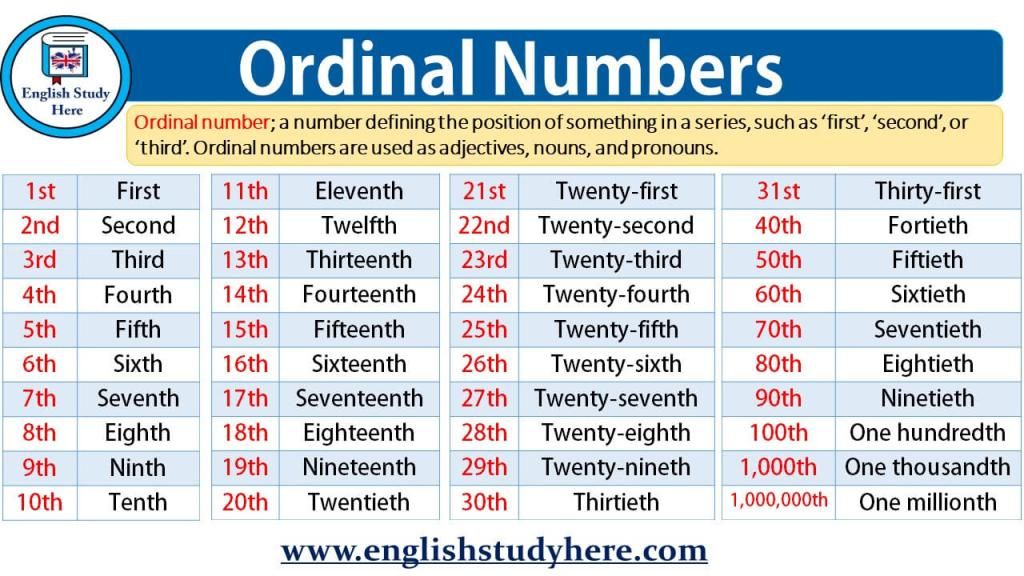
List of Ordinal Numbers from 1 to 100
The list of ordinal numbers from 1 to 100 can be learned easily and is quite helpful for specifying the order of any given object. You can use the combinations from this list to find out the ordinal numbers from 100 onward. Observe the table given below in order to understand how ordinal numbers are written. You might be able to pick up a pattern after referring to the first twenty ordinal numbers.
| 1st: First | 21st: Twenty-First | 41st: Forty-First | 61th: Sixty-First | 81st: Eighty-First |
| 2nd: Second | 22nd: Twenty-Second | 42nd: Forty-Second | 62nd: Sixty-Second | 82nd: Eighty-Second |
| 3rd: Third | 23rd: Twenty-Third | 43rd: Forty-Third | 63rd: Sixty-Third | 83rd: Eighty-Third |
| 4th: Fourth | 24th: Twenty-Fourth | 44th: Forty-Fourth | 64th: Sixty-Fourth | 84th: Eighty-Fourth |
| 5th: Fifth | 25th: Twenty-Fifth | 45th: Forty-Fifth | 65th: Sixty-Fifth | 85th: Eighty-Fifth |
| 6th: Sixth | 26th: Twenty-Sixth | 46th: Forty-Sixth | 66th: Sixty-Sixth | 86th: Eighty-Sixth |
| 7th: Seventh | 27th: Twenty-Seventh | 47th: Forty-Seventh | 67th: Sixty-Seventh | 87th: Eighty-Seventh |
| 8th: Eighth | 28th: Twenty-Eighth | 48th: Forty-Eighth | 68th: Sixty-Eighth | 88th: Eighty-Eighth |
| 9th: Ninth | 29th: Twenty-Ninth | 49th: Forty-Ninth | 69th: Sixty-Ninth | 89th: Eighty-Ninth |
| 10th: Tenth | 30th: Thirtieth | 50th: Fiftieth | 70th: Seventieth | 90th: Ninetieth |
| 11th: Eleventh | 31st: Thirty-First | 51st: Fifty-First | 71st: Seventy-First | 91st: Ninety-First |
| 12th: Twelfth | 32nd: Thirty-Second | 52nd: Fifty-Second | 72nd: Seventy-Second | 92nd: Ninety-Second |
| 13th: Thirteenth | 33rd: Thirty-Third | 53rd: Fifty-Third | 73rd: Seventy-Third | 93rd: Ninety-Third |
| 14th: Fourteenth | 34th: Thirty-Fourth | 54th: Fifty-Fourth | 74th: Seventy-Fourth | 94th: Ninety-Fourth |
| 15th: Fifteenth | 35th: Thirty-Fifth | 55th: Fifty-Fifth | 75th: Seventy-Fifth | 95th: Ninety-Fifth |
| 16th: Sixteenth | 36th: Thirty-Sixth | 56th: Fifty-Sixth | 76th: Seventy-Sixth | 96th: Ninety-Sixth |
| 17th: Seventeenth | 37th: Thirty-Seventh | 57th: Fifty-Seventh | 77th: Seventy-Seventh | 97th: Ninety-Seventh |
| 18th: Eighteenth | 38th: Thirty-Eighth | 58th: Fifty-Eighth | 78th: Seventy-Eighth | 98th: Ninety-Eighth |
| 19th: Nineteenth | 39th: Thirty-Ninth | 59th: Fifty-Ninth | 79th: Seventy-Ninth | 99th: Ninety-Ninth |
| 20th: Twentieth | 40th: Fortieth | 60th: Sixtieth | 80th: Eightieth | 100th: Hundredth |
Ordinal Numbers 1 to 20
Ordinal numbers from 1 to 20 are different from the rest.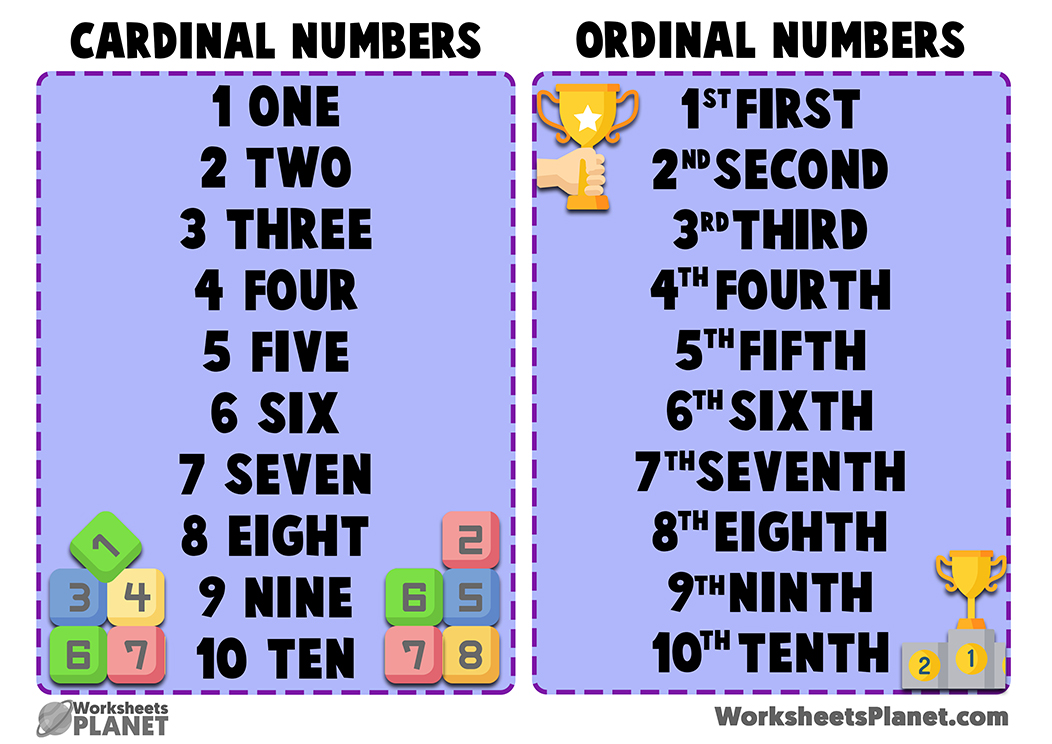 After the number 20, a repeated pattern of ordinal numbers can be observed. Ordinal numbers from 1 to 20 can be listed as follows. 1 - First, 2 - Second, 3 - Third, 4 - Fourth, 5 - Fifth, 6 - Sixth, 7 - Seventh, 8 - Eighth, 9 - Ninth, 10 - Tenth, 11 - Eleventh, 12 - Twelfth, 13 - Thirteenth, 14 - Fourteenth, 15 - Fifteenth, 16 - Sixteenth, 17 - Seventeenth, 18 - Eighteenth, 19 - Nineteenth, 20 - Twentieth.
After the number 20, a repeated pattern of ordinal numbers can be observed. Ordinal numbers from 1 to 20 can be listed as follows. 1 - First, 2 - Second, 3 - Third, 4 - Fourth, 5 - Fifth, 6 - Sixth, 7 - Seventh, 8 - Eighth, 9 - Ninth, 10 - Tenth, 11 - Eleventh, 12 - Twelfth, 13 - Thirteenth, 14 - Fourteenth, 15 - Fifteenth, 16 - Sixteenth, 17 - Seventeenth, 18 - Eighteenth, 19 - Nineteenth, 20 - Twentieth.
☛ Related Topics
- Cardinal Numbers
- Ordinal Numbers Worksheets for Kindergarten
- Numbers
- Rational Numbers
- Prime Numbers
- Composite Numbers
- Even Numbers
- Odd Numbers
- Real Numbers
- Natural Numbers
- Irrational Numbers
- Counting Numbers
Ordinal Numbers Examples
-
Example 1: What is the 3rd letter in the word: SUMMERS?
Solution:
In the given word, SUMMERS, the first letter is 'S'.
 The second letter is 'U'. Similarly, we count the position of the letters in order, like, first, second, third, and so on which denotes ordinal numbers. So, we can see that the letter 'M' comes in the 3rd position. Therefore, the third letter in the given word is 'M'.
The second letter is 'U'. Similarly, we count the position of the letters in order, like, first, second, third, and so on which denotes ordinal numbers. So, we can see that the letter 'M' comes in the 3rd position. Therefore, the third letter in the given word is 'M'. -
Example 2: Sam, Jenny, Mary, and Jack are standing in a queue in the given order. Who is in the fourth position?
Solution:
From the given information, we can say that: Sam is in the first place, Jenny is in the second place, Mary is in the third place, and Jack is in the fourth place. Therefore, Jack is standing in the fourth position. Here, 4th is an ordinal number because it denotes the position of Jack.
-
Example 3: State true or false with respect to ordinal numbers.
a.) An ordinal number is a number that denotes the position or place of an object.
b.) Ordinal numbers are written as 1st, 2nd, and 3rd, and so on.

Solution:
a.) True, an ordinal number is a number that denotes the position or place of an object.
b.) True, ordinal numbers are written as 1st, 2nd, and 3rd, and so on.
go to slidego to slidego to slide
Ready to see the world through math’s eyes?
Math is a life skill. Help your child perfect it through real-world application.
Book a Free Trial Class
Practice Questions on Ordinal Numbers
go to slidego to slide
FAQs on Ordinal Numbers
What Does Ordinal Number mean?
Ordinal numbers are the numbers that specify the position of objects. For example, when we say that the books are kept on the 3rd shelf, here 3rd is an ordinal number. Similarly, first, second, twentieth, fiftieth, and so on are ordinal numbers.
What is the Difference Between Cardinal and Ordinal Numbers?
Cardinal numbers denote the count of any object.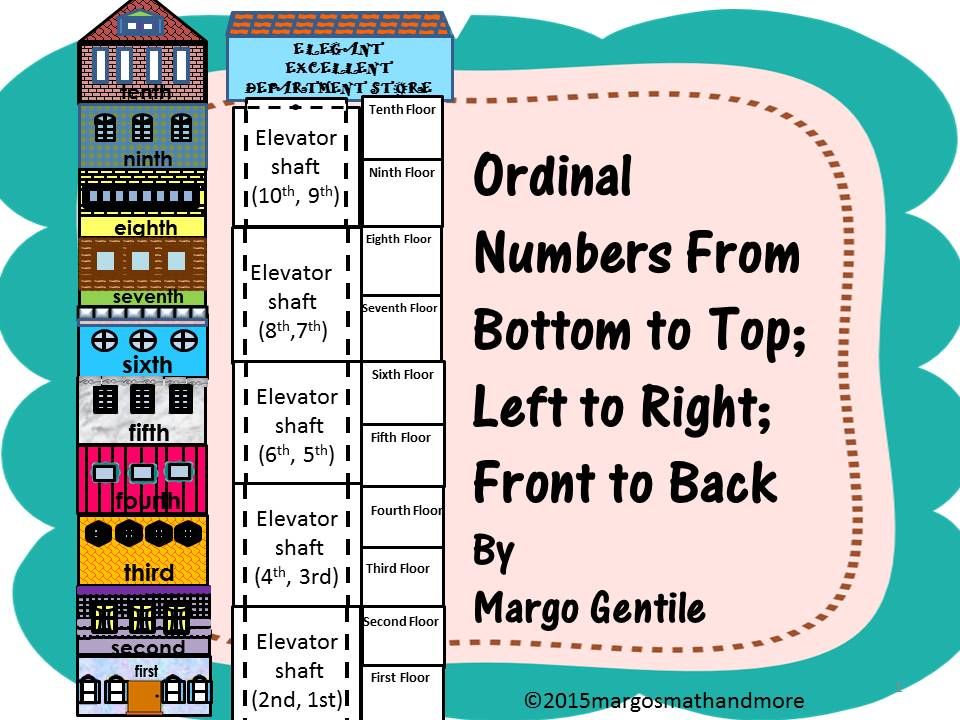 For example, natural numbers like 1, 2 3, and so on are cardinal numbers. On the other hand, ordinal numbers denote the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, and so on, are ordinal numbers.
For example, natural numbers like 1, 2 3, and so on are cardinal numbers. On the other hand, ordinal numbers denote the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, and so on, are ordinal numbers.
How to Write Dates with Ordinal Numbers?
Ordinal numbers are used to mention the dates in English. For example, if we need to write the date of Christmas, we write the month and then the ordinal number of the day. In this case, we say that Christmas is on December 25th. Here, 25th is an ordinal number.
Is Zero an Ordinal Number?
No, 0 cannot be considered an ordinal number. Specifying the position of anything as 0th or zeroth does not give a logical explanation.
How to Write Ordinal Numbers?
Ordinal numbers have a suffix added at the end. They can be written as first, second, third, and so on when expressed in words. When ordinal numbers are expressed as numerals, the last two letters of the words are added to the respective numbers, like, 1st, 2nd, 3rd, 4th, and so on.
Why do we use Ordinal Numbers?
We use ordinal numbers for specifying the position or order of something. For example, the pens are kept in the 3rd drawer from the top, or, Ria stays on the second floor of the apartment. Here, the respective numbers specify the position or order of the object or people, whatever the case may be.
What are Ordinal Numbers From 1 to 10?
The ordinal numbers from 1 to 10 are as follows: 1st: First, 2nd: Second, 3rd: Third, 4th: Fourth, 5th: Fifth, 6th: Sixth, 7th: Seventh, 8th: Eighth, 9th: Ninth, and 10th: Tenth.
What is the Ordinal Number of 1?
The ordinal of 1 is written as First. In the numeral form, it is represented as 1st.
Download FREE Study Materials
Worksheets on Ordinal Numbers
The sequence numbers in Purchase Orders
| are used in the following cases:
Please note that you need to change the Order Quantity. After receipt:
Sequence number 3 corresponds to line type Reorder . You must estimate the underdelivered quantity. If you agree on an additional order, you can specify a delivery date for this additional order. If a sequence number already exists for this delivery date, the underdelivered quantity is added to the order quantity on the date in question. If the order quantity has not yet been determined for the specified date, a new sequence number is generated. LN also checks that the delivery address matches the shipping address. nine0008
| |||||||||||||||||||||||||||||
Races and confirmation numbers
of the serial number and confirmation number are the most important in the TSR segment heading, as they play a key role in the functioning of the data of reliable data transfer. However, before discussing the role of these fields in the reliable transfer mechanism, let's look at the values that TCP places in these fields. nine0008
TCP treats data as an unstructured ordered stream of bytes. This approach is manifested in the fact that TCP assigns sequence numbers not to segments, but to each transmitted byte. Based on this, the sequence number of the segment is defined as the sequence number of the first byte of this segment. Consider the following example. Let host A wants to send a stream of data to host B over a TCP connection. The TCP protocol on the transmitting side implicitly numbers each byte of the stream. Let the size of the transferred file be 500,000 bytes, the MSS value be 1000 bytes, and the first byte of the stream be 0. As shown in Fig. 3.27, TCP breaks the data stream into 500 segments. The first segment is assigned sequence number 0, the second segment is assigned sequence number 1000, the third segment is assigned sequence number 2000, and so on. Sequence numbers are entered in the sequence number fields of each TCP segment. nine0008
This approach is manifested in the fact that TCP assigns sequence numbers not to segments, but to each transmitted byte. Based on this, the sequence number of the segment is defined as the sequence number of the first byte of this segment. Consider the following example. Let host A wants to send a stream of data to host B over a TCP connection. The TCP protocol on the transmitting side implicitly numbers each byte of the stream. Let the size of the transferred file be 500,000 bytes, the MSS value be 1000 bytes, and the first byte of the stream be 0. As shown in Fig. 3.27, TCP breaks the data stream into 500 segments. The first segment is assigned sequence number 0, the second segment is assigned sequence number 1000, the third segment is assigned sequence number 2000, and so on. Sequence numbers are entered in the sequence number fields of each TCP segment. nine0008
Now consider the acknowledgment numbers. Recall that the TCP protocol provides full-duplex data transfer, that is, through a single TCP connection, data between hosts A and B can be transmitted simultaneously in both directions. Each segment outgoing from host B contains the sequence number of the data transmitted from host B to host A. The acknowledgment number that host A places in its segment is the sequence number of the next byte that host A expects from host B. Consider the following example. Suppose host A has received all bytes numbered 0 to 535 sent by host B and is forming a segment to send to host B. Host A expects the next bytes sent by host B to be numbers starting with 536 and puts the number 536 in the confirmation number field of your segment. nine0008
Each segment outgoing from host B contains the sequence number of the data transmitted from host B to host A. The acknowledgment number that host A places in its segment is the sequence number of the next byte that host A expects from host B. Consider the following example. Suppose host A has received all bytes numbered 0 to 535 sent by host B and is forming a segment to send to host B. Host A expects the next bytes sent by host B to be numbers starting with 536 and puts the number 536 in the confirmation number field of your segment. nine0008
Consider another situation. Let host A receive two segments from host B, the first of which contains bytes 0 to 535 and the second contains bytes 900 to 1000. This means that for some reason the bytes 536 to 899 were not received by Host A. In this case, Host A waits for missing bytes and puts the number 536 in its segment acknowledgment number field. Since TCP acknowledges received data up to the first missing byte, it is said to support general handshaking.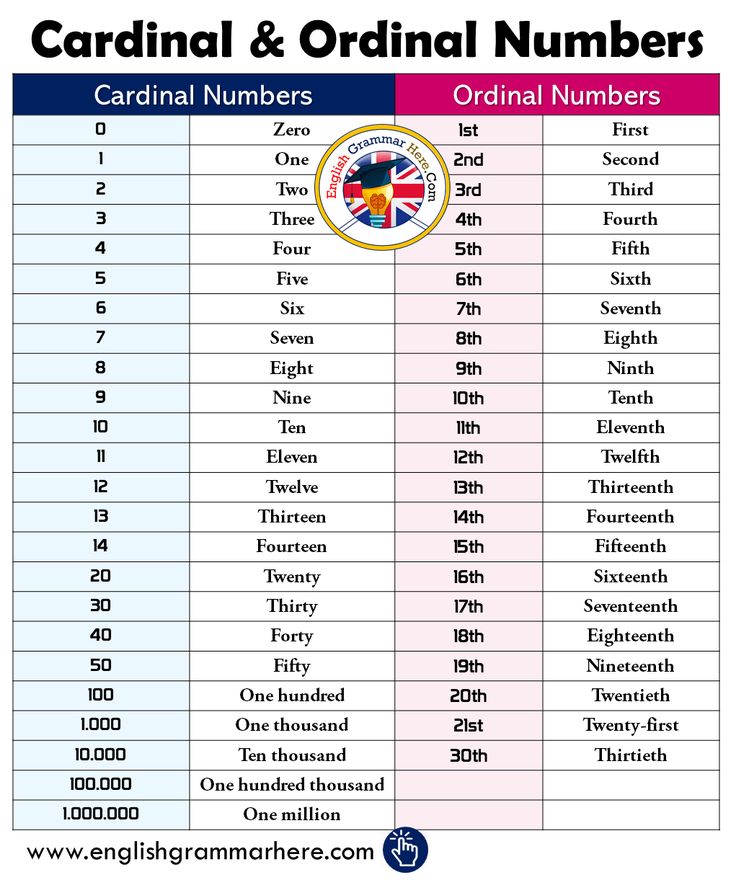 nine0008
nine0008
The last example demonstrates a very important aspect of how the TCP protocol works. The third segment (containing bytes 900-1000) was received by host A earlier than the second (containing bytes 536-899), that is, out of order. The question arises: how does the TCP protocol react to a violation of the order? It turns out that the protocol specification gives TCP programmers complete freedom in resolving this issue. However, two main approaches stand out: the receiving end can either immediately ignore the out-of-order segments, or keep the received segments until the missing data is received. The first approach simplifies programming, while the second improves the efficiency of communication lines. nine0008
Fig. 3.27 the first sequence number is 0, but in practice the parties to the TCP protocol choose a starting number at random. This is due to the need to minimize the probability of finding a segment in the network that is formed by another (already closed) TCP connection between the same two hosts, but which can be mistakenly attributed to an existing TCP connection.


 The sum of order quantities may be lower than the total (total) order quantity. If you save the order line, the total order quantity is updated. nine0008
The sum of order quantities may be lower than the total (total) order quantity. If you save the order line, the total order quantity is updated. nine0008 










