1St grade math skills

First Grade Online Lesson Plans

View Our Lesson Demos!

A first grade math curriculum should teach students the fundamentals in a way that is not just effective, but also fun. In addition to giving students a solid foundation, first grade math fluency also arms students with the tools and confidence they need to learn more advanced concepts down the road.

If a child can’t keep up with a first grade math curriculum, not only will they fall behind and, in turn, lose confidence, but they’ll also lose interest in the subject. Additionally, the skills and concepts that students learn in first grade math aren’t just limited to use in their academic studies. First grade math fluency also helps students become better problem solvers and logical thinkers.

What Math Should a 1st Grader Know

Students will acquire tons of new math skills in first grade. This knowledge will serve as a foundation for what they will learn in second grade math and also expand on what they learned in kindergarten. As they go into first grade, students should be familiar with a number of concepts in order for them to be successful and learn more advanced topics and math strategies. These include, but are not limited to:

• Be able to count, identify and write numbers
• Perform one-digit addition and subtraction
• Have an understanding of quantity (more and less)
• Familiarity with patterns and shapes
• Knowledge of place value (ones, tens, etc.)

The ideal math curriculum for first grade should not only build on these skills and ensure mastery of new concepts, but also make learning fun by engaging and motivating students.

Math Objectives for 1st Grade

Once you’ve selected the ideal math curriculum, it is important to set some attainable goals. Below is a sample of what some of these math goals should be:

• Count to 100; county by 5s and 10s to 100; count by 2s to 40
• Represent numbers on a number line
• Add and subtract 2-digit numbers
• Write the date; tell time; read a calendar
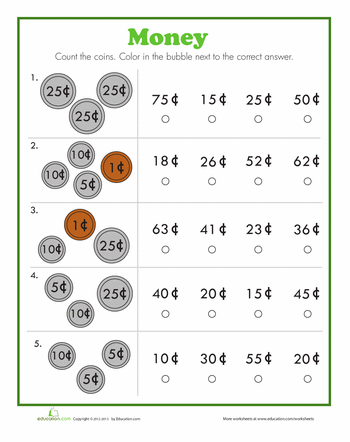
• Count and create coin combinations; add and subtract money
• Identify, sort and classify 2-dimensional shapes
• Understanding the value of money

Towards the end of the year, if your child has already achieved most of their first grade math goals you can give them a head start for the next year by having them practice math facts. This will solidify what they learned in first grade and prepare them for their second grade math learning targets.

1st Grade Math Scope & Sequence

Chapter 1: “Number Sense”

Lesson 1: Read Numbers –

Read whole numbers up to 100. Use one-to-one correspondence to count objects up to 100.

Lesson 2: Compare Numbers –

Compare and order whole numbers up to 100 by understanding the concepts of greater than, less than, and equality.

Lesson 3: Ordinal Numbers –

Match ordinal numbers with an ordered set of up to ten items. Identify first, second, and third by name.

Lesson 4: Count Numbers –

Count forward and backward by ones and count forward by tens from any number less than 100.

Lesson 5: Place Value –

Identify the place value of a digit in whole numbers to 100. Identify the value of digits up to the hundreds place.

Lesson 6: Compare with Place Value –

Group objects by tens and ones. Compare and order whole numbers up to 100 using place value.

Lesson 7: Count by Twos and Fives –

Count forward by twos and fives up to 50.

Lesson 8: Odd and Even Numbers –

Model and identify even and odd numbers.

Chapter Test: Number Sense

 Chapter 2: “Fractions”

Lesson 1: Equal and Unequal Parts –

Identify equal and unequal parts of wholes.

Lesson 2: Halves and Fourths –

Identify and demonstrate fractions (1/2, 1/4) as parts of whole and parts of a set using concrete materials and drawings.

Lesson 3: Thirds –

Identify and demonstrate thirds and 1/3 of wholes using concrete materials and objects.

Lesson 4: Equal Fractions –

Identify equivalent fractional parts as a whole.

Chapter Test: Fractions

 Chapter 3: “Operations”

Lesson 1: Adding and Subtracting –

Demonstrate understanding of the meaning of addition and subtraction by using language such as put together, take away, increase, decrease, compare, and find the difference. Relate informal language to mathematical language and symbols.

Lesson 2: Place Value –

When given any number up to 100, identify one more than, one less than, 10 more than, and 10 less than.

Lesson 3: Equal Numbers –

Using diagrams and/or numerical expressions, represent equivalent forms of the same number up to 12.

Lesson 4: One-digit Addition –

Solve one-digit addition problems.

Lesson 5: One-digit Subtraction –

Solve one-digit subtraction problems.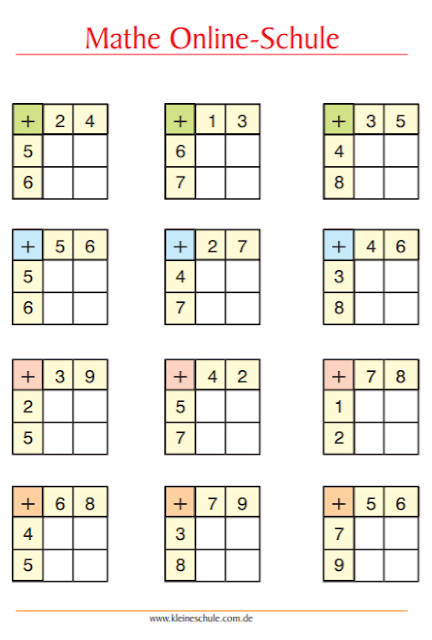

Lesson 6: Sum of Three Addends –

Find the sum of three one-digit numbers.

Lesson 7: Two-digit Addition –

Solve two-digit addition problems.

Lesson 8: Zero as a Placeholder –

Explain the meaning of zero and its function as a placeholder. Explore adding and subtracting zero.

Lesson 9: Addition and Subtraction Strategies –

Solve for basic addition and subtraction facts by using strategies such as counting on, counting back, doubling, doubling plus one, and making ten.

Lesson 10: One-Digit Word Problems –

Solve addition and subtraction one-digit word problems by selecting the proper operation.

Lesson 11: Problem Solving Strategies –

Choose an appropriate method, such as using concrete materials, mental math, or paper and pencil to solve real-world addition and subtraction problems.

Lesson 12: Estimation Language –

Use the appropriate language of estimation such as about, near, closer to, and between to identify and describe numbers in real-world situations.

Lesson 13: Estimate –

Estimate reasonable answers to compare amounts, count objects, and solve basic facts.

Chapter Test: Operations

 Chapter 4: “Money”

Lesson 1: Coin Values –

Identify and name the values of coins (penny, nickel, dime) and show different combinations of coins that equal the same value, up to 75¢. Recognize and use the cents sign.

Lesson 2: Count Money –

Identify and count money to equal an amount using the fewest coins.

Lesson 3: Model Money Amounts –

Identify and count money to equal an amount using the fewest coins.

Lesson 4: Add and Subtract Money –

Solve simple addition and subtraction problems involving the use of pennies, nickels, and dimes up to 50¢.

Chapter Test: Money

 Chapter 5: “Patterns”

Lesson 1: Sort Using One Attribute –

Sort and classify objects by one attribute.

Lesson 2: Sort Using Two Attributes –

Sort and classify objects by two or more attributes.

Lesson 3: Rules for Sorting –

Justify rules for sorting and classifying.

Lesson 4: Build Patterns –

Use one attribute to create a pattern. Identify errors in repeating patterns.

Lesson 5: Classify Patterns –

Classify, describe, and extend patterns of objects using a wide variety of attributes (i.e., size, shape, color).

Lesson 6: Picture and Number Patterns –

Predict and extend pictorial patterns. Identify and generate patterns in number pairs by adding to a T-chart.

Lesson 7: Repeating and Growing Patterns –

Explore and create repeating patterns and growing patterns and generate rule for such patterns.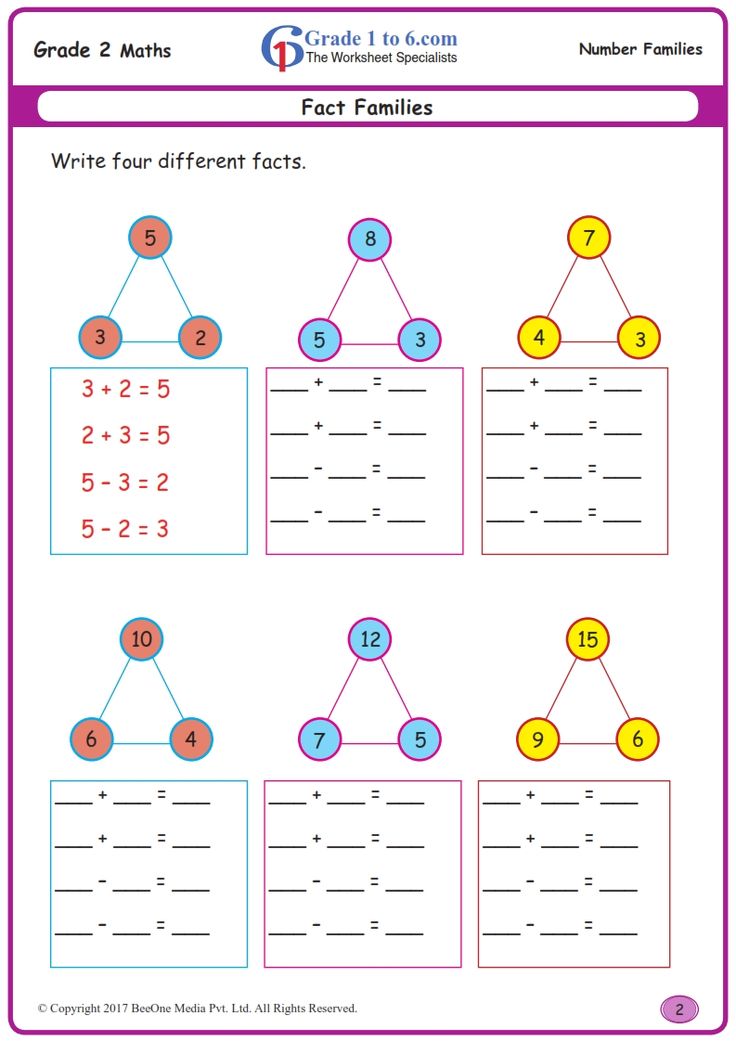

Lesson 8: Patterns on a Hundreds Chart –

Explore patterns of numbers on a hundreds chart.

Lesson 9: Skip Counting –

Use patterns to skip count by 2s, 5s, and 10s to 100. Understand and identify odd and even numbers.

Lesson 10: Extend Number Patterns –

Predict and extend existing numerical patterns using addition.

Chapter Test: Patterns

 Chapter 6: “Algebra”

Lesson 1: Order Property –

Use the Commutative Property of Addition in solving problems.

Lesson 2: Add and Subtract Numbers –

Using objects and pictures, model situations that involve the addition and subtraction of whole numbers.

Lesson 3: Fact Families –

Identify fact families by understanding the patterns in related addition and subtraction sentences.

Lesson 4: Number Sentences –

Using objects, create models that represent a variety of number sentences including the missing addend.

Lesson 5: Equal and Unequal –

Use concrete objects and pictorial representations to explore equalities and inequalities.

Lesson 6: Greater Than and Less Than –

Use concrete objects to solve number sentences with equalities and inequalities using the symbols <, =, >.

Lesson 7: Solve for Unknown Numbers –

Solve addition and subtraction problems with an unknown number represented by a geometric shape.

Chapter Test: Algebra

 Chapter 7: “Shapes”

Lesson 1: Straight and Curved Lines –

Compare plane figures based on their straight and curved lines.

Lesson 2: Open and Closed Shapes –

Identify open and closed figures.

Lesson 3: Plane and Solid Shapes –

Identify circles, triangles, and rectangles (including squares), and describe the shape of balls, boxes, cans, and cones. Sort shapes by attributes (sides, curves, corners).

Lesson 4: Special Plane Shapes –

Recognize plane shapes such as hexagons, trapezoids, and rhombi.

Lesson 5: Attributes of Plane Shapes –

Describe and compare attributes (sides, vertices, angles) of two-dimensional shapes.

Lesson 6: Name Solid Shapes –

Recognize solid shapes such as spheres, cylinders, cones, and cubes.

Lesson 7: Attributes of Solid Shapes –

Describe and compare attributes (edges, vertices, faces) of three-dimensional shapes.

Lesson 8: Congruent Shapes –

Identify congruent two- and three-dimensional shapes.

Chapter Test: Shapes

 Chapter 8: “Positions”

Lesson 1: Positions of Objects –

Describe relative positions of objects or shapes using words such as top, middle, on, inside, and outside.

Lesson 2: Direction Words –

Interpret directional words such as left, right, up, and down.

Lesson 3: Position Words –

Identify, locate, and move objects according to positional words such as to the left, above, and behind.

Lesson 4: The Number Line –

Locate, plot, and identify known and unknown numbers on a number line from 0 to 20 by ones and from 1 to 100 by tens.

Chapter Test: Positions

 Chapter 9: “Using Shapes”

Lesson 1: Slides and Turns –

Identify slides and turns with objects.

Lesson 2: Congruent Shapes –

Identify matching pairs of congruent figures that have been turned or flipped.

Lesson 3: Symmetry –

Identify lines of symmetry in two-dimensional shapes.

Chapter Test: Using Shapes

 Chapter 10: “Spatial Sense”

Lesson 1: Build Shapes –

Create two-dimensional and three-dimensional shapes using other shapes (e. g., two squares make a rectangle).

Lesson 2: Plane and Solid Shapes –

Recognize two- and three-dimensional shapes from various perspectives.

Lesson 3: Perimeter and Area –

Compare perimeter and area of two-dimensional shapes in terms of less than, equal to, or greater than.

Lesson 4: Shapes Around Us –

Recognize geometric shapes in the environment.

Lesson 5: Pattern Blocks –

Use pattern blocks to form shapes. Identify combined shapes in nature, art, and architecture.

Chapter Test: Spatial Sense

 Chapter 11: “Time”

Lesson 1: Calendar –

Identify the names of the week and months of the year using a calendar.

Lesson 2: Passage of Time –

Identify the keywords that name the passage of time such as yesterday, afternoon, night, and day.

Lesson 3: Tools for Telling Time –

Identify tools for measuring time such as clocks and calendars and name parts of each tool.

Lesson 4: Time to the Hour and Half-hour –

Tell time on analog and digital clocks to hour and half hour, and relate time events using shorter/longer.

Lesson 5: Time to the Hour and Half-hour –

Tell time on analog and digital clocks to hour and half hour, and relate time events using shorter/longer.

Lesson 6: Elapsed Time –

Solve simple real-world problems involving elapsed time to the hour and half hour and minutes.

Chapter Test: Time

 Chapter 12: “Length”

Lesson 1: Non-standard Units –

Use nonstandard units to estimate and measure lengths.

Lesson 2: Compare Lengths –

Compare the length of two or more objects by using direct comparison or by using nonstandard units.

Lesson 3: Customary Units –

Use customary units to measure, compare, and order objects according to lengths, in inches and feet.

Lesson 4: Tools and Units –

Choose the appropriate unit and tool to measure length.

Lesson 5: Metric Units –

Use metric units to measure, compare, and order objects according to lengths.

Chapter Test: Length

 Chapter 13: “Weight”

Lesson 1: Non-standard Units –

Use nonstandard units to estimate and measure weights.

Lesson 2: Compare Weights –

Compare the weight of two or more objects by using direct comparison or by using nonstandard units.

Lesson 3: Customary Units –

Compare the weight of two or more objects using customary units and identify the tools for measuring weight.

Lesson 4: Metric Units –

Use metric units to measure, compare, and order objects according to weights.

Chapter Test: Weight

 Chapter 14: “Capacity”

Lesson 1: Non-standard Units –

Use nonstandard units to estimate and measure capacity.

Lesson 2: Compare Capacity –

Compare the capacity of two or more containers using direct comparison.

Lesson 3: Customary Units –

Compare the capacity (in cups, pints, and quarts) of two or more containers. Identify the tools for measuring capacity.

Lesson 4: Metric Units –

Use metric units to measure, compare, and order objects according to capacity.

Chapter Test: Capacity

 Chapter 15: “Temperature”

Lesson 1: Measure Temperature –

Using a Fahrenheit thermometer, tell temperature to the nearest 10 degrees. Match temperature in degrees Fahrenheit to the feeling outside of a warm or cold day.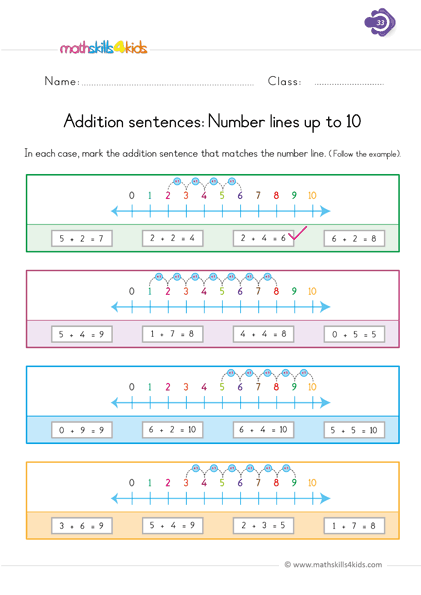

Lesson 2: Compare Temperature –

Compare temperatures in degrees Fahrenheit of two or more objects. Identify tools for measuring temperature.

Chapter Test: Temperature

 Chapter 16: “Graphing”

Lesson 1: Tally Table –

Sort objects into categories and create a tally table.

Lesson 2: Pictographs –

Organize and record data in pictographs.

Lesson 3: Bar Graphs –

Organize and record data in bar graphs.

Chapter Test: Graphing

 Chapter 17: “Using Data”

Lesson 1: Compare Data –

Interpret data and explore range and mode in simple graphs.

Lesson 2: Make Predictions –

Use data to make predictions about events or situations.

Chapter Test: Using Data

 Chapter 18: “Probability”

Lesson 1: Certain or Impossible –

Identify whether an event is certain, possible, or impossible.

Lesson 2: Most and Least Likely –

Identify the likelihood of a given event.

Chapter Test: Probability

Why Choose Time4Learning First Grade Math Homeschool Curriculum

Without a thorough understanding of foundational math skills, students will find it difficult to keep up with a first grade math curriculum. As we all know, in order to keep a young child engaged and to instill a lifelong love of learning they need to enjoy the lessons.

Time4Learning makes learning fun for first graders through interactive, multimedia-based lessons that feature colorful animations, funny characters, and catchy songs — all of which help children learn, retain information, and have fun. With a simple-to-follow format that builds on previous material, students are able to expand their knowledge and build their first grade math fluency in order to master concepts in number sense, addition, subtraction, estimation, money, patterns, and more.

In addition to providing an award-winning curriculum for students, Time4Learning can help your student achieve all their first grade math goals and objectives with our flexible, student-paced curriculum. It also offers convenient tools for parents that help you save time and homeschool with confidence. Learn more about our online first grade homeschool curriculum, designed to help your child learn and master their fundamental concepts.

1st Grade Math Skills, What Your Child Will Learn, Komodo Math

• Math Tips
• Education
• 1st

Your child is heading to first grade! After the year in kindergarten, your first grader will be ready for some amazing growth. For many children, first grade is the year that they bloom as readers and mathematicians. Get ready to support your child’s mathematical growth by learning about first grade math skills.  

In first grade, you can expect your child to learn about: 

1. Addition and subtraction facts to 20 

Now that your child has mastered the idea of adding and subtracting, they’re ready to practice math facts. This means getting faster when answering addition and subtraction problems to 20. 

Help your child develop fluency by asking basic addition and subtraction problems - we find that using treats can help keep kids interested! If your first grader needs support, encourage the use of physical objects or fingers as problem-solving tools. 

2. Addition and subtraction as inverse operations 

Your child probably understands the concept of addition as “putting together” and subtraction as “taking apart.” In first grade, children are encouraged to see the connections between addition and subtraction. Your child will learn how addition and subtraction are inverse operations, or that one is the opposite of the other, and create “fact families” of related addition and subtraction problems.  

When working with addition and subtraction, ask your child to see connections. For example, if your child has four dolls and three cars, ask how many toys there are in all. Then ask how many toys there would be if the four dolls are taken away. 

3. Count and write within 120 

Your child has probably mastered counting to 20. But in first grade kids will learn to count all the way up to 120! That’s not all. Kids will be expected to not only count, but write, the numbers. This is great practice for understanding multi-digit numbers. 

At home: Encourage your child to write numbers whenever possible. Talk about how two-digit numbers are made up of tens and ones and how three-digit numbers are made up of hundreds, tens, and ones. Just looking closely at multi-digit numbers together can be a great learning opportunity. 

4. Add within 100 

Now that your child has an understanding of numbers past 100 as well as basic addition and subtraction facts, it’s time to practice adding within 100. Children will practice adding one-digit numbers to two-digit numbers using strategies like counting on and number charts. Children can practice adding larger numbers with the help of a 1-100 chart. 

First graders are also ready to practice adding and subtracting 10s to and from two digit numbers. 

At home: Help your child see patterns when adding and subtracting 10s. For example, after solving a problem like 59 - 10 = 49, point out to your child that 49 has one less 10 than 59. This is another great way to learn about place value. 

5. Measure objects

In first grade, kids learn how to measure using rulers and more unusual things like paper clips. After taking measurements, children compare and order objects by length.

At home: Kids love measuring things around the house, so keep a couple of rulers handy.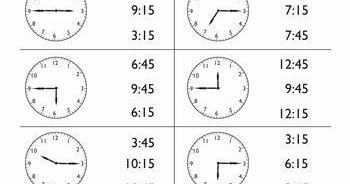 Pay attention to how your child is using a ruler and taking measurements. Sometimes kids don’t quite measure from end to end, so they might need a bit of help...  

6. Tell time to hour and half hour 

One of the trickiest concepts first graders will learn is to tell time. Using analog clocks is confusing, especially when kids are more used to seeing digital clocks. In first grade, your child will learn about the big and little hands of a clock and will practice telling time to the hour and half hour. 

At home: Get hold of an analog clock for your home (either a real one or one made just for learning). Talk with your child about the time and how the hands move around the clock. Remember to just focus on telling time to the hour and half hour to start! 

7. Understand basic fractions

First graders also get an introduction to fractions as equal shares. They will learn how to divide into equal groups and learn basic fractions like ½, ⅓, and ¼. First graders usually have a good understanding of fairness,  so practicing making equal shares should be a relatively easy task for them!

At home: Help your child to divide pizzas, pies, and sandwiches into equal shares. As you do, talk about the fractions of the whole that you created. 

First graders are ready to dive deep into mathematical concepts. Find time to connect with your child about classroom learning and get ready to have some fun! 

Found this useful? Check out our grade by grade math guides from Kindergarten to 5th grade

Written by Lily Jones, Lily loves all things learning. She has been a kindergarten & first grade teacher, instructional coach, curriculum developer, and teacher trainer. She loves to look at the world with curiosity and inspire people of all ages to love learning. She lives in California with her husband, two kids, and a little dog.

About Komodo – Komodo is a fun and effective way to boost K-5 math skills. Designed for 5 to 11-year-olds to use in the home, Komodo uses a little and often approach to learning math (15 minutes, three to five times per week) that fits into the busy family routine. Komodo helps users develop fluency and confidence in math – without keeping them at the screen for long.

Find out more about Komodo and how it helps thousands of children each year do better at maths – you can even try Komodo for free. 

Back to School - 5 Tips to Help you Ease Back into the Routine

Here are some steps you can take to ease children back from full vacation mode so that the first week of school doesn't knock you sideways.

Mindset - The Path to Mastery

People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.

PECULIARITIES OF THE DEVELOPMENT OF MATHEMATICAL ABILITIES IN FIRST CLASS STUDENTS | Article on mathematics (Grade 1) on the topic:

FEATURES OF THE DEVELOPMENT OF MATHEMATICAL ABILITIES IN FIRST CLASS STUDENTS

Gnatiuk Natalia Vadimovna, primary school teacher

Annotation: The article describes the relevance and necessity of developing mathematical abilities in students of educational institutions. The reasons for the low level of mathematical education in the Russian Federation are described. Various points of view on the definition of the concept of mathematical abilities by foreign and domestic scientists are considered. The main components included in the structure of mathematical abilities are given. The effectiveness of the development of mathematical abilities during the period of study in elementary school is argued. Experimental methods of work in the classroom are given, aimed at developing mathematical abilities in first-grade students. Experimental work on the use of TRIZ technology to develop the mathematical abilities of students, as well as innovative methods of work that allow not only to form a system of mathematical representations, but also increase motivation for learning mathematics and develop creative abilities are described.

Key words: mathematical abilities, mathematics, elementary school, first grade students, the concept of mathematical development of the Russian Federation.

The problems of development of mathematical abilities in schoolchildren have traditionally been the subject of special attention of teachers of various educational organizations. However, these issues have gained particular relevance in recent years. This is explained, firstly, by the introduction of the Concept of Mathematical Education in the Russian Federation, the purpose of which is to bring Russian mathematical education to a leading position in the world [1]. This is explained by the fact that a high level of mathematical education among the population of the country will ensure the creation of an innovative economy that will improve the standard of living among Russians.

The relevance of this study is also determined by changes in the socio-economic sphere, the development of technology, as well as an increase in the amount of information, which causes a special need for personnel with a sufficiently high level of mathematical abilities.

A significant contribution to the study of mathematical abilities was made by such prominent representatives of certain trends in psychology as A. Binet, E. Trondike and G. Reves, as well as outstanding mathematicians A. Poincaré and J. Hadamard.

For example, W. Betz defines mathematical abilities as the ability to clearly understand the inner connection of mathematical relations and the ability to think accurately in mathematical concepts. However, a more complete and deeper understanding of the nature of mathematical abilities is reflected in the definition of our compatriot V.A. Krutetsky. In his work “Psychology of Mathematical Abilities of Schoolchildren”, he defines mathematical abilities as individual psychological characteristics (primarily features of mental activity) that meet the requirements of educational mathematical activity and determine, all other things being equal, the success of creative mastery of mathematics as an educational subject, in particular, relatively fast, easy and deep mastery of knowledge, skills in the field of mathematics [3].

Mathematical abilities, like any other, are a set of mental qualities that have a complex structure. V.A. Krutetsky, considering the structure of mathematical abilities, singled out 4 main components [3]: obtaining mathematical information, processing mathematical information, mathematical memory, and also mathematical orientation. It is worth noting the fact that computational abilities and the ability to spatial representations, according to V.A. Krutetsky, were optional components of mathematical abilities, albeit useful ones.

For a long time, psychologists were of the opinion that only empirical thinking is inherent in younger students. However, D.B. Elkonin and V.V. Davydov developed and experimentally substantiated the proposition that it is possible to form theoretical thinking in younger schoolchildren, but for this, their assimilation of relevant subject knowledge (mathematical, linguistic, etc.) must occur through specific educational activities. The need for the formation of mathematical abilities already in elementary school is also due to the fact that in the period from 3-4 years to 8-9years there is a rapid development of the child's intellect.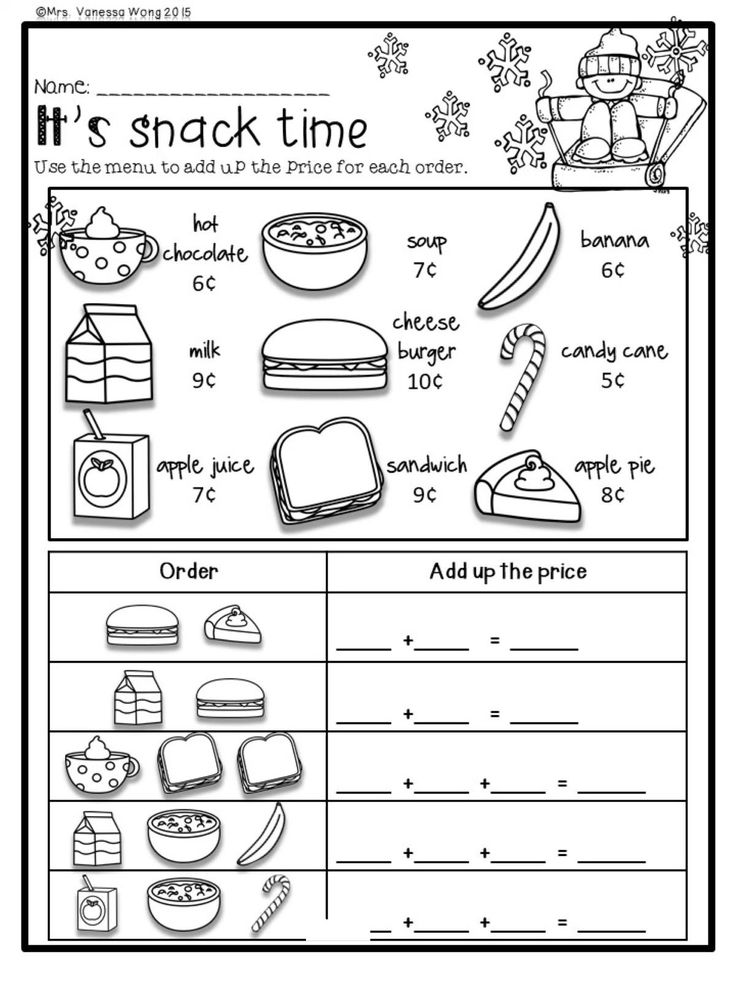 Therefore, during the period of primary school age, the possibilities for developing any abilities, including mathematical ones, are the highest.

Naturally, a child's success in learning is determined not only by his abilities. Great importance in the formation of mathematical abilities is given to the content and methods of teaching, as well as the attitude of the student to the discipline being taught. At the same time, the presence of poorly developed abilities in younger students not only frees the teacher from the need to develop them, but, on the contrary, motivates them to develop them to the extent possible.

The teacher should pay special attention to the selection of students who show a penchant for mathematical abilities. However, do not forget about the rest of the students. In this regard, in his work, the teacher needs to combine collective and individual methods of work in order to activate the activity of students in this way.

Thus, in order to develop mathematical abilities, a set of tasks for first grade students was developed and adapted.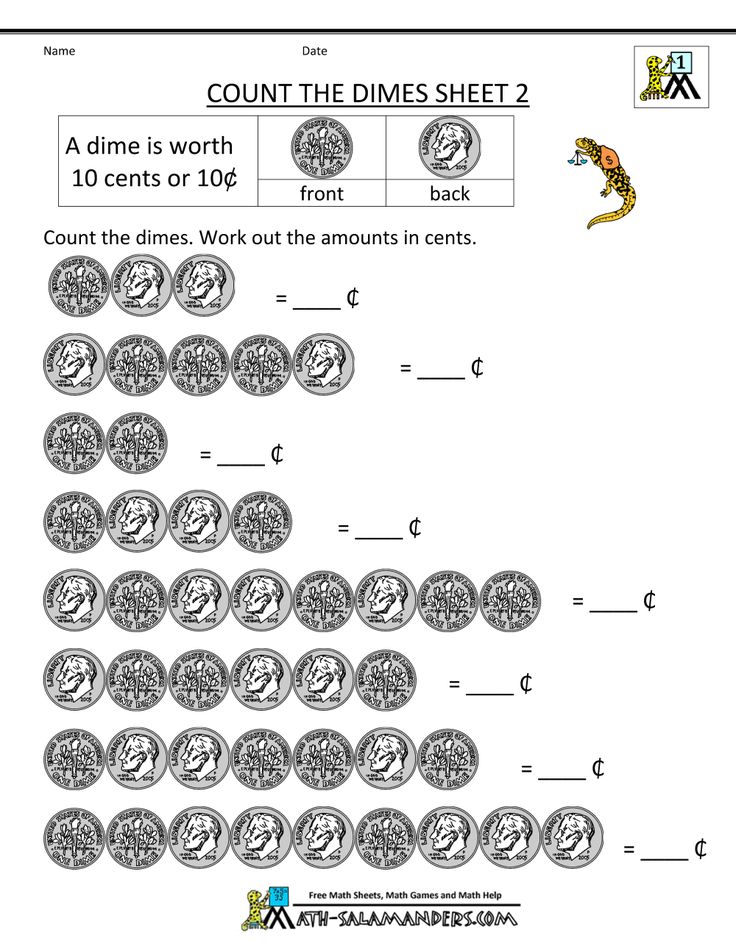 It is worth noting the fact that these tasks are also aimed at developing motivation and interest in learning mathematics, increasing the effectiveness of mathematical education and developing the general outlook of students. This set of tasks was tested not only directly in mathematics lessons, but also in extracurricular activities.

One of the directions of this work was the development of thinking flexibility in first grade students. Unfortunately, already at the initial stage of education, children tend to act according to ready-made stereotypes and reproduce only one way to solve a mental problem. The problem of students is that they do not notice the possibility of multiple answers, and also do not know how to find effective solutions. Therefore, to develop the flexibility of thinking, a set of tasks is used, the solution of which allows several options. These problems are called combinatorial, because they deal with combinations. When solving such problems, younger students choose all possible solutions. Also, in order to develop the flexibility of thinking, tasks are proposed that are inverse to this one, tasks with reverse motion and tasks with an alternative condition

The main direction of work on the development of mathematical abilities was the development of the main component - logical thinking. Tasks aimed at the development of logical thinking can be divided into four groups:

1. Tasks for the development and improvement of attention. Such tasks include finding moves in ordinary, as well as numerical labyrinths. The degree of difficulty of such labyrinths is quite high, because they have an extensive network of paths, moving along which, it is necessary to perform certain tasks of a computational nature. Also, tasks for comparing two pictures are quite effective.
2. Tasks for the development of perception and imagination. In tasks of this type, it is necessary to imagine the nature of one or another transformation, for example, to imagine the whole that should be composed of the proposed parts, to find the missing part among the many given parts to obtain the whole, to correlate the dimensions of the areas of several given figures by eye, to describe and depict the mutual arrangement of several geometric shapes or objects, etc.
3. Tasks for the development of various types of memory - visual, auditory, visual-figurative and verbal-logical memory of children. For this, didactic games are used; visual dictations, the content of which is enriched by the studied mathematical material. Within one minute, all the figures are shown to the students at the same time, after which the children must reproduce them in a notebook from memory.
4. Tasks for the development of thinking are a set of content-logical tasks aimed at developing and improving mental operations: comparison, analysis, synthesis, generalization and classification, solving logical problems. The ability to compare is practiced when comparing two numbers, examples, tasks, equations, two figures, and then a group of examples, tasks, etc. When performing tasks of this type, it is very important to draw the attention of children to the fact that a sign of dividing given objects into groups is not set and they have to determine it themselves.

The use of innovative teaching technologies, one of which is TRIZ technology, played a very important role in the development of mathematical abilities in first grade students. TRIZ - the theory of inventive problem solving - is one of the models of perspective education. The theory of inventive solution is a unique tool for searching for non-trivial ideas, developing creative and strong thinking, forming creative individuals and teams.

One of the methods of working with TRIZ technology was the establishment of the correct sequence of actions described in the problem. That is, before starting to solve the problem, students need to arrange all its elements in the correct sequence. These methods of work allow you to consolidate knowledge about the main structural elements of the task (condition, question).

Another method of working with TRIZ technology is to consider the object under study from the point of view of describing it in terms of shape, color, size, and material.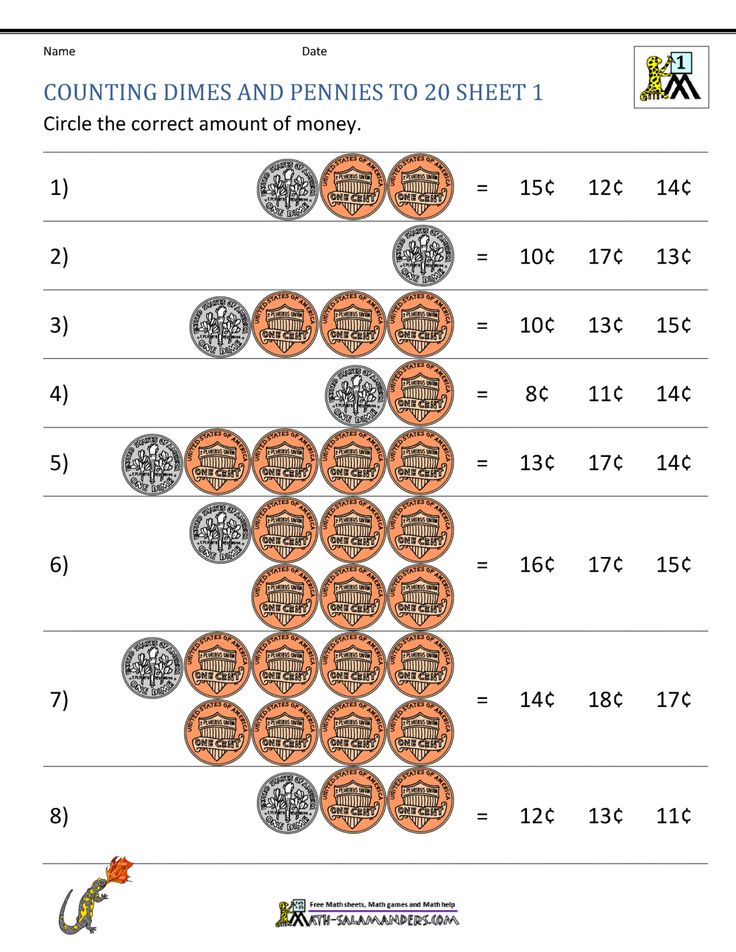 Unfortunately, in mathematics lessons, this type of work can only be used when describing any quantities or new geometric shapes. In the same lessons, it is also possible to use another “Five Senses” technique, where in order to study a new object, it is necessary to use all five senses: sight, hearing, touch, smell and taste. These methods of work allow you to consider the object under study from all sides, as well as to study it in more detail and in detail. At the same time, in such lessons, the student himself acquires new knowledge through his feelings and actions, as a result of which the new acquired knowledge will be much stronger than if the teacher simply told the students about it.

Such an innovative teaching method as "Create a passport" was used in the lessons to describe the studied geometric shapes. This universal method of compiling a generalized characteristic is aimed at systematizing, generalizing the knowledge gained; to identify essential and non-essential features of the phenomenon under study; creating a brief description of the concept under study, comparing it with other similar concepts.

In order to develop mathematical abilities, the innovative Droodle method was also used. It is a drawing, on the basis of which it is impossible to say exactly what it is. In this image, there are dozens of different situations, and there is no single correct answer. In reality, 20-30 different interpretations are possible for each image.

Thus, the introduction of the described teaching methods into the educational process of elementary school contributes to the development of mathematical abilities of younger students, as evidenced by such factors as increasing motivation to study mathematics, improving computational skills, as well as improving academic performance in mathematics. Thanks to the developed mathematical abilities, students not only will not experience difficulties in teaching mathematics in the future (provided that the described work is continued), but will also be able to reach a high level of mathematical education.

REFERENCES:

1. The concept of the development of mathematical education in the Russian Federation (approved by the order of the Government of the Russian Federation of December 24, 2013 N 2506-r)
2. Krutetsky, V. A. Psychology of mathematical abilities of schoolchildren [Text] / V.A. Krutetsky. - M .: Publishing house "Institute of Practical Psychology", 1998. - 416 p.

Mathematics in grade 1 - what should a child be able to do?

Global development does not stand still, so the requirements for a person and his capabilities are constantly increasing. Including such a category of the population as schoolchildren. They need to work almost without rest in order to withstand the competition of their peers.

The level of knowledge of first graders has also become quite high. Schools do not have strict requirements for future students, but still, yesterday's kindergarteners must be prepared for basic subjects. It will be easier for a child to study in the first grade if he knows letters and sounds, can read by syllables, hold a pen correctly, and even better be able to write letters and know the alphabet well. As for mathematics in the first grade, there are also some requirements: you need to know simple geometric shapes, count up to 10, and preferably up to 20, understand what direct and reverse ordinal counting is, navigate on a sheet of paper.

Both the educational and moral readiness of children is important. Parents are worried about the future first-grader, because even knowing everything that is needed, he can get confused and nervous. And school interviews are held precisely for this, so that teachers can understand how capable and prepared the child is.

How can I help my child learn the school curriculum in mathematics in the first grade?

Many parents from the first grade strive to teach their children to study well - to get only A's. But at the same time, they forget to emphasize that the most important thing is to gain knowledge. Even first-graders often have a problem that the grades are good, but there is very little knowledge. After all, it’s easy to just memorize the material in order to answer well at the blackboard the next day. It is difficult to understand and understand the topic in order to fix it forever.

Therefore, parents should convey to their children that the most important thing is to understand mathematics, learn how to apply it in life, consciously perform exercises, not solve examples in the classroom mechanically, but only with full understanding and without haste. For conscious learning, the development of logic and non-standard critical thinking also helps. Thanks to them, it will be easier for the student to understand mathematics and apply its laws in life.

Math assignments in Grade 1

First-graders' education is mainly based on what children learned in pre-school lessons. The past is repeated, and the complication of the material occurs very gradually.

Mathematics assignments in grade 1 are the study of a straight line, a point, a broken line, simple geometric shapes, both written and mental counting. Considering that the basis of algebra is the multiplication table, then in the first grade there is preparation for its study: fundamental knowledge is gained, which in the second grade allows you to master the multiplication table.

In addition, of course, students learn to find figures in the world around them, broaden their horizons, try to apply in life the calculation that they have already mastered.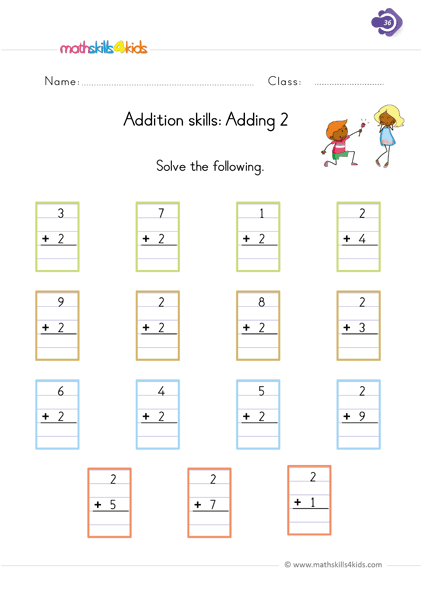 They also solve puzzles, puzzles, easy entertaining tasks, the simplest examples. Despite the fact that this is a school, teachers try to teach the material in an interesting way, and pick up tasks that are exciting and in a playful way.

Math puzzles and quick wits

In addition to learning numbers, rules and counting, it is important to give your child to solve various puzzles and puzzles. It is non-standard tasks that help a child develop his brain, learn how to find a solution, are not afraid of difficulties, apply mathematical tricks. Simple examples will only help to work out the skill of arithmetic calculations, and you can develop further only using non-standard thinking.

The modern Amamatika method from the AMAKids Intelligence Development Academy includes an online platform and math game simulators that allow you to develop all the abilities of children in the field of mathematics at once.

In order to teach students to easily solve problems of any complexity, as well as apply the “queen of sciences” in life, our textbooks and manuals offer interesting tasks with missing numbers, unbroken crosswords and puzzles, mathematical puzzles for grade 1 and for older children, fascinating mazes , tasks for ingenuity. Knowing how to apply non-standard methods of solving, the child does not experience fear of tasks of increased complexity. He takes on any challenge with interest.

Math Simulator Grade 1

The Amamatika platform and simulator will help you not only succeed in school, but also teach you how to find an approach to complex tasks, teach financial literacy and the basics of programming, help develop analytical thinking, spatial imagination. Mathematics is a complex subject, but if you approach learning in a structured way and adhere to a proven methodology, a student will be able to understand and consolidate even the most difficult topics.

On our convenient online platform, students can pull up any mathematical direction - you just need to go to the required section and start doing the exercises. The first grade math simulator will provide a correct understanding of the subject and lay the necessary foundations for further learning.

Also on the gaming platform there are sections with arithmetic, geometry, tasks, as well as tasks on financial literacy, programming and games for the development of logic, memory and attention.

Learn more

• 
  Word writing for kids
• 
  Reading skills stories
• 
  Children's books about going to school
• 
  Can rhyming words
• 
  Short stories for children to read
• 
  Adjectives of children
• 
  Importance of emergent literacy
• 
  Importance of meditation
• 
  Good night love story
• 
  Word hunting games
• 
  Phonological awareness definition