Algebra for first grade
Algebraic Thinking – Mathematics Methods for Early Childhood
What is algebraic thinking?
As you read the Kansas Mathematics Standards, you will notice the Domain “Operations and Algebraic Thinking” in all grade levels preK grade 12. Furthermore, algebraic thinking and concepts permeate all areas of mathematics. Algebra is more than manipulating symbols or a set of rules, it is a way of thinking.
According to the K-5 Progression on Counting & Cardinality and Operations & Algebraic Thinking (2011), algebraic thinking begins with early counting and telling how many in a group of objects, and builds to addition, subtraction, multiplication, and division. Operations and Algebraic Thinking is about generalizing arithmetic and representing patterns.
Algebraic thinking includes the ability to recognize patterns, represent relationships, make generalizations, and analyze how things change. In the early grades, students notice, describe, and extend patterns; and they generalize about those patterns. Elementary students use patterns in arrays, and they look at patterns to learn basic facts. According to NCTM Past-President Cathy Seeley, “the development of algebraic thinking is a process, not an event. It is something that can be part of a positive, motivating, enriching school mathematics experience” (Seeley, 2004).
Algebra must be incorporated into the elementary classroom as students see patterns, make generalizations, and move across representations. It is essential that algebra instruction focus on sense making, not symbol manipulation (Battista & Brown, 1998). According to Earnest and Balti, “When elementary teachers are unfamiliar with early algebra, lessons designed and labeled as algebraic may become arithmetic exercises; the algebra then remains hidden from both the teacher and students in the implementation. The result is that the algebra standard is only superficially addressed” (Earnest & Balti, 2008).
Blanton and Kaput (2003) suggest teachers “algebrafy” their current curriculum materials and ask students to discover patterns and make conjectures and generalizations, and justify their answers. They also recommend that teachers use these prompts to extend students’ thinking:
They also recommend that teachers use these prompts to extend students’ thinking:
- Tell me what you were thinking.
- Did you solve this in a different way?
- How do you know this is true?
- Does this always work?
Therefore, all elementary teachers must support algebraic thinking and create a classroom culture that values “students modeling, exploring, arguing, predicting, conjecturing, and testing their ideas, as well as practicing computational skills” (Blanton & Kaput, 2003).
Key ideas that underscore algebraic thinking are:
- Equality and the concept of equivalence
- Students often have the misconception that the equal sign means “the answer is” when it really means “the same as.” True/false equations are a way to expose students to the meaning of equality, such as 5 + 2 = 3 + 4, or 8 = 2 + 6.
- Inequality
- Develop in your students a conceptual understanding of greater than and less than as relational symbols, and not rely on memory tricks.

- Develop in your students a conceptual understanding of greater than and less than as relational symbols, and not rely on memory tricks.
- Positive and negative numbers
- Students should be exposed to some negative numbers in the early grades. When teachers say, “You can’t take 6 from 3,” or “You can’t subtract a small number minus a big number,” teachers are giving students information that just isn’t true.
- Problem solving and critical thinking
- Students who have problem solving and critical thinking skills can solve problems in new contexts and can generalize to new situations.
- Making generalizations
- It is important that students discover patterns, which includes mathematical rules, in order to make conjectures about the growing pattern.
- Patterns
- “We need to train children to look for, and to expect to find, patterns in all math work that they do” (Bahr, 2008).
- Variables
- Variables are unknown and can change and are represented by symbols. Teachers should explicitly explain to students that the one-letter symbol is an abbreviation (Bahr, 2008).

- Variables are unknown and can change and are represented by symbols. Teachers should explicitly explain to students that the one-letter symbol is an abbreviation (Bahr, 2008).
- Relational thinking
- Relational thinking focuses on the why behind the right answer. For example, 5 x 3 = 15, but why? It is because there are three groups and each group has five.
- Symbolic representation of mathematical ideas
- Learning that equations communicate the relationship between numbers is crucial for a conceptual understanding behind the symbols.
Source: Algebraic Thinking (de Garcia, 2008)
Connecting Number and Operations and Algebraic Thinking
In kindergarten through grade 3, all of the Operation and Algebraic Thinking standards are related to Number and Operations in Base Ten.
Kindergarten
Students in kindergarten solve addition and subtraction problems in various ways as they make sense of and understand the concepts of addition and subtraction. Kindergarten students should see addition and subtraction equations, and should be encouraged to write equations, such as 4 + 3 = 7 and 7 – 3 = 4, but do not require this of students at this level. It is critical that students see the relationship between numbers, and teachers need to provide students those experiences to manipulate numbers using objects, drawings, mental images, etc. so that students can progress from the concrete, to the pictorial, to the abstract levels.
It is critical that students see the relationship between numbers, and teachers need to provide students those experiences to manipulate numbers using objects, drawings, mental images, etc. so that students can progress from the concrete, to the pictorial, to the abstract levels.
Kindergarten students work with numbers through 10 as they solve word problems. Be sure to focus on these three problem types: Result Unknown, Change Unknown, and Start Unknown. See Chapter 4 for more information regarding these types of problems as well as Table 1 in the Appendix of the Kansas Mathematics Standards.
Beginning in kindergarten, students should also see the equal sign as a relational symbol, not as an action to find the answer. Help students see the relationship between both sides of an equation as having the same value.
First Grade
All of the first grade standards under the Domain of Operations and Algebraic Thinking were addressed in Chapter 4 as students represent and solve addition and subtraction problems, apply the properties of operations and see the relationship between addition and subtraction, and add and subtract within 20.
Some students misunderstand the meaning of the equal sign, and it is critical to correct this misconception early. The is a relational symbol meaning “the same as.” The equal sign is not an operations symbol. Many children believe the equal sign means “the answer is,” which is incorrect. Consider the problem 3 + 7 = 9 + 1. There is no answer, although the two sides are the same. Also give students problems where the equal sign is at the beginning of the problem, for example, 8 = 3 + 5.
The Operations and Algebraic Thinking tasks in the Illustrative Mathematics website is a good resource for connecting number sense to algebraic thinking.
Second Grade
All of the second grade standards under the Domain of Operations and Algebraic Thinking were addressed in Chapters 4, 5, and 7 as students represent and solve addition and subtraction problems, use mental strategies to add and subtract within 20, determine even and odd, and use addition to find the total number of objects in a rectangular array.
The common computation situation types teachers should focus on are in Table 1: Common Addition and Subtraction Situations in the Kansas Mathematics Standards. These situation types are result unknown, change unknown, and start unknown. Refer to “Chapter 9: Whole Number Computation” for more information on these situation types.
As students solve one- and two-step problems, expect them to use manipulatives such as base-ten blocks, a number line, hundreds charts, etc. In second grade, do not focus on traditional algorithms or rules, but instead on the meaning of the operations.
The Operations and Algebraic Thinking tasks in the Illustrative Mathematics website is a good resource for connecting number sense to algebraic thinking. Illustrative Mathematics Grade 2 Operations & Algebraic Thinking tasks
Third Grade
All of the third grade standards under the Domain of Operations and Algebraic Thinking were addressed in Chapters 5 and 7 as students represent and solve multiplication and division problems and understand the relationship between multiplication and division and understand the properties of multiplication. Furthermore, third grade students solve problems involving the four operations and identify and explain the .
Furthermore, third grade students solve problems involving the four operations and identify and explain the .
The Operations and Algebraic Thinking tasks in the Illustrative Mathematics website is a good resource for connecting number sense to algebraic thinking. Illustrative Mathematics Grade 3 Operations & Algebraic Thinking tasks
Algebraic Thinking and Algebraic Concepts across the Elementary Grades
Kindergarten
In kindergarten, students identify, duplicate, and extend simple number patterns in preparation for creating rules that describe relationships (NCTM, 2006). Students in kindergarten see addition and subtraction equations as they decompose a set of objects into two sets. Students decompose numbers 1-10 at this level by using objects or drawings. They should record each decomposition by drawing a picture. If students write an equation, they must also share a pictorial representation or show using manipulatives. Additionally, students use the symbols +, -, and = in their decompositions.
Additionally, students use the symbols +, -, and = in their decompositions.
Kindergarten students should have multiple opportunities to use Ten-Frames as they “make ten.” For example, consider the following three ways that students may solve this problem: A package has 10 pencils in it. There are 7 pencils in the package. How many pencils are missing?
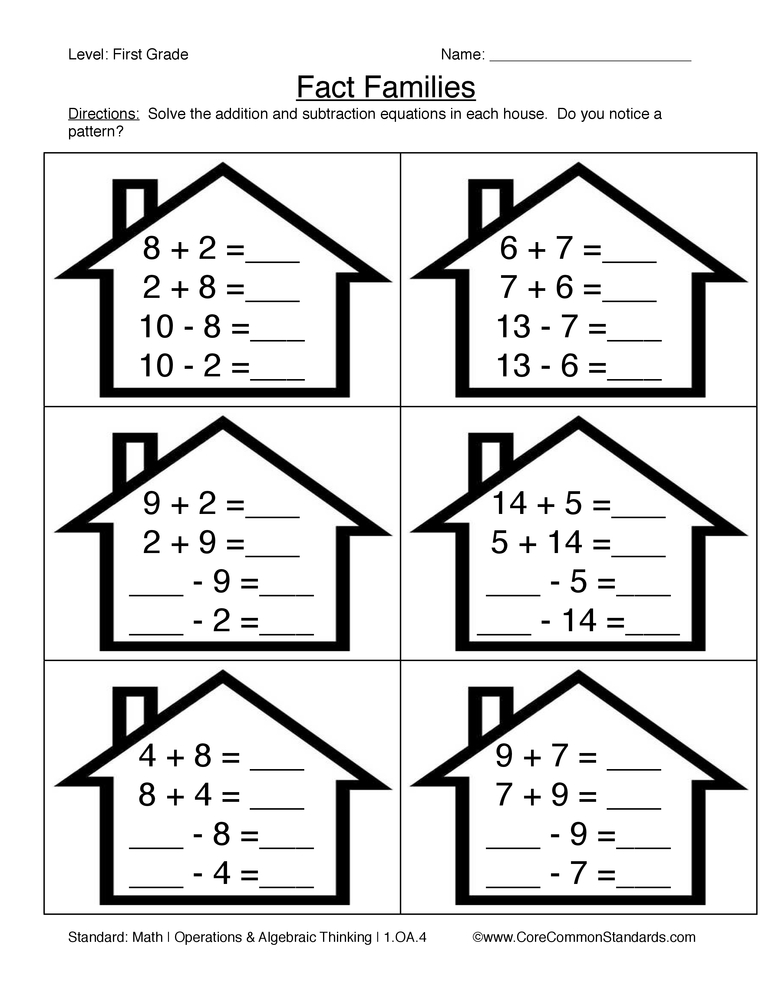
Kindergarten students solve problems fluently, which means efficiently, accurately, and flexibly. Accuracy means getting a correct answer, efficiently means solving a problem in a reasonable amount of steps, and flexibly means using strategies such as make ten, counting on, using doubles, using the commutative property, using fact families, etc. Fluency does not mean knowing the answer instantly. Read the paper, “Fluency is More than Speed” by clicking here.
First Grade
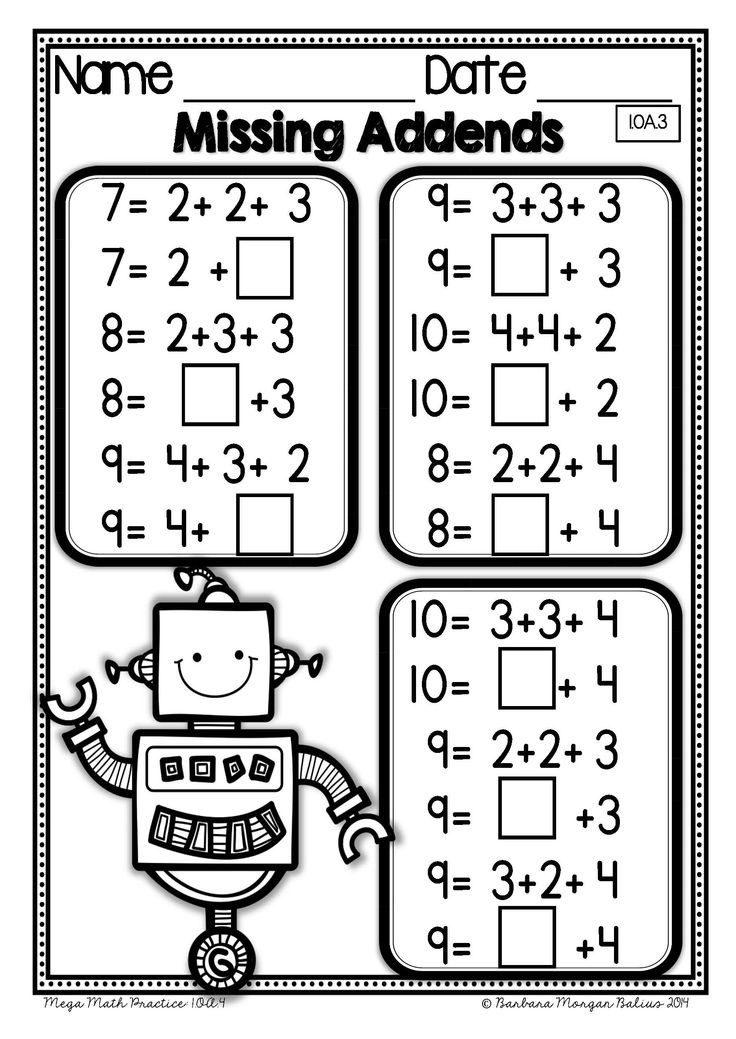
First grade students identify, describe, and apply number patterns and properties in order to develop strategies for basic facts (NCTM, 2006). Students in first grade solve addition and subtraction word problems with 20. At this level, do not use letters for the unknown symbols; instead use a box, picture, or a question mark.
Students in first grade solve addition and subtraction word problems with 20. At this level, do not use letters for the unknown symbols; instead use a box, picture, or a question mark.
Example:
In first grade, students are learning to as they model addition and subtraction with objects, fingers, and drawings. This is foundational to algebraic thinking and problem solving. It is critical that students understand the problem situation and represent the problem.
Check out Greg Tang’s Word Problem Generator here. You can select the operation, the problem type, the unknown variable, and how many problems to generate.
As students solve word problems, it is critical that they not rely on keywords. When students use keywords when solving a problem, they will strip the numbers from the problem and do not consider the context of the problem. In addition, many “keywords” have multiple meanings, such as altogether and left. The use of a keyword strategy does not develop sense-making and does not build structures for more advanced learning. Instead, discuss what the problem is asking and move the question to the beginning of the problem. Act out the problem, and write the corresponding equation.
Instead, discuss what the problem is asking and move the question to the beginning of the problem. Act out the problem, and write the corresponding equation.
Second Grade
In second grade, students use number patterns to extend their knowledge of properties (NCTM, 2006). They represent and solve addition and subtraction problems within 100. Continue to expect students to use base-ten blocks, hundreds charts, number lines, drawings, or equations to support their understanding.
Students in second grade are becoming fluent (efficient, accurate, and flexible) as they mentally add and subtract within 20. Give students multiple opportunities to write equations with two equal addends, such as 2 + 2 = 4 or 3 + 3 = 6. This lays the foundation for multiplication.
Third Grade
Third grade students understand the properties of multiplication and see the relationship between multiplication and division (NCTM, 2006). This is a fundamental step in developing algebraic readiness. Students focus on two models of division: and .
Students focus on two models of division: and .
In second grade, students used rectangular arrays to find the total number of objects, and wrote equations to represent the sum, such as a 5 x 5 array could be written as 5 + 5 + 5 + 5 + 5 = 25. See the modules at EngageNY for resources teaching algebraic thinking for third grade students. Students use the properties of multiplication (commutative, associate, and distributive properties) as they multiply and divide, and understand part/part/whole relationships as they make the connections between multiplication and division. To develop algebraic thinking and reasoning, students explain an arithmetic pattern using the properties of operations.
Algebraic thinking is a Domain throughout the mathematics standards. Beginning in kindergarten, students solve addition and subtraction problems by representing them in various ways. Additionally, they learn about basic operations and quantitative relationships as they model problems and look at mathematical properties and relationships (Stramel, 2021). Read more about Operations and Algebraic Thinking in the K-5 Learning Progressions document.
Read more about Operations and Algebraic Thinking in the K-5 Learning Progressions document.
The Most Important Math Concepts Kids Learn In 1st Grade
Your child has progressed from kindergarten to first grade. That’s exciting news! There is so much learning to come their way, especially from their first grade math class.
Math skills and concepts build on each other from grade to grade, which is why children need to get a firm foundation so they can handle the more complex challenges as they progress in school.
As a concerned parent, you might be wondering what some of these mathematical concepts will be and, more importantly, how you can help your child master them. You don’t have to figure it out on your own.
Here, we will give you a breakdown of what to expect from your child’s math class. We’ll also add a few tips on how to help your young learner thrive through it all.
Let’s get started!
Why Is Math Important?
Math is taught in the classroom, but that doesn’t mean that’s the only place it’s relevant. We use it every day!
We use it every day!
From the hexagonal bee combs to the circles, semi-circles, and crescents of the phases of our moon, mathematics is an essential part of the world we live in, and learning it helps us make sense of everything around us.
Did you know that math skills can also be linked to music? Children who play musical instruments use the same part of the brain when doing math. This is why studies have shown that music students do better in mathematics than their non-musical peers.
Sports and mathematics also have an interesting connection. Just think about all the coordination involved in performing well in certain sports. Research has shown that these skills can also be used to learn math.
In addition, mathematics helps us be stronger logical thinkers. Since most young kids tend to enjoy math time, it’s essential to foster this natural love for the subject just as much as we want to encourage children’s love for reading.
Helping children develop a love for mathematics generally works well when approached actively as a problem-solving skill rather than a rote memory task. Math helps children thrive in various aspects of their lives.
Math helps children thrive in various aspects of their lives.
So, how do we get there? It all starts with the foundation.
Below are the key first grade math concepts your child will soon learn and some tips on how you can support them on their journey.
8 Important First Grade Math Concepts
1) Numbers And Counting
At first grade level (and for the next few years in school), learning different numbers and counting will form a significant part of your child’s mathematics lessons.
By the end of the first grade, your child will have learned to:
- Count and write numbers from 1 to 100
- Count by 1s, 2s, 5s, and 10s
- Count backward
- Count onward from any number
- Count backward from any number
There are different ways to help your child grasp numbers and counting at home, and hands-on activities work best.
An effective strategy is to help your child visualize what all these numbers mean. For example, instead of just memorizing the numbers, they can count bears, large dried beans, or even craft sticks.
2) Addition And Subtraction
In first grade math, your young learner will start adding and subtracting numbers up to 30. They will also solve basic word problems with the help of drawings, objects, and equations.
By the end of the first grade, your child will have been shown how to:
- Add three one-digit numbers
- Write and show an understanding of the mathematical symbols (+, -, =)
- Solve problems involving one and two-digit numbers
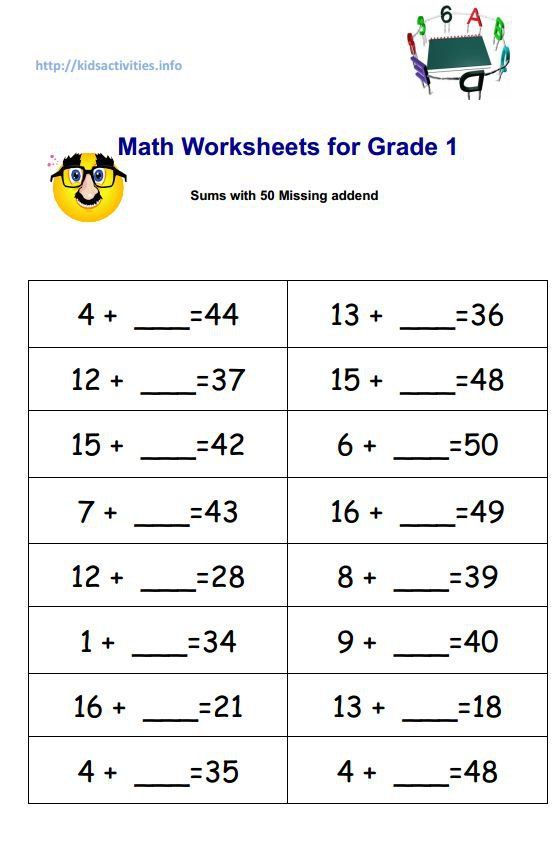
- Solve problems involving an unknown. For example, 1 + _ = 4
Addition and subtraction are two math skills that can be demonstrated in everyday life situations. This makes it relatively easy to practice at home!
For instance, you might ask, “If you have two teddy bears and granny buys you three more, how many teddy bears will you have in total?” Or, “There were six strawberries in the fridge. Daddy ate some strawberries. There are now four left. How many did daddy eat?”
3) 2-D Shapes
During pre-k, children get introduced to different shapes. In first grade, they will continue to extend their understanding of them.
In first grade, they will continue to extend their understanding of them.
By the end of the first grade, your child may be able to:
- Examine the attributes of different shapes (number of sides, faces, etc.)
- Name the 2-D shapes
To help your child grasp these shapes at home, continue to point out and name the 2-D shapes in the world around you (circles, triangles, pentagons, etc.).
When doing so, remember to always highlight the attributes (e.g., this book has four equal sides, so it’s a square).
4) Sorting And Patterns
Understanding and sorting patterns also forms a part of first grade math.
Your first grader will learn to:
- Sort different objects by attributes such as color, shape, and function. For example, sorting a mixed group of blocks so that the red, blue, green, and yellow blocks are separated.
- In addition, if these blocks are placed in a pattern (e.g., green, yellow, green, yellow, etc.), your child should be able to both predict which color will come next and create their own identical pattern.
 This skill will help develop your child’s logical thinking.
This skill will help develop your child’s logical thinking.
Continue to allow your young learner to play with fun building blocks and create their own patterns to help them master this skill.
5) Fractions
Montessori material. Children’s hands. The study of mathematics School and kindergarten. Whole and part. FractionsAs a first-grader, your child will be introduced to fractions as equal shares and basic fractions such as ½, ⅓, and ¼. For children to fully grasp these concepts, it’s essential to keep things intuitive.
For example, you can start by helping them understand that a half is two equal parts, a third is three equal parts, and so forth. They also need to understand that although three is bigger than two, ⅓ is smaller than ½.
Fractions can be tricky for kids to learn, which is why it’s important to use practical and everyday items.
For example, you can help your young learner examine the fractions of a full pizza. Then, as you divide the pizza into different slices, talk about the parts that you’ve created from the whole.
The concept of equal shares can also be demonstrated from one object and a group. For instance, you can have ½ of a single item (e.g., ½ of a cookie), or you can have ½ of a group of objects (e.g., ½ of four cookies is two cookies).
6) Number Place Values
With all the counting in first grade math, your child will naturally be introduced to the concept of place values. For instance, understanding that in the number 288, the 2 is worth 2 “hundreds” (or 200).
There are various activities you can do at home to help your young learner with this concept, including:
- Using number lines
- Base ten blocks
For more ideas to help with number place values and other 1st grade math concepts, take a look at the book Games for Math: Playful Ways to Help Your Child Learn Math, From Kindergarten to Third Grade by HOMER’s very own Peggy Kaye.
7) Time
Telling time (both digital and analog) is an important life skill that kids learn from first grade. The concept of elapsed time will also be introduced at this stage.
The concept of elapsed time will also be introduced at this stage.
In first grade math, your child will learn to:
- Tell time to the nearest hour, half-hour, and quarter-hour (sometimes even to five minutes)
- Make the connection between time and events (e.g., shorter, longer, after, before)
Understanding the analog clock can be tricky for a child who’s only exposed to digital clocks. So help your young learner by buying one (or making one for learning) to hang up at home.
You can then speak to your child about what it means when the hands move. To make things easier, start by helping them tell time to an hour and half-hour before progressing to quarter-hours.
8) Measurements And Comparisons
First grade math also involves some measuring and unit comparisons.
Your child will learn how to measure using a ruler and, after taking measurements, compare and order objects by length. First-graders will also learn how to compare the weights and volumes of different objects.
To help your young learner at home, keep rulers nearby and take measurements together of some of the objects they love (e.g., stuffed toys, cookies, etc.).
Bonus tip: If you’re a regular baker, why not help them see how you use measuring tools to create their favorite treats? Yum!
Helping Your Child With First Grade Math
We’ve already mentioned a few ways in which you can help your first grader with math at home. In addition to the above, playing math games is a fun and easy way to practice math at home!
Here are some examples of more math activities your young learner will enjoy at home:
- Fill in a number grid puzzle
- Build objects with legos and measure
- Number Hunt, Hopscotch, Is It A Number, and Find A Number
Math Is All Around Us
Helping your child grasp first grade math concepts at home is easier when you focus on the fact that mathematics is a part of our everyday lives. It is in the shape of road signs, the parts of sliced pizza, and even the watches on our wrists!
Sometimes kids (and parents) forget that math can be lots of fun. So whenever you can, incorporate games and activities to bring a little excitement to all the learning.
So whenever you can, incorporate games and activities to bring a little excitement to all the learning.
Will this help your child become our next best mathematician? Only time will tell. But one thing is for sure — all of the great mathematicians started somewhere. Even Isaac Newton had to master first grade math!
For more ideas and inspiration, visit the HOMER Learn & Grow app.
Author
Algebra: lessons, tests, assignments.
- Items
-
-
Numeric expressions. Algebraic expressions
-
Mathematical language
-
Mathematical models of real situations
-
Linear equation with one variable.
 Solution algorithm
Solution algorithm -
coordinate line. Numeric spans
-
-
-
Coordinate plane. Point coordinates
-
Linear equation ax + by + c = 0. Linear equation graph
-
Linear function y = kx + m.
 Linear function graph
Linear function graph -
Linear function y = kx, its properties
-
Mutual arrangement of graphs of linear functions
-
-
-
The concept of a system of linear equations with two variables
-
Solving systems of linear equations.
 Substitution method
Substitution method -
Solving systems of linear equations. Addition method
-
System of linear equations as a mathematical model
-
-
-
The concept of a degree with a natural indicator
-
Commonly used degrees
-
Basic properties of degrees with a natural exponent
-
Multiplication and division of powers with the same natural exponents
-
The concept of a degree with a zero exponent
-
-
-
The concept of a monomial.
 Reduction of a monomial to standard form
Reduction of a monomial to standard form -
Addition and subtraction of similar monomials
-
Product of monomials and raising a monomial to a power
-
Division of monomials
-
-
-
The concept of a polynomial.
 Reducing a polynomial to standard form
Reducing a polynomial to standard form -
How to add and subtract polynomials
-
How to multiply a polynomial by a monomial
-
How to multiply a polynomial by a polynomial
-
Application of abbreviated multiplication formulas
-
How to divide a polynomial by a monomial
-
-
-
The concept of factoring polynomials
-
Factorization.
 Taking the common factor out of brackets
Taking the common factor out of brackets -
Factorization. Grouping method
-
Factorization. Using Abbreviated Multiplication Formulas
-
Factorization. A combination of different methods
-
Applying Factoring to Reduce Algebraic Fractions
-
The concept of identity
-
-
-
Quadratic function y = x² and its graph
-
Solving Equations Graphically
-
Writing a function in the form y \u003d f (x)
-
-
-
Digital Olympiad
-
International Olympiad YaKlass
-
-
-
The concept of algebraic fraction
-
Application of the basic property of an algebraic fraction
-
How to add and subtract algebraic fractions with equal denominators
-
How to add and subtract algebraic fractions with different denominators
-
How to multiply, divide and raise algebraic fractions
-
Simplifying Rational Expressions
-
Solution of rational equations
-
-
-
Sets of natural numbers, integers, rational numbers
-
Set of rational numbers
-
The concept of a square root
-
The concept of an irrational number
-
The set of real numbers and its geometric model
-
-
-
Modulus of a real number and its geometric meaning
-
Square root function y = √x, its properties and graph
-
Basic properties of square roots
-
Transformation of irrational expressions
-
-
-
Quadratic function y = ax² and its properties.
 Parabola
Parabola -
The function y = k/x and its properties. Hyperbola
-
How to plot a function y = f(x + l)
-
How to plot a function y = f(x) + m
-
How to plot a function y = f(x + l) + m
-
Quadratic function y = ax² + bx + c
-
Solving quadratic equations using function graphs
-
-
-
What are quadratic equations
-
Ways to solve quadratic equations
-
Solving a rational equation that reduces to a quadratic one
-
Using Rational Equations to Solve Problems
-
Simplified formula for solving a quadratic equation
-
Application of Vieta's theorem
-
Solving an irrational equation that reduces to a quadratic one
-
-
-
The concept of numerical gaps
-
Properties of numerical inequalities.
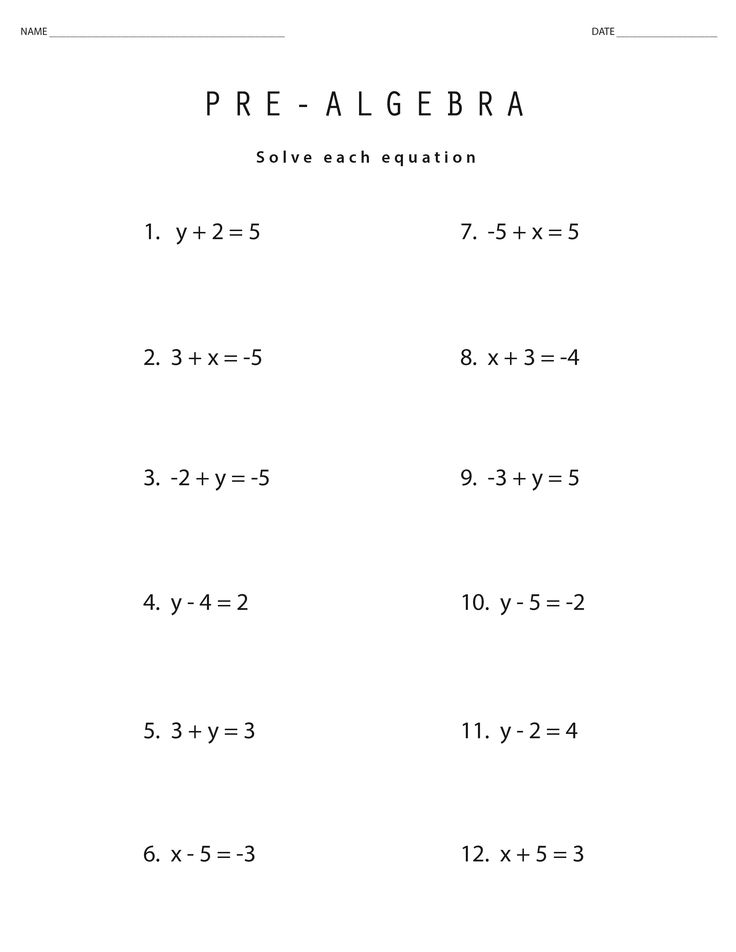 Properties of inequalities of the same meaning
Properties of inequalities of the same meaning -
How to solve a linear inequality
-
Methods for solving quadratic inequalities
-
The concept of monotonicity of a function. Investigation of functions for monotonicity
-
Approximate values by deficiency (by excess)
-
The concept of a degree with a negative integer exponent
-
Standard form of a positive number
-
-
-
Digital Olympiad
-
International Olympiad YaKlass
-
-
-
Repetition of ways to solve linear and quadratic inequalities
-
Solving rational inequalities by the interval method
-
Sets and subsets.
 Union and intersection of sets
Union and intersection of sets -
Systems of rational inequalities
-
-
-
The concept of a system of rational equations
-
Methods for solving systems of rational equations
-
Using systems of rational equations to solve problems
-
-
-
Definition of a numeric function and how to define it
-
Main function properties
-
Even and odd functions.
 Definition of even and odd
Definition of even and odd -
Power function with natural exponent
-
Power function with negative integer exponent
-
cube root function
-
-
-
The concept of a numerical sequence.
 Sequencing Methods
Sequencing Methods -
Arithmetic progression. Properties of an arithmetic progression
-
Geometric progression. Properties of a geometric progression
-
-
-
Elements of combinatorics. Combinatorial problems
-
Elements of statistics.
 Information processing methods
Information processing methods -
Elements of the theory of probability. Finding the Probability
-
Relative frequency and statistical probability of an event
-
-
-
International Olympiad YaKlass
-
-
-
Integers.
 Repetition
Repetition -
Rational numbers. Repetition
-
Irrational numbers. Repetition
-
-
-
Reversible and inverse functions
-
The concept of a periodic function (profile)
-
-
-
Number circle on the coordinate plane
-
Finding the values of sine and cosine, tangent and cotangent
-
Numeric argument of trigonometric functions
-
Angular argument of trigonometric functions
-
Properties of the function y = sin x and its graph
-
Properties of the function y = cos x and its graph
-
Periodicity of trigonometric functions, even, odd
-
Harmonic vibrations (profile)
-
Properties of functions y = tg x, y = ctg x and their graphs
-
Functions y = arcsin a, y = arccos a, y = arctg a, y = arcctg a (profile)
-
-
-
Arc cosine and solution of the equation cos x = a
-
Arcsine and solution of the equation sin x = a
-
Arc tangent and arc tangent.
 Solution of the equations tg x = a, ctg x = a
Solution of the equations tg x = a, ctg x = a -
Methods used to solve trigonometric equations
-
-
-
Formulas for the sine of the sum and difference, the cosine of the sum and difference
-
Tangent of sum and difference
-
Casting formulas.
 General rule
General rule -
Formulas for sine, cosine, tangent of a double angle
-
Reduction formulas, or half angle formulas (profile)
-
Formulas for sums of trigonometric functions
-
Formulas for products of trigonometric functions
-
Auxiliary angle introduction method (profile)
-
-
-
Numeric sequences and their properties
-
The concept of the limit of a numerical sequence
-
How to find the sum of an infinite geometric progression
-
Limit of a function at a point.
 Limit of a function at infinity
Limit of a function at infinity -
Definition of a derivative. Geometric and physical meaning of the derivative
-
Calculation of derivatives. Differentiation rules
-
How to get the equation of the tangent to the graph of a function
-
Investigation of functions for monotonicity and extrema
-
Investigation of convexity and inflection, plotting functions
-
Using the derivative to find the largest and smallest values
-
-
-
The concept of the nth root of a real number
-
nth root function
-
Properties of the root of the nth degree.
 Transformation of irrational expressions
Transformation of irrational expressions -
Ways to simplify expressions containing radicals
-
The concept of a degree with a rational exponent, properties of degrees
-
Properties of power functions and their graphs
-
-
-
Properties of an exponential function and its graph
-
Methods for solving exponential equations
-
Methods for solving exponential inequalities
-
The concept of a logarithm.
 Basic logarithmic identity
Basic logarithmic identity -
Properties of a logarithmic function and its graph
-
Basic properties of logarithms
-
Methods for solving logarithmic equations
-
Methods for solving logarithmic inequalities
-
Transition to a new base of the logarithm
-
Systems of exponential and logarithmic equations
-
Systems of logarithmic and exponential inequalities
-
Derivative of exponential and logarithmic function
-
-
-
The concept of antiderivative
-
Indefinite and definite integrals.
 Integration methods
Integration methods -
Calculating areas using integrals
-
-
-
Sum rule
-
product rule
-
Permutations.
 Permutations without repetition
Permutations without repetition -
Accommodations. Placements with repetitions
-
Combinations and their properties
-
Pascal's triangle. Binomial theorem
-
-
-
What are random events?
-
Event combinations.
 Opposite events
Opposite events -
Event Probability
-
Addition of probabilities
-
independent events. Probability multiplication
-
Statistical Probability
-
-
-
random variables
-
Central trends
-
Scatter measures
-
Probability distribution law.
 Law of Large Numbers
Law of Large Numbers
-
-
-
Equivalence of equations. Equivalence theorems for equations
-
General methods for solving equations
-
Equivalence of inequalities. Systems and collections of inequalities
-
Equations and inequalities with two variables
-
General methods for solving systems of equations
-
Equations and inequalities with a parameter
-
-
Collection of interactive models
Algebra tutors in Ivanovo
11713
The site Repetit. ru has a database of experienced tutors in algebra. Classes will be useful for those who want to improve their knowledge, eliminate gaps in knowledge and prepare for university entrance. When choosing a teacher, pay attention to the professional achievements of teachers, lesson prices and student reviews.
ru has a database of experienced tutors in algebra. Classes will be useful for those who want to improve their knowledge, eliminate gaps in knowledge and prepare for university entrance. When choosing a teacher, pay attention to the professional achievements of teachers, lesson prices and student reviews.
Expand
Popular categories of math tutors: Preparation for the exam Preparation for the OGE (GIA) School course Tutors at home Skype lessons Higher Mathematics
Found 11713 tutors
Reset filters
Julia Konstantinovna
school teacher Experience 16 years
from 1,000 rubles / hour
freeSofia Alexandrovna
school teacher Experience 5 years
The tutor has a video presentation watch video presentation
from 1 100 rubles / hour
freeTatyana Borisovna
Private teacher Experience 46 years
from 700 rubles / hour
freeDaria Andreevna
Private teacher Experience 3 years
from 2,000 rubles / hour
freeIrina Vladimirovna
school teacher Experience 19 years
from 600 rubles / hour
freeAnastasia Nikolaevna
Student Experience 4 years
from 600 rubles / hour
freeAndrey Vladimirovich
Private teacher Experience 30 years
from 700 rubles / hour
freeAlexey Gochevich
Student Experience 4 years
from 400 rubles / hour
freeAlexey Petrovich
school teacher Experience 20 years
from 600 rubles / hour
freeAnna Vasilievna
school teacher Experience 19 years
from 550 rubles / hour
freeAlgebra tutor reviews
The tutor is competent, attentive, explains the material well. The school was invited to an elective in mathematics, so they stopped classes. If there are any problems, we will definitely return to this teacher.
The school was invited to an elective in mathematics, so they stopped classes. If there are any problems, we will definitely return to this teacher.
Keulimjay Barlykovich is an excellent teacher! He quickly found an approach to the child, managed to interest the subject. We are engaged with pleasure and the first results have appeared. This week 5 in Algebra and 5 in Geometry. Many thanks for the help!
We thank Elena Dmitrievna for preparing for the exam. She is a true professional in her field. The teacher achieved a complete understanding of the topic. Constantly there was a check of assimilation and fixing of the passed material. The lessons were meaningful. I definitely recommend Tutor!
- Moscow and Moscow region
- St.
 Petersburg and Leningrad region
Petersburg and Leningrad region - Abakan and the Republic of Khakassia
- Anadyr and Chukotka Autonomous Okrug
- Arkhangelsk and Arkhangelsk region
- Astrakhan and Astrakhan region
- Barnaul and Altai Territory
- Belgorod and Belgorod region
- Birobidzhan and Jewish Autonomous Region
- Blagoveshchensk and Amur Region
- Brest and Brest region
- Bryansk and Bryansk region
- Velikiy Novgorod and Novgorod region
- Vitebsk and Vitebsk region
- Vladivostok and Primorsky Krai
- Vladikavkaz and Rep.
 North Ossetia Alania
North Ossetia Alania - Vladimir and Vladimir region
- Volgograd and Volgograd region
- Vologda and Vologda region
- Voronezh and Voronezh region
- Gomel and Gomel region
- Gorno-Altaisk and the Republic of Altai
- Grodno and Grodno region
- Grozny and Republic of Chechnya
- Yekaterinburg and Sverdlovsk region
- Ivanovo and Ivanovo region
- Izhevsk and the Udmurt Republic
- Irkutsk and Irkutsk region
- Yoshkar-Ola and the Republic of Mari El
- Kazan and the Republic of Tatarstan
- Kaliningrad and Kaliningrad region
- Kaluga and Kaluga region
- Kemerovo and Kemerovo region
- Kirov and Kirov region
- Kostroma and Kostroma region
- Krasnodar and Krasnodar Territory
- Krasnoyarsk and Krasnoyarsk Territory
- Mound and Kurgan region
- Kursk and Kursk region
- Kyzyl and Republic of Tyva
- Lipetsk and Lipetsk region
- Magadan and Magadan region
- Maykop and the Republic of Adygea
- Makhachkala and the Republic of Dagestan
- Minsk and Minsk region
- Mogilev and Mogilev region
- Murmansk and Murmansk region
- Nazran and Republic of Ingushetia
- Nalchik and Kabardino-Balkarian Republic.

- Naryan-Mar and Nenets Autonomous Okrug
- Nizhny Novgorod and Nizhny Novgorod region
- Novosibirsk and Novosibirsk region
- Omsk and Omsk region
- Eagle and Oryol region
- Orenburg and Orenburg region
- Penza and Penza region
- Permian and Perm region
- Petrozavodsk and Republic of Karelia
- Petropavlovsk-Kamchatsky and Kamchatka
- Pskov and Pskov region
- Rostov-on-Don and Rostov region
- Ryazan and Ryazan region
- Salekhard and Yamalo-Nenets Aut.
 county
county - Samara and Samara region
- Saransk and Republic of Mordovia
- Saratov and Saratov region
- Sevastopol
- Simferopol and Republic of Crimea
- Smolensk and Smolensk region
- Stavropol and Stavropol Territory
- Syktyvkar and Komi Republic
- Tambov and Tambov region
- Tver and Tver region
- Tomsk and Tomsk region
- Tula and Tula Region
- Tyumen and Tyumen region
- Ulan-Ude and Republic of Buryatia
- Ulyanovsk and Ulyanovsk region
- Ufa and Republic of Bashkortostan
- Khabarovsk and Khabarovsk Territory
- Khanty-Mansiysk and Khanty-Mansiysk Aut.












