Cardinal number of a set example
Cardinal Numbers - Meaning, Examples, Sets
Cardinal numbers are numbers that are used for counting. They are also known as natural numbers or cardinals. A set of cardinal numbers starts from 1 and it goes on up to infinity. We use cardinal numbers to answer the question "how many?". For example, how many students are going to the school picnic? The answer could be any number like 20, 23, 30, etc. So, all these numbers come in the category of cardinal numbers. In this article, we will explore the world of cardinal numbers and understand the difference between cardinal and ordinal numbers.
| 1. | What are Cardinal Numbers? |
| 2. | Difference Between Cardinal and Ordinal Numbers |
| 3. | List of Cardinal Numbers from 1 to 100 |
| 4. | Cardinal Numbers of a Set |
| 5. | FAQs on Cardinal Numbers |
What are Cardinal Numbers?
A cardinal number describes or represents how many of something are present. Example 2 apples, 5 flowers, etc. It quantifies an object. It does not have values as fractions or decimals. Cardinal numbers are counting numbers, they help to count the number of items. Let's have a look at cardinal numbers examples. Ana wants to count the number of people standing in a queue at a billing counter. Can you help her? Ana started to count using Natural numbers.
Ana counted 1, 2, 3, 4, and 5. There are 5 people standing in a queue at the billing counter. Counting numbers are cardinal numbers! Now, Let's consider another example, Noah kept eight apples in a basket. The number eight denotes how many apples are there in the basket, irrespective of their order.
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on. The smallest cardinal number is 1 as 0 is not used for counting, so it is not a cardinal number.
Difference Between Cardinal and Ordinal Numbers
All the natural numbers are also referred to as cardinal numbers. Cardinal numbers are used for counting. While an ordinal number is a number that denotes the position or place of an object. Example: 1st, 2nd, 3rd, 4th, 5th, etc. Ordinal numbers are used for ranking. Here is an example that explains cardinal and ordinal numbers:
Cardinal numbers are used for counting. While an ordinal number is a number that denotes the position or place of an object. Example: 1st, 2nd, 3rd, 4th, 5th, etc. Ordinal numbers are used for ranking. Here is an example that explains cardinal and ordinal numbers:
In the above image, we can see a team of 4 workers on the construction site. This is an example of cardinal numbers.
In the above image, we can see the position of the runners in the running event. First, second, third, and so on. This is an example of ordinal numbers. Let's discuss ordinal and cardinal number differences in the table below:
| Cardinal Numbers | Ordinal Numbers |
|---|---|
| They are counting numbers that represent quantity. | They are based on the rank or position of an object in a given list or order. |
Cardinal numbers give us the answer of 'how many?'. |
Ordinal numbers give us the answer of 'where'. For instance, where does the object lies in the list? |
| Examples are 1, 2, 3, 4, 5, 10, etc. | Examples are 1st, 2nd, 3rd, 4th, 5th, 10th, etc. |
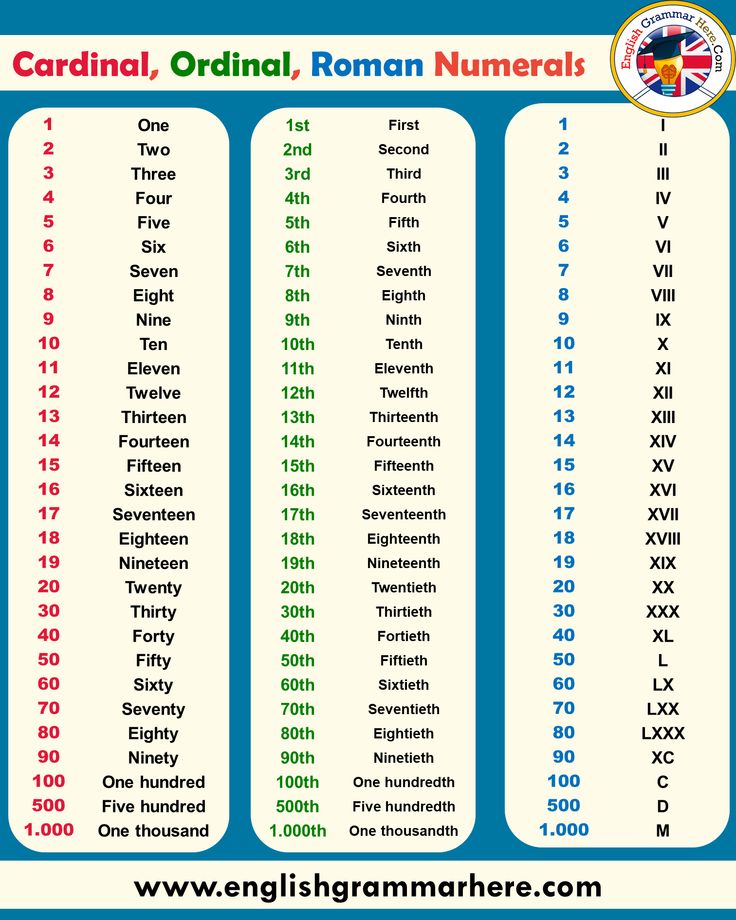
List of Cardinal Numbers from 1 to 100
Given below are the basic and most important cardinal numbers, which form the base for other counting numbers.
| 1 - One | 6 - Six |
| 2 - Two | 7 - Seven |
| 3 - Three | 8 - Eight |
| 4 - Four | 9 - Nine |
| 5 - Five | 10 - Ten |
| 10 - Ten | 60 - Sixty |
| 20 - Twenty | 70 - Seventy |
| 30 - Thirty | 80 - Eighty |
| 40 - Forty | 90 - Ninety |
| 50 - Fifty | 100 - Hundred |
Given below is the list of all cardinal numbers from 1 to 100. It will also help you to see how we write cardinal numbers in words like 21- twenty-one.
It will also help you to see how we write cardinal numbers in words like 21- twenty-one.
Cardinal Numbers of a Set
In the case of a set, the cardinal number is the total number of elements present in it. In other words, the number of distinct elements present in a set is the cardinal number of the set. The cardinal number of a set A is represented as n(A). For example, the cardinal number of set W = {1, 3, 5, 7, 9} is n(W)=5, as there are 5 elements in it.
Think Tank:
- Maria wrote January 1, 2020, as today’s date in her notebook. Does the number 1 in the date, represent a cardinal number?
- There are _______ people in the line ahead of me. I am the 7th person in the line.
Important Notes:
- Cardinal numbers help us to count the number of things or people in or around a place or a group.
- The collection of all the ordinal numbers can be denoted by the cardinal.

- Cardinal numbers can be written as words such as one, two, three, etc.
- Cardinal numbers tell how many items, whereas ordinal numbers show position or ranking.
Related Articles
Check out these interesting articles to know more about cardinal numbers and its related articles.
- Ordinal Numbers
- Whole Numbers
- Natural Numbers
- Difference Between Natural and Whole Numbers
Cardinal Numbers Examples
-
Example 1: Kate has a list of numbers as shown - 7, 8th, 10, Two, Fourth, 2nd. Identify the cardinal numbers.
Solution:
7, 10 and two help us in counting, whereas 8th, fourth and 2nd helps us in identifying the position. Thus, 7, 10, and two are cardinal numbers.
-
Example 2: Help Ryan, to calculate the number of vowels in "NUMBERS".
 Also, identify the number of alphabets used to form this word.
Also, identify the number of alphabets used to form this word.Solution:
(i) We know that a, e, i, o, and u are the vowels and in the given word u and e are used. Therefore, 2 vowels are used to form this number (2 is the required cardinal number).
(ii) We start counting from N to S, we see that "Numbers" has 7 alphabets in all. Therefore, a total of 7 alphabets are required to form the given word and here 7 is a cardinal number.
go to slidego to slide
Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations with Cuemath.
Book a Free Trial Class
Practice Questions on Cardinal Numbers
go to slidego to slidego to slide
FAQs on Cardinal Numbers
What is a Cardinal Number Example?
Cardinal numbers are used for counting. Some examples of cardinal numbers are 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 100, etc. In our daily life, we use cardinal numbers a lot. Even a small child uses this mathematical concept without knowing the term for it. They do count how many toys they have, how many people are there around them, how many friends they have, how many subjects do they study at school, etc.
In our daily life, we use cardinal numbers a lot. Even a small child uses this mathematical concept without knowing the term for it. They do count how many toys they have, how many people are there around them, how many friends they have, how many subjects do they study at school, etc.
What is the Smallest Cardinal Number?
The smallest cardinal number is 1 (one) as whenever we count, we always start from 1.
How do you Find Cardinal Numbers?
Cardinal numbers can be found by counting. We start by 1 and then go on as per the number sequence.
How is Cardinal Number Different from the Ordinal Number?
Cardinal numbers are numbers that represent the number of items(quantity) while ordinal numbers represent the rank or position of an item in the given list.
What is a Cardinal Number in Sets?
In set A, if there are a total of 25 elements then 25 is the cardinal number of set A represented by n(A).
Can Cardinal Numbers Negative?
No, cardinal numbers cannot be negative. They are positive integers or natural numbers, as we always count the number of items starting from number 1, and then it goes up to infinity.
They are positive integers or natural numbers, as we always count the number of items starting from number 1, and then it goes up to infinity.
Is Zero a Cardinal Number?
No, 0 is not a cardinal number as cardinal numbers represent quantity, and 0 means nothing or no quantity.
What is the Biggest Cardinal Number?
There are infinite natural numbers. Therefore, there are as many cardinal numbers as natural numbers. There can be no generalization of the biggest natural number and so does for the biggest cardinal number.
What are Cardinal Numbers? Definition, List, Examples, Facts
What Are Cardinal Numbers?
Cardinal numbers are numbers that are used for counting real objects or counting things. They are also known as “counting numbers” or “cardinals.” We commonly use cardinal numbers or cardinals to answer the question starting with “How many?”
So, how to find the cardinal numbers around us? Let’s see an example.
Example:
How many dogs are in the given picture?
To know the total number of dogs, we need to count the dogs given in the image.
There are 8 dogs in all. Here, 8 is the cardinal number.
Related Games
Cardinal Numbers: Definition
The numbers that we use for counting are called cardinal numbers. They tell us the quantity of objects.
Cardinal Numbers Examples: 2 bananas, 5 suitcases, 100 points, a million dollars, etc.
Cardinal numbers do not include fractions or decimals. Cardinal numbers are natural numbers or positive integers. The smallest cardinal number is 1.
Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on.
The smallest cardinal number is 1.
If we count a bag filled with a million dollars, we get a cardinal number: “one million!”
Example:
Related Worksheets
Cardinal Numbers in Words
We can also write cardinal numbers in words. For the first 10 numbers, we can write the cardinal numbers as:
- 1 – One
- 2 – Two
- 3 – Three
- 4 – Four
- 5 – Five
- 6 – Six
- 7 – Seven
- 8 – Eight
- 9 – Nine
- 10 – Ten
List of Cardinal Numbers
Here’s a list of cardinal numbers up to 100, in figures and in words:
Cardinal Numbers as Multiples of 100:
We can count further and list a few larger cardinal numbers as well:
What Is Cardinality?
The cardinality of a group or a set represents how many elements or numbers are present in a group or in a set.
For example, if a pencil set has 10 pencils in it, then the cardinality of pencils is 10.
Cardinal Number of a Set
The number of elements in a set is known as the cardinal number of that set. If A is a finite set and it has N elements, then the cardinal number of set A is given by n(A) $=$ N.
Note: The cardinal number of an empty set is always zero.
For example, what is the cardinal number of a set if the set is defined as A $=$ {2, 5, 7, 9, 11, 15, 19, 22, 24}?
The cardinal number of set A is 9. Hence, n(A) $=$ 9
Cardinal Numbers vs. Ordinal Numbers
As we discussed, the cardinal numbers are used for counting. They include all the natural numbers. However, an ordinal number is a number that is used to represent the position or order of an object. Examples:
1st rank, 2nd in a queue, 3rd row, tenth floor, etc.
Ordinal numbers are used for ranking or ordering.
Here’s an example that explain the difference between cardinal and ordinal numbers:
In the image given above, we can see a group of 8 children on the picnic spot. Here, 8 represents the cardinal number.
In the above image, we can see the position of the kids in a running event. Here, first, second, third, fourth, fifth are ordinal numbers.
Difference between Cardinal Numbers and Ordinal Numbers
Nominal Numbers
Nominal numbers, as the name suggests, are used to name an object or a thing in a set of groups. They help us in the identification of objects. It is not used to represent the quantity or the position of an object.
For example:
- Social security number
- Zip code number
- Cell phone number
In the image given below, the numbers 22, 18 are nominal numbers since they are used on the jerseys to represent players or to identify players.
Conclusion
In this article, we learnt about the Cardinal Numbers. Cardinal Numbers are the numbers used for counting numbers. To read more such informative articles on other concepts, do visit SplashLearn. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Cardinal Numbers are the numbers used for counting numbers. To read more such informative articles on other concepts, do visit SplashLearn. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
1. Kathy has a list of numbers as shown: 10, 9, 7th, 22, Third, Five, 21st. Identify the cardinal numbers.
Solution: The cardinal numbers are used for counting. The cardinal numbers are 10, 9, 22 and Five.
2. Help Mark calculate the number of consonants in “INDEPENDENCE.” Also identify the number of alphabets used to form this word.
Solution: The consonants are alphabets other than vowels. The vowels are a, e, i, o and u. The number of consonants INDEPENDENCE are 7. The number of alphabets in the word INDEPENDENCE are 12.
3. Write the cardinality of the flowers in the vase.
Solution: There are 5 flowers in the vase. So, the cardinality is 5.
4. What is the position of the strawberry from the left?
Solution: The strawberry is at the second position from the left. Here, second is the ordinal number.
5. How many kites are there in all? What is a cardinal number here?
Solution: On counting, we get:
There are 8 kites. 8 is the cardinal number since we used it for counting.
Practice Problems
1
How many two-digit numbers are there?
89
90
91
92
Correct answer is: 90
The smallest two-digit number is 10 and the greatest two-digit number is 99.
From 1 to 99, there are 99 numbers. Out of them 9 numbers (1 to 9) are one-digit numbers.
So, we will subtract 9 from 99 to find the two-digit numbers.
Number of two-digit numbers $= 99 – 9 = 90$
2
The cardinality of the set A $= {12, 18, 23, 65}$ is
4
10
18
Cannot be defined.
Correct answer is: 4
Since the number of elements in the set is 4, the cardinality of the set is 4.
3
Which of the following is not a cardinal number?
23
Sixty-one
4th
77
Correct answer is: 4th
4th is not a cardinal number as it tells us about the position of something.
4
For which of the following are cardinal numbers used?
To find the number of objects
To identify the rank or order of something
To identify objects
All of these
Correct answer is: To find the number of objects
We use cardinal or natural numbers for finding the number of objects.
5
76 is a $\underline{}$ number.
Ordinal
Cardinal
Nominal
None of these
Correct answer is: Cardinal
76 is a natural number and hence, it is cardinal.
Frequently Asked Questions
Which is the smallest cardinal number?
The smallest cardinal number is 1.
Can cardinal numbers be negative?
No, cardinal numbers cannot be negative. They are positive integers or natural numbers, as we count the number of items starting from number 1, and then it goes up to infinity.
Is 0 a cardinal number?
No, we can not count 0 things.
Which is the biggest cardinal number?
The biggest cardinal number is infinity.
Can we do operations with the cardinal numbers?
Yes, we can do operations with the cardinal numbers. We can add, subtract, multiply, and divide the cardinal numbers.
Are all whole numbers cardinals?
All whole numbers are not cardinal numbers. 0 is a whole number but not a cardinal number as we can never say that the number of objects is 0.
What is the Cardinal Counting Principle?
When you count a number of objects in a group, the total number of items is the last word said while counting.
- Number
- First
- Ordinal Numbers
6.3. Fuzzy sets: basic definitions
Generalization of the notion of membership. In the considered examples, the characteristic function took the values 0 or 1. Suppose that the characteristic function takes any value from . Then the element may not belong to the set , belong to some extent, or be an element of the set .
Fuzzy set . Fuzzy subset (fuzzy set) of a set is a set of ordered pairs , where is the membership function of an element to a set , which characterizes the degree of membership of an element in this set, or, in other words, the measure of correspondence of an element of a universal set to the properties of a fuzzy set . In the case of a continuous set, the following notation is used to define a fuzzy set: .
Lots of accessories. The set of values of the membership function is called Numerous accessories . If , then is an ordinary set, i.e., a crisp set can be considered as a limiting case of a fuzzy set. There are many accessories later in this tutorial.
If , then is an ordinary set, i.e., a crisp set can be considered as a limiting case of a fuzzy set. There are many accessories later in this tutorial.
Cardinality of the fuzzy set. Let a fuzzy set be given on the universal set . The cardinality of the fuzzy set or its Cardinal number is defined as follows: .
Example 28. On the universal set, we define the following fuzzy set:
.
Let's define the cardinal number of the fuzzy set :
Membership of an element in a fuzzy set can also be denoted as follows: .
There is a special terminology to determine the degree of belonging of an element to a fuzzy set. Thus, the fuzzy set given in Example 28, contains the element to a small extent, does not contain , to a small extent contains , to a large extent - and , and contains the element .
Example 29. The fuzzy set of small natural numbers can be given, for example, as follows:
Values are subjective.
The carrier of the fuzzy set. The carrier (support) of the fuzzy set (supp) is the set of elements for which . A fuzzy set is called empty if its support is the empty set.
The kernel of the fuzzy set. The kernel of the fuzzy set () is the set of elements for which .
Height of fuzzy set . The value ( for discrete universal sets) is called Height fuzzy set ().
Normal and subnormal fuzzy sets . Fuzzy set Normally if its height is 1. If its height is less than 1, then the fuzzy set is called Subnormal . Any non-empty subnormal fuzzy set can be transformed to a normal one by normalizing its membership function:
.
Unimodal fuzzy sets. A fuzzy set is called Unimodal if only for one .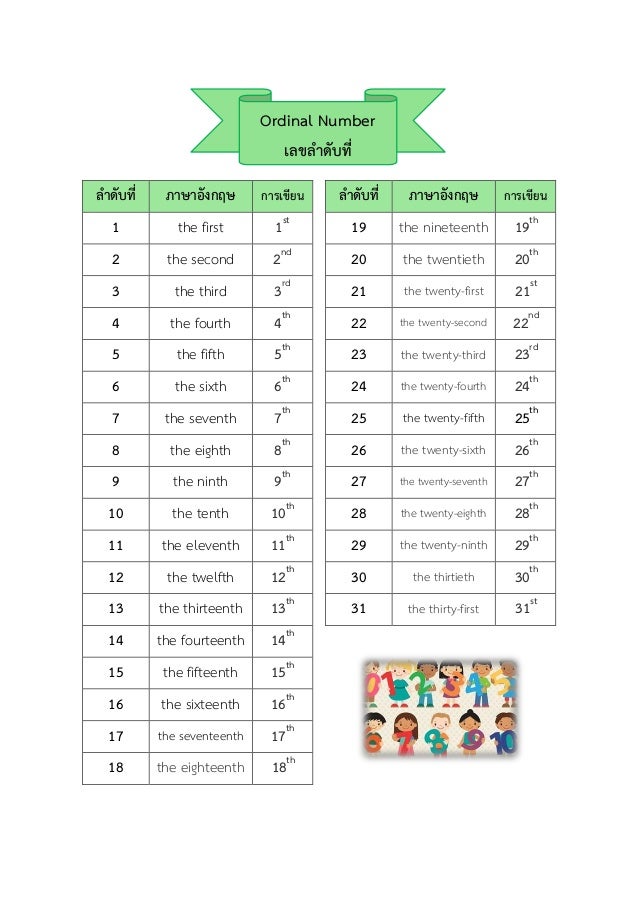
Transition points of fuzzy sets. Elements for which are called Transition points of the fuzzy set .
Convex fuzzy sets . Fuzzy set is called Convex if:
.
Example 30. Let the universal set be the set of real numbers, i.e. . Let's define a fuzzy set as a set of numbers close to a number (Fig. 4).
Figure 4
The membership function can be specified as follows: , where . The exponent is chosen depending on the degree of proximity to . For example, to describe a set of numbers very close to , you can take ; for a set of numbers not very far from , .
Example 31. On the universal set of Example 28 A fuzzy set is given. For a fuzzy set: 1) determine its cardinality; 2) determine the carrier, core and height; 3) find out if it is normal or subnormal. If is subnormal, convert it to normal; 4) check whether the resulting set is unimodal; 5) determine the transition points.
If is subnormal, convert it to normal; 4) check whether the resulting set is unimodal; 5) determine the transition points.
Solution.
1. By definition, the power (cardinal number) of a fuzzy set given on a finite universal set is determined by the formula: .
Then .
2. Let's use the definitions of support, core and height of fuzzy set. Obviously, , , .
3. The given fuzzy set is subnormal. Let us construct the corresponding fuzzy normal set . To do this, we calculate the values of the element membership function according to the formula:
.
We have: , similarly: , , , , . Thus, a fuzzy normalized set .
4. The set is unimodal, since it contains only one element , for which .
5. The set has a single transition point – , since only .
Multiplication of fuzzy sets by a number. If is a positive number such that , then for a fuzzy set the membership function is defined as follows: .
Comparison of fuzzy sets. Consider two fuzzy sets and , defined on the universal set .
It is said that is contained in , i.e., if for any . Graphically, this means that the curve defining the fuzzy set is located above the similar curve of the fuzzy set . If the inclusion condition is not satisfied for all , then we say about Degrees of inclusion in , which is defined as , where is the set on which the inclusion condition is satisfied.
Two fuzzy sets and Are equal to if they are contained in each other, i.e. if for any .
-level subset. A -level subset of a fuzzy set , , is a crisp subset of elements for which . The set is also called the -section of the fuzzy set . In this case, if , then one speaks of a strong section, and if , then one speaks of a weak section. Occurs Important property : if , then .
For problems of analysis and synthesis of fuzzy sets, Decomposition theorem: a fuzzy set can be decomposed into its -level sets as follows: , where is the product of a number by the set .
Example 32. On the universal set we define the fuzzy set . Find all subsets of the fuzzy set:
According to the fuzzy set decomposition theorem, the given fuzzy set is represented as follows:
,
< Previous
Geometric (planar) model of the natural series / Sudo Null IT News
which cryptanalysis is performed. For an RSA cipher, such a model of its element must be the models of an odd number, which the cryptanalyst seeks to factorize.
This article is the first in a series that will show various models of the natural number series (NSN), a single number and some others, as well as approaches to solving the factorization problem based on these models.
Introduction
Are we familiar with the natural series of numbers? How much do we know about him? Yes, these are positive integers that follow one after another, starting with one (1) and increasing by 1 in each successive number, and so on to infinity (∞).
Still all the numbers of the NRF are divided into two classes according to divisibility by 2: even and odd. One is an odd number (zero is not included in the NRF), two ( 1 + 1 = 2) is even, two is followed by three (2 + 1 = 3) is odd again, followed by an even four ( 3 + 1 = 4 ). So in NRF odd and even numbers alternate.
Numbers multiplied by themselves are squares in the NRF. They take their specific places in the NRF, so that they form the same sequence alternating in evenness - odd - even square. Between the squares of neighboring numbers, the difference is always an odd number of positions occupied by non-squares. It follows from this that the sum of 1 + 3 + . ..+ 2k - 1 = k 2 , where k the number of odd consecutive numbers is equal to the square of the number of terms. This is an informal discussion of the NRF.
..+ 2k - 1 = k 2 , where k the number of odd consecutive numbers is equal to the square of the number of terms. This is an informal discussion of the NRF.
And how is NRF determined in theory? A non-empty set N = {1, 2, 3,...} with a unary operation S is called a natural series of numbers, here S denotes a mapping of N to N that satisfies the conditions or the following Peano axioms:
- for any a ∊ N, 1 ≠ S a ;
- for any a, b ∊ N , if S a = S b , then a = b ;
- any subset N , c 1 ∊ N , which together with each element a contains the element S and , is the same as N . Element S a of set N is usually called the element immediately following a .
The natural series of numbers is a completely ordered set. In number theory, it is proved that the following conditions are:
In number theory, it is proved that the following conditions are:
- a + 1 = S a , a + S b = S(a + b) ;
- a 1 = a , a S b = a b + a ,
where a and b are any elements from N , define in the set N , binary operations (+) and (·).
System
A natural number is one of the basic concepts of the mathematics of natural numbers and can be interpreted as the cardinal number of a non-empty finite set. The set N = {1, 2,...} of all natural numbers and operations on them: addition (+) and multiplication ( ) form a system of natural numbers  In this case, the axiom of induction is fulfilled: any subset of the set N containing 1 and together with each element a is the sum of a + 1 , the same as N .
In this case, the axiom of induction is fulfilled: any subset of the set N containing 1 and together with each element a is the sum of a + 1 , the same as N .
In deductive scientific theories, axioms are the basic assumptions, i.e. axioms are basic propositions, self-evident principles. From the axioms within the framework of such theories, all their content is extracted by deduction.
In fact, a purely formal approach, although it provides a certain rigor and evidence of the results, is very limited and gives little practice. We can see the manifestation of limitations in the absence of solutions to actual problems of modern mathematics: establishing the simplicity of a number, finding the discrete logarithm, divisors of a large natural number, etc. It should be noted that the time and effort spent on finding answers by specialists is very significant.
One of the branches of additive number theory is the study of summation of sequences. An important situation is when, as a result of summing a limited number of sequences, all sufficiently large numbers are obtained or, in another variant, all natural numbers are obtained, which is essentially equivalent to the NRF modeling.
An important situation is when, as a result of summing a limited number of sequences, all sufficiently large numbers are obtained or, in another variant, all natural numbers are obtained, which is essentially equivalent to the NRF modeling.
The theory introduces the concept of a basis k -th order, which is understood as a multiple ( k -fold) sum of the sequence P with itself k times and thus all natural numbers are formed. Further summation of the sequence P to the previous result k = k + 1 th time does not change the resulting basis.
For example, Lagrange's theorem is known that any natural number is the sum of four squares. Thus, the sequence of squares Q is a 4th order basis [1]. It is known [2, 3] that a sequence of cubes forms a 9th order basis. The last result is proved in a more complicated way.
Truncated NRF models (not all natural numbers are present in the model), in which the presence of only sufficiently large numbers is obligatory, are obtained with a smaller number of sequence terms. So from the theorem of I.M. Vinogradov [1], it follows that it is enough to sum the sequence P + P + P three times, where P is a sequence of prime numbers, and this sum will contain all sufficiently large odd numbers. Thus, the sequence P forms a 4th order basis for sufficiently large numbers. The sequence of cubes in this situation forms a 7th order basis for sufficiently large numbers. Such, in general, are the results of rigorous number theory.
So from the theorem of I.M. Vinogradov [1], it follows that it is enough to sum the sequence P + P + P three times, where P is a sequence of prime numbers, and this sum will contain all sufficiently large odd numbers. Thus, the sequence P forms a 4th order basis for sufficiently large numbers. The sequence of cubes in this situation forms a 7th order basis for sufficiently large numbers. Such, in general, are the results of rigorous number theory.
When presenting the material, we will not resort to rigorous proofs, in terms of provisions they are not yet available, and where they are, they take up a lot of space
As mentioned above, it is proposed to supplement the model of an odd number with a planar model of a natural series of numbers. This model is convenient because it contains all odd numbers, and potential knowledge of their position (the coordinates of the cell with the number) leads to almost instantaneous factorization. It remains to find a way to localize a given number (pointing to its cell). The numerical examples given below in the text illustrate the capabilities of the proposed model and, I hope, stimulate the reader to search for a solution to the named problem.
The numerical examples given below in the text illustrate the capabilities of the proposed model and, I hope, stimulate the reader to search for a solution to the named problem.
Previously, it was shown that the use of a geometric (planar) model of a natural series of numbers in the form-plane allows us to formulate the problem of factorization of large numbers (LFP) in terms and concepts of this model and reduce it essentially to determining the coordinates of an integer point of a hyperbola characterized by a modulus of comparison N RSA cipher, which is available to all network subscribers. The use of another available key parameter (encryption exponent e ), found factors and modulus provides a simple calculation of the private key of the cipher d and access to the original message view.
The most difficult part of the cryptanalytic attack is the search for an integer point of the hyperbola with a known modulus N . With a huge bit depth of RSA numbers, a segment of a hyperbola branch lying in a selected area of unreliable key parameters (NKP) contains a single integer point among an infinite number of other points. The search for such a point by enumeration algorithms is a long and laborious process, which boils down to checking whether the calculated point belongs to the set of natural numbers. The procedure is essentially simple: the natural value of one coordinate of the cell is specified and the integer value of the second coordinate is determined, or it is specified and calculated.
The search for such a point by enumeration algorithms is a long and laborious process, which boils down to checking whether the calculated point belongs to the set of natural numbers. The procedure is essentially simple: the natural value of one coordinate of the cell is specified and the integer value of the second coordinate is determined, or it is specified and calculated.
Among the many possible NRF models, the following one, designated as Г s∓ , seems to be very effective. The model satisfies almost all the requirements usually imposed on them.
Let us formulate a number of provisions to substantiate the choice of the model under consideration:
- Г s∓ — the model contains all the odd numbers of the NRF, and it is always necessary to factorize an odd number, since the even numbers are easily divisible by powers of two.
- Ratios that implement the factorization of a number are formulas for abbreviated calculations, sums and differences of equal powers of variables, among which the most preferred ratio is: x 0 )(x 1 - x 0 )
- All odd numbers in NRF lie between the squares of numbers of different parity.

- Any composite odd natural number can be represented by the sum of an odd number of terms - odd consecutive numbers, and possibly not uniquely.
- The sum from paragraph 4 is easily converted into the product of the middle term (larger db divisor N ) by the number of terms (smaller dm divisor N ).
- The value in each cell at the intersection of the horizontal and vertical submodels Г 2- , on the one hand, is equal to the difference of the squares of the numbers of these lines, and on the other hand, is equal to the product of the numbers of the short and long diagonals occurring in this cell.
- The values of the numbers in the cells of the diagonals are a multiple of the number of the diagonal in which they lie.
Design description D 2∓
To build a model on a plane, two intersecting orthogonal coordinate numerical axes are set, directed x 1 - vertically down and x 0 - horizontally to the right. The points of the axes, equidistant from one another, are marked with numbers of the natural series. The intersection of the axes is marked with zero. Lines are drawn through the marked points, forming the boundaries of the strips of perpendicular directions. A lattice pattern appears on the plane, a kind of parquet from cells of size 1x1 . In the work, we will limit the fragment of the plane to the possibilities of the pictorial representation and select the main diagonal in it, like the main diagonal of a numerical matrix. Associate with each cell under the main diagonal the value N(x 1 , x 0 ) = x 1 2 - x 0 2 N(x 1 , x 0 ) = x 1 2 + x 0 2 , where x 1 and x 0 are the coordinates of cell (x 1 , x 9025 9025)
The points of the axes, equidistant from one another, are marked with numbers of the natural series. The intersection of the axes is marked with zero. Lines are drawn through the marked points, forming the boundaries of the strips of perpendicular directions. A lattice pattern appears on the plane, a kind of parquet from cells of size 1x1 . In the work, we will limit the fragment of the plane to the possibilities of the pictorial representation and select the main diagonal in it, like the main diagonal of a numerical matrix. Associate with each cell under the main diagonal the value N(x 1 , x 0 ) = x 1 2 - x 0 2 N(x 1 , x 0 ) = x 1 2 + x 0 2 , where x 1 and x 0 are the coordinates of cell (x 1 , x 9025 9025)
Visual representation of the model
Note that the cells of such a discrete plane are unique, and the values in them can be repeated. With this definition, the parity of the values in the cells corresponds to the alternating order, like the color of the cells on a chessboard. In this case, the cells will be called even or odd, respectively. The cells placed under the main diagonal form a half-plane, which we will call G 2- (G from the word hyperbole), and above the main diagonal - K = G 2+ (K from the word circle). We denote the generalized model as Г s∓ , where s — can take the values 2, 3,…, etc.
With this definition, the parity of the values in the cells corresponds to the alternating order, like the color of the cells on a chessboard. In this case, the cells will be called even or odd, respectively. The cells placed under the main diagonal form a half-plane, which we will call G 2- (G from the word hyperbole), and above the main diagonal - K = G 2+ (K from the word circle). We denote the generalized model as Г s∓ , where s — can take the values 2, 3,…, etc.
sides or top, one to the other) horizontal (H i ) , vertical (V i ) , oblique (sets of cells-points adjacent to the vertices or cells without contact, forming the direction of lines with breaks - rays): long (D i ) and short (K i ) diagonals, which contain either only even values and are called even or odd diagonals formed by odd cells. Short diagonals end and start at the points of the coordinate axes with the same coordinates (diagonal numbers).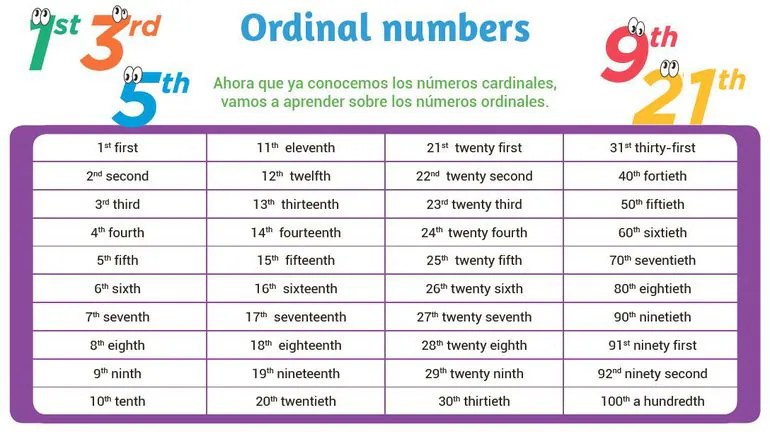 Long diagonals (D i ) run parallel to the main one (numbered (D 0 ) ) have only starting points on the coordinate axes and continue down to ∞. Their position above and below (D 0 ) is characterized by matching numbers and to distinguish them, the diagonals of the upper half-plane are provided with an additional (+) sign (D i + ) . Odd diagonal (D 1 + ) starts on axis x 0 cell with 1 and contains odd numbers in its cells. The odd diagonal D 1 starts on the x 1 axis with a cell with N=1 and contains all odd numbers without exception, sorted in ascending order. This ensures the requirement for the NRF model to contain all odd numbers.
Long diagonals (D i ) run parallel to the main one (numbered (D 0 ) ) have only starting points on the coordinate axes and continue down to ∞. Their position above and below (D 0 ) is characterized by matching numbers and to distinguish them, the diagonals of the upper half-plane are provided with an additional (+) sign (D i + ) . Odd diagonal (D 1 + ) starts on axis x 0 cell with 1 and contains odd numbers in its cells. The odd diagonal D 1 starts on the x 1 axis with a cell with N=1 and contains all odd numbers without exception, sorted in ascending order. This ensures the requirement for the NRF model to contain all odd numbers.
Within the framework of this model, a convenient opportunity arises to explore hypothetical numerical patterns and solve, for example, the problems of determining and localizing Pythagorean triples of numbers, factoring a number into factors (factorization), determining multiple cells containing the same values, and their location, and other number-theoretic tasks.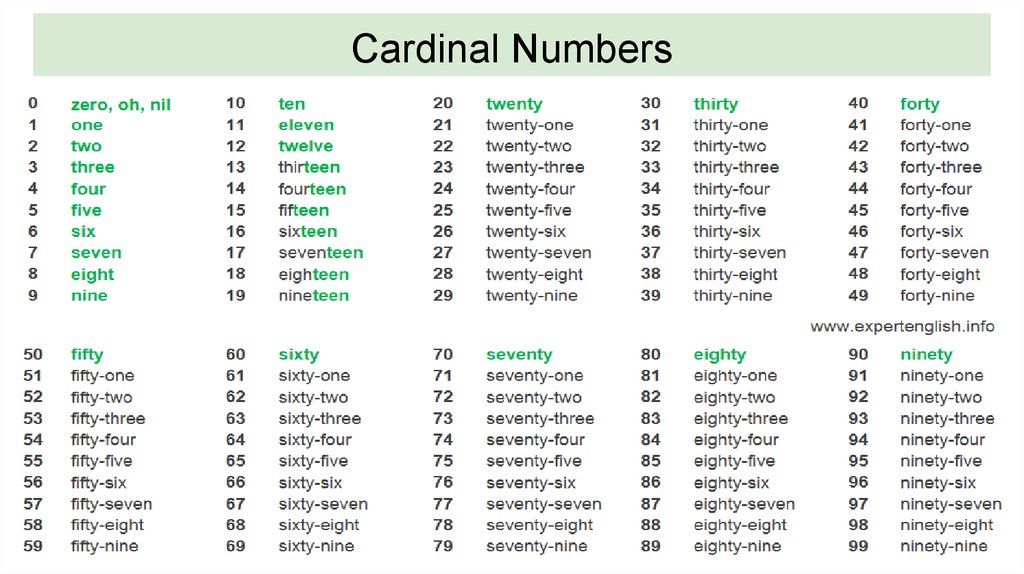 In addition, there are good opportunities for visual display of results.
In addition, there are good opportunities for visual display of results.
Dependences of numbers in organized cells
Under the organization of cells, we mean the belonging of some (semantically distinguished) cells to some image, specified by a mathematical dependence of either coordinates, or values in cells, or both. We will use the properties of the resulting images to solve number-theoretic problems, in particular, for the ZFBC. Let's start with very simple images of straight lines, rays. G 2- — the model provides their visualization.
Example 1 . Consider the lower semi-plate g 2- and numbers in cells with coordinates (x 1 , x 0 ) , where coordinate x 1 x 0 0 0 0 0 0258 0 0258 0 0 0258 0 0258 0 0258 0 = kx 0 , the proportionality coefficient changes monotonously k = 2,3,4,. ...∞ , which is briefly written as k=2(1)∞ . With a change in the coordinate x 0 = 0(1)∞ , i.e. from zero to infinity with a step of 1 and with a fixed value of k , cells and natural values in them belonging to lines (rays) with discontinuities will be calculated . So at k = 2 , the resulting cells are located in the middle of the horizontal segments of the lower half-plane, and the line takes the form of a ray-bisector (designated B3 ) of the lower half-plane. At k = 3 , the resulting cells are located in the middle of the segments of the short diagonals of the lower half-plane, and the line takes the form of another ray-bisector (indicated by B8 ) of the lower half-plane.
...∞ , which is briefly written as k=2(1)∞ . With a change in the coordinate x 0 = 0(1)∞ , i.e. from zero to infinity with a step of 1 and with a fixed value of k , cells and natural values in them belonging to lines (rays) with discontinuities will be calculated . So at k = 2 , the resulting cells are located in the middle of the horizontal segments of the lower half-plane, and the line takes the form of a ray-bisector (designated B3 ) of the lower half-plane. At k = 3 , the resulting cells are located in the middle of the segments of the short diagonals of the lower half-plane, and the line takes the form of another ray-bisector (indicated by B8 ) of the lower half-plane.
Let some number N ∊ Г 2- be given, and it lies in one of the cells of the oblique line (ray) formed by the conditions of the example. Then you can get the following relation for the beam model:
at k = 2 , we have N (x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 - - 0 2 = x 0 2 (k 2 - 1) = 3x 0 2 . Beam B3 ;
Beam B3 ;
At k = 3 , we have N (x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 - - 0 2 = x 0 2 (k 2 - 1) = 8x Beam B8 ;
at k = 4 , we have N (x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 - X 0 0 0 0258 0 0258 0 0 2 (k 2 - 1) = 15x 0 2 . Beam B15 ;
at k = 5 , we have N (x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 -. Beam B24 ;
The main property of such rays for ZFBC is that the numbers in the cells of the rays are determined by one coordinate x 0 , i.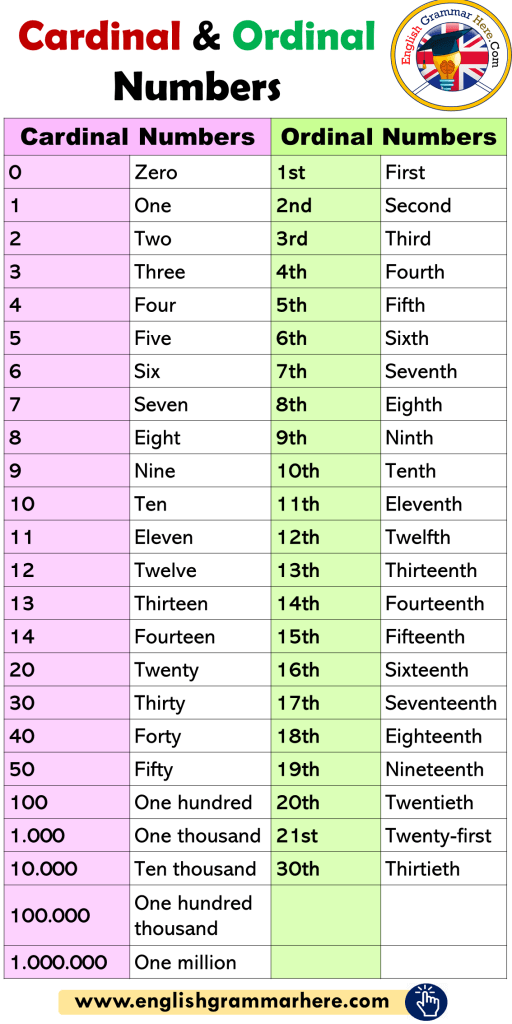 e. value N (x 1 , x 0 ) = N (KX 0 , X 0 ) = (KX 0 ) 2 - X 0 2 = X 2 (k 2 - 1) in a cell belonging to one of the rays becomes a function of only one coordinate x 0 . The presence of the number N , the fact that it belongs to a cell of a particular beam, provides the determination of the second coordinate and the receipt of the solution of the ZFBCH in a fraction of a second, which practically does not depend on the word length of the number. The value of the second coordinate is found from the ratio of the half-plane ray model x 1 = kx 0 N = 968 and N = 507 ∊ Г 2- are models, and each lies in one of the cells of the oblique straight line formed by the relation for some k , for example, k = 2 we get N(x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 - x 0288 = x = x = x = x = x = x = x = x = x = X k 2 - 1) = 3x 0 2 = 968.
e. value N (x 1 , x 0 ) = N (KX 0 , X 0 ) = (KX 0 ) 2 - X 0 2 = X 2 (k 2 - 1) in a cell belonging to one of the rays becomes a function of only one coordinate x 0 . The presence of the number N , the fact that it belongs to a cell of a particular beam, provides the determination of the second coordinate and the receipt of the solution of the ZFBCH in a fraction of a second, which practically does not depend on the word length of the number. The value of the second coordinate is found from the ratio of the half-plane ray model x 1 = kx 0 N = 968 and N = 507 ∊ Г 2- are models, and each lies in one of the cells of the oblique straight line formed by the relation for some k , for example, k = 2 we get N(x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 - x 0288 = x = x = x = x = x = x = x = x = x = X k 2 - 1) = 3x 0 2 = 968.
- Checking whether the given number belongs to one of the possible rays of the half-plane Г 2- . The value of N = 968 We check for belonging to the beam B3 , divide N by 3 , the number N = 968 is not divided by a boc by 3 , we check the belonging to the next ray , divide by 8 8 8 8 8 8 8 8 8 . 968 / 8 \u003d 121 \u003d 11 2 \u003d x 0 2 .
- We found that the number N = 968 lies in the cell belonging to the beam B8 , and the cell has the coordinate x 0 = 11 . The second coordinate of the cell is determined from the ratio of the beam model x 1 = kx 0 = 3 ∙ 11 = 33 . The presence of cell coordinates ensures the factorization of the number in it:)(x 1 -x 0 ) = (33+11)(33-11) = 44 ∙ 22 = 968 .
 Factorization completed successfully.
Factorization completed successfully.
For the second number N = 507 we perform the same actions.
- The first check confirms that the cell with the number N = 507 belongs to the beam B3 , and gives the division result 507 / 3 = 169 = 13 2 = x 0
2. Cell coordinate x 0 = 13 . Other coordinate x 1 \u003d 2 x 0 \u003d 2 ∙ 13 \u003d 26 .
This coordinate can be found in another way. It has independent value (value) and is applicable in other situations. From the total ratio N (x 1 , x 0 ) = x 1 2 - x 0 2 = (KX 0 ) 2 - X - X - X - X - X - X - X = x 0 2 (k 2 - 1) = 3x 0 2 = 507 .
- We find the division of N / 3 = 507 /3 = 169 Value x 0 2 and summing with N This square we find a square of other coordinates x 1 2 = N + X 0 2 = 507 + 169 = 676 .
- We find the division of N / 3 = 507 /3 = 169 Value x 0 2 and summing with N This square we find a square of other coordinates x 1 2 = N + X 0 2 = 507 + 169 = 676 .