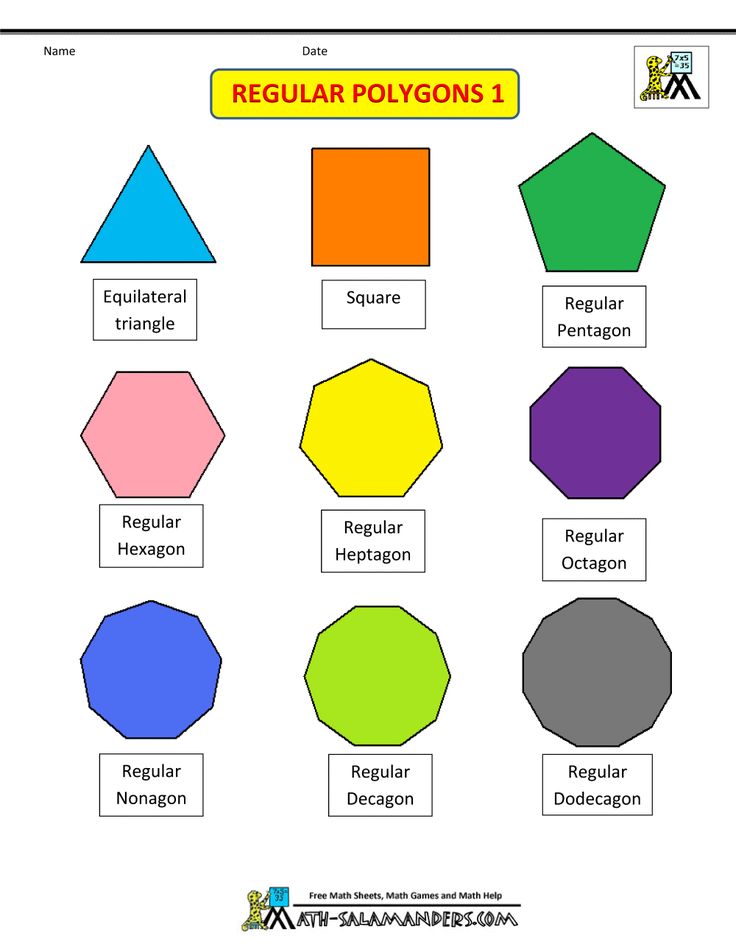
Definition of math concepts

How Math Concepts and Math Skills Work Together and Why You Should Care

Sometimes people use the words “math skills” and “math concepts” interchangeably. They are not the same, but they do go hand and hand. Understanding how new math skills and concepts work together will give you a new perspective on math education and math challenges.

Definition of Skills
Skills are actions. People do them. People master math skills the same way they master musical skills or sports skills. They practice the actions and steps intentionally, correctly and frequently. They may even go to a special place to practice the skill.

Definition of Concepts
Concepts are ideas. People understand them. People learn concepts by thinking, discussing, reading, listening and/or writing about them.

Similarities Between Skills and Concepts
Both can be learned and they are each the point of education.
Both have a natural progression, or order, in which they should be taught.
Both are a huge component of math success.

1. Education
Most of education focuses on skills. Skills are easier to observe and grade because a person can demonstrate skills. Proving that you understand a concept is difficult. Teachers try to measure a student’s understanding by asking them to write about, discuss or draw concepts. Even then, students are still limited in showing their understanding by their language, writing or artistic skills. For example, most adults in the U.S. understand the concept of basic nutrition. How many adults in the U.S. could explain basic nutrition in a foreign language? Our limited skill set in the foreign language would limit how well we could prove our understanding.

Retaining concepts is easier than retaining skills. What happens when we don’t practice a skill? We lose the skill. Most adults can think of a skill that they frequently practiced as child, but don’t practice now (piano for example). Chances are that their younger selves were much better at that skill than their current self.

If you understand a concept, you have that understanding forever. You may need to think about it before you remember all the details, but the underlying concept will always be there. You will always be able to build upon the concepts you understand and your previous understanding makes learning easier and faster.

2. Progression
Skills build on top of each other. When learning to swim, most children learn to float around the same time as learning to flutter kick. They are both beginning level skills. They must master all the beginning level skills before attempting an advanced skill, like swimming in open water or attempting the butterfly stroke.

Concepts are also best taught progressively. Our brains use neural pathways to make connections. Our understanding of underlying concepts pave the way for understanding new concepts. The deeper and broader our knowledge base is, the easier it is for us to connect it to new concepts.

3. Math Success
Skills are the “how-to” parts of math. Children should master adding and subtracting before starting multiplication. They must know how to multiply and divide before attempting percentages.

Concepts are the underlying ideas of math. Concepts are ideas like equality and symbolic representation. Many math concepts build upon each other. A child who has a solid understanding of the relationship of quantity and numbers, or “number sense”, will find the concept of “wholes and parts”, naturally makes sense.

How Skills and Concepts Work Together
Understanding concepts makes learning skills easier. Mastering skills, especially thinking skills, makes learning concepts easier. Each prepares the brain differently.

People might be able to do a skill without understanding “why” it works. Understanding why a skill works in sports is helpful, but not critical. Can you imagine swim lessons at the neighborhood pool to 5 year-olds including a study of fluid dynamics and propulsion?

People might also have a concept about something, without the skill to execute it. Many adults understand the concept of bacteria and wound maintenance, but they still go to a skilled professional to get stitches. Some people call this “book smarts” versus “street smarts.” Understanding the why helps you build your knowledge base and your retention of skills.

Most people in life don’t care about what others understand. They care about what others do. A conceptual understanding helps build skill sets faster.

How Skills and Concepts Work Together in Math
Math skills and concepts should be taught simultaneously. Children who learn math skills without learning the underlying concepts, will find math can get very confusing. Their lack of understanding will limit their ability to apply math in a variety of problem solving situations. Without understanding a concept, we are forced to rely on remembering and practicing a skill. For example, let’s say a 5th grader learned how to divide fractions using the "copy, dot, flip" method but never understood the concept behind why that process worked. Then the 5th grader progresses to 6th grade and stops practicing dividing fractions because they are learning new skills. When that child stops practicing, he will then likely forget how to divide fractions. This will be a problem when dividing fractions comes up again in algebra and advanced math. The child who has both the skills and the concepts will be much better prepared.

Children who learn math concepts without learning the skills, will struggle to apply what they know. Knowing the difference between concepts and skills helps to identify the problems that arise in math.

How we Approach Skills and Concepts at Mathnasium
At Mathnasium of Littleton we focus on teaching foundational math skills like Counting, Numerical Fluency (adding and subtracting and multiplication facts), time and money and the order of operations while also teaching concepts such as Number Sense, Wholes and Parts, and Proportional Thinking. These latter are concepts that also involve skills. Additionally, thinking is a skill that must be practiced. Thinking skills enable a child to learn the concepts and we never neglect to teach concepts. We encourage our students to ask us questions and we ask them questions to promote deep thinking and conceptual understanding.

The progression of skills and concepts and how they work together is exactly why at Mathnasium of Littleton, we work hard to close math gaps.

For more information about our methods, click here. The result is stronger math skills with a deeper understanding of mathematical concepts. Our motto is: “We Make Math Make Sense!”

Give us a call today! 303-979-9077

Articles referenced in this post:

Practice Makes Perfect so Perfect Practice is Essential

Multiple Practice Sessions Provide Better Learning than Cramming

Where Does your Child Go To Practice Math?

Is Mathematical Understanding Really Necessary?

Worried Your Child has Not Memorized the Multiplication Tables?

4 Tips for Figuring Out Percentages the Easy Way

Learning Math Symbols in Elementary School Takes Time

Prepare Your Child for Calculus Starting in Second Grade

Is Your Child Dependent on Algorithms and is that a Bad Thing?

Why Does Mathnasium of Littleton Focus on Foundational Math Skills?

Counting … Its More Complex Than You Imagine

Teaching Number Sense

Focus on Math: Wholes and Parts

Focus on Math: Proportional Thinking

What is Numerical Fluency?

Multiplication Fluency is Coming to Mathnasium of Littleton

Focus on Math: Learning About Money

Does Your Child Ask Questions in Math Class?

Focus on Math: Order of Operations

Understanding Mathematical Reasoning

Understanding Math Learning Gaps

Mathematical Concepts and Definitions | The Philosophy of Mathematical Practice

Navbar Search Filter Oxford AcademicThe Philosophy of Mathematical PracticePhilosophy of Mathematics and LogicBooksJournals Mobile Microsite Search Term

Navbar Search Filter Oxford AcademicThe Philosophy of Mathematical PracticePhilosophy of Mathematics and LogicBooksJournals Microsite Search Term

Advanced Search

Cite Icon Cite
Permissions
Share
- Twitter
- More

Cite

Tappenden, Jamie,

'Mathematical Concepts and Definitions'

in Paolo Mancosu (ed. )

The Philosophy of Mathematical Practice

(

Oxford,

2008;

online edn,

Oxford Academic

, 1 Feb. 2010

), https://doi.org/10.1093/acprof:oso/9780199296453.003.0010,

accessed 10 Dec. 2022.

Select Format Select format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Navbar Search Filter Oxford AcademicThe Philosophy of Mathematical PracticePhilosophy of Mathematics and LogicBooksJournals Mobile Microsite Search Term

Navbar Search Filter Oxford AcademicThe Philosophy of Mathematical PracticePhilosophy of Mathematics and LogicBooksJournals Microsite Search Term

Advanced Search

Abstract

This chapter lays some preliminary groundwork for answering the question: What kind of success have we attained when we introduce a ‘good’ mathematical concept or definition? What sort of contribution is this to our mathematical knowledge? It develops two mathematical examples from algebraic number theory: the Legendre symbol and the definition of prime number. The question is studied in connection with the contrast of ‘real’ versus ‘nominal’ definitions in general, and with current philosophical theories of natural properties.

Keywords: concept, definition, mathematical knowledge, Legendre symbol, prime number, real definition, nominal definition, natural properties

Subject

Philosophy of Mathematics and Logic

You do not currently have access to this chapter.

Sign in

Get help with access

Institutional access

Access to content on Oxford Academic is often provided through institutional subscriptions and purchases. If you are a member of an institution with an active account, you may be able to access content in one of the following ways:

IP based access

Typically, access is provided across an institutional network to a range of IP addresses. This authentication occurs automatically, and it is not possible to sign out of an IP authenticated account.

Sign in through your institution

Choose this option to get remote access when outside your institution. Shibboleth / Open Athens technology is used to provide single sign-on between your institution’s website and Oxford Academic.

Click Sign in through your institution.
Select your institution from the list provided, which will take you to your institution's website to sign in.
When on the institution site, please use the credentials provided by your institution. Do not use an Oxford Academic personal account.
Following successful sign in, you will be returned to Oxford Academic.

If your institution is not listed or you cannot sign in to your institution’s website, please contact your librarian or administrator.

Sign in with a library card

Enter your library card number to sign in. If you cannot sign in, please contact your librarian.

Society Members

Society member access to a journal is achieved in one of the following ways:

Sign in through society site

Many societies offer single sign-on between the society website and Oxford Academic. If you see ‘Sign in through society site’ in the sign in pane within a journal:

Click Sign in through society site.
When on the society site, please use the credentials provided by that society. Do not use an Oxford Academic personal account.
Following successful sign in, you will be returned to Oxford Academic.

If you do not have a society account or have forgotten your username or password, please contact your society.

Sign in using a personal account

Some societies use Oxford Academic personal accounts to provide access to their members. See below.

Personal account

A personal account can be used to get email alerts, save searches, purchase content, and activate subscriptions.

Some societies use Oxford Academic personal accounts to provide access to their members.

Viewing your signed in accounts

Click the account icon in the top right to:

View your signed in personal account and access account management features.
View the institutional accounts that are providing access.

Signed in but can't access content

Oxford Academic is home to a wide variety of products. The institutional subscription may not cover the content that you are trying to access. If you believe you should have access to that content, please contact your librarian.

Institutional account management

For librarians and administrators, your personal account also provides access to institutional account management. Here you will find options to view and activate subscriptions, manage institutional settings and access options, access usage statistics, and more.

Purchase

Our books are available by subscription or purchase to libraries and institutions.

Purchasing information

1. Mathematical concepts

Lecture #2

in mathematics

Topic: "Mathematical concepts”

Plan:

Mathematical concepts
Scope and content concepts. Relations between concepts
Definition concepts
Requirements to definition of concepts
Some species definitions

concepts, which are studied in the initial course mathematics is usually represented in the form four groups. The first one includes concepts related to numbers and operations above them: number, addition, term, more, etc. The second includes algebraic concepts: expression, equality, equation and others. The third is geometric concepts: line, segment, triangle etc. The fourth group is formed by the concepts associated with quantities and their measurement.

How to study such an abundance of different concepts?

Before All you need to do is to understand the concept as a logical category and features mathematical concepts.

AT logic concepts are considered as a form thoughts reflecting objects (objects or phenomena) in their essential and general properties. The language form of the concept is a word or group of words.

Compose the concept of an object means to be able to to distinguish it from others similar to it objects. Mathematical concepts have a number of features. home is that the mathematical objects to be compiled concept does not exist in reality. Mathematical objects are created by the mind person. These are ideal objects reflecting real objects or phenomena. For example, in geometry one studies the shape and size of objects, without taking into account their other properties: color, mass, hardness, etc. From all this distracted, abstracted. That's why in geometry instead of the word "object" say "geometric figure".

result abstractions are and such mathematical concepts like "number" and "value".

Generally mathematical objects exist only in the thinking of man and in those signs and symbols that form a mathematical language.

To It can be added to what has been said that, by studying spatial forms and quantitative relations of the material world, mathematics not only uses different methods abstraction, but abstraction itself acts as a multi-step process. Mathematics considers not only concepts that emerged in the study real objects, but also concepts arising from the first. For example, the general concept of a function as a correspondence is a generalization of the concepts of specific functions, i.e. abstraction from abstractions.

To master general approaches to learning concepts in the elementary course of mathematics, The teacher needs knowledge about the volume and the content of the concept, about the relationship between concepts and about the types of definitions of concepts.

Any mathematical object has certain properties. For example, a square has four sides right angles equal to diagonals. Can specify other properties.

Among the properties object distinguish between essential and insignificant. Property feel essential to an object if it inherent in this object and without it, it is not may exist. For example, for square essential are all the properties mentioned above. Not essential for square ABCD property "side AD horizontal. " If the square is turned then side AD will be located differently (Fig. 26).

That's why, to understand what is given mathematical object know its essential properties.

When talking about a mathematical concept, then usually means a set of objects, denoted by one term (word or group of words). So, speaking of a square, refers to all geometric shapes, which are squares. Think that the set of all squares is the scope of the concept of "square".

Generally volume concepts are the set of all objects, denoted by one term.

Any concept has not only volume, but also content.

Contents concepts are the set of all essential object properties reflected in this concept .

Consider, For example, the concept of "rectangle".

Volume concepts are many different rectangles, and in its content includes such properties of rectangles, how "to have four right angles", "to have equal opposite sides", "to have equal diagonals”, etc.

Between scope of the concept and its content there is a relationship: if increases the scope of the concept, then it decreases content and vice versa. For example, the scope of the concept of "square" is part of volume of the concept of "rectangle", and in the content of the concept of "square" contains more properties than in the content of the concept "rectangle" ("all sides are equal", diagonals are mutually perpendicular and etc.).

Any the concept cannot be grasped without realizing it relationships with other concepts. That's why it is important to know in what respects to be concepts, and to be able to establish these connections.

Relations between concepts are closely related to relationships between their volumes, i.e. sets.

Let's agree concepts are capitalized Latin alphabet: a, b, c,...,z.

Let two concepts a and b are given. Their volumes will be denoted respectively by A and V.

If a BUT B (A ≠ B), then they say that the concept of a - specific in relation to the concept b , a concept b - generic in relation to the concept a .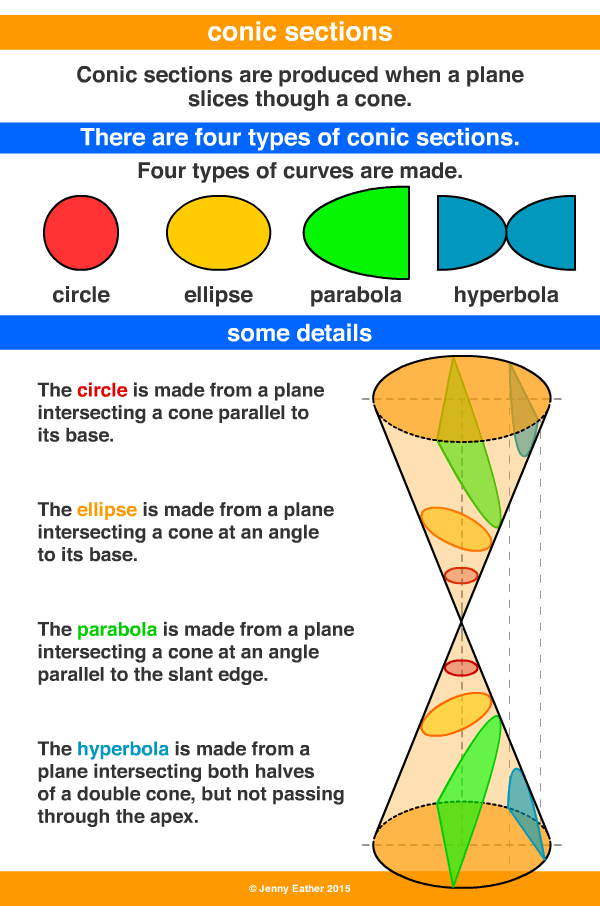

For example, if a is a "rectangle", b - "quadrilateral", then their volumes A and B are in relation to inclusion (A B and A ≠ B), since every rectangle is a quadrilateral. That's why it can be argued that the concept "rectangle" - specific in relation to to the concept of "quadrilateral", and the concept "quadrangle" - generic in relation to the concept of a rectangle.

If a A = B, then they say that concepts a and b are identical.

For example, identical concept of "equilateral triangle" and "equiangular triangle" because their volumes match.

If a sets A and B are not related inclusions, then we say that the concepts a and b are not related to genus and species and are not identical. For example, not related such relations of the concept of "triangle" and "rectangle".

Consider in more detail the relation of genus and species between concepts. First, the concepts of gender and species are relative: the same concept may be generic to one concept and species in relation to another. For example, the concept of "rectangle" - generic in relation to the concept of "square" and specific in relation to the concept "quadrilateral".

Secondly, for a given concept, one can often specify several generic terms. Yes, for the concepts of "rectangle" are generic are the concepts of "quadrilateral", parallelogram, polygon. Among them, you can specify the nearest. For the concept of "rectangle" to the nearest is the concept of "parallelogram".

Thirdly, the species concept has all the properties generic concept. For example, a square being a species concept in relation to to the concept of "rectangle", has all the properties of a rectangle.

Since the volume concepts - set, convenient, setting relations between the volumes of concepts, depict them using Euler circles.

Set, for example, relationship between the following couples concepts a and b, if:

1) a - "rectangle", b - "rhombus";

2) a - "polygon", b - "parallelogram";

3) a - "straight", b - "line segment".

AT case 1) the volumes of concepts intersect, but not one set is a subset of another (Fig. 27).

Consequently, It can be argued that these concepts and b are not related to genus and species.

AT case 2) the data volumes of the concept are regarding inclusion, but do not match - every parallelogram is polygon, but not vice versa (Fig. 28). Therefore, it can be argued that the concept of "parallelogram" - specific in relation to the concept of "polygon", and the concept of "polygon" is generic in relation to the concept of "parallelogram".

AT case 3) the volumes of concepts do not intersect, since not a single segment is possible say he is direct, and neither one line cannot be named segment (Fig. 29).

Consequently, these terms are not related genus and species.

O concepts of "line" and "segment" can be say they are for whole and part: A segment is a part of a line, not a type of it. And if the species concept has all the properties generic concept, then the part is not necessarily has all the properties of the whole. For example, a segment does not have such property of the straight line, as its infinity.

Features of mathematical concepts. The scope and content of the concept. Definition of concepts. The structure of the definition of the concept through the genus and specific differences

Ostensive definitions are such definitions that introduce the concept by demonstrating, showing the objects that are denoted by this term.

Mathematics, unlike other sciences, studies the world around us from a special perspective. Any mathematical objects are the result of separating quantitative and spatial properties and relationships from objects and phenomena. That. mathematical objects do not really exist. These are ideal concepts, they exist only in human thinking and in those signs and symbols that form the mathematical language. Moreover, in the formation of mathematical concepts, in addition to abstraction, they are credited with such properties that no real object possesses.

Basic mathematical concepts: point, line, plane, plural, number, magnitude, arithmetic operation.

Any mathematical concept is characterized by a term, scope and content.

A term is a word or a group of words that is used to name the elements of some set. The scope of a concept is the set of all objects denoted by the same term. There are essential and non-essential properties of objects. The property will be essential if it is inherent in the object, and without it the object cannot exist. Minor - the absence of which does not affect the essential objects.

The content of concepts is the plurality of all interconnected essential properties of this concept or this object.

a-the concept of a parallelogram; in-the concept of a rectangle; √vs√a generic for in; in-species for a; c-the concept of a quadrilateral. √а с√с

The same concept, for example, a parallelogram, can be generic for the concept of a rectangle or specific for the concept of a quadrilateral.

The concept of an isosceles triangle. And a rectangular triangle. They are not in genus-species relationships. There is a relationship between the concepts of part and whole.

For example, a ray is part of a line, a line segment is part of a line, an arc is part of a circle.

If concepts are in genus-species relationships, then there is such a relationship between the volume of the concept and its content: the larger the volume, the less its content, and vice versa.

Definition of concepts is a logical operation that reveals the content of a concept. It indicates those essential properties that are sufficient for its recognition. Definitions are divided into explicit and implicit (indirect). Explicit definitions take the form of equality, the coincidence of two concepts.

Example: Parallelogram called. a quadrilateral whose sides are pairwise parallel. a is in; a-parallelogram (defining concept; c-quadrilateral whose sides are pairwise parallel (defining concept; a=r+v

Defined concept=generic concept+specific difference

Genus-species: The bisector of the angle is called the ray emerging from the vertex of the angle and bisecting an angle/ r-generic concept: ray v-species concept: emerging from the vertex of an angle and dividing the angle in half Explicit definition by gender and aspect difference is rarely used in elementary school Example: Defining an even number, rectangle, square, multiplication .

Explicit definitions can also have another structure: a) genetic definitions. A triangle is a figure consisting of 3 points that do not lie on the same straight line, and 3 segments connecting them in series. A generic concept and method of construction.

b) recurrent (recursion-return) An arithmetic progression is a numerical sequence, each member of which, starting from the second, is equal to the previous one, added with a constant for this sequence number d (difference).