Different types of shapes in math
Different Shape Names (with Useful List, Types) • 7ESL
Pin
Are you looking for different shape names in English? Here you will find a list of shapes with different types and useful example sentences. If you work in a business that requires the use of mathematics, for example then it would be very important that you are aware of the English names for shapes.
However, this may not be the only reason that you need to learn this information. When taking part in day-to-day conversations, you will need to learn the shape names in order to describe something or be able to understand what someone is talking about, for example, if a person tells you about ‘the square plate.’ Here, you can learn shape names and further expand your vocabulary.
Table of Contents
Shapes
What Are Shapes?
Shapes are geometric figures, or the pattern an outline falls into. Shapes are often drawn (whether by ink, pencil, or digitally), but they occur in life, also. Frequently, people picture 2D (two-dimensional, or flat) images when they hear the word “shapes,” so most of the objects listed in this lesson will be 2D shapes, but some will be 3D as well.
Different Types of Shapes
There are many, many different types of shapes, and there are names for basically all of them. The following list focuses on more common shapes that you’re more likely to encounter or to need or want to know the name of.
Shape names with pictures
Pin
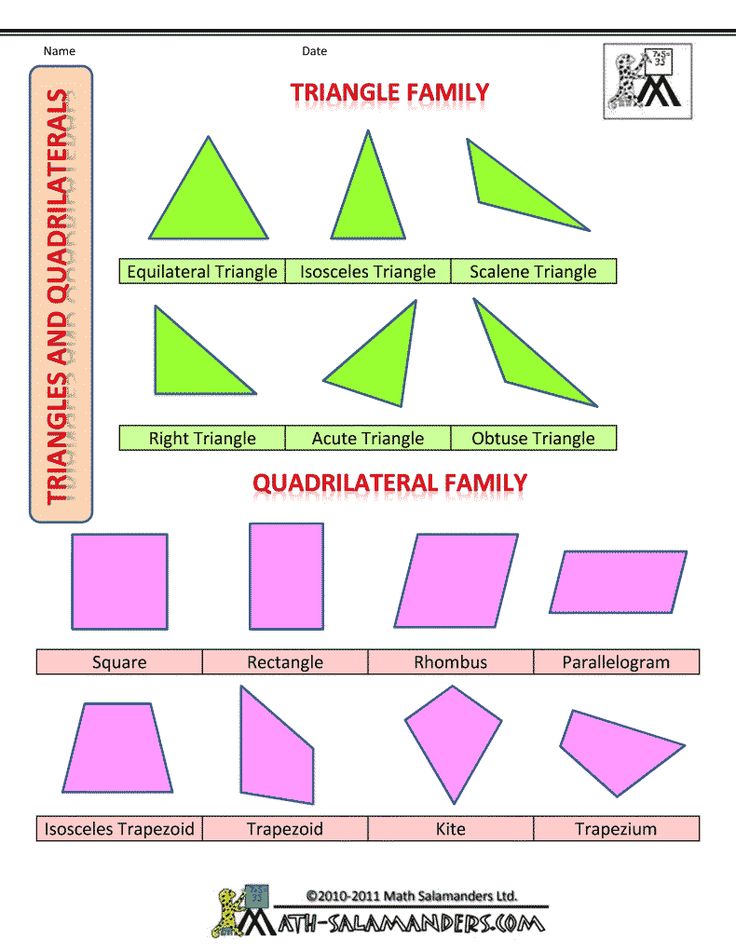
Two-Dimensional (Flat) Shapes
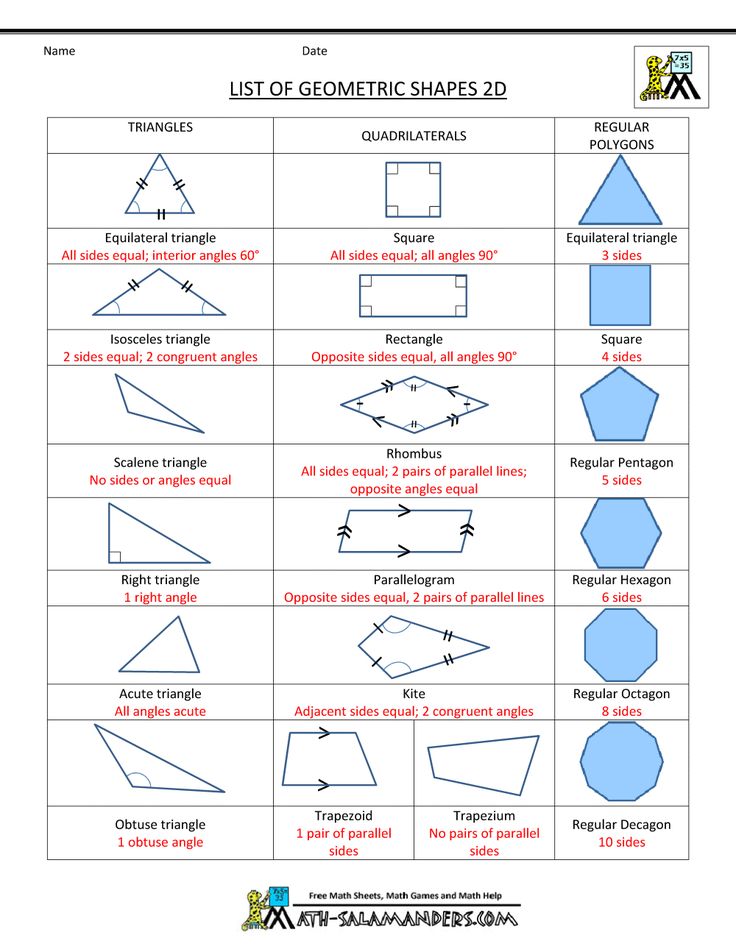
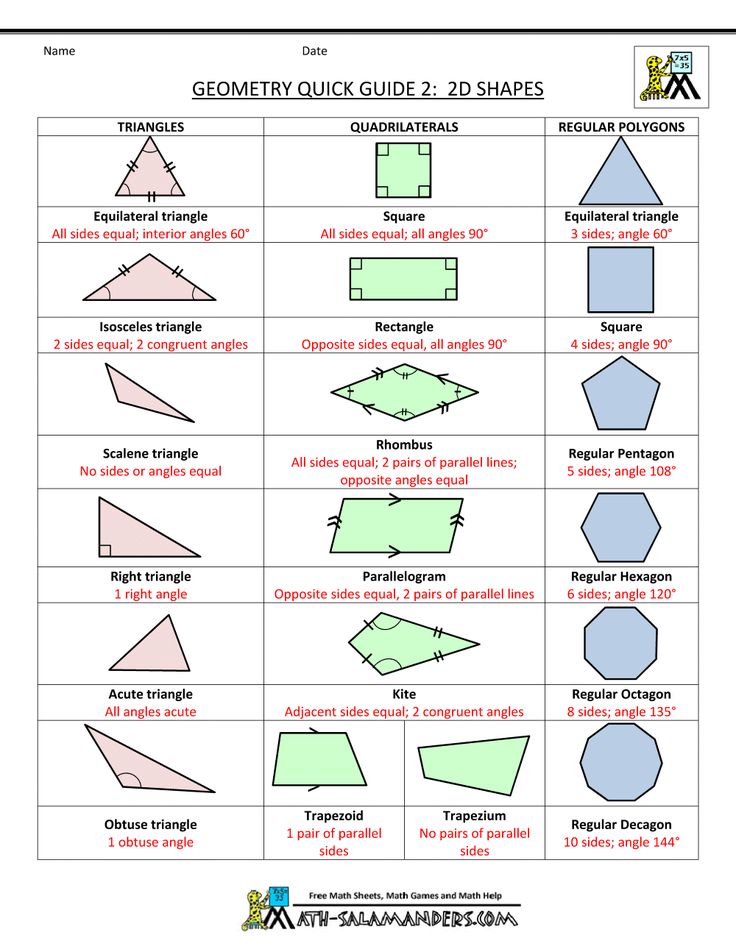
- Circle: A circle is an equally round shape. Picture the lid of a jar, flat, from above. That is a circle. The wheels on a car are circular, as well. So are the holes in most lined paper and notebooks.
- Oval: An oval is basically a circle that’s been a little squished. The cups of over-the-ear headphones are generally referred to as oval. So is the profile of an egg.
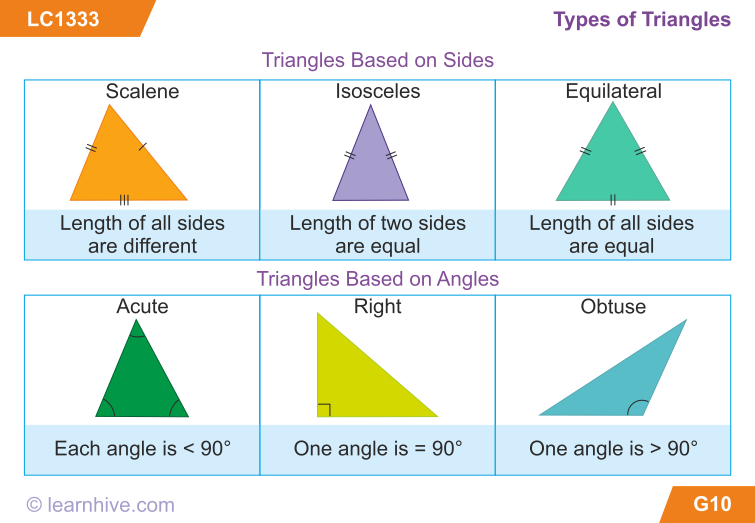 Some make a distinction between circles that have been squished in the middle versus circles that have been squished at the top, the former being called an ellipse, but common usage treats both as ovals.
Some make a distinction between circles that have been squished in the middle versus circles that have been squished at the top, the former being called an ellipse, but common usage treats both as ovals. - Rectangle: A rectangle is a shape with four sides, made up of two sets of parallel lines, with four right angles (90 degree angles; picture a capital L). It doesn’t matter whether the sets of sides are the same length. Picture a plain piece of printing paper. This is a rectangle, with one set of sides (generally the top and bottom) shorter than the other set of sides (generally the left and right).
- Square: A square is a very specific type of rectangle, one with four equal sides. Some boxes have a square footprint. Origami paper is square.
- Triangle: A triangle is a shape with three straight sides. These sides can be any length, with any degree of angle, as long as the three sides are joined at their ends. Many warning signs are triangular.
 A slice of a round pizza is mostly triangular (the crust is a little too rounded to be perfect).
A slice of a round pizza is mostly triangular (the crust is a little too rounded to be perfect). - Pentagon: A pentagon is a shape with five sides. A basic drawing of a house, with two lines for the roof, a line for each side, and a line for the bottom is generally a pentagon.
Shapes with more sides are generally named based on how many sides they have. A hexagon has six sides, heptagon has seven, and an octagon has eight.
Three-Dimensional Shapes
Three-dimensional shapes are ones that aren’t just flat on paper, but also take up room vertically. Only a few are really commonly named.
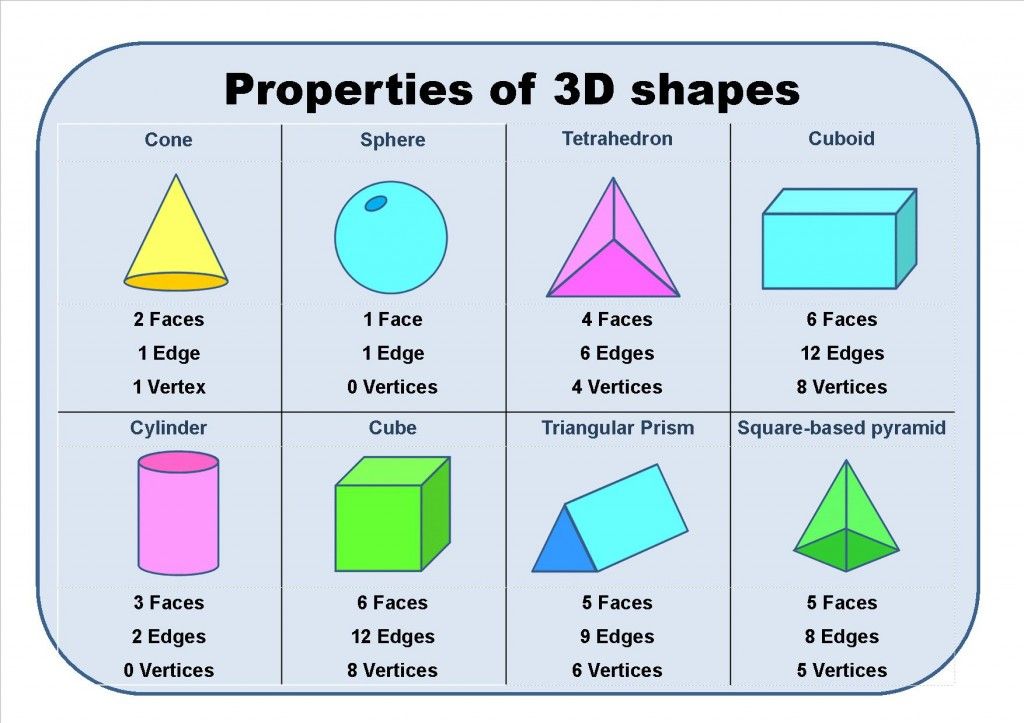
- Sphere: A sphere is a 3D circle, like a ball.
- Cube: A cube is a 3D square, like a box.
- Pyramid: A pyramid is a 3D triangle. The giant structures in Egypt are pyramids, as is the Luxor in Las Vegas.
Shape Names
It’s important to build a good vocabulary, in any language.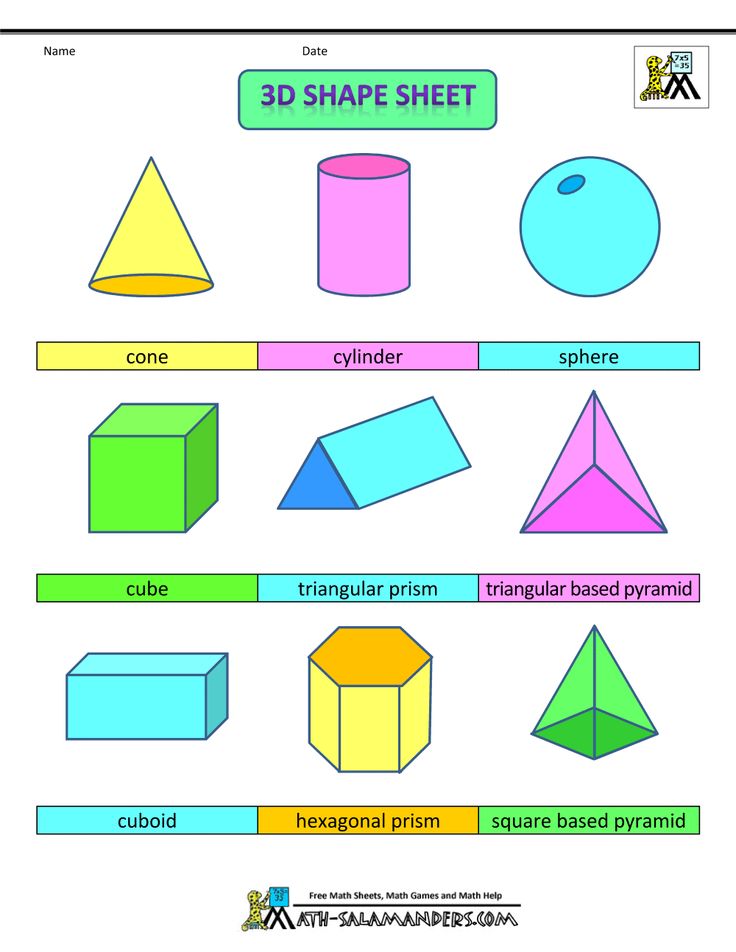 The more words you know and understand, the better you can communicate. Even if you don’t use the words often, understanding them allows you to follow along with a conversation, even if it ventures a little outside of your comfort zone. This lesson is specifically focused on different types of shapes.
The more words you know and understand, the better you can communicate. Even if you don’t use the words often, understanding them allows you to follow along with a conversation, even if it ventures a little outside of your comfort zone. This lesson is specifically focused on different types of shapes.
- Nonagon
- Octagon
- Heptagon
- Hexagon
- Triangle
- Scalene triangle
- Right triangle
- Parallelogram
- Rhombus
- Square
- Pentagon
- Circle
- Oval
- Heart
- Cross
- Arrow
- Cube
- Cylinder
- Star
- Crescent
The math student measured each side of the nonagon until he had measurements for all nine edges.
Pin
OctagonThe sectional shape is a quarter of an octagon.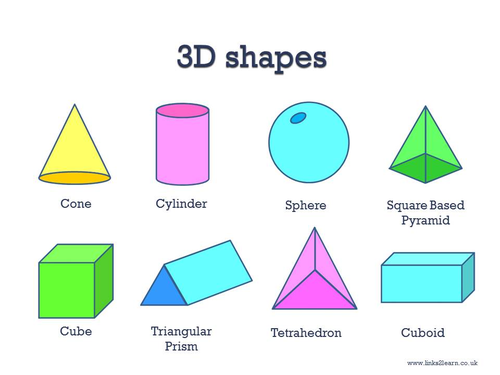
Pin
HeptagonThe pagoda has a base of heptagon.
Pin
HexagonA hexagon is a six – sided figure.
Pin
TriangleThe sum of all the angles of a triangle is 180 degrees.
Pin
Scalene triangleA scalene triangle is a triangle that has three unequal sides.
Pin
Right triangleThe hypotenuse is the longest side of a right triangle.
Pin
ParallelogramThese are the opposite sides of the parallelogram.
Pin
RhombusA rhombus is a simple quadrilateral whose four sides all have the same length.
Pin
SquareThe interior angles of a square are right angles or angles of 90 degrees.
Pin
PentagonDraw a pentagon, a regular five-sided figure.
Pin
CircleThe students sit in a circle on the floor.
Pin
OvalThe shape of the earth is an oval.
Pin
HeartThe pool was in the shape of a heart.
Pin
CrossThe cross is the symbol of Christianity.
Pin
ArrowIt flew straight as an arrow.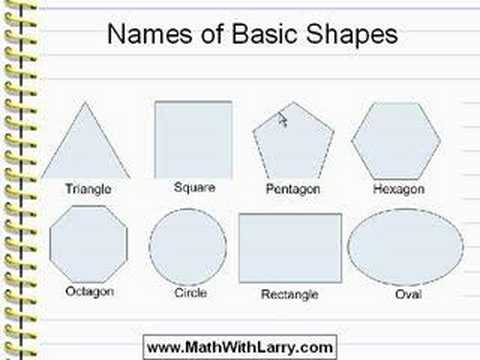
Pin
CubeThe box was cube-shaped.
Pin
CylinderThe cylinder is rotated 180 degrees.
Pin
StarShe cuts these paper into star-shaped.
Pin
CrescentHe has a crescent–shaped knife.
Pin
Shapes | PictureLearn different shapes with images to improve and expand your vocabulary, especially shapes and colors vocabulary words in English.
PinShapes: Different Shape Names (with Useful List, Types)Shapes Names VideoThere are shapes everywhere, and so references to them happen frequently. Hopefully, after this lesson, you’re feeling prepared to deal with shapes!
Hopefully, after this lesson, you’re feeling prepared to deal with shapes!
Shapes – Definition with Examples
What are Shapes?
In geometry, a shape can be defined as the form of an object or its outline, outer boundary or outer surface.
Everything we see in the world around us has a shape. We can find different basic shapes such as the two-dimensional square, rectangle, and oval or the three-dimensional rectangular prism, cylinder, and sphere in the objects we see around us. These geometric shapes appear in objects we see as credit cards, bills and coins, finger rings, photo frames, dart boards, huts, windows, magician’s wands, tall buildings, flower pots, toy trains, and balloons.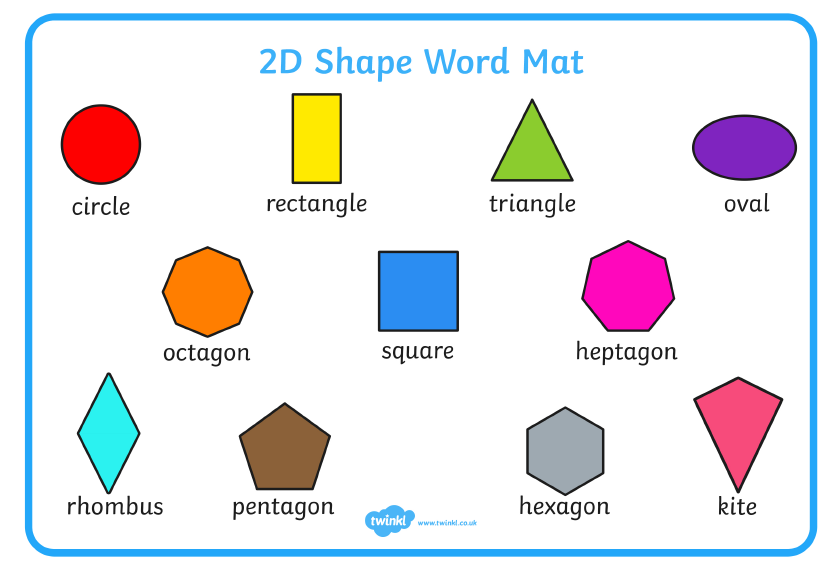
Different Types of Shapes
Shapes can be classified into open and closed shapes.
| In geometry, an open shape can be defined as a shape or figure whose line segments and/or curves do not meet. They do not start and end at the same point. | In geometry, a closed shape can be defined as an enclosed shape or figure whose line segments and/or curves are connected or meet. They start and end at the same point. |
Closed geometric shapes can further be put into two broad categories, namely two-dimensional and three-dimensional shapes.
| The 2-Dimensional shape is flat. | A 3-Dimensional Shape is a solid shape. |
| It has two dimensions, that is, length and width. | It has two dimensions, that is, length, width, and depth. |
Here’s a list of 2-D or two-dimensional shapes with their names and pictures:
| Two-Dimensional Geometric Shapes |
Here’s a list of 3-D or three-dimensional shapes with their names and pictures:
| Three-Dimensional Geometric Shapes |
The color, overall size, and orientation called the non-defining attributes of a two-dimensional or three-dimensional shape do not define or affect the shape in any way.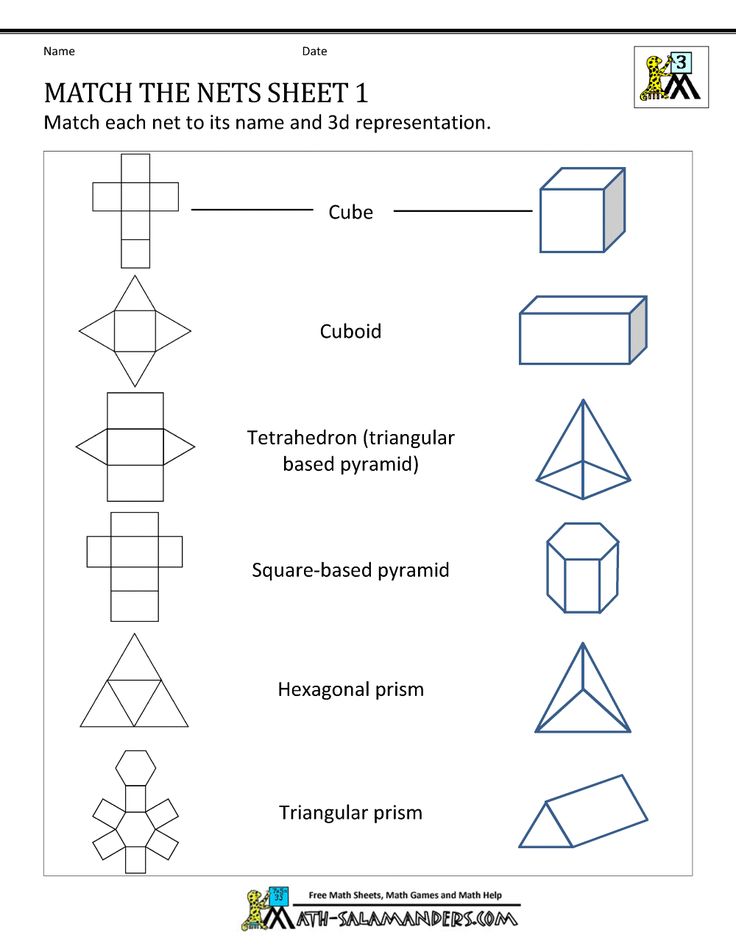 These attributes can change without any effect on the shape.
These attributes can change without any effect on the shape.
On the other hand, defining attributes such as the number of sides (parallel or non-parallel, straight or curved), vertices, edges, and faces of a shape, whether the shape is open or closed, and the angle measures determine the shape of a two-dimensional or three-dimensional object. Any change in these defining attributes will change the shape.
Solved Examples on Shapes
Example 1: Name the shapes.
- A polygon with 6 sides.
- Outline of a door.
- When you fold square corner to corner.
- A square and a triangle on top of it.
Solution:
- Hexagon
- Rectangle or quadrilateral
- Triangle
- Pentagon
Example 2: Classify the given letters as open shape or closed shape.
C, D, L, M, O, S, U, V, Z
Solution:
Open shape: C, L, M, S, U, V, Z
Closed shape: D, O
Example 3: Identify the solid shape of given objects.
- Globe
- Book
- Cold drink can
- Dice
Solution:
- Sphere
- Cuboid
- Cylinder
- Cube
Example 4: Why is the crescent-shaped moon not a polygon?
Solution:
Crescent shape moon is not a polygon as it has curved lines.
Practice Problems
1
What is 8-sided polygon known as?
hexagon
heptagon
octagon
quadrilateral
Correct answer is: octagon
A polygon with 8 sides is known as octagon.
2
How many dimensions does a solid shape have?
1
2
3
depends on the shape
Correct answer is: 3
All solid shapes are 3-dimensional shapes.
3
Which of the following statements is incorrect?
closed shapes can have only straight sides.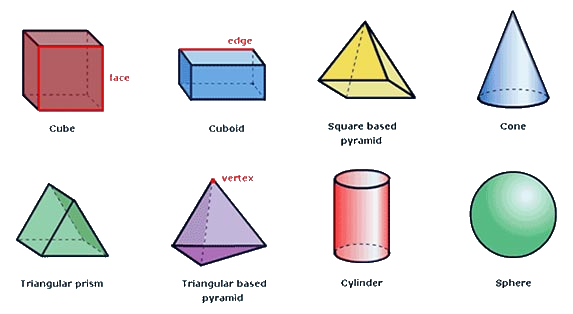
closed shapes have definite area.
start and end point of a closed shape are the same.
start and end point of a open shape are the different.
Correct answer is: closed shapes can have only straight sides.
Closed shapes are shapes whose start and end points are the same. It is not necessary that it is formed by only straight sides.
Basic geometric shapes
Each of us, both adults and children, noticed how many geometric shapes exist around us. We meet them everywhere, in all the objects around us. Where are geometric shapes found in our lives?
Where are geometric shapes found in our lives?
Each of us - both an adult and a child - noticed how many geometric shapes exist around us. We meet them everywhere, in all the objects around us.
People have long been interested in the variety of geometric shapes. Even for primitive people, the shape of the objects surrounding them played an important role.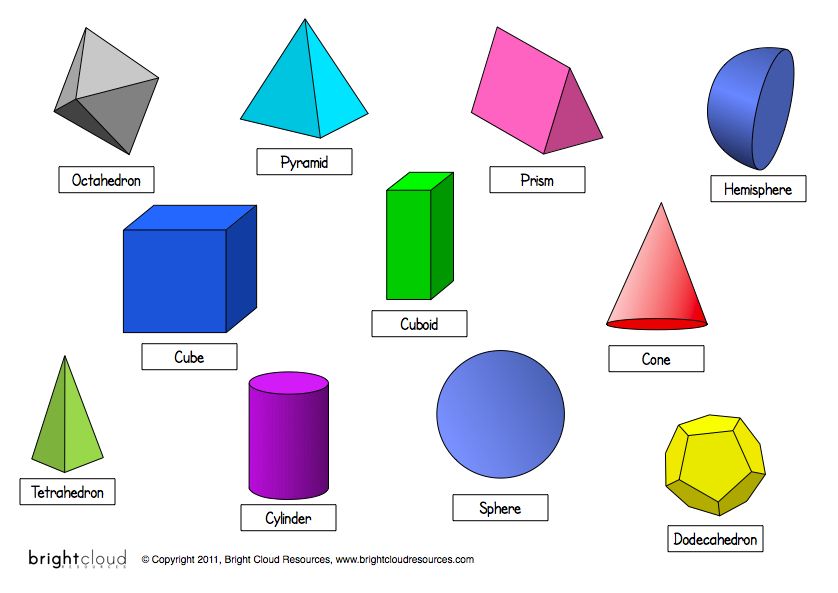 Mastering the world, people got acquainted with the simplest geometric shapes. At first they made tools of relatively regular shape, then they learned how to improve them. At that time, of course, there were no special names for geometric shapes. They were invented much later. When people began to build houses, they had to understand even more deeply the features of different figures in order to understand what shape walls and roofs should be given, what shape logs or stone blocks should be. Without knowing it, a person was constantly studying figures: women, making clothes, hunters - spearheads or boomerangs of complex shape, fishermen, making such bone hooks so that the fish would not fall off them.
Mastering the world, people got acquainted with the simplest geometric shapes. At first they made tools of relatively regular shape, then they learned how to improve them. At that time, of course, there were no special names for geometric shapes. They were invented much later. When people began to build houses, they had to understand even more deeply the features of different figures in order to understand what shape walls and roofs should be given, what shape logs or stone blocks should be. Without knowing it, a person was constantly studying figures: women, making clothes, hunters - spearheads or boomerangs of complex shape, fishermen, making such bone hooks so that the fish would not fall off them.
One cannot live without this knowledge in the modern world.
Where are geometric shapes found in our lives?
Perhaps someone thinks that the various lines of the figure are "found" only in the books of learned mathematicians. However, if you look around, it becomes clear that many objects have a shape similar to the main geometric shapes. We just don't always notice it. Many wonderful geometric shapes are found in the nature around us. The field has the shape of a rectangle, the river has a curved line, the lake has a circle, a salt crystal has the shape of a cube, an ordinary pea, a dew drop has the shape of a ball. Beautiful and varied polyhedrons - crystals of rock crystal. But in everyday life, the basic geometric shapes are also everywhere. These are buildings, structures, transport, apartment interiors, even dishes and clothing. For example, a woman's skirt is a trapeze, a plate is a circle, a house is a square and a triangle, and a cylinder is in a pipe.
We just don't always notice it. Many wonderful geometric shapes are found in the nature around us. The field has the shape of a rectangle, the river has a curved line, the lake has a circle, a salt crystal has the shape of a cube, an ordinary pea, a dew drop has the shape of a ball. Beautiful and varied polyhedrons - crystals of rock crystal. But in everyday life, the basic geometric shapes are also everywhere. These are buildings, structures, transport, apartment interiors, even dishes and clothing. For example, a woman's skirt is a trapeze, a plate is a circle, a house is a square and a triangle, and a cylinder is in a pipe.
Knowing all the figures, their types, names and properties is very important. Systematizes knowledge about geometric shapes and studies their properties of mathematical science - geometry. This science is very important, its application is simply priceless at all times and regardless of profession. Neither a worker, nor an engineer, nor an architect, nor an artist can do without knowledge of geometry. And it is very important to start mastering this science at an early age.
And it is very important to start mastering this science at an early age.
The iSmart educational platform will be a great help to your child. The main types of geometric shapes, their properties, tasks for finding the area of figures and much more are on the platform in the "Mathematics" section. Here are collected several thousand tasks for the development of these topics, which are not repeated during repeated development. Being engaged in, primary school students will thoroughly understand the basics of geometry. This will give them a good base in the subject for their middle and high school studies. In addition, interactive tasks are colorful, interesting, and exciting.
So,
The simplest types of shapes
The two basic shapes are a point and a line. The accumulation of points and lines forms various geometric shapes. Each of them is individual, differs in its parameters, their forms are very diverse. Figures are simple and complex, flat and voluminous.
Point
Point is the smallest, but at the same time the most important object in geometry. This is the smallest geometric figure, but it is it that is necessary for constructing other figures on the plane and is the basis for all other figures. It does not contain such properties as length, height, volume, area, does not have measuring features and characteristics. It only matters where it is located. The point is indicated by a capital letter of the Latin alphabet or a number. For example, A, B, C or 1, 2, 3.
Any more complex geometric figure is a set of points , which have a certain property that is characteristic only for this figure.
The simplest figures are a ray and a segment.
- A ray is a part of a line that has a starting point but no end. This is a one way extension.
- Segment is a component of a straight line bounded by two points.
 It has a beginning and an end, so it is measured. The length of a line can be determined by measuring the distance between its ends.
It has a beginning and an end, so it is measured. The length of a line can be determined by measuring the distance between its ends.
Line
A line is formed from a set of dots arranged one after another and connected to each other. Lines are closed and open, straight and curved, as well as broken.
- Closed - when the start and end parts of the direction are located at the same point. An inverse version is obtained from an open line.
- Open - when the beginning and end of the line are not connected.
- Straight continuous line unchanged.
- Curve is not a straight line.
- Polyline - when segments are not connected at an angle of 180 degrees.
An infinite number of lines can be drawn through one point, but only one straight line and many curves can be drawn through two points.
Basic geometric shapes
Connected points form lines, and interconnected lines form basic geometric shapes on a plane.
Geometric figures are flat or two-dimensional (2D) and three-dimensional or three-dimensional (3D). They are bounded by the closed surface of their outer boundary.
If all points of a figure are in the same plane, then it is flat. Flat figures that everyone knows: point, square, rectangle, triangle, circle, semicircle, circle, oval, rhombus, trapezoid.
And if all the points of a geometric figure are not in the same plane, then it is voluminous. These include a ball, cone, cylinder, sphere, pyramid, etc.
Let's analyze flat figures.
Triangle
Triangle is a figure that is formed when three line segments connect three points that do not lie on the same line. These three points are called vertices, and the segments are called sides.
There are three kinds of triangles:
- Rectangular - when one angle is right, the other two are less than 90 degrees.

- Acute - when the degree of its angles is greater than 0 but less than 90 degrees.
- Obtuse - when one angle is obtuse, that is, more than 90 degrees, and the other two are acute.
Triangles have the following properties:
- in a triangle opposite the larger angle lies the larger side and vice versa;
- the sum of the angles of a triangle is always 180 degrees;
- all angles of an equilateral triangle are 60 degrees;
- in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs (but this is already studied in high school).
The vertices of triangles are indicated by capital letters of the Latin alphabet: A, B, C, etc.
Examples of triangles:
from center distance.
Circle
The part of the plane inside the circle is called circle . That is, the circle is the boundary of the circle. And the distance from the center of the circle to any point on it is called the radius. The diameter of a circle is a line segment that connects two points on a circle and passes through its center. The diameter of a circle is equal to two of its radii.
That is, the circle is the boundary of the circle. And the distance from the center of the circle to any point on it is called the radius. The diameter of a circle is a line segment that connects two points on a circle and passes through its center. The diameter of a circle is equal to two of its radii.
Rectangle
Rectangle is a figure consisting of four sides and four right angles, which has:
- opposite sides are equal;
- the diagonals are equal and bisect at the point of intersection;
- around a rectangle it is possible to circumscribe a circle centered at the point of intersection of its diagonals and with a radius equal to half of the diagonals.
Square
Square is the same rectangle with:
- all sides are equal;
- all angles are equal and equal to 90 degrees;
- the diagonals are equal and perpendicular;
- the centers of the inscribed and circumscribed circles coincide and are located at the point of intersection of its diagonals.
Trapezium
A quadrilateral in which two sides are parallel and two are not is called a trapezoid . If the sum of the lengths of the bases of a trapezoid is equal to the sum of the lengths of the sides, then a circle can be inscribed in it.
Parallelogram and rhombus
Parallelogram is a quadrilateral whose opposite sides are pairwise parallel.
Rhombus is a parallelogram with equal sides.
A parallelogram has the following properties:
- opposite sides and angles are equal;
- the sum of any two adjacent angles is equal to 180 degrees;
- the diagonals intersect and the intersection point is bisected;
- each diagonal divides the figure into two equal triangles.
Basic quantities and their formulas
All geometric shapes have their own characteristics and their own value. The most common are such quantities as area and perimeter. They are used in everyday life, in construction and in other areas. For example, during renovation or new construction, the amount of materials needed and the scope of work cannot be determined without calculating the area and perimeter in advance.
The most common are such quantities as area and perimeter. They are used in everyday life, in construction and in other areas. For example, during renovation or new construction, the amount of materials needed and the scope of work cannot be determined without calculating the area and perimeter in advance.
Perimeter
The perimeter is the closed boundary of a flat geometric figure, which separates its inner area from the outer one. Any closed geometric figure has a perimeter:
In the figure, the perimeters are marked with a red line. The perimeter of a circle is often called the length.
The perimeter is measured in units of length: mm, cm, dm, m, km.
Designated by capital Latin P .
Area
Area is the part of the plane occupied by a closed flat geometric figure, that is, that part of the plane that is inside the perimeter. It is she who gives us basic information about its size. Any flat closed geometric figure has a certain area.
In the figure, the areas of the figures are colored in different colors.
To measure the area of a figure means to find how many times another figure is placed in a given figure, taken as a unit of measurement. Area is measured in square units of length. Area units include: mm 2 , cm 2 , m 2 , km 2 , etc. S (square) - a sign of the area.
Perimeter and area calculation
Perimeter is the length of the closed contour of the geometric figure. You can, of course, measure the length of all sides with a ruler and add them. But it is better to use special formulas for calculating the perimeter, this will greatly simplify the task.
- Square: perimeter = 4 * side.
- Triangle: perimeter = side 1 + side 2 + side 3.
- Irregular polygon: perimeter = sum of all polygon sides.
- Circle: circumference = 2 * π * radius = π * diameter (where π is pi (a constant approximately equal to 3.
 14), radius is the length of the line connecting the center of the circle and any point lying on this circle, Diameter is the length of a line segment passing through the center of a circle and connecting any two points on the circle.
14), radius is the length of the line connecting the center of the circle and any point lying on this circle, Diameter is the length of a line segment passing through the center of a circle and connecting any two points on the circle.
To calculate the area of the figure, you will also need the corresponding formula. Different formulas apply to different figures. To calculate the area of standard geometric shapes, you can use the following formulas:
- Parallelogram: area = base * height
- Square: area = side 1 * side 2
- Triangle: area = ½ * base * height radius is the length of the line segment connecting the center of the circle and any point lying on this circle.The square of the radius is the value of the radius multiplied by itself).
So, we have listed the main and most common geometric shapes and their properties. The iSmart educational platform will help your child learn basic geometric shapes, their types, names and properties through fun activities. Benefits of exercising on iSmart smart trainers:
Benefits of exercising on iSmart smart trainers:
- interactive tasks are more like a game;
- they can be practiced many times and will not be repeated;
- the platform will form an individual learning path based on knowledge diagnostics;
- just 20 minutes of lessons a day is enough to see progress in learning in a short time.
In addition, classes will help you free up your time, because the child will be able to study independently, and the parent will receive reports and monitor the dynamics of learning. The iSmart learning method is based on the latest scientific practices: microlearning and behavioral analysis.
The iSmart educational platform offers preparation for tests, tests, VPR, olympiads, as well as the study of additional subjects that are not included in the school curriculum.
Types of quadrilaterals. Geometry square. Geometry rectangle. Parallelogram geometry.
- Alphaschool
- Articles
- Quadrangle types
Different types of quadrilaterals have different properties, which are determined by the different aspect ratio and angles of the quadrilateral. It is entirely possible to have a quadrilateral in which no two sides and no two angles are the same. On the other hand, any two or more sides may be equal in length, and any two or more angles may be the same size. In addition, one or both pairs of opposite sides may be parallel. Many configurations result in shapes with specific names, and at least some of those names are probably familiar to you. Examples of various configurations are shown below, along with a name given to each form and a brief description of its characteristics.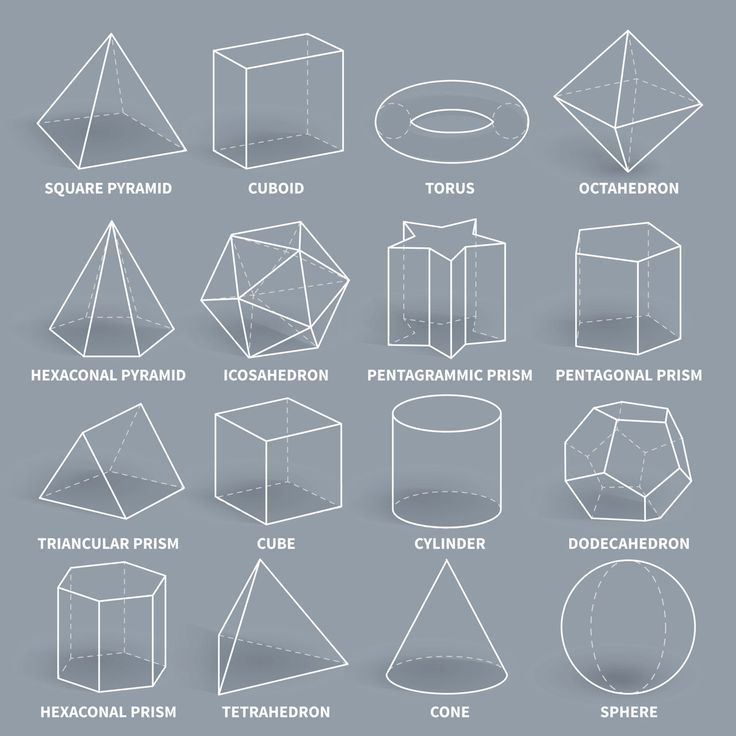
Square is the simplest type of quadrilateral. A square is called equilateral because all four sides are the same length, i.e. a square is a regular polygon and all four interior angles are ninety degrees. The diagonals in a square have the same length, cross each other perpendicularly, that is, intersect at right angles. By definition, a square is also a rectangle, parallelogram and rhombus.
- A square has four equal sides and four right angles.
Rectangle - A quadrilateral where all four interior corners are right angles (i.e. ninety degrees), only opposite sides are of equal length. Adjacent sides can be of different lengths. By definition, a rectangle is also a parallelogram.
- Only opposite sides of the rectangle must be equal
Parallelogram - Both pairs of opposite sides are parallel (hence the name), opposite sides are equal, and opposite angles are equal in magnitude. The diagonals, although of the same length, when the parallelogram is a square or a rectangle, always separate each other. The diagonal divides the parallelogram into two equal triangles. Successive angles are complementary (that is, they are always one hundred and eighty degrees). Note that a parallelogram in which adjacent sides are of different lengths and in which all interior angles are oblique is sometimes called a rhombus (as opposed to a rhombus, which is a parallelogram in which all four sides are the same length).
The diagonals, although of the same length, when the parallelogram is a square or a rectangle, always separate each other. The diagonal divides the parallelogram into two equal triangles. Successive angles are complementary (that is, they are always one hundred and eighty degrees). Note that a parallelogram in which adjacent sides are of different lengths and in which all interior angles are oblique is sometimes called a rhombus (as opposed to a rhombus, which is a parallelogram in which all four sides are the same length).
- The parallelogram shown here is a rhombus
A rhombus-rhombus is an equilateral parallelogram, that is, it has four sides of equal length. Since it is a parallelogram, opposite sides are parallel, opposite angles are of equal magnitude, successive angles are complementary (i.e. they are one hundred and eighty degrees), and diagonals separate each other. The diagonals of the rhombus also cut through the interior angles and are orthodiagonal (i. e., intersect at right angles).
e., intersect at right angles).
- Rhombus-equilateral parallelogram
A trapezoid is a convex quadrilateral in which two sides are parallel and the other two sides are not parallel. The figure below shows three possible options for the trapezoid. The figure on the left shows an isosceles trapezoid in which the angles adjacent to each of the parallel sides are equal. The central figure has one side perpendicular to both parallel sides, so the trapezoid contains two right angles. The last, rightmost, figure has sides of different lengths, and all internal angles are different.
More lessons and assignments in mathematics with the teachers of our online school "Alpha". Sign up for a trial lesson now!
Sign up for a free knowledge test!
By clicking the "Sign up" button I accept the terms of the User Agreement and Privacy Policy
Our teachers
Hmayak Vardanyan
Math tutor
Experience (years)
Education:
Peoples' Friendship University of Russia
Conducted classes:
Form of study:
Remote (Skype)
Maria Valerievna Zagrebina
Math tutor
Experience (years)
Education:
Udmurt State University
Conducted classes:
Form of study:
Remote (Skype)
Alina Vladimirovna Vaulina
Math tutor
Experience (years)
Education:
Ural Federal University B. N. Yeltsin
N. Yeltsin
Conducted classes:
Form of study:
Remote (Skype)
Items
- Maths
- Physics
- Chemistry
- Russian language
- English language
- Social science
- Russian history
- Biology
- Geography
- Informatics
Specializations
- Preparation for the OGE in mathematics
- Preparing for the Unified State Examination in Mathematics (profile level)
- Preparation for the exam in chemistry
- Grammar of Russian language
- Preparation for the exam in English
- English for beginners
- Tutor for preparation for VPR in English
- VPR in physics
- VPR in social studies
- Preparation for the exam in computer science
Similar items
- Arc length formulas
- Surface area of the pyramid
- Distance between points on a coordinate line
- National Research University Higher School of Economics (Computer Security): passing score, reviews, schedule
- MEPhI: Applied Informatics
- RUDN University: Faculty of Ecology and Nature Management
- USE in mathematics, profile level.

Learn more











