Learning counting to 20

What All Teachers Ought To Know

Math tips and strategies for building number sense to 20 in Kindergarten and first grade: An extensive list of number sense activities and resources are included: books, materials, math manipulatives, and FREE activities!

The math tips and strategies you need for building number sense to 20 are right here. You will have everything you need to quickly implement and bring a wealth of number sense activities, games, and centers into your classroom or home.

Building Number Sense to 20

The activities, books, resource suggestions (including a FREE one) cover a ton of number sense concepts and are perfect for Kindergarten and first grade. Plus, find valuable number sense materials and manipulative suggestions, as well as freebies you can access today! Warning: It’s LONG but filled with so much you won’t want to miss anything!

Why is Building Number Sense Important?

Children need opportunities to learn and experience numbers. Learning to count, identify numbers, and understand quantity are a few of the essential concepts. Repeated experiences build understanding and fluency with numbers. These experiences help expand knowledge and learn new ideas. A strong number sense is vital for future understanding of more complex math topics.

The activities below are ones that have been used successfully. Use them as they are described or adapt them to your own needs. Be flexible. Have conversations about numbers and encourage questions. When there is an opportunity to order, count, match, or describe with a child, go for it! They benefit from seeing numbers in natural, fluid ways.

Make time for fun and engaging number activities daily and watch fluency develop.

Number Sense Concepts & Activities

Build Number Sense Through Counting

It is crucial to count with children every day. Repeated oral counting helps them hear what numbers sound like and to learn their order. Using math manipulatives, like counting chips, can help build a connection to verbal counting and counting objects. This one-to-one counting is an important skill that needs to be practiced often.

Activities

• Count out loud as a class starting at one and building to higher and higher numbers.
• Sit with a partner or in a circle and take turns counting by 1’s.
• As counting develops, teach number patterns and counting by 2’s, 5’s, and 10’s.
• Use a number chart to see what numbers look like visually. Point to each number as it is said.
• Encourage kids to practice one-to-one counting with small objects. Have small groups of objects set up in a center for them to count.
• Provide number cards (like those seen below) for kids to represent with counting chips.

Build Number Sense by Matching Numbers to Quantities

Provide materials for kids to count and connect with objects and numbers. This encourages children to see that numbers are more than words. Teach children that numbers have many representations, such as dots, fingers, counters, numerals, objects, ten frames, etc.

Activities

• Match two different types of objects together, such as five counting bears and a domino that shows five dots.
• Use links to create a number chain for a number.
• Work up to showing quantity with more than two types of objects (as seen in the photo).
• Have many different items available for activities, such as dice, dominoes, number magnets, bears, counting chips, cubes, and number cards.

• Match number cards from a card deck or game of Uno with dots on dominoes. Find every number combination on the dominoes.

• Complete number puzzles that have a different number representation on each piece. They help kids see that numbers can be modeled in many ways. These number puzzles to 20 are available as a FREE download further on.

• Encourage one-to-one counting with clip cards. Kids count groups of objects and clip the numeral that matches to the correct quantity.

• Ten frames are great for organizing numbers so that they can be easily counted. Matching numeral cards with ten frame representations is simple, yet effective at connecting quantity with numbers.

Build Number Sense with Number of the Day

When kids see numbers in many ways at once in a repeatedly, their number sense develops. Pick a number of the day starting at one and dissect it during your math block.

Activities

• Learn about a specific number for each day that you have been at school. Teach and dissect that number during calendar time. Represent that number on a number line, count to that number, show that number with straws or cubes, etc.
• Use a number of the day poster or anchor chart to break numbers down. Create your number of the day poster with the FREE poster templates.
• Encourage kids to participate and show their understanding on paper or mini whiteboards. Ask a question, such as “How do we show 5 with tally marks?” and allow them time to try on their own. This makes an excellent fluency building warm-up to math lessons.
• Read more tips on starting a number of the day routine in your classroom.

Build Number Sense by Ordering Numbers

Provide opportunities for kids to put numbers in order. While they put numbers or objects with numbers on them into the correct order, they are counting and building number sense.

Activities

• Provide opportunities with using a number line and number chart that puts numbers in order for us.
• Give sets of numbers to order correctly by finding them on the number line.
• Cover different numbers on a number chart with sticky notes and ask kids for the missing numbers.
• Build Lego stacks by putting the pieces together in an order written on the blocks.

• Work together with a partner to order number cards from 0 to 20. Create a number caterpillar like the one seen below.

• Number puzzles are a fun way to order numbers. Put the strips in the right order to reveal a picture.

• Puzzles are simple and easy to create. Take an old puzzle and write numbers on the back of each piece.
• Grab a piece of paper and write numbers in rows. Cut out pieces randomly and trade with a partner. Put the puzzle back together again for practice.

• Complete a number order maze starting at 0. This activity can be reused when put into a pocket protector.

Build Number Sense with Place Value Activities

Teaching kids about place value should begin with teaching them to see ten in many ways. Move on to illustrating numbers with base ten blocks.

Activities

• Practice making groups of ten things. Group straws, beans, counters, or any small objects.
• Teach counting by 10’s to count groups. Extend to teaching groups first and then singles.
• Make groups of ten to get to the 100th day.
• Show and examine a tens block and ones block. Discuss that a tens block has ten ones put together.
• Use base ten blocks to represent numbers. Do plenty of examples where kids must use and count blocks. Use a chart to help count the blocks.
• Say “Show (or draw) me 14 with place value blocks!”
• Represent the number of tens and ones on place value mats (seen below). Ask questions like “How many ones are there?” or “How many groups of ten?”. Make sure they understand what each number within the number stands for (i.e., the 1 in 18 is a ten and not a one).

• Represent a number in different ways: expanded form, standard form, word form, numeral, etc. Worksheets like the one below, can help build this connection.

Reading and Writing Numerals

Kids are constantly surrounded by numbers in their environment. They quickly learn to recognize the individual numerals 0 to 9 through different experiences. Continue to encourage this familiarity by having numbers on the wall. Posters, number lines, and calendars are helpful tools.

Activities

• Build numbers with playdough in a math center. Even something as simple as this playdough numbers activity here.
• Print numbers from 0 to 9 daily in different ways – in booklets, on whiteboards during math lessons, etc.
• Draw numbers on paper and give students do-a-dot markers or bingo dabbers to dot numbers.

• Use a Boogie Board (seen below) or whiteboard to practice numbers over and over quickly.

• Trace numbers frequently and repeatedly to build coordination and correct form. The mini-book below encourages this, as well as locating numbers.

• Encourage the correct formation of numbers by teaching it explicitly. The posters (seen below) are helpful tools to use and post on the wall.
• Catchy number poems help students visualize and remember number formation. Use your whole body to make actions or draw in the air.

Reading and Writing Number Words

Teach kids how to read number words as they learn to read. Teach each number word one at a time and how to spell them phonetically (when applicable).

Activities

• Have number posters with both the numeral and number word on it.
• Include number words on spelling lists so that kids learn to read and spell number words.
• Use a number of the day routine to teach and focus on one word each day.
• Match numbers word cards with numeral cards (seen below).
• Play memory with a partner with number words and numeral cards. Look for pairs (twelve and 12).

• Build recognizing and speed with mental math flash cards. Flashcards to kids, and they race to call out what they see (tally, numerals, number words, etc.).

Build Number Sense by Counting On and Back

Teach the strategy of counting on and back from a number to prepare kids for addition and subtraction.

Activities

• Give students a number and a group of small objects to count on. Ask, “How many more do I have?” given 7 to start and a group of 9 counters to count on with.
• Play games with small objects and decks of cards where counting on is needed.
• Play a group counting game called ‘Around the World.’ Say a number, and each person counts on and says the next number as you go around the circle.
• Use small objects to count on or back from a number given (cubes, counters, dice, etc.).
• Put numbers in backward order. Take the ordering activities seen above and reverse them.

Build Number Sense through Estimating

Provide lots of opportunities for kids to guess how many things they see in their day to day lives. Ask prompting questions to encourage this thinking. Make sure kids know that they are estimating and that these are just guesses. Stress that estimates do not need to be exact but that they should be thoughtful. With more practice, estimations should become closer to the actual number of objects.

Activities

• Fill clear or open containers with different sized objects for kids to guess. Keep them simple and work up in difficulty and size of objects. Smaller objects and bigger containers are usually harder.
• Create an Estimation Station,” where containers are set up with objects inside. Kids can take a close look and make estimates.

• As a whole group activity, grab a pile of objects to show quickly. Cover them and have kids make guesses.
• Play ‘Show & Hide’ with a partner. Use a cup and put some small counting bears inside. Quickly show a partner, and then hide them. They make an estimate, and then you count together to check.

Build Number Sense by Comparing Numbers

As familiarity with numbers grow, so does an ability to compare numbers with each other. Provide opportunities to compare numbers daily. Ask questions about which number is bigger, smaller, or the same.

Activities

• Use a chart or number line to compare numbers.
• Use small objects to make comparing easier. Say “Show 11 and 15 with cubes”. Ask, “Which number is smaller?”.
• Teach the symbols < > and = and what they each mean. Use the alligator strategy (The alligator likes to eat the bigger number) to remember the signs and what they mean.
• Create number towers. Kids use cubes to form towers to represent numbers. Compare two towers to see which is the tallest and, therefore, the bigger number. The alligator eats the bigger tower.
• Compare numbers with math tools and indicate the correct symbol on clip cards (seen below). As kids become fluent, they should recognize the correct symbol without support.

The activities seen in this post can be found in the following resources found on Teachers Pay Teachers.

Numbers to 5 for Kindergarten

Numbers to 10 for Kindergarten

Numbers 11-20 for Kindergarten

Mindful Math Kindergarten Curriculum

Numbers to 10 for First Grade

Numbers to 20 for First Grade

Mindful Math First Grade Curriculum

Free Number Sense Puzzles to 20

Prep this fun set of number puzzles for your classroom centers and help kids build their number sense!

Grab 20 FREE number puzzles with different representations on each piece by clicking the image below.

Number Sense Books

I Spy Numbers by Jean Marzollo
1,2,3 Peas by Keith Baker
ChickaChicka 1,2,3 by Bill Martin Jr.
Splash! by Ann Jonas (counting)
The Very Hungry Caterpillar by Eric Carle (counting)
How Do Dinosaurs Count to 10? by Jane Yolen
Number Everywhere by Elliot Kaufman
10 Black Dots by Donald Crews
How Many Bugs in a Box? by David Carter
How Many Snails? by Paul Giganti, Jr.
Ten Sly Piranhas by William Wise
None the Number by Oliver Jeffers
Zero the Hero by Joan Holub
More or Less by Stuart Murphy
Tally O’Mally by Stuart Murphy
Place Value by David Adler
What’s the Place Value by Shirley Duke
Quack and Count by Keith Baker
Betcha! by Stuart J. Murphy

Number Sense Materials

Try the Mindful Math Comprehensive Program

Read about the Mindful Math program and how it can change your math block in positive ways! This comprehensive math curriculum is available for Kindergarten, first grade, and second grade.

Learn More about Teaching Number Sense

Building Number Sense free email series

Number of the Day Activities

5 Tips for Building Math Fluency

PIN

FREE Number Sense Email Series

Sign up for the building number sense email series filled with effective strategies, must try activities, and FREE resources to build routines in your classroom. Everything you need to help kids grow their number sense and have fun at the same time!

First Name

Personal Email Address

We use this field to detect spam bots. If you fill this in, you will be marked as a spammer.

I'd like to receive the free email course.

What Children Know and Need to Learn about Counting

Print resource

  Print resource or save as PDF

Print feature not currently compatible with Firefox.

DREME TE

Print resource

  Print resource or save as PDF

Print feature not currently compatible with Firefox.

Children Develop an Everyday Math

Context and overview
Young children, even infants, develop essentially non-verbal basic concepts of quantity: more/less, order, same, and adding/subtracting. Children learn most of these things on their own, without much adult help. Children often use these concepts in everyday life, for example, to determine who has more or less ice cream. Children’s concepts and procedures are useful under certain conditions but need to be enriched. (Perhaps that’s why number was invented: the shepherd needs to know not only that he has a lot of sheep, but exactly how many. ) This is what children know and what they need to learn at roughly ages three, four and five.

More/less
Children need to be able to see that there are more objects here than there. They often solve this problem not by counting but by physical appearance. "This flock of geese in the sky must be larger because it covers a greater area than does the other flock." This approach is often adequate but can lead to wrong answers and confusion.

Order
Judgments of more or less are sufficient for many purposes, but sometimes a comparison between more than two things needs to be made. Thus the idea of order, which includes subtle ideas:

• In a group of three objects, the second item is larger than the one preceding it but smaller than the one following it. 
• Also, the item that was first can become last under a new order.

Again young children tend to rely too much on appearances to solve the problems.

Same number
The idea of same number evolves, even without adult assistance, through several stages:

• The first step is seeing that two groups identical in shape and arrangement are also the same in number.  Thus, if a brown bear and a yellow canary are placed directly below another brown bear and yellow canary, both rows are the same in number (as well as in shape, color, and arrangement). 
• The second step is seeing that two groups differing in color or shape can still be the same in number. Thus, if a brown bear and a yellow canary are placed directly under a pink pig and blue heron, both rows are the same in number (and arrangement, although they differ in shape and color).
• The third step is seeing that two groups differing only in arrangement are the same in number. Thus, if a brown bear and a yellow canary are not placed directly under a pink pig and blue heron but instead lie elsewhere, both groups are the same in number (although they differ in arrangement, shape and color).
• The fourth is seeing that one group, when rearranged, has the same number as it did before it was moved around. Thus, if the child first sees a brown bear and a yellow canary in one arrangement, which is then transformed, the child realizes that the number did not change from what it was before the rearrangement.
• The fifth is first seeing that two amounts are the same number when they look similar, for example five eggs in a row and five egg cups in a row both have the same number. But then if there is a transformation (for example spreading the eggs apart so that the line of eggs is longer than the line of egg cups), the child has to be able to understand that the eggs and egg cups are the same in number even though the two lines look different.

The idea of adding as resulting in more and subtracting in less
Children learn that:

• When you add something to an existing set, the result is that you have more than you had at first.
• If you start with two groups of the same number, and by magic (while the child is not looking), one set is now more numerous than the other, you must have added to one or subtracted from the other
• You don’t have to count to arrive at these judgments concerning more and concerning addition and subtraction: you can solve the problem by reason alone.

Later instruction needs to build on all of these ideas when written numbers are introduced.

Learning the Counting Words

Context and overview
In everyday life, we use counting words all the time, selecting items from the supermarket (“we need two bananas”) or playing “10, nine, eight, … blast off!” Children love counting as high as they can, like grown-ups. They may even be interested in the name of the highest number. Fluency in the counting words aids later computation.

Rote memory plus 
At first, children memorize the counting words from about one to 10 or so. But their learning doesn’t involve only memory. Children learn some ideas and rules about number too, namely that proper order is essential; numbers are different from letters; and you are not supposed to skip or repeat numbers when you count.

Structure
Later, children pick up the underlying structure of number: ten is the basic unit (20, 30, etc.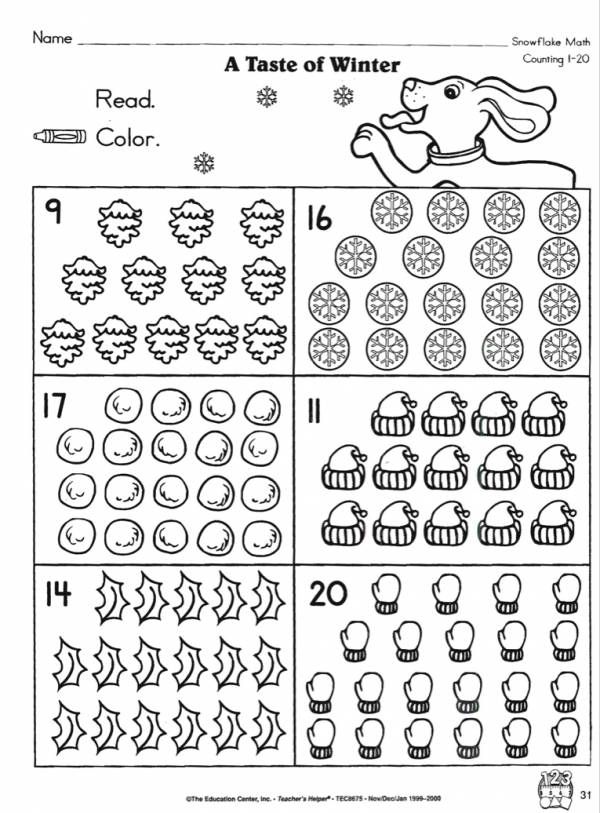 ) and we tack units onto the tens (twenty-one etc.). The rules for saying the English counting words from eleven to nineteen are especially hard to learn because they are poorly designed. Eleven should be "ten-one," just like twenty-one. Fifteen should be "ten-five," like twenty-five. The East Asian languages get this right, but English and many other languages do not. By contrast, English is fairly well designed for the number words beginning with twenty.  Each of the tens words resembles a unit word. Forty is like four; eighty like eight, and so on. Fifty comes before sixty. (A fairly minor problem is that twenty should sound more like two and ideally should be “two-ten;” thirty should be “three-ten” and so on). After saying a tens word, the child appends the unit words, one through nine. Learning to count to 20 and beyond is a child's first experience with base-ten ideas.  In this case, teaching needs to stress the base-ten pattern underlying the counting numbers: the structure. We need to “instructure” (teach the structure) not “instruct.”

Counting Things: How Many Are There?

Context and overview
Children’s ideas about same, more, less, and order are heavily influenced by perception and by their own imperfect logic (for example, that what looks like more is more). These are good ideas but lack precision, so children need help in taking the next step. The counting words that children learn early on can be used for enumeration; in determining the exact number of a collection, it is the cardinal number that tells how many. Accurate enumeration and understanding of cardinal number are fundamental for all arithmetic (and measurement) and are not as simple as they seem. Rather they involve key mathematical ideas and strategic thinking.

Principles needed to understand enumeration
Enumeration refers to using the counting words to figure out the number of objects. (This includes any object, from imaginary monsters to marbles.) Children must learn to follow several rules and principles to enumerate accurately. This set of rules is fundamental:

• Say number words in their proper order.
• Match one number word with only one thing (one-to-one correspondence between number word and thing).
• Count each thing once and only once.

Given these rules and principles, there are several ways to enumerate with accuracy. Children need to be able to:

• "See” small numbers (up to four or so) without counting. This is subitizing, which can reduce the drudgery of counting.
• Count one object at a time.
• Point at objects.
• Push objects aside to keep track of which ones have been counted.
• Put objects in a line or other orderly arrangement.
• Count on the fingers.
• Group objects into convenient groups that can be subitized or counted.
• Group by 10s.  
• Check the answer.

Children need to learn to use these approaches in appropriate situations. For example, if there are only two objects, subitizing may useful, but if there are nine, then pushing objects aside may be indicated. 

Understanding cardinality
Children who enumerate accurately also need to understand the result achieved. Suppose a child accurately counts five things. Correct enumeration alone does not necessarily mean that the child understands cardinality. Asked how many there are, the child may simply count the objects another time. For that child, answering the question of how many simply activates the counting routine but does not provide an understanding of the result. Children need to learn several things about cardinal number. The core idea is that correct enumeration yields the cardinal value of set. The last number word does not refer to the last object counted but to the set as a whole. When we count, the number one refers to the first object; two refers not to the second object counted but to the two objects in the new group, and so on.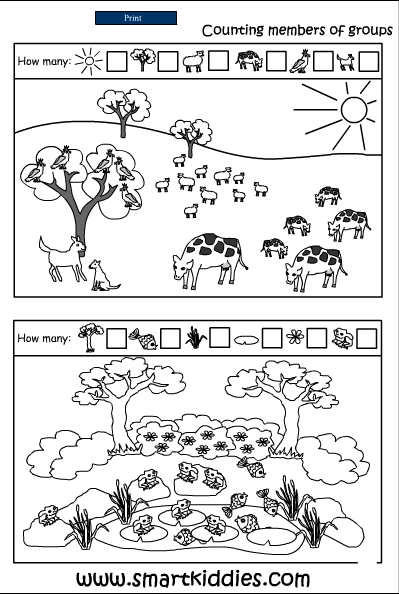  Furthermore, once the child has determined that there are five objects in the set, it does not matter if they are hidden, or if the objects are simply rearranged (say from a straight line to a circle). There are still five objects. This is conservation of number.

Common mistakes or misconceptions
When counting, children often rely too heavily on physical appearance, just as they did in determining more or less. One goal of teaching should be to help children learn that reason must trump appearance. Children need to think abstractly about tangible things. Eventually, they need to embed understanding of cardinal number (for example, the abstract idea that there are five objects here) within the larger system of number, for example, that five comes after four and is half of 10.

Everyday Numerical Addition and Subtraction

Context and overview
Next we need to understand how concepts of more/less, order, same, adding and subtracting without exact number (knowing that adding means making a set larger even if you don't know of the exact number), and enumeration get elaborated to create numerical addition and subtraction.  Children learn some of this on their own, but adults can and should help.

Understanding addition
These concepts need to be learned to understand addition (subtraction is similar):

• Addition can be thought of in several ways, including combining two sets, increasing the size of one set, and jumping forward on a number line.
• Simple counting is also adding, one at a time.
• The order of addition makes no difference (the commutative property).
• Adding zero changes nothing.
• Different combinations of numbers can yield the same sum.
• Addition is the inverse of subtraction.

Strategies used to add (or subtract)
Children often begin by using concrete objects and fingers to add but gradually learn mental calculation and remember some of the sums.

• Using concrete objects, children may do the following to solve a simple problem like 3 + 2: They may count all ("I have three here and two there and now I push them together and count all to get five") or they may count on from the larger ("I can start with three and then say, four, five. ")
• Approaching the problem mentally, children may solve the problem by derived facts, building on what is known ("I know that two and two is four, so I just add one to get five") and by memory ("I just know it!").

More features of numerical addition and subtraction

• It’s always useful to have backup strategies in case one doesn’t work. For example, if unsure about memory, the child can always count to get the answer.
• It’s important for the child to be able to check the answer.
• It’s important for the child to explain why 3 + 2 gives five as the answer, since proof is a social act requiring language.
• The child needs to learn different strategies for different set sizes. (Counting one by one is good for adding small sets but tedious and inefficient for larger sets.)
• The child should also be able to describe how he got the answer. (Self-awareness is one aspect of metacognition. Of course, remembering what you just did is essential for describing it in words. )
• Language is vital for describing one’s work and thinking, and to convince others; children need to learn mathematical vocabulary.
• The child should be able to apply the math in real situations or stories about real situations (such as word problems).

Number Sense

Context and overview
Children need to develop number sense, a concept that is notoriously difficult to define in a simple and exclusive way. I like to think of it as mathematical street smarts, which can be used in just about any area of number, including those discussed above. Number sense, which helps the child to make sense of the world, has several components, each of which undergoes a process of development. 

Thinking instead of calculating
Number sense involves using basic ideas to avoid computational drudgery, as when the child knows that if you add two and three and get five, then you don’t have to calculate to get the answer to three-and-two.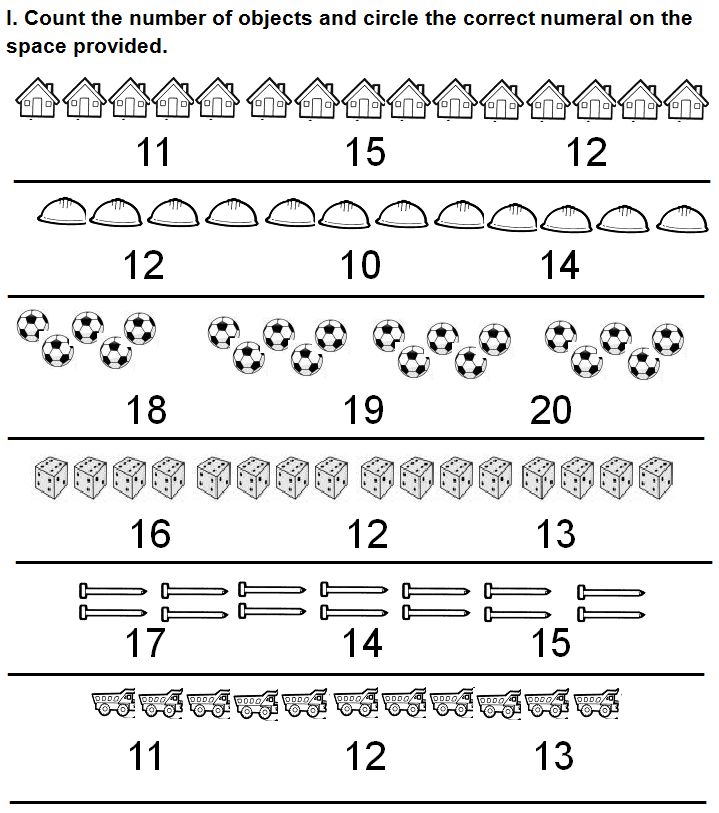  

Use what is convenient
Number sense involves breaking numbers into convenient parts that make calculation easier, as when we mentally add 5 + 5 + 1 instead of 5 + 6. 

Knowing what’s plausible or impossible
Number sense may involve a “feel” for numbers in the sense of knowing whether certain numbers are plausible answers to certain problems (if you are adding two and three you know that the answer must be higher than three; anything lower is not only implausible but impossible).

Understanding relationships
Number sense involves intuitions about relationships among numbers. (For example, "this is 'way bigger' than that.")

Fluency
Number sense involves fluency with numbers, as when the child knows immediately that eight is bigger than four, or sees that there are three animals without having to count.

Estimation
This involves figuring out the approximate number of a group of objects and is related to the notion of plausible answers.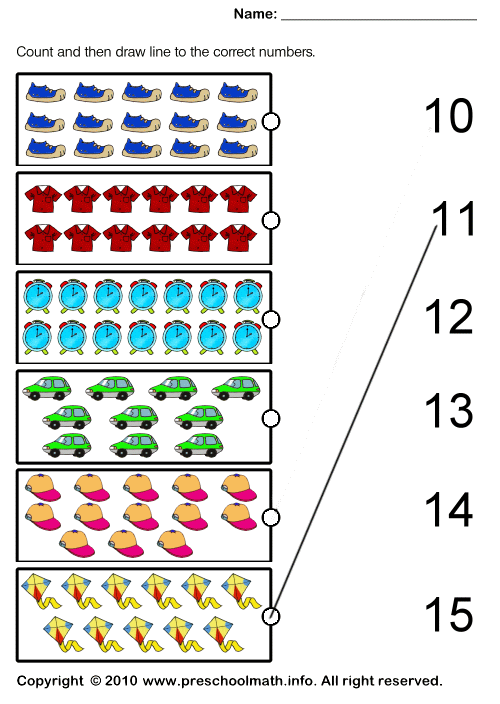

The Transition to Written, Symbolic Math

Context and overview
Formal, symbolic mathematics can provide children with more powerful tools and ideas than those provided through their informal everyday math. Formal math (and its use of symbols) developed in several cultures and is now virtually universal. Children need to learn it.

Everyday origins and formal math
Children encounter math symbols in everyday life: elevator numbers, bus numbers, television channels and street signs are among the many. Often parents, television, and software activities introduce some simple symbolic math, such as reading the written numbers on the television or on playing cards. 

Schools certainly have to teach formal math. But doing so is not easy. Even if they are competent in everyday math, children may have trouble making sense of and connecting their informal knowledge to what is taught in school. Teachers often do not teach symbolism effectively.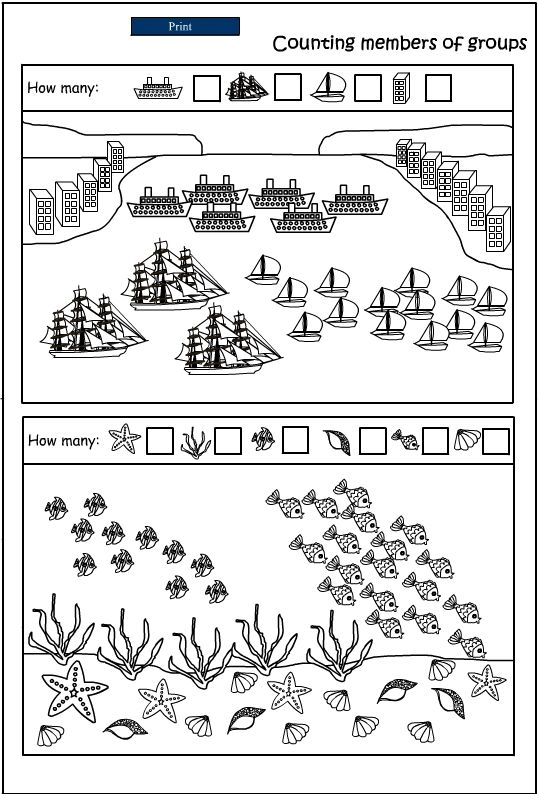  If children get off on the wrong symbolic foot, the result may be a nasty fall down the educational stairs. So the goal for teachers is to help children, even beginning in preschool, to understand why symbols are used, and to use them in a meaningful way to connect already-known informal mathematics to formal symbolic mathematics. The teacher needs to “mathematize” children’s everyday, personal math; that is, help children connect their informal system with the formal mathematics taught in school. It’s not ill-advised or developmentally inappropriate to introduce symbols to young children, if the activity is motivating and meaningful. On the contrary, it is crucial for the teaching of symbols to begin early on, but again, if and only if it is done in a meaningful way.

Here are key issues surrounding the introduction of formal math to young children:

Young children have a hard time connecting numerals and the symbols of arithmetic (+ and -) to their own everyday math 
They may add well but be confounded by the expression 3 + 2.  It is as if the child is living in alternate realities: the everyday world and the “academic” (in the pejorative sense) world. The everyday world makes sense and the world of school does not. You think for yourself in the former and do what you are told in the latter.

The equals sign (=) is a daunting challenge
The teacher intends to teach the equals sign as "equivalent," and thinks she has, but the child learns it as “makes” (e.g., 3 + 2 makes 5). This is a tale of how child egocentrism meets teacher egocentrism but neither talks with the other.

The solution
We should not avoid teaching symbols but need to introduce them in a meaningful way. This means taking account of what children already know and relating the introduction of symbols to that prior knowledge. It also means motivating the use of symbols. Thus if you want to tell a friend how many dolls you have at home, you need to have counted them with number words (symbols) and then use spoken words (“I have five dolls”), written words (“I have five dolls” written on a piece of paper or a computer screen), or written symbols (5) to communicate the result.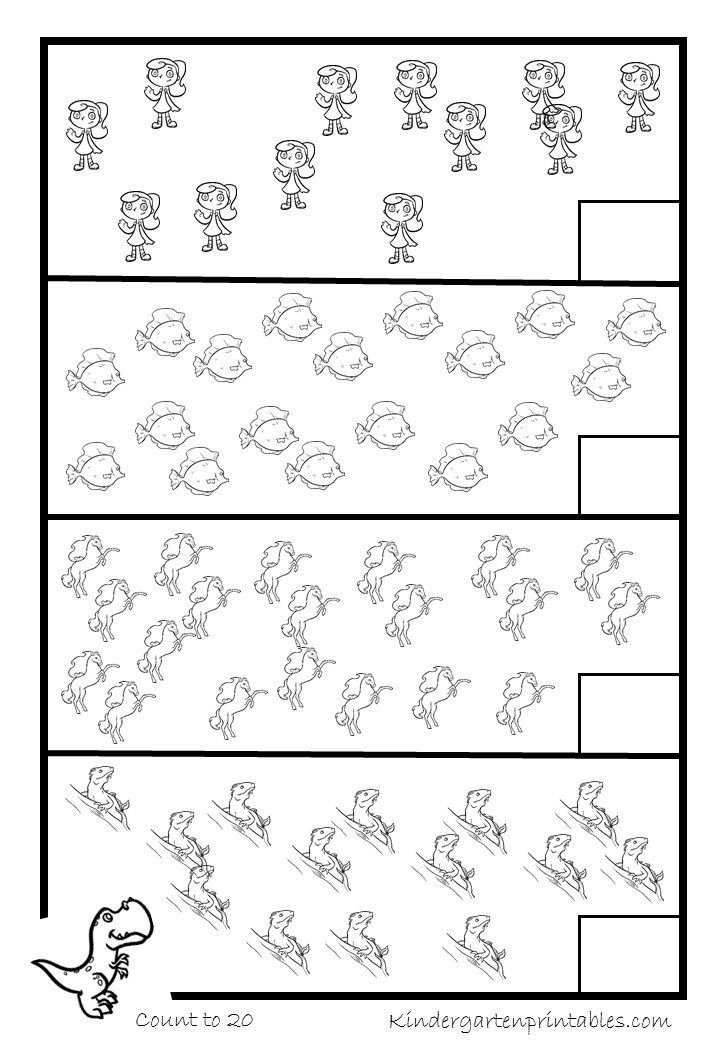

Manipulatives can help
Use of manipulatives can be effective in teaching symbolism and formal math, but they are often utilized badly. The goal is not to have the child play with concrete objects but to use these objects to help the child learn abstract ideas. The goal of manipulatives is to get rid of them by putting them in the child’s head to use as needed in thought. For example, suppose the child learns to represent tens and ones with base-ten blocks. Given the mental addition problem 13 plus 25, the child may understand that each number is composed of 10s (the 10 by 10 squares) and some units (the individual blocks), and that solving the problem involves adding one 10 and two more, which is easy, and then figuring out the number of units. The mental images of the 10s and ones provide the basis for her calculation, part of which may be done by memory (one plus two is three) and part of which may be done by counting on her fingers (five fingers and three more give eight).

Conclusion

The basics of number are interesting and deep. Although young children develop a surprisingly competent everyday mathematics, they have a lot to learn and teachers can help.

Resource Type

Handout

Learning to count up to 20

At the age of 4-5, children are ready to learn counting up to 20. Start with forward counting, gradually moving on to learning backward counting.

Developing online math tasks for children from 2 to 11 years old

Direct quantitative counting

Learn with your child the names of numbers from one to twenty and their spelling. Your child probably already knows how to count to ten. For better memorization of numbers from 11 to 19explain how they are formed: they consist of 10 and one more of the numbers 1, 2, 3,4, 5, 6, 7, 8, 9. Put ten identical objects or counting sticks in a row. This is "twenty" - Old Russian ten. Place one other object or stick of a different color on top. It turned out eleven - "one" to "twenty". Show how the other numbers of the second ten turned out. There are two tens in the number 20.

The next step is to remember the numbers. An excellent simulator for learning numbers is the number line. You can use a regular ruler. Looking at the ruler, the child will not only remember the spelling of numbers and their arrangement in order, but also learn to distinguish: the numbers that are located to the right - more, to the left - less. Encourage such exercises with a ruler. Call the child numbers in random order, let him write down the numbers under your dictation. As an assistant at first, he can use a ruler.

Do simple game exercises:

Name the neighbors. You name a number, the child - neighboring numbers located on both sides of the number line. This exercise not only helps to remember numbers, but also teaches the child to increase and decrease by one.

Quantitative account

Repeat the formation of numbers from eleven to twenty with your child, tell them that numbers up to one hundred are formed in the same way: a number indicating the number of tens + "twenty" and a number indicating the number of units. The only exception is the number "forty", it must be remembered.

Counting skills within the first hundred are well developed by the Connect by Dots exercises. You can also perform simple game exercises with your child:

"Name the neighbors of round numbers." The greatest difficulty for children is the transition to round numbers. This exercise is designed to reinforce this skill. Name a round number, let the child name the neighboring numbers that are on both sides of it on the number line. This exercise also teaches the child to increase and decrease by one.

“We pronounce the numbers one by one”. The essence of the exercise: counting up to one hundred, say the numbers in turn with the child. Explain to him that you need to pronounce the number that comes after the one named. You can connect a few more people to the game to make the game more fun.

In addition to counting straight, practice counting backwards, paying special attention to naming numbers in the forward and backward order with the transition through the round number.

Practice writing numbers. Pay attention to the fact that the child writes and “reads” the number from left to right. Children often make mistakes in recognizing numbers, for example, instead of the number 21 they say 12 . Written numbering, like oral numbering, is associated with the number of digits, remind the child that tens are written first, then units. Pay special attention to writing round numbers, in which 0 is written in place of units (they are not in this number). If you miss this moment, you may encounter the fact that the child will write the number 45 as 405.

"Counting and counting". In every possible situation, enlist the help of the child in counting and counting objects. When counting, the child needs to determine the number of items. Make sure that you count according to the rules: in the process of counting, point to objects in order, touching them with your finger. If you count out of order, you can get confused and miss one or more items. Count everything in a row - steps, steps, toys. When counting, the child needs to count a certain number of items, for example, bring 7 pencils or 2 sweets.

"Forbidden number". An adult calls a number up to 10, a child shows it on his fingers. Before that, a number is selected that is forbidden to be shown. When an adult calls this number, the child simply clap his hands. The game consolidates the understanding of the relationship between the name of the number and the quantity that it denotes.

Countdown

After your child has learned counting up to 20, you can start learning backward counting up to 20. Do this in stages - first from 5, then from 10, and only then from 20. To practice skills countdown do exercises:

"How much is left." Going down the stairs, count together with the child how many steps are left, seeing the approaching bus, count the seconds before the doors open, count the seconds before the green traffic light.

Walking games. Play board games with two dice. During the game, the child will need to calculate how many steps he will need to make a move, as well as “walk”, forward or backward.

"Count in range". The adult names the tasks for the child, and the child completes them. For example, count up to 9 to 5, from 17 to 11. The exercise teaches the child to vary numbers, count in a certain range, trains attention.

Do these simple exercises throughout the day, at home or on your way home, and your child will be great at counting from 1 to 20 and back!

Educational online math exercises for children from 2 to 11 years old

Learning to count to 20 - Math tasks in pictures

• Home
• Learning to count to 20

Addition and subtraction tables up to 20 are used to teach a child the skill of finding the sum or difference of two numbers, help to quickly get the result without actually performing arithmetic operations. They can be used as assistants in calculations for grade 1 students and not only in math lessons to solve examples. You can download and print our tables for free at the bottom of the page.

Published in Mathematics for children 4, 5, 6, 7 years old - print and study

What is the composition of a number? And how can we help children develop understanding? When a child understands the composition of a number, he understands that numbers are made up of other numbers. They "see numbers inside" other numbers: first, the child sees that all numbers are made up of ones, and then that they can be made up of pairs of large numbers. So, for example, 5 consists of "five ones", or of "1 and 4", or of "2 and 3". In this article, we have prepared for you tables, number houses and simulators for teaching preschoolers and grade 1 students the composition of numbers up to 20, which you can print for free.

Published in Mathematics for children 4, 5, 6, 7 years old - print and practice

Learning to count up to 20 with the help of a simulator to consolidate the composition of the number up to twenty. The task is suitable for children of elementary grades (6-7 years old). In tasks, the child will have to solve examples for addition and subtraction, writing down the answers in the tables provided. This is a good training for children who are learning math counting. According to the example given, you can independently come up with similar tasks for classes with your children.

Published in Mathematics for children 4, 5, 6, 7 years old - print and practice

In this task, we learn to count up to 20 by connecting even and odd numbers from 1 to 20. These are exercises that will be a good tool when teaching a kid math. In these tasks, the child will have to, connecting even or odd numbers, draw a path for cartoon characters, while repeating not only counting to 20, but also learning the concept of even and odd numbers.

Published in Math for children 4, 5, 6, 7 years old - print and study

The task for children "Count. Underwater World" is a great opportunity to test not only the knowledge of the child, but also his attention. Ask the kid what other inhabitants, besides those shown in the picture, he knows, what underwater plants he knows, share your knowledge with him. Mathematical problems will be interesting for children from 3 years old.

Published in Mathematics for children 4, 5, 6, 7 years old - print and practice

Fun Jobs "Learning to count to 20 - For little fidgets" it will be much easier for a child to decide under your strict guidance. Read the task to the child, and if he can already read on his own, check whether he correctly understood the proposed condition of the problem. If the child is very young and still does not know how to count, ask him only to find objects, and at the same time count aloud yourself. Such activities well develop the attention of the child and his memory.

Published in Math for children 4, 5, 6, 7 years old - print and study

Fun tasks for children "Counting to 20" will be of interest to children aged 5-7 who have consolidated their knowledge of counting up to 10 and are learning to count up to 20.

Learn more

• 
  Skills preschoolers need to learn
• 
  Rhymes with stories
• 
  Rhymes and stories for kids
• 
  Children english short stories
• 
  Beginning sound activities kindergarten
• 
  At sounds words
• 
  Five little ducks went out one day
• 
  Alphabet a story
• 
  Child paper games
• 
  Syllables in our
• 
  Thanksgiving place cards