Everyday math kindergarten
Everyday Mathematics
Kindergarten Lesson Lists
Common Core State Standards (CCSS) Edition Lesson List
Expand All | Collapse All
Ongoing Daily Routines
| Lesson | |
|---|---|
| 1 | Number of the Day |
| 2 | Attendance Routine |
| 3 | Job Chart Routing |
| 4 | Monthly Calendar Routine |
| 5 | Daily Schedule Routine |
| 6 | Weather Observation Routine |
| 7 | Recording Daily Temperature Routine |
| 8 | Survey Routine |
Unit 1: Section 1: Opener
| Lesson | |
|---|---|
| 1-1 | Partner Match |
| 1-2 | Introduction to Pattern Blocks |
| 1-3 | Multisensory Counts |
| 1-4 | Countdown to Zero |
| 1-5 | Getting to Know Numbers (1-9) |
| 1-6 | Introduction to Sorting |
| 1-7 | Sand and Water Play |
| 1-8 | Birthday Graphs |
| 1-9 | Sound and Motion Patterns |
| 1-10 | Patterns with Color |
| 1-11 | Coin Comparisons |
| 1-12 | Give the Next Number Game |
| 1-13 | Body Height Comparisons |
| 1-14 | Finger Count Fun |
| 1-15 | Shape Puzzles |
| 1-16 | Ten Frames |
| 1-P1 | Numbers in Our World |
Unit 2: Section 2
| Lesson | |
|---|---|
| 2-1 | Shape Collages |
| 2-2 | Shapes by Feel |
| 2-3 | Which Way Do I Go? |
| 2-4 | Spin a Number Game |
| 2-5 | Patterns All Around |
| 2-6 | Playful Oral Counting Games |
| 2-7 | Preparation for Number Writing |
| 2-8 | Matching Coin Game |
| 2-9 | Number Board |
| 2-10 | Tricky Teens |
| 2-11 | Listen and Do (10-19) |
| 2-12 | Teen Partners |
| 2-13 | Estimation Jars |
| 2-14 | Number Stories: Stage 1 |
| 2-15 | Symmetry Painting |
| 2-16 | Symmetry in Nature |
| 2-P2 | Mathematics and Our Bodies |
Unit 3: Section 3
| Lesson | |
|---|---|
| 3-1 | Number Books |
| 3-2 | Macaroni Necklaces |
| 3-3 | Roll and Record |
| 3-4 | The Pan Balance |
| 3-5 | Domino Concentration Game |
| 3-6 | Monster Squeeze Game |
| 3-7 | Measurement with Objects |
| 3-8 | Pocket Problems |
| 3-9 | Number Card Games |
| 3-10 | Probability Stories |
| 3-11 | Probability Tray |
| 3-12 | Pan Balance 2: Leveling |
| 3-13 | Train Games |
| 3-14 | Favorite Colors Graph |
| 3-15 | Count by 10s |
| 3-16 | Teen Frame Game |
| 3-P3 | Fun with Games |
Unit 4: Section 4
| Lesson | |
|---|---|
| 4-1 | Number Line Mathematics |
| 4-2 | Top-It Card Games |
| 4-3 | The Pattern-Block Template |
| 4-4 | The Addition Symbol (+) |
| 4-5 | Follow My Pattern |
| 4-6 | Interrupted Counts |
| 4-7 | Meet the Calculator |
| 4-8 | Roll and Record with Two Dice |
| 4-9 | Body and Rope Shapes |
| 4-10 | Shape Comparisons |
| 4-11 | The Subtraction Symbol (-) |
| 4-12 | Slate Activities |
| 4-13 | Introduction to Attribute Blocks |
| 4-14 | "What's My Rule?" Fishing Game |
| 4-15 | Number Stories, Stage 2 |
| 4-16 | Two-Digit Numbers |
| 4-P4 | Class Celebration |
Unit 5: Section 5
| Lesson | |
|---|---|
| 5-1 | Order of Daily Events |
| 5-2 | Patterns with Craft Sticks |
| 5-3 | Find The Block Game |
| 5-4 | Guess My Number Game |
| 5-5 | Count with Calculators |
| 5-6 | Measurement with Children's Feet |
| 5-7 | How Big Is a Foot? |
| 5-8 | Count by 5s |
| 5-9 | Introduction of Tally Marks |
| 5-10 | The Raft Game |
| 5-11 | Standard and Nonstandard Feet |
| 5-12 | Tools for Measuring Length |
| 5-13 | Pet Bar Graph |
| 5-14 | Attribute Spinner Game |
| 5-15 | Introduction to the Number Grid |
| 5-16 | Number-Grid Search Game |
| 5-P5 | Project 5: The 100th Day of School |
Unit 6: Section 6
| Lesson | |
|---|---|
| 6-1 | Introduction of the Penny |
| 6-2 | Introduction of the Nickel |
| 6-3 | Solid Shape Museum |
| 6-4 | Counts to Measure Time |
| 6-5 | Surveys and Graphs |
| 6-6 | I Spy with Shapes |
| 6-7 | Introduction of the Dime |
| 6-8 | Coin Exchanges |
| 6-9 | Comparison Number Stories |
| 6-10 | Count by 2s |
| 6-11 | Divide Groups in Half |
| 6-12 | Read My Mind Game |
| 6-13 | Tools for Measuring Time |
| 6-14 | Skip Count with Calculators |
| 6-15 | Symbolic Representations of Patterns |
| 6-16 | Division of Whole Objects into Halves |
| 6-P6 | Project 6: Maps and Mapping |
Unit 7: Section 7
| Lesson | |
|---|---|
| 7-1 | Money Cube Game |
| 7-2 | Class Collections |
| 7-3 | Class Number Story Book |
| 7-4 | Marshmallow and Toothpick Shapes |
| 7-5 | Introduction of the Quarter |
| 7-6 | Dice Addition and Subtraction Games |
| 7-7 | Late-in-the-Year Counting |
| 7-8 | 10s and 1s with Craft Sticks |
| 7-9 | Name Collections with Craft Sticks |
| 7-10 | Number Scrolls |
| 7-11 | Decade Count |
| 7-12 | Plus or Minus Game |
| 7-13 | Double Digits with Dice |
| 7-14 | Numbers in Sequence |
| 7-15 | "What's My Rule?" with Patterns |
| 7-16 | Bead String Name Collections |
| 7-P7 | Project 7: Weaving |
Unit 8: Section 8
| Lesson | |
|---|---|
| 8-1 | Ones, Tens, Hundreds Game |
| 8-2 | How Long Is an Hour? |
| 8-3 | The Hour-Hand Clock |
| 8-4 | High Roller Game |
| 8-5 | Introduction to Function Machines |
| 8-6 | Number Gymnastics Game |
| 8-7 | Introduction of the $1 Bill |
| 8-8 | One-Dollar Game |
| 8-9 | Name Collection Posters |
| 8-10 | "What's My Rule?" with Numbers |
| 8-11 | Hour-Hand, Minute-Hand Story |
| 8-12 | Time Match Game |
| 8-13 | Missing Number Problems |
| 8-14 | Number Stories with Calculators |
| 8-15 | Pan Balance with Uniform Weights |
| 8-16 | Introduction of the $10 Bill |
| 8-P8 | Project 8: Math Outdoors |
3rd Edition Lesson List
Expand All | Collapse All
Unit 1: Section 1
| Lesson | |
|---|---|
| 1-1 | Partner Match |
| 1-2 | Introduction to Pattern Blocks |
| 1-3 | Multisensory Counts |
| 1-4 | Countdown to Zero |
| 1-5 | Getting to Know Numbers (1-9) |
| 1-6 | Introduction to Sorting |
| 1-7 | Sand and Water Play |
| 1-8 | Birthday Graphs |
| 1-9 | Sound and Motion Patterns |
| 1-10 | Patterns with Color |
| 1-11 | Coin Comparisons |
| 1-12 | Give the Next Number Game |
| 1-13 | Body Height Comparisons |
| 1-14 | Finger Count Fun |
| 1-P1 | Numbers in Our World |
Unit 2: Section 2
| Lesson | |
|---|---|
| 2-1 | Shape Collages |
| 2-2 | Shapes by Feel |
| 2-3 | Which Way Do I Go? |
| 2-4 | Spin a Number Game |
| 2-5 | Patterns All Around |
| 2-6 | Playful Oral Counting Games |
| 2-7 | Preparation for Number Writing |
| 2-8 | Matching Coin Game |
| 2-9 | Number Board |
| 2-10 | Tricky Teens |
| 2-11 | Listen and Do (10-19) |
| 2-12 | Teen Partners |
| 2-13 | Estimation Jars |
| 2-14 | Number Stories: Stage 1 |
| 2-15 | Symmetry Painting |
| 2-16 | Symmetry in Nature |
| 2-P2 | Mathematics and Our Bodies |
Unit 3: Section 3
| Lesson | |
|---|---|
| 3-1 | Number Books |
| 3-2 | Macaroni Necklaces |
| 3-3 | Roll and Record |
| 3-4 | The Pan Balance |
| 3-5 | Domino Concentration Game |
| 3-6 | Monster Squeeze Game |
| 3-7 | Measurement with Objects |
| 3-8 | Pocket Problems |
| 3-9 | Number Card Games |
| 3-10 | Probability Stories |
| 3-11 | Probability Tray |
| 3-12 | Pan Balance 2: leveling |
| 3-13 | Train Games |
| 3-14 | Favorite colors Graph |
| 3-15 | Count by 10's |
| 3-16 | Teen Frame Game |
| 3-P3 | Fun with Games |
Unit 4: Section 4
| Lesson | |
|---|---|
| 4-1 | Number Line mathematics |
| 4-2 | Top-It Card Games |
| 4-3 | The Pattern-Block Template |
| 4-4 | The Addition Symbol (+) |
| 4-5 | Follow My Pattern |
| 4-6 | Interrupted Counts |
| 4-7 | Meet the Calculator |
| 4-8 | Roll and Record with Two Dice |
| 4-9 | Body and Rope Shapes |
| 4-10 | Shape Comparisons |
| 4-11 | The Subtraction Symbol (-) |
| 4-12 | Slate Activities |
| 4-13 | Introduction to Attribute Blocks |
| 4-14 | "What's My Rule?" Fishing Game |
| 4-15 | Number Stories: Stage 2 |
| 4-16 | Two-Digit Numbers |
| 4-P4 | Class Celebration |
Unit 5: Section 5
| Lesson | |
|---|---|
| 5-1 | Order of Daily Events |
| 5-2 | Patterns with Craft Sticks |
| 5-3 | Find the Block Game |
| 5-4 | Guess My Number Game |
| 5-5 | Count with Calculators |
| 5-6 | Measurement with Children's Feet |
| 5-7 | How Big is a Foot? |
| 5-8 | Count by 5's |
| 5-9 | Introduction of Tally Marks |
| 5-10 | The Raft Game |
| 5-11 | Standard and Nonstandard Feet |
| 5-12 | Tools for Measuring length |
| 5-13 | Pet Bar Graph |
| 5-14 | Attribute Spinner Game |
| 5-15 | Introduction to the Number Grid |
| 5-16 | Number-Grid Search Game |
| 5-P5 | The 100th Day of School |
Unit 6: Section 6
| Lesson | |
|---|---|
| 6-1 | Introduction of the Penny |
| 6-2 | Introduction of the Nickel |
| 6-3 | Solid Shape Museum |
| 6-4 | Counts to Measure Time |
| 6-5 | Surveys and Graphs |
| 6-6 | I Spy with Shapes |
| 6-7 | Introduction of the Dime |
| 6-8 | Coin Exchanges |
| 6-9 | Comparison Number Stories |
| 6-10 | Count by 2's |
| 6-11 | Divide Groups in Half |
| 6-12 | Read My Mind Game |
| 6-13 | Tools for Measuring Time |
| 6-14 | Skip Count with Calculators |
| 6-15 | Symbolic Representations of Patterns |
| 6-16 | Division of Whole Objects into Halves |
| 6-P6 | Maps and Mapping |
Unit 7: Section 7
| Lesson | |
|---|---|
| 7-1 | Money Cube Game |
| 7-2 | Class Connections |
| 7-3 | Class Number Story Book |
| 7-4 | Marshmallow and Toothpick Shapes |
| 7-5 | Introduction of the Quarter |
| 7-6 | Dice Addition Games |
| 7-7 | Late-in-the-Year Counting |
| 7-8 | 10's and 1's with Craft Sticks |
| 7-9 | Name Collections with Craft Sticks |
| 7-10 | Number Scrolls |
| 7-11 | Decade Count |
| 7-12 | Plus or Minus Game |
| 7-13 | Double Digits with Dice |
| 7-14 | Numbers in Sequence |
| 7-15 | "What's My Rule?" with Patterns |
| 7-16 | Bead String Name Collection |
| 7-P7 | Weaving |
Unit 8: Section 8
| Lesson | |
|---|---|
| 8-1 | Ones, Tens, Hundreds Game |
| 8-2 | How Long Is an Hour? |
| 8-3 | The Hour-Hand Clock |
| 8-4 | High Roller Game |
| 8-5 | Introduction to Function Machines |
| 8-6 | Number Gymnastics Game |
| 8-7 | Introduction of the $1 Bill |
| 8-8 | One-Dollar Game |
| 8-9 | Name Collection Posters |
| 8-10 | "What's My Rule?" with Numbers |
| 8-11 | Hour-Hand, Minute-Hand Story |
| 8-12 | Time Match Game |
| 8-13 | Missing Number Problems |
| 8-14 | Number Stories with Calculators |
| 8-15 | Pan Balance with Uniform Weights |
| 8-16 | Introduction of the $10 Bill |
| 8-P8 | Math Outdoors |
Related Links
Advice from Teachers
See advice from Everyday Mathematics teachers on working with parents, using technology in the classroom, pacing, and more.
Professional Development
The UChicago STEM Education offers strategic planning services for schools that want to strengthen their Pre-K–6 mathematics programs.
On the Publisher's Site
McGraw-Hill Education's website features supplemental materials, games, assessment and planning tools, technical support, and more.
Explore Reports
Downloadable Resources
2015-2016
Everyday Math 4
Downloadable Resources
Showing:
- Overview Overview
- Kindergarten Kindergarten
- 1st Grade 1st Grade
- 2nd Grade 2nd Grade
- 3rd Grade 3rd Grade
- 4th Grade 4th Grade
- 5th Grade 5th Grade
- 6th Grade 6th Grade
- Showing:
- Overview
- K
- 1
- 2
- 3
- 4
- 5
- 6
Report Overview
Summary of Alignment & Usability: Everyday Math 4 | Math
Math K-2
Math 3-5
Math 6-8
Report for {{ report.
 grade.shortname }}
grade.shortname }}Overall Summary
Gateway {{ gateway.number }}
Viewing:
- Gateway {{ gateway.number }} Gateway {{ gateway.number }}
Indicator {{ indicator.name | indicatorName }}
Narrative Evidence Only
Viewing:
- Gateway {{ gateway.number }} Gateway {{ gateway.number }}
"Entertaining mathematics in kindergarten"
Entertaining mathematics in kindergarten.
Currently, taking into account the introduction of federal state educational standard for preschool education targets have changed at the stage of completion of preschool education. Who should be our graduate? First of all, having mastered the basic cultural methods of activity, showing initiative and independence in different activities - play, communication, cognitive research activities, design, etc., which has formed prerequisites for educational activity. Therefore, before us, teachers, it becomes relevant search for such forms and methods of working with children that will help a preschooler become successful, first in kindergarten, then at school.
The main task of the educator is to arouse interest in knowledge, and interest gradually develops the skills of mastering knowledge, then this the process turns into a need for systematic mental activity.
At preschool age, the foundations of knowledge are laid, necessary for the child at school. Mathematics is a complex science which can cause certain difficulties during schooling. To In addition, not all children have inclinations and have a mathematical warehouse mind, therefore, when preparing for school, it is important to form the foundations for the child mathematical representations.
To In addition, not all children have inclinations and have a mathematical warehouse mind, therefore, when preparing for school, it is important to form the foundations for the child mathematical representations.
Mathematical development of preschoolers means qualitative changes in the cognitive activity of the child, which occur as a result of the formation of elementary mathematical representations and related logical operations.
Teaching children mathematics in senior preschool age contributes to the formation and improvement intellectual abilities: the logic of thought, reasoning and action, flexibility of the thought process, ingenuity and ingenuity, development creative thinking.
Precision and rigor of mathematics as a science should in no way result in the dryness of its presentation to children. That's why it is necessary to widely use the game form of learning, which contributes to development of children's interest in mathematics, more emotional perception stingy mathematical laws and qualitative assimilation of these laws.
To increase the level of mathematical development, activity of children, to develop their interest in mathematics, you need to use entertaining material: puzzles, mazes, didactic games, sheets with tasks for self-fulfillment, hand-made manuals for individual lessons with children.
Logic games of mathematical content educate the child has a cognitive interest, the ability to creative search, desire and the ability to learn. Entertaining math problems contribute to the child's the ability to quickly perceive cognitive tasks and find the right ones for them solutions. The child begins to understand that for the correct solution of the logical tasks need to be focused.
Smart tasks, puzzles, entertaining games are of great interest to the child. Children can, without being distracted, for a long time exercise in the transformation of figures, shifting sticks or other objects along model, according to his own design. In such classes, important qualities are formed personality of the child: independence, observation, resourcefulness, ingenuity, perseverance is developed.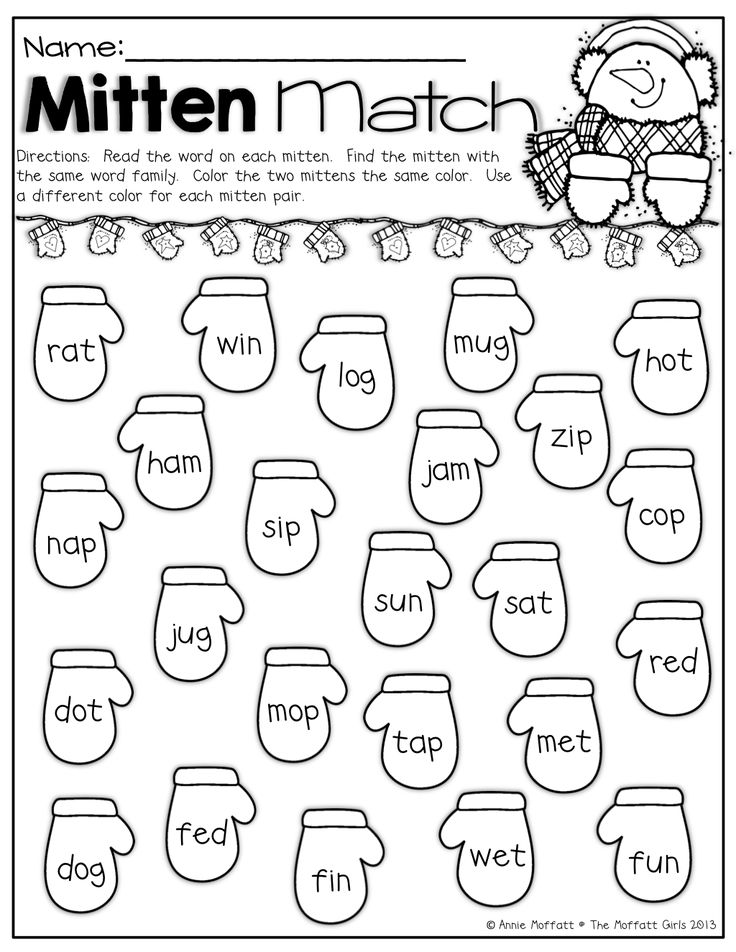
A special place for the developing environment of kindergarten groups be assigned to the center of entertaining mathematics - this is specially allotted, thematically equipped with games, manuals and materials, and a certain artistically designed place. You can organize it using the usual items of children's furniture: a table, a wardrobe, a secretary, providing free access of children to the materials located there. To these same children they are given the opportunity to choose the game they are interested in, a manual of mathematical content and play individually or together with other children, a small subgroup.
The Center for Entertaining Mathematics is not only the possibility of providing children with materials for creativity and opportunities to act with them at any moment, but also the atmosphere in the team. She is is woven from a sense of external security when the child knows that his manifestations will not receive a negative assessment of adults, and feelings of inner looseness and freedom due to the support of adults for his creative endeavors.
Tasks "Center for Entertaining Mathematics" :
elementary mathematical activity. Development of qualities and properties personality of the child, necessary for the successful mastery of mathematics in further: purposefulness and expediency of search actions, desire to achieve a positive result, perseverance and resourcefulness, independence.
2. Teaching children the need to occupy their own free time is not only entertaining, but also requiring mental tension, intellectual effort games. entertaining math material in the preschool and subsequent years should become a means organization of useful leisure, to promote the development of creativity.
The creation of the center is preceded by the selection of game material, which is determined by the age capabilities and level of development of children groups. A variety of entertaining material is placed in the center, so that so that each of the children could choose a game for themselves. These are board games. games for the development of logical thinking, leading children to the development of checkers and chess, puzzle (stick and mechanical) ; logical tasks and cubes, labyrinths; games to compose a whole from parts, to recreate silhouette figures from special sets of figures; movement games.
games for the development of logical thinking, leading children to the development of checkers and chess, puzzle (stick and mechanical) ; logical tasks and cubes, labyrinths; games to compose a whole from parts, to recreate silhouette figures from special sets of figures; movement games.
When organizing a center for entertaining mathematics, one must proceed from the principles of the availability of games for children at the moment, put in the corner such games and game materials, the development of which by children is possible on different level. From the assimilation of the given rules and game actions, they move on to inventing new games.
To encourage team play, creative activities of preschoolers, it is necessary to use magnetic boards, flannelographs with a set of figures, counting sticks, sketchbooks tasks invented by them, composed figures.
During the year as children master games their types should be diversified, more complex games should be introduced with a new entertaining material.
In the game, the child acquires new knowledge, skills, skills. In didactic games, it is possible to form new knowledge, introduce children to ways of doing things. Their main purpose is to exercise children in distinguishing, highlighting, naming sets of objects, numbers, geometric shapes, directions, etc. Each of the games solves a specific the task of improving mathematical (quantitative, spatial, temporary) representations of children.
Mathematical games are games in which mathematical constructions, relationships, regularities. To find an answer (solutions like as a rule, a preliminary analysis of the conditions, rules, content of the game or tasks. In the course of the solution, the use of mathematical methods and inferences or the like.
Preparatory group children looking for or by a combination of mental and practical trials, or only mentally. All this gives grounds for asserting the possibility of involving preschoolers in in the course of solving entertaining tasks to the elements of creative activity. At children are formed the ability to search for solutions through assumptions, to implement samples of different nature, guess.
At children are formed the ability to search for solutions through assumptions, to implement samples of different nature, guess.
Availability of relevant material in the group allows not only to stimulate the initially inherent in preschoolers curiosity, but also to develop their cognitive interests further.
So, to objects for research in real action experts refer to a wide range of materials, from specially developed to natural and cultural:
• Material for sensory development (puzzles, mosaics, pyramids, lacing, etc.)
• Natural objects (collections of minerals, seeds, playing with sand and water, etc.)
• Cultural objects (magnifying glass, scales, thermometer and etc.)
To implement the principle of visibility during FEMP specially created manuals are used (figurative and symbolic materials) :
• Sets of pictures with images (geometric shapes, household items, animals, plants, etc.)
• Cut-out pictures, folding cubes, puzzles
• Paired pictures for comparison
• Stories in pictures
• Variety of toys (3D and flat figurines of animals, sets of dummies of vegetables, fruits, etc. )
)
images in the form of diagrams, drawings, maps, globes, etc.
• Collection material (collection stamps, coins, etc.)
and numerical characters: a set of numbers and letters, alphabetic tables.
There are a number of proprietary techniques that are successfully are used in the construction of work by teachers of preschool educational institutions.
- Gyenes blocks
The main purpose of using didactic material: teach how to solve logical problems on partitioning by properties; familiarize children with geometric shapes and shape of objects, size; assimilation elementary skills of algorithmic culture of thinking; development of cognitive processes of perception of memory, attention, imagination; development of creative abilities.
- Kuizener sticks
Allows modeling of numbers, properties, relationships, dependencies between them using color and length. Purpose of use sticks Kuizener : development of the ability to group objects by color and size; mastering the methods of measurement using a conditional measure; development of quantitative ideas, the ability to distinguish between quantitative and ordinal count, establish equality and inequality of two groups of objects; development of the ability to distinguish and name in the process of modeling geometric figures, silhouettes, objects and others.
- Educational games by Voskobovich
Educational games are relevant for children from two years and older. The game can start with elementary manipulation elements and end with the solution of complex multi-level tasks.
Voskobovich's games also take into account the interests of the child. Children in the course of an exciting game process make new discoveries and get emotional satisfaction from their tasks. Majority educational games are accompanied by special teaching aids with illustrated fairy tales in which you need to complete interesting tasks or answer questions.
Geocont
Construction game Geocont presented in the form of a plywood board with carnations, which are located on it in a certain sequences. The game comes with a set of colored rubber bands and an illustrated a manual containing creative tasks of various levels of complexity. Children are not they just do tasks, but travel with baby Geo, help him with constructing multi-colored geometric shapes to overcome various obstacles in the Purple Forest. The manual describes the schemes of drawings, which in the result should be obtained in children.
The manual describes the schemes of drawings, which in the result should be obtained in children.
Voskobovich Square
This game is also called Maple Leaf , Eternal Origami , Klondike , Transformer Square and etc. "Voskobovich Square" consists of 32 multi-colored triangles glued on a flexible fabric base and located on a certain distance from each other. "Voskobovich Square" possible easy to transform, creating a variety of voluminous and flat figures : airplane, candy, crow house, etc. These figures can be collected according to proposed schemes or come up with your own images.
- Games according to the Nikitin method
Nikitin's educational games are aimed at development logical and figurative thinking. They are presented in the form of puzzles, aimed at recognition and completion of images.
The main difference between Nikitin's games is that, when playing in them, the child acts as an active side and he is brought up not the ability to perform work according to the proposed template, and develops a logical and figurative thinking, creativity, the ability to recognize and build an image, the ability to independence.
“Fold the pattern”
Consists of 16 wooden cubes (rib size 3 cm, where each face has its own color. Cubes must be in box. First, look at the cubes together with the child, name the color of the side cubes, fold a solid track, and then make it colored. Promotes the development of spatial imagination, attention, ability analyze and combine.
Unicube
Consists of 27 wooden cubes. Bring the child into the world three-dimensional space. The game teaches to be attentive and accurate.
Mathematical entertainment refers to : puzzles, rebuses, labyrinths, spatial transformation games, etc. They are interesting in content, entertaining in form, different unusual solution, paradoxical result.
For example : puzzles can be arithmetic (guessing numbers), geometric (paper cutting, wire bending), alphabetic (anagrams, crosswords, charades) . There are puzzles designed only for the game of fantasy and imagination.
Of the variety of puzzles, the most acceptable at senior preschool age, puzzles with sticks. They are called tasks of ingenuity of a geometric nature, since in the course of solving, both as a rule, there is a transfiguration, the transformation of some figures into others, and not only change in their number.
At preschool age, the most simple puzzles. To organize work with children, you must have sets of ordinary counting sticks for compiling visually presented puzzle tasks. In addition, tables with graphically depicted on them with figures that are subject to transformation. On the back of the tables it is indicated which transformation should be done and which figure should get as a result. From solving puzzle problems with the help of a teacher (on based on partial prompts, use of leading questions, confirmation partial solution), children move on to fully independent rapid problem solving.
Riddles, joke problems and entertaining questions meet children with extraordinary enthusiasm. They are capable activate the mental activity of the child, develop the skills to notice main and essential properties, separating them from secondary ones.
They are capable activate the mental activity of the child, develop the skills to notice main and essential properties, separating them from secondary ones.
Joking tasks are entertaining game tasks with mathematical meaning. To solve them, you need to show more resourcefulness, ingenuity, understanding of humor than knowledge in mathematics. The structure, content, question in these problems are unusual. They are only indirectly reminiscent of a math problem. The essence of the task, i.e. the main, thanks to which one can guess the solution, give an answer, masked by external secondary conditions.
Children are very active in perceiving joke tasks, puzzles, logical exercises. They are persistently looking for a solution that leads to a result. In the event that an entertaining task is available child, he develops a positive emotional attitude towards her, which stimulates mental activity. The child is interested in the final goal : fold, find the right shape, transform, which captivates him.
Joking tasks can create a favorable emotional background, cheer up.
Mathematical riddles are intricate questions or descriptions of some subject, phenomena that the child must guess. Since riddles are mathematical, then they will definitely contain numbers, it will be necessary to produce computing actions.
In riddles of mathematical content an object is analyzed from a quantitative, spatial, temporal point view, the simplest mathematical relations are noticed.
A special place among mathematical entertainment occupy games for compiling planar images of objects, animals, birds, houses, ships from special sets of geometric shapes. The sets of figures are not chosen arbitrarily, but are parts of a figure cut in a certain way: a square, a rectangle, a circle or oval. They are interesting for children and adults. Children are fascinated by the result - compose seen on the sample or conceived. They are included in the active practical the activity of selecting the method of arranging the figures in order to create a silhouette.
Tangram Game, Columbus Egg , Magic circle , Mongolian game , Vietnam game , Pentamimo and other
To successfully prepare children for schooling not only certain knowledge is required, but also the ability to consistently and think logically, guess, mentally strain.
And precisely the tasks of ingenuity, puzzles, logic games teach children to plan their actions, think about them, look for an answer, guess the result, while showing creativity.
Such work activates mental activity child, develops in him the qualities necessary for professional skill, no matter what area he then worked.
During games and exercises with entertaining Mathematical material children master the ability to search for solutions on one's own. The educator equips children only with a scheme and direction analysis of an entertaining problem, leading to the final result decision (correct or erroneous) . systematic exercise in solving problems in this way develops mental activity, independence thoughts, creative attitude to the educational task, the initiative of children.
A child should not draw on his knowledge of mathematics not only from kindergarten math classes, but also from my daily life, from observations of the phenomena of the world around him. Here in the first place the child's parents come out. The help of parents who wish to contribute is invaluable. their contribution to the development and upbringing of their own child. Joint Search problem solving helps organize learning for children and adults that does not only contributes to a better assimilation of mathematics, but also enriches the spiritual world child, establishes connections between elders and younger, necessary for them in further to solve life's problems.
Parents should be reminded that compulsory education useless and even harmful. Tasks must begin with Suggestions: "Shall we play?"
Task discussion should start when the child is not very excited and is not busy with any interesting business: after all, he they offer to play, and the game is voluntary!
Practice with using entertaining material develops in children the ability perceive cognitive problems, find new ways of solving them.
Children begin to realize that in each of entertaining tasks concluded some trick. Find her without concentration and reflection is impossible.
Mathematical games help to educate children's cognitive interest, the ability to research and creative search, desire and ability to learn. Entertaining tasks, games, puzzles contribute to the formation and development such personality traits as purposefulness, perseverance, independence. Performing practical actions using entertaining material develops in children the ability to perceive cognitive tasks, to find new solutions for them.
Entertaining mathematical material is a good means of educating children already at preschool age of interest in mathematics, logic and evidence of reasoning, the desire to show mental tension, to concentrate attention to the problem.
Thus, didactic games and game exercises of mathematical content - the most famous and frequently used in modern practice of preschool education, types of entertaining mathematical material. In the process of teaching preschoolers mathematics, the game directly is included in the OOD, being a means of generating new knowledge, expanding, clarification, consolidation of educational material. Didactic games justify themselves in solving problems of individual work with children, and are also carried out with all children or with a subgroup in their free time.
In the process of teaching preschoolers mathematics, the game directly is included in the OOD, being a means of generating new knowledge, expanding, clarification, consolidation of educational material. Didactic games justify themselves in solving problems of individual work with children, and are also carried out with all children or with a subgroup in their free time.
As children learn ways to solve logical tasks to find the missing figure and tasks to find features the main difference in the teaching methodology is the direction of the teacher task analysis. Children are told only a general method for finding solutions through visual and mental comparison. Analysis and decision process problem is closely intertwined with the proof of the solution.
Methodically selected material (riddles, joke tasks, entertaining questions) promotes the development of logical thinking, observation, resourcefulness, speed of reaction, interest in mathematical knowledge, formation of search approaches to solving any problem.
"Methods and techniques for the formation of elementary mathematical representations among preschoolers" - JV "Kindergarten No. 2, secondary school No. 30, Syzran"
Message on the topic:
elementary mathematical concepts in preschoolers”
Mathematical knowledge of a preschooler is a directly important basis in the mental development of a child. Thanks to mathematical knowledge, children learn to: analyze, compare, synthesize, perform computational operations, think logically, distinguish between geometric shapes, name their features, navigate in space. Preschool children develop memory, attention, thinking. The knowledge gained in kindergarten, children apply in everyday life. Therefore, the task of the teacher: to arouse children's interest in educational activities, to give the necessary elementary mathematical knowledge, to lead children to independent answers, search for solutions. The teacher must find an approach to each child and give this knowledge to all children.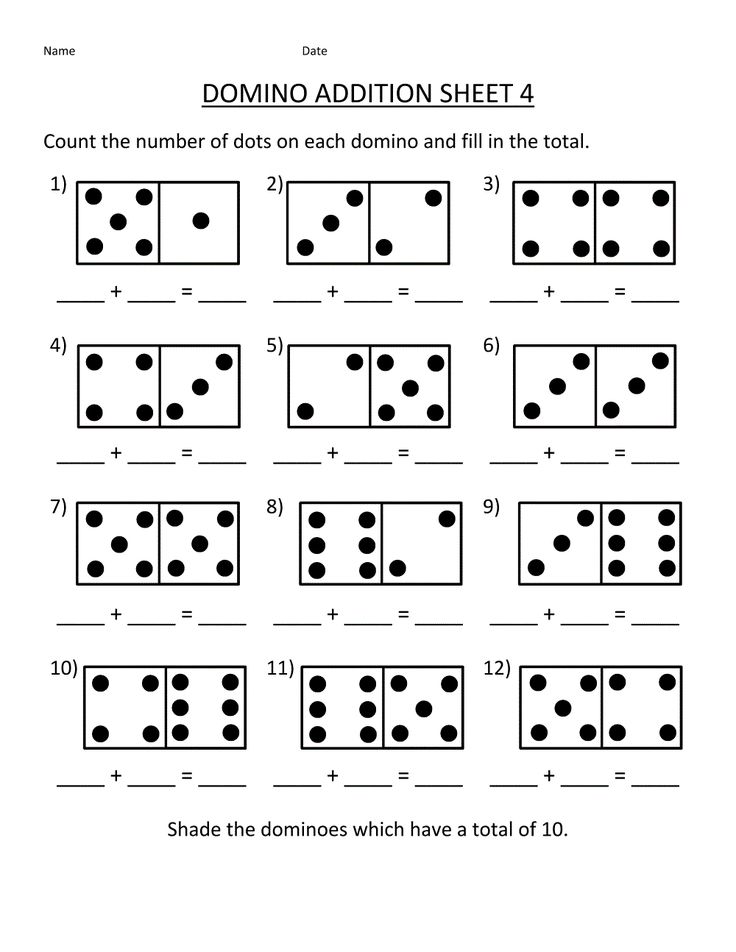
Methods and techniques for the formation of mathematical representations in preschoolers.
In the process of forming elementary mathematical concepts in preschool children, the teacher uses a variety of teaching methods:
- practical,
- visual,
- verbal,
- gaming.
When choosing a method, a number of factors are taken into account:
program tasks to be solved at this stage;
age and individual characteristics of children;
availability of the necessary teaching aids, etc.;
The teacher's constant attention to a reasonable choice of methods and techniques, their rational use in each specific case ensures:
— successful formation of elementary mathematical concepts and their reflection in speech;
- the ability to perceive and highlight the relationship of equality and inequality (by number, size, shape), sequential dependence (decrease or increase in size, number), identify quantity, shape, size as a common feature of the analyzed objects, determine relationships and dependencies;
- orientation of children to the application of mastered methods of practical actions (for example, comparison by comparison, counting, measurement) in new conditions and an independent search for practical ways to identify, detect signs, properties, and connections that are significant in a given situation. For example, in the conditions of the game, to identify the sequence, the pattern of alternation of features, the commonality of properties.
For example, in the conditions of the game, to identify the sequence, the pattern of alternation of features, the commonality of properties.
In the formation of elementary mathematical representations, the leading method is a practical method.
Its essence lies in the organization of children's practical activities aimed at mastering strictly defined methods of action with objects or their substitutes (images, graphic drawings, models, etc.).
Characteristic features of the practical method in the formation of elementary mathematical concepts:
— performance of various practical actions;
— wide use of didactic material;
- the emergence of ideas as a result of practical actions with didactic material:
- development of counting skills, measurement and calculation in the most elementary form;
- wide use of formed ideas and mastered actions in everyday life, play, work, i.e. in various types of activity.
This method involves the organization of special exercises that can be offered in the form of a task, organized as actions with demonstration material, or proceed in the form of independent work with handout didactic material.
Exercises can be collective - they are performed by all children at the same time, and individual - they are carried out by an individual child at the teacher's board or table. Collective exercises, in addition to mastering and consolidating knowledge, can be used for control.
Individual, performing the same functions, also serve as a model for which children are guided in collective activities.
Game elements are included in the exercises in all age groups: in the younger ones - in the form of a surprise moment, imitation movements, a fairy-tale character, etc.; in seniors, they acquire the character of a search, a competition.
From the point of view of children's manifestation of activity, independence, creativity in the process of performance, reproductive (imitative) and productive exercises can be distinguished.
The game as a method of teaching and the formation of elementary mathematical representations involves the use in the classroom of individual elements of different types of games (plot, mobile, etc.), game techniques (surprise moment, competition, search, etc. Currently a system of so-called learning games has been developed.0005
All didactic games on the formation of elementary mathematical representations are divided into several groups:
- Games with numbers and numbers
- Time travel games
- Orientation games in space
- Games with geometric shapes
- Logic games
Visual and verbal methods in the formation of "elementary" mathematical representations are not independent, they accompany practical and game methods.
Techniques for the formation of mathematical representations.
Kindergarten widely uses methods related to visual, verbal and practical methods and applied in close unity with each other: This is the main method of teaching, it has a visual-practical-effective nature, is performed using a variety of didactic means, makes it possible to form skills and abilities in children. It has the following requirements:
It has the following requirements:
- clarity, dissection of the display of methods of action;
- coordination of actions with verbal explanations;
- accuracy, brevity and expressiveness of speech accompanying the show:
- activation of perception, thinking and speech of children.
- Manual for self-exercises. This technique is connected with showing the educator methods of action and follows from it. The instruction reflects what and how to do in order to get the desired result. In the older groups, the instruction is given in full before the start of the task, in the younger ones it precedes each new action.
- Explanations, explanations, instructions. These verbal devices are used by the educator when demonstrating a method of action or in the course of performing a task by children in order to prevent errors, overcome difficulties, etc. They should be specific, short and figurative.

Demonstration is appropriate in all age groups when getting acquainted with new actions (application, measurement), but it requires activation of mental activity, excluding direct imitation. During the development of a new action, the formation of the ability to count, measure, it is desirable to avoid repeated display.
Mastering the action and improving it is carried out under the influence of verbal techniques: explanations, instructions, questions. At the same time, the speech expression of the mode of action is being mastered.
- Questions for children.
Questions activate the perception, memory, thinking, speech of children, provide comprehension and assimilation of the material. When forming elementary mathematical representations, a series of questions is most significant: from simpler ones aimed at describing specific features, properties of an object, the results of practical actions, i.e., ascertaining, to more complex ones that require establishing connections, relationships, dependencies, their justification and explanation, use the simplest proofs.
Most often, such questions are asked after the educator demonstrates the sample or the children complete the exercises. For example, after the children have divided the paper rectangle into two equal parts, the teacher asks: “What did you do? What are these parts called? Why can each of these two parts be called a half? What shape are the parts? How to prove that the squares are obtained? What should be done to divide the rectangle into four equal parts?
Basic requirements for questions as a methodological device:
- accuracy, concreteness, conciseness:
- logical sequence;
— variety of formulations, i.e. the same question should be asked in different ways
— optimal ratio of reproductive and productive questions depending on the age of the children and the studied material;
- give children time to think;
- the number of questions should be small, but sufficient to achieve the didactic goal;
- prompting questions should be avoided.
The teacher usually asks the whole group a question, and the called child answers it. In some cases, choral responses are possible, especially in younger groups. Children need to be given the opportunity to think about the answer.
Children's answers should be:
- short or complete, depending on the nature of the question;
- independent, conscious;
- accurate, clear, loud enough;
- grammatically correct (observance of the order of words, the rules for their agreement, the use of special terminology).
In working with preschoolers, an adult often has to resort to the method of reformulating the answer, giving it the correct sample and offering to repeat it. For example: “There are four mushrooms on the shelf,” says the baby. “There are four mushrooms on the shelf,” the teacher clarifies.
- During the formation of elementary mathematical concepts in preschoolers comparison, analysis, synthesis, generalization are not only
as cognitive processes (operations), but also as methodological techniques that determine the path along which the child's thought moves in the process of learning.
Comparison is based on establishing similarities and differences between objects. Children compare objects by quantity, shape, size, spatial arrangement, time intervals by duration, etc.
Analysis and synthesis as methodological devices act in unity. An example of their use is the formation in children of ideas about "many" and "one", which arise under the influence of observation and practical actions with objects.
- Modeling is a visual-practical technique that includes the creation of models and their use in order to form elementary mathematical concepts in children. The reception is extremely promising due to the following factors:
- the use of models and modeling puts the child in an active position, stimulates his cognitive activity;
- the preschooler has some psychological prerequisites for the introduction of individual models and elements of modeling: the development of visual-effective and visual-figurative thinking.
Models can play different roles: some reproduce external connections, help the child to see those that he does not notice on his own, others reproduce sought-after but hidden connections, not directly perceived properties of things.
Models are widely used in the formation of time representations
- : model of parts of the day, week, year, calendar;
- quantitative; numerical ladder, numerical figure, etc.), spatial: (models of geometric shapes), etc.
- when forming elementary mathematical representations, subject, subject-schematic, graphic models are used.
- Experimentation is a method of mental education that provides the child with self-identification through trial and error of connections and dependencies hidden from direct observation. For example, experimentation in measurement (size, measurement, volume).
- Monitoring and evaluation .
These techniques are interrelated.