First grade math equations

Check Out These 50 First-Grade Math Word Problems of the Day

Opening your daily math lesson with a Math Word Problem of the Day is an excellent way to set the stage for learning. We all know that word problems are difficult for young learners to grasp, even when the mathematical operation portion of the problem is basic.

Incorporate these first grade math word problems one day at a time at the start of your math block to build confidence, critical thinking skills, and a learning community. Students will get used to reading slowly for meaning, while also identifying key information. Encourage students to write out equations and draw pictures to explain their thinking, since this helps them see the light when they are stuck!

ADVERTISEMENT

Topics covered include addition, subtraction, multiplication, and comparison. All you need to do is post one of these first grade math word problems on your whiteboard or projector screen. Then let kids take it from there!

Want this entire set of word problems in one easy document? Get your free PowerPoint bundle by submitting your email here.

1. I had 6 pencils, and my teacher gave me 4 more. How many pencils do I have now?

2. Gina’s dog got 3 treats on Sunday and 0 treats on Monday. How many treats did Gina’s puppy get in all?

3. Joel went to the zoo with his family. During the first hour he was there he saw a bear, 2 tigers, and 3 lions. How many animals did Joel see in his first hour at the zoo?

4. Jackson sorted his toy cars by color. He has 6 blue cars, 5 green cars, and 4 black cars. How many cars does Jackson have in all?

5. Ben has 2 green balloons and 4 yellow balloons. How many balloons does he have altogether?

6. There are 3 kids in the Clark family. Tina is 3, Joshua is 4, and Samantha is 7. If you add up all their ages, what is the sum of the Clark kids?

7. If you go for a swim and 6 of your friends come along, how many friends are swimming in total?

8. Rachel’s mom had some flowers in a vase. 3 of the flowers wilted and Rachel’s mom took them out of the vase. Now there are 5 flowers in the vase. How many flowers were in the vase to start with?

9. Hayden’s cat had a litter of kittens. 3 kittens were gray, 2 kittens were spotted, and 7 kittens were black. How many kittens did Hayden’s cat have?

10. Pedro brought in 3 red leaves and 6 yellow leaves from the playground. How many leaves does he have in all?

11. Gabriella read 3 books on Monday, 6 books on Tuesday, and 4 books on Wednesday. How many books did Gabriella read in all?

12. If you have 3 cats, 2 guinea pigs, and a bunny. How many cute little noses do they have altogether?

13. If there are 3 inches of snow on the ground in the morning and we get 3 more inches of snow by dinner time. How many inches of snow did we get that day?

14. My cat has 4 paws and my brother’s dog has 4 paws. How many paws are there in all?

15. I had 10 pennies, but I lost 2 of them. How many pennies do I have now?

16. Santiago read 7 books over the summer. Ryan read 5 books. How many more books did Santiago read than Ryan?

17. Andrew put 10 stickers on his notebook. When he got to school he noticed some of the stickers had fallen off. Now Andrew only has 6 stickers on his notebook. How many stickers fell off Andrew’s notebook?

18. Nicole likes to help her mom pick tomatoes from their garden. She counted 9 tomatoes in the garden. 6 tomatoes were red and the rest were green. Nicole and her mom picked all the red tomatoes. How many green tomatoes did Nicole and her mom leave in the garden?

19. My sister and I have 20 pennies. If my sister has 10 pennies, how many pennies do I have?

20. The zoo had 8 tigers. 3 of the tigers moved to another zoo. How many tigers were left?

21. Esther read 3 poems. Magenna read some more poems. Altogether they read 7 poems. How many poems did Magenna read?

22. Haley’s dad bought 8 cheeseburgers. Haley ate 1 of them. How many cheeseburgers does Haley’s dad have left?

23. If you boil 7 eggs in water, and the number of eggs that float is one more than the number that sink, how many eggs float?

24. Rasheed loves to eat jellybeans. His favorite jellybeans are the yellow ones. There were 12 jellybeans in his bag. Rasheed removed all the yellow jellybeans and ate them, leaving 6 jellybeans in his bag. How many yellow jellybeans did Rasheed eat?

25. The gym teacher had 5 basketballs. The next week the gym teacher got some new basketballs. Now the gym teacher has 9 basketballs. How many new basketballs did the gym teacher get?

26. Jamal has 6 toy airplanes and his brother has 4 toy airplanes. How many more toy airplanes does Jamal have than his brother?

27. Antonio has some marbles. His brother Alex gives him 5 more. Now Antonio has 8 marbles. How many marbles did Antonio have to begin with?

28. If you have an 8-pack of crayons and you give your friend 3 of them to use during drawing time. How many crayons do you have in your pack now?

29. Emily has 4 pink erasers and some white erasers. She has 7 erasers in all. How many white erasers does Emily have?

30. Angel serves pizza at her birthday party. The pizza has 12 slices. 8 slices of pizza are eaten by Angel and her guests. How many slices of pizza are left?

31. If you have 9 toys on the floor and your little brother has 6 toys on the floor. How many more toys on the floor do you have?

32. There are 8 windows in the classroom. Some of the windows have decorations on them, 2 of them don’t have any directions. How many windows have decorations?

33. On Saturday, you brought home some fish from the pet store. If 15 of your 18 fish have stripes. How many of your fish are without strips?

34. 8 birds flew to the top of a fence. Some birds flew away and 6 birds stayed. How many birds flew away?

35. There were 6 books on Noah’s shelf. Olivia took some of the books. Now there are 2 books on the shelf. How many books did Olivia take?

36. Ethan has some folders in his backpack and 4 folders in his desk. He has 8 folders altogether. How many folders are in his backpack?

37. Liam has 8 t-shirts. 5 of them have superheroes on them, and the rest are solid colors. How many of Liam’s t-shirts are solid colors?

38. Mary was putting together a 20 piece puzzle. After she finished, she discovered that only 18 pieces were there. How many pieces were missing?

39. Nicholas has 7 cousins. Some of his cousins are girls and 3 of his cousins are boys. How many girl cousins does Nicholas have?

40. It snowed for 6 hours on Monday and 4 hours on Tuesday. How many more hours did it snow on Monday?

41. Charlie’s mom baked 12 chocolate chip cookies for dessert. Charlie ate 2 cookies and his mom and 1 cookie. How many chocolate cookies were left?

42. Melanie has 16 purple pens. Dante has 10 blue pens. Melanie has ____ more pens than Dante has.

43. Sofia has 75 pennies in her bank. How many more pennies will she need to have 100 pennies in her bank?

44. There were 9 cups of soda on the table. Some of the cups were knocked over, and 6 were still standing. How many cups of soda were knocked over?

45. Griffin has 20 board games. Some were under his bed, and 15 were in his closet. How many board games were under Griffin’s bed?

46. Antonio spotted 3 deer sitting at the top of a hill, but all he could see were their eyes. How many eyes did Antonio see in all?

47. Desmond saw 5 bunnies. He counted all of their ears. How many bunny ears did Desmond count?

48. Katie counted all of her toes, and then she counted all her mom’s toes. How many toes did Katie count altogether?

49. Which weighs more? A 15-pound red fox or a 24-pound wild turkey?

50. Which weighs more: a 150-pound white-tailed deer or a 110-pound kangaroo?

Enjoying these first grade math word problems? Check out our first grade hub for even more resources.

Get a PPT version of these word problems.

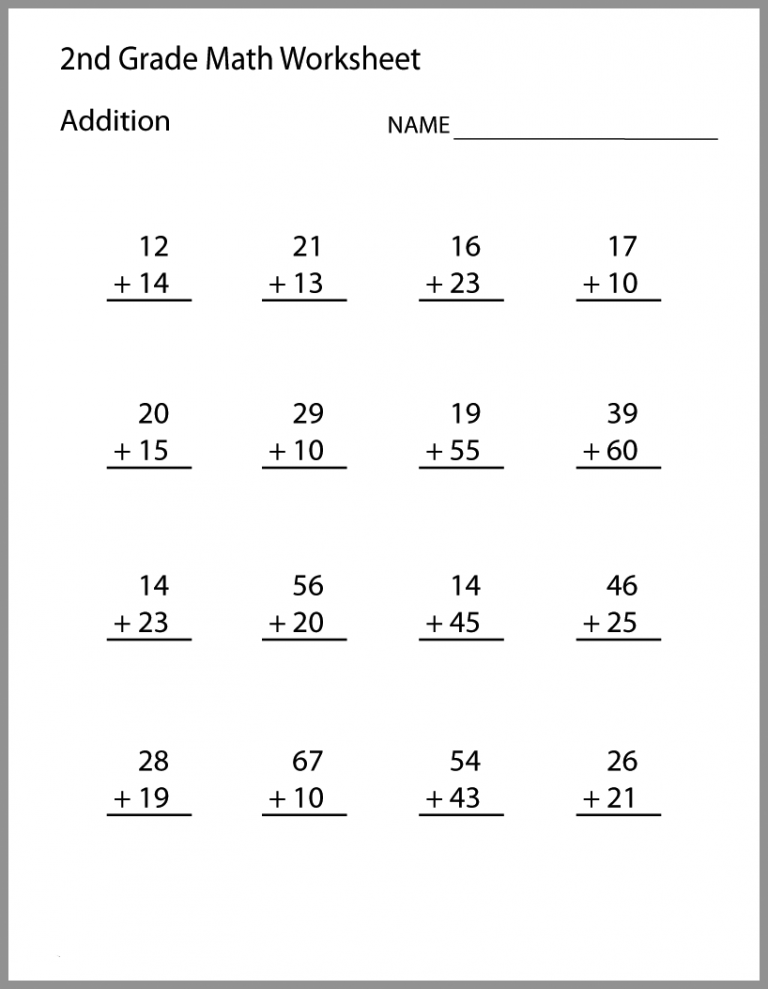
1st Grade Math Worksheets

Rich with scads of practice, the CCSS aligned printable 1st grade math worksheets with answer keys help kids solve addition and subtraction problems within 20, extend their counting sequence, understand place value and number systems, measure length and compare sizes, tell time, count money, represent and interpret data, and know the attributes of 2D and 3D shapes in geometry. Our free math worksheets for grade 1 kids give you a peek into what's in store!

All

Addition

Subtraction

Patterns

Counting

Place Value

Number System

Measurement

Time

Money

Data & Graphs

Geometry

Explore 2,200+ First Grade Math Worksheets

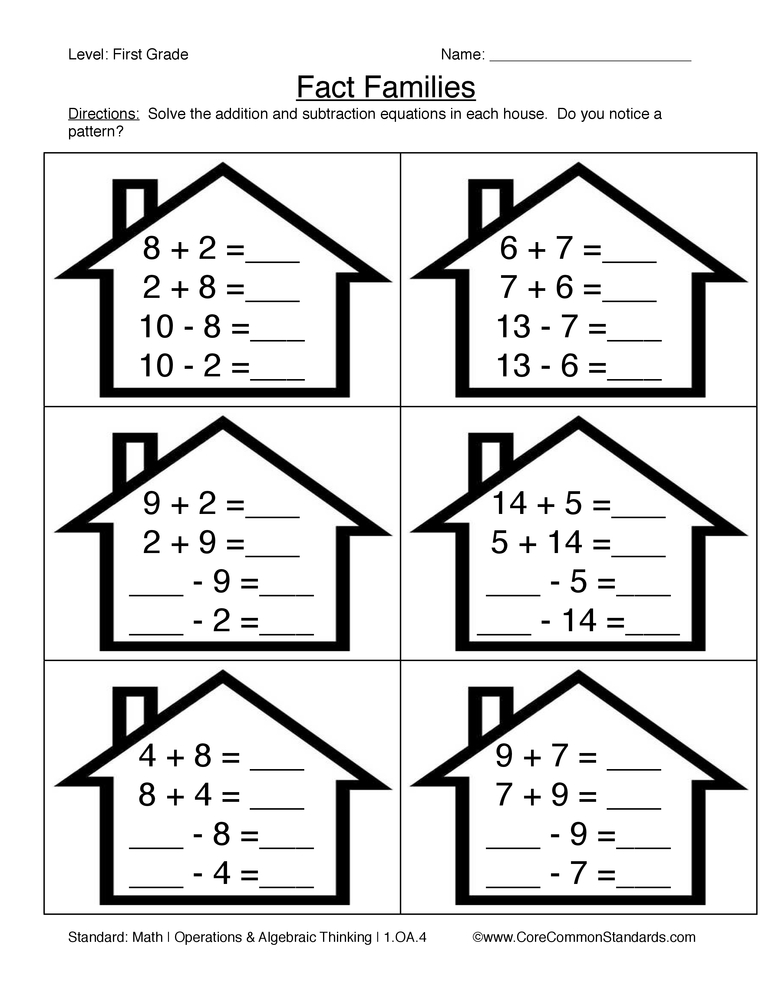
Counting and Adding Pictures

The pictures in two groups present a fascinating array of addition equations for 1st grade kids. Count the pictures in the two groups separately, and then combine the two to find the total number.

Subtracting on Number Lines | 0 to 10

Get the little hoppers to draw hops on the number lines in these printable grade 1 math worksheets and complete the subtraction equations involving numbers up to 10.

Identifying the Next Picture in a Repeating Pattern

Develop pattern awareness in kids with this set of pdf worksheets. Study the pattern, identify the pattern's core or terms that repeat in the same order and make a logical prediction of what comes next.

Reading and Writing Numbers from 1 to 25

Fluency with numbers is vital in first grade math. Task kids to look at the top of this printable chart, identify and read the numbers from 1 to 25 repeatedly, and copy them to complete the table.

Base Ten Blocks | Tens and Ones

Visualizing numbers is easy with place value blocks or base-10 blocks. Get kids to count the units and rods in the base-10 blocks and write the base-10 numerals.

Identifying Greater and Smaller 2-Digit Numbers

Cracking these 1st grade math worksheet pdfs is a true measure of your place value skills. Compare 2-digit numbers using symbols in Part A. Circle the greater number in Part B, and the smaller number in Part C.

Ordering Objects from the Shortest to the Longest

Arranging objects of three different sizes from the shortest to the longest, numbering them 1, 2, and 3 respectively, is all that is expected of grade 1 kids.

Telling Time | Hourly Increment

With these pdf math worksheets for grade 1 kids at your disposal, the time is ripe to practice reading clocks to tell the time in whole hours, and choosing the clock face that depicts the specified time.

Counting Dimes

Develop skills in counting the dimes and expressing the amount in dollars, trading dimes for dollars, and converting between them in word problems with this compilation of first grade math worksheet pdfs.

Counting Tally Marks

Let's travel back in time and practice counting using tally marks. First grade kids have a blast reading and counting each set of tally marks and writing the value it represents.

Identifying 2D Shapes | MCQ

Can the little architects of grade 1 distinguish between a rectangle and a square? Watch them recognize the two-dimensional figures and check the appropriate option that best describes each.

Number Line Addition | 0 to 10

This stack of 1st grade math worksheets has pre-drawn hops on the number lines. The starting-point of the hops, and the number of hops are the two addends and the endpoint is the sum.

Writing Subtraction Equations from Number Lines | 0 to 10

Examine the hops on the number line; identify the minuend, subtrahend, and the difference. Once this is done, completing the subtraction sentence is not a hard nut to crack!

Repeating Patterns | Cut and Glue Activity

Add a spark of fun with repeating picture patterns in this bundle of printable math worksheets for 1st grade kids. Comprehend the pattern, cut out the graphics and glue the one that comes next in order.

Display Chart - Numbers 1 to 25 | Theme based

The crawling number snails get kids to instantly memorize numerals from 1 to 25. This show-and-tell chart comprising snails-shells inscribed with numbers is a compulsive-print.

Next »

"Equation" Grade 1 EMC "School 2100"

Lesson topic: "Equation" Grade 1 EMC "School 2100".

Objectives: Educational: To form an idea about the equation, how to solve the equation (based on the relationship between the part and the whole). To form the ability to solve equations of the form a ± x \u003d b, x - a \u003d b based on the relationship between the part and the whole. Improve the ability to solve problems to find the whole or parts.
Promote development mathematical speech, working memory, voluntary attention, visual and effective thinking.
Cultivate a culture of behavior in frontal work, individual work.
Form UUD:
- Personal: ability to self-assessment based on the criterion of success in educational activities.
- Regulatory UUD: the ability to determine and formulate the goal in the lesson with the help of a teacher; pronounce the sequence of actions in the lesson; work according to a collectively drawn up plan; evaluate the correctness of the action at the level of an adequate retrospective assessment; plan your action in accordance with the task; make the necessary adjustments to the action after its completion, based on its assessment and taking into account the nature of the errors made; express your guess.
- Communicative UUD: the ability to formulate one's thoughts orally; to listen and understand the speech of others; jointly agree on the rules of behavior and communication at school and follow them.
- Cognitive UUD: the ability to navigate in your knowledge system: to distinguish the new from the already known with the help of a teacher; acquire new knowledge: find answers to questions using a textbook, your life experience and information received in the lesson.

Planned result:

Subject: Understand what an “equation” is, “solve an equation”. Know how to solve an equation (based on the relationship between the part and the whole).
Be able to solve equations of the form a ± x = b, x - a = b based on the relationship between the part and the whole. Be able to solve problems to find the whole or parts, read mathematical expressions, inequalities, equalities.

Personal: Be able to conduct self-assessment based on the criterion of success in educational activities.
Meta-subject: Be able to define and formulate the goal in the lesson with the help of a teacher; pronounce the sequence of actions in the lesson; work according to a collective plan; evaluate the correctness of the action at the level of an adequate retrospective assessment; plan your action in accordance with the task; make the necessary adjustments to the action after its completion, based on its assessment and taking into account the nature of the errors made; make a guess ( Regulatory UUD). Be able to formulate their thoughts orally; listen and understand the speech of others; jointly agree on the rules of behavior and communication at school and follow them ( Communicative UUD).
To be able to navigate in one's knowledge system: to distinguish the new from the already known with the help of a teacher; acquire new knowledge: find answers to questions using the textbook, your life experience and the information received in lesson (Cognitive UUD).

Basic concepts : Equation, equation solution, part, whole.

Resources: main , additional: Demidova T.E., Kozlova S.A., Tonkikh A.P. Maths. Textbook for 1st grade. Part 2. Pg. 60 - 61., presentation "Equation"

Organization of space: frontal work, individual work, group work, work in pairs.

PROGRESS OF THE LESSON:

1. Motivation for learning activities. Interview.

- Today is January 22nd. And we are live on the math lesson in the 1st grade, we will try to interview the students of this class before the start of the lesson.

– Is this lesson any different from previous math lessons? How?

– If there are guests at the lesson, do you have to work in some other way?

– What is your goal?

– What do you expect from this lesson?

Are you worried? What about your teacher?

– Do you think the lesson will be successful?

-Why do you study mathematics?

- Is the math lesson very important?

– Thank you all. I wish you success.

- I am sure that you guys will not let me down and will be exemplary and smart students throughout the lesson.

II. Knowledge update. A moment of cleansing.

1 3 2 4

- Come up with tasks (Continue the pattern, add.)

Mental counting "Funny tasks."

1. Seryozha will soon be 10 years old,
   Dima is not yet six.
   Dima still can't,
   Grow up to Seryozha.
   And how many years younger,
   The boy Dima, than Seryozha? (4)

2. Five tits sat on a branch,
   Two jackdaws flew to them.
   Count fast, kids,
   How many birds are sitting on the branch? (7)

3. Children were skating,
   There were ten of them together.
   Nine of them are boys.
   And the girls? How many? (1)

- I liked your answers and we can move on.

Silence game with numerical fans.

- Look, numerical expressions are recorded on the board:

- What are numbers called when added? (Addendum, addendum, sum. )

- What are numbers called when subtracted? (Reduced, subtracted, difference.)

2. Discovery of new knowledge and formation of the topic of the lesson.

Group work.

- Guys, I suggest you work in groups. Complete the tasks on the cards. When working, remember the rules of working in a group. Choose who will write, who will answer, the rest suggest.

a + 2 ... a - 2

k + 5 ... 5 + k - 3 \u003d 7

10 - x \u003d 6

y + 3 \u003d 8

- Have you completed all the tasks? Which ones didn't work out? (10 - x = 6)

- Why didn't it work out? (We didn't have such a badge, we didn't solve it.)

- What do you think the purpose of our lesson will be? (Find out what these expressions are called.) LEARN ... ..

- What groups can these mathematical records be divided into? (Equalities and inequalities, alphabetic and numeric expressions.)

- Is the expression that you could not fulfill - is it equality or inequality? EQUALITY

- Why couldn't you decide? (There is an unknown number. )

-What assumptions do you have about how equalities with an unknown number (component) can be called.

- Does anyone know him? (Equation.) - Let's check. Whether he is right or not.

- What name would you think of?

- Why?

-How to solve such equality?

- Look at the left side of the expression, then the right side. What are they made of?

- What sign stands between the parts (=), then the left and right parts must be equal.

– What do we do to make the parts equal? (It is necessary to equalize the left and right parts.)

- Such equalities in mathematics are called equations. EQUATION

- Read in unison. Well done!

- What is the topic of our lesson? (Equation.)

- Based on the topic of the lesson, let's try to plan our lesson, identify goals. Use the words written on the screen.

1. Learn……(What are these expressions called.)

2. Learn.. . (read, write, solve equations)

3. Let's find a way ... (solution of equations).

- An equation is an equation that has an unknown component.

- Do you think "x" and "y" are numbers or letters? (Letters.)

- What letters do they look like? ("Ha" and "y".)

- These letters denoted unknown numbers.

- An unknown number in equations is most often denoted by Latin letters, for example, X (x), Y (y).

- In mathematics, all the most secret and unknown are marked with X. ( Showing a plate with X ). They call him "Mr. X" ( I post his portrait ).

- Wherever he appears, there is a mystery to be revealed.

– What do we not know? ( Part. )

- What is the name of the component? (When adding, it is a term; when it is a difference, it is subtracted.)

- How to find the part? Need to decide. But as?

- Let's solve our equation. What is X equal to?

- How can you calculate? We use the selection method.

- The value of X is called the solution to the equation. SOLUTION OF THE EQUATION

10 - x = 6 equation y + 3 = 8

x = 4 solution of the equation y = 5

- Let's try to substitute the solution of the equation into the equation instead of the letter, then the correct equality should turn out.

- An unknown number in the equation can be anywhere on the left side of the equation.

- Probably everyone is eager to learn how to solve equations? Then let's get started!

- It is important for us to correctly write down the solution of the equation in writing. To solve it , we define an algorithm of actions. Attention, we read the first step.

1st step: select part and whole;

2nd step: remember the rule;

Step 3: solve .

- We select such numbers instead of x and y so that the correct inequalities are obtained.

- And now let's read and write the equation in a notebook, together with me.

III. Primary fastening.

- Open your textbooks to page 60. Read the text in the orange box.

- And now let's try to solve the equation from the textbook on page 60 No. 3.

- Read the equations (“On the chain”.)

on the board:

- Compare the equation. What did you notice? What is the difference? (Two equations for addition and two for subtraction.)

- Note the parts and the whole.

- Good! The parts and the whole are noted, that is, the first step of solving the equation is completed. Write the first equation in your notebook, showing the parts and the whole, and solve it. Who wants to work behind the board? (One student does this work at the blackboard.)

4 + y \u003d 5

- What is unknown: the whole or the part? (In the equation 4 + y = 5, the part is unknown.)

- How to find the unknown part? (From the whole 5, subtract the known part of 4.)

- We completed the second stage - remembered the rule.

- So, let's execute the third stage : 5 - 1 = 4 . So y = 1.

- Test: 4 + 1 = 5. Answer: 1.

- By what action did you find the part? (Subtraction.)

- How will we work with the equation x - 2 = 8?

- Select the part and the whole.

- Remember the rule. (To find the whole, you need to add the part to the part.)

- Solve: 8=2+10. Answer: 10.

- By what action did you find the whole? (Addition.)

- Complete the tasks in writing in a notebook.

- Pay attention to seating at the desk.

- We will solve the remaining equations orally.

- Conclusion: So, which rule will help in solving each type of equation? (To find a part, you need to subtract another part from the whole. To find the whole, you need to add the parts.)

Physical culture minute.

The teacher shows cards with numbers, depending on this, the students perform movements.

- How many times do we stamp our feet?

- How many times shall we clap our hands?

- How many times will we sit down?

- We'll bend over now.

- We will jump exactly that much.

IV. Training tasks.

Work in pairs.

- Discuss in pairs where the equation is solved correctly.

3 + x = 4 y - 3 = 4

x = 7 y = 7

Answer: 7. Answer: 7.

- All pairs are ready. Who will answer? (There is an error in the solution of the first equation.)

- Prove. (In the equation 3 + x \u003d 4, the part is unknown. To find it, you need to subtract the known part 3 from the whole 4. 4 - 3 \u003d 1. x \u003d 1 Answer: 1.)

A) Problem of Vova Kolesnikov (No. 5 p. 61 )

4 aspens and 3 lindens grow near the river. How many trees are on the river?

- Read the problem.

- What is known? What do you need to know?

- What is known about aspens, lindens?

- Read the question, what do you need to find?

- Complete the diagram.

-What is not known in the diagram?

-What is the arithmetic operation to find the part?

-Write down the solution and the answer yourself.

Perform the task, check with the standard

10 - 4 = 6 (s.)

Answer: 6 traces.

-Which of you will try to compose and write down an equation for this scheme? Options for writing on the board: x + 4 \u003d 10 or 10 - y \u003d 4

-So is it possible to solve the problem with an equation? (Yes. )

V. Independent work.

B) Petya Zaitsev's problem (No. 5 p. 61 ) Solve the problem yourself.

10 tracks in the snow. 4 tracks were left by magpies, and the rest by crows. How many tracks did the crows leave?

Write down the solution in your notebook. (Check with comments.)

"Self-assessment":

1) What was task ? (Solve the problem yourself.)

2) Did you manage to get the result ? (It was possible to get the result.)

3) Completely correct or with an error? (We solved the problem completely and correctly.)

4) Completely independently or with help? (We completed the task on our own.)

Physical Minute . Game "Where is the equation?" to the music of the song " Terribly interesting is everything that is unknown ".

- Clap your hands if this is an equation.

The teacher shows the expressions on slide .

X - 4 =2

U + 1 = 7

K = 8

9 - y = 4

VI. Summary of the lesson. Reflection.

It's time to sum up the result of our lesson .

- Did you like the lesson?

- What exactly did you like?

-What task did you find most interesting in the lesson?

- What topic did you get acquainted with at the lesson?

- What did you learn at the lesson?

- Let's repeat the algorithm of actions again. So, to solve the equation you need………

- Who was it difficult?

- How would you rate your work?

- In the next lessons we will continue to solve equations.

- The lesson is over, thank you all for your work. Well done!

How to solve linear equations - formulas and examples of solving simple equations

Understanding the equation

Equation is a mathematical equation in which one or more quantities are unknown. The value of the unknowns must be found in such a way that when they are substituted into the example, the correct numerical equality is obtained.

For example, take the expression 2 + 4 = 6. When calculating the left side, the correct numerical equality is obtained, that is, 6 = 6.

An equation can be called the expression 2 + x = 6, with an unknown variable x, the value of which needs to be found. The result should be such that the equal sign is justified and the left side is equal to the right side.

The root of the equation is the same number that, when substituted for the unknown, equalizes the expressions on the right and left.

To solve equation means to find all possible roots or make sure that there are none.

Solve an equation with two, three or more variables - these are two, three or more values ​​of the variables that turn this expression into a true numerical equality.

Equivalent equations are those in which the sets of solutions coincide. In other words, they have the same roots.

Demo lesson in mathematics

Find out which topics are “lame” for you, and then analyze them without cramming formulas and boring lectures.

What are the types of equations

Equations can be different, the most common are linear and quadratic.

A feature of the transformations of algebraic equations is that a polynomial of unknowns must remain on the left side, and zero on the right.

Linear equation looks like this: ax + b = 0, where a and b are real numbers. Here's what will help in solving:

• if a ≠ 0 - the equation has a single root: x \u003d -b: a;

• if and = 0 - the equation has no roots;

• if a and b are equal to zero, then the root of the equation is any number.

The quadratic equation looks like this: ax2 + bx + c = 0, where the coefficients are a , b and c are arbitrary numbers, a ≠ 0.

Numerical coefficient is the number that stands for an unknown variable.

In addition to linear and square, there are other types of equations that we will get acquainted with next time:

• cubic,
• fourth degree equations,
• irrational and rational,
• systems of linear algebraic equations and others.

Online mathematics courses for grade 7 will help consolidate new knowledge in practice with a talented teacher.

How to solve simple equations

To learn how to solve simple linear equations, you need to remember the formula and two basic rules.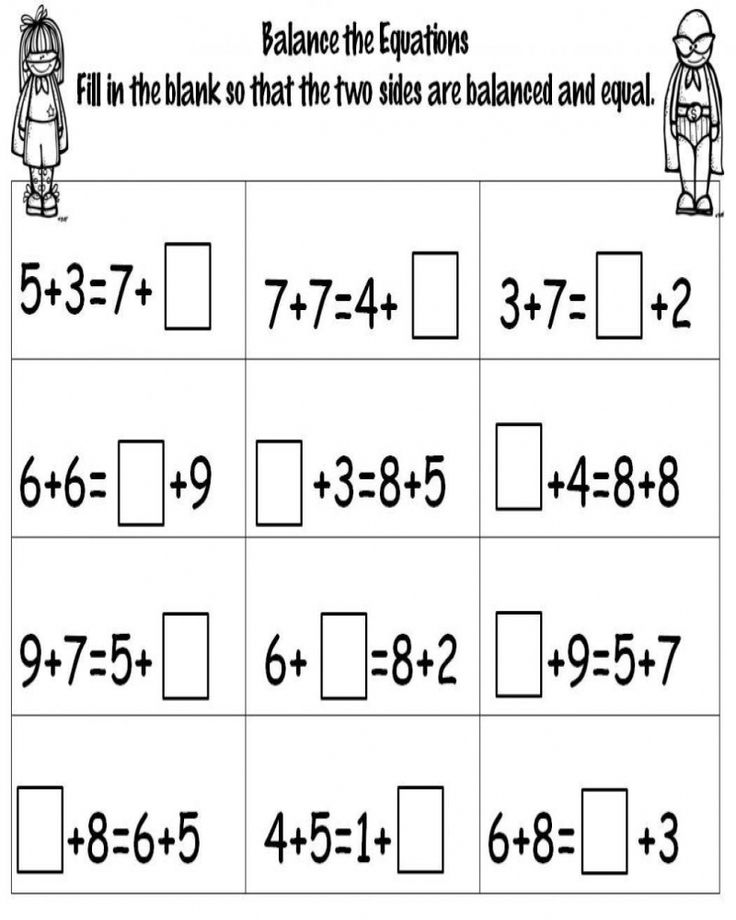

1. Transfer rule. When transferred from one part to another, the term of the equation changes its sign to the opposite.

For example, consider the simplest equation: x+3=5.

Let's start with the fact that each equation has a left side and a right side.

Move 3 from the left side to the right side and change the sign to the opposite.

You can check: 2 + 3 = 5. That's right. The root is 2.

We solve another example: 6x = 5x + 10.

How we solve:

1. Move 5x from the right side to the left. We change the sign to the opposite, that is, to minus.

   6x - 5x = 10

2. We give similar ones and complete the solution.

   x=10

Answer: x = 10.

2. Division rule. In any equation, you can divide the left and right sides by the same number. This can speed up the resolution process. The main thing is to be careful not to make stupid mistakes.

Let's apply the rule when solving the example: 4x=8.

With an unknown x , there is a numerical coefficient - 4. They are united by the action - multiplication.

0714 x was one.

Divide each part by 4. What it looks like:

Now reduce the fractions we have obtained and complete the solution of the linear equation:

How we solve:

1. Divide both parts by -4 so that the coefficient at the unknown becomes equal to one.

   -4x = 12 | : (-4)
   x = −3

Answer: x = −3.

If the minus sign is in front of the brackets, and it was removed in the course of calculations, it is important not to forget to change the signs inside the brackets to the opposite ones. This simple fact will help prevent offensive mistakes, especially in high school.

Recall that not every linear equation has a solution - sometimes there are simply no roots. Occasionally, zero may appear among the roots - it's okay, this does not mean that the decision was wrong. Zero is the same number as the rest.

There are few ways to solve linear equations, you only need to remember one algorithm that will be effective for any problem.

To quickly memorize the solution and the formula of a linear equation, download or print the algorithm - keep it in your phone, textbook or on your desktop.

Free English lessons with a native speaker

Practice 15 minutes a day. Learn English grammar and vocabulary. Make language a part of life.

Examples of linear equations

Now we know how to solve linear equations. It remains to practice on the tasks in order to feel more confident on the control ones. Let's decide together!

Example 1. How to solve the equation correctly: 6x + 1 = 19.

We solve it like this:

1. Move 1 from the left side to the right side with a minus sign.

   6x = 19 − 1

2. Subtract.

   6x = 18

3. Divide both parts by the factor in front of x, i.e. 6.

   x = 3

Answer: 3.

5x - 15 + 2 = 3x - 12 + 2x - 1