First grade problem solving

Check Out These 50 First-Grade Math Word Problems of the Day

Opening your daily math lesson with a Math Word Problem of the Day is an excellent way to set the stage for learning. We all know that word problems are difficult for young learners to grasp, even when the mathematical operation portion of the problem is basic.

Incorporate these first grade math word problems one day at a time at the start of your math block to build confidence, critical thinking skills, and a learning community. Students will get used to reading slowly for meaning, while also identifying key information. Encourage students to write out equations and draw pictures to explain their thinking, since this helps them see the light when they are stuck!

Topics covered include addition, subtraction, multiplication, and comparison. All you need to do is post one of these first grade math word problems on your whiteboard or projector screen. Then let kids take it from there!

Want this entire set of word problems in one easy document? Get your free PowerPoint bundle by submitting your email here.

1. I had 6 pencils, and my teacher gave me 4 more. How many pencils do I have now?

2. Gina’s dog got 3 treats on Sunday and 0 treats on Monday. How many treats did Gina’s puppy get in all?

ADVERTISEMENT

3. Joel went to the zoo with his family. During the first hour he was there he saw a bear, 2 tigers, and 3 lions. How many animals did Joel see in his first hour at the zoo?

4. Jackson sorted his toy cars by color. He has 6 blue cars, 5 green cars, and 4 black cars. How many cars does Jackson have in all?

5. Ben has 2 green balloons and 4 yellow balloons. How many balloons does he have altogether?

6. There are 3 kids in the Clark family. Tina is 3, Joshua is 4, and Samantha is 7. If you add up all their ages, what is the sum of the Clark kids?

7. If you go for a swim and 6 of your friends come along, how many friends are swimming in total?

8. Rachel’s mom had some flowers in a vase.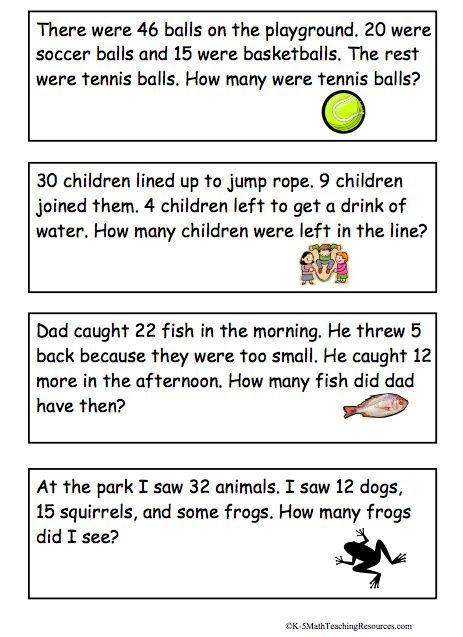 3 of the flowers wilted and Rachel’s mom took them out of the vase. Now there are 5 flowers in the vase. How many flowers were in the vase to start with?

9. Hayden’s cat had a litter of kittens. 3 kittens were gray, 2 kittens were spotted, and 7 kittens were black. How many kittens did Hayden’s cat have?

10. Pedro brought in 3 red leaves and 6 yellow leaves from the playground. How many leaves does he have in all?

11. Gabriella read 3 books on Monday, 6 books on Tuesday, and 4 books on Wednesday. How many books did Gabriella read in all?

12. If you have 3 cats, 2 guinea pigs, and a bunny. How many cute little noses do they have altogether?

13. If there are 3 inches of snow on the ground in the morning and we get 3 more inches of snow by dinner time. How many inches of snow did we get that day?

14. My cat has 4 paws and my brother’s dog has 4 paws. How many paws are there in all?

15. I had 10 pennies, but I lost 2 of them. How many pennies do I have now?

16. Santiago read 7 books over the summer. Ryan read 5 books. How many more books did Santiago read than Ryan?

17. Andrew put 10 stickers on his notebook. When he got to school he noticed some of the stickers had fallen off. Now Andrew only has 6 stickers on his notebook. How many stickers fell off Andrew’s notebook?

18. Nicole likes to help her mom pick tomatoes from their garden. She counted 9 tomatoes in the garden. 6 tomatoes were red and the rest were green. Nicole and her mom picked all the red tomatoes. How many green tomatoes did Nicole and her mom leave in the garden?

19. My sister and I have 20 pennies. If my sister has 10 pennies, how many pennies do I have?

20. The zoo had 8 tigers. 3 of the tigers moved to another zoo. How many tigers were left?

21. Esther read 3 poems. Magenna read some more poems. Altogether they read 7 poems. How many poems did Magenna read?

22. Haley’s dad bought 8 cheeseburgers. Haley ate 1 of them. How many cheeseburgers does Haley’s dad have left?

23. If you boil 7 eggs in water, and the number of eggs that float is one more than the number that sink, how many eggs float?

24. Rasheed loves to eat jellybeans. His favorite jellybeans are the yellow ones. There were 12 jellybeans in his bag. Rasheed removed all the yellow jellybeans and ate them, leaving 6 jellybeans in his bag. How many yellow jellybeans did Rasheed eat?

25. The gym teacher had 5 basketballs. The next week the gym teacher got some new basketballs. Now the gym teacher has 9 basketballs. How many new basketballs did the gym teacher get?

26. Jamal has 6 toy airplanes and his brother has 4 toy airplanes. How many more toy airplanes does Jamal have than his brother?

27. Antonio has some marbles. His brother Alex gives him 5 more. Now Antonio has 8 marbles. How many marbles did Antonio have to begin with?

28. If you have an 8-pack of crayons and you give your friend 3 of them to use during drawing time. How many crayons do you have in your pack now?

29. Emily has 4 pink erasers and some white erasers. She has 7 erasers in all. How many white erasers does Emily have?

30. Angel serves pizza at her birthday party. The pizza has 12 slices. 8 slices of pizza are eaten by Angel and her guests. How many slices of pizza are left?

31. If you have 9 toys on the floor and your little brother has 6 toys on the floor. How many more toys on the floor do you have?

32. There are 8 windows in the classroom. Some of the windows have decorations on them, 2 of them don’t have any directions. How many windows have decorations?

33. On Saturday, you brought home some fish from the pet store. If 15 of your 18 fish have stripes. How many of your fish are without strips?

34. 8 birds flew to the top of a fence. Some birds flew away and 6 birds stayed. How many birds flew away?

35. There were 6 books on Noah’s shelf. Olivia took some of the books. Now there are 2 books on the shelf. How many books did Olivia take?

36. Ethan has some folders in his backpack and 4 folders in his desk. He has 8 folders altogether. How many folders are in his backpack?

37. Liam has 8 t-shirts. 5 of them have superheroes on them, and the rest are solid colors. How many of Liam’s t-shirts are solid colors?

38. Mary was putting together a 20 piece puzzle. After she finished, she discovered that only 18 pieces were there. How many pieces were missing?

39. Nicholas has 7 cousins. Some of his cousins are girls and 3 of his cousins are boys. How many girl cousins does Nicholas have?

40. It snowed for 6 hours on Monday and 4 hours on Tuesday. How many more hours did it snow on Monday?

41. Charlie’s mom baked 12 chocolate chip cookies for dessert. Charlie ate 2 cookies and his mom and 1 cookie. How many chocolate cookies were left?

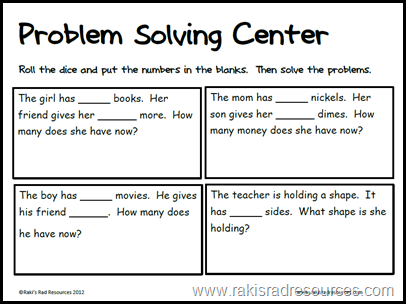
42. Melanie has 16 purple pens. Dante has 10 blue pens. Melanie has ____ more pens than Dante has.

43. Sofia has 75 pennies in her bank. How many more pennies will she need to have 100 pennies in her bank?

44. There were 9 cups of soda on the table. Some of the cups were knocked over, and 6 were still standing. How many cups of soda were knocked over?

45. Griffin has 20 board games. Some were under his bed, and 15 were in his closet. How many board games were under Griffin’s bed?

46. Antonio spotted 3 deer sitting at the top of a hill, but all he could see were their eyes. How many eyes did Antonio see in all?

47. Desmond saw 5 bunnies. He counted all of their ears. How many bunny ears did Desmond count?

48. Katie counted all of her toes, and then she counted all her mom’s toes. How many toes did Katie count altogether?

49. Which weighs more? A 15-pound red fox or a 24-pound wild turkey?

50. Which weighs more: a 150-pound white-tailed deer or a 110-pound kangaroo?

Enjoying these first grade math word problems? Check out our first grade hub for even more resources.

Get a PPT version of these word problems.

Visual Models for Problem Solving in 1st Grade

As students enter 1st grade, they continue to work on math comprehension using early structures, like the Kindergarten journal we introduced last week, but now we begin to add visual models to the mix!

Let’s recap a child’s developmental journey through problem solving:

1. In the early childhood years, a child needs lots of developmentally appropriate experience interacting with real objects in a physical world. 
2. The physical world is captured in a quantitative picture, which young children observe and use as a springboard for mathematical conversations.
3. We transition into a more structured math work mat to help young students be able to connect numbers to words and words to numbers, still using familiar situations from real life.
4. The math work mat gives way to a formal math journal in Kindergarten that makes use of math comprehension skills. It provides a structure for students to explain their understanding of numbers within real world situations that will carry on throughout elementary school. 

Each of the stages of development builds on the skills developed in the previous step, so it is important that students aren’t rushed through these stages. The goal is to teach students the why behind the how so they aren’t just memorizing procedures but truly understand what is happening as they solve problems.

This 1st grade year is the last stage in the Math5Littles progression, in my opinion. After this, there isn’t much scaffolding, so we really want to carefully implement all the previous stages of problem solving before we turn the students loose, because we don’t want them to start guessing and checking. In taking students on this developmental journey, we are trying to build them a solid foundation for visual models to help them to understand problem solving.  

When I was teaching 1st grade, I remember a strategy that we used for problem solving called the C.U.B.S. method. Each of those letters stood for a step in the problem solving process so students could remember what to do: C – circle the numbers, U – underline the word, B – box the operation, S – solve the problem. Seems like a simple process that gives kids a really great structure to start to understand what words problems are asking, right? But what I realized is that this strategy doesn’t hold up long term.

As a child was reading a part-whole addition or part-whole subtraction story, the boxing and underlining worked great. But when we got to comparison problems, it all fell apart.

“Shannon has 5 lollipop and Scott has 4 more lollipops than Shannon. How many do they have all together?” 

I watched students follow that procedure with this type of problem. They circled the 4 and 5, underlined important information and put a box around the words all together, which means add because we’ve all seen the T-charts of addition/subtraction vocabulary – it says difference, it means we’re going to subtract, if you see all together, we’re going to add. But that strategy gives me 4, 5, and all together. If you go back to the question, you’ll realize the answer isn’t 9.

As I often do, I asked myself why? Why isn’t it 9? A little more reading comprehension is required to decode that answer. The problem says I had 5 lollipops. Scott had 4 more than me, which means he also had 5. Adding that up, he had 9 and I had 5, so there were 14 all together.  

Why are we teaching kids procedures with concepts they don’t understand? Sometimes the strategies that we teach in math are conditional, meaning they only work for a certain amount of kids or a certain length of time. Then you have to worry about teaching them when to apply it and the rules for applying it, and what was meant to make things easier for students ends up being more complicated.

When we start working with strategies, I want to be able to find that vertical zip, meaning if I show you how this strategy might work in first grade, it has to work as the child gets older too so that they don’t have to learn a whole new set of strategies every year because every teacher teaches it differently.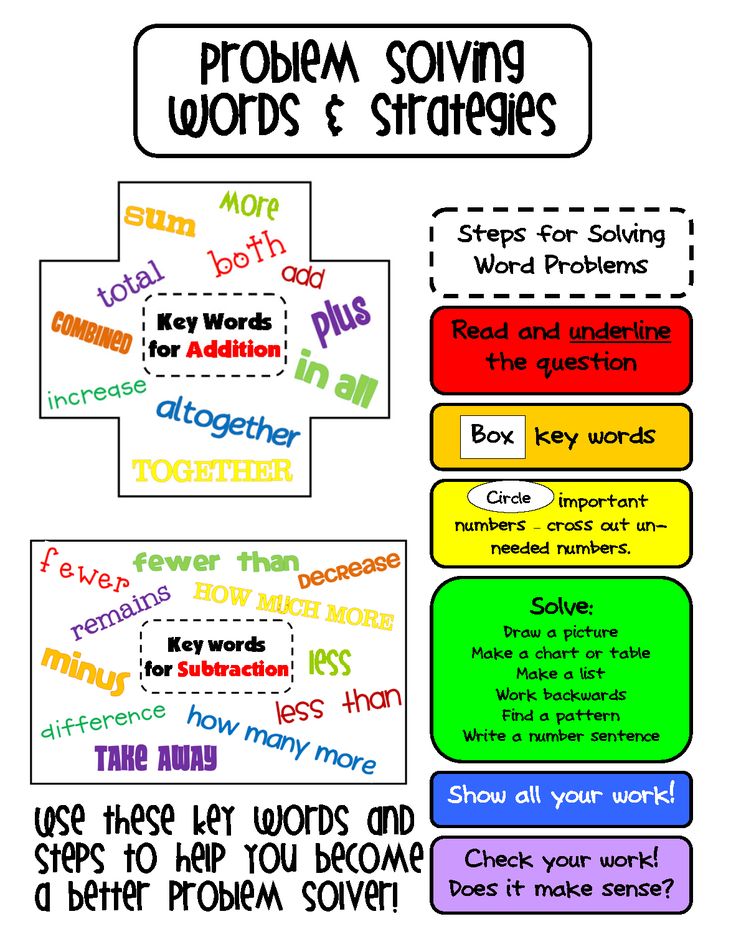 Honestly, the CUBS method would probably work for 75% of the problems in first grade. Students are doing more advanced part-whole addition problems, part-whole subtraction, part-whole missing addends, and they’ll start doing a few multi-step problems, all of which fit in the part-whole family, for which the CUBS method works well. But when you move out of that genre of problems, it falls apart. 

This is why, even in the Kindergarten journal, we use a coding system for our story problems. It’s for teachers and students to start to learn the different characteristics of the types of story problems that are out there, which will put them further ahead.

In the Kindergarten journal, we featured part-whole addition, part-whole subtraction, part-whole missing addend, a few problems with teen numbers, and a mixed review. The journal is very structured because it is intended to start students thinking about what they’re reading in the story problem: We have a story, a sentence form, a quick draw area, a number bond, a 10-frame, and a computation area. As they transition to 1st grade, how do we remove some of that scaffolding while still keeping it developmentally appropriate?

We have to be really careful with the way we make this transition, because very quickly, students can jump to the “circle the numbers, box the word” strategy and many times they just appeal to us because they don’t know what to do. It’s a word problem and it’s confusing, so they just add because we’re talking about adding that week. 

Additive comparison problems, where I have an amount and you have the same amount but you may have more or less than I do, are introduced after students have spent some time working on multi-step part-whole problems.

This type of problem is really a play on language, in my opinion, which makes it really confusing for kids to understand exactly what it is asking. So, we really want kids to take a step back to understand the additive comparison problems, which are coded AC in our journals. I find that building these problems with unfix cubes is a good way to start.

Let’s take this problem: Shannon has 10 pet rocks and Sherry has 4 pet rocks. How many more rocks does Shannon have than Sherry?

In some ways it seems like this might be a missing addend problem, but in fact we’re really comparing my pet rocks to Sherry’s pet rocks and we’re asking how many more does one have than the other. This really requires students to take it to the concrete level and make a bar model with unifix cubes.

I put 10 cubes to represent Shannon’s pet rocks, and then I’ll use different color cubes to show Sherry’s 4. Then, I want to compare the lengths of those two bars and figure out what the problem is really asking, which is the gap between where Sherry’s bar stops and Shannon’s bar stops. The question mark is asking for how many more does Shannon have? 

Sometimes, the language of an additive comparison problem might be reversed and say how many less does Sherry have? Since it is a play on words, which sometimes becomes confusing for students, we really need to put thought into how we go about teaching kids to do a problem like this.

If I were to line up all the programs we work with, every one of them has bit of a different name for visual models: model drawings, tape diagrams, bar models, unit bars. We’re going to universally call them visual models for word problems. 

These aren’t the little quick draws we’ve been doing in Kindergarten because, as students get older and the problems get more complex, I’m not going to be able to draw 13 ducks and then 9 more because it will take too long! Instead, I want to put it into a visual model that has these units.

This first grade year is a transitional time where kids are going from the quick draw to what I’m going to call proportional bars, which have a length of individual cubes that are representative of the quantities we’re talking about in the problem.

Say Erin has 4 books, but then she goes to the library and gets 3 more. Each cube or square represents a book, which helps kids go from the quick draw they did in Kindergarten to more formal structure. We could still put an X in the box to represent books that Erin had, and a circle in the boxes to represent the books that she got from the library, just to differentiate the two. The drawing is a comprehension tool, and we really focus less on answering the question than we do figuring out how to solve it. I think that’s the most misunderstood part of visual models.

I just was working with a first grade teacher last week on a Zoom call, and this teacher had not been able to attend our workshop on their campus about visual models. She, like most teachers I work with, didn’t understand why visual models were so important. She thought her students should be able to do quick draws and didn’t understand why they had to do boxes. She told me she was a big proponent of encouraging students to solve problems in different ways, so why would she possibly want to teach students a procedure like this and make them solve word problems in this way. 

After I took her through the same progression of problem solving we’ve been going through in our blog the past few weeks, she was sold! I took her up through fifth grade to help her see why it is that, in 1st grade, we’re asking students to stop doing quick draws and start to use a visual model that has a unit bar with different pieces.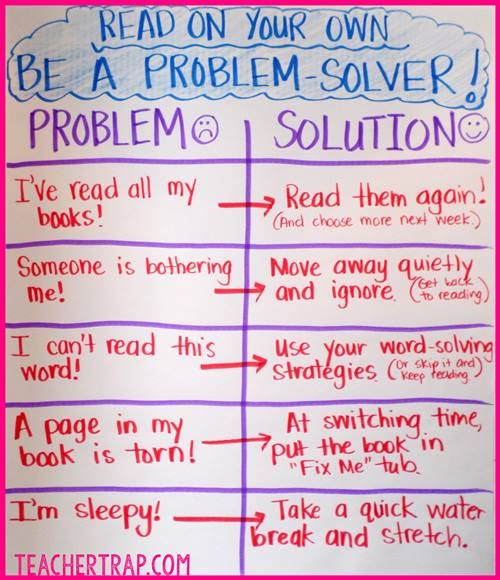 This proportional model is also a great transition into using a non-proportional bar.

Let’s say I had 92 pet rocks and Sherry has 45 pet rocks. A quick draw clearly won’t work for this problem, and I don’t have enough room on my paper to draw a proportional model for those numbers. But I can draw a longer bar that represents Shannon’s rocks, write in 92 rocks, and draw a shorter bar to show Sherry’s 45 rocks so I could see the proportionality. 

The hardest thing to remember when we do visual models for word problems is that it actually has nothing to do with math! We’re not actually solving the problem on the model; we are solely using a reading comprehension strategy.  

One of the biggest misconceptions we addressed when we started rolling out the 1st grade journal samples that I’ll be using in this video, was that the total doesn’t go on the line. If the problem asks for a total, we represent that in the visual model with a question mark. 

We also want to make sure that we label the visual model. For example, putting a B above the books that Erin had and an L above the books she got at the library. 

The whole point of this process is to provide a systematic way for students to work through problems that doesn’t stop working after 1st grade or when you start working on a different type of story problem. In fact, this strategy carries through multiplicative comparison problems and fractions, all the way into ratios and proportions in middle school. 

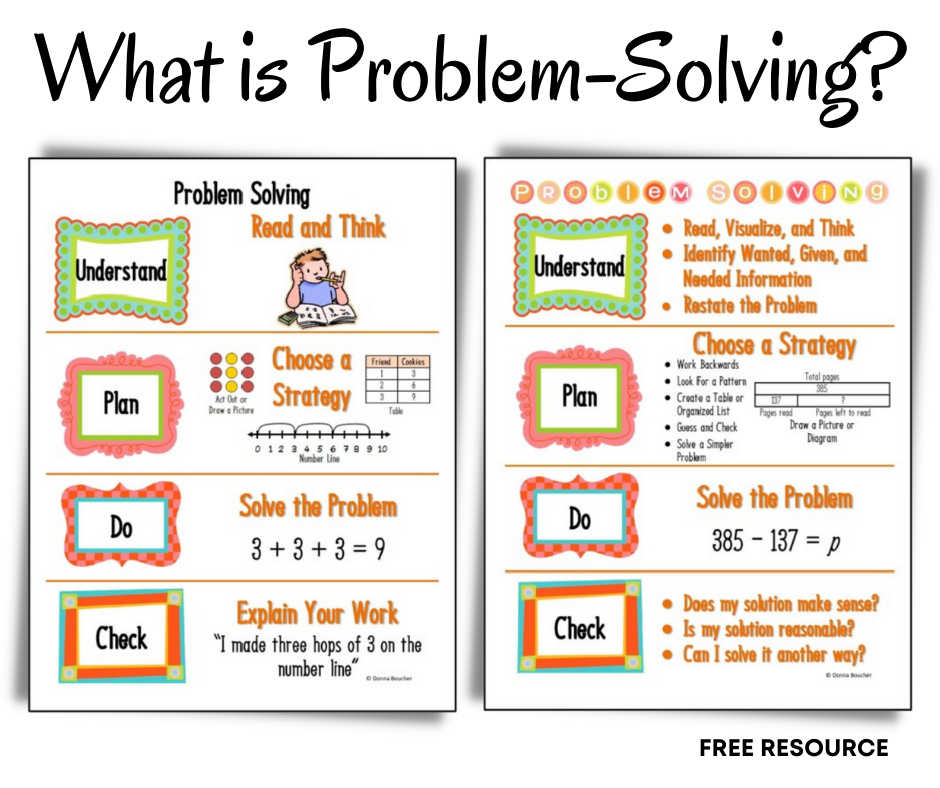
This step by step checklist that we use helps ensure that students will start to become more independent with this process as they go. We introduce it a little bit in Kindergarten as a more teacher-led process, but it is integrated into the first grade classroom as well where kids have a step-by-step visual model process to solve. As you can see in the examples, we have Professor Barble explaining the steps.

Read the problem. Then, have someone read it and repeat it, and every time a new piece of math information is presented, we’re going to put a chunk. So, as kids are reading the problem, they start to learn how to dissect what’s being asked. 

Not all first grade students will be able to read the story problem, but this process is modeled day after day after day in the first grade classroom, so eventually the child will become independent. 

I’m going to read a story problem: Mark has 9 strawberries, 6 of them are small. The rest are large. How many strawberries are large? 

Then, I’ll go back and read it in chunks: Mark has 9 strawberries. This is a new piece of mathematical information, so students will repeat that statement back and highlight or put a line there. The students also like to say chunk! Then we continue reading: Six of them were small. I’ll stop, repeat it, and the students say chunk! as they mark that chunk in their journals. Now we have two pieces of mathematical information. Let’s continue: The rest were large. Repeat and then chunk! So, we’ve got three sections of information that the problem has given us that we need to replicate in our visual model.  Finally, How many strawberries are large? Repeat that and then chunk!

By going through the problem slowly and methodically, students can really see these sections that they’re reading, and, as they’re going on to the subsequent steps of solving the problem, they can actually check off that they’ve included all the chunks of information in their visual model. 

Create a sentence form. What is a sentence form? Simply put, it is stating what the problem is asking in a complete sentence. I can’t tell you how many times I’ve seen students solve story problems, and actually forget what they’re being asked because they’ve gotten so into the arithmetic and figuring out what they’re doing! So this step keeps them focused on what the problem is actually asking.

In our problem, it asked me how many strawberries are large? To put it in a sentence form, I would say: Mark has ____ large strawberries. I like to say Hmm for the ____  as we’re reading it out loud.

In Kindergarten, we provide the sentence for students, leaving the blank space for their answer. But in 1st grade, we take some of the scaffolding away. It might say “There were _____ large ____” and the students have to fill in the blanks.

The sentence form is a great way to make sure that kids are comprehending what they’re reading. Generally, students in first grade have a difficult time trying to create a sentence form, because they aren’t yet developmentally ready to give you a complete answer in reading. But students will be required to do a sentence form in 2nd through 5th grade so we can be sure they understand the problems being asked, so it’s really great practice to start in 1st grade with the scaffolding.

Proportional model. We start the 1st grade year with a proportional model.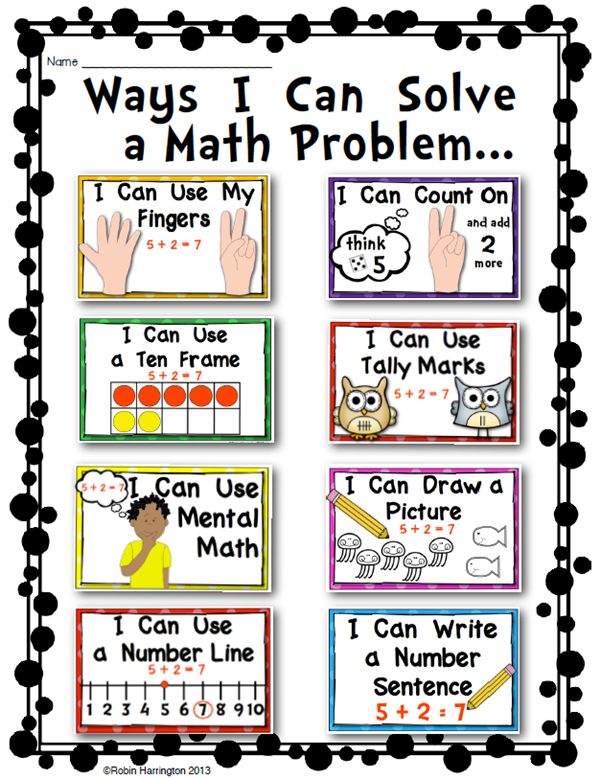 We may scaffold here for the who or the what, and students will eventually start to learn what goes in that visual model. In this case, we’re talking about all of Mark’s strawberries, even though the question itself is only asking about how many of them are large.

In a proportional model, you might see the 9 squares. This is a missing addend problem so that title is going to have PWMA at the top, and there will be exactly nine squares. Some people might think that’s giving it away, but remember the goal of visual models? It’s not to solve the problem but understand what’s going on in the problem, so we’re more concerned about whether or not the student can label the drawing correctly. 

In this example, the student would total the bar at 9 and check off the first chunk of the problem that we read earlier –  Mark has nine strawberries.

The next part says “6 of them are small.” In 6 of my boxes, I’ll make six Xs, or I might make small circles, and at the top I can either write small or abbreviate with an s.  

Then it says “the rest are big.” I could label that other section of the boxes B for big, or write the whole word if I wanted. Then,  I need to put a question mark above that section between 9 (the total number of strawberries) and 6 (the number of small strawberries). That section represents the large strawberries, which is what my sentence form reminds me that I’m looking for. 

Technically, a student could just look at this easy proportional model and say there are 3 large strawberries because it’s right there in front of them. So some people might think this journal is just too easy, but at the end of the day, students are solidifying the process. They’re going back up to the problem and putting a check when they add Xs or circles for the six small strawberries. They’re putting in a check when they’ve talked about putting in the large strawberries. Then they put a question mark to show what we’re looking for. There’s a lot of detail that we’re looking for kids to have to interact with the text in math to show the comprehension.  

In some of our schools, we will do a unit bar at the bottom of the page. In the 1st grade journal we’ve created for Math5Littles, we’re going to leave the bar off and introduce the non-proportional bar a little bit later in the year. There is nothing wrong with having a model of the proportional bar and then underneath it having the non-proportional bar. In our journal, we plan to show the proportional bar, and then bring in both types of bars so that kids could see the relationship between the two. If where about this non proportional bar, where would I slice it to put the nine in? And then where’s my question mark? is it labeled? etc. 

The integral parts of visual models are: labelling the who or what, taking the bar and adjusting it based on the information that’s given, and writing in their question mark. Then it’s time to solve!

Computation. Although this step might not seem necessary because our sample problem is so simple, and to first graders after they do so many, it seems simple and both teachers and students might wonder why they’re even doing it, but I can promise that these problems will become more complex, very quickly. In our 1st grade journal, we will feature this look at the proportional bar, and then transition to having proportional and non proportional models, and then eventually just leaving it blank and having the student put in a non proportional bar to see that they can develop this progression. 

The goal is, by the end of their first grade year, students should be able to solve problems with larger numbers and a non-proportional bar. You certainly don’t want to rush that progression. 1st grade is a really nice scaffold for students to get to that point of independence, because when we get to 2nd grade, we don’t do a whole lot of scaffolding. There are more open-ended sentences, more blanks, and students are doing more of the work.

Additionally, we want to mix up the types of problems we’re solving, give students time to understand them. You might do three days of part-whole addition to see if they can get it under their belt. Then do some part-whole subtraction, then mix the two to see if students are just following a pattern where we’re adding today or subtracting today. We want to know that they can really apply what they’re learning. Multi-step problems, where students have to add and then subtract, or vice versa, are next. Give students lots of good practice, and then mix it up again to see if they’re really following the words, or if they’re just learning a procedure. The last type of problem that we would integrate in the first grade is additive comparisons. 

In the video tutorials, you’ll see aspects of four different problems being displayed. Some will have the proportional bar, some will have the proportional and the non proportional and some just won’t have it just so you can get an overall idea of what this looks like as we go.

[yotuwp type=”playlist” id=”PL76vNL0J-a405ysBIwEwXfaMp5883yGh5″ ]

As you watch the videos, think about how you could set this up in your classroom, starting with some of the sample problems that we’re offering as a free download today. We will be releasing a full 1st grade journal soon, so stay tuned! 

Join us next week for problem solving in 2nd grade: What are the different problems that 2nd grade is going to encounter? How are journals coded?  As we start to look at how journals are coded, which you certainly could use these tutorial videos right away in your classroom or in your distance learning by thinking about story problems in a different way.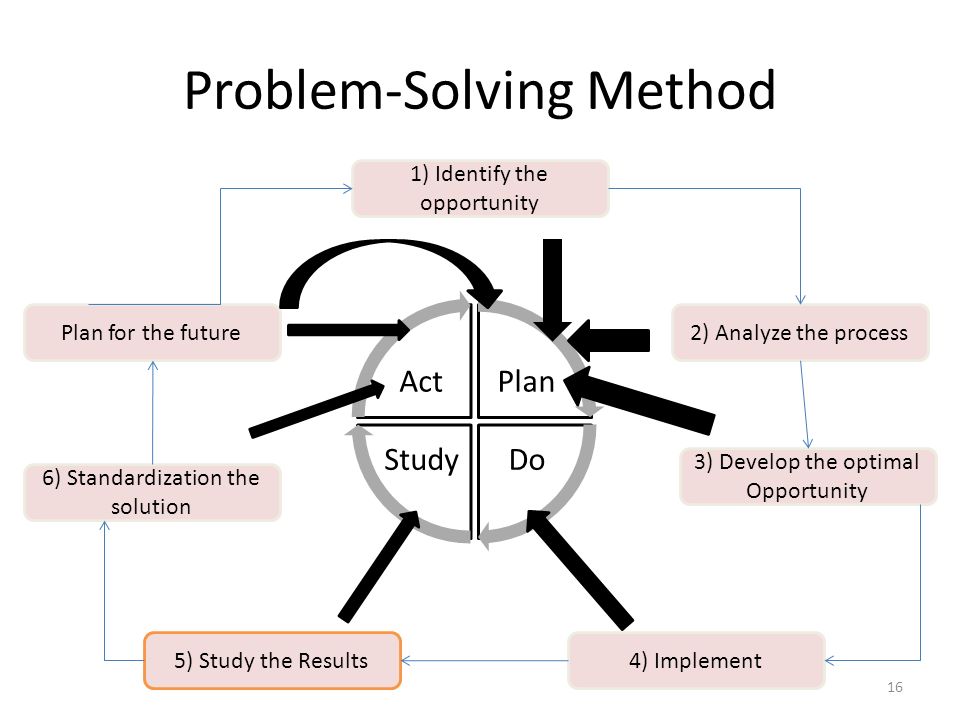

entertaining tasks and examples in pictures with answers and solutions

Entertaining mathematics

1st grade

Why do kids love LogicLike tasks more than tasks from math textbooks? The professor and his team will teach each child to click both typical and non-standard math problems.

Select the child's age

to get started!

Preschooler

First grader

LogicLike.com children learn to reason, develop logic, ability to mathematics and cognitive interest.

Recommended thematic courses

online for grade 1

Logic course and thinking Begin

Preparing for Olympics Begin

Why do children and parents choose LogicLike?

What kind of mathematics do children in the 1st grade need?

The following story often happens: when preparing for the 1st grade the child liked to solve entertaining tasks, puzzles, examples and tasks. Passes the first a quarter and a capable child begins to get bored of the monotonous or too simple for him assignments.

If you were looking for a mental counting simulator or want to check how much your child has learned school curriculum, you will love the collection of math tests for grade 1 from LogicLike.

The LogicLike team knows how to captivate a first grader mathematics and charge with the desire to learn how to solve any problems. We have more 3500 entertaining tasks, awards, achievements, student rating, personalized certificates.

Try the full fun math course and logics from LogicLike

• Flexible mind and confidence! When children decide tasks and puzzles on LogicLike, they train the "wiggles" and develop ingenuity.
• Foundation for IT! Algorithms, patterns, logic - we have all this. We teach to work with information, train memory and thinking - we form the potential for success in IT professions.
• We increase progress! Regular classes of 20-30 minutes develop logical and mathematical capabilities. As a result - high grades at school, prizes at olympiads and competitions, interest in learning increases.

Start the course!

Entertaining mathematics for first graders online

Mathematics classes on LogicLike begin with entertaining logical problems, unusual examples, puzzles and other tasks in pictures that you want to solve. In the course we alternate mathematical and logical problems, patterns, figures in space and other types assignments.

Popular categories of assignments for grade 1

Selections from the training course LogicLike

• Simple addition and subtraction
• Enlargement, reduction by several units
• Composite tasks
• Text logic and math
• Examples for addition and subtraction for class 1
• Math puzzles for 1st class

Addition and Subtraction Problems

Simple task to find sums

To decide click Start!

Three girls took 1 balloon in each hand.
How many balls do they have?

Watch answer

Answer:

6.

Mindfulness task

To decide click Start!

There are two sweets, one cake and three pears on the plate.

How many fruits are on the plate?

Watch answer

Answer:

3.

Subtraction problem

To decide click Start!

There were 7 liters of water in a 12-liter barrel, and 8 liters in a bucket.
Water from a bucket filled the barrel to the top.

How many liters of water are left in the bucket?

Find out the answer

Answer:

3.

We have everything you were looking for

Text and logical tasks

Tasks mathematics

Examples and tasks

Shapes in space: 2D and 3D

Start classes!

We have built the educational process in an understandable and exciting way for anyone child format, from simple to complex.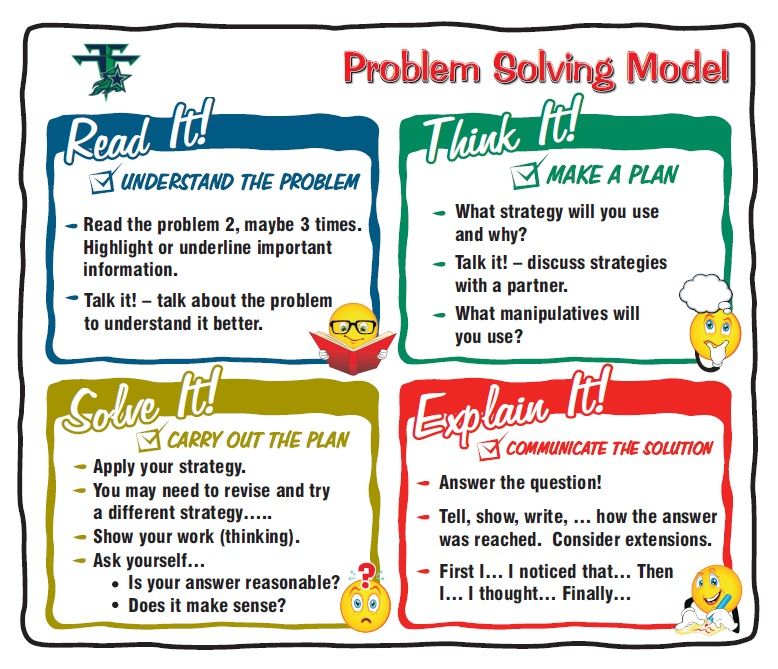

Tasks to increase and decrease the number by several units

What will be the result?

To decide click Start!

Find out the answer

Answer:

5 apples.

Age problem

Yura was born 2 years earlier than Vanya.
Yuri is now 5 years old.

How old is Vanya?

Find out the answer

Answer:

3.

Finding the Unknown term and difference

To decide click Start!

An evil virus hid the numbers in the examples.
Put the correct numbers back in their places.

Find out the answer

Answer:

2 + 3=5
3 − 2 = 1

You can see examples of Olympiad tasks for 1 class or start To activities on the site.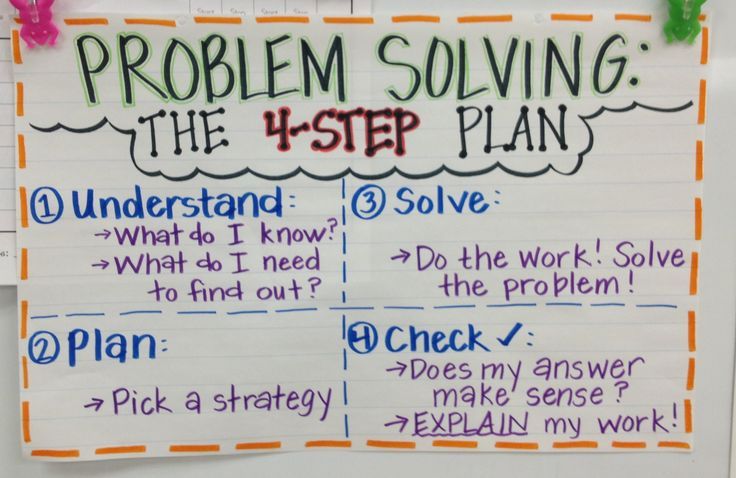

Day after day more 100,000 children

go through 10-20 tasks on the LogicLike website. And how much can you?

Solve problems

Downloads: tasks for developing counting skills

For those who do not currently have the opportunity to study online, we have prepared small selections assignments for paperwork. You can download and print tasks for practicing oral skills invoices in pdf format.

To "warm up" the child's interest in mathematics, we recommend starting with 1 sheet a day.

• Entertaining tasks for grade 1 for addition and subtraction within 10.
• Entertaining tasks for first graders: addition and subtraction up to 10.

What is the best online course?

We recommend that future and present first graders practice 15-20 minutes a day.

Compound tasks for first graders

Tasks in two or three actions develop memory, logic and mathematical speech.

Composite difference problem comparison

To decide click Start!

Condition: The purple monster ate 4 whole oranges, and the red monster ate 7 halves of the same oranges.

Question: Who ate more oranges?

Show solution

Answer:

Violet.

Solution
1 whole orange = 2 halves.
4 whole oranges = 2 + 2 + 2 + 2 = 8 halves.
8 > 7 means Purple ate more than Red.

Multi-action task on balancing

To decide click Start!

Condition: A rabbit is 2 kg lighter than a puppy.

Questions: What the scale will be higher if the puppy is placed on the left side of the scale, and the rabbit on right? How after that you need to place the weights on the scales so that they come to equilibrium?

Find out the answer and solution

Solution
1. A rabbit is lighter than a puppy, so the right one is lighter. the bowl with the rabbit will rise up.

2. In order for the balance to balance, the weight on the bowl rabbit should be 2 kg heavier than the kettlebell that we will add to the puppy.

It turns out that you need to put on a bowl with a puppy weight in 1 kg, and on a bowl with a rabbit - in 3 kg.

Suggested tasks are part of the LogicLike educational platform. Start learning!

Develop logic and mathematical thinking

• Child-friendly theory . Video tutorials, tips and hints will help the student to independently deal with even very complex tasks.
• Making math fun . game form and step-by-step methodology make the learning process interesting and effective.
• All materials on one site . 17 categories, over 3500 exciting challenges! The LogicLike team creates new ones every week interesting tasks that help children understand and love logic and mathematics.

Text Boolean

Fedya has equal number of sisters and brothers.

Who is more in the family: sons or daughters?

Show answer

Answer:

more sons (Fedya is also a son).

To decide click Start!

Kolya and Nadia have the same items.
Anya has a jump rope.

Distribute items to all children.

Find out the answer

Answer:

Kolya and Nadi - balls. Ira and Anya have jump ropes.

Want more examples of similar tasks? See logic puzzles for 1 class.

Take the full course from LogicLike!

• 3 steps to start the path to the heights of logic 😎:
• 1. Solve 5 problems
• 2. Save account
• 3. Show the platform to the child and solve together 10-15 tasks.

Math tasks for logic

Task with figures on verbal-logical thinking

To decide click Start!

Condition: The professor thought of a figure and gave two clues:
- it is not square and not blue;
- it is round or triangular.

Question: What did the Professor guess?

Find out the answer

Answer:

orange triangle.

Take hint

Prompt

Solving similar mathematical puzzles promotes the development of verbal-logical thinking , trains possession skills basic methods of thinking: highlighting essential and insignificant features of objects, generalization, comparison, derivation of the investigation and others.

Continue the pattern

To decide click Start!

Find a pattern and continue the series with numbers.

Find out the answer

Answer:

20.

Comment:
The difference between each successive number and the previous one increases by 1 (+1, +2, +3…).

You can see other rules for 1st grade or start training.

Did you like the material? Share with friends!

Connect to LogicLike!

More than 150,000 children from all over the world have already do math and logic at LogicLike.com.

Start learning! Start learning

We will teach a child

Reasoning and making decisions

Solve any logic problem

Think flexible and non-standard

Other collections of tasks by age

Tasks for preschoolers

Tasks for grade 2

Tasks for grade 3

Tasks for grade 4

You are here: LogicLike Math and Logic Online Simulator in mathematics for grade 1

tasks for counting and logic

Actual

• How to teach a child to count
• Tasks for adding to first -graders
• Option 1
• Option 2
• Option 3
• Option 4
• Purpose Tasks for first -graders
• Option 1
• Option 2
• Option 4 9004
• Tasks comparison for first graders
• Logic tasks for first graders
• Instead of a conclusion

When sending a child to first grade, parents always dream that their child will study well and receive only the highest marks in all subjects. And if it is not at all difficult to teach a child to read, then it is not always easy for children to understand and solve mathematical problems. In order for a first-grader to succeed in mathematics at school, parents either hire a tutor, which is not always financially justified, or try to work with their children on their own. In this material, we will tell you how to pull up a first-grader in mathematics at home, talk about different types of problems and methods for solving them.

How to teach a child to count

Parents of first-graders should remember that at the age of 5-7 years, abstract thinking is still poorly developed in children. Remember the tale of Pinocchio, when he counted the apples that “Someone” allegedly took. Similarly, a 5–7-year-old child is not yet able to imagine the condition of the problem.

It is best to use visual aids that the child can see and touch. These can be counting sticks, cubes or pictures cut out of cardboard (for example, a set of cardboard hedgehogs, flowers, leaves, etc. ). Lay out in front of the child the entire condition of the task from visual materials: there was so much, so much was added or taken away. So it will be easier for him to understand the condition of the problem and it will be easier to find its solution.

Another important point in teaching children is that the child must learn to distinguish tasks from each other by type. To do this, you can target it to some keywords. For example, if the task mentions the words "added", "brought", "arrived", "ran" and others denoting joining, then this is an addition problem.

Understanding what type a particular problem belongs to, the child will learn to determine the required solution algorithm and successfully cope with the task.

Addition problems for first graders

As already mentioned, addition problems have a common feature - attachment. Another sign of addition tasks is the phrase “how much” in the task question.

The child must learn to clearly understand that if there is something added to the condition, then he needs to add up the available numbers. The child must understand what the first term, the second term and the sum are, and be able to find them in the task condition.

In order for a child to master mental counting well, he needs to regularly practice mental counting. If you are on vacation, at least once a day, ask him examples to develop memory. You can even study on the way to school or in the section.

Five to ten examples daily will not tire a first-grader too much, but will bring many benefits for his further studies.

Below are addition problems for first graders. For convenience, we have divided them into options, so that when studying at home, you can solve already completed tasks with your child.

Option 1

• Natasha read 5 books during the holidays, and Katya read 4 books. How many books did the children read together during the holidays?
• There were 6 apples on one branch of the apple tree, and 7 on the other. How many apples were there on both branches of the apple tree?
• There are potted flowers on the window in the classroom. The first window has 2 flowers, the second has 3 flowers, and the third has 1 flower. How many flowers are in the class?
• Alyosha's family has 2 boys and 1 girl. Tanya's family has 1 girl and 1 boy. Serezha has 2 boys in the family, and Katya has only 1 girl. How many girls live in the families of all children? And how many boys?
• According to the results of assessments for the 1st quarter in the 1-A class, 10 excellent students, 14 good students and 2 three students. In the 1-B grade - 8 excellent students, 12 good students and 3 three students. And in 1-B - 11 excellent students, 11 good students and 4 three students. How many excellent students, good students and three students in the entire parallel of the first classes?

Option 2

• Natasha is 8 years old, how old will she be in 3 years? In 4 years, in 10 years?
• In the stationery store, Nastya liked the felt-tip pens for 18 rubles. She has 10 rubles, 5 rubles, 2 rubles and 1 ruble. Will the girl have enough money to buy?
• 6 girls and 12 boys went for a walk. How many children went out for a walk?
• Sasha has a pack of counting sticks. Of these, 10 are red, 8 are blue and 12 are yellow. How many sticks are in the pack?
• 4 girlfriends and 5 friends came to Polina's birthday party. How many children will sit at the festive table? (here it is important that the child does not forget to count Polina herself, the answer in the problem is 10 children).
  

  Variant 3

• Children came to the park and saw birds swimming on the lake: 8 swans and 12 ducks. How many birds were swimming in the lake?
• Children were planting saplings at school. Petya planted 2 seedlings, Anton planted 3, Natasha and Katya planted 2 seedlings. How many seedlings did the children plant in total?
• There were sweets in a box on the table. Masha ate 5 candies, Alena - 3 candies, Nastya - 6 candies, and Kolya ate 6 candies and the box was empty. How many sweets were in the box from the very beginning?
• There are 20 postcards in Marina's collection. Yulia also has 20 postcards. How many postcards do girls have?
• Seva had 20 stamps, he was presented with 4 more stamps. How many stamps did Seva have in total?

Option 4

• Mom planted 20 cucumber bushes and 17 tomato bushes. How many plant bushes did mom plant in total? On Monday, 8 tables were brought to the canteen, on Tuesday - 7 tables, and on Thursday - 10 more. How many tables did the canteen receive in a week?
• Pasha and dad went camping. On the first day they walked 12 km. In the second - 10 km, in the third - 8, and in the fourth - 11. What path did dad and Pasha cover?
• The zoo has 12 monkeys, 8 tigers, 2 elephants, 6 bears and 4 raccoons. How many animals are in the zoo?

Important! If every day you solve one version of addition tasks with a child, then on the control tests he will show brilliant results.

• There are 13 boys and 12 girls in Grade 1-A. There are 12 boys and 15 girls in grade 1-B, and 10 boys and 12 girls in grade 1-C. How many boys and how many girls are there in all first grades?

Subtraction tasks for first graders

Subtraction tasks also have their own characteristics and features. In the condition, you can always find some of the characteristic phrases: “how much is left”, “there were so many, of them ...”, “there were so many, so many left / flew away / ran away / deteriorated, etc.” and others. Here it is also important to understand what the first term, the second term and the sum are, to be able to find them in the task condition, because subtraction problems are the inverse of addition. And the concepts here are slightly different: reduced, subtracted, difference.

Below are subtraction problems for first graders. For convenience, we also divided them into options so that when doing homework, children can solve already completed tasks.

Here there are tasks both for finding the remainder (“how much is left”) and for decreasing (“by how much the number has changed”).

Option 1

• Andrei lives on the 7th floor, and Alena 3 floors below. What floor does Alena live on?
• Volodya has 17 cars, but Sasha has none. Volodya gave Sasha 8 cars. How much does he have left?
• Natasha is 12 years old, and her brother Seryozha is 7 years younger. How old is Seryozha?
• There were 10 apple trees in the garden, and 4 less pear trees. How many pears grew in the garden?
• On the first day Mila read 24 pages in the book, and on the second day she read 3 less. How many pages did Mila read on the second day?

Option 2

• Children receive books in the school library. Petya took 8 books, Alyosha took 2 books less than Petya, and Vanya took 3 books more than Alyosha. How many books did each boy take? How many books did they take together?
• There were 25 berries in a vase on the table. Marina ate 4 berries, Alice ate 6 berries, Mila ate 3 berries, and Katya finished the rest of the berries. How many berries did Marina and Alice eat? Mila and Katya How many berries did Katya eat?
• There were 10 plates on the table and 6 less in the sink. How many dishes were in the sink?
• Serezha is 15 years old, his sister Larisa is 4 years younger. And the youngest brother Boris is 7 years younger than Larisa. How old are Larisa and Boris?
• Mom planted 30 cucumber bushes, 17 bushes sprouted. How many cucumber bushes were lost in total?

Option 3

• The children went to the forest for mushrooms. Dima found 10 russula and 7 white mushrooms. Tanya found 3 less russula and 2 less white ones. How many and what kind of mushrooms did Tanya find?
• The first house has 12 entrances, the second house has 4 entrances less than the first one. And in the third house there are 6 entrances less than in the first. How many entrances are in each of the houses?
• There are 23 apples in the first basket, and 11 less apples in the second. How many apples are in both baskets?
• 12 girls took part in the performance, and 3 less boys. How many boys were in the play?
• There are 15 roses in one vase and 8 less in another. How many roses are in the second vase?

Option 4

• Sweets cost 30 rubles, and bread is 15 rubles cheaper. How much does bread cost?
• Grandmother baked pies. With potatoes 30 pieces, with jam 10 less than with potatoes, and with cabbage 5 less than with potatoes. How many and what kind of pies did grandma bake?
• There were 20 men on the bus. There were 5 fewer women than men, and 7 fewer children than women. How many people were on the bus in total?
• Children receive books in the school library. Sasha took 5 books, Misha took 2 books less than Sasha, and Serezha took 2 books more than Misha. How many books did each boy take? How many books did they take together?
• 20 buckets of water were used to water the garden. 12 buckets went to the beds with cabbage. How much went to the beds with carrots?

Comparison tasks for first graders

• Comparison tasks are aimed at finding some number, less or more than the original. In principle, to some extent they can be attributed to addition or subtraction tasks, so we decided not to describe these tasks by options, but to give several similar examples:
• There were 10 cats on the roof: 7 black and 3 grey. How many more black cats than gray ones?
• In the village, my grandmother has chickens and ducks. There are 18 chickens and 15 ducks. How many more chickens than ducks.
• Tanya has 3 dolls, and Dina has 4 more. How many dolls does Dina have? How many dolls does Tanya have less?
• Marina is 14 and Misha is 9. How many years is Marina older than Misha?
• There are 8 cars in the garage. Of these, 3 trucks and 5 cars. How many fewer trucks than cars?
• Dima was presented with gifts for his birthday. First, mom and dad gave 2 gifts, then friends brought 5 gifts. How many more gifts did Dima have?
• On the first day of vacation, Yura solved 5 problems, on the second - 7, and on the third - 2. How many more problems did Yura solve on the second day?
• How many problems less than the first did Yura solve on the third day? And how many fewer problems did he solve on the third day than on the second?
• Sonya had 3 oranges and 10 apples. How many more apples than oranges?
• Olya has 3 hares and 2 squirrels. Mila has 5 dolls and 1 bear. Who has more toys and by how many?
• Cows were grazing in the meadow. 7 goats came to them and in total there were 15 animals in the meadow. How many cows were there?
  

  Logic tasks for first graders

  Articles with teachers' recommendations and lists of exercises and tasks have already been devoted to the development of logical thinking. Here we present several logical tasks that will allow not only to develop, but also to train the logic of first graders.

• Which is easier? A kilogram of cotton wool or a kilogram of nails? Tea, compote and cocoa were poured into a glass, mug and cup. There is no cocoa in the mug. There is no cocoa in the cup, and no compote. What was poured into what?
• How many fingers are on 3 hands?
• How many paws do 4 cats have?
• How many hands do 10 children have?
• Lena and Misha saw 2 ships in the sea. How many ships did each of the children see?
• Kitten tails sticking out from under the bed. How many kittens are there if 7 tails are visible?
• Dogs hid behind the fence. You can see 12 paws from under the fence, how many dogs are behind the fence?
• There are 5 peaches and 8 pears on the table. How many apples and plums will there be in total?
• There are 2 glasses of milk on the table. Petya drank the milk and put the camp on the table. How many glasses are on the table?
• Vanya left the school. 3 girls walked towards him. How many children left school?
• Seven first graders went from home to school: Petya, Masha, Liza, Grisha, Tolya, Misha and Larisa, and 4 second graders: Seryozha, Tanya, Mila and Vanya. How many girls went to school?
• To get into the theater 2 daughters and 2 mothers needed 3 tickets. How could this happen?
• Misha is 2 years older than Lena. How much older will he be than Len in 5 years?
• Lena and Milana planted 10 flowers each and finished the work at the same time. Milana started work earlier. Which of the girls worked slower?

Instead of a conclusion

Mathematical development of first-graders is of great importance in their education. By solving examples and problems, the child acquires new experience, knowledge and skills. Learns to think logically and mathematically, find solutions from various situations, more successfully master related sciences in further studies.

Children's progress should not be left to chance, and every effort should be made to help them in this difficult task, like studying in the first grade.

Learn more

• 
  Games to play with five year olds
• 
  Sight words 4 year olds
• 
  Average reading level for 3rd grade
• 
  Beginning reading free worksheets
• 
  What is letter sound correspondence
• 
  Social skills group activities for adults
• 
  Help child reading comprehension
• 
  A spelling game
• 
  Math terms starting with k
• 
  The learning web
• 
  Lower case abc chart