First second third fourth fifth sixth seventh eighth
Ordinal Numbers | Vocabulary | EnglishClub
We use ordinal numbers to talk about the "order" of things or to define a thing's position in a series.
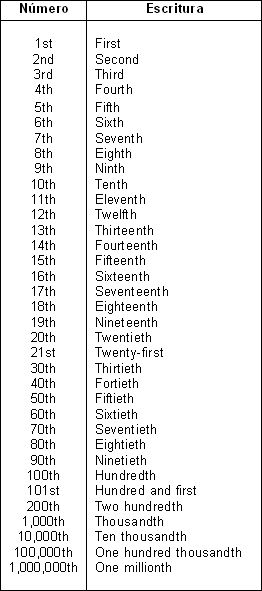
| first | 1st |
| second | 2nd |
| third | 3rd |
| fourth | 4th |
| fifth | 5th |
| sixth | 6th |
| seventh | 7th |
| eighth | 8th |
| ninth | 9th |
| tenth | 10th |
| eleventh | 11th |
| twelfth | 12th |
| thirteenth | 13th |
| fourteenth | 14th |
| fifteenth | 15th |
| sixteenth | 16th |
| seventeenth | 17th |
| eighteenth | 18th |
| nineteenth | 19th |
| twentieth | 20th |
| twenty-first | 21st |
| twenty-second | 22nd |
| twenty-third | 23rd |
| twenty-fourth | 24th |
| thirtieth | 30th |
| thirty-first | 31st |
| fortieth | 40th |
| fiftieth | 50th |
| sixtieth | 60th |
| seventieth | 70th |
| eightieth | 80th |
| ninetieth | 90th |
| hundredth | 100th |
| hundred and first | 101st |
| hundred and fifty-second | 152nd |
| two hundredth | 200th |
| thousandth | 1,000th |
| millionth | 1,000,000th |
| billionth | 1,000,000,000th |
| trillionth | 1,000,000,000,000th |
Note that after the
numeral or digit, we write the last two letters of the word. For example, we take the last two letters of first and add them to the digit 1 to make 1st.
Transcript:
Well I placed a bet on a horse
and I hoped it would win
I was glued to the television
watching the racing
But it wasn't 1st (first) or 2nd (second)
3rd (third) or 4th (fourth)
5th (fifth), 6th (sixth)
7th (seventh) of course
8th (eighth)
9th (ninth)
10th (tenth)
11th (eleventh)
12th (twelfth)
13th (thirteenth)
14th (fourteenth)
15th (fifteenth)
or 16th (sixteenth)
17th (seventeenth)
18th (eighteenth)
19th (nineteenth)
20th (twentieth)
21st (twenty-first)
22nd (twenty-second)
23rd (twenty-third)
24th (twenty-fourth)
25th (twenty-fifth)
26th (twenty-sixth)
27th (twenty-seventh)
28th (twenty-eighth)
29th (twenty-ninth)
30th (thirtieth)
Not even 31st (thirty-first)!
Nowhere to be seen
32nd (thirty-second)
33rd (thirty-third)
34th (thirty-fourth)
35th (thirty-fifth)
36th (thirty-sixth)
37th (thirty-seventh)
38th (thirty-eighth)
39th (thirty-ninth)
40th (fortieth)
Uh huh.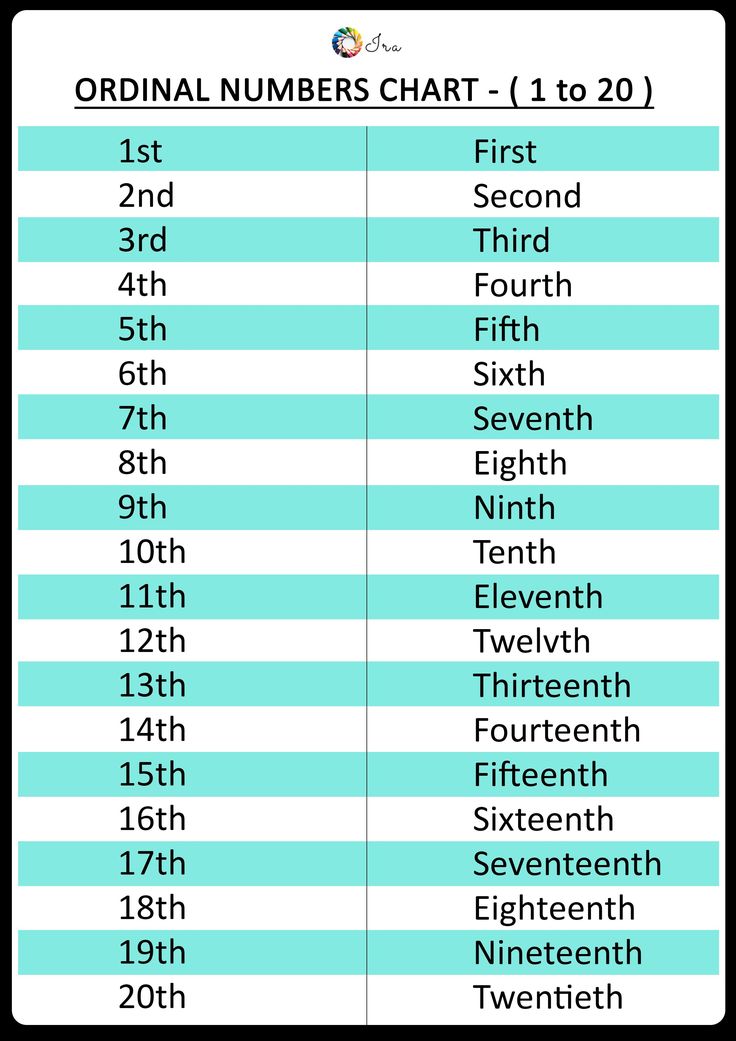 ..
..
I'll carry on counting
41st (forty-first)
42nd (forty-second)
43rd (forty-third)
44th (forty-fourth)
45th (forty-fifth)
46th (forty-sixth)
47th (forty-seventh)
48th (forty-eighth)
49th (forty-ninth)
50th (fiftieth)
Nowhere to be seen
60th (sixtieth)
70th (seventieth)
80th (eightieth)
90th (ninetieth)
100th (hundredth)
101st (hundred and first)
No, I came in last
152nd (hundred and fifty-second)
What a donkey!
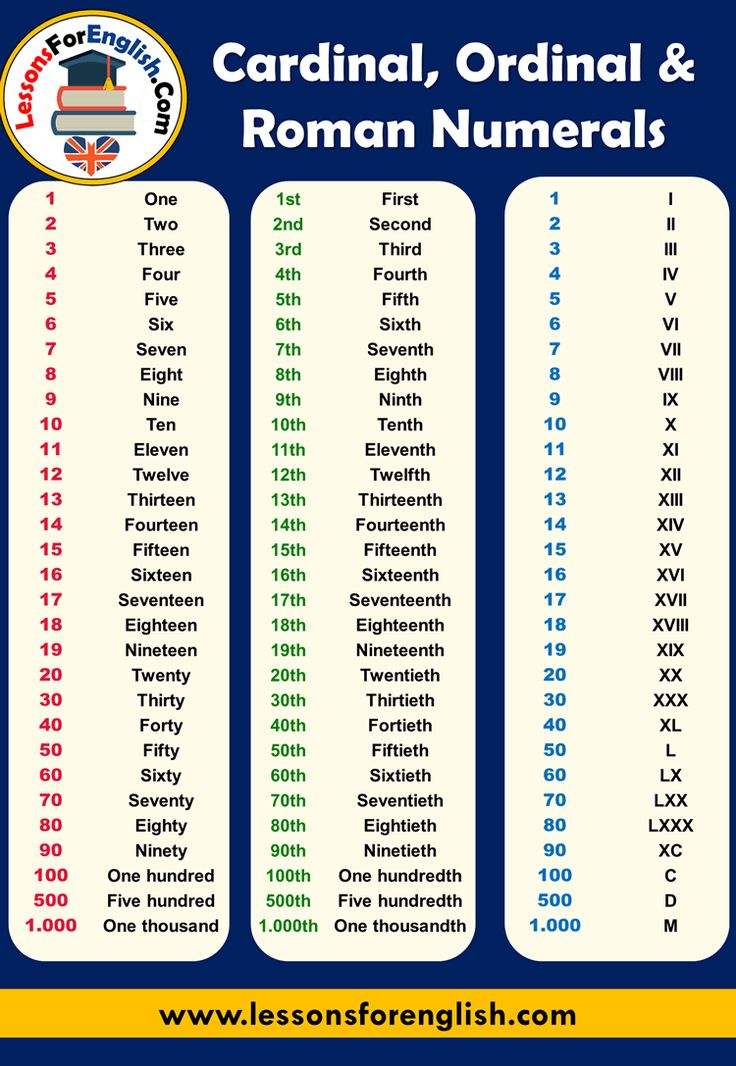
What are Ordinal Numbers? Definition, List, Examples, Facts
What are Ordinal Numbers?
Numbers that are used to represent the rank or position of an object or a person are known as ordinal numbers. They are also referred to as positioning or ranking numbers.The sequence of ordinal numbers vary on the parameters that are based on the positions that are defined, such as weight, height, marks, size, etc. Such numbers are also known as ordinals.
How to Write Ordinal Numbers?
Ordinal numbers or ordinals are written using numerals as prefixes and adjectives as suffixes.
For example, 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 8th and so on. We can easily identify an ordinal number: it talks about positioning.
So, if we were to say, “Bring me the bottle of jam that is lying on the 4th shelf.”, one would know that the ordinal number here is 4, which informs us about the position of the jam bottle.
The above picture shows different floors of a building. Here, we can use ordinal numbers to define the position of the floors.
The numbers 1st (first), 2nd (second), 3rd (third), 4th (fourth), 5th (fifth), 6th (sixth), 7th (seventh), 8th (eighth), 9th (ninth) and 10th (tenth) tell us about the positions of various floors in the building. Therefore, all of them are the ordinal numbers.
Applications of Ordinal Numbers
Ordinal numbers are a great way to talk about the order of something. For example, the order of dates. These numbers are only used when data is provided and the data is to be arranged in order.
For example: Someone who has performed well throughout the year may get the chance to be valedictorian. They would be first in line. But someone who performed well, but was unable to score as much as the person before in various tests and exams, may be second in line to be valedictorian. The person who has not performed well at all, has the least amount of chance.
They would be first in line. But someone who performed well, but was unable to score as much as the person before in various tests and exams, may be second in line to be valedictorian. The person who has not performed well at all, has the least amount of chance.
The picture given below shows some athletes competing in a 500-m race. We can also use ordinal numbers to define their positions in order to see who the winner and runners-up of the race are.
Other examples of ordinal numbers are as follows:
- Jennifer always ranks 2nd in the class.
Here 2nd is the ordinal number that tells you about the position that Jennifer has secured.
- Jane is standing at the 5th place in the queue.
Hereby the ordinal number is 5th, we understand Jane’s position in the queue.
- Jenny came 3rd in the race.
Here, 3rd is the ordinal number which tells you about the place that Jenny has secured in the race.
- The 10th table is reserved.
Here, the ordinal number 10th refers to the number of table reservations made.
Ordinal Numbers 1
– 50 listOrdinal Numbers 51
–100 listOrdinal Numbers v. Cardinal Numbers
The type of numbers that are used for counting the number of objects or persons are known as cardinal numbers. This type of numbers are used for representing the cardinality of the number of elements in a set.
Cardinality means to know about the number of elements in a set.
Cardinal numbers can be the natural numbers that we use while we are counting like one, two, three, four, five and so on.
On the other hand, ordinal numbers are used to determine the rank or position of any object or person. We write ordinal numbers using numbers as prefixes and adjectives as suffixes.
Let us understand the difference with the help of an example.
Some students were asked to collect marbles.
Tom collected 1, Jane collected 2, and Clove collected 3 marbles.
Here the numbers 1, 2, 3 are cardinal numbers as they represent the quantity of marbles.
Now, the one who scores maximum wins. So, Clove stands 1st, Jane stands 2nd and Tom stands 3rd.
Here the numbers 1st, 2nd and 3rd are ordinal numbers as they represent the position of the students.
Ordinal Numbers v. Nominal Numbers
A set of numbers that are used for labeling certain items or places so that they can be identified easily are known as nominal numbers. Whenever we have to identify an object uniquely, we use nominal numbers. These numbers are not of much use because they are just going to give information about location and not about its quantity, quality, etc. Nominal numbers can be used as area codes, on number plates of vehicles, etc. Operations such as addition, subtraction, multiplication and division are meaningless on nominal numbers.
For example: In a phone number like 202 588-6500, the number is a nominal number.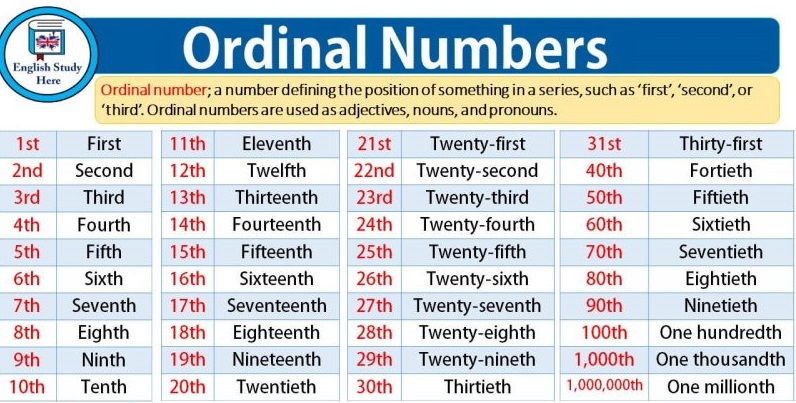 Even if we apply an operation, it will not give us anything meaningful.
Even if we apply an operation, it will not give us anything meaningful.
On the order hand, the ordinal numbers tell us about the rank or position of any object or person.
For example: Sophia lives in the 34th house on San Pablo Avenue, California.
Fun Fact!
11, 12 and 13 are the only numbers to use a suffix ‘–th’ but all other numbers ending with 1 use ‘–st’, those ending with 2 use ‘–nd’ and those ending with 3 use ‘–rd’.
Solved Examples
Example 1: Which English alphabet is 12th from the beginning?
Solution: The alphabet that is 12th from the beginning is L.
Example 2: Kim, Kethy, Kiah and Kaina are sitting in the line in alphabetical order. What is the position of Kiah from the beginning?
Solution: According to alphabetical order, the order in which they’re sitting would be: Kaina, Kethy, Kiah, Kim. So, Kiah is at the 3rd position.
3. Christmas lies on the _____ of December.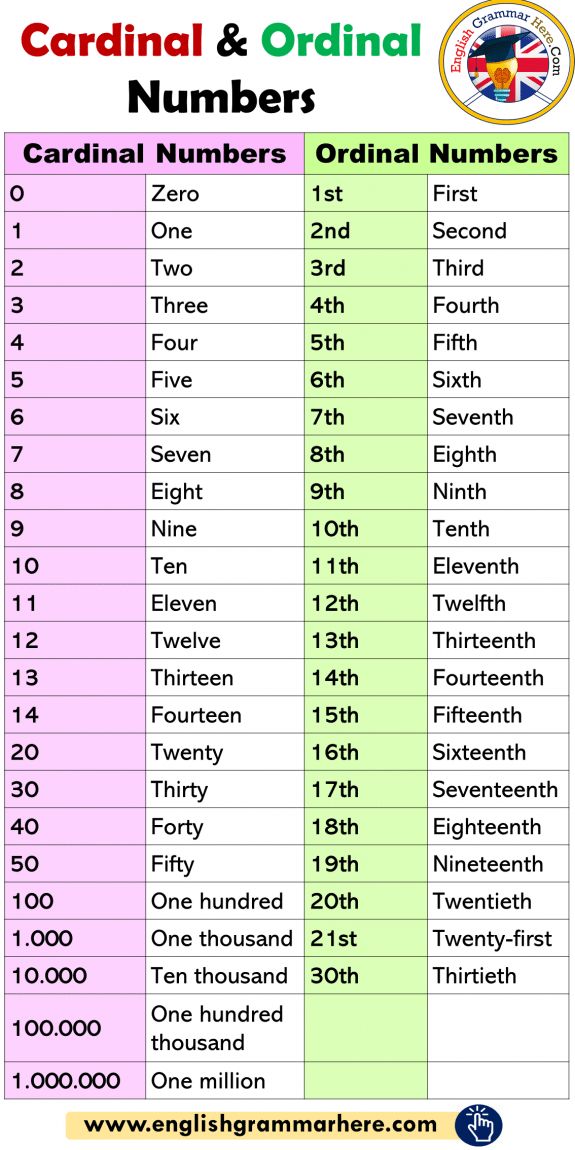 Solution: Christmas lies on the 25th of December.
Solution: Christmas lies on the 25th of December.
Practice Problems
1
Which one of the following denotes an ordinal number?
The vehicle number of Sarah is KL23AB89.
There are 9 apples on the tree.
Catheline came 4th in the drawing competition.
None of these
Correct answer is: Catheline came 4th in the drawing competition.
In the option C, the number 4th is telling about the position of Catheline in the drawing competition.
2
How do you write 51 in ordinal numbers?
51
51st
51th
51rd
Correct answer is: 51st
The ordinal number for 51 for 51st.
3
In the word, “COMPENSATION”, which are the fourth and tenth letters?
M and O
M and N
P and I
E and O
Correct answer is: P and I
The fourth letter is P and the tenth letter is I.
Frequently Asked Questions
Is 0 an ordinal number?
No, we cannot write 0 as an ordinal number.
What are exceptional ordinal numbers?
Exceptional ordinal numbers are the ordinal numbers that do not end with -th. For example: 1st (first), 2nd (second), 3rd (third), etc.
Who invented ordinal numbers?
Ordinal numbers were invented by Georg Cantor in 1883.
Natural numbers: definition, examples, properties
Definition of a natural number
Natural numbers are numbers that we use to count something specific, tangible.
These are what are called natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, etc.
ascending order. The first hundred can be viewed in the table.
| Singularities of natural numbers |
|---|
|
What operations are possible on natural numbers
Sign up for math courses for students in grades 1-11!
Math Demo Lesson
Find out which topics are “lame” for you, and then analyze them without cramming formulas and boring lectures.
Decimal notation of a natural number
At school, we go through the topic of natural numbers in the 5th grade, but in fact, a lot of things can be intuitively clear to us even earlier. Let's talk about important rules.
We regularly use numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. When writing any natural number, you can use only these digits without any other symbols. We write the numbers one by one in a line from left to right, using the same height.
We write the numbers one by one in a line from left to right, using the same height.
Examples of correct writing of natural numbers: 208, 567, 24, 1467, 899112. These examples show us that the sequence of numbers can be different and some can even be repeated.
077, 0, 004, 0931 are examples of incorrect notation of natural numbers, because zero is on the left. The number cannot start from zero. This is the decimal representation of a natural number.
Quantitative meaning of natural numbers
Natural numbers carry a quantitative meaning, that is, they act as a tool for numbering.
Imagine that we have a banana 🍌 in front of us. We can record that we see 1 banana. In this case, the natural number 1 is read as "one" or "one".
But the term "unit" has another meaning: that which can be considered as a whole. An element of a set can be denoted by a unit. For example, any tree from a set of trees is a unit, any leaf from a set of leaves is a unit.
Imagine that we have 2 bananas 🍌🍌 in front of us. The natural number 2 is read as "two". Further, by analogy:
| 🍌🍌🍌 | 3 items ("three") |
| 🍌🍌🍌🍌 | 4 items ("four") |
| 🍌🍌🍌🍌🍌 | 5 items ("five") |
| 🍌🍌🍌🍌🍌🍌 | 6 items (“six”) |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 items ("seven") |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 items ("eight") |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 items ("nine") |
The main function of a natural number is to indicate the number of objects.
If the entry of a number matches the number 0, then it is called "zero". Recall that zero is not a natural number, but it can mean the absence. Zero items means none.
Zero items means none.
One-digit, two-digit and three-digit natural numbers
A one-digit natural number is such a number, which consists of one sign, one digit. Nine single-digit natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Two-digit natural numbers are those that include two signs, two digits. The numbers may be repeated or different. For example: 88, 53, 70.
If the set of items consists of nine and one more, then we are talking about 1 dozen (“one dozen”) items. If one ten and one more, then we have 2 dozen (“two tens”) and so on.
Basically, a two-digit number is a set of single-digit numbers, where one is written on the right and the other on the left. The number on the left shows the number of tens in the natural number, and the number on the right shows the number of ones. There are 90 two-digit natural numbers in total.
Three-digit natural numbers are numbers that include three digits and three digits.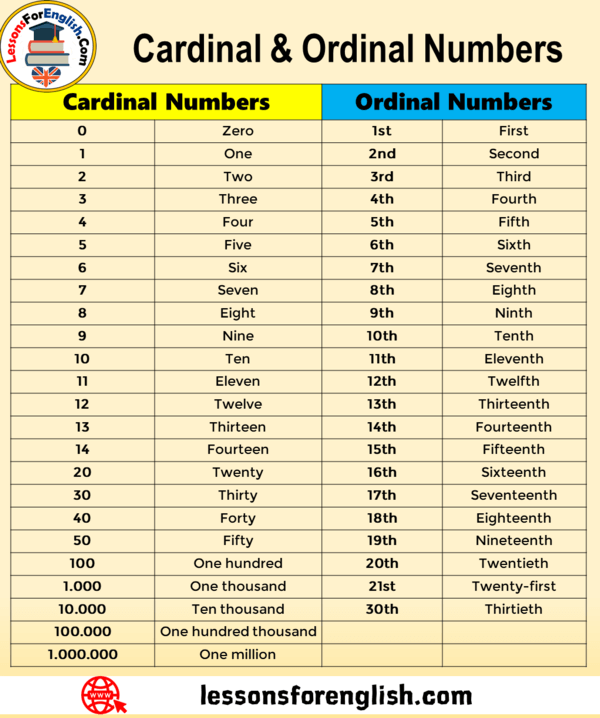 For example: 666, 389, 702.
For example: 666, 389, 702.
One hundred is a set of ten tens. One hundred and another hundred - 2 hundreds. Let's add another hundred - 3 hundreds.
This is how a three-digit number is written: natural numbers are written one after the other from left to right.
The rightmost single digit indicates the number of units, the next one indicates the number of tens, the leftmost one indicates the number of hundreds. The number 0 indicates the absence of units or tens. So 506 is 5 hundreds, 0 tens and 6 ones.
Four-digit, five-digit, six-digit and other natural numbers are defined in the same way.
Multivalued natural numbers
Multi-digit natural numbers consist of two or more digits.
1,000 is a set with ten hundred, 1,000,000 is a thousand thousand, and one billion is a thousand million. A thousand million, just imagine! That is, we can consider any multi-valued natural number as a set of single-valued natural numbers.
For example, 2873206 contains: 6 ones, 0 tens, 2 hundreds, 3 thousand, 7 tens of thousands, 8 hundreds of thousands and 2 millions.
How many natural numbers are there?
One-digit 9, two-digit 90, three-digit 900, etc.
Properties of natural numbers
We already know about the features of natural numbers. And now we will tell you in detail about their properties:
| set of natural numbers | infinite and starts with one (1) |
| each natural number is followed by another | it is more than the previous one by 1 |
| the result of dividing a natural number by one (1) | is itself a natural number: 5 : 1 = 5 |
| the result of dividing a natural number by itself | unit (1): 6 : 6 = 1 |
| commutative law of addition | the sum does not change from the rearrangement of the places of the terms: 4 + 3 = 3 + 4 |
| combination law of addition | the result of adding several terms does not depend on the order of operations: (2 + 3) + 4 = 2 + (3 + 4) |
| commutative law of multiplication | from rearranging the places of factors, the product will not change: 4 × 5 = 5 × 4 |
| combination law of multiplication | the result of the multiplication of factors does not depend on the order of actions; you can at least like this, at least like that: (6 × 7) × 8 \u003d 6 × (7 × 8) |
| distributive law of multiplication with respect to addition | to multiply the sum by a number, you need to multiply each term by this number and add the results: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| distributive law of multiplication with respect to subtraction | to multiply the difference by a number, you can multiply by this number separately reduced and subtracted, and then subtract the second from the first product: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| distributive law of division with respect to addition | to divide the sum by a number, you can divide each term by this number and add the results: (9 + 8) : 3 = 9: 3 + 8 : 3 |
| distributive law of division with respect to subtraction | to divide the difference by a number, you can divide by this number first reduced and then subtracted, and subtract the second from the first product: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Digits of a natural number and the value of the digit
Recall that its value depends on the position on which the digit stands in the record of the number. So, for example, 1123 contains: 3 units, 2 tens, 1 hundred, 1 thousand. At the same time, we can formulate it differently and say that in a given number 1123, the digit 3 is located in the units digit, 2 in the tens digit, 1 in the hundreds digit and 1 serves as the value of the thousands digit.
So, for example, 1123 contains: 3 units, 2 tens, 1 hundred, 1 thousand. At the same time, we can formulate it differently and say that in a given number 1123, the digit 3 is located in the units digit, 2 in the tens digit, 1 in the hundreds digit and 1 serves as the value of the thousands digit.
The digit is the position, the location of the digit in the record of a natural number.
Each category has its own name. The most significant digits are always on the left, and the least significant ones are on the right. To remember faster, you can use a table.
The number of digits always corresponds to the number of digits in the number. This table contains the names of all digits for a number that consists of 15 characters. The following digits also have names, but they are used extremely rarely.
The lowest (lowest) digit of a multi-digit natural number is the units digit.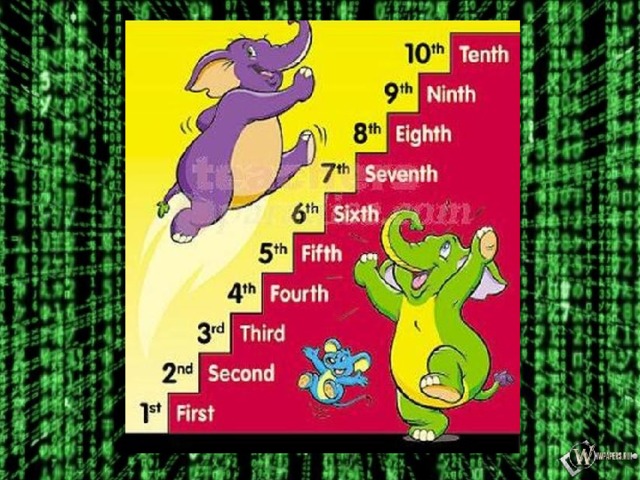
The highest (highest) digit of a multi-digit natural number is the digit corresponding to the leftmost digit in the given number.
You must have noticed that textbooks often put small spaces when writing multi-digit numbers. This is done so that natural numbers are easy to read. And also to visually separate different classes of numbers.
Class is a group of digits that contains three digits: units, tens and hundreds.
Decimal number system
People at different times used different methods of writing numbers. And each number system has its own rules and features.
Decimal number system is the most common number system in which ten digits are used to write numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
In the decimal system, the value of one and of the same digit depends on its position in the number entry. For example, the number 555 consists of three identical digits. In this number, the first digit from the left means five hundred, the second - five tens, and the third - five units. Since the value of a digit depends on its position, the decimal number system is called positional.
For example, the number 555 consists of three identical digits. In this number, the first digit from the left means five hundred, the second - five tens, and the third - five units. Since the value of a digit depends on its position, the decimal number system is called positional.
Question for self-test
How many natural numbers can be marked on the coordinate ray between points with coordinates:
-
0 and 15;
-
20 and 50;
-
100 and 130?

 The natural series is infinite.
The natural series is infinite.  + text | 8-10 cells + text
+ text | 8-10 cells + text  + video analysis | 6 cells + video analysis | 7 cells + video analysis | 8 cells + video analysis | 9 cells + video analysis | 10 cells + video analysis
+ video analysis | 6 cells + video analysis | 7 cells + video analysis | 8 cells + video analysis | 9 cells + video analysis | 10 cells + video analysis 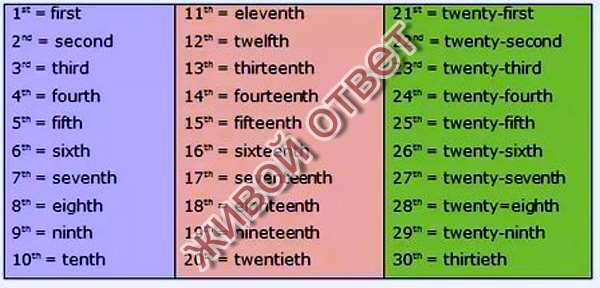 + video analysis | 6-7 cells. + video analysis | 8-10 cells + video analysis
+ video analysis | 6-7 cells. + video analysis | 8-10 cells + video analysis 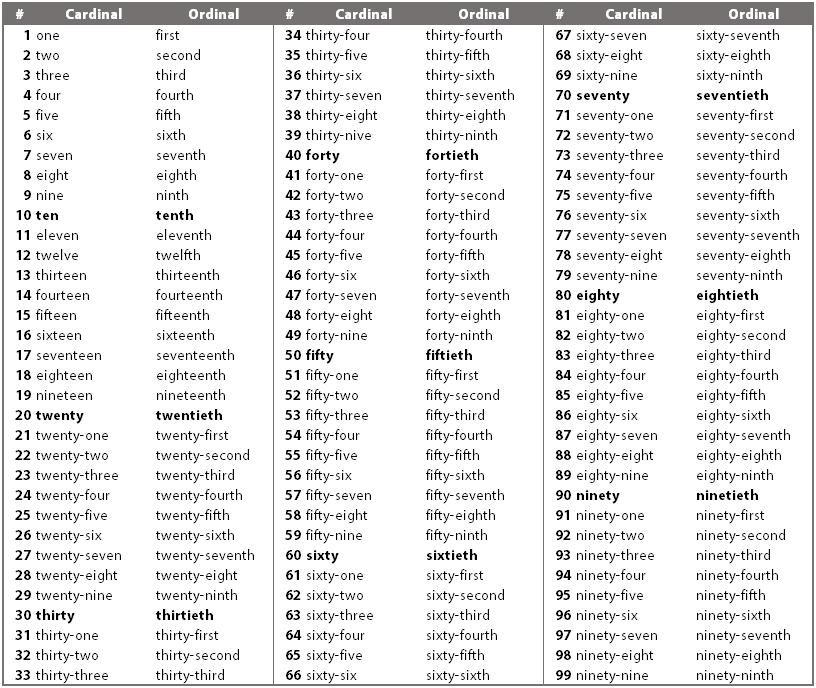 | 5 cells | 6 cells | 7 cells | 8 cells | 9 cells | 10 cells
| 5 cells | 6 cells | 7 cells | 8 cells | 9 cells | 10 cells  + text | 6-7 cells. + text | 8-10 cells + text
+ text | 6-7 cells. + text | 8-10 cells + text 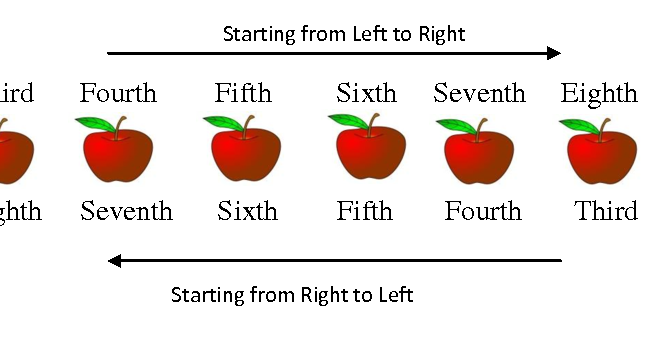 | 4 cells | 5 cells | 6 cells | 7 cells | 8 cells | 9 cells | 10 cells
| 4 cells | 5 cells | 6 cells | 7 cells | 8 cells | 9 cells | 10 cells  + audio
+ audio 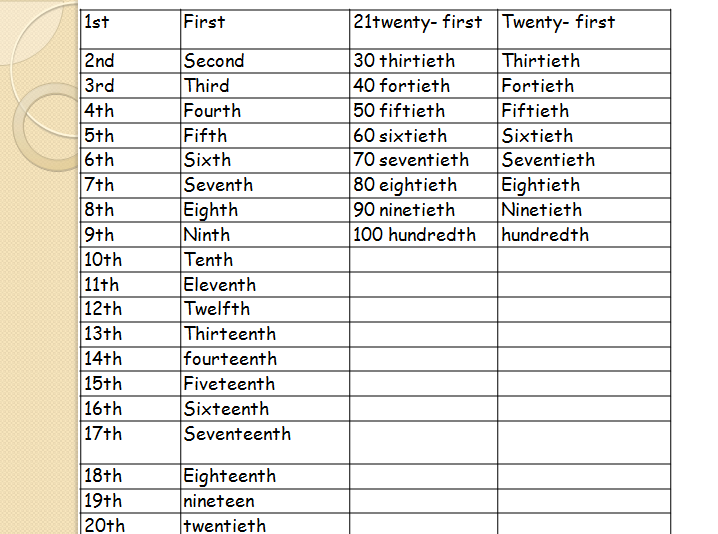 | 6-7 cells. | 8 cells | 9-10 cells
| 6-7 cells. | 8 cells | 9-10 cells  | 8-10 cells
| 8-10 cells  practice
practice  | 8 cells | 9 cells | 10 cells | 11 cells
| 8 cells | 9 cells | 10 cells | 11 cells 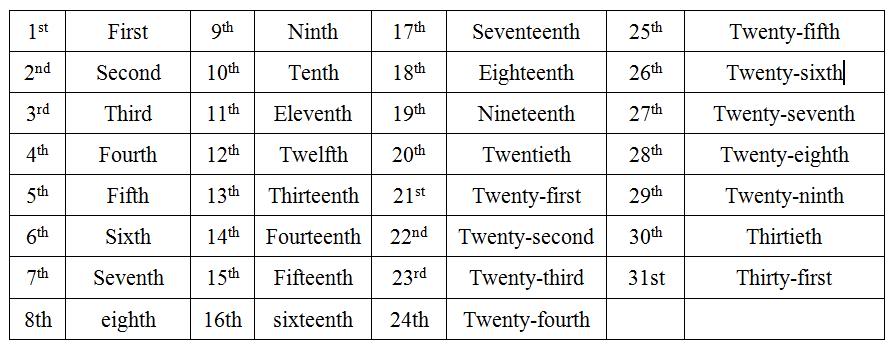 + audio
+ audio