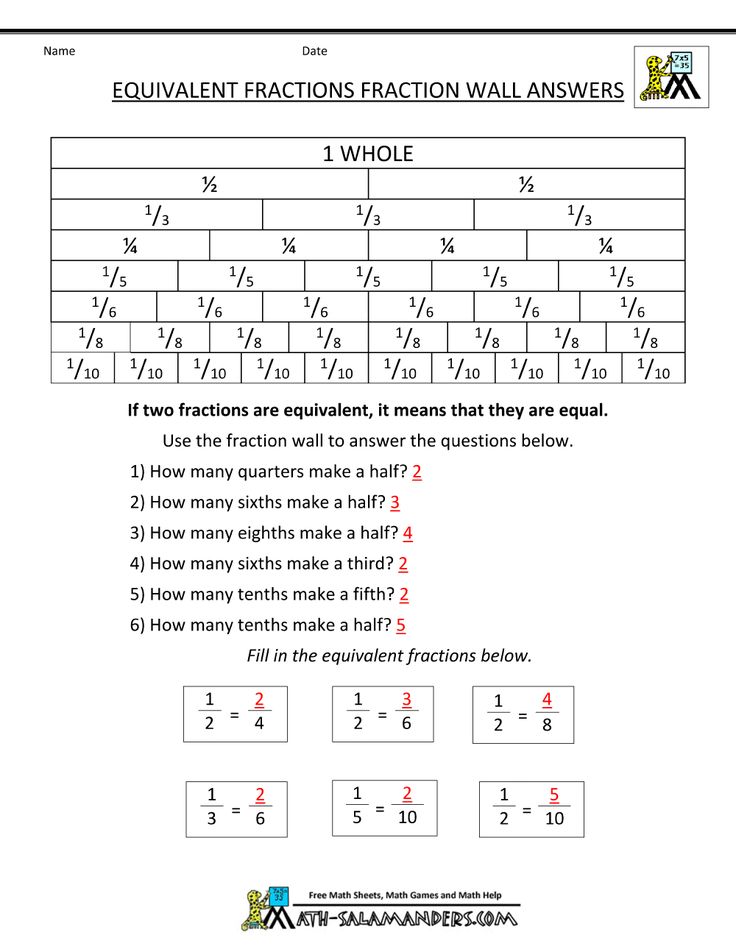
Fractions activities for 1st grade
Fraction activities, games, and read alouds for 1st and 2nd grade
Happy Tuesday! I know many of you are on Spring Break this week but I wanted to share several fraction activities and games that are great for 1st grade and 2nd grade. There are lots of fun ones that will help amp up the engagement during your fraction unit. Our state standard focuses on fractions of a whole – not of a set.
Alrighty, let’s start planning!
FRACTION ACTIVITIES AND GAMES
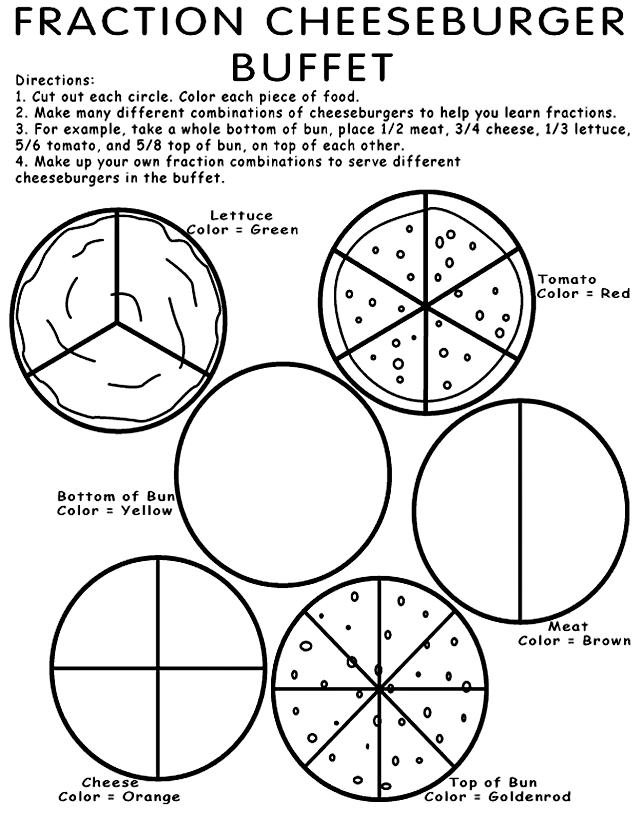
For years now I’ve used sticky notes to introduce fractions and partitioning shapes in 1st grade. Over the years I collected sticky notes in various shapes and sizes…anytime I’m out and about and see unique shapes, I throw ’em in the cart. Amazon is also a great place to find lots of sticky notes. I have this pack and they’re great.
I always start off introducing equal and unequal when partitioning the different shapes. These anchor charts are easy to make and kids love them. I gave each student a sticky note and let them add it to the chart under the correct category – this is a great way to get lots of discussion and thinking going. Of course relating this to sharing food is a great way to connect to the real world.
Sticky notes are also great for students to use to fold, draw, and cut the shapes into various fractions. This Book of Fractions is a great activity to hold all their sticky note shapes.
Here are a few other fraction activities and games for partitioning shapes to create different fractions.
Spin and Make can be used in partners, independently, stations, or as a whole group. If using it as a whole group, simply project the activity onto your white board and use a magnetic spinner on the board. These are my favorite; I’ve used them for years. To play, students spin the spinner, create the shape they land on and partition it into the corresponding amount of pieces.
For Fraction Wreaths, students color in the circles to create their own fractions.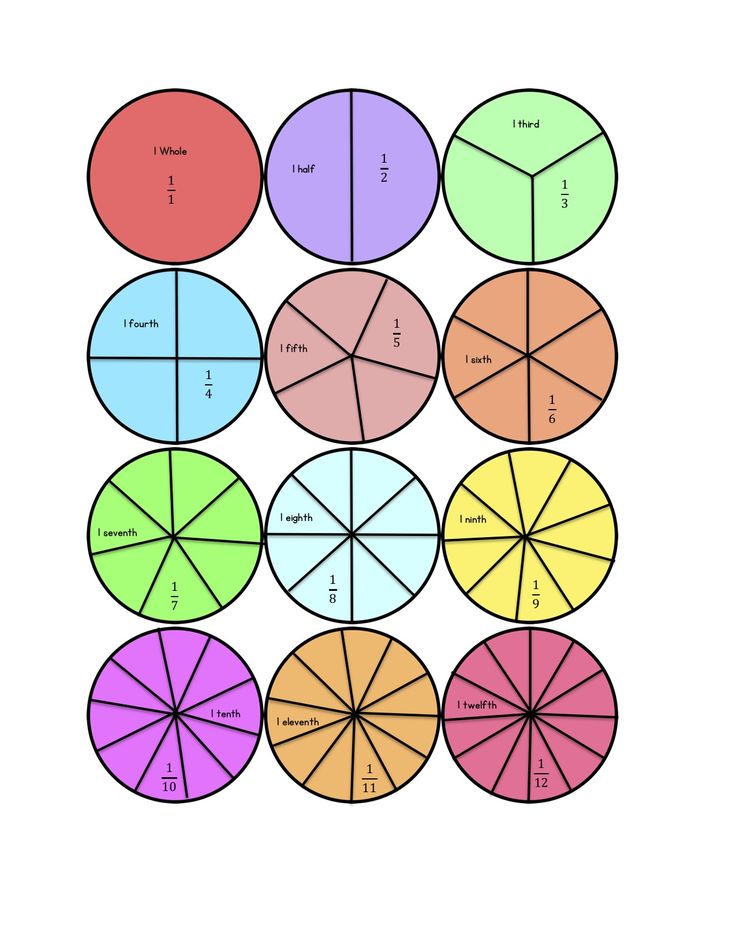
Afterwards, they write the fraction in word form and/or number form. The colors of the wreath can be changed out to match the season….Christmas could be red bow and green strips…fall could be brown bow and yellow strips, etc. The wreath is a paper plate with the middle cut out. Easy peasy!
Next up is a class favorite from a few years ago. We played this with place value (see here) and lemme’ just tell ya’…it was a HIT! Loads of fun, meaningful, easy prep, peer collaboration…talk about engagement!
To play: group your students in table groups (this could be played independently but peer collaboration is my favorite!) and give each group a fraction card and several sticky notes. I like to give each table group a different color – this makes it easy to quickly see which table group is having trouble with the skill, etc.
Hang the different fraction posters around the room (square model, circle model, rectangle model, word form, numerator, denominator)…
Students will work together as a table group to represent the fraction on their card in the various forms that are on the posters.
After they have it the form of their fraction on their sticky note, they stick it to the correct poster. Y’all! They love it! It’s such a fun fraction game! Plus, it helps the different forms of fractions and ways that fractions are represented, STICK.
Spin It is another fraction game that is a blast. This is projected onto your whiteboard and used with a magnetic spinner. There are several different Spin It slides available here. To play: students (or you) spin the spinner, and students write the word form on their desks with an expo marker….or they could verbally tell you the fraction. You can play in table teams and make it a race to write the correct fraction first. My class always liked to play Spin It in table groups.
Flip and Share is a partner game where students take turns flipping over two cards and comparing them.
Tic-Tac-Find is another fun partner game to practice reading and identifying fractions.
Fraction Walk is a “Write the Room” activity and Read, Match, Scoot is played like the classic game of Scoot.
I love using these type of activities for assessments.
I love this craftivity and hativitiy to wrap up the fraction unit!
And because you gotta get those grades in…Fraction Match Up sort and these Flip Books work well for informal assessments!!
There are several other flip book options here.
Whew. That was a lot, but I hope these activities will create engagement in your classroom and make learning about fraction fun for you and your students!
You can find all these activities here or Pin the picture below to your Pinterest board.
Oh and here are few old fraction freebies.
Before I go, I’ve rounded up some fraction read alouds for you. These are available on Amazon (affiliate links included), but you could definitely check your school or local library to see if they have them.
A Fraction’s Goal – Parts of a Whole
Fraction Fun
Full House: An Invitation to Fractions
Fractions in Disguise
Fraction Action
Give Me Half
If I were a Fraction
Twinderlla, A Fractioned Fairy Tale
Peg and Cat: The Pizza Problem
22 Fun and Free Fraction Games and Activities For Kids
Fractions can be a challenge to teach.
That’s why it’s important to have a wide array of activities on hand to help kids learn this tricky concept. These fraction games are a fun way to give them practice, in the classroom or at home.
1. Sort sticky notes
Divide sticky notes into sections, then have kids sort them onto anchor charts. We especially love using fun shapes like hearts or stars!
Learn more: Smitten With First
2. Connect fractions to learn and win
Repurpose a Connect Four set to play fraction games! The goal is to match not only your colors but the fractions themselves. For instance, you need four one-fourths in a row, but only three one-thirds, so there’s strategy involved, too.
Learn more: No Time for Flash Cards
3. Explore the Fraction of the Day
Fractions are one of those math concepts we actually use quite a bit in everyday life. Make them part of routine practice by posing a new Fraction of the Day question each morning.
Learn more: Runde’s Room
4.
Grab the fun of fraction SpoonsIf you’ve played Spoons before, you know the drill. Match four of a kind (this time using free printable fraction cards found at the link below), and you get to grab for a spoon—and so does everyone else! The loser takes one letter of the word SPOON, and play continues.
Learn more: Games 4 Gains
5. Get them in order
Comparing fractions is definitely a bit of a challenge. This simple free printable game tasks kids with putting a series of four fractions in order from smallest to largest. They can race to see who finishes first or just challenge themselves to get the right answer.
Learn more: Get Them in Order/Math Geek Mama
6. Fight it out in a fraction war
Your kids probably already know how to play War with cards. This version just adds a fraction aspect. Students deal two cards: a numerator and a denominator, and then determine whose fraction is the largest. The winner keeps all four cards, and play continues until the cards are gone.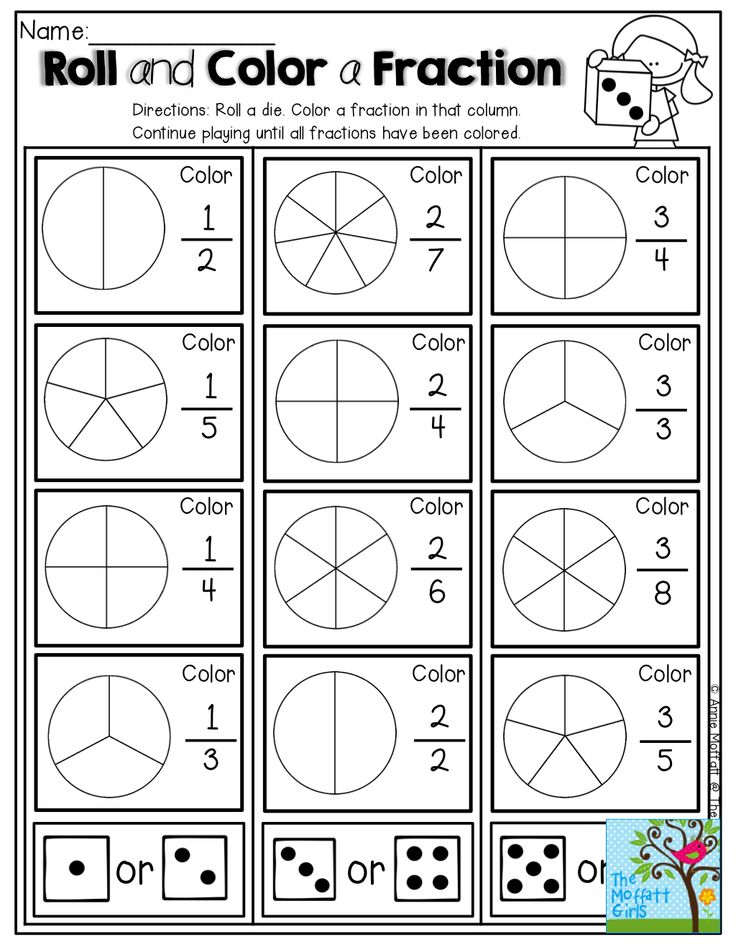
You can also play using these free printable fraction cards.
7. Noodle around with fractions
It’s so easy to make these pool noodle math manipulatives, which you can then use for all kinds of fraction games. Learn how to make them and get ideas for using them here.
8. Build excitement with LEGO fraction games
Visualizing what fractions represent is easier (and a lot more fun) when you use LEGO bricks! Lay them out side by side or build towers. No matter how you play, this is a sure-fire hit.
Learn more: JDaniel4’s Mom
9. Try making paper plate fractions
Such a fun, colorful way to play with fractions and equivalencies! Get the full instructions here.
10. Boogie down with newspaper fractions
Turn the music up! Start out with a full paper as each student’s dance floor, then fold down to one half. Continue folding the paper into smaller and smaller dance floors and watch kids get creative as they try to stay on the paper.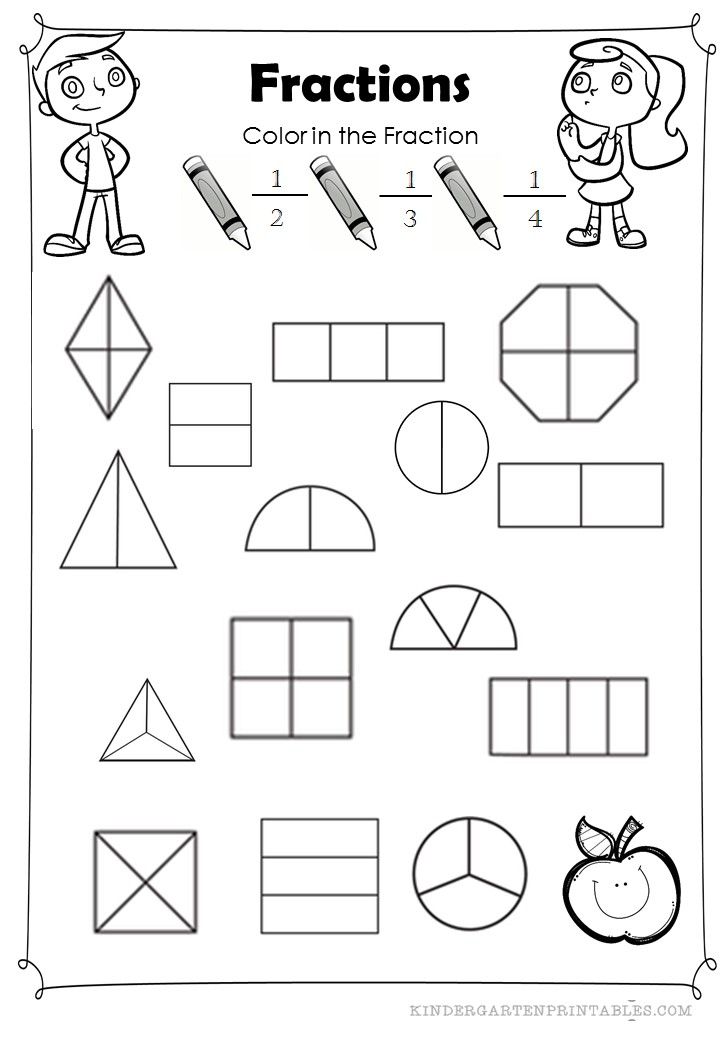
Learn more: Mrs. King’s Music Class
11. Move onto Fraction Avenue
This is such a fun activity! Grab the free printable street scene at the link. Then, have kids follow the directions to add details. For instance, 2/8 of the homes have dogs outside. Ask kids to reduce the fraction, then draw the correct number of pups.
Learn more: Ashleigh’s Education Journey
12. Jump into fraction hopscotch
It’s hopscotch—with a fraction games twist! Draw a hopscotch board on the playground (or outline one with tape on your classroom or hallway floor). Label the squares with fractions instead of whole numbers. Kids throw a marker and jump to where it lands, then name the equivalent fractions for that square.
Learn more: Capturing Classroom Ideas
13. Turn your name into fractions
Who knew there were so many fractions hiding inside your own name? Pose these questions to students, and ask them to find their own fractions too.
Learn more: Tunstall’s Teaching Tidbits
14. Have a fraction picnic
Provide a variety of food images cut from magazines or printed out from the Internet. Students plan a picnic and choose the food they want to bring along. Using a ruler and scissors, cut portions of their food choices and glue them to a paper plate. Finally, label each item with the fraction name. Bon appétit!
Learn more: Fraction Picnic/E is for Explore
15. Put a spin on the fraction fun
Kids get a kick out of stuff that spins, so they’ll love these free printable fraction games. Since the spinners are just pencils and paper clips, every kid can have their own as they practice their fraction skills. Get the whole free set of games here.
16. Color your way to fraction bingo
There’s learning and strategy involved when you play fraction bingo. Kids color in portions of the circles in an effort to get five in a row, based on the fractions the teacher calls out.
Of course, the best part is getting to shout “BINGO!”
Learn more: School Time Snippets
17. Reduce fractions and race to the finish
Kids draw a card (the free printable cards and board are at the link below) and reduce the fraction shown. They then move along the board to the next square that matches. First to the end wins!
Learn more: 123Homeschool4Me
18. Draw on their creativity with fraction Pictionary
Can you draw a fraction—without using any numbers? That’s the challenge of this fractions game. Kids can draw single objects divided to represent fractions or be more creative. For example, they might draw three apples and two oranges to represent three-fifths.
Learn more: Fraction Pictionary/E is for Explore
19. Get into a fraction fiasco
Once they get the rules down, kids will be adding fractions and checking each other’s work in this free printable game. You’ll find all the instructions and the game board at the link below.
Learn more: Learn With Math Games
20. Do the math with domino fractions
Dominoes are like ready-made fractions! Multiply (or add, subtract, or divide) them and reduce the results. Turn it into a race to see who can finish—correctly—first.
Learn more: Relentlessly Fun, Deceptively Educational
21. Play with pattern blocks
If you’ve already got pattern blocks on hand, put them to good use in some fractions games. In this one, kids spin to find out how many blocks they get to add to their board in an effort to be the first to build six complete shapes.
Learn more: Pattern Block Fractions/Math Geek Mama
22. Shake it up with number bonds
All you need is a plastic cup and two-sided counters. Kids shake the cup and pour the counters on the table, then count how many of each color landed face up. For example, if 13 counters were rolled, six red and seven blue landed face up. Six and seven are both parts of thirteen (the whole).
Have students write the number bond and fractions for each color.
Learn more: Number Bond Fractions/E is for Explore
What are your favorite fraction games for kids? Come and share in our WeAreTeachers HELPLINE group on Facebook.
Looking for more math games? Try this roundup of online math games for every grade level.
Fractions - how to explain actions with fractions to a child
The topic of fractions is one of the most difficult for schoolchildren. To understand them for an unprepared child, and even more so to perform operations with them, can be quite difficult. But even the most difficult task can become simple and understandable if approached correctly. For children, you need to use fantasy, visualization and elements of the game. And also to remain calm and patiently explain, even if it needs to be done many times.
How to explain the essence of fractions to a child?
The word "fraction" seems to speak for itself - it means crushing, division.
In the school curriculum, they begin to study fractions only in the 5th grade, having mastered all the actions with integers. But it is advisable to start acquaintance with them in advance, even at the senior preschool age. This forms spatial representations in children and trains logical thinking.
First you need to explain the concept of shares to the child. This is very easy to do with illustrative everyday examples. The simplest and most affordable is food. For example, a pie is a whole. It can be divided into several identical parts. One piece of such a pie will be called one share of all possible. Dividing the cake into four parts, one piece is called one fourth.
Anything can be divided this way: apples, oranges, chocolate bars, candies in a box, etc. Another great visual material for learning fractions is Lego bricks. With their help, you can divide the whole into equal parts very easily. Children quickly memorize the shape of the cubes, and they do not need to constantly recalculate the number of protruding elements on them.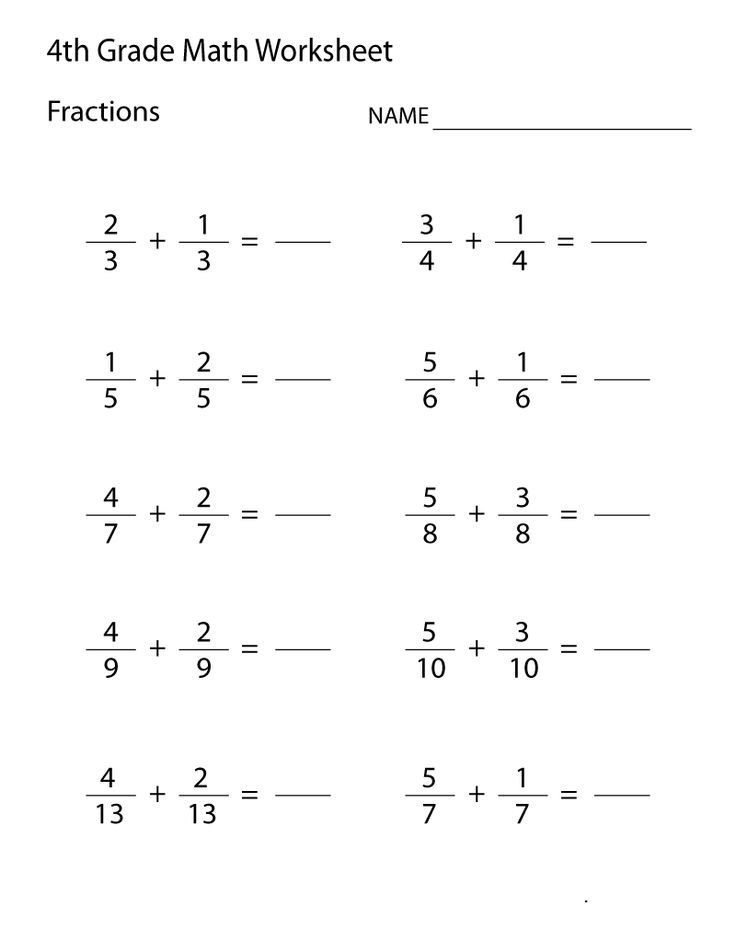
If a child sees the practical use of fractions and their demand in real life, it will be easier for him to understand them and realize the importance of obtaining mathematical knowledge and skills.
What do you need to know about fractions?
1. A fraction is a non-integer number, it denotes the number of parts of a whole.
2. A fraction is less than a whole.
3. The more parts the whole is divided into, the smaller these parts are, and vice versa - the fewer parts, the larger they are, respectively.
To denote shares in mathematics, the concept of an ordinary fraction is used. With its help, you can record absolutely any number of shares you need.
An ordinary fraction consists of two parts, called the numerator and denominator. They are written separated by a horizontal line or a line slanted to the right. The denominator is written below or to the right of the fractional bar, it shows the total number of parts from the whole by which it was divided.
And the numerator is written at the top or to the left of the fractional line and shows how many parts of the whole have now been taken.
Let's get back to our pie. It is obvious that it is realistic to divide it into any number of equal parts. Depending on how many parts it is divided into, the denominator of the fraction also changes. For a pie divided by one straight line into two parts, the denominator will be 2, for a pie divided into three parts - 3, etc. The numerator, in turn, shows how many parts are now taken. If you take only one part out of two, then you get a fraction 1/2, only two out of three - 2/3, etc.
What are mixed fractions?
In mathematics, correct and improper fractions are distinguished. Correct - those whose numerator is less than the denominator. For example: 1/3 , 2/5 , 4/12 . But it also happens that the numerator becomes larger than the denominator. If you explain in detail, then more parts of the pie were taken than there were those into which it was divided.
This is quite possible in life and in mathematics.
In such fractions, you can separate the whole part and the remaining fraction after that. That is, it will be seen how many whole pies are taken and plus a certain number of its parts. You need to imagine well what is described, or even check it in practice, and not just memorize the formulas. Then the reduction of fractions will be performed by the child meaningfully and accurately.
To convert an improper fraction to a mixed number, first divide the numerator by the denominator. As a result, we almost always get an integer and some kind of remainder. An integer and must be written as an integer part. And the remainder is sent to the numerator of the fractional part. Only the denominator remains unchanged.
Fractions with the same number above and below the fractional bar are also called incorrect: 6/6 , 12/12 , etc. Obviously, they can be turned into 1. Visually, this is taken as many pieces of the pie as it is and was divided, that is, the whole pie.
Examples:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Task:
Find the whole part of improper fractions:
- 15/4,
- 22/12,
- 30/7.
You can do the opposite procedure - turn a mixed number into an improper fraction. This operation is often used in mathematical calculations, so it will be useful to learn about it. To do this, you must first multiply the integer part and the denominator. Then add the resulting number to the numerator, and leave the denominator the same.
Examples:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Job:
1. Convert improper fraction to mixed number:
- 27/4,
- 18/5,
- 45/7.
2. Perform the inverse of the first task - turn the mixed number into an improper fraction:
- 3 4/5;
- 12 7/11.
Decimals
Fractions whose denominators contain numbers that are multiples of ten - 10, 100, 1000, etc. - in mathematics can be denoted as follows. The integer part is written first, and then the numerator from the fractional part, separated by a comma.
For example, let's try to write 5 4/10 as a decimal fraction. We write the integer part (5), put a comma and then write the numerator of the fractional part (4). We get: 5.4 . This fraction is read like this: "five whole and four tenths." A number represented in this form is called a decimal.
There are also decimals without an integer part. For example: 7/100 . How to be in that case? To write down a similar fraction, write zero, put a comma and then write down the numerator of the fraction - 0.07 . Such a fraction is read as "zero point, seven hundredths."
Decimals are very handy, they are used in exact calculations.
The decimal system has been used by mankind since ancient times. It is intuitive and simple.
Reference:
Convert the following fractions to decimals:
- 8/10,
- 4/100,
- 7/1000.
Reduction of fractions
Reduction of fractions is performed in order to simplify them. If the numerator and denominator of a fraction are such that they are divisible by the same number (have a common divisor), then you can simply divide them by this number, thereby simplifying the fraction. This mathematical operation is called fraction reduction. To understand this, consider a couple of such examples.
Example 1. Reduce the fraction 8/12
The solution is as follows. The largest number that both 8 and 12 are divisible by is 4. Therefore, to reduce the fraction, simply divide its numerator and denominator by 4:
8/12 = 8:4 / 12:4 = 2/3
Example 2. Reduce the fraction 10/25
Solution.
The largest number that both 10 and 25 are divisible by is 5. Therefore, to reduce the fraction, we divide its numerator and denominator by 5:
10/25 = 10:5 / 25:5 = 2/5
A fraction is called in which the numerator and denominator have only one common divisor - one.
Reference:
Reduce the following fractions:
- 6/18,
- 20/40;
- 7/21.
Addition of fractions
First, let's analyze the addition of fractions with the same denominators. In this case, the operation is extremely simple. The numerators of fractions are added, but the denominator remains the same.
Examples:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Reference:
Add fractions with the same denominators:
But things get more complicated if you need to add fractions with different denominators. In this case, it is necessary to reduce the fractions to the smallest common denominator.
To do this, you need to find the least common multiple. This is a number that is divisible by both of these numbers without a remainder. For example: 3/7 + 2/6 . The least common multiple for numbers 7 and 6 will be 42.
Next, we look for additional factors for each of the fractions. To do this, we divide the least common multiple found at the previous stage in turn by the denominator of each of the fractions:
- 42 / 7 = 6 - this will be an additional factor for 3/7;
- 42 / 6 = 7 is, respectively, an additional factor for 2/6.
Both parts of each of our fractions, both the numerator and the denominator, are multiplied by our own multiplier, defined above:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
We add the resulting fractions in the same way as the fractions with the same denominators already analyzed above:
- 18/42 + 14/42 = 32/42
If possible, the fraction is reduced.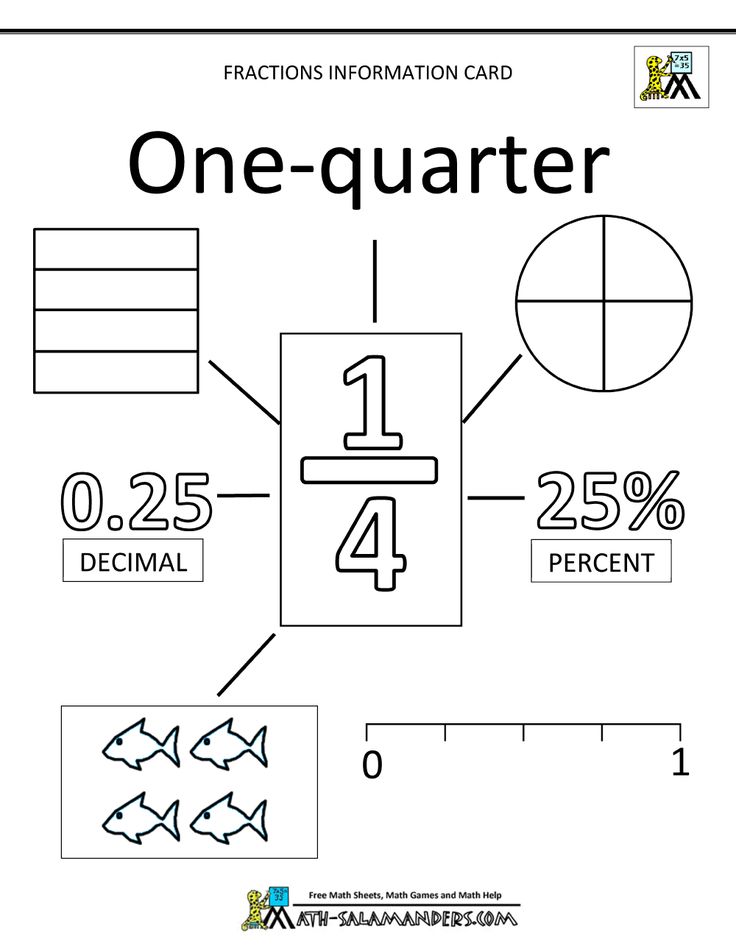
If the fraction turned out to be incorrect, then the whole part should be selected from it.
Task:
Add fractions with different denominators:
Subtraction of fractions
This operation is carried out similarly to addition. To subtract two fractions with the same denominators, you need to find the difference between their numerators, and leave the denominator the same.
Example:
7/9 - 2/9 = (7-2) / 9 = 5/9
Task:
Subtract fractions with the same denominator:
you also have to find the least common multiple and additional factors. Then, by analogy with addition, subtract.
Example:
6/7 - 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Reference:
Subtract fractions with different denominators:
Multiply fractions
There are two options for multiplying fractions.
Let's consider each of them in detail.
Multiplication of ordinary fractions
In this case, the numerators of both fractions are multiplied - this will be a new numerator. The denominators of both fractions are also multiplied - this will be the new denominator.
Example:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
If possible, reduce fractions before multiplying. This will make the next steps easier.
Example:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Multiplication of mixed fractions
To do this, you need to turn the fractions into improper ones and then follow the algorithm given in the first paragraph.
Example:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Job:
Multiply fractions:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Division of fractions
Having mastered multiplication, division can also be handled easily. The rule for dividing fractions is as follows: when dividing one fraction by another, you need to multiply the first by the reciprocal (inverted) second fraction. Or, in other words, multiply the numerator of the first by the denominator of the second (this will be the new numerator), and multiply the denominator of the first by the numerator of the second (this will be the new denominator).
Example:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
There are times when a fraction needs to be divided by an integer. In this case, the fraction should be represented as an improper fraction. Her numerator will be this whole number, and the denominator will be just one. Next, you need to act according to the already familiar rule for dividing fractions from the previous case.
Example:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Reference:
Divide fractions:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Comparison of fractions
If fractions with the same denominator are compared, it is obvious that the larger one will be the one with the larger numerator.
Example:
1/5 < 4/5 because the denominators are the same and the numerator 1 is less than 5.
Example:
1/2 > 1/8 , since the numerators are the same, but the denominator of 8 is greater than 2.
Fractions with different denominators cannot be compared so easily. You must first determine their common denominator and reduce both fractions to it. The rules for this operation were given above. We get fractions that can be compared very easily.
Example:
Compare fractions 2/5 and 1/10 . To do this, we bring them to a common denominator - 10. We get 4/10 and 1/10 . Now we compare fractions that already have the same denominators: 4/10 > 1/10 .
There is one secret to remember. If one of the compared fractions is incorrect, then it is always greater than the correct one. If you think about and remember the properties of fractions, then everything becomes clear. After all, an improper fraction will always be greater than one, while a correct one, on the contrary, will always be less.
Task:
Determine which fractions are shown in the picture and compare them:
So, we have considered fractions, the rules of all actions with them. We hope that our explanations and recommendations will be very useful. Start introducing your kids to fractions before school. Having mastered these concepts well, the child will then easily cope with the recording of fractions and with actions with them.
Mathematics and logic for children 7-13 years old
Developing logical thinking through solving plot mathematical problems in an interactive game format
learn more
See also:
- Multiplication table for children
- How to explain to a child the composition of a number?
Fractions
Fractions is a topic about which half of the inhabitants of our planet stumble.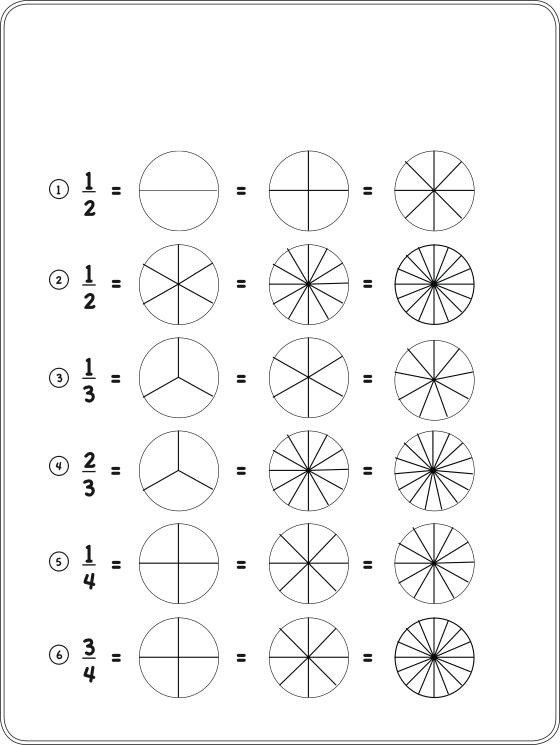
If you ask people from what topic they started having problems with mathematics, then most of them will answer - with fractions.
These people cannot be reproached. Fractions are indeed not an easy topic. The topic of fractions requires a lot of patience and attention, especially if a person is studying it for the first time.
But there is good news. If you are patient and master fractions, then we assure you that further study of mathematics will become simple and interesting for you.
And if you have studied the previous lesson well, which was called division, then you can be sure that you have already mastered fractions by half.
What is a fraction?
In simple terms, a fraction is a part of something. This "something" can be anything - food, money, a number. In the people, a fraction is called a share. The word "fraction" itself also speaks for itself - a fraction means crushing, division, division.
Consider a real life example.
We bought ourselves a pizza to eat during the day. Suppose we decide to divide it into four parts in order to gradually eat one piece at a time.
Look at this picture. Imagine that this is our pizza divided into four slices. Each piece of pizza is a fraction, because each piece individually is a part of the pizza.
Let's say we ate one piece. How to write it down? Very simple. Draw a small line first:
At the bottom of this line is how many slices the pizza was divided into. The pizza was divided into four pieces. This means that four is written at the bottom of the line:
And at the top of this line is written how many slices of pizza were eaten. One piece was eaten, so we write a unit on top:
Such records are called fractions . A fraction consists of a numerator and a denominator.
The number written on top is called as the numerator of the fraction .
The number written below is called the denominator of the fraction .
In our example, the numerator of the fraction is one, and the denominator of the fraction is four. This fraction can be read like this: "one fourth" or "one piece out of four" or "one fourth" or "quarter" - these are all synonyms.
Now imagine that we have eaten another slice of the same pizza that has been divided into four slices. How to write such a fraction?
Very simple. We write 2 at the top (since two pieces have already been eaten), and at the bottom we write 4 (since there were 4 pieces in total):
two fourths" .
Now imagine that we divided the pizza not into four parts, but into three.
Let's say we ate one slice of this pizza. How to write such a fraction?
Very simple. Again, a small line is drawn. At the bottom of this line, the number 3 is written, since the pizza is divided into three parts, and at the top of this line, the number 1 is written, since one piece is eaten:
This fraction reads like this: "One third" or "One piece out of three" or "One third" or "Third" .
If we eat two slices of pizza, then such a fraction will be called "two-thirds" and written as follows:
Now imagine that we divided the pizza into two parts, or as the people say: "in half" :
Let's say we ate one of these two pieces. How to write such a fraction?
Draw a line again. At the bottom of this line we write the number 2, since the pizza is divided into two parts, and at the top we write the number 1, since one piece is eaten:
"one half" or "half".
The fractions that we have now examined are called ordinary .
In general, there are two types of fractions: ordinary and decimal . At the moment we are looking at common fractions fractions . A fraction is a fraction that consists of a numerator and a denominator. Decimal fractions will be discussed a little later.
The denominator of a fraction is a number that shows how many equal parts something can be divided into. Let's get back to our pizza. Equally, this pizza can be divided into 2 parts and 3, and 4, and 5, and 6. Depending on how many parts we divide the pizza into, the denominator will change.
The following picture shows three pizzas that are divided differently. The first pizza will have a denominator of 2. The second pizza will have a denominator of 3. The third pizza will have a denominator of 4.
The numerator shows how many parts are taken from something. For example, if you divide a pizza into two parts, as in the first picture, and take one part for a meal, it will turn out that we took ( one part out of two ), or as people say "half" pizza.
Using variables, a fraction can be written like this:
where a is the numerator, b is the denominator.
The next thing to know is that common fractions are proper and improper .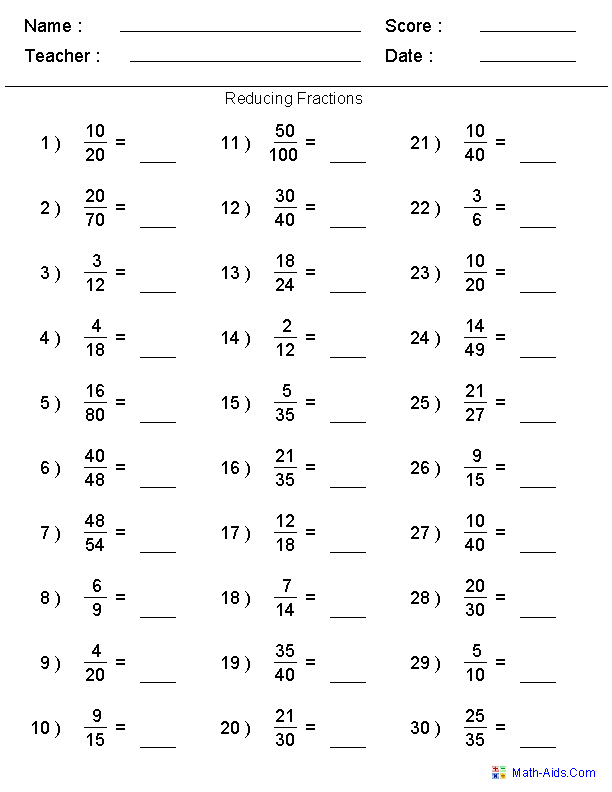
A regular fraction is a fraction whose numerator is less than the denominator. For example, the following fractions are correct:
Why are such fractions called proper? Remember that a fraction is a part of something. After all, it would be more logical if this part is less than where this part was taken from. For example, if the pizza is divided into four parts, and we take ( one fourth of ), then our slice will be smaller than all four slices combined ( than one whole pizza ). Therefore, such fractions are called proper.
With an improper fraction, everything is exactly the opposite. An improper fraction is a fraction whose numerator is greater than the denominator. For example, the following fractions are improper:
It can be seen that these fractions have a numerator greater than the denominator. Why are such fractions called improper? Remember that a fraction is a part of something. The denominator shows how many parts it is divided into.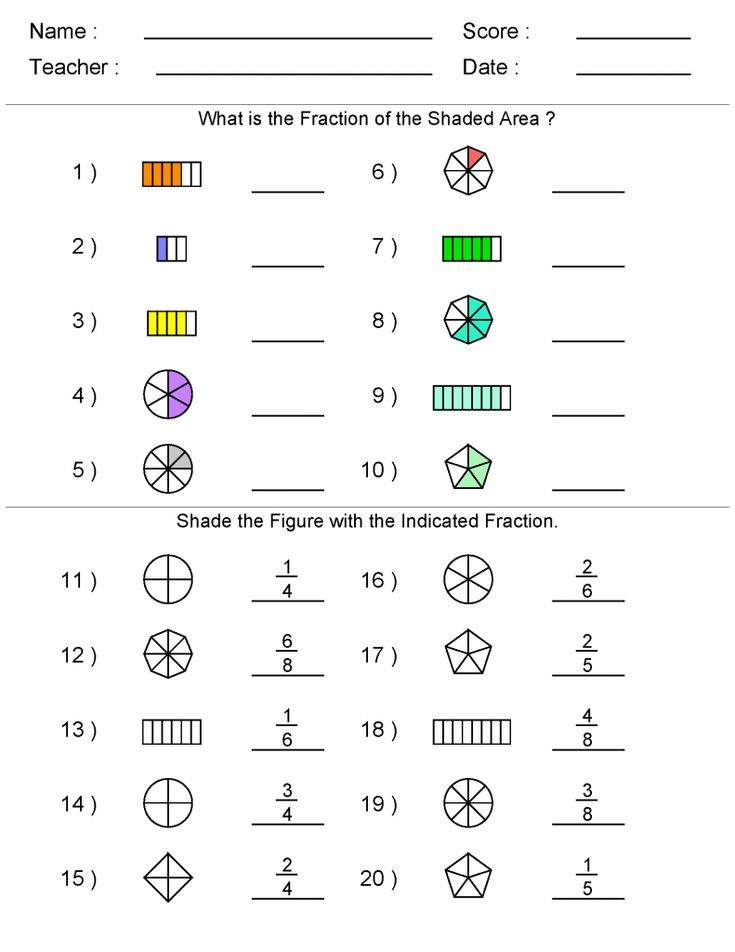
And the numerator shows how much of this something was taken.
Now let's take an improper fraction as an example and apply it to our pizza. The denominator is 2, which means the pizza is divided into two parts, and the numerator is 9. It turns out that nine pieces were taken out of two. But how can you take nine pieces if there are only two? The answer is no. Therefore, such fractions are called improper.
A fraction with the same numerator and denominator is also called an improper fraction. For example:
In general, such fractions should not even be called fractions. And that's why. Consider, for example, a fraction. Let's apply it to our pizza.
Let's say we want to eat pizza. The denominator is 2, which means the pizza is divided into two parts. And the numerator is 2, so two parts are taken. In fact, the whole whole pizza is taken, and if we eat this pizza, then we will eat not part of the pizza, but the whole pizza. In other words, we will eat not a fraction, but a whole part of the pizza.
Therefore, a fraction that has the same numerator and denominator is called an improper fraction.
A fraction means division
A line in a fraction that separates the numerator from the denominator means division. She says that the numerator can be divided by the denominator.
For example, consider the fraction . The fractional line says that the four can be divided into two. We know that four divided by two is two. We put an equal sign (=) and write down the answer:
We can conclude that any division of numbers can be written using fractions. For example:
These are the simplest examples. It can be seen that they have no residue. The rest is a little more complicated, but more interesting. We will talk about this in the next topic, which is called "selecting the integer part of a fraction."
Selection of the integer part of the fraction
Calculate the fraction . Five divided by two will be two and one remainder:
5 : 2 = 2 (1 remainder)
Check: (2 × 2) + 1 = 4 + 1 = 5
But now we have dealing with fractions, which means that you must answer in fractional form.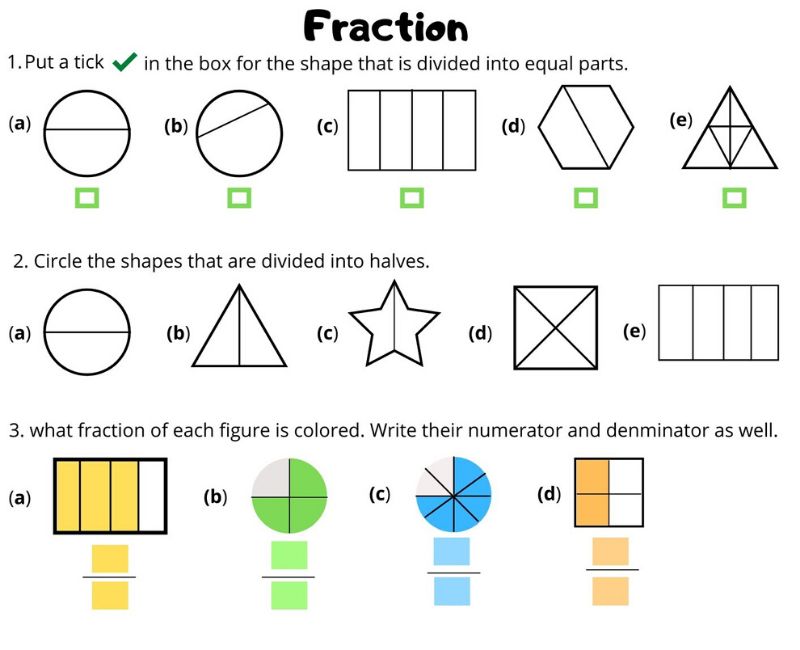
To better understand how this is done, consider an example from life.
Imagine that you have 5 apples and decide to share them with your friend. And to share honestly, so that everyone gets equally. How to share these 5 apples?
Obviously, each of you will get two apples, and you will cut the remaining one apple in half with a knife and also divide among yourself:
Look carefully at this picture. It shows how five apples are divided between you and your friend. Obviously, everyone got two whole apples and half an apple.
Now we return to the fraction and answer its question. What is five divided by two? We look at our drawing and answer: if five apples are divided by two, then each will get two whole apples and half an apple. So we write:
Schematically it looks like this:
In our example, we selected the integer part of the fraction and got a new fraction . Such a fraction is called mixed .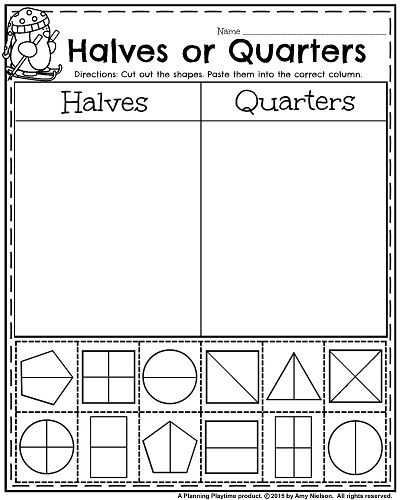
A mixed fraction is a fraction that has an integer part and a fractional .
In our example, the integer part is 2, and the fractional part is
Be sure to remember these concepts! Better yet, write it down in your workbook.
You can select the integer part only for improper fractions. Recall that an improper fraction is a fraction whose numerator is greater than the denominator. For example, the following fractions are improper and have their integer part highlighted:
To isolate the integer part, it is enough to know how to divide numbers with a corner. For example, let's select the integer part of the fraction. We write down this expression with a corner and solve:
After the solution of the example is completed, a new fraction is assembled like a children's designer. It is important to understand what goes where. The quotient is taken as the integer part, the remainder is taken as the numerator of the fractional part, and the divisor is taken as the denominator of the fractional part.
In principle, if you know the multiplication table well and can quickly perform elementary calculations in your mind, then you can do without corner entries. In schools, by the way, this is exactly what is required - so that students do not waste time on simple operations, but immediately write down the answers.
But if you're just starting out in math, we recommend that you write down every little thing.
Let's consider one more example of extracting an integer part. Let it be required to select the integer part of the fraction
We write this expression as a corner and solve it. Then we collect the mixed fraction:
Received:
Converting a mixed number to an improper fraction
Any mixed number is obtained by isolating the whole part in an improper fraction. For example, consider an improper fraction. If you select an integer part in it, then it turns out
But the reverse process is also possible - any mixed number can be converted into an improper fraction.
To do this, the integer part must be multiplied by the denominator of the fractional part and the result obtained should be added to the numerator of the fractional part. The result obtained will be the numerator of the new fraction, and the denominator will remain unchanged.
For example, let's convert a mixed number to an improper fraction. We multiply the integer part of 2 by the denominator of the fractional part:
2 × 3 = 6
Then we add the numerator of the fractional part to 6:
6 + 1 = 7
The resulting seven will be the numerator of the new fraction, and the denominator 3003 will remain unchanged:
The detailed solution looks like this:
And with the help of variables, the translation of a mixed number into an improper fraction can be written as follows:
Example 2. Convert mixed number to improper fraction.
Multiply the integer part of the mixed number by the denominator of the fractional part and add to the numerator of the fractional part, and leave the denominator unchanged:
divided by the same number, you get an equal fraction.
This means that the value of the fraction will not change. For example, consider the fraction . We multiply its numerator and denominator by the same number, for example, by the number 2
We got a new fraction. If you believe the basic property of a fraction, then the fractions and are equal to each other. Is it so? Let's check it by drawing these fractions as pizza slices:
Look closely at these two drawings. The first drawing illustrates the fraction (one piece out of two) and the second one illustrates the fraction (two pieces out of four) . If you look closely at these pieces, you can make sure that they have the same size. The only difference is that they are cut differently. The first pizza was cut into two pieces and one piece was taken from it. And the second pizza was cut into four pieces, and two pieces were taken from it.
Therefore, you can put an equal sign (=) between fractions and because they are equal to the same value:
Consider a fraction.
Let's divide its numerator and denominator by the same number, for example, by the number 2
We got a new fraction. If you believe the basic property of a fraction, then the fractions and are equal to each other. Is it so? Let's check it out by drawing these fractions as pizza slices:
Look closely at these two drawings. The first drawing illustrates the fraction (four pieces out of eight) , and the second illustrates the fraction (two pieces out of four) . If you look closely at these pieces, you can make sure that they have the same size. The only difference is that they are cut differently. The first pizza was cut into eight pieces and four pieces were taken from it. And the second pizza was cut into four pieces, and two pieces were taken from it.
Therefore, you can put an equal sign (=) between the fractions and because they are equal to the same value:
Now we have fully tested how the main property of the fraction works, and made sure that it works great.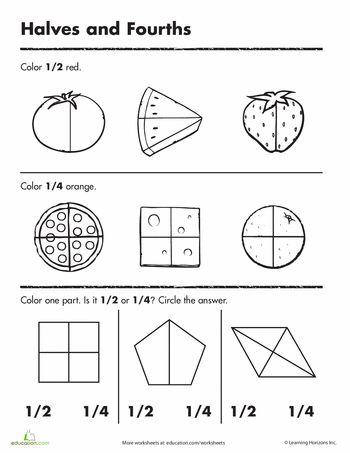
The number by which the numerator and denominator are multiplied is called additional factor . Remember this for sure!
Fraction reduction
Fractions can be reduced. To shorten means to make a fraction shorter and easier to read. For example, a fraction looks much simpler and prettier than a fraction.
If, when solving examples, a large and ugly fraction is obtained, then you need to try to reduce it.
The reduction of a fraction is based on the basic property of a fraction. Therefore, before studying the reduction of fractions, be sure to study the basic property of a fraction.
Dividing the numerator and denominator by their greatest common divisor is called abbreviation .
Example 1. Reduce the fraction
So, you need to divide the numerator and denominator of the fraction by the greatest common divisor of the numbers 2 and 4.
In this case, the fraction is simple and it is easy to find the GCD for it.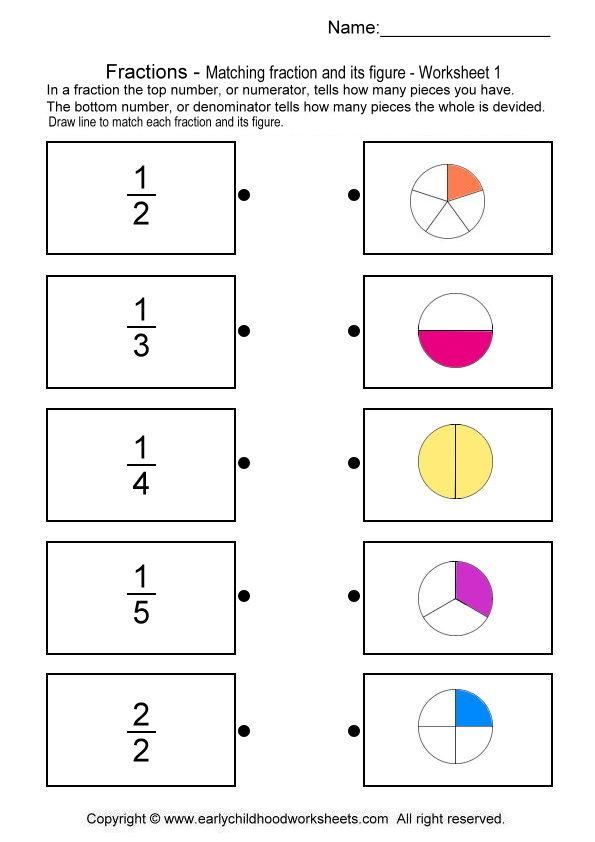
The GCD of the numbers 2 and 4 is the number 2. This means that the numerator and denominator of the fraction must be divided by 2
As a result, the fraction turned into a simpler fraction. The value of the original fraction did not change, since the reduction implies dividing the numerator and denominator by the same number. And this action, as mentioned earlier, does not change the value of the fraction.
The illustration shows fractions and pizza slices. Before reduction and after reduction they have the same dimensions. The only difference is that they are divided in different ways.
Example 2. Reduce the fraction
20
Example 3 . Reduce the fraction
To reduce the fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor of the numbers 32 and 36. and the denominator are prime numbers, then such a fraction cannot be reduced - it is not reduced.
Such fractions are called irreducible . For example, the following fractions are irreducible:
Recall that prime numbers are numbers that are only divisible by 1 and themselves.
Second method of fraction reduction
The second method is a shortened version of the first method. Its essence lies in the fact that a detailed explanation of what the numerator and denominator was divided into is skipped.
For example, let's return to the fraction. We reduced this fraction by 4, that is, we divided the numerator and denominator of this fraction by the number 4
Now imagine that there is no construction in this expression, and the answer is immediately written. The following expression will be obtained:
The bottom line is that the number by which the numerator and denominator are divided is kept in mind. In our case, the numerator and denominator are divided by 4 - this number will be kept in mind.
First, we divide the numerator by the number 4. We write the received answer next to the numerator, having previously crossed it out:0003
Then we collect a new fraction. We send the new number 8 instead of 32 to the numerator, and send the new number 9 instead of 36 to the denominator
There is a kind of replacement of one fraction for another. The value of the new fraction is equal to the value of the previous fraction, since the main property of the fraction is triggered, which says that if the numerator and denominator of a fraction are multiplied or divided by the same number, then a fraction equal to it will be obtained.
Also, fractions can be reduced by first decomposing the numerator and denominator into simple factors.
For example, let's reduce the fraction by first decomposing the numerator and denominator into simple factors:
So, we decomposed the numerator and denominator of the fraction into factors.
Now we apply the second method of reduction. In the numerator and in the denominator, we select by the factor and divide the selected factors by the GCD of these factors.
Let's cancel by three in the numerator and in the denominator. To do this, we divide these triples by 3 (by their greatest common divisor). We get the following expression:
You can reduce by three more in the numerator and in the denominator:
There is nothing more to reduce further. The last three in the denominator simply cannot be reduced because there is no factor in the numerator that could be reduced along with this triple.
We write down a new fraction, in the numerator and in the denominator of which there will be new factors.
Received an answer. This means that when a fraction is reduced, a new fraction is obtained.
It is not recommended to use the second method of fraction reduction and the method of decomposition into prime factors of the numerator and denominator if a person has just begun to study mathematics.
Practice shows that this is difficult in the early stages.
So if you're having trouble using the second method, then use the good old reduction method: divide the numerator and denominator of the fraction by their greatest common divisor. The expression in this case is simple, understandable and beautiful. So the previous example can be solved the old way and looks like this:
Compare this expression with the expression we got when we used the second way:
The first expression is much clearer, neater and shorter. Is not it?
Tasks for independent solution
Task 1. Write the following figure as a fraction:
Show the solution
Task 2. Write the following figure as a fraction:
Show the solution 900. the following figure:
Show the solution
Task 4. Write the following figure as a fraction:
Show the solution
Task 5. Write the following figure as a fraction:
Show the solution
Task 6.
Select the whole parts in the following fractions:
Show the solution
Task 7. Select the integer parts of the following fractions:
Show the solution
Task 8. Convert improper mixed fractions: 9003 solution
Task 9. Convert mixed fractions to improper, without describing how the integer part is multiplied by the denominator of the fractional part and the result is added to the numerator of the fractional part
show the decision
Task 10. Reduce the next shot by 3
show the solution
Task 11. Reduce the next shot in the 3rd in the second way
Show solution
Task 12. Reduce the next shot by 5
show the decision
Task 13. Reduce the following fraction by 5 in the second way
Show the solution
Task 14. Reduce the following fractions:
Show the solution
Task 15. Reduce the following fractions in the second way:
Show the solution
Task 16.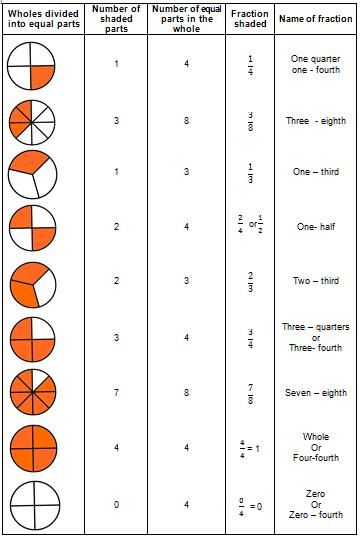
Write the following figure as a fraction:
Show the solution
Task 17. Write the following figure as a fraction:
Show the solution
Task 18. Write the following figure 2 as a fraction: Show solution
Task 19. Write the following figure as a fraction:
Show solution
Task 20. Write the following figure as a fraction:
Show solution
Task 21. Draw the following fraction:
Show the solution
Task 22. Draw the following fraction:
Show the solution
Task 23. Draw the following fraction:
Show the solution Task 24. Draw the following fraction as a picture:
Show the solution
Task 25. Draw the following fraction as a picture:
Show the solution
Task 26. Draw the following fraction as a picture:
Show the solution
Task 27. Draw the following fraction in the form of a picture:
Show the solution
Task 28. Draw the following fraction in the form of a picture:
Show the solution
Task 29.
