How to play number games
10 Super Fun Classroom Games With Numbers
Kids must practice numbers and counting a lot before they can use them confidently and fluently. For kids, this can be quite challenging, especially if English is not their first language. An incredibly effective way to teach English numbers is through playing games.
On this page, you can find ten incredibly fun games with numbers that you can use in your class to teach English numbers to kids. If you like the game ideas on this page, check out our other post about guessing games for more inspiration for your next classroom activity.
Related: Numbers Lesson Plan / Numbers 1 to 100 Spelling Chart
1: One, Two, or Three, Game
This counting game with numbers is incredibly fun and helps beginner learners to practice basic numbers. To start, choose a number that you are going to count to. A good number for this is 31, but you can use any number. Students will take turns counting until they reach 31.
When it’s their turn, students have the choice to say one number, two numbers, or three numbers. The student who says the last number (31) is out.
So, for example, the first student may decide to say two numbers and say “one, two”. Then, the next student may decide to say three numbers and say ” three, four, five”. The next student then may choose to say one number and say “six”. The game continues like this until one student says the last number (31) and is out. This game is great for practicing basic numbers but can also be used with ordinal numbers (first, second, third, etc.) and to practice the date.
2: One, Two, Three, Stand-Up Game
As well as practicing numbers, this game is great to use as a warm-up activity. To begin, choose a number to count to. The number you choose will depend on your class size and how difficult you want the game to be. For this example, let’s choose the number 5. Then, tell the students that when the teacher says ‘Go!’, one student from the class must stand up and say the first number (one).
Then, another student must stand up and say the next number (two). And so on until they get to five. Any student can stand up at any time they want. If two students stand up at the same time and say the same number, then they lose.
If you have a large class, then an alternative way to play this game is to divide the class into teams. Give each team 3 chances to get to five. If they succeed, then they get a point for their team.
3: Zingo Number Bingo
Zingo is an award-winning game that develops children’s counting, addition, and number recognition skills. It is a fast-paced and exciting bingo/matching game.One set can be played by up to 6 players. To play, each student will have a different ‘zingo card’. Then students will take turns in sliding the ‘zinger’ to reveal a number card. The student must then try to match that number card to a number picture on his/her zingo card. The first student to fill up his/her zingo card is the winner. All the materials that come with the Zingo game are durable and can be re-used.
So, by having a few sets of this game in your classroom you will have a fun and exciting numbers game to use in your class for years to come.
4: Number Guessing Games
How Many Game
Please enable JavaScript
A great way to practice numbers while also teaching ‘How many?’ and plural nouns is to play a fun numbers guessing game. Here is one of Games4esl’s ‘Telepathy Games’ about animals and numbers.
In this game, students will be asked, ‘How many (puppies)?’ and then they will see two possible answers. They must choose ONE and write it down. To help them guess the answer they can use ‘Telepathy’ to read the teacher’s mind.
This kind of game is so simple, but kids absolutely love it! Especially when they guess it correctly. For more ESL activity videos, check out our videos page.
5: Liar Game
This fun ESL card game can be used to review numbers. For this game, prepare a set of number cards for each student (for this example, we will use a set of 10 cards numbered 1-10).
Give one set of cards to each student and put them into groups of 3/4.
Next, ask students to put all their cards face down in the middle of the group and mix them up. Once the cards are mixed, ask students to take 10 random cards and tell them not to show the cards to the other students. Now the liar game can begin.
Students will take turns and MUST put down the cards in numerical order. As they put down the card, they must say that number out loud. For example, the first student should place the number one card face down in the middle and say “one”. Then, the next student must place the number 2 card in the middle and say “two”. If a student doesn’t have the next number card, he/she must lie! So, in this example, the next number is 3. If the student doesn’t have the number 3 card, then he/she must put down a different card while saying “three”.
If, at any point during the game, a student thinks that another student is lying about the card that they placed down, then they can accuse them and shout, “Liar!”.
If they are correct and the student was lying, then the student who lied must pick up all the cards in the middle. If a student accuses another student of being a liar, but they did not lie, then the student who shouted “Liar!” must pick up all the cards in the middle. This game is a lot of fun and can be used with other topics, not just numbers.
6: Number Swap
This fun counting game will help students practice numbers while testing their concentration. To play, decide a number that you are going to count to. Let’s say 21 for this example. Then ask students to make a circle. Next, point at one student to start the counting. That student should say “one”, then the next student should say “two”, and so on, clockwise around the circle. The student who says “21” gets to swap one of the numbers for a silly word (e.g. number 3 = banana).
Next, the counting starts again, but this time instead of saying the number 3, students should say ‘banana’. If students forget, and say number 3, then the counting starts again at 1.
If they count to 21 without making a mistake, then they choose another number to replace with a silly word.
Once you have 3 or 4 silly words the game becomes incredibly fun and it will really test your students’ concentration.
7: Dice Game – Draw A Monster
This game is great for practicing basic numbers and body parts at the same time. To play, write the parts of a body on the board. For example, eyes, ears, mouth, nose, head, arms, legs, etc. Then for each body part, roll the dice (or ask a student to roll the dice) and write that number next to the body part word.
Next, tell students that they must draw a monster with the same number of body parts as is written on the board. Give students 10 minutes or so to draw their monster, and then students can show their monsters to the class.
Another way to play this game is to give each student a die. That way, each student will have a very different monster. Then, when showing the monster to the class, the students can describe their monster using sentences and numbers (e.
g., “It has five eyes.” “It has three mouths.“, etc.).
8: Make A Group Number Game
This is a very active game to practice numbers that will get your students up out of their seats. For this game, you need a lot of space, so if possible, play this game outside. If not, you can play in the classroom if it is safe to do so.
To play, students must walk around while listening to music. When the music stops, the teacher will shout, “Make a group of (4).”, and students must quickly try to get into a group of that number. The students who do not get into a group of that number are out.
9: Bingo Games
Bingo games are wonderfully simple to make and are very effective when teaching numbers. Here are two variations of bingo you can try in your English class:
Classic Bingo – Ask students to draw a 3×3 grid of squares and then choose nine numbers between 1-20 (or whichever numbers you are teaching) and write them in the squares.
Then, the teacher will call out a number, and if that number is on the students’ bingo sheet, then they should cross it out.
A student gets bingo when they cross out all the numbers in a horizontal, vertical, or diagonal line. To make the game last longer, you can tell students that they must make 2/3 lines of bingo to win. Alternatively, make a bigger bingo grid of 12 (3×4) squares or 16 (4×4) squares to make the game more challenging.
Line Bingo – To play line bingo, you need to prepare some number cards for the students. Give each student a set of number cards ( around 8 – 10 cards is best). Then ask students to arrange their cards in a horizontal line in any order they choose. Once students have done that, the game can begin.
As the teacher calls out a number, students should check their line of cards to see where that number is. If the number is on the left end or the right end of the line, then the student can turn that card over. If it is in the middle of the line, then the student cannot turn it over.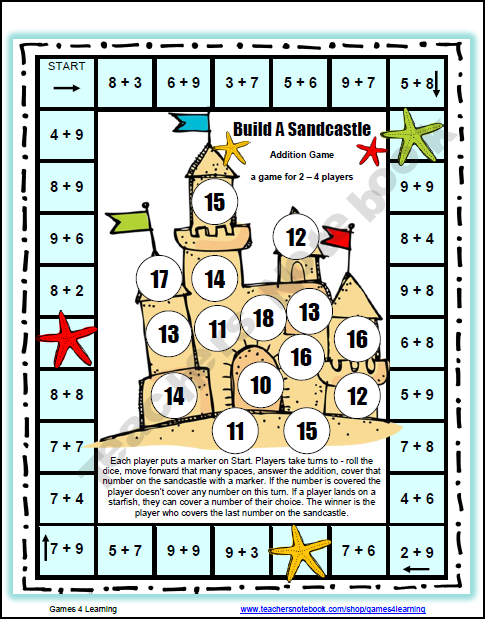
The aim of the game is to turn over all the cards to get bingo.
10: Number Puzzles
Puzzles can be a great way to review numbers and practice reading and writing out the words. An easy way to quickly make your own puzzles for class is to use a puzzle maker. To make your own word searches, simply type in the number of words you want to practice into this word search maker. To make a numbers crossword puzzle, simply type in your words and clues into this crossword maker.
Thanks for reading. I hope you found some fun games with numbers for your next class. Before you go, don’t forget to check out our free lesson resources, including classroom games, PPT Games, Worksheets, and more.
5 Math Games Every Classroom Needs to Play
Guest post by Leigh Langton
Hey guys! It’s Leigh from The Applicious Teacher! I am super excited to be blogging at Corkboard Connections today. I’m sharing a practice that I use to help increase my students’ engagement and number sense during my math block.
Do you play games in your classroom? Wait… what?! No time? Well… you should make time! Especially during your math time. To me, math and games go together like Nutella and pretzels. Delicious separate, but amazing together.
As a third grade teacher, I know how limited our time can be, so I am here to share with you 5 math games you should take the time to play this year! All of these games are fun, easy, and require little to no prep. They are math games that I’ve played for years with my second graders. When I moved up to third, I was able to easily modify these games for my new “big kids”.
First up… 100’s Game
This game can be played in a k-5 classroom. It is perfect for building number sense and it’s only prerequisite is that students can count. There’s no supplies needed to play and my kids loved playing this as a “brain-break” before math.
Here’s how to play…
Have your class stand in a circle. Moving in a clockwise direction, have the students count out loud until they get to a hundred.
The person who says, “100” sits down. The last person standing, WINS!
The idea is simple, but can be modified for your students. In second grade we’d count by 5’s,10’s, and 25’s (to help with money later on in the year). For third, we count the multiples of numbers. For numbers that don’t have a multiple of 100, I choose the last number in the sequence of 12 as the “end number.”
Other Variations
Students sit down on a certain multiples (like the multiples of 7) Students don’t say the multiple. Students can count by ones to a hundred, but all the multiples of say, 4, are “off limits.” If a student says them, they sit down. You could also change it to student don’t say the divisors (perfect for those 4th/5th graders who need more practice with their facts!)
101 and Out…
This paper and pencil game works well in second to fifth grade classrooms and can be played by teams of students (like boys against girls) or in pairs.
To play you will need a sheet of paper, a pencil, and one dice. The object of the game is to score as close to 101 without going over or “out.”
To play, students take turns rolling the dice. As they roll, they can either take the number as a one or a ten. For example, if a student rolls a 5, they could take it as a 5 or a 50. Students keep a running record of their total as they play.
I love how the kids start to form a strategy for what numbers they want to roll next. It’s a great way to build mental math strategies. To introduce this game, I usually play it as, “The Teacher vs. The Class”. This allows time for modeling while keeping the kids in on the action. What class doesn’t love beating the teacher? They always want to play again if I win the round.
This game works best in longer stretches, so multiple rounds can be played. I usually like to use it at the beginning of the year as a class game before math centers. It then becomes an easy and fun game for the kiddos to play during math centers.
Back 2 Back
Seriously, hands down, my class’ favorite game to play! This game is perfect for inside recess as the whole class can play at once and everyone is excited for the game.
This game requires some “brain sweat”, so it works well for grades 2-5. There are two different versions of this game. Supplies needed are minimal: a writing surface, writing utensils, and someone who is quick with their math facts for a “caller.”
The object of the game is to guess the other player’s number before they guess yours. To play, two students come up to the board and stand back to back (hence the name). This allows for the students to write on the board, but blocks their view of the other person’s number.
The “Caller” states, “Numbers Up”. This signals the two students write a number of their choice on the board. I usually play with numbers 2-9 to keep kiddos from dwelling in the 0’s and 1’s easy train, but you can play with numbers as high or as low as needed for your group of kids.
The caller then states the sum (for younger students) or product (3rd-5th) of the two numbers. The students use their understanding of math facts to figure out what they other person’s number is when added or multiplied by their number. The first player to say the other person’s number wins the round. The “loser” gets to choose the next person to come to the board.
Please be warned… this game can get a little rowdy as students win and lose rounds and somehow the teacher always gets pulled up to “clear out” a player who’s been up a little too long… But it’s a lot of fun and well worth the 10-20 minutes! Beats the repetitious practice drills of flashcards!
Guess My Number
This next game is very versatile and can be modified in so many ways! It can be played in kindergarten all the way through 5th grade classrooms. To play, you need a number chart and a dry erase marker. This game can be played whole group, in pairs or in small groups of 3-4.
To begin, one student chooses a number.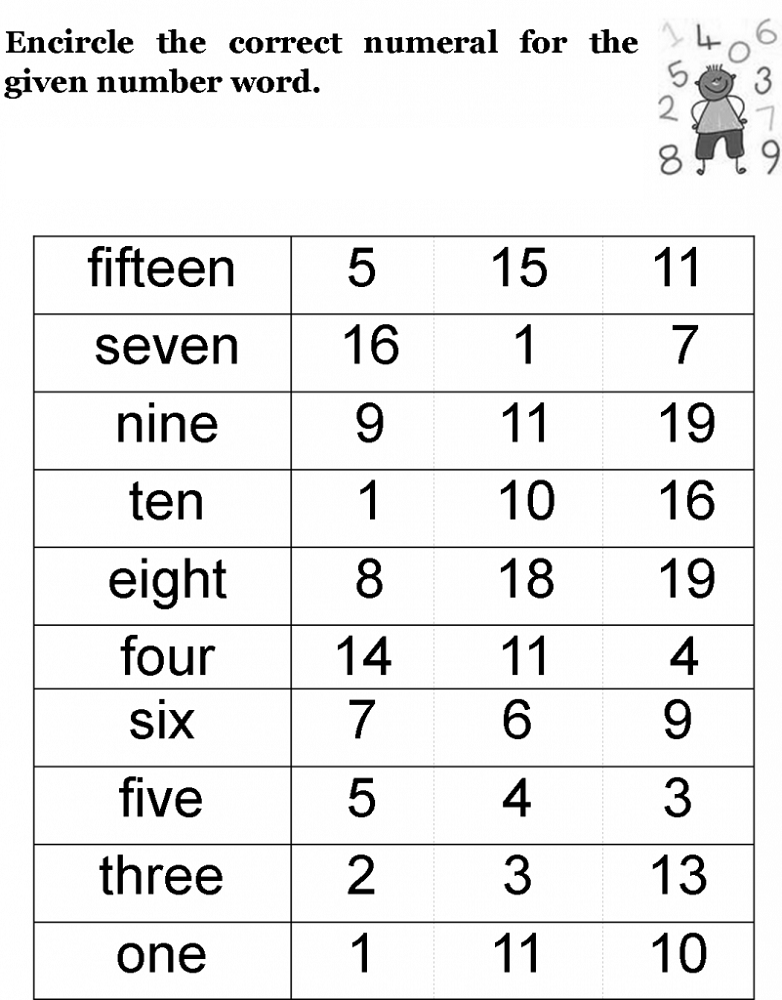
The other players try to guess the number by asking a series of questions. The student crosses off numbers it can’t be and circles numbers it could. The person who guesses the right number, wins and gets to choose the next number.
The best part of this game is that it can be played with laminated personal hundreds charts in small groups.
It can also be played as a whole group game using a large chart.
For third grade, I encourage the use of question clues like “Is it a multiple of 5? Or greater than 70?” To introduce the game, I usually model crossing out numbers as students ask questions about the numbers and help link the clues to finding the right number.
For a kindergarten or first grade classroom, you may want to play with a number line with numbers 1-20. Then, students could ask if the number is bigger or smaller than numbers within that range. A 4th or 5th grade classroom can beef up the game with question clues like, “Is it divisible by 3?” or “Is it a multiple of 5?” The possibilities are endless! Time range to play can be from 5 minutes to 20 minutes and can be used as an inside recess game or a quick brain break before or after a lesson.
Math Fact Top It!
This last game works well in 1st through 5th grade classrooms and is best played in groups of 2-4 students. All that is needed to play are math fact flash cards. You can use addition, subtraction, multiplication or division cards. It just depends on where your students are in their math skills. I like to think of this game as “War for the classroom,” as the rules for the traditional card game apply to this math fact version.
To play, students divide the flash cards evenly among all players. Then, on the count of three, all students throw down a card. The card with the highest sum or product wins all the cards in play. This can be modified to lowest difference or quotient. If students have the same answer, then they play each other again, with the winner capturing all the cards in play. Students play until all the cards are won. The student depending on the flashcards you are using. with the most cards at the end wins. I find this game works best in math centers and is an easy way for students to practice their math facts in a new and unique way!
Download Freebie with Game Directions
So go forth and play! Get your students engaged and learning in the new year! If you’re not sure you’ll remember all these games I shared today, I’ve compiled all the directions in one file for you.
It’s available here at my TpT store!
Leigh is a wife, mother, and a second-grade- turned-third-grade teacher. She currently resides in Central Florida where she has been teaching for 7 years. When Leigh isn’t teaching or writing for her teacher blog, The Applicious Teacher, she enjoys snuggling up with a good book, running a few miles, or spending time with her family.
To win this game with numbers, you need to learn how to avoid patterns / Sudo Null IT News
you such a simple number game. Let's say you and I take turns crossing off numbers from the list {1, 2, 3, ..., 9}. The last person to cross out a number so that the three crossed out numbers are not in a row wins. Let's play! You are the first. nine0006
Suppose after four moves we have crossed out the following numbers:
1 2 3 4 5 6 7 8 9
Your turn again. If you cross out 4, you lose, because then you will make a sequence of three numbers, 3-4-5.
You will also lose by striking out a 7 due to the 7-8-9 sequence. It is only safe to cross off 1, 2, or 6. However, no matter what number you cross off, I will cross off one of the remaining ones and win, leaving you with no safe moves. nine0004
This is a simple game with interesting mathematical background. One approach is to make gaps so that the opponent has no choice but to cross out the third number from the sequence, something like this: Another approach is to make moves next to the opponent's moves to force him to finish with a sequence of three numbers on either side, for example:
1 2 3 4 5 6 7 8 9
But regardless of the style of play, one fact is mathematically predetermined: after six moves, someone has to win. It is impossible to cross out seven or nine numbers so that there are no consecutive three numbers among them (check if you don’t believe me - there will be exercises on this at the end of the article). In this case, we say that 6 is the "upper bound" on the number of moves that can be made in this game.
So while sometimes we don't know the best move, we know for sure that our game won't last more than six moves. We can expand this task. A game using numbers from 1 to 15 cannot go longer than 10 steps, and in general, if the size of the playing field is divisible by 3, then a maximum of 2/3 numbers can be crossed out. Finding such an upper bound is a step towards understanding the game. For example, we could use the upper bound to look for a winning strategy, or as a basis for reasoning about what happens if the playing field is not a multiplier of three. And while it may not seem like much information about the upper bound, it is much more than can be said for similar games with slightly different rules. nine0006
Let's, for example, change the rules so that the first player to cross out three numbers in sequence with any step loses. That is, you lose if you cross out not only 2-3-4 (step 1), as in the original, but also 1-3-5 (step 2), or 1-4-7 (step 3). Such sequences are called arithmetic progressions.
It is a sequence of numbers with the same step size, or "progression difference".
Let's go back to the very first playing field and apply the new rules. You go first. And you lost. nine0006
1 2 3 4 5 6 7 8 9
If you cross out 1, you get the sequence 1-3-5. If 2 - 2-5-8. If 4 - 3-4-5. If 6 - 3-6-9. If 7 - 7-8-9. Any move completes the arithmetic progression. Please note that in such a game you have to track much more. As a result, the game becomes much more difficult. And the upper bound on the number of safe steps becomes much harder to find.
The most interesting thing for mathematicians is to turn a simple game with numbers into a game against mathematics itself. Their goal is to figure out how long a game can be played before someone loses, on a game board of arbitrary size. In other words, if we have a list of numbers of any length, how many numbers can you cross off before you hit an arithmetic progression? The rules sound pretty simple, but we don't really know the answer to this question.
And we know even less about the variants of this game. Let's play a little more and see where the math takes us. nine0006
In our arithmetic progression game, the set of safe moves is essentially the Salem-Spencer set. This is a subset of the set {1, 2, 3, 4, 5, 6, 7, 8, 9} that does not contain an arithmetic progression. Then the upper bound is simply the largest possible Salem-Spencer subset on our playing field. However, finding the right moves that allow us to find this set can be quite difficult. Let's see why.
Let's start with a new field. No one can lose the first two turns, so let's just cross out 3 and 5.
1 2 3 4 5 6 7 8 9
Now we need to choose the third number - and then it's time to start thinking. Just like in the original game, we don't want to end the progression, and we don't want to cross out the number between the crossed out ones or on either side of the already crossed out ones. For example, we cannot choose 4, because we get the sequence 3-4-5; we can't choose 1 because we get 1-3-5; we can't choose 7 because we get 3-5-7.
8 is a safe choice, so let's make it. nine0006
1 2 3 4 5 6 7 8 9
Now things get more complicated. Our concern is all about the same thing - we need to try not to end the progression, and not cross out the numbers between the crossed out ones or on both sides of them. However, we need to track much more progressions already. Now you need to try not to end the progression, given the three existing pairs of crossed out numbers.
On the one hand, it is clear what to expect. For each pair, we need to avoid moves that will give us a progression in the middle or both ends. However, things are not as predictable as we would like. 3 and 5 eliminate three options: 1, 4, and 7. But 3 and 8 don't eliminate anything, because with them we need to avoid numbers like -2, 5.5, and 13, and they aren't even on the board. 5 and 8 eliminate only 2 since we can't choose 6.5 or 13.
We know that each choice eliminates some options in the future, but how much depends on what you choose.
Because of this heterogeneity, it is difficult to count all the possibilities and determine the upper bound for all possible playing fields.
Let's get back to our game. It can be seen that 6 is a safe move, so we cross it out.
1 2 3 4 5 6 7 8 9
That's it. There are no more safe moves left. We already know that 1, 2, 4 and 7 lose, while choice 9gives us a progression of 3-6-9. We've gone as far as we can.
This means that the set of our moves, {3, 5, 6, 8}, is a Salem-Spencer set. But is it the maximum? We cannot increase this set, but can another strategy lead to a larger set? Does {1, 2, 3, 4, 5, 6, 7, 8, 9} have a larger subset in which no triple of numbers gives an arithmetic progression?
There are: {1, 2, 6, 8, 9}. This is the set of five safe moves in our game, and hence the Salem-Spencer set. And it is maximal, since it is already known that for {1, 2, 3, 4, 5, 6, 7, 8, 9} the maximum size of the Salem-Spencer set will be 5.
But in the general case, for a set of n elements {1, 2, 3, ..., n}, we do not always know the answer. We actually know the answers for sets with n ≤ 209 by now. is to set certain boundaries. And even this is difficult to do, in part because of the irregular behavior that we have already observed. Crossing out a new number can eliminate a lot of options, or a little. Irregularity can be estimated from the graphs below showing the sizes of the largest possible Salem-Spencer subset for the set {1, 2, 3, ..., n} for different n. nine0006
In our game, where n = 9, the size of the largest possible Salem-Spencer set is 5. But look, if we add 10 to the playing field, this does not change the size of the largest possible Salem-Spencer set. It will remain equal to 5.
| The size of the set {1,2,3,…,n} | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | nine0118 910 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Salem-Spencer maximum subset size | 1 | 2 | 2 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
On the other hand, when going from 12 to 13 and 14, the maximum size grows from 6 to 7 and 8.
And then you have to add six more integers to the set to increase the maximum size of the Salem-Spencer subset by only 1.
| Set size {1,2,3,…,n} | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| Salem-Spencer maximum subset size | 6 | 6 | 7 | 8 | 8 | 8 | nine0118 88 | 8 | 9 |
Advances such as Roth's theorem and Szémeredy's theorem set limits on the size of these sets and their variations, often using complex mathematics (eg, ergodic theory and Fourier transforms) and huge values. For example, Fields Prize winner Timothy Gowers, in his work on a generalization of Szemeredi's theorem, established an important upper bound on the size of a set of length k that does not contain an arithmetic progression.
But if we wanted to calculate this upper bound for our game, where n=9(the size of the playing field) and k = 3 (the length of the arithmetic progression we want to avoid), we would have to do a calculation involving 2 4096 , a number with over 1200 digits!
These bounds are not useful for everyday tasks, but they give us some mathematical control over sets that we do not yet understand very well. For example, until recently we didn't have such limits for "polynomial sequences", a generalization of arithmetic progression that also uses addition and exponentiation. It turns out that polynomial sequences such as 2+3, 2+3², 2+3³, and so on, are even more difficult to keep track of than our simple arithmetic progressions, which makes the game of subset selection free of polynomial sequences even more difficult. for understanding. However, setting an upper limit is another step towards understanding them, and this is the goal of mathematicians in any game with numbers. nine0006
1.
Prove that in the game using {1, 2, 3, 4, 5} by the original rules (the first player to cross out three numbers from the sequence with step 1 loses), the first player has a winning strategy.
Solution
If the first player crosses out 3, he can always win. If in response the second player crosses out 1 or 5, then the first player crosses out another number from this pair. If the second player crosses out a 2, the first player crosses out a 5. If the second player crosses out a 4, the first player crosses out a 1.
2. Does any of the players have a winning strategy in the game using {1, 2, 3, 4, 5, 6} according to the original rules?
Solution
Second. Let's say the first one chooses one of the numbers {1, 2, 3}. Then the second one must choose a number from the same set next to the one chosen by the first one. For example, if the first one chose 3, then the second one chooses 2.
Now the first one has to choose a number from {4, 5, 6}. Whichever he chooses, the second player will have a winning move. If the first player immediately chooses a number from {4, 5, 6}, then the same strategy works for the second player - he must also choose a number from {4, 5, 6}. nine0004
3. Prove that in the game with {1, 2, 3, 4, 5, 6, 7, 8, 9} it is impossible to play seven times according to the original rules. Hint: Divide the board into the following subsets: {1, 2, 3}, {4, 5, 6} and {7, 8, 9}.)
Solution
If you cross out three numbers from any of the three subsets from the hint, then you will lose. We can theoretically make six moves by crossing out two numbers from each subset. But whichever subset you choose on your seventh move, you'll get three numbers in a row. This argument is known as the “hole in the dovecote” - in order to stuff seven pigeons into three holes, you have to stuff three pigeons into one of them.
Note that this reasoning is similar to the winning strategy from Exercise 2. nine0004
4. Find the largest Salem-Spencer subset of {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}.
Solution
One strategy is to start with the extreme numbers since they can never end up in the middle of an arithmetic progression. Take 1 and 11, which eliminates option 6. Apply the same strategy, cross out 2 and 10, which eliminates 3 and 9, but that's all. From the remaining options {4, 5, 7, 8}, you can choose two more, for example, 4 and 5. Judging by the table above, 6 is the maximum possible size of the Salem-Spencer subset. nine0004
See also:
- "Game theory and its application in life"
- "The Tanezhi problem: a new stage in the development of mathematics?"
- "Full review of the first part of the exam in ShAD 2020"
Didactic game "Number houses" | Teaching aid (preparatory group):
Published on 04/29/2022 - 21:32 - Kuropatkina Nina Mikhailovna
The game "Number houses" is suitable for older children to study numbers, quantitative and ordinal values of numbers and to start acquaintance with the composition numbers within 10.
This encourages children to understand how a number can be formed from other numbers. Children learn to analyze and realize how many can be formed from parts. Also, with the help of this game, the child will learn how to compose and solve simple examples for addition and subtraction. nine0006
Download:
Preview:
Didactic game "Number houses"
Purpose: To consolidate ideas about the composition of numbers from two smaller numbers (within 10).
Material: Houses with windows. Each floor has only one number. A set of cards with numbers and a set of cards with the image of different objects.
Rules of the game
Option 1
The facilitator shows the child a card with a number, and the child must lay out the same number of items shown in the pictures as indicated by the number. And vice versa. The host lays out a certain number of items, and the child selects the number. nine0006
Option 2
The facilitator puts house cards with numbers within 5 in front of the child.
The number on the roof indicates the number of residents on each floor. The child must pick up and put the number on the second window.
Option 3 (complication)
The facilitator puts a large card with a house in front of the child. A certain number lives in each of the houses. The child is invited to think and say what numbers it consists of. Let the child name all the options. After that, he can show all variants of the composition of the number. nine0006
On the topic: methodological developments, presentations and notes
Didactic game "House for animals" (1 junior group)
Purpose of the game: the formation of constructive abilities; sympathy.Material for the lesson...
Didactic game "Houses"
"Houses". Didactic game on FEMPD Didactic game "Houses" on FEM Objectives: Development of the ability to establish a correspondence between the number of objects and a number and vice versa. Development of fine motor skills; develop.
