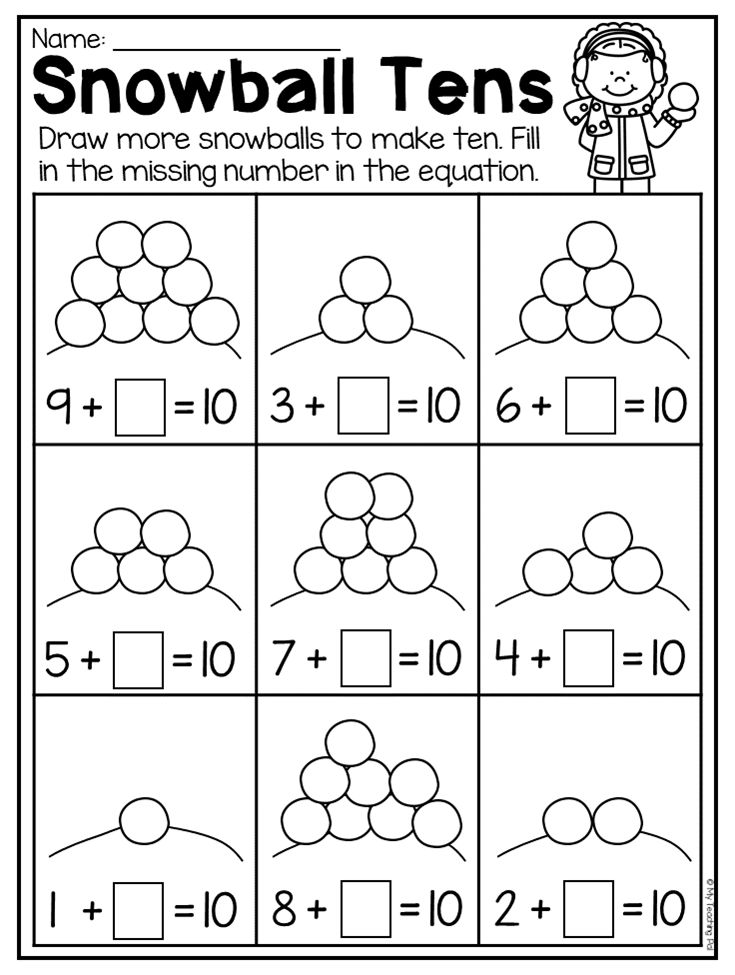
Kindergarten counting activities
14 Counting Activities for Kindergarten
Featured | Math | Numbers
Having a firm grasp on what numbers look like, what they stand for, and how we use them in the real world is the foundation for building a strong number sense and a lifetime of mathematical learning. Kindergarteners need a lot of practice counting, writing, manipulating, and thinking about numbers. The good news is, counting activities for kindergarten are a lot of fun! Read on for 14 ways that your students can practice numbers in your classroom.
Counting Activities for Kindergarten
When it comes to counting and number activities, it is important to give students opportunities to use different manipulatives, materials, and styles of activities. From sorting, building, matching, and playing games, students will love learning more about numbers.
These activities use basic materials that you probably have on hand, such as number cards, dice, spinners, ten frames, craft supplies, and blocks. If you don’t have a certain supply, you can always substitute to make it work for you and your classroom.
#1: Ten-Frame Fill
Ten-frames are the ultimate way to practice number sense. Students flip over number cards and fill in ten-frames with the proper number of counters. There are so many fun things you can use as counters, such as lego cubes, counting bears, bottle caps, colored marbles, cotton balls, shells, mini erasers, etc. By rotating materials often, you can keep this activity fresh and fun for your students, as it will feel new each time.
As your students progress, you can use multiple ten-frames to practice larger numbers.
If you want a done-for-you activity, check out this year-long ten frames unit. There are over 25 themes included, which is sure to keep ten frames fun and fresh all year long.
#2: Domino Match
Dominos are another great manipulative to use with kindergarten.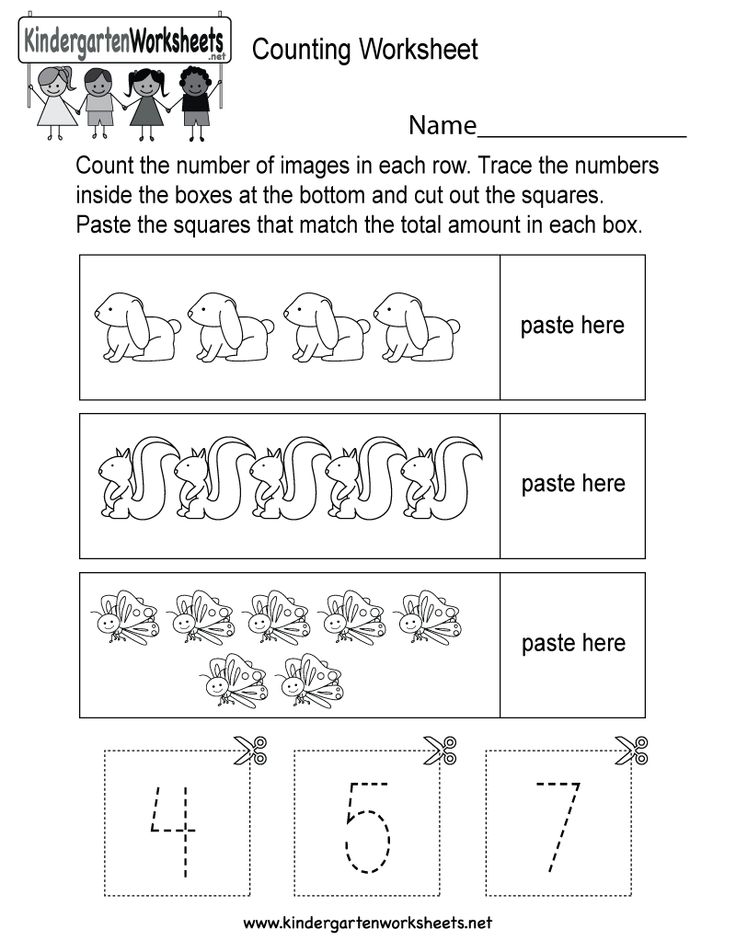 This activity requires a deck of number cards (remove face cards) and a supply of dominos. First, students flip over a number card. Then they find a domino that has that same number of dots and match them up.
This activity requires a deck of number cards (remove face cards) and a supply of dominos. First, students flip over a number card. Then they find a domino that has that same number of dots and match them up.
Another activity students can use dominos for is matching the ends of the dominos according to number. Challenge them to see what creation they can come up with by matching numbers and turning their dominos in different directions. This is also great for problem-solving!
#3: Play Dough Numbers
Using play dough is another great way to practice number sense along with fine motor skills. Before this activity, model how to roll out long “snakes” and form small balls with play dough. Allow your students to practice doing this. Once they’re good and ready, have your students use the play dough “snakes” to form the numbers 1 through 10.
You can also have them make and match the correct number of balls with each number. If you’re looking for some ready-made play dough mats, you can check out these Numbers to 10 Playdough Mats – just print and laminate!
#4: Bingo Dabbers
Using bingo dabbers with counting activities for kindergarten is a ton of fun! There are so many ways to incorporate them as well. One idea is to have students roll a dice and dab that many dots on a large sheet of paper. You can also use a spinner or number cards to select the number.
One idea is to have students roll a dice and dab that many dots on a large sheet of paper. You can also use a spinner or number cards to select the number.
Another idea is to have students form the number using bingo dabbers. Simply write the number in a large print on a piece of paper. Have students use bingo dabbers to trace or dab over the print to form the number. You can also use pre-made no-prep number pages, designed specifically for bingo dabbers. For more ideas on how to use bingo dabbers in the classroom, click here!
#5: Number Puzzles
There are tons of great number puzzles you can find at the dollar store, but you can also make them in just a few simple steps! To make your own, use mini paper plates to create number puzzles. Cut each plate in half using a different pattern. For example, cut one plate using a zig zag pattern, another using a curved line pattern, etc.
For each puzzle, write a number on one half of the plate. On the other half, draw that number of dots. Mix up the pieces of 6-8 puzzles and have students solve the puzzles by matching them up.
Mix up the pieces of 6-8 puzzles and have students solve the puzzles by matching them up.
#6: Build a Tower
Students love to build, and luckily building with manipulatives is great for counting, fine motor skills, problem solving, and spatial awareness! Students can roll dice, flip a number card, or spin a spinner to select a number. Then, they use plastic counting cubes to build a tower that matches the number. To take this activity one step further, have your students arrange the towers in number order.
#7: Magnetic Numbers
Magnetic numbers come in handy for several counting activities for kindergarten. One idea is to put them in a container or basket. Have students select them, one at a time, and put them in order on their desk or a magnetic board.
Another way they can use magnetic numbers it to practice counting on with number mats. Students will look at the first number on the mat and count on using magnetic numbers (or they can use the printable number cards included).
#8: Number Link-Up
This activity uses plastic links, which are fun for kids and also is great for building fine motor skills and coordination. Students select a number card and count out that number of plastic links. They will then link them together to show the number. If you have different colors, students can also practice patterns while doing this activity.
#9: Make the RecipeThis is such a fun counting activity for kindergarten! First, line muffin tins with paper liners. Mark each paper liner with a different number. Students will take a tin and a supply of magnetic numbers and match the magnets to the correct muffin cup. There are a lot of variations you can do with this activity, too!
Instead of writing the number, you could mark different numbers using dots on each paper liner and have students match the magnetic number to the dots. You could also have students count out the correct number of plastic bears, mini erasers, large beads or buttons, etc.
Kids love this activity, and as a bonus, it’s great for building strength in those little hand muscles. Prepare a stack of paper plates by writing a number in the center of each.
Give students a basket of small pom-poms. Students will choose a plate and use tongs or chunky tweezers to pick up the correct number of pom-poms and place them on each plate.
#11: Stringing Up Numbers
For this activity, you will need pipe cleaners and plastic beads. Before the activity, model how to curl the end of the pipe cleaner so the beads don’t fall off.
Have students curl one end of their pipe cleaner. Students will then draw a number card and string that many plastic beads onto the pipe cleaner. They will curl the other end when they are done and move onto a new number and pipe cleaner.
#12: Deal the CardsThis would be a fun partner activity for students to play to work on counting. All you need is an ordinary deck of playing cards and a number mat for each player.
Students take turns flipping over a card and placing it on the number mat. If a number already has a card on top of it, the student puts the card face down in front of them. Once the mat is completely filled with numbers, students count up their cards to see who has the fewest cards left.
#13: Make a Deposit
For this activity, you will need used paper towel and toilet paper tubes. You can ask families to donate these or save them from your home.
Once you have a large supply, write a number at the top of each tube. Put a basket of small items on the table. You can use pom-poms, plastic counting cubes, plastic bears, colorful discs, etc.
Students will look at the number on the tube and count out that many items. They will drop them into the tube. They love hearing the different sounds the objects make!
When they think they have deposited the right amount of items, they can pull the tube up and count the items on the table, practicing the concept again.
#14: Digital Task Cards
Boom cards are digital task cards that are fun, interactive, and self-checking! This set of interactive, self-checking Number to 10 Mini Deck Boom cards work on a variety of number sense skills.
These digital activities can be used with many learning platforms or as a technology center. Students will listen to the audio directions and complete the task on the digital card by dragging and dropping the objects on the screen. Kids love these!
I hope these counting activities for kindergarten will inspire the young mathematicians in your classroom. Rotate these activities into your independent practice stations, math centers, or early finisher activities. You can adapt each activity with different numbers and materials to meet the needs of your students.
For more math activities to build number sense with numbers to 10, check out this blog post.
What is your favorite part of teaching math to your students?
Post Tags: #counting#math#number sense#numbers
Similar Posts
Hands-On Counting Activities for Kindergarten
misskindergarten Leave a Comment
Kindergarten teachers know that learning how to count is more than just reciting numbers in order. Students need to understand the meaning behind the numbers they are saying! This helps our young learners build a foundation for future math skills such as addition and subtraction. My favorite way to help students practice one-to-one correspondence is with hands-on counting activities. Keep reading for ten of my favorites!
Students need to understand the meaning behind the numbers they are saying! This helps our young learners build a foundation for future math skills such as addition and subtraction. My favorite way to help students practice one-to-one correspondence is with hands-on counting activities. Keep reading for ten of my favorites!
10 Hands-On Counting Activities for Kindergarten
1. Ten Frame
One of the best ways to help students with one-to-one correspondence is to use a ten frame. This helps students keep track of the items as they count as they put one item in each box of the frame. (My students love using mini erasers and stickers!) Plus, introducing students to ten frames will help them prepare for future math concepts and investigations.
2. Play Dough
I love to use play dough during math lessons because it’s a great way to incorporate some engaging fine motor practice. To use play dough as a hands-on counting activity, you can have students pinch and roll small balls and place them in a row or on a ten frame (I like to use these play dough mats). Students can then squash each ball of play dough as they count them. This is a fun way to help students practice accurate counting and one-to-one correspondence!
Students can then squash each ball of play dough as they count them. This is a fun way to help students practice accurate counting and one-to-one correspondence!
3. Bingo Daubers
Bingo daubers are always a hit in the kindergarten classroom, so they’re a great option for counting practice! Students can use daubers to represent a particular number on a piece of paper. For example, they will create eight dots on their paper for the number eight. My personal favorite, though, are count and dab activities! Students count a number of objects and then dab the correct answer on the worksheet. Count and dab activities are perfect for math centers!
4. Number Lines
It’s important for our young learners to get familiar with number lines for future math skills, so I always like to use number lines as a hands-on activity. Counting on a number line is another helpful way for students to visualize the quantities of a given number. Students can practice showing the number of “jumps” it takes to get to each number.
5. Task Cards
There are countless ways that you can use task cards to help students practice one-to-one correspondence and counting. These simple, hands-on activities can be incorporated into the classroom at various points of the school day, such as centers, small group instruction, interventions, or even morning work! You can also use them to incorporate counting into other areas of the math curriculum, such as counting the vertices and sides of 2D shapes! If you’d like to read more about how I use math task cards in the classroom, check out this post.
6. Counting Games
A fun way to practice counting and one-to-one correspondence is with board games! Students are able to practice navigating the board as they count the correct number of spaces. However, you can also turn task cards into fun and engaging counting games! For example, this monster counting freebie can be used as a counting game if you turn the task cards face-down on the table and have students take turns selecting a monster. After choosing a card, they place the correct number of googly eyes on their monster as they count. Something as simple as having students choose their task cards from a face-down pile can bring a lot of engagement to math practice!
After choosing a card, they place the correct number of googly eyes on their monster as they count. Something as simple as having students choose their task cards from a face-down pile can bring a lot of engagement to math practice!
7. Count and Reveal
In addition to task cards, count and reveal activities are another hands-on math center idea. This self-correcting activity is perfect for students to practice one-to-one correspondence and counting. After counting the number of objects shown on the cards, students say the number and then lift the flap to see if they are correct. The addition of the clothes pins to this activity means that students are strengthening their fine motor skills, as well!
8. Roll and Cover
Roll and cover activities are a fun way for students to practice counting. After rolling dice, students can count the number of dots on the dice and then cover the corresponding number on their roll and cover mats. The game continues until they have covered each number. This is a very effective way to fit in a lot of counting repetition because students love to play this game over and over!
This is a very effective way to fit in a lot of counting repetition because students love to play this game over and over!
9. Printable Number Books
One of the best reasons to use printable books in kindergarten is that students love to share their creations with friends and family. Encouraging our students to talk about what they work on in school is a great way to solidify what they’ve been learning. After practicing the number concepts as they create these little number books, students will often talk about these same concepts when they take the books home to family. This is a great way to encourage students to continue to count and talk about numbers!
10. Morning Work Tubs
If you use morning work tubs in your classroom, be sure to add hands-on counting activities to your morning routine! Students will be able to get more practice with one-to-one correspondence as they ease into a day of learning. Counting tasks are perfect for morning work because students are usually able to complete these tasks independently. Check out this post for my favorite math ideas for morning work tubs!
Check out this post for my favorite math ideas for morning work tubs!
Number Practice for Kindergarten
To save you some time and money, I have created a bundle of numbers centers and numbers printables that will help you add variety to your counting practice! This bundle is full of hands-on fine motor activities, low-prep printables, no-prep worksheets, and even technology. You can find this bundle in my shop if you’d like to see everything that’s included!
Save These Hands-On Counting Activities
Short on time? Be sure to save this post to your favorite math board on Pinterest. You’ll be able to refer back to this post any time you’re looking for some fun counting activities for kindergarten!
Math, Number Sense
Previous Post First Grade Morning Work Ideas and Tips
Next Post Kindergarten Crafts for the Entire Year
Number Formation Posters
Make learning numbers fun with these poems to teach the correct number formation. Print them out and back them on cute paper to match your room decor. You can grab these for FREE by signing up for my email list.
First Name
Your email address
Print them out and back them on cute paper to match your room decor. You can grab these for FREE by signing up for my email list.
First Name
Your email address
Hello, I’m Hadar
Welcome to Miss Kindergarten. I’m so happy you’re here!
If you are looking for hands-on, engaging kindergarten activities, you came to the right place! I’m here to save you time by sharing tried and true kindergarten resources, and hopefully spark some ideas for your own kindergarten lesson plans!
Whether you need ideas to teach reading, sight words, math, or even some fun crafts, I have you covered. My ultimate goal is to help passionate educators and parents to young kids gain their valuable time back!
If you want to stay connected with Miss Kindergarten, please follow me on social media and be sure to sign up for the newsletter below.
More About Me Contact Me
Teaching preschoolers to count by means of project activities
%PDF-1. 7 % 10 obj > /Metadata 4 0 R /ViewerPreferences 5 0 R >> endobj 6 0 obj /Title >> endobj 20 obj > endobj 3 0 obj > endobj 40 obj > stream
7 % 10 obj > /Metadata 4 0 R /ViewerPreferences 5 0 R >> endobj 6 0 obj /Title >> endobj 20 obj > endobj 3 0 obj > endobj 40 obj > stream
 32 841.92] /Contents[115 0 R 116 0 R 117 0 R] /group> /Tabs /S /StructParents 0 /Annots [118 0R] >> endobj 80 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 119 0 R /group> /Tabs /S /StructParents 1 >> endobj 9 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 120 0R /group> /Tabs /S /StructParents 2 >> endobj 10 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 121 0 R /group> /Tabs /S /StructParents 3 >> endobj 11 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 122 0 R /group> /Tabs /S /StructParents 4 >> endobj 12 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 123 0 R /group> /Tabs /S /StructParents 5 >> endobj 13 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents[115 0 R 116 0 R 117 0 R] /group> /Tabs /S /StructParents 0 /Annots [118 0R] >> endobj 80 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 119 0 R /group> /Tabs /S /StructParents 1 >> endobj 9 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 120 0R /group> /Tabs /S /StructParents 2 >> endobj 10 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 121 0 R /group> /Tabs /S /StructParents 3 >> endobj 11 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 122 0 R /group> /Tabs /S /StructParents 4 >> endobj 12 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 123 0 R /group> /Tabs /S /StructParents 5 >> endobj 13 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 125 0 R /group> /Tabs /S /StructParents 6 >> endobj 14 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 128 0 R /group> /Tabs /S /StructParents 7 >> endobj 15 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 129 0 R /group> /Tabs /S /StructParents 8 >> endobj 16 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 130 0 R /group> /Tabs /S /StructParents 9 >> endobj 17 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 131 0 R /group> /Tabs /S /StructParents 10 >> endobj 18 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 132 0R /group> /Tabs /S /StructParents 11 >> endobj 19 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 133 0R /group> /Tabs /S /StructParents 14 >> endobj 20 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 125 0 R /group> /Tabs /S /StructParents 6 >> endobj 14 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 128 0 R /group> /Tabs /S /StructParents 7 >> endobj 15 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 129 0 R /group> /Tabs /S /StructParents 8 >> endobj 16 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 130 0 R /group> /Tabs /S /StructParents 9 >> endobj 17 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 131 0 R /group> /Tabs /S /StructParents 10 >> endobj 18 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 132 0R /group> /Tabs /S /StructParents 11 >> endobj 19 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 133 0R /group> /Tabs /S /StructParents 14 >> endobj 20 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 134 0 R /group> /Tabs /S /StructParents 15 >> endobj 21 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 135 0 R /group> /Tabs /S /StructParents 16 >> endobj 22 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 136 0R /group> /Tabs /S /StructParents 17 >> endobj 23 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 137 0 R /group> /Tabs /S /StructParents 18 >> endobj 24 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 138 0 R /group> /Tabs /S /StructParents 19 >> endobj 25 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 139 0R /group> /Tabs /S /StructParents 20 >> endobj 26 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 140 0R /group> /Tabs /S /StructParents 21 >> endobj 27 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 134 0 R /group> /Tabs /S /StructParents 15 >> endobj 21 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 135 0 R /group> /Tabs /S /StructParents 16 >> endobj 22 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 136 0R /group> /Tabs /S /StructParents 17 >> endobj 23 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 137 0 R /group> /Tabs /S /StructParents 18 >> endobj 24 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 138 0 R /group> /Tabs /S /StructParents 19 >> endobj 25 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 139 0R /group> /Tabs /S /StructParents 20 >> endobj 26 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 140 0R /group> /Tabs /S /StructParents 21 >> endobj 27 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 141 0 R /group> /Tabs /S /StructParents 22 >> endobj 28 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 142 0 R /group> /Tabs /S /StructParents 12 >> endobj 29 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 143 0 R /group> /Tabs /S /StructParents 23 >> endobj 30 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 144 0 R /group> /Tabs /S /StructParents 24 >> endobj 31 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 145 0 R /group> /Tabs /S /StructParents 25 >> endobj 32 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 146 0R /group> /Tabs /S /StructParents 26 >> endobj 33 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 147 0R /group> /Tabs /S /StructParents 27 >> endobj 34 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 141 0 R /group> /Tabs /S /StructParents 22 >> endobj 28 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 142 0 R /group> /Tabs /S /StructParents 12 >> endobj 29 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 143 0 R /group> /Tabs /S /StructParents 23 >> endobj 30 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 144 0 R /group> /Tabs /S /StructParents 24 >> endobj 31 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 145 0 R /group> /Tabs /S /StructParents 25 >> endobj 32 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 146 0R /group> /Tabs /S /StructParents 26 >> endobj 33 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 147 0R /group> /Tabs /S /StructParents 27 >> endobj 34 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 148 0R /group> /Tabs /S /StructParents 28 >> endobj 35 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 149 0R /group> /Tabs /S /StructParents 29 >> endobj 36 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 150 0 R /group> /Tabs /S /StructParents 13 >> endobj 37 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 151 0 R /group> /Tabs /S /StructParents 30 >> endobj 38 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 152 0 R /group> /Tabs /S /StructParents 31 >> endobj 39 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 153 0 R /group> /Tabs /S /StructParents 32 >> endobj 40 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 154 0 R /group> /Tabs /S /StructParents 33 >> endobj 41 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 148 0R /group> /Tabs /S /StructParents 28 >> endobj 35 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 149 0R /group> /Tabs /S /StructParents 29 >> endobj 36 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 150 0 R /group> /Tabs /S /StructParents 13 >> endobj 37 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 151 0 R /group> /Tabs /S /StructParents 30 >> endobj 38 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 152 0 R /group> /Tabs /S /StructParents 31 >> endobj 39 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 153 0 R /group> /Tabs /S /StructParents 32 >> endobj 40 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 154 0 R /group> /Tabs /S /StructParents 33 >> endobj 41 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 155 0R /group> /Tabs /S /StructParents 34 >> endobj 42 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 156 0 R /group> /Tabs /S /StructParents 35 >> endobj 43 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 157 0R /group> /Tabs /S /StructParents 36 >> endobj 44 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 158 0 R /group> /Tabs /S /StructParents 37 >> endobj 45 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 159 0 R /group> /Tabs /S /StructParents 38 >> endobj 46 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 160 0 R /group> /Tabs /S /StructParents 39 >> endobj 47 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 161 0 R /group> /Tabs /S /StructParents 40 >> endobj 48 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 155 0R /group> /Tabs /S /StructParents 34 >> endobj 42 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 156 0 R /group> /Tabs /S /StructParents 35 >> endobj 43 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 157 0R /group> /Tabs /S /StructParents 36 >> endobj 44 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 158 0 R /group> /Tabs /S /StructParents 37 >> endobj 45 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 159 0 R /group> /Tabs /S /StructParents 38 >> endobj 46 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 160 0 R /group> /Tabs /S /StructParents 39 >> endobj 47 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 161 0 R /group> /Tabs /S /StructParents 40 >> endobj 48 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 162 0 R /group> /Tabs /S /StructParents 41 >> endobj 49 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 163 0 R /group> /Tabs /S /StructParents 42 >> endobj 50 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 164 0 R /group> /Tabs /S /StructParents 43 >> endobj 51 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 165 0 R /group> /Tabs /S /StructParents 44 >> endobj 52 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 166 0 R /group> /Tabs /S /StructParents 45 >> endobj 53 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 167 0 R /group> /Tabs /S /StructParents 46 >> endobj 54 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.
32 841.92] /Contents 162 0 R /group> /Tabs /S /StructParents 41 >> endobj 49 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 163 0 R /group> /Tabs /S /StructParents 42 >> endobj 50 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 164 0 R /group> /Tabs /S /StructParents 43 >> endobj 51 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 165 0 R /group> /Tabs /S /StructParents 44 >> endobj 52 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 166 0 R /group> /Tabs /S /StructParents 45 >> endobj 53 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 167 0 R /group> /Tabs /S /StructParents 46 >> endobj 54 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841. 92] /Contents 169 0 R /group> /Tabs /S /StructParents 47 >> endobj 55 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 171 0R /group> /Tabs /S /StructParents 48 >> endobj 56 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 172 0R /group> /Tabs /S /StructParents 49 >> endobj 57 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 173 0R /group> /Tabs /S /StructParents 50 >> endobj 58 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 174 0 R /group> /Tabs /S /StructParents 51 >> endobj 59 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 175 0 R /group> /Tabs /S /StructParents 52 >> endobj 60 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 176 0 R /group> /Tabs /S /StructParents 53 >> endobj 61 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841.
92] /Contents 169 0 R /group> /Tabs /S /StructParents 47 >> endobj 55 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 171 0R /group> /Tabs /S /StructParents 48 >> endobj 56 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 172 0R /group> /Tabs /S /StructParents 49 >> endobj 57 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 173 0R /group> /Tabs /S /StructParents 50 >> endobj 58 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 174 0 R /group> /Tabs /S /StructParents 51 >> endobj 59 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 175 0 R /group> /Tabs /S /StructParents 52 >> endobj 60 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 176 0 R /group> /Tabs /S /StructParents 53 >> endobj 61 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841. 92 595.32] /Contents 177 0R /group> /Tabs /S /StructParents 54 >> endobj 62 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 178 0R /group> /Tabs /S /StructParents 55 >> endobj 63 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 179 0 R /group> /Tabs /S /StructParents 56 >> endobj 64 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841.92 595.32] /Contents 180 0 R /group> /Tabs /S /StructParents 57 >> endobj 65 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 181 0 R /group> /Tabs /S /StructParents 58 >> endobj 66 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 182 0 R /group> /Tabs /S /StructParents 59 >> endobj 67 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 183 0 R /group> /Tabs /S /StructParents 60 >> endobj 68 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
92 595.32] /Contents 177 0R /group> /Tabs /S /StructParents 54 >> endobj 62 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 178 0R /group> /Tabs /S /StructParents 55 >> endobj 63 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 179 0 R /group> /Tabs /S /StructParents 56 >> endobj 64 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 841.92 595.32] /Contents 180 0 R /group> /Tabs /S /StructParents 57 >> endobj 65 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 181 0 R /group> /Tabs /S /StructParents 58 >> endobj 66 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 841.92 595.32] /Contents 182 0 R /group> /Tabs /S /StructParents 59 >> endobj 67 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 183 0 R /group> /Tabs /S /StructParents 60 >> endobj 68 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 185 0R /group> /Tabs /S /StructParents 61 >> endobj 69 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 187 0R /group> /Tabs /S /StructParents 62 >> endobj 70 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 188 0 R /group> /Tabs /S /StructParents 63 >> endobj 71 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 189 0 R /group> /Tabs /S /StructParents 64 >> endobj 72 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 190 0 R /group> /Tabs /S /StructParents 65 >> endobj 73 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 191 0 R /group> /Tabs /S /StructParents 66 >> endobj 74 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.
32 841.92] /Contents 185 0R /group> /Tabs /S /StructParents 61 >> endobj 69 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 187 0R /group> /Tabs /S /StructParents 62 >> endobj 70 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 188 0 R /group> /Tabs /S /StructParents 63 >> endobj 71 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 189 0 R /group> /Tabs /S /StructParents 64 >> endobj 72 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 190 0 R /group> /Tabs /S /StructParents 65 >> endobj 73 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 191 0 R /group> /Tabs /S /StructParents 66 >> endobj 74 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841. 92] /Contents 192 0 R /group> /Tabs /S /StructParents 67 >> endobj 75 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [193 0 R 194 0 R] /MediaBox [0 0 595.32 841.92] /Contents 195 0 R /group> /Tabs /S /StructParents 68 >> endobj 76 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /annotations[196 0 R 197 0 R 198 0 R 199 0 R 200 0 R 201 0 R 202 0 R] /MediaBox [0 0 595.32 841.92] /Contents 203 0 R /group> /Tabs /S /StructParents 71 >> endobj 77 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [204 0R] /MediaBox [0 0 595.32 841.92] /Contents 205 0 R /group> /Tabs /S /StructParents 79 >> endobj 78 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [207 0R] /MediaBox [0 0 595.32 841.92] /Contents 208 0 R /group> /Tabs /S /StructParents 81 >> endobj 790 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 209 0 R /group> /Tabs /S /StructParents 83 >> endobj 80 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
92] /Contents 192 0 R /group> /Tabs /S /StructParents 67 >> endobj 75 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [193 0 R 194 0 R] /MediaBox [0 0 595.32 841.92] /Contents 195 0 R /group> /Tabs /S /StructParents 68 >> endobj 76 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /annotations[196 0 R 197 0 R 198 0 R 199 0 R 200 0 R 201 0 R 202 0 R] /MediaBox [0 0 595.32 841.92] /Contents 203 0 R /group> /Tabs /S /StructParents 71 >> endobj 77 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [204 0R] /MediaBox [0 0 595.32 841.92] /Contents 205 0 R /group> /Tabs /S /StructParents 79 >> endobj 78 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /Annots [207 0R] /MediaBox [0 0 595.32 841.92] /Contents 208 0 R /group> /Tabs /S /StructParents 81 >> endobj 790 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 209 0 R /group> /Tabs /S /StructParents 83 >> endobj 80 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 210 0R /group> /Tabs /S /StructParents 84 >> endobj 81 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 211 0 R /group> /Tabs /S /StructParents 85 >> endobj 82 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 212 0R /group> /Tabs /S /StructParents 86 >> endobj 83 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 213 0 R /group> /Tabs /S /StructParents 87 >> endobj 84 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 214 0R /group> /Tabs /S /StructParents 88 >> endobj 85 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 215 0R /group> /Tabs /S /StructParents 89 >> endobj 86 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 216 0R /group> /Tabs /S /StructParents 90 >> endobj 87 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.
32 841.92] /Contents 210 0R /group> /Tabs /S /StructParents 84 >> endobj 81 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 211 0 R /group> /Tabs /S /StructParents 85 >> endobj 82 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 212 0R /group> /Tabs /S /StructParents 86 >> endobj 83 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 213 0 R /group> /Tabs /S /StructParents 87 >> endobj 84 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 214 0R /group> /Tabs /S /StructParents 88 >> endobj 85 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 215 0R /group> /Tabs /S /StructParents 89 >> endobj 86 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 216 0R /group> /Tabs /S /StructParents 90 >> endobj 87 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595. 32 841.92] /Contents 217 0R /group> /Tabs /S /StructParents 91 >> endobj 88 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 218 0R /group> /Tabs /S /StructParents 92 >> endobj 89 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 219 0 R /group> /Tabs /S /StructParents 93 >> endobj 90 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 220 0 R /group> /Tabs /S /StructParents 94 >> endobj 91 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 221 0R /group> /Tabs /S /StructParents 95 >> endobj 92 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 222 0 R /group> /Tabs /S /StructParents 96 >> endobj 93 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 223 0 R /group> /Tabs /S /StructParents 97 >> endobj 94 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 217 0R /group> /Tabs /S /StructParents 91 >> endobj 88 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 218 0R /group> /Tabs /S /StructParents 92 >> endobj 89 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 219 0 R /group> /Tabs /S /StructParents 93 >> endobj 90 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 220 0 R /group> /Tabs /S /StructParents 94 >> endobj 91 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 221 0R /group> /Tabs /S /StructParents 95 >> endobj 92 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 222 0 R /group> /Tabs /S /StructParents 96 >> endobj 93 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 223 0 R /group> /Tabs /S /StructParents 97 >> endobj 94 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 224 0 R /group> /Tabs /S /StructParents 98 >> endobj 95 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 225 0 R /group> /Tabs /S /StructParents 99 >> endobj 96 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 226 0 R /group> /Tabs /S /StructParents 100 >> endobj 97 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 227 0 R /group> /Tabs /S /StructParents 101 >> endobj 98 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 228 0 R /group> /Tabs /S /StructParents 102 >> endobj 99 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 230 0 R /group> /Tabs /S /StructParents 103 >> endobj 100 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.
32 841.92] /Contents 224 0 R /group> /Tabs /S /StructParents 98 >> endobj 95 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 225 0 R /group> /Tabs /S /StructParents 99 >> endobj 96 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 226 0 R /group> /Tabs /S /StructParents 100 >> endobj 97 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595.32 841.92] /Contents 227 0 R /group> /Tabs /S /StructParents 101 >> endobj 98 0 obj > /ExtGState> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 228 0 R /group> /Tabs /S /StructParents 102 >> endobj 99 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 230 0 R /group> /Tabs /S /StructParents 103 >> endobj 100 0 obj > /ExtGState> /XObject> /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox[0 0 595. 32 841.92] /Contents 232 0 R /group> /Tabs /S /StructParents 104 >> endobj 101 0 obj > endobj 102 0 obj > endobj 103 0 obj > endobj 104 0 obj > endobj 105 0 obj > endobj 106 0 obj > endobj 107 0 obj > endobj 108 0 obj > endobj 109 0 obj > endobj 110 0 obj > endobj 111 0 obj > endobj 112 0 obj > endobj 113 0 obj > endobj 114 0 obj > stream x
32 841.92] /Contents 232 0 R /group> /Tabs /S /StructParents 104 >> endobj 101 0 obj > endobj 102 0 obj > endobj 103 0 obj > endobj 104 0 obj > endobj 105 0 obj > endobj 106 0 obj > endobj 107 0 obj > endobj 108 0 obj > endobj 109 0 obj > endobj 110 0 obj > endobj 111 0 obj > endobj 112 0 obj > endobj 113 0 obj > endobj 114 0 obj > stream x The system of teaching children to count in kindergarten
Stages of formation of quantitative representations
1. Pre-numeric activity
2. Counting activity
3. Computational activity
The first learning task
- development of practical counting activity based on comparing sets with elements of another.
- It is advisable to simultaneously teach children to lay out objects with their right hand from left to right, which prepares the child's hand and eyes to follow the row from left to right in accordance with the direction of the letters in the row.
 nine0004
nine0004
The content of quantitative representations of preschoolers
Pre-numerical activity
- See and name the essential features of objects;
- See the whole set and select its elements;
- Name a set and list its elements;
- Make up a set of individual elements and subsets;
- Divide a set into classes;
- Compare sets by number by one-to-one correlation; nine0004
- Create equal sets;
- Merge and unmerge sets.
Counting
Accounting:
- Knowledge of numerals and naming them in order;
- Ability to relate numerals to elements of the set "one to one";
- Highlighting the total number.
Possession of the concept of number:
- Understanding the independence of the result of a quantitative calculation from its direction, location of the elements of the set and their qualitative characteristics; nine0004
- Understanding the quantitative and ordinal value of a number.

- The concept of the natural series of numbers and its properties
- Knowledge of the sequence of numbers;
- Knowledge of the formation of neighboring numbers from each other;
- Knowledge of relationships between adjacent numbers.
Computational activity
Knowledge
- of relationships between neighboring numbers, nine0023 formation of neighboring numbers,
- composition of numbers from units,
- composition of numbers from two smaller numbers,
- digits and signs +, -, =, <, >;
- Ability to compose and solve arithmetic problems.
Possession of
- oral and written numbering,
- arithmetic operations of addition and subtraction,
- by groups.
Such a sequence in teaching will ensure the transition of children from the activity of counting to the activity of calculation, will gradually free children from excessive connection with visual material, and will make it possible to operate with numbers. nine0005
nine0005
Stages of development of accounting activity (A.M. Leushina)
| Stage | Age | Target | Ways | Result |
| 1 stage | nine0130 familiarization with the structure of the set | selecting individual elements in a set and compiling a set from individual elements | Children compare contrasting sets: many and one. | |
| Stage 2 | 3-4 years | nine0123 teach to compare adjacent sets element by element, i.e. compare sets that differ in the number of elements by one | application, application, comparison | children must learn to establish equality from inequality by adding one element, i.e. increasing, or removing, i.e. decreasing, the set |
| Stage 3 | nine0123 4-5 years | introduce children to the formation of the number | comparison of adjacent sets, establishing equality from inequality (they added one more item, and they became equal - two, four, etc.). | the total of the account, indicated by the number |
| Stage 4 | 5-6 years | nine0130
| understanding of the basic principle of the natural series: each number has its place, each subsequent number is one more than the previous one, and vice versa, each previous one is one less than the next. | |
| Stage 5 | 6-7 years nine0135 | children's understanding of counting in groups of 2, 3, 5. |
| leading children to understand the decimal number system.
|
| Stage 6 | 7 years… | children mastering the decimal number system | nine0123 | In the seventh year of life, children get acquainted with the formation of numbers of the second ten, begin to realize the analogy formed by any number based on the addition of one (increase: numbers by one). Understand that ten units make one ten. |
The first stage can be correlated with the second and third years of life. The main goal of this stage is to get acquainted with the structure of the set. The main methods are the selection of individual elements in the set and the compilation of the set from individual elements. Children compare contrasting sets: many and one. nine0005
The second stage is also pre-numerical, but during this period, children learn to count in special mathematics classes.
The goal is to teach how to compare adjacent sets element by element, i.e. compare sets that differ in the number of elements by one. The main methods are superposition, application, comparison. As a result of this activity, children must learn to establish equality from inequality by adding one element, that is, increasing, or removing, that is, reducing, the set. nine0005
nine0005
The fourth year of life
The main thing is the perception of the boundaries of the set
The law of conservation of quantity is not recognized by children immediately
Easier to perceive individual elements. They do not see the boundary of the multitude
The multitude is perceived as a whole unity, but it is difficult to single out individual elements
The third stage conditionally correlates with the education of children of the fifth year of life. The main goal is to familiarize children with the formation of numbers. nine0005
Characteristic methods of activity - comparison of adjacent sets, establishment of equality from inequality (one more item was added, and they became equal - two, four, etc.).
Result - the total of the account, indicated by a number. Thus, the child first masters the account, and then realizes the result - the number.
The fourth stage of mastering counting activity is carried out in the sixth year of life. At this stage, children are introduced to the relationship between adjacent numbers of the natural series. nine0005
At this stage, children are introduced to the relationship between adjacent numbers of the natural series. nine0005
The result is an understanding of the basic principle of the natural series: each number has its place, each subsequent number is one more than the previous one, and vice versa, each previous one is one less than the next.
The fifth stage of learning to count corresponds to the seventh year of life. At this stage, children understand the account in groups of 2, 3, 5.
The result is to bring children to an understanding of the decimal number system.
This usually ends the education of preschool children. nine0005
The sixth stage of the development of counting activity is connected with mastering the decimal number system by children. In the seventh year of life, children get acquainted with the formation of the numbers of the second ten, begin to realize the analogy formed by any number based on the addition of one (increase: numbers by one). Understand that ten units make one ten. If you add ten more units to it, you get two tens, etc. A conscious understanding of the decimal system by children occurs during the period of schooling. nine0005
Understand that ten units make one ten. If you add ten more units to it, you get two tens, etc. A conscious understanding of the decimal system by children occurs during the period of schooling. nine0005
Sub-numeric activity
| Features of the development of quantitative representations in children | Guidelines for the formation of quantitative representations in DOW |
|
|
Accounting
| Features of the development of quantitative representations in children | Guidelines for the formation of quantitative representations in DOW |
|
 We consider mutually inverse relationships at the same time (more - less) We consider mutually inverse relationships at the same time (more - less) |
Computing
| Features of the development of quantitative representations in children | Guidelines for the formation of quantitative representations in DOW nine0135 |
|
|


 If you add ten more units to it, you get two tens, and so on.
If you add ten more units to it, you get two tens, and so on. 
 We explain the meaning of the words "impose", "attach", "enclose". We teach to lay out and pronounce: “one flower - one butterfly ... Handout cards can first be divided into squares, then into stripes, then we proceed to work on the table
We explain the meaning of the words "impose", "attach", "enclose". We teach to lay out and pronounce: “one flower - one butterfly ... Handout cards can first be divided into squares, then into stripes, then we proceed to work on the table