Kindergarten counting and cardinality activities
Counting and Cardinality FREEBIES — Keeping My Kiddo Busy
KINDERGARTEN MATH - UNIT 1
I am thrilled to be sharing this huge Counting and Cardinality Unit with you!
This is the math unit we start the year with in kindergarten.
The kids love all of the hands-on activities we get to do, and I love how easy it is to keep them engaged.
Try a few FREEBIES right here on this blog post. We are learning about 1:1 correspondence, numbers 1-20, using number lines and ten frames, more than/less than and so much more.
This entire unit is aligned to the common core math standards as well as almost all state standards.
It comes complete with:
Pre/post assessments
Math centers worksheets
No-prep activities
Standards checklists
…and so much more
All the planning and prep work are done for you!
WATCH THIS QUICK VIDEO ABOUT COUNTING AND CARDINALITY
“Learning seems to be more like a game with these worksheets, than school work. Very fun to use.”
“This bundle is amazing and is so helpful to make sure each standard is mastered!”
“Absolutely brilliant resource. I'm so excited to start using it.”
“This is going to make things so much more easier and organized . This is a wonderful product. Thanks so much for making it.”
“This. Is. Amazing!!! Thank you!!”
I break down the kindergarten math standards into five main units.
Right now, we are tackling COUNTING & CARDINALITY.
I did my best to organize this unit as I do all my math units – so it is easy for you to implement and use.
I actually teach it a little differently than some teachers. I focus on numbers 0-10 in the fall and then come back in late January to teach the teen numbers through 20.
This unit is set up so you can do this, or if you prefer to tackle 0-20 all at once it is up to you!
I keep my math units in three-ring binders.
I use page protectors to keep my lessons and black lines organized – no more filing cabinets to dig through!
I love this because it keeps my papers nice and smooth, and it is so easy to flip through and see what I have to grab exactly what I need.I start each unit by sending home standard checklists to parents so they know what their student will be learning.
I also keep a color version in my Counting & Cardinality Unit binder as an easy visual reminder for me as I am writing my weekly lesson plans.
I include this exact same checklist (with just a slightly different header) to send home after the unit is complete so parents know the standards their child mastered, and what they still need to work on.
This way parents stay involved and aware with what we are doing in math.
You can even make a copy of the child's pre/post test that correlate with the standards checklists. There are no surprises at report card time and I love writing little notes about every child's improvement - big or small!
This is a peek at what I use for pre/post tests for this unit. This assessment is a FREEBIE (at the end of this blogpost).
The tests are pretty much exactly the same, but the numbers, pictures, etc. are different. This will give you accurate data for growth.
We are mandated to give pre and post tests for our math units so we can chart progress. These tests cover all the standards in the unit and two versions are also included if you choose to "split" the unit and do numbers 1-10 separately. Both version are included for your convenience.
When I teach my students how to count, I always have students put their counting bears (or whatever objects they're using) in a line. - If they don’t line them up, their bears are in a big pile and students forget which ones they have counted and they end up confused.
Having objects in a linear fashion also helps with left to right progression.
I've it broken the worksheets down into numbers 1-3 to start and then 4-6, 7-9, etc.
These worksheets are a perfect reinforcement of what we are practicing during our lessons. To start, I have students point to 1 object and say one number. Then they pick up their "magic counting finger" and point to the next object and say the next number.
Practice showing numerals on ten frames and number lines.
CCSS.MATH.CONTENT.K.CC.C.6 Identify whether the number of objects in one group is greater than, less than, or equal to the number of objects in another group, e.g., by using matching and counting strategies.1
CCSS.MATH.CONTENT.K.CC.C.7 Compare two numbers between 1 and 10 presented as written numerals.
This gum ball more/less activity is a freebie at the bottom of this blog post.
We start with K.CC.C.6 - telling whether the number of objects is more than/less than.The gum ball, flower baskets and lady bug worksheets simply have student count the objects and color which one has more. The number line at the bottom helps them see which quantity is larger, or more.
Once we do these three worksheets, we can move on to having them count the objects and then write the number below in the box.
The bumble bee, butterfly and apple tree worksheets have students do this extra step of writing the number in the boxes. Again, the number line at the bottom helps them see which quantity is larger, or more.
Finally, students can do the worksheet where they can just look at the numerals and decide whether to circle < or >
One more, one less is also a tricky concept for students to master.
Once they really grasp the terms more and less, I can move on to this standard of one more, one less.
By now my students are familiar with number lines and know how to use them as a reference tool.
There are cut and paste as well as fill in the blank worksheets.
I scaffold the more than/less than worksheets for my students.
This is a trickier concept for them to understand!
Next, we move on to counting on, or K.CC.A.2 Count forward beginning from a given number within the known sequence (instead of having to begin at 1).
Sometimes we do these as partners, and I break these worksheets into numbers 0-10 and teen numbers.
We do a lot of fun skip counting activities in class, and these worksheets are great reinforcement. Counting by 5s is not a kindergarten CCSS standard, but it is included to use if you wish.
Lastly, the worksheets cover writing numbers 1-20. I scaffold this with a few different options, but this is also a great check to see where your kids are at.
I don't generally just use worksheets as a lesson; however they are wonderful to use as reinforcement after an activity, for small groups, homework, etc.
Do you use interactive math journals?
They are a lot of work to set up, and then to train your students what you expect and to get going, but then they are awesome!
This bundle comes with tons of journal prompts and activities for the entire unit.If you prefer not to use journals, these printables can also just be used as self-starters, exit slips or worksheets.
COUNTING & CARDINALITY MATH CENTERSHow fun are these centers for students to practice the standards in a fun, hands-on way?!
Most use materials you already have in your classroom - locking cubes, color poms or beads, clay or play dough, dry erase markers, dice, etc.
So many fun activities and games for you students to practice the counting and cardinality standards.
These also work great for morning work tubs or small groups. We play some of the game with our "big kid" buddies and the kids have a blast while practicing the standards.
TRY FREEBIES FROM THIS UNIT!
CLICK HERE
Ready to get started?
There are over 180 pages or worksheets, journals, tests, checklists and centers in this unit! All the prep work is done for you!
READ THE REVIEWS
“This is an excellent practice for students with counting and cardinality. There are pretests/posttests, worksheets, and center station activities. I have purchased two of the units so far, and I plan to get the rest. You can't beat the price.”
“This is an amazing resource thank you!”
“These kinder-friendly worksheets are excellent to assess the standards! The pre/post tests for each section!! The graphics are cute and appropriate.
I love the frog to "hop" on the number lines. Thank you for creating and sharing!”
“This has helped me so much when it comes to planning my math. Definite has made my lesson a lot easier.”
“I am so excited to have all these resources available. It will make it easier to show parents what skills we are working on, pretest and post tests will be great assessment tools and having it all in one bundle takes a lot of stress off my shoulders.”
CLICK HEREDon’t forget! I offer a FREE kindergarten math made easy email course.
How do I teach the math standards in a fun, hands-on way to my kindergarten students?
Let me walk you through exactly how to do this with my FREE Kindergarten Math Made Easy Email Course!
It is free to sign up, and lesson ideas along with standards based, freebie printable worksheets, assessments and activities will show up in your inbox every day for the next week.
CLICK HERE to learn more.
Common Core, Counting & Cardina..., FREEBIES, Math, Math Centers, Uncategorized, [email protected]8 Comments
0 LikesCounting and Cardinality Activities For Kindergarten and First Grade
Are you looking for a counting and cardinality activity book for mastering essential math skills? Perhaps, a cut and paste activity book to build math confidence and independence?
The math cut and paste worksheets found in this activity book is for comprehensive practice of numbers 1 through 20. It combines the math worksheets from my previous post, Counting and Cardinality Activities: Numbers 1-20 with deeper number practice.
Each math task aligns with the Common Core Standards. For example, understanding the relationship between numbers and quantity and the connection of quantity to cardinality (K.
CC.B.4.)
Your students will also work on other core standards such as understanding that the last number said tells the number of objects counted. In other words, the number of objects is the same regardless of their arrangement or the order in which they were counted (K.CC.B.4b)
They will also learn that each successive number name refers to a quantity that is one larger (K.CC.B.4c). Additionally, your students will learn to count to answer “how many?” in a linear or rectangular array of numbers 1-20. (K.CC.B.5).
This math workbook comes with worksheets in color and black/white enabling you to use it in creative and scaffolded ways.
Identifying, Counting, Tracing and Coloring Activity Book: Numbers 1-20
As a SPED teacher, I loved materials in color that I could easily transform into interactive workbooks for my autism classroom. Students on the spectrum require high motivation built into their learning tools; activity books have that feature. For this reason, we took the time required to modify our materials, as needed.
You can copy, print, cut, laminate and velcro the color version of the workbook; hole-punch and place laminated sheets in a binder for a powerful teaching and learning tool. Your students will love learning and interacting with these durable, brightly illustrated and fun worksheets. Plus, your students who are not writers or who are non-verbal, can engage in the lessons and demonstrate their skills in a functional way.
The black and white print version is not only a great ink saver, but a wonderful way to engage those early finishers. You can use them to manage the pace. For example, they will have to identify, read, trace, color, cut and paste—demonstrating many higher order and functional skills.
Counting and CardinalityThe numbers 1-20 worksheets targets skills in telling how many objects are in a rectangular array with 3 answer choices. Additionally, it also targets skills in understanding that numbers can be expressed in numeral and word symbols..gif)
The number writing worksheets will guide your students in writing the numbers 1-20 with correct number formation.
This counting and cardinality activity book will help your students build strong foundational skills in math.
I hope you found this article useful and beneficial. If you need additional materials to address any prerequisite skills, you may want to check out, Community Helpers Math Activities-Number Concepts to 10 in my TPT store. Your students can work on number sequence, 1:1 number correspondence to build number sense through counting, tracing, writing and building numbers.
A great majority of my activities are available digitally on the Easel by TPT platform. You can assign the work to your students on Easel and they can access it from any device. Additionally, you’ll be able to monitor their progress and give them timely feedback right on the platform. You also have the ability to further customize.
Lastly, I invite you to join the vortex2learning club and gain exclusive access to the freebie library of resources— a growing collection of educational lessons, activities, printables, worksheets, workbooks and more.
You will be given a password that will allow you access at any time and you will want all these resources in your classrooms.=)
Read more
Sharing is caring!
2 shares
Games on the water and in the water for children in the pool
Health work in the preschool educational institution > Physical education for children
Tyurina Oksana Nikolaevna, instructor in physical education of MBDOU No. 54 “Iskorka”, Naberezhnye Chelny
Games in the water 9 9
The role of play in activities with children can hardly be overestimated. Whenever there is any problem in mastering new movements, the game may be the only means to solve these problems. In a game situation, the child, without hesitation, will perform the movement that for some reason he could not decide to perform consciously. At the stage of preparatory exercises for learning to swim, for some children, one of the difficult moments is the “immersion” exercise.
To solve this problem, given the age of the child, you can come up with several options for games on the theme of "immersion". Classes in the water with children under the general health program may include elements of preparation for mastering the preparatory exercises of the swimming training program. For example, games like: "Kitten washes"; "Summer rain" ...
Watering the flowers game. Each child calls himself a flower. The children are in the water. The command is given: “we water the flowers!” Having scooped up water with his palms, the child pours it on his head. Seeing that one of the children is not doing the exercise, the teacher says: “The bell dries up! Water it, please!” (A child can “feel” himself and Sasha and a “bell” at the same time!)
Even in such simple games, the teacher should actively participate in the game, using his role, activate the children’s imagination, encouraging everyone with praise, including unexpected elements. Children will gladly take on the role of kittens when they hear, for example: “how well a little white kitten washes! And you little black kitten, wash your nose! What clean kittens! What good fellows!” While playing the game “Summer Rain” with the children, the teacher at some point says: “Look! Rainbow ”and raises woven colored cords above his head.
In the game “Water the flowers”, the teacher “admires the flowers”: “What a beautiful tulip! Pour it some more!” It is possible to get the expected result using games in the classroom only if the children enthusiastically, with interest, perform all the actions and enjoy it. Having introduced children to several games, they can be used in classes in any sequence, several times, alternating with any movements. For example, you can organize the game "Funny Bunnies". Children stand at the bottom of the pool, the teacher says: “You are all bunnies! We went for a walk on the lawn. Let's jump!" Children, bending their arms to their chest, move along the bottom in jumps.
Teacher: Butterflies fly. Children pretend to be butterflies. "But the bugs are washing." The children are washing. “The flowers in the meadow are drying up! Let's water the flowers!" The children are watering the flowers. "The rain has gone!" In conclusion, he says: “What glorious hares! What a wonderful walk they had!” Five-year-old children can already be offered games that contain the “immersion” exercise.
But before you start the game, teach all the children the breath-holding exercise. Then, on the side, he teaches children to perform the “immersion” exercise. If at least one child in the group can complete the exercise, then immersion can be included in the games. It should be remembered that this element of the game is performed solely at the personal request of each child!
Below are some examples of such games.
Game "Who wants to visit the duck?" By jumping (or walking) from one ledge to another, children can “visit the duck”. The duck house is a floating hoop on the surface of the water. To enter it, you need to inhale, hold your breath, sit down near the hoop and stand inside it. Then, in the same way, exit the duck house and continue moving to the side. The hoop must not be touched by hand. Some of the children will want to visit the duck, while others will simply move from one side to the other. Every time praise those who came to visit the duck.
Without judging those who are not yet ready to dive, the teacher emphasizes: “The duck is glad to see everyone at home!” Those who "came to visit the duck" at the end of the lesson can be given a gift from the duck (e.g. duck stencils) .
Niagara Falls game. At the beginning of the lesson, the teacher briefly tells the children about the mountains, about the fact that in the mountains the rivers form waterfalls, large and small. There is a beautiful rainbow in the spray of the waterfall. You can swim by standing under the stream of the waterfall. There will also be a waterfall in class today! In the pool on the side, the teacher prepares a bucket of water from the pool. Children along the bottom of the pool move along its sides, and when they come to the place where the teacher stands, he says, “Who wants to swim under the waterfall, come!” pours water from a bucket in a small stream. You can give buckets to each child so that everyone has a waterfall.
Have everyone come up with a name for their waterfall. Emphasize to children that you can only water yourself. There should not be a situation that someone waters the child when he is not yet ready for such actions!
Games help the teacher to create a situation where the child's mind gets the feeling that he is not being taught, but he is learning himself, he wants to learn how to perform a specific action, he wants to learn how to swim!
When planning games in the classroom, the teacher must provide for all the details of the organization of the movement of children in the water, provide for all safety measures for the life and health of children. Playing children are not always able to control their behavior and adequately respond to the situation. He must clearly represent all possible scenarios in the game scenario in order to intervene in time if necessary and prevent undesirable situations.
Children aged 6-7 begin their swimming program. When some of the children from the group have mastered the “immersion” exercise, you can offer them the game “Sleeping Crocodile”.
You can add a competition element to it. Before the start of the game, the teacher reminds that before diving into the water, you need to inhale and hold your breath.
Description of the game. The water surface of the children's pool is blocked across the dividing path with floats. On the side, where one of the ends of the track is fixed, an image of the head of a crocodile is placed (cut out of paper or other material) , on the opposite side - an image of a crocodile's tail.
Children must cross from one ledge (from one "shore") to the other without "waking up the crocodile", that is, without touching the path with either their hands or head (when diving) .
At the command of the teacher, the children walk along the bottom of the pool towards the opposite side, approach the dividing path (to the “crocodile”) , perform the “immersion” exercise (hold their breath, squat while plunging into the water and stand on the other side of the track) .
Then they continue to move to the side along the bottom.
Organization of the game. Large group activity (up to 5 people) .
Three "baskets" (any three containers) are located near the "crocodile's head". Two baskets are empty, one is filled with "apples" (small balls or marbles) . One empty basket belongs to the "crocodile", the other belongs to the children. If one of the children, while doing the exercise, touched track ("Woke up the crocodile") , "apple" is placed in the "crocodile" basket. If the child completed exercise (“did not wake up the crocodile”) , then “the apple is placed in the children's basket. The duration of the game depends on the number of "apples". The basket with "apples" is empty - the game is over. The teacher calculates: how many "apples" are given to the "crocodile", how many "apples" are there in the children's basket?
Lesson with a large group of children (from 8 people) .
Children divided into two teams (for example, "Brave" and "Brave") . On the side near the "head of the crocodile" there is a basket with "apples" and three empty baskets ("crocodile", "Brave" and "Brave") . On the command "Brave" (for example, 4 people), start moving to the opposite side. If all the children have successfully completed the exercise, then 4 "apples" are placed in their basket, if, for example, two "woken up the crocodile" (touched the track) , then 2 "apples" are placed in the "crocodile" basket, 2 apples are placed in crocodile basket, 2 apples are placed in the crocodile basket, 2 apples are placed in the Brave basket. Then the "Brave" do the same.
At the end of the game, the winner is determined by the number of "apples".
How many activities to play this game? As long as it takes for all children to learn to dive into the water. Today the dividing path is a “sleeping crocodile”, tomorrow it is a “sleeping fish”, next time it is a “dachshund dog”.
The more interesting the lessons, the more successful the development of new movements.
By connecting several hoops floating on the surface of the water, you can organize the game "We go to visit."
Each hoop is someone's house, which can be reached by diving into the water. For example, the red hoop is the duck's house (you can put a floating toy on the surface) , the blue hoop is the dolphin's house. Children, moving along the bottom of the pool and performing the “immersion” exercise, enter the “house” (squat, plunging into the water, and stand inside the hoop) . Then, in the same way, they leave the "house" (from the hoop) , getting into the next "house" (into the hoop) . Hoops can not be touched with hands. Children should be reminded to inhale and hold their breath before diving into the water. Before going to visit, the children, being on the side, march in place and sing a couple of lines from the Winnie the Pooh song in chorus: “Whoever visits in the morning, he acts wisely! Param, param, burum, burum! That’s what morning is for!”
Divers game.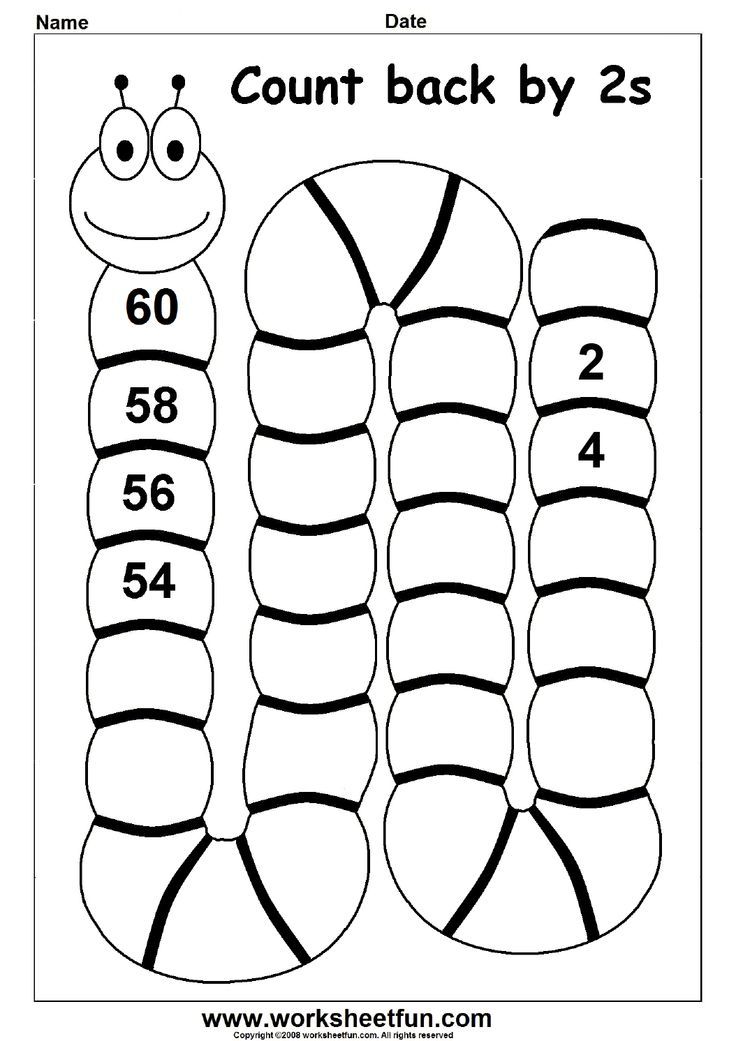
Immersion in water (and moving underwater with voluntary movements) in order to collect toys from the bottom can also be turned into a game. By setting different tasks for the children (to collect objects of the same color, or shape, or size) , the teacher can maintain the children's interest in a particular game for a long time, while solving several problems at once. For example, to collect toys of a certain color or shape, you need to dive into the water and open your eyes in the water.
The games used in swimming lessons place special demands on the teacher.
Firstly, the teacher must be an "artist", he must know and represent the entire scenario of the game lesson, remember his "text". He needs to lead the game and at the same time be mentally and a participant in the events. The whole mood of the classes, intonations, emotions, actions of the teacher should be planned in advance. Children should feel that not only do they believe that this is not a track, but a “crocodile”, but the teacher is also sure of this.
Second, we should not forget that the rules of the game should be explained briefly, focusing on the main points. For example, in the game “sleeping crocodile”, the teacher tells the children: “This is a sleeping crocodile. You must move from this ledge to that one without waking the crocodile. You can not touch it with your hands and touch your head. He approached, sat down and stood on the other side. The first time you can play the game without "apples". Then he adds: “There are apples in the basket. How many children wake up the crocodile, so many apples we give to him. These explanations are sufficient. Children know what to do. When the moment comes to share the “apples”, the teacher, shifting the “apples” into baskets, comments: “In the “Brave” team, two “woke up the crocodile”, so we give 2 “apples” to the “crocodile”. Two did not disturb the "crocodile", we will put 2 "apples" in the "Brave" basket. As the game progresses, children will understand the principle of counting "apples".
Children love to play games they like. This can be used in swimming lessons. Having mastered the “dive” exercise, children should master the “floating” exercise. All games that help to master this exercise have an element of "floating" (the exercise can be called "float" or "ball") . Simple exercises like “Which ball is better?”, “Which ball will lie on the surface longer?”. We should not forget that training takes place first on the side, and then in the water.
In game "Journey through the lake where the crocodile lives" used inventory from previous games. The "sleeping crocodile" familiar to children lies on the side. The children are in the water. On command, they begin to move along the bottom from one side to another. When the children have gone a few steps, the teacher, raising the "crocodile's head" above the side, says: "The crocodile is waking up! Everyone turned into a "ball"! Children perform the exercise "floating up". Then the children continue to move forward.
The game continues. The game can be made more difficult. The teacher can give commands designed to perform various exercises: “The crocodile is waking up, everyone is hiding!” - children perform the exercise "immersion". .. A few hoops on the surface of the water will add a new element to the game. The teacher says: “The crocodile is waking up! Everyone hid in the houses! Children, having completed the “immersion” exercise, find themselves in the middle of the hoops.
You can invite children to perform the exercise “floating up”, standing in the middle of a hoop floating on the surface of the water, calling this game “Give the duck a ball”. Each child "comes to visit the duck" (performs a "dive") and gives her a "ball" (floating up) . Several floating hoops connected together can be used in the game Gift for a Friend. Each hoop contains a small floating toy (fish, doll...) ; the child chooses to whom to give the ball, and in the corresponding hoop performs a “float”.
The game can be an integral part of the lesson, it is possible that all lessons take place in the form of a game (the goal and objectives of each specific lesson are taken into account) .
By organizing games, provide each child with the opportunity to independently regulate their actions in the water. Elements of games in which several children hold each other's hands should not be included in the lessons. There should be no situations where a child pushes (even if unintentionally) another or tries to submerge him in water. Any unexpected movement of the child in such cases can cause negative emotions, significantly complicating the process of learning to swim! The very process of learning to swim should be interesting for children. It is necessary to regularly note the progress of each child and remind the children what they have already learned, what exercises they have mastered, what is to be learned and what is to be learned in the next lessons.
Having mastered the “lying” exercise (“asterisk”) , children can perform it in games using the “starfish” plot.
For example, in the game "Sea". Children stand in the water, the teacher says: “There is wind on the sea! The waves are rising! Children create “waves” at the surface of the water with their hands. Then the teacher says: “Starfish appear on the surface of the sea”, the children perform the “lying” exercise. As in previous games, this exercise can be used in combination with other exercises.
Game "Ships" can be included in the lesson when children master the exercises "sliding on the chest, on the back." Each child turns into a "ship" that goes out to sea. Which ship sailed farthest?
In addition to educational games, classes often include general developmental games. Often these games have an element of competition. For example, in the game Postman. At the command of the teacher, children, while in the water, take “letters” from the side (small swimming boards or other objects) . Moving along the bottom, they carry the "letters" to the address (to the opposite bank) , trying to reach the "addressee" as quickly as possible.
There are many variants of the Postman game. For example, you can change the way of movement (walking, running, jumping) and the number of times the "mail" is delivered.
Children love ball games. Light, inflatable balls are suitable for training in water. In the game "Let's put things in order" , you can use not only balls, but also other inflatable toys. 8 children divided into two teams - "dexterous" and "skillful". One team (4 people) is in the water near one side, the other team is near the opposite side. A dividing path with floats is stretched across the middle of the pool. 5-6 balls or inflatable toys float on the water in each half of the pool. At the command of the teacher, the children begin to move along the bottom in their own half of the pool and throw balls (or toys) to the side of the opponent, trying to clear their area. When the moment comes in the game that all the balls are on the same site, the teacher gives a signal to end the game.
The winner is the team that managed to "put things in order" by throwing all the balls to the opponent's side. It should be noted that this game makes children move actively, and therefore children are able to show interest in it for a certain time (before feeling tired) . When the children begin to move less actively, even if there was no moment that all the balls were on the same side, the game should end. The teacher announces that the game ended in a draw and praises everyone for an interesting game. If a rope is stretched over the water, children can throw balls to each other through it.
Watermelon Cart Game. Each child is a ship that carries a watermelon from one coast to another. "Watermelon" - the belly of the child. It is important that when moving in the water in the crawl on the back, the stomach is at the surface of the water (not immersed in water) . The child swam from side to side correctly - he brought the "watermelon", lowered his stomach below the surface of the water - did not take it.
If you organize a competition between two teams, then the team that brings the most "watermelons" wins.
When teaching the movements of the legs using the breaststroke method, you can introduce a new character into the plot of the lesson - “The Frog”, since the movements of the swimmer's legs are similar to the movements of the frog's hind legs.
Using the acquired skills, children can move from side to side like “watermelon trucks”, like “frogs”. For example, children stand in the water: four at one side, they are “watermelon carriers”, four at the other, they are “frogs”. Team: “The watermelon carriers have sailed. The children are doing the exercise. When four swim to the opposite side, the following command sounds: “The frogs swam! The other "four" performs its exercise.
Even at the stage of improving sports methods of swimming, children will be happy to imitate “a bear cub swimming to Aibolit, Performing crawl movements on the chest with their legs and one hand.
Teacher: “The bear cub climbed into the hive for honey with its paw, and the bees bit its paw. The sick paw lies on the surface of the water, the bear cub rows with the other paw.
Children who know how to move in water, at all stages of learning and improvement, willingly play story games, games with a ball, games containing competitive elements.
Even seemingly simple games will become much more interesting for children if an unexpected element is added to the game. For example, if water basketball (rings are hung above the water) or water polo will be played not just by teams of children, but by the “country team” and “city team”, the game will have a new emotional connotation.
Teachers working with children should not forget that games are an essential part of any educational process, especially when it comes to physical education. In each case, the teacher chooses, invents a game, taking into account his own and children's interests and capabilities.
The principle of building a game is important, the idea and creative approach of each teacher to each child is important!
A swimming pool in a kindergarten, where group stability allows the teacher to plan the number of lessons for each group and each child for a year or several years, certainly has an advantage over city swimming pools. It is this circumstance that should be guided by a teacher working in a children's institution with a swimming pool, including in the classes not only the compulsory exercises for teaching swimming, but also a significant number of games. Positive emotions, interest in activities that include games will help orient the child and his parents to regular swimming lessons for a long time.
Improving work in preschool educational institution:
in kindergarten | in preschool | | | | in kindergarten
Mathematical Development Methodology (exam) - Mathematical Development Methodology Cheat Sheet
Mathematical Development Methodology Cheat Sheet
Download all files (4262 kb.
)
Available files (1):
| 262b.doc | 15.02.2014 20:00 | download |
1 2 3 4 5 6 7 8 9... 20
Methods of mathematical development (exam)
time, space.
The FEMP methodology in the system of pedagogical sciences is designed to assist in preparing preschool children for the perception and assimilation of mathematics - one of the most important subjects in school and the comprehensive development of the child.
The FEMP technique has a specific, purely mathematical terminology .
These are:
- set;
- number;
- counting and computing activities;
- value;
- geometric figures;
- time;
- space.
SET is a collection of objects that are considered as a single whole . The world in which a person lives is represented by a variety of sets: a lot of stars in the sky, plants, animals around him, a lot of different sounds, parts of his own body.
Sets are made up of elements. The elements of the set are the objects that make up the set. These can be real objects (things, toys, drawings), as well as sounds, movements, numbers, etc. .
The elements of a set can be not only individual objects, but also their combinations . For example, when counting in pairs, triplets, tens. In these cases, the elements of the set are not one object, but two, three, ten - a set.
Thus, sets are considered as a set, a collection , a collection of any objects and objects, united by a common, for all, characteristic property .
Any property can be considered as belonging to some objects.
For example, some flowers, berries, cars and other objects have the property of being red . The property of being round is possessed by the moon, the ball, the wheels of bicycles and cars, parts of various machines and machine tools, etc.
Thus, each property is associated with a set (objects) that have this property.
It is also said that the set is characterized by the given property - or the set is given by specifying the characteristic property.
Under the characteristic property of a set is meant such a property, which all objects belonging to a given set (elements of this set) have, and not a single object that does not belong to it, i.e. this item is not its element.
If some set A is specified by specifying the characteristic property P , then this is written as follows:
A = { x | P ( x )}
and reads like this: “ A is the set of all x such that x has the property P ”, or, in short, “A is the set of all x having the property R ". When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property.
Thus, if the set A is given by the characteristic property P , then this means that it consists of all objects that have this property, and only of them.
If any a has the property P , then it belongs to the set A , and, conversely, if the object a belongs to the set A , then it has the property P .
An infinite set of objects can have some property, only a finite set can have another. Therefore, the sets are subdivided into end and end .
A finite set can be specified by direct enumeration of all its elements in an arbitrary order. For example, the set of children of a given group living on Sadovaya Street can be described using a characteristic property: { x | x - lives on Sadovaya Street) or listing all its elements in an arbitrary order: {Lena, Sasha, Vitya, Ira, Kolya}.
It is quite clear that an infinite set cannot be specified by listing all of its elements .
Mathematics mostly deals with infinite sets (numbers, points, figures and other objects), but the basic mathematical ideas and logical structures can be modeled on finite sets.
Naturally, in pre-mathematical preparation usually deals with finite sets .
COUNT - first and main mathematical activity , based on element-by-element comparison of finite sets.
NUMBER is the general invariant category of the set , which is an indicator of the cardinality of the set. This is just a sound designation.
Theoretical foundations for the formation of elementary mathematical representations in preschoolers include a detailed study of only the system of natural numbers . Therefore, when we say "numbers", we mean natural numbers.
DIGITS - a system of characters (“letters”) for writing numbers (“words”) (numerical characters). The word “digit” without specification usually means one of the following ten characters: 0 1 2 3 4 5 6 7 8 9 (so-called “Arabic numerals”). Combinations of these numbers generate two (or more) digit numbers.
The number has 2 values : cardinal and ordinal.
With a quantitative value of , we are interested in the number of elements in the set. We use the question HOW MUCH? and we start counting with the cardinal number ONE.
With the ordinal value of a number, we are interested in the place of the number among others or the ordinal number of the element in the set. The question is WHICH COUNTS? and set the direction of the account. Ordinal numbers are used, counting begins with the word FIRST.
When we talk about quantity, it does not matter the direction of the count, the object from which the count began. The final number does not change. With an ordinal count, the final number may change.
COUNTING ACTIVITY is considered as an activity with specific elements of the set, in which a relationship is established between objects and numerals. The study of numerals and sets of objects leads to the assimilation of counting activities.
CALCULATION ACTIVITY - is an activity with abstract numbers, carried out by means of addition and subtraction.
The simple naming of numerals will not be called counting activity. The system of computational actions is formed on the basis of quantitative knowledge.
VALUE is the quality and property of an object, with the help of which we compare objects with each other and establish a quantitative characteristic of the compared objects.
Concept the value in mathematics is considered as the main one.
A direct answer to the question "what is a quantity?" no, since the general concept of magnitude is a direct generalization of more specific concepts: length, area, volume, mass, speed, etc.
The size of an object is its relative characteristic , emphasizing the length of individual parts and determining its place among homogeneous ones. The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.
Size of item, i.e. Item size is determined by based on comparison of only. It is impossible to say whether it is a large or a small object, it can only be compared with another.
The perception of magnitude depends on the distance from which the object is perceived, and also on the magnitude of the object with which it is compared . The farther an object is from the one who perceives it, the smaller it seems, and vice versa, the closer it is, the larger it seems.
The characteristic of the size of the object also depends on its location in the space . The same object can be characterized either as high (low), or as long (short). This depends on whether it is in a horizontal or vertical position. So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short.
The value of an item is always relative , it depends on which item it is compared to . Comparing an object with a smaller one, we characterize it as a larger one, and comparing the same object with a larger one, we call it a smaller one.
So, the magnitude of a particular object is characterized by the following features : comparability, variability and relativity.
1) comparability , carried out:
- overlay,
- application,
- measurement using a conditional measure,
- comparison by eye.
2) relativity - depends on the object with which we are comparing, on the distance at which we are comparing, on the location in space.
3) variability . Size is closely related to size. And size is a property of magnitude variability. Each item has its own generic purpose. It can change its dimensions without changing its essence.
GEOMETRIC FIGURE is an abstract concept with the help of which we personify all the objects around us in form.
A geometric figure is the presence of points on a plane, limited by space.
Figures are flat (circle, square, triangle, polygon…) and spatial (ball, cube, parallelepiped, cone...), which are also called geometric bodies.
GEOMETRIC BODY is a closed part of space bounded by flat and curved surfaces.
If the surface bounding the body consists of planes, then the body is called a polyhedron . These planes intersect along straight lines, which are called edges, and form the faces of the body. Each of the faces is a polygon whose sides are the edges of the polyhedron; the vertices of this polygon are called the vertices of the polyhedron.
Some polyhedra with a certain number of faces have special names : tetrahedron - tetrahedron, hexahedron - exahedron, octahedron - octahedron, dodecahedron - dodecahedron, twenty-sided - icosahedron.
What is a geometric FORM?
SHAPE is the outline, the outer appearance of an object.
Form (lat. forma - form, appearance) - the mutual arrangement of the boundaries (contours) of the subject, object, as well as the relative position of the points of the line.
TIME is a philosophical concept, which is characterized by the change of events and phenomena and the duration of their existence.
Time has properties :
- fluidity (time cannot be stopped)
- irreversibility and uniqueness
- duration .
SPACE is a quality by which relations such as neighborhoods and distances are established.
Orientation in space implies orientation towards oneself, away from oneself, from other objects, orientation on the plane and orientation on the ground.
2. Subject and tasks of the course "Methods of mathematical development and teaching of mathematics". Connection of the methodology of mathematical development with other sciences.
The method of forming elementary mathematical concepts in the system of pedagogical sciences is designed to assist in preparing preschool children for the perception and assimilation of mathematics - one of the most important subjects in school, to contribute to the education of a comprehensively developed personality.
Having stood out from preschool pedagogy, the methodology for the formation of elementary mathematical representations has become an independent scientific and educational area.
The subject of her research is the study of the basic patterns of the process of formation of elementary mathematical representations in preschoolers in the context of public education.
The range of tasks solved by the methodology is quite extensive:
- scientific substantiation of program requirements for the level of development of quantitative, spatial, temporal and other mathematical representations of children in each age group;
- determination of the content of factual material to prepare a child in kindergarten for mastering mathematics at school;
- improvement of the material on the formation of mathematical representations in the kindergarten curriculum;
- development and implementation in practice of effective didactic tools, methods and various forms of organizing the process of developing elementary mathematical concepts;
- implementation of continuity in the formation of basic mathematical concepts in kindergarten and the corresponding concepts in school;
- development of the content for the training of highly qualified personnel capable of carrying out pedagogical and methodological work on the formation and development of mathematical concepts in children at all levels of the preschool education system;
- scientifically based development of guidelines for parents on the development of mathematical concepts in children in a family setting.
The general task of methodology is to study and develop the practical foundations for the process of forming elementary mathematical representations in preschool children. It is solved from the standpoint of the Marxist-Leninist theory, which will develop a unified view of the world, having discovered the laws of development of nature, society, and the individual, and serves as the methodological, ideological basis of science.
The formation of elementary mathematical concepts is a purposeful and organized process of transferring and mastering knowledge, techniques and methods of mental activity provided for by the program requirements Its main goal is not only preparation for the successful mastery of mathematics at school, but also the comprehensive development of children.
The methodology for the formation of elementary mathematical representations in children in kindergarten is associated with many sciences , and above all with those whose subject matter is different aspects of the personality and activity of a preschool child, the process of upbringing and learning.
She has the closest connection with preschool pedagogy . The methodology for the formation of elementary mathematical representations is based on the tasks of teaching and mental education of the younger generation developed by preschool pedagogy and didactics: principles, conditions, ways, content, means, methods, forms of organization, etc. This connection is mutual in nature: research and development of problems the formation of elementary mathematical concepts in children, in turn, improve the pedagogical theory, enriching it with new factual material.
Multilateral contacts exist between private methods that study the specific patterns of the process of raising and teaching young children: the method of forming elementary mathematical representations, speech development, theory and methods of physical education, etc.
Preparing children for learning mathematics at school cannot be carried out successfully without connection with the methodology of elementary teaching of mathematics and those aspects of mathematics itself , which are the theoretical basis for teaching preschoolers and primary school students .
Reliance on these sciences allows, firstly, to determine the volume and content of knowledge that should be mastered by children in kindergarten, and serve as the foundation of mathematical education; secondly, to use teaching methods and means that fully meet the age characteristics of preschoolers, the requirements of the principle of continuity.
Education should be built taking into account the patterns of development of cognitive activity, the personality of the child , which is the subject of study of psychological sciences . Perception, representation, thinking, speech not only function, but also intensively develop in the learning process.
Psychological features and patterns of perception by a child of a variety of objects, numbers, space, time serve as the basis for developing a methodology for the formation of elementary mathematical representations. Psychology determines the age capabilities of children in acquiring knowledge and skills that are not something frozen and vary depending on the type of education.
The rational construction of the learning process is associated with the creation of optimal conditions based on the anatomical and physiological characteristics of young children. The regularities of the course of physiological processes in preschoolers serve as the basis for determining the duration of classes for the formation of elementary mathematical representations for each age group of the kindergarten, determine their very structure, the combination and alternation of various methods and means of teaching, different types of activities (inclusion of physical education minutes, dosing of educational cognitive tasks, etc.).
Communication with various sciences creates a theoretical basis for the methodology for the formation of mathematical representations in children in kindergarten.
3. Stages of development of the methodology of mathematical development: empirical, classical, modern.
Issues of mathematical development of preschool children are rooted in classical and folk pedagogy.
Various counting rhymes, proverbs, sayings, riddles, nursery rhymes were good material in teaching children to count, they made it possible for the child to form concepts about numbers, shape, size, space.
In the course of mastering them, children not only mastered the recalculation of objects, but also the ability to perceive and realize changes occurring in the reality around them: natural, color, spatial and temporal; quantitative, changes in shape, size, location, proportions. This ensured the natural development in children of certain ideas, ingenuity and ingenuity.
The first printed educational book by I. Fedorov "Primer" (1574) included thoughts about the need to teach children to count in the process of various exercises.
In the XIII-XIX centuries. questions of the content and methods of teaching mathematics to preschool children and the formation of their ideas about size, measurement, time and space can be found in the pedagogical works of Ya.
A. Comenius, M.G. Pestalozzi, K.D. Ushinsky, L.N. Tolstoy and others.
Views of teachers of the XIII—XIX centuries. on the content and methods of developing mathematical concepts in children - this is the first stage in the development of the methodology - empirical.
Teachers of that era, under the influence of the requirements of developing practice, came to the conclusion that it was necessary to prepare children for learning mathematics at school. They made certain proposals about the content and methods of teaching children, mainly in a family setting. It must be said that they did not develop special manuals for preparing children for school, but included their main ideas in books on education and training.
Thus, the Czech humanist thinker and teacher Ya.A. Comenius (1592-1670) in the book "Mother School" (1632) recommends even before school to teach the child to count within twenty, the ability to distinguish numbers greater-smaller, even-odd, to compare objects by size, to recognize and name some geometric shapes, to use in practice with units of measurement: inch, span, step, pound, etc.
I. G. Pestalozzi (1746-1827), a Swiss democratic teacher, pointed out the shortcomings of the teaching methods existing at that time, which were based on cramming, and recommended teaching children to count specific objects, understand operations on numbers, and the ability to tell time . The teaching methods proposed by him presuppose the transition from simple elements to more complex ones, the widespread use of visualization, which facilitates the assimilation of numbers by children. The ideas of J. G. Pestalozzi later (mid-19th century) served as the basis for reform in the field of teaching mathematics at school.
Progressive ideas in teaching children arithmetic before school were expressed by the Russian democrat teacher, the founder of scientific pedagogy in Russia, K. D. Ushinsky (1824-1871). He considered it important to teach the child to count individual objects and their groups, to perform addition and subtraction, to form the concept of ten as a unit of account.
However, all this was just wishes, without any scientific justification.
Writer and teacher Leo Tolstoy published in 1872 "ABC", one of the parts of which was called "Account". Criticizing the existing teaching methods, L.N. Tolstoy suggested teaching children to count "forward" and "backward" within a hundred and numbering, based on children's practical experience gained in the game.
Methods for developing ideas about number and form in children were reflected and further developed in the systems of sensory education of the German teacher F. Fröbel (1782-1852), the Italian teacher Maria Montessori (1870-1952), etc.
In the classical systems of sensory learning F. Fröbel (1782-1852) and M. Montessori (1870-1952) presented a methodology for introducing children to geometric shapes, sizes, measurement and counting, drawing up rows of objects by size, weight, etc.
F. Fröbel saw the tasks of teaching counting in the assimilation of a number of numbers by children of preschool age.
He created the famous "Gifts" - a special manual for the development of constructive skills in unity with the knowledge of numbers, shapes, sizes, spatial relationships. F. Fröbel was convinced that the development of "spatial" imagination and thinking at preschool age creates the conditions for the transition to the assimilation of geometry at school. The "gifts" created by F. Fröbel are still being used as didactic material to familiarize children with number, shape, size and spatial relationships.
M. Montessori, relying on the ideas of self-development and self-learning, recognized the need to create a special environment for mastering numbers, shapes, sizes, as well as written and oral numbering. She suggested using special material for this: counting boxes, bundles of colored beads strung in dozens, abacus, coins, and much more.
M. Montessori's pedagogical activity proceeded most effectively in the first half of the 20th century. The use of materials for the development of mathematical representation in children in the education and upbringing of a child was based on a certain style of interaction between an adult and a child; the need to monitor the behavior of children in a specially created environment; organizing joint free work with the child, etc.
The M. Montessori system provides for the development of the child's sensorimotor sphere and, in the future, intellect. The "golden" mathematical material, which is especially distinguished by its significance, is first mastered by the child as a set of beads in different quantities, then in symbols (numbers), after that - as a means of mastering the ability to compare numbers. Thus, the decimal number system is presented to the child visibly and tangibly, which leads to the successful mastery of arithmetic.
The section “Logic and Counting” is extensively represented in the M. Montessori system: the study of figures, sizes, methods of measurement, projection, modeling of sets. The following benefits are most interesting: “Figures from carnations”, “Mathematical sun”, “Fold the pattern”, “Combine the sets”.
In general, teaching mathematics according to the M. Montessori system began with a sensory impression, then a transition was made to understanding the symbol (i.e., from the concrete to the abstract), which made mathematics attractive and accessible even for 3-4-year-old children.
So, advanced teachers of the past , Russian and foreign, recognized the role and necessity of primary mathematical knowledge in the development and education of children before school , at the same time singled out account as a means of mental development and strongly recommended that children be taught it as early as possible from about three years of age. Learning was understood by them as "exercise" in performing practical, playful actions using visual material, using the experience accumulated by children in distinguishing numbers, time, space, measures in a variety of children's activities.
The questions of the methodology of mathematical development are of particular importance in the pedagogical literature of elementary school at the turn The authors of the methodological recommendations at that time were advanced teachers and methodologists. The experience of practical workers was not always scientifically substantiated, but it was tested in practice.
Over time, he improved, stronger and more fully revealed progressive pedagogical thought.
In the late 19th - early 20th century methodologists needed to develop a scientific foundation for the arithmetic technique . A significant contribution to the development of the methodology was made by advanced Russian teachers and methodologists P.S. Guriev, A.I. Goldenberg, D.F. Egorov, V.A. Evtushevsky, D.D. Galanin and others.
Formation of the methodology for the development of elementary mathematical concepts in the 19th — early 20th centuries. was also under the direct influence of ideas for reforming school teaching methods arithmetic. Two directions stand out in particular : the so-called method of studying numbers, or the monographic method, is associated with one of them, and the method of studying actions, which is called computational, is associated with the other.
According to the method of studying numbers, in the development of the German methodologist A.
V. Grube the teaching of arithmetic was carried out "from number to number." Each of the numbers allegedly accessible to "direct contemplation" was compared with each of the previous numbers by establishing a difference and multiple ratio between them. Actions seemed to follow from knowledge by heart of the composition of numbers. Monographic method received the definition of a method that describes a number.
In the process of studying each number , fingers, strokes on a blackboard or in a notebook, sticks served as the material for counting. For example, when studying the number 6, it was proposed to decompose the sticks one by one. Questions were asked: “How many sticks made up the number?”, “Count one stick at a time to get six, etc. After each group of such exercises, the actions were recorded in the form of a table, the results of which were memorized in order to subsequently perform arithmetic operations from memory without resorting to calculations.
In the 70s 19th century Opponents of the monographic method began to appear. Dissatisfaction with the method grew, and in the 80-90s. Russian mathematicians sharply criticized it, contrasting it with the method for studying actions , or, otherwise, computational method .. Method for studying actions (computational) - involved teaching children to calculate and understand the meaning of arithmetic operations. The training was based on decimal concentrations. Within each concentration, not individual numbers were studied, but counting and operations with numbers.
Both methods (both monographic and computational) played a positive role in the further development of the methodology, which absorbed the techniques, exercises, didactic means of one and the other methods.
At the end of the 19th - beginning of the 20th centuries. the ideas of teaching mathematics without coercion and didacticity, amusing, but without excessive entertainment were widely disseminated.
Mathematicians, psychologists, teachers developed mathematical games and entertainment, compiled collections of tasks for ingenuity, transformation of figures, solving puzzles (V. A. Latyshev, N. N. Amenitsky, I. P. Sakharov, A. P. Domoryad, V. Arene and etc.).
The authors tried to give a clear logic of construction, unusualness to joke problems, arithmetic rebuses, puzzle problems, problems of dividing a whole into parts, etc. In the course of solving such problems, the ability to think correctly, the logic and consistency of thought, a sharp mind and savvy. Tasks for ingenuity, ingenuity teach children to apply their knowledge to various cases of life, teach them to self-control, and most importantly, they contribute to the development in children of the ability to independently look for a solution.
A number of books were published specifically with the aim of developing the abilities of children, in particular, “Funny Arithmetic” by N. N. Amenitsky and I. P. Sakharov. It offered a lively and amusing solution to various practical problems and issues, which stimulated manifestations of children's amateur performance.
