Learn how to do math

How To Learn Math Fast: A System For Success

Many people struggle with math. It tends to be one of the most common subjects that people have trouble with. But with the right training, practice and effort, it can become easier. For those who want to learn how to be good at math, it may require extra practice. Here are a few best practices to learn math fast.

Begin With Foundations

Math is a subject that relies on the foundations when introducing sequential topics. For example, you’ll start with the basics like adding, subtracting, dividing, and multiplying. Then, as you build on your knowledge, you can master harder subjects in math like algebra, geometry, and calculus.

If you have no idea how to divide or add, then algebra will certainly be confusing. And you won’t be able to advance to calculus without a solid foundation in trigonometry and algebra. That’s why it is imperative to understand the foundations and build from there.

The Importance Of Number Sense

A lot of people start learning math by memorization. This means that they’ll take a times table (multiplication) and memorize what 9×9 is, for example. While this tactic can work, it could also cause problems in the future. If you’re taking a test and have a sudden burst of anxiety, you may forget whatever you have memorized.

Instead, it’s useful to have a grasp on number sense. Here’s an example of one method that makes this work. If you want to understand what 9×9 is, you may take 10×9 and know that it’s 90. Then, since you’re looking for nine groupings of nine, rather than 10, you’d subtract 9 from 90 to get to 81.

There’s more to number sense than that, but that’s the general idea. You want to really grasp how numbers and mathematical functions work over memorization.

Set Goals

Once you’ve mastered the basics of math, you can set goals as to what you want to focus on. If you’re looking to be good with algebra, then there’s no need to focus on geometry. Once you know what type of math you need to master, you can find the shortest path and spend energy getting good with those topics.

Tips And Tricks To Learn Math Fast

Math is diverse, so there’s no one method for how to be good at math. However, there are tried and true best practices to help you improve with each step along your journey.

Let’s take a look at what they include:

1. Practice

As with any subject or discipline, the best way to get better is to practice. You can find practice problems online or in workbooks. Also, if you’re currently in school and enrolled in a math class, be sure to do all your classwork and homework. There’s no doubt that your teacher will serve as a good resource to give you extra practice problems.

2. Understand Mistakes

Math is one of the subjects where your work really matters to get to the solution. It’s also entirely objective, as in there’s only one right answer because it’s based in numbers. As such, you’ll want to really understand your mistakes within your process of solving problems. This way, you can rectify errors and potentially arrive at the right solution.

3. Grasp Concepts

While math is based in numbers, there are broad concepts to help understand different types of math problems. Sometimes, students make the question harder than it actually is. Be sure to read math questions slowly and make sure you grasp the question before starting to work on the solution.

4. Get Help When Needed

It’s okay to ask for help. Even if you think you know the concept and understand the question, you may need extra guidance to lead you in the right direction. Consider getting a math tutor, asking a peer, or seeking help from your professor/teacher.

Number Tricks

Here are a few specific number tricks for foundation math to help you learn math fast.

5. Round When Adding

Adding more than two numbers at a time can become tricky to do mentally. One quick way to add numbers is to round them first. For example, say you want to add 317 and 518. You can round these up for 320 and 520 and more easily see that the sum is 840. Then, you’ll just have to deduct the difference between 320-317 (3) and 520-518 (2), so 3+2=5. The answer would be 840-5=835.

6. Multiply By 5s

There’s a specific trick for multiplying by 5 and it goes like this:

• For 5* even number, take half the even number and add a 0 to the side. Example: 5*6 — half of 6 =3, add a 0 to make it 30. 5*6=30
• For 5* odd number, deduct 1 from the odd number and take half of it, then add a 5 to the side. Example: 5*7 — one less than 7 is 6, half of 6 is 3, add a 5 to the side then the answer is 5*7=35

7. Multiplying Numbers That End In 0

When numbers end in 0 and you are multiplying them, simply multiply the digits that are not 0s and then add the total number of 0s back on the end. For example, if you want to multiply 1,000×4,000, then you’d take 4*1=4 and add 6 0s which would make the answer 4,000,000.

Educational Tips And Tricks

When you’re enrolled in school, whether it’s primary, secondary or higher education, you’ll want to practice these educational tips and tricks.

Following these tips will help you in math and any subject you’re trying to master.

8. Don’t Skip Class

Even if you are enrolled in online college and can more easily miss out on attending lectures, it’s not a good idea! This is especially true when it comes to math because missing just one class can cause you to miss the foundational lesson that each sequential lesson will build upon.

9. Repeat Work At Home

With any subject, but especially math, it helps to redo classwork at home. This will aid in better understanding the problems and solutions. Additionally, it’s an extra type of practice.

10. Get Extra Help

Math tends to be a subject that requires extra aid outside of the classroom. This may be in the form of hiring an outside tutor or attending online math classes. While there is always one right answer for math problems, there may sometimes exist multiple ways to reach the right answer. Perhaps the method you learn inside your class isn’t the best method for you. That’s why outside tutors or help may be just what you need to learn math fast.

11. Break The Question Down

If a problem seems hard to approach, try to break it up into its components. For math, this would be: arithmetic, algorithms or geometry. Do as much as you can within a solution and then seek help if needed.

The Bottom Line

No matter what subject you’re trying to master, learning takes time and everyone has different methods that work for them. However, when it comes to learning math fast, the primary requirement is to have a strong hold of the basics. Then you can work on building upon each concept with practice, extra help, and useful tips and tricks.

How to Learn Math: For Students | Course

GSE-YEDUC115-S

Stanford Graduate School of Education

Enroll Now

Format

Online, edX

Tuition

$0. 00

How to Learn Math is a class for learners of all levels of mathematics. It combines really important information on the brain and learning with new evidence on the best ways to approach and learn math effectively. Many people have had negative experiences with math, and end up disliking math or failing. This class will give learners of math the information they need to become powerful math learners, it will correct any misconceptions they have about what math is, and it will teach them about their own potential to succeed and the strategies needed to approach math effectively. If you have had past negative experiences with math this will help change your relationship to one that is positive and powerful.

The course will feature Jo and a team of undergraduates, as well as videos of math in action - in dance, juggling, snowflakes, soccer and many other applications. It is designed with a pedagogy of active engagement.The course will run from May/June to the end of December, 2014.

Course Concepts and Structure

The course will consist of six short lessons, taking approximately 20 minutes each. The lessons will combine presentations from Dr. Boaler and a team of undergraduates, interviews with members of the public, cutting edge research ideas, interesting visuals and films, and explorations of math in nature, sport and design.

Part 1: The Brain and Math Learning.

1. Knocking Down the Myths About Math.

   Everyone can learn math well. There is no such thing as a math person. This session give stunning new evidence on brain growth, and consider what it means for math learners.

2. Math and Mindset

   When individuals change their mindset from fixed to growth their learning potential increases drastically. In this session participants will be encouraged to develop a growth mindset for math.

3. Mistakes and Speed

   Recent brain evidence shows the value of students working on challenging work and even making mistakes. But many students are afraid of mistakes and think it means they are not a math person. This session will encourage students to think positively about mistakes. It will also help debunk myths about math and speed.

Part 2: Strategies for Success.

1. Number Flexibility, Mathematical Reasoning, and Connections

   In this session participants will engage in a number talk and see different solutions of number problems to understand and learn ways to act on numbers flexibility. Number sense is critical to all levels of math and lack of number sense is the reason that many students fail courses in algebra and beyond. Participants will also learn about the value of talking, reasoning, and making connections in math.

2. Number Patterns and Representations

   In this session participants will see that math is a subject that is made up of connected, big ideas. They will learn about the value of sense making, intuition, and mathematical drawing. A special section on fractions will help students learn the big ideas in fractions and the value of understanding big ideas in math more generally.

3. Math in Life, Nature and Work

   In this session participants will see math as something valuable, exciting, and present throughout life. They will see mathematical patterns in nature and in different sports, exploring in depth the mathematics in dance and juggling. This session will review the key ideas from the course and help participants take the important strategies and ideas they have learned into their future.

Instructors

Dr. Jo Boaler is a Professor of Mathematics Education at Stanford University and founder of youcubed. Former roles have included being the Marie Curie Professor of Mathematics Education at the University of Sussex, England, a mathematics teacher in London comprehensive schools, and a lecturer and researcher at King’s College, London. She is the editor of the Research Commentary Section of The Journal for Research in Mathematics Education (JRME), and the author of seven books including What’s Math Got To Do With It? (2009) Penguin, US, and The Elephant in the Classroom (2010) Souvenir Press, UK. She is the author of the first MOOC on mathematics learning for teachers and parents, a White House presenter, and an advisor to the PISA team at the OECD.

Mathematics from scratch. Step-by-step study of mathematics

“Mathematics from scratch. Step by Step Math for Beginners is a new project designed for people who want to learn math on their own from scratch.

Let's say right away that there are no easy solutions and statements like " Buy this book and pass math for 5" or " Master math for 12 hours " you will not see here. Mathematics is a big science that should be mastered consistently and very slowly.

The site is a math lesson, which is arranged according to the principle "from simple to complex". Each lesson covers one or more topics from mathematics. Lessons are broken down into steps. Start learning from the first step and then ascending.

Every lesson passed must be learned. Therefore, without understanding one lesson, you cannot move on to the next, since each lesson in mathematics is based on understanding the previous one. If you didn’t understand the lesson the first time, don’t be discouraged. Be aware that some people have taken months and years to understand just one single topic. Despair and despondency are definitely not your way. Read, study, try and try again.

Mathematics is well learned when a person opens a textbook on his own and teaches himself. At the same time, a certain discipline is developed, which is very helpful in the future. If you stick to the principle "from simple to complex", you will be surprised to find that mathematics is not so difficult. Perhaps even it will seem interesting and exciting to you.

What will the knowledge of mathematics give you? First, confidence. Not everyone knows mathematics, so knowing that you know at least some part of this serious science makes you special. Secondly, having mastered mathematics, you can easily master other sciences and be able to think much more broadly. Knowledge of mathematics allows you to master such professions as a programmer, accountant, economist. No one will argue that these professions are in great demand today.

In general, go for it friend!

We wish you good luck in learning mathematics!

• Step 1. Numbers
• Step 2: Basic Operations
• Step 3. Expressions
• Step 4. Substitutions in expressions
• Step 5 Beginner Shocks
• Step 6. Multiply
• Step 7. Division
• Step 8. Procedure
• Step 9. The laws of mathematics
• Step 10 Divisors and Multiples
• Step 11. NOD and NOK
• Step 12. Fractions
• Step 13. Working with fractions
• Step 14 Mixed Numbers
• Step 15: Compare fractions
• Step 16 Units
• Step 17. Using Fractions
• Step 18. Decimals
• Step 19 Decimal Operations
• Step 20: Use decimals
• Step 21 Rounding Numbers
• Step 22. Periodic fractions
• Step 23: Unit Conversion
• Step 24 Relationships
• Step 25. Proportion
• Step 26. Distance, speed, time
• Step 27. Direct and inverse proportionality
• Step 28. Interest
• Step 29. Negative numbers
• Step 30 Modulo
• Step 31. What is a set?
• Step 32. Adding and Subtracting Integers
• Step 33. Multiplication and division of integers
• Step 34 Rational Numbers
• Step 35. Comparing rational numbers
• Step 36: Adding and Subtracting Rational Numbers
• Step 37. Multiplying and dividing rational numbers
• Step 38: Learn more about fractions
• Step 39 Letter Expressions
• Step 40. Bracketing the common factor
• Step 41. Expanding brackets
• Step 42: Simple Math Problems
• Step 43. Problems with fractions
• Step 44 Interest Problems
• Step 45. Movement tasks
• Step 46 Performance
• Step 47. Statistics elements
• Step 48: Introduction to Equations
• Step 49: Solving Problems with Equations
• Step 50: Solving Problems with Proportions
• Step 51. Systems of linear equations
• Step 52: Inequality Overview
• Step 53. Systems of linear inequalities with one variable
• Step 54. Set Operations
• Step 55. Degree with natural indicator
  
• Step 56. Degree with integer exponent
  
• Step 57. Perimeter, area and volume
  
• Step 58. Monomials
  
• Step 59. Polynomials
• Step 60: Reduced multiplication formulas
  
• Step 61. Factoring a polynomial
  
• Step 62. Division of polynomials
  
• Step 63. Identity transformations of polynomials
• Step 64. Square root
• Step 65. Square Root Algorithm
  
• Step 66 Quadratic Equation
• Step 67. Quadratic equation with even second coefficient
  
• Step 68. Vieta's theorem
  
• Step 69. Factoring the square trinomial
• Step 70. Generalized concept of the modulus of a number
  
• Step 71 Equation with modulo
• Step 72. Solving Equations with Modulus by the Interval Method
  
• Step 73. Inequalities with modulo
  
• Step 74. Solving inequalities with modulus using the interval method
  
• Step 75: Taking the square root of both sides of the equation
  

New lessons coming soon. Stay with us!

Join our new Vkontakte group and start receiving notifications about new lessons

Basic operations

The basic operations that are used in mathematics are addition, subtraction, multiplication and division.

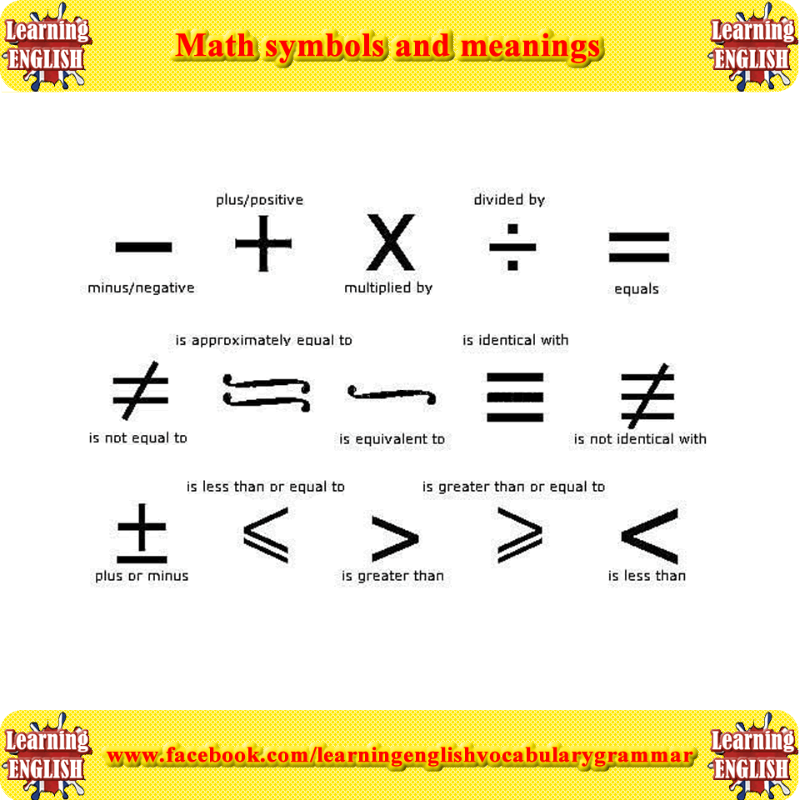
In addition to these operations, there are also relational operations such as: equal to (=), greater than (>), less than (<), greater than or equal to (≥), less than or equal to (≤), not equal to (≠).

In general, operations can be divided into two types:

1. action operations;
2. relation operations.

Action operations are:

• addition (+)
• subtraction (-)
• multiplication (×)
• division ( ÷ ).

Operations of relation are:

• is equal to (=)
• more (>)
• less than (<)
• greater than or equal to (≥)
• less than or equal to (≤)
• is not equal (≠).

Let's start with relational operations. The word relationship speaks for itself. Examples from life: something is related to something. Dad is related to mom. This relationship is called marriage:

There are many examples of relationships. We can say that our beautiful world, which develops harmoniously, also consists of relationships.

If five is greater than three, then we say that "five is greater in relation to three" and write as 5 > 3 (read: five is more than three) . The acute angle of the ratio sign should be directed towards the smaller number. In this example, the number 3 is less than the number 5, so the acute angle of the ratio sign is directed towards the number 3.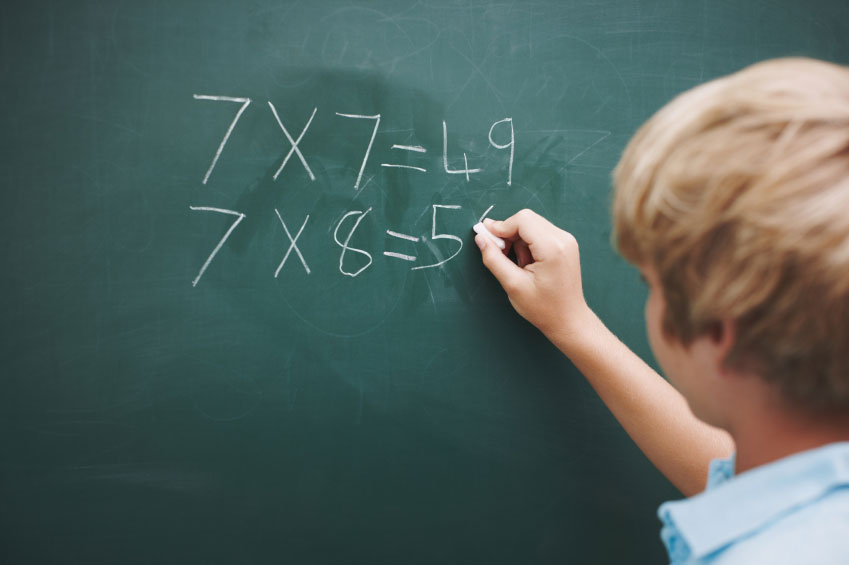

Another example. The number 11 is less than the number 15. This phrase can be written like this:

11 < 15

In mathematics, laws, formulas, equations, and functions can be written using relations. It can be written that one expression is equal to another, or some action is unacceptable in relation to some object, number, law.

For example, the famous phrase “you cannot divide by zero” is written as follows:

Let's not get ahead of events and run ahead. Let's just say that in this expression, instead of a and b , any numbers can stand. But then it says that b should not be equal to zero.

The equal sign = is placed between values ​​and indicates that these values ​​are equal to each other.

For example, " five equals five" is written as 5 = 5. It is clear that two fives are equal to each other. In addition to simple numbers, more complex expressions can be connected with the equal sign, for example: 9 + x + y = 4 + 5 + x + y .

Another example: if one large watermelon weighs 20 kg, and two small watermelons weigh 10 kg each, then an equal sign can be put between a 20 kg watermelon and two 10 kg watermelons. This ratio can be read like this: "one watermelon weighing 20 kilograms is equal to the weight of two watermelons, each of which weighs 10 kg" . After all, 20 kg = 10 kg + 10 kg.

Not equal sign ≠ is placed between values ​​when they are not equal to each other.

For example, 5 ≠ 7. Clearly, five is not equal to seven. More examples: Excellent student is not equal to the dual -breeder, the dog is not equal to the cat, tangerine is not orange :

Excellent student ≠ Two

Dog ≠ Cat

Mandarin ≠ Orange