List mathematical concepts

10 Math Concepts You Can't Ignore

Sets and set theory

A set is a collection of objects. The objects, called elements of the set, can be tangible (shoes, bobcats, people, jellybeans, and so forth) or intangible (fictional characters, ideas, numbers, and the like). Sets are such a simple and flexible way of organizing the world that you can define all of math in terms of them.

Mathematicians first define sets very carefully to avoid weird problems — for example, a set can include another set, but it can't include itself. After the whole concept of a set is well-defined, sets are used to define numbers and operations, such as addition and subtraction, which is the starting point for the math you already know and love.

Prime numbers go forever

A prime number is any counting number that has exactly two divisors (numbers that divide into it evenly) — 1 and the number itself. Prime numbers go on forever — that is, the list is infinite — but here are the first ten: 2 3 5 7 11 13 17 19 23 29 . . .

It may seem like nothing, but . . .

Zero may look like a big nothing, but it's actually one of the greatest inventions of all time. Like all inventions, it didn't exist until someone thought of it. (The Greeks and Romans, who knew so much about math and logic, knew nothing about zero.)

The concept of zero as a number arose independently in several different places. In South America, the number system that the Mayans used included a symbol for zero. And the Hindu-Arabic system used throughout most of the world today developed from an earlier Arabic system that used zero as a placeholder. In fact, zero isn't really nothing — it's simply a way to express nothing mathematically. And that's really something.

Have a big piece of pi

Pi (π): The symbol π (pronounced pie) is a Greek letter that stands for the ratio of the circumference of a circle to its diameter. Here's the approximate value of π:

π ≈ 3.1415926535…

Although π is just a number — or, in algebraic terms, a constant — it's important for several reasons:

Geometry just wouldn't be the same without it. Circles are one of the most basic shapes in geometry, and you need π to measure the area and the circumference of a circle.

Pi is an irrational number, which means that no fraction that equals it exactly exists. Beyond this, π is a transcendental number, which means that it's never the value of x in a polynomial equation (the most basic type of algebraic equation).

Pi is everywhere in math. It shows up constantly (no pun intended) where you least expect it. One example is trigonometry, the study of triangles. Triangles obviously aren't circles, but trig uses circles to measure the size of angles, and you can't swing a compass without hitting π.

Equality in mathematics

The humble equals sign (=) is so common in math that it goes virtually unnoticed. But it represents the concept of equality — when one thing is mathematically the same as another — which is one of the most important math concepts ever created. A mathematical statement with an equals sign is an equation. The equals sign links two mathematical expressions that have the same value and provides a powerful way to connect expressions.

Bringing algebra and geometry together

Before the xy-graph (also called the Cartesian coordinate system) was invented, algebra and geometry were studied for centuries as two separate and unrelated areas of math. Algebra was exclusively the study of equations, and geometry was solely the study of figures on the plane or in space.

The graph, invented by French philosopher and mathematician René Descartes, brought algebra and geometry together, enabling you to draw solutions to equations that include the variables x and y as points, lines, circles, and other geometric shapes on a graph.

The function: a mathematical machine

A function is a mathematical machine that takes in one number (called the input) and gives back exactly one other number (called the output). It's kind of like a blender because what you get out of it depends on what you put into it. Suppose you invent a function called PlusOne that adds 1 to any number. So when you input the number 2, the number that gets outputted is 3:

PlusOne(2) = 3

Similarly, when you input the number 100, the number that gets outputted is 101:

PlusOne(100) = 101

It goes on, and on, and on . . .

The very word infinity commands great power. So does the symbol for infinity (∞). Infinity is the very quality of endlessness. And yet mathematicians have tamed infinity to a great extent. In his invention of calculus, Sir Isaac Newton introduced the concept of a limit, which allows you to calculate what happens to numbers as they get very large and approach infinity.

Putting it all on the line

This pattern continues forever, with each value being halved, which means you can never get to the other side of the room. Obviously, in the real world, you can and do walk across rooms all the time. But from the standpoint of math, Zeno's Paradox and other similar paradoxes remained unanswered for about 2,000 years.

The basic problem was this one: All the fractions listed in the preceding sequence are between 0 and 1 on the number line. And there are an infinite number of them. But how can you have an infinite number of numbers in a finite space? Mathematicians of the 19th century — Augustin Cauchy, Richard Dedekind, Karl Weierstrass, and Georg Cantor foremost among them — solved this paradox. The result was real analysis, the advanced mathematics of the real number line.

Numbers for your imagination

The imaginary numbers (numbers that include the value i = √ - 1) are a set of numbers not found on the real number line. If that idea sounds unbelievable — where else would they be? — don't worry: For thousands of years, mathematicians didn't believe in them, either. But real-world applications in electronics, particle physics, and many other areas of science have turned skeptics into believers.

So, if your summer plans include wiring your secret underground lab or building a flux capacitor for your time machine — or maybe just studying to get a degree in electrical engineering — you'll find that imaginary numbers are too useful to be ignored.

The Most Important Math Concepts Kids Learn in Pre-K

Although there’s a lot of emphasis placed on emergent reading, experts show that pre-k math skills are just as important for your child’s learning development.

Understanding what skills your child will be exposed to as a math beginner will give you an idea of what concepts you can emphasize in fun, easy ways at home!

Fortunately, kids are exposed to many math concepts from a very young age — putting puzzles together, sorting objects, and even playing with building blocks. These activities all help build a good foundation for math.

In this article, we’ll take you through the most important pre-k math concepts so you can encourage and motivate your budding mathematician!

Table Of Contents

• What Are The Components Of Pre-K Math?
• Basic Pre-K Math Checklist
• Pre-K Math Development
• 9 Fun Pre-K Math Activities

What Are The Components Of Pre-K Math?

There are five basic components of pre-k math. They act like umbrella terms, each with many different elements hidden inside their broad concepts.

Your child will become acquainted with all of these essential concepts when they begin learning pre-k math.

1) Numbers And Counting

Children typically start with the bedrock of math — numbers! They’ll learn number names and how to write numbers, typically beginning with 1-10.

Counting is not easy business! While your child learns how to count — first with physical objects, then conceptually — they are bound to make mistakes here and there. This is perfectly all right. Counting will take time to master.

Most of kids’ initial exposure will be through representational counting. This could mean counting the number of strawberries in their lunch box, how many blocks are on the floor, and so on. These counting activities will set the stage for a strong foundation in counting.

By understanding that numbers represent objects, your child will begin to understand one-to-one correspondence (each object counted gets its own number and only that number) as well as the counting principle that when counting the number of objects, the last number counted equals the amount present.

Over time, a child’s reliance on physical objects for counting will decrease. They’ll depend more on conceptual counting as their skills develop.

This conceptual counting is called “number sense.” They’ll understand that quantities, whether tangible or theoretical, are countable. They’ll also learn that numbers can be compared: two or more numbers can have a more-than, less-than, or same-as number relationship.

There are many fun ways to get your child comfortable with numbers and counting at home without making it feel burdensome.

Here are a few simple yet effective strategies you can try:

• Encourage your child to touch and count objects they see in everyday life — for example, a bunch of bananas or a stack of books.
• After they count a set of objects, help them write down the corresponding number on a piece of paper.
• Have your child compare different items using the appropriate language. For example, “Let’s count the number of blueberries and strawberries on the plate. Are there more strawberries than blueberries?”
• Hang a simple number line on the wall or tape one to your refrigerator. Throughout the day, point to each number with your child and count from 1-10 together.
• Ask your child to help set the table by counting out the right number of forks and spoons. Once they have collected them, they can count them again as they put one at each place setting.

These simple activities allow children to make sense of numbers. And the more they practice counting principles outside of the classroom, the more they’ll realize how relevant they are to everyday life.

2) Addition And Subtraction

Once your child has a firm grasp on counting and is developing number sense, they’ll explore the relationships between numbers more often. Describing how numbers are the same or different will lead into learning how to combine two numbers to make a new number!

Similar to the last concept, children will typically learn how to add and subtract by relying on counting activities with tangible objects. For example, you could set up two separate groups of apples and ask how many you will have if you join them together.

The first group may have three apples, while the second group has two apples. At first, many children will count one group and then start over to count the second group. It is a good idea to count both groups individually and then bring them together and count the total amount.

This is their first introduction to addition! The same idea works for subtracting. What happens when you begin with five apples and then take away two of them?

“Taking away” objects may be a little harder for your child to master at first. This is why many children will remove apples first and then count the remaining apples rather than counting backward.

To help, practice counting backward together. Pretend to be a rocket ship, and start counting down from five to one, gradually increasing the beginning number each time. After you get to one, shout, “Blastoff!” and jump into the air as high as you can. This fun game can help your child become more comfortable with counting down.

Pictures can also help your child master addition and subtraction concepts. For addition practice, present one sheet of paper with three apples and another with two. Then say, “Count the apples on both pieces of paper. How many apples do you have total?”

For subtraction problems, present this scenario: “On our paper, we have five apples total. How many apples will you see if I cover up two of them?” Then, count the remaining apples together.

Pictures are an effective way for your child to visualize mathematical problems. But, if you prefer not to draw, you can also use real objects instead. You could get out several apples (stuffed animals, cups, or whatever) and count them. Then, use those items for math practice.

Remember that adding and subtracting are basically making comparisons between numbers or establishing relationships between them. There are many strategies a child might use to solve a problem, which is a good thing since our main goal is to help children think mathematically.

3) Geometry And Spatial Reasoning

Shapes are everywhere in our world, which will be one of your greatest assets when it comes to teaching your child about shapes and spatial reasoning.

They’ll start out by learning about the basic 2-D shapes that are used in math: squares, triangles, circles, rectangles, rhombuses, and ovals. Learning how to draw these basic shape illustrations can be helpful for their learning process.

Some of these shapes you’ll be able to reference easily in your day-to-day life. This will help reinforce your child’s understanding of the shapes after their initial introduction.

For example, when making breakfast with your child, you could hold up a plate and ask them, “What shape is this? Do you think it’s a square or a circle?”

Other shapes, like triangles or rhombuses, may be a little harder to find hanging around. Challenge your child to find these shapes in nature. Are there any flower petals in your garden that are shaped like triangles (or an aloe vera plant hanging in their windowsill)?

Encourage your child to be creative with identifying shapes! It will help them with learning geometry in the long run.

Next, learning 3-D shapes will come after learning 2-D shapes. Like their flatter cousins, 3-D shapes are all around the world, too! Your child’s soccer ball is a sphere; the paper towel roll in the kitchen is a cylinder.

We recommend learning the basic form of these shapes and how they appear first. Then, you can use the natural 3-D shapes in your child’s environment to reinforce their learning!

Point out shapes when you see them and play a shape version of “I Spy” to practice. If your child has a set of blocks, talk about the different shapes of the blocks. Challenge them to use only one shape to build something. Then, see what they can make by using all of the shapes.

Kids also learn about spatial reasoning by discovering how to describe the shapes they see and play with. They can compare them with dimensional adjectives like “big” and “small,” or characteristics of their shape like “straight” and “curvy.”

This includes the spatial relationship between different objects, too. Look out for observations using location adverbs like “under,” “beside,” or “around.” These are all different ways for your child to “measure” or observe how shapes take up space.

4) Sorting And Patterns

We categorize things in our daily lives without even realizing it. Your child probably already does this, too — they may arrange their stuffed animals or toys in a certain way. For example, they may keep farm animals separated from dinosaurs.

Sorting and patterns are related to categorical reasoning. In the same way grocery stores sort out items by their parallel uses, your child will learn how to sort things based on their characteristics and how they are the same or different from other objects.

They’ll sort objects by weight, shape, quantity, texture, color, and other traits, often without even realizing it!

It’s important to note here that sorting and counting aren’t sequential. Your child might begin sorting before they begin counting, in fact.

For instance, if you want your child to sort a bowl of fruit, you can ask them to count all of the strawberries. They’ll sort the strawberries from the rest of the fruit. If you ask them to count the red fruit, they’ll sort out strawberries, cherries, and watermelon and count them together.

Once a child has learned to isolate characteristics, they can begin to identify, extend, and even create patterns. Your child will learn how to:

• Copy a pattern
• Identify the parts that repeat and continue a pattern
• Correct a mistake in a pattern
• Explain a pattern
• Create their own patterns

To encourage your child to explore patterns, take a few moments to build a pattern for them when you play together. Use whatever materials you have available and create a simple AB pattern, such as truck, car, truck, car.

Next, point to each object. Say its name aloud. Then, when you get to the end of the row, ask them what comes next. If they aren’t sure, grab the next object and put it down. Once you’ve completed one round, start at the beginning and repeat each item to reinforce the pattern.

5) The Language Of Math

Part of learning how to do math means learning how to “speak” math. We don’t mean your child will turn into C-3PO — just that they will learn how to use mathematically correct language, or how to tell a story with math terms.

This can happen in daily life. While picking at an afternoon snack, your younger child may say, “Hey! My brother has more crackers than me!” Then you might agree to “add” to the cookies on the younger child’s plate so that both plates are “equal.”

These skills may be naturally exciting for your child — they’ll feel like they’re learning how to speak “grown up!” Show them how fun it is to incorporate mathematically appropriate language into their daily speech and use it to tell stories about what’s going on around them.

Using words to describe things in their lives will help them give ownership over ideas and observations. Motivate them to think about the order of the world around them and use different words to describe them, such as:

• More than
• Less than
• Shape names
• Light or heavy
• Small or big

Mastering math language will help them in their quest to become robust mathematicians! It’ll also help them develop a strong vocabulary so they’re better prepared for kindergarten.

Basic Pre-K Math Checklist

Now that you know some of the concepts your child will be learning in pre-k math, let’s look at some of the skills they’ll build during this time.

• Rote count to 10
• Use one-to-one correspondence to count up to 10 objects and tell how many there are altogether
• Recognize basic shapes (circle, triangle, square)
• Understand the concept of quantity (more/less)
• Sort objects by one characteristic
• Understand and use directional terms, such as up, down, in, out
• Pick what object goes next in a simple pattern

While these aren’t all of the math skills your child might learn in pre-k, they will give your child a solid mathematical foundation to build on in kindergarten. And they’re all skills you can practice in fun ways!

Pre-K Math Development

As your child grows and learns, they’ll work through three phases of mathematical development: concrete, representational, and abstract. They’ll likely be in the concrete stage at the beginning of pre-k.

During this phase, students need hands-on activities and real-world examples to help them understand mathematical concepts. This is why math manipulatives are so crucial in the early years. It’s also essential to present math concepts in a very concrete way during this stage.

For example, if you’re teaching your child about numbers, don’t just tell them that five is more than three. Instead, show them five objects and three objects, and let them count for themselves. This will help them understand the concept of more and less.

As your child continues to learn and practice a mathematical concept, they can move into the representational phase. Here, students can count pictures or images instead of actual objects. For example, they realize that numbers can be represented by lines or drawings.

Then, they’ll be ready to try the abstract stage. At this point, children understand that numbers can be represented by symbols. They don’t need manipulatives or visual aids to do math problems. They can start using numbers and symbols such as + or – to solve math problems.

The activities above will help your child to build their understanding of mathematical concepts so they can move through the different stages.

But, in pre-k, it’s important to focus on the process, not the answer. So don’t worry if your child doesn’t get the solution right away. Let them work through the problem and try to figure it out for themselves.

A strong foundation in pre-k math sets children up for success when they start kindergarten. By providing opportunities for them to explore and experiment with math, you can help them develop the skills they need to be successful in school and beyond.

9 Fun Pre-K Math Activities

Now that you’re clear on all of the exciting new math concepts your pre-kindergartener will be exposed to and what skills they’ll practice, let’s talk about some games and activities you can play at home to help your child hone them.

We’ve already discussed some math activities you can incorporate into everyday life. Now, we’re sharing our list of fun games to encourage your young learner to love math even more.

1) What Did I Do?

This game helps reinforce counting, adding, and subtracting. It’s quick to play, so it’s perfect for when you have a few extra minutes.

What You’ll Need

• Small objects (e.g., paper clips)

What To Do

Place some paper clips (or any other small objects) in your hand, and let your child count how many you have. After they’ve done this, put your hands behind your back and either add or remove some.

Next, show your child the new quantity and ask them to count how many there are now. You can ask your child questions, such as, “Did I add or take away some paper clips?” or “How many did I add or take away?”

For even more fun and learning opportunities, take turns playing the game. And when it’s your turn to guess, it’s OK to guess wrong — “I think you took away 10!… No! I added two!” This back and forth offers lots of laughs and critical thinking for your little mathematician.

Remember that because your child is in pre-k, the concepts of addition and subtraction are still new. Therefore, it’s best to keep the number of objects used in this game low (e.g., 1-10 clips) so they aren’t confused or overwhelmed.

2) Math Tic-Tac-Toe

Add a mathematical twist to the classic game of Tic-Tac-Toe!

What You’ll Need

• Paper
• Pencil
• Ruler
• Markers (or colored pencils)

What To Do

Start by dividing your sheet of paper into squares by drawing lines (three horizontal by three vertical). In traditional tic-tac-toe, you’d leave these squares blank until the game starts. Not this time.

For this version of the game, you’ll need to fill each box with dots and have your child tell you how many dots are in a box before placing their X or O in it. The first player to get three Xs or Os wins!

The Xs or Os don’t have to be in order at this point, but you can add that requirement as a challenge once your child gets the hang of playing the game.

This activity helps kids work on their counting skills while also incorporating lots of fun.

3) NumberBow

Your child will add numbers to create a beautiful rainbow in this game.

What You’ll Need

• Two dice
• Two sheets of paper
• Colored pencils (or crayons)
• Pencil

What To Do

Draw two identical rainbow-shaped boards (one on each sheet of paper) with numbered boxes on the rainbows. (You can check out this link for reference.). The aim of the game is to color the numbered boxes in.

To play, each player throws two dice, then adds the numbers from the throw together and colors in the corresponding box on their rainbow.

For example, if your child throws a three and a one, they’d need to add 3+1 and color in the “4” box. If they’ve already colored that box in, they’d have to wait for their next turn. Each player gets 10 turns to have the most colorful rainbow at the end!

While this is an effective game to help your child work on their addition skills, some children might experience difficulty adding larger numbers together (e. g., 5 and 6). If you need to help them, that’s OK!

Remember that exposure and repetition are very beneficial for young learners.

4) Fill The Cup

This game can be challenging for younger children, so if it causes frustration, play other math games until your child is more comfortable with adding and counting.

What You’ll Need

• Dice
• Plastic cup
• Small objects that are easy to count (e.g., paper clips, dried beans, pebbles, etc.)

What To Do

To begin the game, players roll the dice at the same time. The number rolled indicates the number of items you can add to your cup. For example, if you roll a five, you add five dried beans. The goal for your child is to be the first one to fill their cup.

At the pre-kindergarten stage, some children might not be comfortable with the steps needed to play this game (rolling the dice, reading the number aloud, adding the items to the cup). So, before starting, take a few minutes to get them used to the process.

If you notice that it’s still too challenging, you can make it easier by choosing to roll the dice for each other. In this option, you can roll the dice and then help your child read the number and add the right amount of items to their cup.

Whichever variation you choose, this is a fun and engaging way to help children learn numbers and practice counting.

5) Stand Up, Sit Down

Kids enjoy playing this active game where they get to use their bodies and their brains! (Note: This game requires more than one child player, so it’s a great activity for siblings or to do when your child has a friend over.)

What You’ll Need

• Index cards
• Marker

What To Do

Write the numbers 1-10 on the index cards (one number per card) and hand three to each participant. Then, say a math equation (or word problem) out loud.

If the answer matches a number they’re holding, the child will stand. If they don’t have the answer, they remain seated.

For example, if the question is, “If I have three dried beans and I throw away one, how many do I have left?”, the child with “2” would then need to stand up and show their card.

The player who has the least number of cards left at the end of five rounds wins. Note: To make it easier, you can give children small items (e.g., blocks, dried beans, paper clips, etc.) to help them count.

Stand Up, Sit Down is also helpful for children learning shapes. Instead of writing numbers on the cards and handing them out, you can draw different 2-D and 3-D shapes that children learn in pre-k (as discussed above) and hand those out.

To play, someone describes a shape and the player who has that shape stands up and says what it is. For example, “If you are holding a shape that has three sides, stand up right now!”

When the child stands up, they’ll need to say that their shape is a triangle, and they get the point. In this version of the game, the player with the most points at the end wins.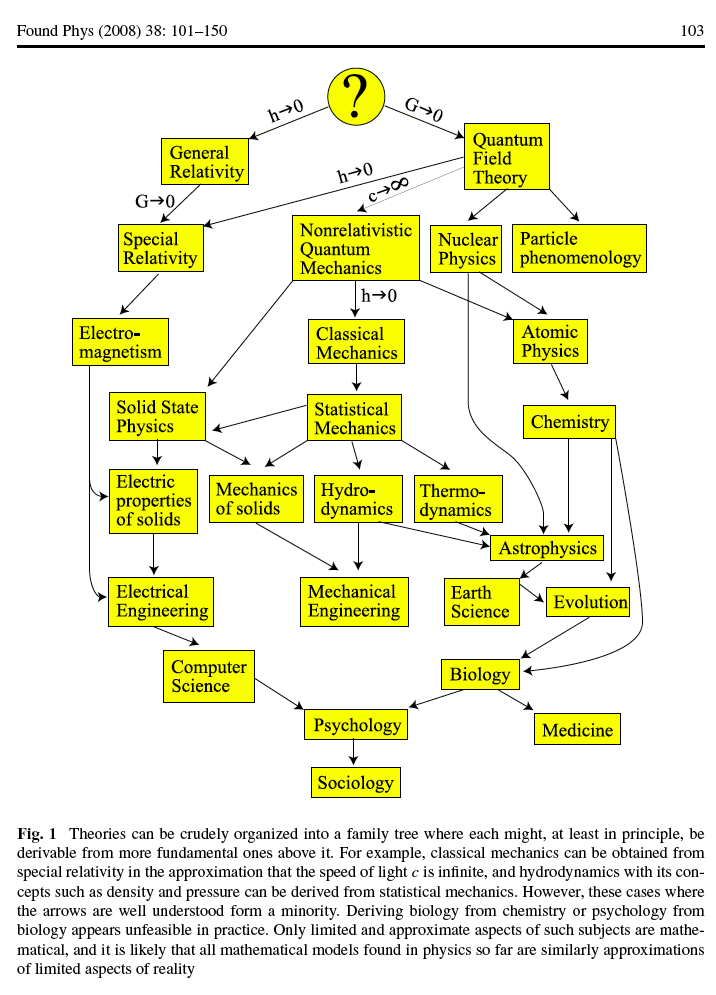

Using this game allows children to learn the names and attributes of the different 2-D and 3-D shapes they get exposed to in pre-kindergarten.

6) Who Has More?

This game is perfect for helping kids understand the concepts of more and less, which are critical in early math development.

What You’ll Need

• A small bowl or container
• A teaspoon
• A handful of objects (e.g., buttons, pennies, cereal pieces, etc.)

What To Do

Place the objects in one bowl. Have your child scoop a teaspoon of them out and count them. Then, you do the same and see who got the most. That person’s the winner!

Note: Counting past 10 is difficult at this age, so you’ll want to use big enough items (such as large kidney beans) and stick to a teaspoon for scooping so your child doesn’t end up with more than 10 per spoonful.

7) Read Math Books

Help your child develop a love for math by reading math-related books together.

What You’ll Need

• A mathematical-themed book to read together (see some recommendations below)

What To Do

Grab one of the following books and snuggle up with your little one for a math-themed storytime. As you read, point out any mathematical concepts in the book.

• From the Garden by Michael Dahl
• The Shape of Me and Other Stuff by Dr. Seuss
• The Button Box by Margarette S. Reid
• A Pair of Socks by Stuart J. Murphy
• The Berenstain Bears and the Spooky Old Tree by Stan and Jan Berenstain
• Pattern Fish by Trudy Harris

When you finish reading, discuss any new math concepts your child learned. You could even do a related activity or two to reinforce what they’ve learned.

8) In The Box

This game helps your child practice prepositions or direction words, like “under,” “behind,” and “in front of.” These concepts are essential for mathematical development as well as reading comprehension.

What You’ll Need

• A stuffed animal
• An empty box large enough for the animal to fit inside

What To Do

Ask your child to put the animal inside the box.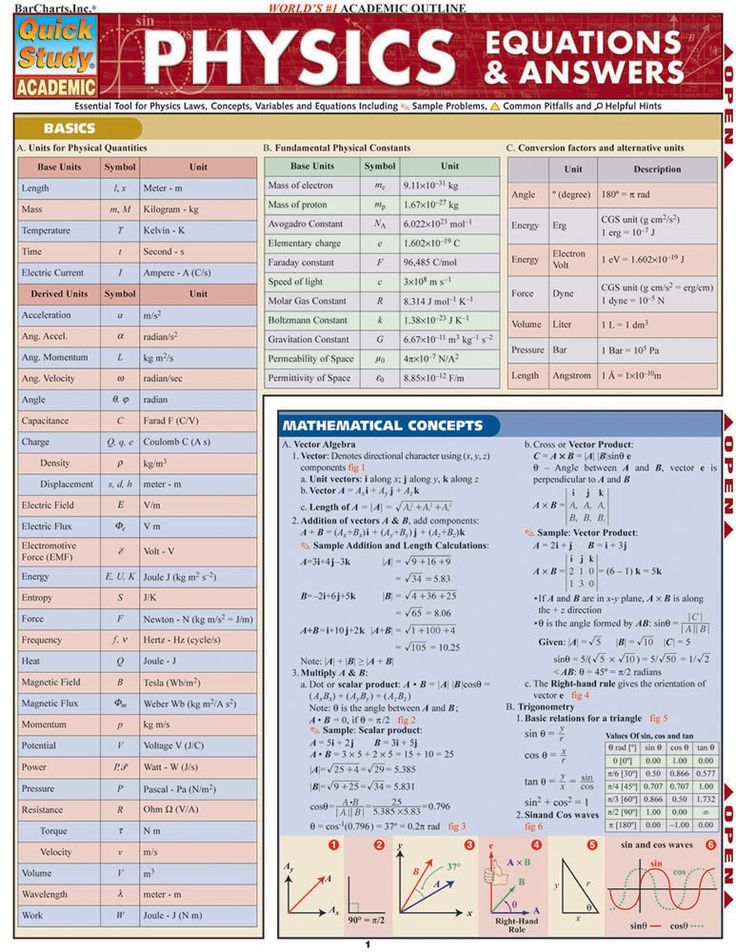 If they have difficulty understanding what you mean, give them some clues. For example, you could say, “Put the animal in the box so that its head is sticking out,” or “Put the animal in the box so that only its tail is showing.”

Once the animal is in the box, ask them to describe where it is using prepositions. So, they might say, “The animal is in the box.”

Then, take the animal out and place it behind the box. Ask your child to describe its location again. For example, they might say, “The animal is behind the box.”

Next, let them take a turn placing the animal in, on, under, next to, etc. the box. When they’re done, you describe where it is. Continue taking turns as you practice different prepositions.

9) Number Line Race

This game helps kids with number recognition as well as one-to-one correspondence.

What You’ll Need

• Number cards (we recommend the ones from the HOMER Explore Numbers Kit)
• A die

What To Do:

Spread the cards out in numerical order, with a bit of space between each one. They should form a line on the floor, though it doesn’t need to be perfectly straight.

Have your child stand on the card with the number one on it. Hand them the die and let them roll it. Call out the number they rolled. Next, ask them to move that many numbers forward, moving from one index card to the next as they count aloud.

If they land on a number that would take them off the end of the line, they start from the beginning for their next throw (each player gets five throws). Then, it’s your turn! Start on one and see how far you can get, too.

The person to end on the card with the highest number is the winner!

Encouraging A Love Of Pre-K Math At Home

Pre-k math isn’t just reserved for pre-k classes. You can help your child explore the exciting world of pre-k math right from your home!

HOMER is always here to help and happy to be your at-home learning partner. Our Learn & Grow app offers tons of opportunities for your child to develop their pre-k math skills from conception to execution.

Our games are personalized to accommodate your child’s specific interests. They include pattern-identification games like Ribbons or shape-building games like the Castle Creator.

Your child can also explore the Shapery Bakery, where they help the cute, cuddly Tisa the Cat by sorting treats based on their shape. All that and so much more can help your child develop their pre-k math skills!

Author

Mathematical concepts | Educational and methodological material on mathematics on the topic:

Slide 1

Methods of mathematics Primary school teacher: Anikina Tatyana Yurievna

Slide 2

Mathematical concepts Concepts, their scope and content. The relationship of genus and species between concepts. Explicit and implicit definitions of concepts. Algorithm for solving the problem of recognition using the definition through the genus and specific difference. Examples of explicit and implicit definitions of concepts.

Slide 3

Concepts, their scope and content Concepts related to numbers and operations on them: number; addition; term; more. Algebraic concepts: expression; the equation; equality. Geometric concepts: segment; straight; triangle. Quantities and their measurement: centimeter; meter; kilometer.

Slide 4

The scope of a concept is the set of all objects denoted by one term. is the set of all essential properties of the object reflected in this concept. Content of concept

Slide 5

Relationship Scope of a concept Content of a concept sets. ! If A with B (A=/ B), then a is specific in relation to the concept b, and the concept b is generic in relation to the concept a. If A = B, then the concepts a and b are identical. If the sets A and B are not connected by an inclusion relation, the concepts a and b are not in relation to the genus and species and are not identical.

Slide 7

Properties: 1) The concepts of genus and species are relative. 2) For a given concept, it is often possible to specify several generic concepts. 3) A species concept has all the properties of a generic concept. and implicit definitions of concepts Defined concept Generic concept Specific difference Defining concept + A definition is usually a sentence that explains the essence of a new term (or designation). !

Slide 10

Remember!!! 3. The definition should be clear 2. There should be no vicious circle in the definition (or their system) 4. The same concept can be defined in different ways. 1. The definition must be proportionate

Slide 11

Algorithm: Name the concept (term) being defined. 2. Indicate the closest generic (in relation to the defined) concept. 3. List the properties that distinguish the defined objects from the scope of the generic, i.e. state the difference. 4. Check whether the rules for defining the concept are met (is it proportionate, is there a vicious circle, etc.)

Slide 12

Explicit definitions Have the form of equality, coincidence of two concepts. The general scheme of such definitions is: "A is (by definition) B". Here A and B are two concepts, and it does not matter whether each of them is expressed by one word or a combination of words. Geometry is the science of the properties of geometric shapes. A molecule is the smallest particle of a substance that retains all the chemical properties of this substance. This definition is by display. They are used to introduce terms, by demonstrating the objects that these terms designate.

Slide 14

X + 6 = 15 is an equation An example of a contextual definition can be the definition of an equation and its solution given in a mathematics textbook for grade II (Moro M.I., Bantova M.A. Mathematics: Textbook for 2 class of a four-year elementary school.) Here, after writing + 6 \u003d 15 and a list of numbers 0,5,9,10, there is a text: “To what number must 6 be added to get 15? We denote the unknown number with the Latin letter X (x): To solve an equation means to find an unknown number. In this equation, the unknown number is 9, since 9+6=15. "Explain why the numbers 0.5 and 10 are not appropriate."

Slide 15

2*7 >2*6 is inequality 17-5=8+4 is equality inequalities) from other sentences, it does not indicate the properties characteristic of these concepts. They only associate terms with the objects they define.

Slide 16

Geometric shapes Definition of a segment, ray, angle, polyline. The main properties of these figures. The content of these concepts in elementary education in mathematics; types of definitions. Task examples.

Slide 17

Definition of a segment, ray, angle, polyline A segment is a straight line passing through two points. is a system of two points A and B belonging to the line a. The points located between A and B are called the points lying inside the segment AB, the points A and B are called the ends of the segment AB. - A B is a part of a straight line, which consists of all points of this straight line lying between two given points of it. These points are called the ends of the segment.

Slide 18

Main property: Of the three points on a line, one and only one lies between the other two. Two points are enough to draw a straight line.

Slide 19

A ray is a part of a straight line that has a beginning but no end. - The beam is limited on one side and can be extended in a straight line only in one direction, as far as desired. - A ray with origin O is a set of all points of a straight line lying on one side of O.

Slide 20

О A ray is a part of a straight line, which consists of all points of this straight line, lying on one side of its given point. This point is called the starting point of the beam.

Slide 21

An angle is a figure formed by two rays with the same origin. A B The rays forming an angle are called the sides of the angle, and their common beginning is the apex of the angle. An acute angle is an angle that is less than a right angle. An obtuse angle is an angle that is greater than a right angle. A right angle equal to 90 is a set of two rays with a common origin, lying on different lines. - - From

Slide 22

Basic properties: Each angle has a certain degree measure greater than zero. A straight angle is 180. The degree measure of an angle is equal to the sum of the degree measures of the angles into which it is divided by any ray passing between its sides.

Slide 23

Polyline - B A C D E Polyline ABCDEG . Points A, B, C, D, E, G are the vertices of the polyline. The segments AB, BC, CD, DE, EG are the links of the broken line. G is a figure that consists of points A1, A2,……A n and segments A1A2, A2A3,…..A n A n connecting them.

Slide 24

Main property: The length of the polyline is not less than the length of the segment connecting its ends. The length of a broken line is the sum of the lengths of its links.

Slide 25

Examples of tasks What is the broken line that has the most links? Less links? Which polyline has 3 vertices? 4 peaks? How to find out which segment is larger?

Slide 26

How can you draw a right angle on unlined paper? How to make 4 right angles with just two segments? And now 2 sharp and 2 blunt?

Slide 27

Rectangle A quadrilateral with all right angles. - is a parallelogram with all right angles. B A C D

Slide 28

Diagonals of a rectangle are equal Opposite sides are equal Sides do not intersect Diagonals intersect and the point of intersection is bisected

Slide 29

A square - - - - is a rectangle whose adjacent sides are equal. is a rectangle whose diagonals are mutually perpendicular and equal. This is a rhombus that has a right angle. It is a parallelogram in which all sides are equal and the angles are right. B A C D

Slide 30

After drawing the diagonals, we get equal triangles. The diagonals are equal. The diagonals intersect and the intersection point is bisected. The sides do not intersect. Diagonals intersect at right angles.

Slide 31

Example tasks Is this figure a rectangle? Why? How to shift the sticks so that you get 3 identical squares? Which figure has the largest area? Why? Do the calculations.

Mathematical concepts Lecture 2 Popova E A

Mathematical concepts Lecture 2 Popova E. A.

The concepts that are studied in the initial course of mathematics are usually presented in the form of four groups: 1. 2. 3. 4. Concepts related to numbers and operations on them: number, digit, addition, summand, etc. Algebraic concepts: expression, equality , equation, etc. Geometric concepts: straight line, segment, triangle, etc. Concepts related to quantities and their measurement: length, mass, unit of magnitude, etc.

Concepts with the help of which the concept of a number is defined. Concepts related to reading and writing numbers. Concepts related to the operation of Quantities: Natural quantity, number and zero, length, area, mass, volume. Relations and their signs: more - >, less -

Algebraic concepts Geometric concepts Expression: numeric expression and single variable expression. Numerical equality. Numerical inequality. Inequality with one variable. Equation with one variable. Geometric shapes: segment, angle, right angle, triangle, quadrilateral, rectangle, square, circle, circle. Geometric quantities: the length of the segment, the area of ​​\u200b\u200bthe figure, the magnitude of the angle.

n n n The concept is considered as a form of thinking that reflects objects (objects or phenomena) in their essential and general properties. The linguistic form of a concept is a word or a group of words. Concepts do not exist in the objective world. They arise in the human mind and replace the objects and phenomena of this world, being their ideal images. To have a concept of an object means to be able to single out its essential features and distinguish it from all other objects.

Mathematical concepts, like any others, exist only in human thinking and in those signs and symbols that form the mathematical language. n Every mathematical object has certain properties. For example, a square has four sides, four right angles equal to the diagonal. You can specify other properties as well. n

Among the properties of an object, essential and non-essential are distinguished. A property is considered essential for an object if it is inherent in this object and without it it cannot exist. n When talking about a mathematical concept, they usually mean a set of objects denoted by one term (a word or a group of words). n

n n n The scope of a concept is the set of all objects that are generalized in a concept and denoted by one term. The content of a concept is the set of all essential properties of an object reflected in this concept. There is a relationship between the volume of a concept and its content: if the volume of a concept increases, then its content decreases, and vice versa. For example, the concept of "rectangle" The scope of this concept is a set of different rectangles, and its content includes such properties of rectangles as "have four right angles", "have equal opposite sides", "have equal diagonals", etc.

n Any concept cannot be learned without realizing its relationship with other concepts. Therefore, it is important to know in what relationships concepts can be, and to be able to establish these connections. n Relationships between concepts are closely related to relationships between their volumes, i.e., sets. For example, if a is a "rectangle", b is a "quadrilateral", then their volumes A and B are in the inclusion relation (A B and A B), since every rectangle is a quadrilateral. Therefore, it can be argued that the concept of "rectangle" is specific in relation to the concept of "quadrilateral", and the concept of "quadrilateral" is generic in relation to the concept of "rectangle". If A = B, then the concepts a and b are said to be identical. n

n n First, the concepts of genus and species are relative: the same concept can be generic in relation to one concept and species in relation to another. For example, the concept of "rectangle" is generic in relation to the concept of "square" and specific in relation to the concept of "quadrilateral". Secondly, several generic concepts can often be specified for a given concept. So, for the concept of "rectangle", the generic concepts are "quadrilateral", "parallelogram", "polygon". Among them, you can specify the nearest. For the concept of "rectangle" the closest is the concept of "parallelogram". Thirdly, the specific concept has all the properties of the generic concept. For example, a square, being a specific concept in relation to the concept of "rectangle", has all the properties inherent in a rectangle. Since the scope of a concept is a set, it is convenient, when establishing relationships between the scopes of concepts, to depict them using Euler circles.

In the process of thinking, operations are performed with concepts n n n Generalization of a concept is a logical operation that consists in the transition from a concept with a smaller volume (greater content) to a concept with a larger volume (but lesser content). Generalization of a concept is a transition from a specific concept to a generic one. In this case, the volume expands due to the rejection of essential features. For example, generalizing the concept of "rectangle", you can go to the concept of "quadrilateral", discarding such a property as "have all right angles". Concept restriction is a logical operation that consists in the transition from a concept with a large volume to a concept with a smaller volume. The restriction of a concept is the transition from a generic concept to a specific one. In this case, the narrowing of the volume occurs due to the expansion of the content. For example, the concept of "quadrilateral" can be limited by adding to its content the property "have all right angles". As a result, we get the concept of "rectangle". The definition of a concept is a logical operation by which the content of a concept is revealed. According to the method of revealing the content of a concept, explicit and implicit definitions are distinguished. Among explicit definitions in mathematics, definitions through genus and specific difference are most often used.

n Species difference - these are properties (one or more) that allow you to select the defined objects from the scope of the generic concept.

When formulating definitions of concepts through genus and specific difference, they adhere to a number of rules: 1. 2. 3. 4. The definition must be proportionate. This means that the scope of the defined and defining concepts must match. This rule follows from the fact that the defined and defining concepts are interchangeable. There should be no vicious circle in the definition. This means that one cannot define a concept in terms of itself (the defining term must not contain the term being defined) or define it in terms of another, which, in turn, defines in terms of it. The definition must be clear. This is an obvious rule at first glance, but it means a lot. First of all, it is required that the meanings of the terms included in the defining concept be known by the time the definition of the new concept is introduced. One and the same concept can be defined through the genus and specific difference, observing the rules formulated above, in different ways.

The sequence of actions that must be followed when reproducing the definition of a familiar concept or constructing a definition of a new one: 1. 2. 3. 4. Name the concept (term) being defined. Indicate the closest generic (in relation to the defined) concept. List the properties that distinguish the defined objects from the scope of the generic, i.e., formulate the specific difference. Check whether the concept definition rules are fulfilled

n n n When studying mathematics in elementary school, implicit definitions are most often used. In implicit definitions, the content of concepts is revealed indirectly. Among them, contextual and ostensive are distinguished. In contextual definitions, the content of a new concept is revealed through a passage of text, through context, through an analysis of a specific situation that describes the meaning of the introduced concept. Through the context, the connection of the defined concept with others, known, is established, and thus its content is indirectly revealed.

+ 6 = 15 0, 5, 9, 10 To what number must 6 be added to make 15? Let's denote the unknown number with the Latin letter x (x): x + 6 = 15 - this is an equation. Solving an equation means finding an unknown number. In this equation, the unknown number is 9, since 9 + 6 = 15. Explain why the numbers 0, 5 and 10 are not suitable?

Ostensive definitions are definitions that reveal the essential features of objects by indicating or showing them. They are used to introduce terms by demonstrating the objects that these terms denote. For example, in this way it is possible to define the concepts of equality and inequality in elementary school: 2 7 > 2 6 93 \u003d 27 78 - 9 37 17 - 5 \u003d 8 + 4 These are inequalities. This is equality.

n n In elementary mathematics teaching, in addition to contextual and ostensive definitions, techniques are often used that replace the definition. This is, in particular, a description, a comparison. When describing the object under study, the goal is to identify as many of its properties as possible, both essential and non-essential. If the comparison technique is used, then the properties of the introduced concept are revealed in the process of comparing various objects.

Learn more

• 
  How to learn reading comprehension
• 
  Kindergarten social skills lessons
• 
  Things to do before bedtime
• 
  List of verbs for 1st grade
• 
  Kindergarten syllable games
• 
  Cardinal numbers example
• 
  Reading level chart scholastic
• 
  Teach three year old to read
• 
  What is a long vowel
• 
  What is phonological knowledge
• 
  Activities for 3 and 4 year olds