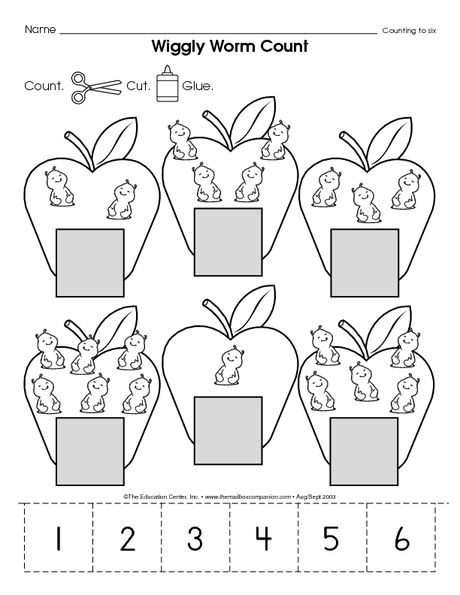
Matching numbers activity
Simple Number Matching Activity - Toddler Approved
How do you teach a toddler numbers? Quick to set up games like this simple number matching activity are my favorite way to introduce numbers to kids.
There are so many ways to embed learning math concepts like counting, measuring, and identifying more and less through simple daily experiences along with easy activities that you can enjoy alongside your child.
When I introduce numbers to kids it is all through play, hands-on experiences, and every day interactions! Games are such a great way to teach new concepts!
Some children might need a more direct approach with more structured learning activities and teaching, but play is a great place to start!
RELATED: Want to introduce more math concepts? Try these 25+ Math activities for toddlers.
What you need for this number matching activity:
Toddler Approved is a participant in the Amazon Services LLC Associates Program, an affiliate advertising program. As an Amazon Associate, I earn from qualifying purchases. Read more about these links in my Disclosure Policy.
- Large roll of paper
- Colored cardstock (cut in half)
- Black marker
- Painter's tape
- Scissors
How to set up this matching activity:
The set up for this number matching activity is so quick!
Just cut a piece of white paper and tape it to the wall!
Next, draw numbers on the paper. I did numbers 1-10.
After that, write the same numbers on the half sheets of cardstock. Stick the cardstock pieces with painters tape around the room on different pieces of furniture so that they are somewhat "hidden."
Encourage your child to go and find the numbers that are stuck around the room and come and match them to the number on the wall.
Pull the numbers off and hide them again. Repeat!
Number recognition (knowing number names) is just one aspect as you start introducing your kids to numbers, counting, and under standing simple match concepts.
EXTENSION:
Want to help your child understand what each number means while you play? Try doing an action to go along with each number when you stick it on the wall.
For example, if your child matches #2, then do 2 jumps.
This will help your child start to realize that numbers are more than just something you see and write. They mean something. It will help them start to understand what 2 means.
RELATED: Learning activities like this can easily be adapted into hunts! Check out these 40+ Simple Learning Hunts that kids love to do again and again.
Do you have any other favorite activities to teach numbers to toddlers? I'd love to hear about them!
Smack the numbers by Sunny Day Family is such hands-on active way to introduce numbers!
137 shares
All Activities, Big Kid, Blog, Gross Motor, Indoor Play, Learn, Math, Preschooler, Quick and Easy, Toddler
Reader Interactions
7 Number Matching Games Your Child Will Want To Play
Whether your child is just starting to learn preschool math or they are becoming a pre-k math whiz, number matching games can be an incredibly helpful, fun way to develop your child’s skills with number recognition.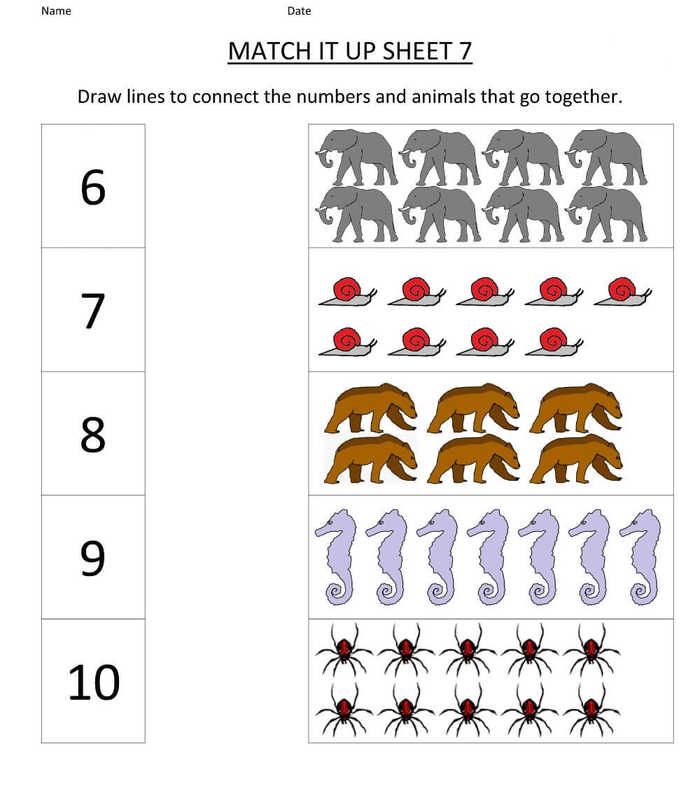
When talking about number recognition, we mean that your child is able to consistently recognize numbers by both name and written number. This process can take some time.
Just as your child must learn how to read letters, they must also learn to “read” numbers. And that can be a lot like learning a new language! Don’t worry; we’re here to help.
About Number Matching
Number matching is an essential skill for young children and can be done in a few different ways:
- Identifying the number name after being given a number of objects
- Matching the amount of objects in a picture with their respective number
- Matching the name of a number with its corresponding number symbol
As we’ve mentioned, this process won’t come naturally. It may take some patience and clear instruction for your child to understand how number names, objects, and number symbols all correspond to one another.
Thankfully, there are easy — and enjoyable! — methods for helping your child learn.
Below, we’ve compiled 7 number matching games to transform this learning experience into a fun activity your child will look forward to.
7 Number Matching Games For Fun Learning
1) How Many Items?
What You’ll Need
- 40 or so small items
- Paper clips and dried kidney beans work well
- 10 pieces of paper
- Each paper should be labeled with a number 1 – 10
What To Do
This game is a great way to master the basics of matching a specific amount of objects with their corresponding number — the perfect activity for preschool math learners!
To play, lay out all of the sheets with numbers. Your child will close their eyes, swirl their arm around, and place their finger on a random number.
They’ll open their eyes and look at the number they chose. For our example, let’s use the number 7. Once your child picks a number, they’ll count out 7 beans (or whatever small item you’re using).
Repeat the process until all 10 numbers are filled.
This activity is great for working on your child’s understanding of one-to-one correspondence (the idea that each object counted corresponds to one and only one number). This activity can also help build a child’s sense of number, which will help when they engage in mental math.
2) Splash Zone!
What You’ll Need
- Colorful chalk
- A spray bottle full of water (or an outdoor water hose)
What To Do
To start, you’ll use the chalk to write out the numbers 1 – 10 in large, bold print on pavement. If your child is a bit younger, feel free to scale back and begin with numbers 1 – 5.
You will then call out a number, and your child will race to spray that specific number with the water bottle. The water will likely erase portions of the number. This is actually a good thing!
When your child is just starting out with number matching, they may become easily confused and mix up numbers. By marking numbers with water, they will know that that number is “unavailable” for the next round.
Make sure you let them know each number can only be sprayed and used one time. You can scale the level of this activity by adding or subtracting the amount of numbers your child is working with.
You can also increase the difficulty by clapping with your hands instead of calling out a number. Your child will have to listen carefully to count how many times you clapped, then spray the correct number.
3) Number Scavenger Hunt
What You’ll Need
- Good weather
- Paper
- Pen
What To Do
You can play this game indoors or outdoors. It’s a great activity for passing the time during a walk around the neighborhood!
Write out a “checklist” of numbers 1 – 10 on the sheet of paper. Make sure the numbers are big, bold, and legible because your child will use the checklist as a reference during your scavenger hunt.
Then, off you go! You will work together to match the numbers on the checklist with the numbers they see in real life.
Mailboxes, clocks, menus at outdoor cafes — numbers could be anywhere! Feel free to play up the detective aspect of the game. It’s part of the fun!
4) Hungry, Hungry Giraffe
What You’ll Need
- A stuffed giraffe (or any animal)
- Green construction paper cut into leaf shapes
- You’ll need 10 leaf shapes
- Each leaf should be labeled with a number 1 – 10
What To Do
For this game, your child will play the zookeeper of a very hungry giraffe. But this giraffe is special because he’s a picky eater — he only eats certain numbers!
You will play the puppeteer and talk on behalf of the giraffe. When the giraffe grumbles about being hungry, he will complain about craving a specific number. For example, he may say, “Wow, I’m starving! If only I had a leaf with the number 7 on it to eat right now…”
Your child will then locate the leaf marked with a 7 and feed it to the picky giraffe.
If they feed the giraffe the wrong number, the giraffe will spit it out.
“Yuck! That doesn’t taste like 7! That was the [number your child gave] leaf! I’m still hungry!”
Your child will probably laugh at the giraffe’s funny reaction. Tell them to try again until they get the right number.
This game is very silly and fun and gives your child multiple opportunities to find the correctly labeled leaf without demotivating them in the process.
5) Fill The Cup
What You’ll Need
- A small cup (you can also cut off the top portion of a larger, plastic cup)
- Large dried beans, pebbles, Cheerios, or other objects that are easy to count
- A pair of dice
What To Do
You and your child will roll your dice at the same time. Depending on what number you roll, you will add that many beans to your plastic cup.
The goal is to finish filling up your cup before the other person. Nothing is more fun than a friendly competition! Your child will excitedly roll their dice and squeal as they count out their items.
Your child must match the dots on the dice to the number of beans they add to play fair, so feel free to help them get used to the process before diving in!
If you notice they’re scooping up too many just to rush and fill their cup, feel free to change the rules of the game. Instead of rolling their own dice, you can roll for one another.
That means if they roll a 6, you count 6 beans into their cup and vice versa. That way they are counting with you — which doubles their practice — and you keep each other accountable!
6) Sticky Ball Match-Up
What You’ll Need
- 10 sheets of paper, each labeled sequentially with a number between 1 and 10
- Tape
- A balled-up piece of paper covered in tape
What To Do
After labeling the sheets of paper, tape them to a wall or flat against the ground.
Then, give your child the sticky ball. You will call out a random number and their goal is to throw the ball on the right sheet of paper and make it stick.
They can try as many times as necessary to “score” and hit the right sheet of paper.
This game is simple but effective and easily scaled. One way to increase the difficulty, for example, is by representing the numbers on the paper with dots instead of number symbols.
Do what’s most appropriate for your child. Number matching games should be challenging but attainable for young learners!
7) Numbered Chocolate Chip Cookies
What You’ll Need
- Cookie dough (without add-ins)
- Chocolate chips
- Dice
What To Do
Number matching games are fun, but they can taste good, too! With this game, the reward is built-in, as you’ll be making cookies together.
Pick your favorite chocolate chip cookie recipe. Before adding chocolate chips to the batter, portion out enough batter to form the cookies.
Each cookie dough ball will get its own dice roll. This will determine how many chocolate chips can go into each cookie. You can play with a pair of dice (instead of one) if you like your cookies extra chocolatey!
Since everyone loves chocolate chips in their cookies, your child’s goal is obviously to get the highest score possible! The goal is to reach 6 (or 12 for a pair of dice) chips per cookie.
If you sneak in a couple of extra chocolate chips, we won’t tell (as long as your child counts them!).
Number Matching Games For Everyone!
We hope these activities sparked your sense of imagination and got you thinking about how exciting number matching games can be for your child.
But here at HOMER, we know that busy families like yours may not have time for a number matching game every day of the week. Some days, it’s time to take a bath and hit the hay before you know it!
For the times when you need a helping hand, we recommend checking out our Learn & Grow app or our Explore Numbers Kit. Our personalized products are perfect for squeezing in reading and math practice for emergent learners without sacrificing a morsel of fun!
Author
4.3. Comparison of adjacent numbers
Compare adjacent numbers means to determine which one more and which is less.
Based on visual material children have already compared adjacent numbers. Based on the "comparison 2 sets, in one of which 1 item more (less) than the other, they were introduced to the methods of obtaining all numbers up to 10. Therefore, they have the representation about the connections between numbers, i.e., which of adjacent numbers greater (less) than any. These ideas need to be deepened. On specific examples, children are revealed constancy of links between adjacent numbers (3 is always greater than 2, and 2 is less than 3, and etc.). It is emphasized from the outset that "more" and "less" are relative terms. every number (except one) is greater than or less than the other, depending on what number is it compared to (3>2, but 3 < 4). Starting to form a show about a certain sequence numbers.
Practical establishment of difference relations between adjacent numbers allows lead children to an understanding of reciprocal relations between them (4 is greater than 3: if k 3 add 1, will be 4; 3 is less than 4: if from 4 subtract 1, it will be 3).
Relations between adjacent numbers will be studied already in preparatory school group.
Children are taught to compare all numbers within 10. Get started it is advisable from comparing the numbers 2 and 3, not 1 and 2.
visual basis comparison of numbers serves as a comparison 2 collections of items. When comparing 2 items with 3 stand out more clearly quantitative ratios than comparing 1 item with 2. 1 item not yet perceived by the child as set with 1 element. brightly the pronounced properties of the object are distracting children from establishing quantitative set ratios.
Show persistence connections between numbers allows repeated comparison of the same adjacent numbers based on matching collections of different items. For example, matching 2 nesting dolls with 3 dice, find out that there are fewer nesting dolls than cubes, and there are more cubes than nesting dolls. So 2 is less than 3 and 3 is greater than 2.
Check if is this always the case. For this 2-3 times change counting material. collate other aggregates consisting of 2 and 3 objects, and conclude that 3 is always greater than 2 and 2 less than 3.
The same way compare 2-3 more pairs of adjacent numbers. The work of children is organized at the same time e different counting material. Alone children match, for example, 4 Christmas trees and 5 mushrooms, others - 4 ducklings and 5 chickens, the third - 4 circles and 5 squares, etc. Find out that in all cases 5 is greater than 4 and 4 is less than 5.
Showdown "more", "less" in relation to each other contributes to the formation of the idea about the reciprocal nature of relations between numbers.
great attention give children exercise in equalization aggregates. Equalizing the aggregates, children practically set difference relationships between adjacent numbers. It is useful to compare aggregates objects of different sizes or occupying different area.
This will allow parallel reinforce ideas of independence the number of objects from their spatial properties.
Mapping collections of items that are different size, shape, etc., allows you to focus the attention of children on the meaning of piece-by-piece correlation techniques items (overlays, applications, etc.) to clarify the relationship "equal", "not equals, greater than, less than. Children begin use these methods as clear evidence of what of 2 compared numbers is greater than or less. The options are tasks that talk about subjects, represented by symbols models of geometric shapes (circles, squares, dots, etc.). Children, for example, guess who was more in the tram: boys or girls if boys represented on the board in large circles, and girls are small. Experience shows that a child of the sixth year of life is easy accepts such an abstraction. Appears the possibility of using "intermediate" means - labels, relationship modeling quantities.
Children are taught to receive not only "equality from inequality", but, conversely, "from equality to inequality", and the comparison of numbers is carried out on the basis of comparison of populations, perceived both visually and hearing, touch, muscle the senses.
Inclusion in active work different analyzers serves to generalize relevant presentations. are given, for example, such tasks: “Raise hand 1 times more (less) than it was buttons on Sasha's card. How many times did you raise your hand? Why?”, “How much are you did you hear sounds? How much to count triangles so that there are 1 more (less) than you heard sounds? Children first compare the numbers, and then take appropriate action. After completing the task, the child must just say how many items put or how many movements performed, but also explain why there are so many, i.e. compare numbers.
Comparing the numbers some children name only one of them: "5 more" or "4 less". Achieving exact answer, the teacher sets suggestive questions, such as: "What number do we compared the number 5?”, “What number is it more less)?" Seizing the opportunity emphasize the relativity of expressions "more", "less", the teacher offers child to compare this number with previous or subsequent.
He says, for example: "You said that 4 less. And if I call the numbers 3 and 4, what Can you tell me about the number 4? The children are convinced that the same number can be more or less than the other depending what number it is being compared to. Therefore, it is necessary to name both compared numbers and indicate which one is greater (less) what. Otherwise the answer will be inaccurate.
Show relativity of expressions "greater than", "less than" allows comparison of several numbers following each other. visual The basis for such a comparison is collections of homogeneous objects (circles, squares, etc.) located horizontal rows exactly under each other friend.
most valuable technique is the construction of a numerical stairs. Mugs painted on 2 sides (squares) blue and red laid out in 5 (10) pieces. rows. Quantity circles in a row increase sequentially by 1, and the "additional" circle turned to the other side. Numeric ladder allows you to visualize certain final sequence natural numbers.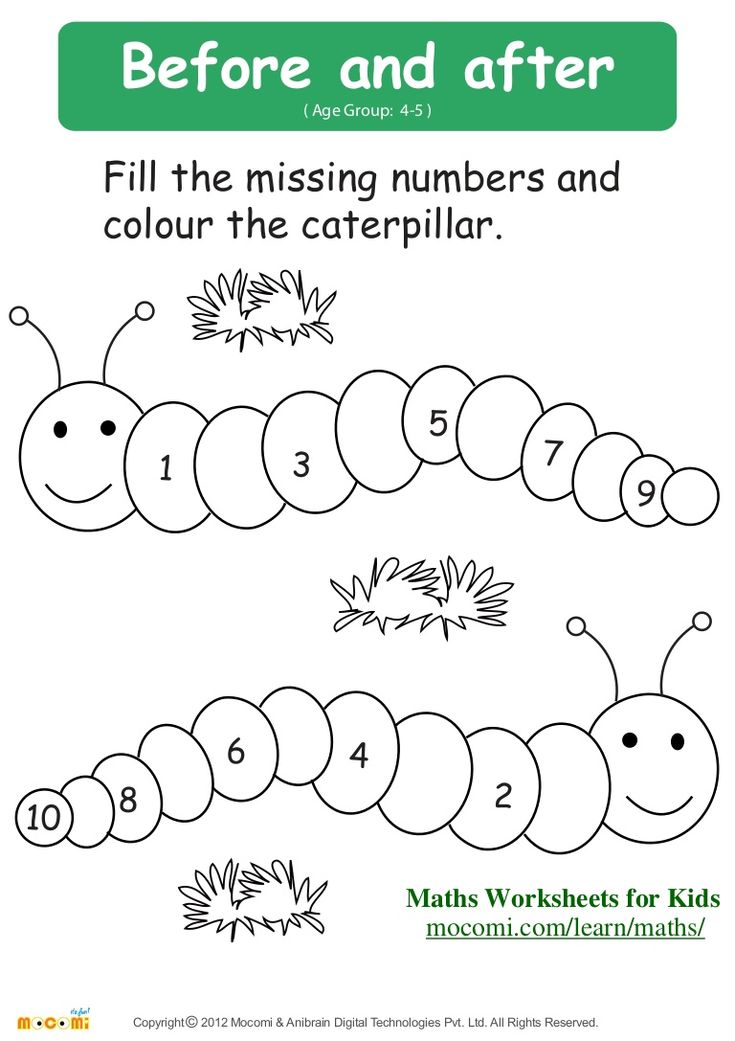
offering in each next row put the same circles, how many in this one, and even 1, the teacher reminds the children how to get the next number (n + 1).
Note. AT senior group are limited to building number ladder within the first heel.
Taking away one by one mug from each row, children remember way to get each previous numbers (n - 1). Next, establish a connection between the number of circles in a row and its serial number. Numbers First compare in pairs, and then each number with the previous and next. Based on visibility children keep score in direct and reverse order.
It is important to, working independently, they built ladder strictly in order, i.e. increased the number of circles of each next row by 1.
Job Compared adjacent numbers combined with exercises in a grouping of geometric shapes, with comparison of the sizes of objects and etc., variety of tasks. So in children form an idea of a certain sequences of numbers and let down them to an understanding of reciprocal relationships between adjacent numbers.
| Methods of mathematical development (exam) 1. Basic mathematical concepts: set, number, digit, natural series of numbers, number system, counting, computing, measuring activity, size, shape, geometric figure, time, space. - many; - number; - counting and computing activities; - value; - geometric figures; - time; - space. SET is a collection of objects that are considered as a whole . The world in which a person lives is represented by a variety of sets: a lot of stars in the sky, plants, animals around him, a lot of different sounds, parts of his own body.  Sets consist of elements. The elements of the set are the objects that make up the set. These can be real objects (things, toys, drawings), as well as sounds, movements, numbers, etc. . Elements of a set can be not only individual objects, but also their combinations . For example, when counting in pairs, triplets, tens. In these cases, the elements of the set are not one object, but two, three, ten - a set. For example, some flowers, berries, cars and other objects have the property to be red . The property of being round is possessed by the moon, the ball, the wheels of bicycles and cars, parts of various machines and machine tools, etc. Thus, each property is associated with a set (objects) that have this property. Thus, if the set A is given by the characteristic property P , then this means that it consists of all objects that have this property, and only of them. An infinite set of objects can have some property, only a finite set can have another. Therefore, the sets are subdivided into end and end . A finite set can be specified by direct enumeration of all its elements in an arbitrary order. For example, the set of children of a given group living on Sadovaya Street can be described using a characteristic property: { x | x - lives on Sadovaya Street) or listing all its elements in an arbitrary order: {Lena, Sasha, Vitya, Ira, Kolya}. It is quite clear that an infinite set cannot be specified by listing all of its elements . Mathematics mostly deals with infinite sets (numbers, points, figures and other objects), but the basic mathematical ideas and logical structures can be modeled on finite sets. Naturally, in pre-mathematical preparation usually deal with finite sets . NUMBER is the general unchanging category of the set , which is an indicator of the cardinality of the set. This is just a sound designation. Concept the value in mathematics is considered as the main one. Direct answer to the question “what is a quantity?” no, since the general concept of magnitude is a direct generalization of more specific concepts: length, area, volume, mass, speed, etc. The size of an object is its relative characteristic , emphasizing the extent of individual parts and determining its place among homogeneous ones. The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.  Item size, i.e. item size , determined by only based on the comparison of . It is impossible to say whether it is a large or a small object, it can only be compared with another. The perception of magnitude depends on the distance from which the object is perceived, and also on the magnitude of the object with which it is compared . The farther an object is from the one who perceives it, the smaller it seems, and vice versa, the closer it is, the larger it seems. The characteristic of the size of the object also depends on its location in the space . The same object can be characterized either as high (low), or as long (short). It depends on whether it is in a horizontal or vertical position. So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short. The value of an item is always relative , it depends on which item it is compared to . Comparing an object with a smaller one, we characterize it as a larger one, and comparing the same object with a larger one, we call it a smaller one. So, the value of a particular object is characterized by the following features : comparability, variability and relativity. 1) comparability implemented by: - overlay, - application, - by measuring with a standard measure, - comparison by eye. 2) relativity - depends on the object with which we are comparing, on the distance at which we are comparing, on the location in space. 3) variability . Size is closely related to size. And size is a property of magnitude variability. Each item has its own generic purpose. It can change its dimensions without changing its essence. A geometric figure is the presence of points on a plane, limited by space. Figures are flat (circle, square, triangle, polygon…) and spatial (ball, cube, parallelepiped, cone...), which are also called geometric bodies. GEOMETRIC BODY is a closed part of space bounded by flat and curved surfaces. If the surface bounding the body consists of planes, then the body is called a polyhedron . These planes intersect along straight lines, which are called edges, and form the faces of the body. Each of the faces is a polygon whose sides are the edges of the polyhedron; the vertices of this polygon are called the vertices of the polyhedron. Some polyhedra with a certain number of faces have special names : tetrahedron - tetrahedron, hexahedron - exahedron, octahedron - octahedron, dodecahedron - dodecahedron, twenty-sided - icosahedron. What is a geometric FORM? SHAPE is the outline, the outer appearance of an object. Form (lat. forma - form, appearance) – the relative position of the boundaries (contours) of an object, object, as well as the relative position of the line points. - fluidity (time does not stop) - irreversibility and uniqueness - duration . SPACE is a quality by which relationships such as neighborhoods and distances are established. Orientation in space implies orientation towards oneself, away from oneself, from other objects, orientation on the plane and orientation on the ground. 2. Subject and tasks of the course "Methods of mathematical development and teaching of mathematics". Connection of the methodology of mathematical development with other sciences. - scientific substantiation of program requirements for the level of development of quantitative, spatial, temporal and other mathematical representations of children in each age group; - determination of the content of factual material to prepare a child in kindergarten for learning mathematics at school; - improvement of the material on the formation of mathematical representations in the kindergarten program; - development and implementation in practice of effective didactic tools, methods and various forms of organization of the process of development of elementary mathematical concepts; - implementation of continuity in the formation of basic mathematical concepts in kindergarten and the corresponding concepts in school; - development of the content of training highly qualified personnel capable of carrying out pedagogical and methodological work on the formation and development of mathematical concepts in children in all parts of the preschool education system; - development on a scientific basis of guidelines for parents on the development of mathematical concepts in children in a family setting. The general objective of methodology is to research and develop the practical foundations for the process of forming elementary mathematical concepts in preschool children. It is solved from the standpoint of the Marxist-Leninist theory, which will develop a unified view of the world, having discovered the laws of development of nature, society, and the individual, and serves as the methodological, ideological basis of science. The formation of elementary mathematical concepts is a purposeful and organized process of transferring and mastering knowledge, techniques and methods of mental activity provided for by program requirements Its main goal is not only preparation for the successful mastery of mathematics at school, but also the comprehensive development of children. The methodology for the formation of elementary mathematical representations in children in kindergarten is associated with many sciences , and above all with those whose subject matter is different aspects of the personality and activity of a preschool child, the process of upbringing and education. She has the closest connection with preschool pedagogy . The methodology for the formation of elementary mathematical representations is based on the tasks of teaching and mental education of the younger generation developed by preschool pedagogy and didactics: principles, conditions, ways, content, means, methods, forms of organization, etc. This connection is mutual in nature: research and development of problems the formation of elementary mathematical concepts in children, in turn, improve the pedagogical theory, enriching it with new factual material. Relying on these sciences makes it possible, firstly, to determine the volume and content of knowledge that should be mastered by children in kindergarten, and serve as the foundation of mathematical education; secondly, to use teaching methods and means that fully meet the age characteristics of preschoolers, the requirements of the principle of continuity. Education should be built taking into account the patterns of development of cognitive activity, the personality of the child , which is the subject of study of psychological sciences . Perception, representation, thinking, speech not only function, but also intensively develop in the learning process. Psychological features and patterns of perception by a child of a variety of objects, numbers, space, time serve as the basis for developing a methodology for the formation of elementary mathematical representations. Psychology determines the age capabilities of children in acquiring knowledge and skills that are not something frozen and vary depending on the type of education. The rational construction of the learning process is associated with the creation of optimal conditions based on the anatomical and physiological characteristics of young children. The regularities of the course of physiological processes in preschoolers serve as the basis for determining the duration of classes for the formation of elementary mathematical representations for each age group of the kindergarten, determine their very structure, the combination and alternation of various methods and means of teaching, different types of activities (inclusion of physical education minutes, dosing of educational cognitive tasks, etc.). Communication with various sciences creates a theoretical basis for the methodology for the formation of mathematical representations in children in kindergarten. 3. Stages of development of the methodology of mathematical development: empirical, classical, modern. In the course of mastering them, children not only mastered the recalculation of objects, but also the ability to perceive and realize changes occurring in the reality around them: natural, color, spatial and temporal; quantitative, changes in shape, size, location, proportions. This ensured the natural development in children of certain ideas, ingenuity and ingenuity. The first printed textbook by I. Fedorov "Primer" (1574) included thoughts on the need to teach children to count through various exercises. In the XIII-XIX centuries. questions of the content and methods of teaching mathematics to preschool children and the formation of their ideas about size, measurement, time and space can be found in the pedagogical works of Ya.A. Comenius, M.  G. Pestalozzi, K.D. Ushinsky, L.N. Tolstoy and others. Views of teachers of the XIII—XIX centuries. on the content and methods of development of mathematical representations in children is The first stage in the development of the methodology is empirical. Teachers of that era, under the influence of the requirements of developing practice, came to the conclusion that it was necessary to prepare children for learning mathematics at school. They made certain proposals about the content and methods of teaching children, mainly in a family setting. It must be said that they did not develop special manuals for preparing children for school, but included their main ideas in books on education and training. Thus, the Czech humanist thinker and teacher Ya.A. Comenius (1592-1670) in the book "Mother School" (1632) recommends even before school to teach the child to count within twenty, the ability to distinguish between larger-smaller, even-odd numbers, compare objects by size, recognize and name some geometric shapes, use in practical activity units of measurement: inch, span, step, pound, etc. I. G. Pestalozzi (1746-1827), a Swiss democratic pedagogue, pointed out the shortcomings of the teaching methods existing at that time, which were based on cramming, and recommended teaching children to count specific objects, understand operations on numbers, and the ability to determine time. The teaching methods proposed by him presuppose the transition from simple elements to more complex ones, the widespread use of visualization, which facilitates the assimilation of numbers by children. The ideas of J. G. Pestalozzi later (mid-19th century) served as the basis for reform in the field of teaching mathematics at school. Methods for developing ideas about number and form in children were reflected and further developed in the systems of sensory education of the German teacher F. Fröbel (1782-1852), the Italian teacher Maria Montessori (1870-1952), etc. The classical systems of sensory learning by F. Fröbel (1782-1852) and M. Montessori (1870-1952) present a methodology for introducing children to geometric shapes, sizes, measurement and counting, drawing up rows of objects by size, weight, etc. F. Fröbel saw the tasks of teaching counting in the assimilation of a number of numbers by preschool children.  He created the famous "Gifts" - a special manual for the development of constructive skills in unity with the knowledge of numbers, shapes, sizes, spatial relationships. F. Fröbel was convinced that the development of "spatial" imagination and thinking at preschool age creates the conditions for the transition to the assimilation of geometry at school. The "gifts" created by F. Fröbel are still being used as didactic material to familiarize children with number, shape, size and spatial relationships. M. Montessori, based on the ideas of self-development and self-learning, recognized the need to create a special environment for mastering numbers, shapes, sizes, as well as written and oral numbering. She suggested using special material for this: counting boxes, bundles of colored beads strung in dozens, abacus, coins, and much more. M. Montessori's pedagogical activity proceeded most effectively in the first half of the 20th century. The use of materials for the development of mathematical representation in children in the education and upbringing of a child was based on a certain style of interaction between an adult and a child; the need to monitor the behavior of children in a specially created environment; organizing joint free work with the child, etc. The section “Logic and Counting” is extensively represented in the M. Montessori system: the study of figures, sizes, methods of measurement, projection, modeling of sets. The following benefits are most interesting: “Figures from carnations”, “Mathematical sun”, “Fold the pattern”, “Combine the sets”. In general, teaching mathematics according to the M. Montessori system began with a sensory impression, then a transition was made to understanding the symbol (i.e.  , from the concrete to the abstract), which made mathematics attractive and accessible even for 3-4-year-old children. So, advanced teachers of the past , Russian and foreign, recognized the role and necessity of primary mathematical knowledge in the development and upbringing of children before school , at the same time singled out account as a means of mental development and strongly recommended that children be taught it as early as possible from about three years of age. Learning was understood by them as "exercise" in performing practical, play actions using visual material, using the experience accumulated by children in distinguishing numbers, time, space, measures in a variety of children's activities. Issues of methods of mathematical development are of particular importance in the pedagogical literature of elementary school at the turn The authors of the methodological recommendations at that time were advanced teachers and methodologists. Directory: attachments -> article -> 448 Download 4. 
|
If some a has the property P , then it belongs to the set A , and, conversely, if the object a belongs to the set A , then it has the property P . 
Various counting rhymes, proverbs, sayings, riddles, nursery rhymes were good material in teaching children to count, they made it possible for the child to form concepts about numbers, shape, size, space. 
However, all this was just wishes, without any scientific justification.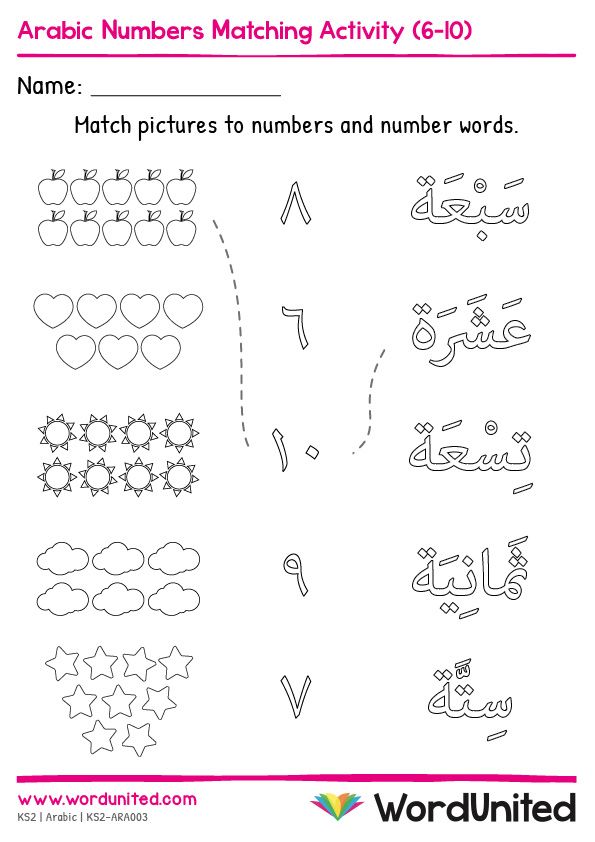 
The M. Montessori system provides for the development of the child's sensorimotor sphere and, in the future, intellect. The "golden" mathematical material, which is especially distinguished by its significance, is first mastered by the child as a set of beads in different quantities, then in symbols (numbers), after that - as a means of mastering the ability to compare numbers. Thus, the decimal number system is presented to the child visibly and tangibly, which leads to the successful mastery of arithmetic. 
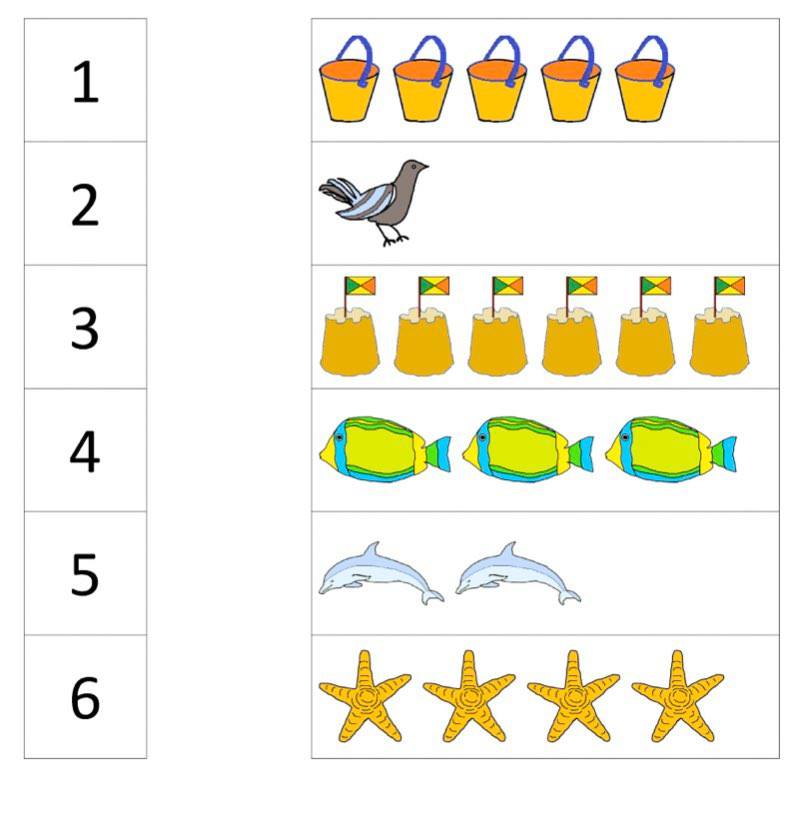The experience of practical workers was not always scientifically substantiated, but it was tested in practice. Over time, he improved, stronger and more fully revealed progressive pedagogical thought. 
