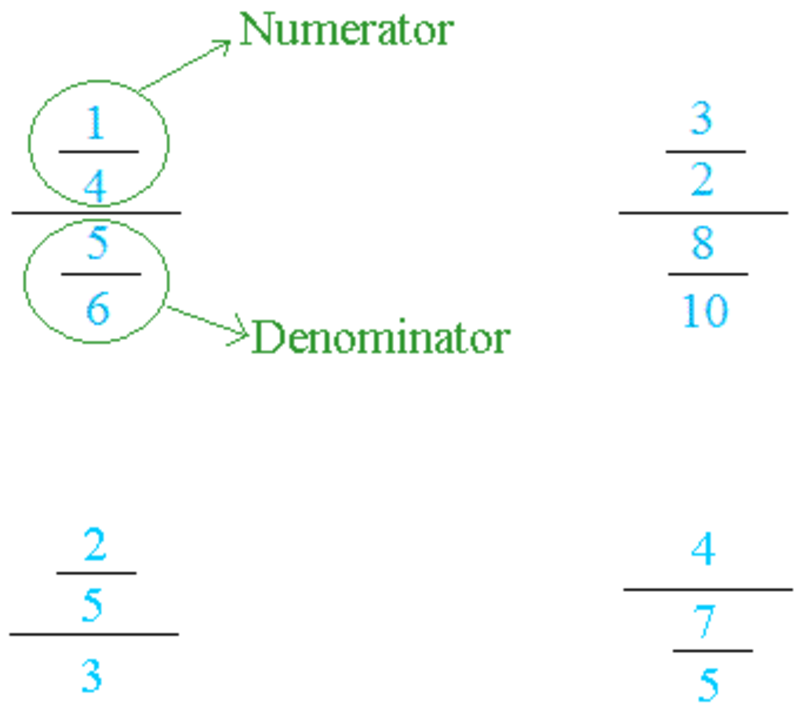
Math concept examples

10 Math Concepts You Can't Ignore

Sets and set theory

A set is a collection of objects. The objects, called elements of the set, can be tangible (shoes, bobcats, people, jellybeans, and so forth) or intangible (fictional characters, ideas, numbers, and the like). Sets are such a simple and flexible way of organizing the world that you can define all of math in terms of them.

Mathematicians first define sets very carefully to avoid weird problems — for example, a set can include another set, but it can't include itself. After the whole concept of a set is well-defined, sets are used to define numbers and operations, such as addition and subtraction, which is the starting point for the math you already know and love.

Prime numbers go forever

A prime number is any counting number that has exactly two divisors (numbers that divide into it evenly) — 1 and the number itself. Prime numbers go on forever — that is, the list is infinite — but here are the first ten: 2 3 5 7 11 13 17 19 23 29 . . .

It may seem like nothing, but . . .

Zero may look like a big nothing, but it's actually one of the greatest inventions of all time. Like all inventions, it didn't exist until someone thought of it. (The Greeks and Romans, who knew so much about math and logic, knew nothing about zero.)

The concept of zero as a number arose independently in several different places. In South America, the number system that the Mayans used included a symbol for zero. And the Hindu-Arabic system used throughout most of the world today developed from an earlier Arabic system that used zero as a placeholder. In fact, zero isn't really nothing — it's simply a way to express nothing mathematically. And that's really something.

Have a big piece of pi

Pi (π): The symbol π (pronounced pie) is a Greek letter that stands for the ratio of the circumference of a circle to its diameter. Here's the approximate value of π:

π ≈ 3.1415926535…

Although π is just a number — or, in algebraic terms, a constant — it's important for several reasons:

Geometry just wouldn't be the same without it. Circles are one of the most basic shapes in geometry, and you need π to measure the area and the circumference of a circle.

Pi is an irrational number, which means that no fraction that equals it exactly exists. Beyond this, π is a transcendental number, which means that it's never the value of x in a polynomial equation (the most basic type of algebraic equation).

Pi is everywhere in math. It shows up constantly (no pun intended) where you least expect it. One example is trigonometry, the study of triangles. Triangles obviously aren't circles, but trig uses circles to measure the size of angles, and you can't swing a compass without hitting π.

Equality in mathematics

The humble equals sign (=) is so common in math that it goes virtually unnoticed. But it represents the concept of equality — when one thing is mathematically the same as another — which is one of the most important math concepts ever created. A mathematical statement with an equals sign is an equation. The equals sign links two mathematical expressions that have the same value and provides a powerful way to connect expressions.

Bringing algebra and geometry together

Before the xy-graph (also called the Cartesian coordinate system) was invented, algebra and geometry were studied for centuries as two separate and unrelated areas of math. Algebra was exclusively the study of equations, and geometry was solely the study of figures on the plane or in space.

The graph, invented by French philosopher and mathematician René Descartes, brought algebra and geometry together, enabling you to draw solutions to equations that include the variables x and y as points, lines, circles, and other geometric shapes on a graph.

The function: a mathematical machine

A function is a mathematical machine that takes in one number (called the input) and gives back exactly one other number (called the output). It's kind of like a blender because what you get out of it depends on what you put into it. Suppose you invent a function called PlusOne that adds 1 to any number. So when you input the number 2, the number that gets outputted is 3:

PlusOne(2) = 3

Similarly, when you input the number 100, the number that gets outputted is 101:

PlusOne(100) = 101

It goes on, and on, and on . . .

The very word infinity commands great power. So does the symbol for infinity (∞). Infinity is the very quality of endlessness. And yet mathematicians have tamed infinity to a great extent. In his invention of calculus, Sir Isaac Newton introduced the concept of a limit, which allows you to calculate what happens to numbers as they get very large and approach infinity.

Putting it all on the line

This pattern continues forever, with each value being halved, which means you can never get to the other side of the room. Obviously, in the real world, you can and do walk across rooms all the time. But from the standpoint of math, Zeno's Paradox and other similar paradoxes remained unanswered for about 2,000 years.

The basic problem was this one: All the fractions listed in the preceding sequence are between 0 and 1 on the number line. And there are an infinite number of them. But how can you have an infinite number of numbers in a finite space? Mathematicians of the 19th century — Augustin Cauchy, Richard Dedekind, Karl Weierstrass, and Georg Cantor foremost among them — solved this paradox. The result was real analysis, the advanced mathematics of the real number line.

Numbers for your imagination

The imaginary numbers (numbers that include the value i = √ - 1) are a set of numbers not found on the real number line. If that idea sounds unbelievable — where else would they be? — don't worry: For thousands of years, mathematicians didn't believe in them, either. But real-world applications in electronics, particle physics, and many other areas of science have turned skeptics into believers.

So, if your summer plans include wiring your secret underground lab or building a flux capacitor for your time machine — or maybe just studying to get a degree in electrical engineering — you'll find that imaginary numbers are too useful to be ignored.

22 Examples of Mathematics in Everyday Life – StudiousGuy

According to some people, maths is just the use of complicated formulas and calculations which won’t be ever applied in real life. But, maths is the universal language that is applied in almost every aspect of life. Yes! You read it right; basic mathematical concepts are followed all the time. You would be amazed to see the emergence of maths from unexpected situations.

Let’s read further to know the real-life situations where maths is applied.

Index of Article (Click to Jump)

How much should I spend today? When I will be able to buy a new car? Should I save more? How will I be able to pay my EMIs? Such thoughts usually come into our minds. The simple answer to such type of question is maths. We prepare budgets based on simple calculations with the help of simple mathematical concepts. So, we can’t say, I am not going to study maths ever! Everything which is going around us is somehow related to maths only.

Application: 

• Basic mathematical operations (addition, subtraction, multiplication, and division)

• Calculation of percentage

• Arithmetic calculations

You know what, maths is the basis of any construction work. A lot of calculations, preparations of budgets, setting targets, estimating the cost, etc., are all done based on maths. If you don’t believe it, ask any contractor or construction worker, and they will explain as to how important maths is for carrying out all the construction work.

Application:

• Preparing budgets

• Taking measurements

• Estimating the cost and profit

• Arithmetic calculations

• Geometry

• Calculus and Statistics

• Trigonometry

I should reduce some body fat! Will I be able to achieve my dream body ever? How? When? Will I be able to gain muscles? Here, the simple concept that is followed is maths. Yes! based on simple mathematical concepts, we can answer to above-mentioned questions. We set our routine according to our workout schedule, count the number of repetitions while exercising, etc., just based on maths.

Application: 

• Basic Mathematical Operations (additions, subtraction, multiplication, and division)

• Logical and Analogical Reasoning

Interior designing seems to be a fun and interesting career but, do you know the exact reality? A lot of mathematical concepts, calculations, budgets, estimations, targets, etc., are to be followed to excel in this field. Interior designers plan the interiors based on area and volume calculations to calculate and estimate the proper layout of any room or building. Such concepts form an important part of maths.

Application:

• Geometry

• Ratios and Percentages

• Mathematical Operations

• Calculus and Statistics

5. Fashion Designing

Just like interior design, maths is also an essential concept of fashion design. From taking measurements, estimating the quantity and quality of clothes, choosing the color theme, and estimating the cost and profit, to producing cloth according to the needs and tastes of the customers, maths is followed at every stage.

Application:

• Basic Mathematical Operations

• Rations and Percentages

• Geometry

The most obvious place where you would see the application of basic mathematical concepts is your neighborhood grocery store and supermarket. The schemes like ‘Flat 50% off, ‘Buy one get one free, etc., are seen in most of the stores. Customers visit the stores, see such schemes, estimate the quantity to be bought, the weight, the price per unit, discount calculations, and finally the total price of the product, and buy it. The calculations are done based on basic mathematical concepts. Thus, here also, maths forms an important part of our daily routine.

Application: 

• Mathematical Operations

• Ratio and Percentage

• Algebra

In your kitchen also, the maths is performed. For cooking or baking anything, a series of steps are followed, telling us how much of the quantity is to be used for cooking, the proportion of different ingredients, methods of cooking, the cookware to be used, and many more. Such are based on different mathematical concepts. Indulging children in the kitchen while cooking anything, is a fun way to explain maths as well as basic cooking methods.

Application:

• Mathematical Algorithm

• Mathematical Operations

• Ratios and Proportions

Maths improves the cognitive and decision-making skills of a person. Such skills are very important for a sportsperson because by this he can take the right decisions for his team. If a person lacks such abilities, he won’t be able to make correct estimations. So, maths also forms an important part of the sports field.

Application:

• Probability

• Mathematical Operations and Algorithm

• Logical Reasoning

• Game Theory

Now managing time is one of the most difficult tasks which is faced by a lot of people. An individual wants to complete several assignments in a limited time. Not only the management, but some people also are not even able to read the timings on an analog clock. Such problems can be solved only by understanding the basic concepts of maths. Maths not only helps us to understand the management of time but also to value it.

Application:

• Logical Reasoning

• Basic Mathematical Operations

• Reasoning

10. Driving

‘Speed, Time, and Distance’ are all these three things that are studied in mathematical subjects, which are the basics of driving irrespective of any mode of transportation. Maths helps us to answer the following question;

• How much should be the speed to cover any particular distance?

• How much time would be taken?

• Whether to turn left or right?

• When to stop the car?

• When to increase or decrease the speed?

Application:

• Logical reasoning

• Numerical Reasoning

• Mathematical Operations

The different car manufacturing companies produce cars based on the demands of the customers. Every company has its category of cars ranging from microcars to luxury SUVs. In such companies, basic mathematical operations are being applied to gain knowledge about the different demands of the customers.

Application:

• Mathematical Operations

• Ratios and Proportions

• Statistics

• Geometry

• Algorithm

Ever wondered how a computer works? How easily it completes every task in a proper series of actions? The simple reason for this is the application of maths. The fields of mathematics and computing intersect both in computer science. The study of computer applications is next to impossible without maths. Concepts like computation, algorithms and many more forms the base for different computer applications like PowerPoint, word, excel, etc. are impossible to run without maths.

Applications:

• Computation

• Algothirm

• Coding Methods

• Cryptography

We all are bored with our monotonous life and we wish to go on long vacations. For this, we have to plan things accordingly. We need to prepare the budget for the trip, the number of days, the destinations, and hotels adjust our other work accordingly, and many more. Here comes the role of maths. Basic mathematical concepts and operations are required to be followed to plan a successful trip.

Application:

• Budgeting

• Algebra

• Calculus

• Mathematical Operations

Every Hospital has to make the schedule the timings of the doctors available, the systematic methods of conducting any major surgery, keeping the records of the patients, records of the success rate of surgeries, number of ambulances required, training for the use of medicines to nurses, prescriptions, and scheduling all tasks, etc. All these are done based on Mathematical concepts.

Application:

• Budgeting

• Operations

• Ratios and Proportions

• Body Mass Index

15. Video Games

Playing video games is one of the most favorite entertainment activities done all over the world, irrespective of the fact that whether you are a kid or an adult. Students usually skip their maths classes to play video games. But, do you know here also they are learning maths? Here, they learn about the different steps and techniques to be followed to win any game. Not only while playing, but the engineers who introduce different games for people also follow the different mathematical concepts.

Applications:

• Game Theory

• Probability

• Computation

• Logical Reasoning

• Geometry

• Algebra

• Calculus

• Statistics

The weather forecasting is all done based on the probability concept of maths. Through this, we get to know about the weather conditions like whether it’s going to be a sunny day or rainfall will come So, next time you plan your outing, don’t forget to see the weather forecasting.

Application:    

• Probability

• Statistics

Though maths is itself a unique subject. But, you would be surprised to know that it forms the base for every subject. The subjects like physics, chemistry, economics, history, accountancy, and statistics every subject is based upon maths. So, next time you say, “I’m not going to study this maths subject ever!” remember, this subject will not going to leave you ever.

Application:

• Mathematical Operations

• Budgeting

• Operations Research

• Algebra

• Linear Programming

• Algorithm

• Ratios and Proportions

Listening to music and dancing is one of the most common hobbies of children. Here also, they learn maths while singing and learning different dance steps. Coordination in any dance can be gained by simple mathematical steps.

Application: 

• Mathematical Operations

The part of maths called ‘Operations Research is an important concept that is being followed at every manufacturing unit. This concept of maths gives the manufacturer a simple idea of performing several tasks under the manufacturing unit like,

• What quantity is to be produced?

• What methods are to be followed?

• How to increase production?

• How the cost of production can be reduced?

• Removing unnecessary tasks.

• Following methods like target costing, ABC costing, cost-profit budgeting, and many more.

Application:

• Operations Research

• Statistics

• Ratios and Probability

• Algebra

20. Planning of Cities

Urban planning includes the concepts of budgeting, planning, setting targets, and many more which all forms part of mathematics. No activity is possible without maths.

Application:

• Trigonometry

• Algebra

• Linear Programming

• Operations Research

Problem-solving skills are one of the most important skills which every individual should possess to be successful in life. Such skills help the individual in taking correct decisions in life, let it be professional or personal. This is all done when the person has the correct knowledge of basic mathematical concepts.

Application:

• Logical Reasoning

• Mathematical Reasoning

• Basic Mathematical Operations

The marketing agencies make the proper plans as to how to promote any product or service. The tasks like promoting a product online, use of social media platforms, following different methods of direct and indirect marketing, door-to-door sales, sending e-mails, making calls, and providing several schemes like ‘Buy one get one free, ‘Flat 50% off, offering discounts on special occasions, etc. are all done based on simple mathematical concepts. Thus, maths is present everywhere.

Application:

• Budgeting

• Percentages

• Ratios

• Algebra

• Probability

• Mathematical Operations 

Mathematical concepts | Educational and methodological material on mathematics on the topic:

Slide 1

Methods of mathematics Primary school teacher: Anikina Tatyana Yurievna

Slide 2

Mathematical concepts Concepts, their scope and content. The relationship of genus and species between concepts. Explicit and implicit definitions of concepts. Algorithm for solving the problem of recognition using the definition through the genus and specific difference. Examples of explicit and implicit definitions of concepts.

Slide 3

Concepts, their scope and content Concepts related to numbers and operations on them: number; addition; term; more. Algebraic concepts: expression; the equation; equality. Geometric concepts: segment; straight; triangle. Quantities and their measurement: centimeter; meter; kilometer.

Slide 4

The scope of a concept is the set of all objects denoted by one term. is the set of all essential properties of the object reflected in this concept. The content of the concept

Slide 5

Relationship Scope of a concept Content of a concept sets. ! If A with B (A=/ B), then a is specific in relation to the concept b, and the concept b is generic in relation to the concept a. If A = B, then the concepts a and b are identical. If the sets A and B are not connected by an inclusion relation, the concepts a and b are not in relation to the genus and species and are not identical. nine0003

Slide 7

Properties: 1) The concepts of genus and species are relative. 2) For a given concept, it is often possible to specify several generic concepts. 3) A species concept has all the properties of a generic concept. and implicit definitions of concepts Defined concept Generic concept Specific difference Defining concept + A definition is usually a sentence that explains the essence of a new term (or designation). ! nine0003

Slide 10

Remember!!! 3. The definition should be clear 2. There should be no vicious circle in the definition (or their system) 4. The same concept can be defined in different ways. 1. The definition must be proportionate

Slide 11

Algorithm: Name the concept (term) being defined. 2. Indicate the closest generic (in relation to the defined) concept. 3. List the properties that distinguish the defined objects from the scope of the generic, i.e. state the difference. 4. Check whether the rules for defining the concept are met (is it proportionate, is there a vicious circle, etc. )

Slide 12

Explicit definitions Have the form of equality, coincidence of two concepts. The general scheme of such definitions is: "A is (by definition) B". Here A and B are two concepts, and it does not matter whether each of them is expressed by one word or a combination of words. Geometry is the science of the properties of geometric shapes. A molecule is the smallest particle of a substance that retains all the chemical properties of this substance. This definition is by display. They are used to introduce terms, by demonstrating the objects that these terms designate. nine0003

Slide 14

X + 6 = 15 is an equation An example of a contextual definition can be the definition of an equation and its solution given in a mathematics textbook for grade II (Moro M.I., Bantova M.A. Mathematics: Textbook for 2 class of a four-year elementary school.) Here, after writing + 6 \u003d 15 and a list of numbers 0,5,9,10, there is a text: “To what number must 6 be added to get 15? We denote the unknown number with the Latin letter X (x): To solve an equation means to find an unknown number. In this equation, the unknown number is 9, since 9+6=15. "Explain why the numbers 0.5 and 10 are not appropriate."

Slide 15

2*7 >2*6 is inequality 17-5=8+4 is equality inequalities) from other sentences, it does not indicate the properties characteristic of these concepts. They only associate terms with the entities they define.

Slide 16

Geometric shapes Definition of a segment, ray, angle, polyline. The main properties of these figures. The content of these concepts in elementary education in mathematics; types of definitions. Task examples.

Slide 17

Definition of a segment, ray, angle, polyline A segment is a straight line passing through two points. is a system of two points A and B belonging to the line a. The points located between A and B are called the points lying inside the segment AB, the points A and B are called the ends of the segment AB. - A B is a part of a straight line, which consists of all points of this straight line lying between two given points of it. These points are called the ends of the segment. nine0003

Slide 18

Main property: Of the three points on a line, one and only one lies between the other two. Two points are enough to draw a straight line.

Slide 19

A ray is a part of a straight line that has a beginning but no end. - The beam is limited on one side and can be extended in a straight line only in one direction as far as desired. - A ray with origin O is a set of all points of a straight line lying on one side of O.

Slide 20

О A ray is a part of a straight line, which consists of all points of this straight line, lying on one side of its given point. This point is called the starting point of the beam.

Slide 21

An angle is a figure formed by two rays with the same origin. A B The rays forming an angle are called the sides of the angle, and their common beginning is the apex of the angle. An acute angle is an angle that is less than a right angle. An obtuse angle is an angle that is greater than a right angle. A right angle equal to 90 is a set of two rays with a common origin, lying on different lines. - - From

Slide 22

Basic properties: Each angle has a certain degree measure greater than zero. A straight angle is 180. The degree measure of an angle is equal to the sum of the degree measures of the angles into which it is divided by any ray passing between its sides.

Slide 23

Polyline - B A C D E Polyline ABCDEG . Points A, B, C, D, E, G are the vertices of the polyline. The segments AB, BC, CD, DE, EG are the links of the broken line. G is a figure that consists of points A1, A2,……A n and segments A1A2, A2A3,…..A n A n connecting them. nine0003

Slide 24

Main property: The length of the polyline is not less than the length of the segment connecting its ends. The length of a broken line is the sum of the lengths of its links.

Slide 25

Examples of tasks What is the broken line that has the most links? Less links? Which polyline has 3 vertices? 4 peaks? How to find out which segment is larger?

Slide 26

How can you draw a right angle on unlined paper? How to make 4 right angles with just two segments? And now 2 sharp and 2 blunt? nine0003

Slide 27

Rectangle A quadrilateral with all right angles. - is a parallelogram with all right angles. B A C D

Slide 28

Diagonals of a rectangle are equal Opposite sides are equal Sides do not intersect Diagonals intersect and the point of intersection is bisected

Slide 29

A square - - - - is a rectangle whose adjacent sides are equal. is a rectangle whose diagonals are mutually perpendicular and equal. This is a rhombus that has a right angle. It is a parallelogram in which all sides are equal and the angles are right. B A C D

Slide 30

After drawing the diagonals, we get equal triangles. The diagonals are equal. The diagonals intersect and the intersection point is bisected. The sides do not intersect. Diagonals intersect at right angles.

Slide 31

Example tasks Is this figure a rectangle? Why? How to shift the sticks so that you get 3 identical squares? Which figure has the largest area? Why? Do the calculations.

Formation of mathematical concepts in elementary school

Author: Grebennikova Anna Andreevna

Formation of mathematical concepts in elementary school

Abstract: The article discusses various ideas on the formation of scientific concepts and their influence on modern ideas about the formation of the concept of number in primary school students.

Keywords: concept, number concept, generalization, various methodological approaches.

When acquiring scientific knowledge, elementary school students encounter different types of concepts. The student's inability to differentiate concepts leads to their inadequate assimilation. nine0003

Logic in concepts distinguishes scope and content. The volume is understood as the class of objects that belong to this concept, are united by it. So, the scope of the concept of a triangle includes the entire set of triangles, regardless of their specific characteristics (types of angles, size of sides, etc.).

The content of concepts includes that system of important properties due to which the process of uniting these objects into one class takes place. In order to reveal the essence of a concept, it is necessary, by means of comparison, to identify what signs will be sufficient to highlight its relationship to other objects. Until the moment when the signs are established, as well as the content, we will not be clear about the essence of the subject that is reflected by this concept. It will definitely be very difficult to separate such an object from adjacent objects, there will be some confusion. nine0003

If, for example, we talk about the concept of a triangle, then the properties can be attributed to such as a closed figure, consisting of three line segments. The set of properties, according to which objects are combined into one class, is usually called sufficient features or necessary features. In some concepts, these features can complement each other, thereby forming a content that allows you to combine objects into one class. An example of such concepts is a triangle, an angle, a bisector, and many others. nine0003

The set of such objects to which this concept will apply is a logical class of objects, which, in turn, is a collection of objects that have common features, and therefore are defined by a common concept. Concepts can be divided into types according to content, volume. It all depends on the nature and number of objects to which they are distributed. If we take the scope of a concept as a criterion, then it should be said here that concepts are divided into general and singular. For example, if the scope of a concept includes one object, then such a concept is called a single one. If we talk about the content, then the concepts can be divided into conjunctive and disjunctive, absolute and concrete, irrelative and relative. Conjunctive should be understood as such concepts that are interconnected by their features, that is, it is not possible to recognize an object of this class by individual features. For example, objects related to the concept of a triangle must necessarily consist of three line segments and be closed. nine0003

In other concepts, the relationship between necessary and sufficient features is different: they do not complement each other, but replace. This means that one feature is equivalent to the other. Such a connection of attributes is called disjunction, and the concepts are respectively called disjunctive. It is also important to take into account the division of concepts into absolute and relative. Absolute concepts can unite objects into classes, according to some features that characterize the essence of these objects. Relative concepts, on the other hand, set themselves the task of uniting them into classes according to the properties that characterize their relationship to other objects. nine0003

Relative concepts cause more serious difficulties for students than absolute concepts. The essence of the difficulties lies precisely in the fact that schoolchildren do not take into account the relativity of concepts and operate with them as with absolute concepts.

In elementary school, each concept is initially introduced through visualization, through observation of specific objects, or through practical operation. In this case, the teacher is trying to build on the knowledge and experience of the children that they received early, perhaps even at preschool age. The teacher fixes acquaintance with the concepts of mathematics with the help of terms or symbols. But this does not mean that various types of definitions are not used at this stage of the work. The definition of a concept is a listing of all the important features of objects that are components of this concept. The definition of a concept by a word will be called a term, for example, “circle”, triangle. The tasks of the definition are very important: to single out and separate a certain concept from all the others, to indicate those essential features without which this concept cannot exist, on which all other features will depend. In the process of teaching children in elementary school, contextual and ostensive definitions are of particular interest among implicit definitions. nine0003

Any passage from the text, whatever the context, in which the concept that interests us occurs, is, in some sense, its implicit definition. Context allows you to put the concept in connection with other concepts, revealing their content.

For example, when working with children such expressions as “find the values ​​of the expression”, “compare the value of the expressions 5 + a and (a - 3) 2, if a = 7”, “read expressions that are sums”, “ read expressions, and then read equations”, we reveal the concept of “mathematical expression” as a record that consists of numbers or variables and signs of actions. It should be noted that almost all definitions that we encounter in life will be contextual definitions, since if we hear an unfamiliar word, we try to figure out its meaning ourselves, based on the general meaning of what was said. Such a phenomenon is present in the system of teaching younger students, since some mathematical concepts are defined in elementary school through the context. nine0003

These are, for example, such concepts as “big - small”, “any”, “any”, “one”, “many”, etc.

Contextual definitions remain largely incomplete and incomplete. They are used in connection with the unpreparedness of the younger student to assimilate the full and, all the more so, the scientific definition.

Ostensive definitions are definitions by demonstration. They resemble ordinary contextual definitions, but the context here is not a passage of some text, but the situation in which the object denoted by the concept finds itself. For example, the teacher shows a square (drawing or paper model) and says "Look - it's a square. " This is a typical ostensive definition. nine0003

In elementary grades, ostensive definitions are used when considering such concepts as “red (white, black, etc.) color”, “left - right”, “left to right”, “number”, “preceding and following number”, "signs of arithmetic operations", "comparison signs", "triangle", "quadrilateral", "cube", etc.

Thanks to the assimilation of the meanings of words in an ostensive way, it is possible to introduce into the child's vocabulary the already verbal meaning of new, previously unfamiliar words, as well as entire phrases. It is ostensive definitions that can connect a concept with objects. In elementary school, there are usually some acceptable definitions, like "We'll use the word 'pentagon' to mean a polygon with five sides." This, one might say, would be a nominal definition. Various explicit definitions are used in mathematics. The most common of them is the definition through the nearest genus and species character. The generic definition is also called the classical one. nine0003

Examples of definitions in terms of genus and species: “A parallelogram is a quadrilateral whose opposite sides are parallel”, “A rhombus is a parallelogram whose sides are equal”, “A rectangle is a parallelogram whose angles are right”, “A square is a rectangle, in which the sides are equal”, “A square is a rhombus with right angles”.

Let's analyze such concept as a square. Speaking about the first definition, it should be said about the nearest generic concept - "rectangle", where the species attribute will be - "all sides are equal." In the second definition, the closest genus is "rhombus", and the specific feature is "right angles". And if we take a genus that will not be the closest, then there will be two specific signs of a square, for example: "A parallelogram is called a square, in which all sides are equal and all angles are right." Some definitions allow us to consider concepts according to the method of its formation, as well as according to the method of its occurrence.

Learn more

• 
  First grade reading activities free
• 
  Kindergarten addition and subtraction activities
• 
  Adding for first graders
• 
  Writing the letter n
• 
  Pictures rhyming words
• 
  Bed time short stories
• 
  Long and short vowels video
• 
  Shaving cream sensory bag
• 
  Preschool number crafts
• 
  Story for baby to sleep
• 
  Children education websites