Math concepts 2nd grade

Math Skills for 2nd Grade, What Your Child Will Learn

• Math Tips
• Education
• 2nd

In second grade math, children begin to work with larger numbers and develop a stronger understanding of place value. Students also learn everyday skills like telling time, working with money, and measuring. 

We parents can help our children succeed in second grade math by finding out more about what they’re going to learn. Over the year, your child will learn how to: 

1. Count within 1,000 

Second graders learn to read and write numbers to 1,000. They practice skip counting by 5s, 10s, and 100s as they notice patterns among numbers. 

At home: Create opportunities for reading and writing three-digit numbers. For example, have your child read the numbers on nutritional labels.
You can also ask your child to verbally skip count by 10s or 100s. Begin by starting at 10 or 100, then challenge your second grader to skip count on from other numbers, such as 60 or 204. 

2.  Understand place value in three-digit numbers

As kids learn to count within 1,000, they’ll be looking at three-digit numbers more closely. By looking at patterns in numbers, kids start to understand place value.

At home: Help your child by asking how many ones, tens and hundreds are in three-digit numbers. 

3. Compare three-digit numbers

After learning about place value and counting within 1,000, second graders will be able to compare three-digit numbers. They will be able to use their knowledge of place value to look at two numbers and tell which one is more or less than the other. Kids will learn how to use the symbols <,>, and = to compare three-digit numbers. 

At home: Help your child practice comparison skills by asking questions like “Which is bigger: 943 or 783?” Push your child’s thinking by asking why one number is bigger than another.

4. Add and subtract within 1,000

In second grade, kids get used to adding and subtracting numbers within 100. They solve one-step and two-step word problems, such as “Timmy had 39 toy cars. He got 12 more, then gave 18 away. How many cars does Timmy have left?”

After working to add and subtract within 100, kids will use their knowledge of three-digit numbers to practice adding and subtracting within 1,000. 

At home: make up some word problems like the one above, using your child's favorite toys or foods.

5. Measurement

Second graders develop their understanding of measurement by estimating lengths and measuring using different units. They compare lengths, similar to the comparison work they do with numbers, and use addition and subtraction to find out how much longer or shorter objects are. 

At home: Give your child a ruler and ask them to measure three different objects in the house. Then have your child put the objects in order from shortest to longest and explain how much longer or shorter each object is than the other ones. 

6. Telling time to the nearest five minutes

In first grade, students were introduced to telling time. Now second graders are able to extend their understanding to tell time to the nearest five minutes. Kids will also be able to tell the difference between AM and PM. 

At home, have your child practice telling time to the nearest five minutes - remind them to use AM and PM!

7. Word problems involving money

Second graders will solve lots of word problems involving addition and subtraction, including money problems.  

At home: Give your child a pile of coins and the job to count the total value. Or play “store” and have your child practice buying objects for different amounts of money, then figuring out how many cents are left. 

8. Picture and bar graphs

In second grade, your child will learn to use picture and bar graphs with up to four categories.

Challenge your child to take surveys at home and represent the data that is collected on a graph. 

Have a wonderful time digging into second grade math! 

Found this useful? Check out our grade by grade math guides from Kindergarten to 5th grade

Written by Lily Jones, Lily Jones loves all things learning. She has been a kindergarten & first grade teacher, instructional coach, curriculum developer, and teacher trainer. She loves to look at the world with curiosity and inspire people of all ages to love learning. She lives in California with her husband, two kids, and a little dog.  

About Komodo – Komodo is a fun and effective way to boost K-5 math skills. Designed for 5 to 11-year-olds to use in the home, Komodo uses a little and often approach to learning math (15 minutes, three to five times per week) that fits into the busy family routine. Komodo helps users develop fluency and confidence in math – without keeping them at the screen for long.

Find out more about Komodo and how it helps thousands of children each year do better at maths – you can even try Komodo for free. 

Back to School - 5 Tips to Help you Ease Back into the Routine

Here are some steps you can take to ease children back from full vacation mode so that the first week of school doesn't knock you sideways.

Mindset - The Path to Mastery

People who have a growth mindset believe that they always have the potential to learn and improve. They are more motivated to persevere with difficult tasks, to take risks and to learn from failure.

2nd Grade Math Concepts|2nd Grade Math Facts|2nd Grade Math

While every state and school district differs slightly, below you will find useful detail surrounding some of the Math concepts children will likely be covering in 2nd Grade Math such as: Addition and Subtraction Math Facts, Adding and Subtracting Larger Numbers, Multiplication and Division Math Facts, Skip Counting and Using a Hundreds Board, Money, Place Value, Telling Time, Measurement, Shapes and Solids, Lines and Angles, Symmetry, Fractions, Data Management and Analysis, Estimating, Area and Perimeter, Capacity and Weight, Decimals, and Patterns.

You will notice that many math concepts and math skills repeat over the Kindergarten, 1st Grade, Second Grade and 3rd Grade levels. This is due to the fact that math concepts build on each other grade by grade.

Math Facts: Addition and Subtraction

Addition and Subtraction Math Facts should be mastered by the end of the 2nd Grade. Students will review Math Fact Addition strategies such as “Doubles” (6+6 or 4+4), “Turnarounds” (2+7 = 7+2), “Near Doubles”, “Almost Doubles” or “Doubles Plus 1” (6+6+12, so 6+7= one more, or 13). Kids will also learn other math strategies for both Addition and Subtraction that will enable them to really master their Math Facts.

Adding and Subtracting Larger Numbers

Children in Second Grade will learn to add and subtract larger numbers (ex: 2-digit numbers such as 46+19, or 72-58). More than one math strategy may be taught to solve these problems, including Mental Math.

Math Facts – Multiplication and Division

Students in Second Grade will begin exploring Multiplication and Division in concrete ways. Kids will learn important vocabulary such as Products (answer to a multiplication question), Quotients (answer to a division question), Remainders, Fact Families, etc. Students will also be placing objects into equal groups, displaying numbers in arrays, and creating number stories.

Skip Counting and Using a Hundreds Board

Students in 2nd Grade will review skip counting by 2s, 5s, and 10s (ex: 2,4, 6, 8, or 5, 10, 15, 20). Frequently, a Hundreds Board is used to visually represent these math concepts, and to assist students in learning them.

Money

Children in Second Grade will count / add pennies, nickels, dimes, quarters, and dollar bills. Students will continue to work on the math concept of making change.

Place Value

Students in Grade 2 will learn that each digit in larger numbers has a value, depending on its position in the number. For example, in the number 52,478, the 5 is worth 5 “ten-thousands” (or 50,000), the 2 is worth 2 “thousands” (or 2,000), the 4 is worth 4 “hundreds” (or 400), the 7 is worth 7 “tens” (or 70), and the 8 is worth 8 “ones”, or simply 8.

Measurement

Second-Graders will have many opportunities to measure in a variety of ways. Grade Two students may continue measuring with non-standard units (ex: hand spans) and standard units (ex: inches, feet, yards, or centimeters, decimeters and meters), as well as temperature in Fahrenheit and Celsius using a thermometer, etc.

Telling Time

Telling Time remains an important math skill that students will continue working on in Second Grade. They will tell time to the hour, half-hour, quarter-hour, 5 minutes and 1 minute using both digital and analog clocks. The math concept of elapsed time will also be reviewed.

Shapes and Solids

Grade 2 students will learn to classify 2-dimensional shapes by shape, color and size. They will also look at various attributes of shapes (ex: number of sides, corners, etc.). Solids (3-D) such as cones, cylinders, prisms, pyramids and spheres will also be reviewed.

Lines and Angles

Second Grade students will learn about Lines, Line Segments, and Parallel Lines, and they will be introduced to Angles as well.

Fractions

Fractional parts of a whole will be investigated (ex: the child will see a circle, and will divide it into several equal parts like halves, thirds, fourths, sixths, etc.) in second grade. Fractions of a group will also be explored (ex: how to divide a class of 24 children into 6 equal groups). 2nd Grade kids will shade in parts of an object to show a specified fraction, and they will explore equivalent fractions using concrete materials such as pattern blocks.

Symmetry

An image that is symmetrical is something that has two sides that are identical. One side could be seen as a “mirror image” of the other side. 2nd Grade students will have opportunities to look for symmetry in everyday objects, as well as create symmetrical patterns of their own. They will determine whether certain objects or pictures display line symmetry, and the number of lines of symmetry in those objects or pictures.

Data Management and Analysis

Children in Second Grade will continue to create various graphs (ex: bar graphs). They will also learn more about data collection, and how to organize and analyze the data. Math concepts such as Median, Mode, and Range will be learned.

Estimating

Students in Grade 2 will use estimating and rounding as useful math strategies to get an approximate answer, and they will also estimate to verify that their answer (to an Addition or Subtraction question) makes sense.

Capacity and Weight

Students in 2nd Grade will begin learning about different types of measuring, such as measuring the contents of a container (Capacity) and the Weight of small objects. Kids will work with both the U.S. Customary Measuring System, and the Metric System. Children will learn terms such as Cups, Pints, Quarts, Gallons, Liters, Ounces, Pounds, Grams and Kilograms. Some equivalent measures will also be explored (ex: 2 Pints = 1 Quart).

Area and Perimeter

Second Graders will explore the concept of Perimeter and Area in concrete ways. For example, students may measure the distance around their textbook, or use pattern blocks to “tile” a surface such as their desk.

Decimals

Students in Second Grade have already had many opportunities to explore numbers that are “less than one” (

Patterns

Grade 2 students have already worked with Color, Shape and Number Patterns, and they will continue to discover new ways to create more complex math patterns. This skill incorporates some adding and subtracting, logical thinking, number sense, etc.

Mathematical concepts | Educational and methodological material on mathematics on the topic:

Slide 1

Methods of mathematics Primary school teacher: Anikina Tatyana Yurievna

Slide 2

Mathematical concepts Concepts, their scope and content. The relationship of genus and species between concepts. Explicit and implicit definitions of concepts.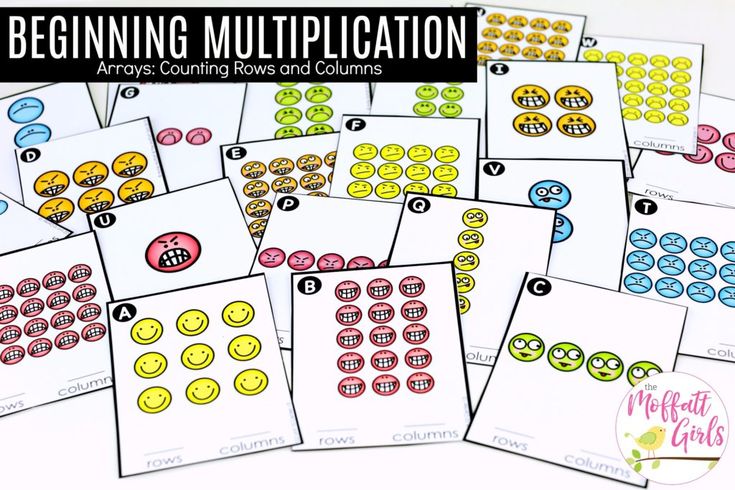 Algorithm for solving the problem of recognition using the definition through the genus and specific difference. Examples of explicit and implicit definitions of concepts.

Slide 3

Concepts, their scope and content Concepts related to numbers and operations on them: number; addition; term; more. Algebraic concepts: expression; the equation; equality. Geometric concepts: segment; straight; triangle. Quantities and their measurement: centimeter; meter; kilometer.

Slide 4

The scope of a concept is the set of all objects denoted by one term. is the set of all essential properties of the object reflected in this concept. Content of concept

Slide 5

Relationship Scope of a concept Content of a concept sets. ! If A with B (A=/ B), then a is specific in relation to the concept b, and the concept b is generic in relation to the concept a. If A = B, then the concepts a and b are identical. If the sets A and B are not connected by an inclusion relation, the concepts a and b are not in relation to the genus and species and are not identical.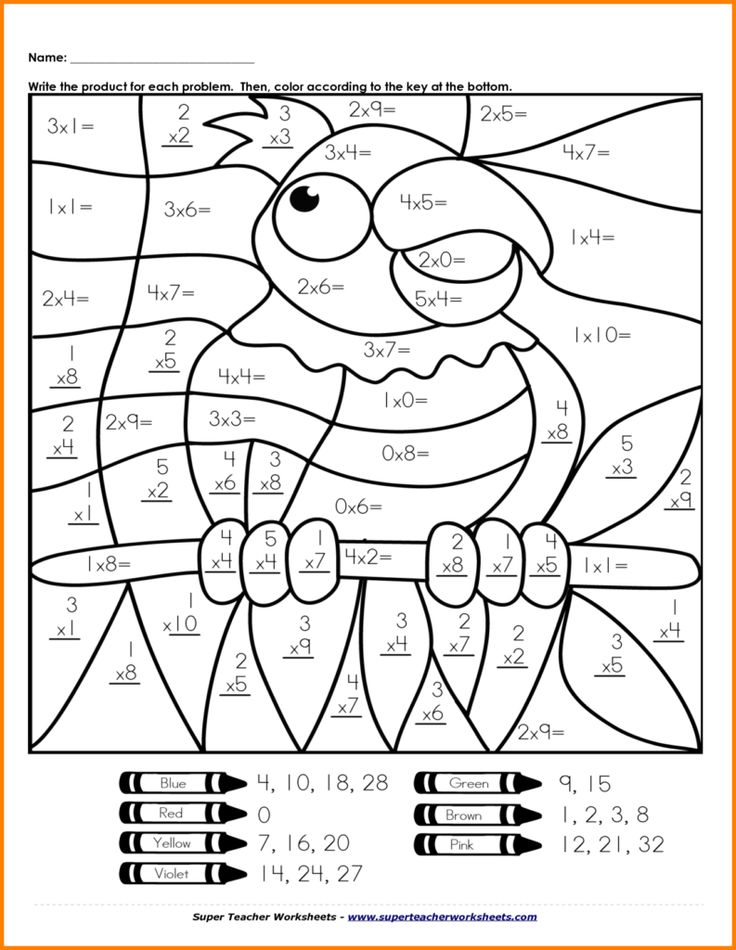

Slide 7

Properties: 1) The concepts of genus and species are relative. 2) For a given concept, it is often possible to specify several generic concepts. 3) A species concept has all the properties of a generic concept. and implicit definitions of concepts Defined concept Generic concept Specific difference Defining concept + A definition is usually a sentence that explains the essence of a new term (or designation). !

Slide 10

Remember!!! 3. The definition should be clear 2. There should be no vicious circle in the definition (or their system) 4. The same concept can be defined in different ways. 1. The definition must be proportionate

Slide 11

Algorithm: Name the concept (term) being defined. 2. Indicate the closest generic (in relation to the defined) concept. 3. List the properties that distinguish the defined objects from the scope of the generic, i.e. state the difference. 4. Check whether the rules for defining the concept are met (is it proportionate, is there a vicious circle, etc. )

Slide 12

Explicit definitions Have the form of equality, coincidence of two concepts. The general scheme of such definitions is: "A is (by definition) B". Here A and B are two concepts, and it does not matter whether each of them is expressed by one word or a combination of words. Geometry is the science of the properties of geometric shapes. A molecule is the smallest particle of a substance that retains all the chemical properties of this substance. This definition is by display. They are used to introduce terms, by demonstrating the objects that these terms designate.

Slide 14

X + 6 = 15 is an equation An example of a contextual definition can be the definition of an equation and its solution given in a mathematics textbook for grade II (Moro M.I., Bantova M.A. Mathematics: Textbook for 2 class of a four-year elementary school.) Here, after writing + 6 \u003d 15 and a list of numbers 0,5,9,10, there is a text: “To what number must 6 be added to get 15? We denote the unknown number with the Latin letter X (x): To solve an equation means to find an unknown number. In this equation, the unknown number is 9, since 9+6=15. "Explain why the numbers 0.5 and 10 are not appropriate."

Slide 15

2*7 >2*6 is inequality 17-5=8+4 is equality inequalities) from other sentences, it does not indicate the properties characteristic of these concepts. They only associate terms with the objects they define.

Slide 16

Geometric shapes Definition of a segment, ray, angle, polyline. The main properties of these figures. The content of these concepts in elementary education in mathematics; types of definitions. Task examples.

Slide 17

Definition of a segment, ray, angle, polyline A segment is a straight line passing through two points. is a system of two points A and B belonging to the line a. The points located between A and B are called the points lying inside the segment AB, the points A and B are called the ends of the segment AB. - A B is a part of a straight line, which consists of all points of this straight line lying between two given points of it. These points are called the ends of the segment.

Slide 18

Main property: Of the three points on a line, one and only one lies between the other two. Two points are enough to draw a straight line.

Slide 19

A ray is a part of a straight line that has a beginning but no end. - The beam is limited on one side and can be extended in a straight line only in one direction as far as desired. - A ray with origin O is a set of all points of a straight line lying on one side of O.

Slide 20

О A ray is a part of a straight line, which consists of all points of this straight line, lying on one side of its given point. This point is called the starting point of the beam.

Slide 21

An angle is a figure formed by two rays with the same origin. A B The rays forming an angle are called the sides of the angle, and their common beginning is the apex of the angle. An acute angle is an angle that is less than a right angle. An obtuse angle is an angle that is greater than a right angle. A right angle equal to 90 is a set of two rays with a common origin, lying on different lines. - - From

Slide 22

Basic properties: Each angle has a certain degree measure greater than zero. A straight angle is 180. The degree measure of an angle is equal to the sum of the degree measures of the angles into which it is divided by any ray passing between its sides.

Slide 23

Polyline - B A C D E Polyline ABCDEG . Points A, B, C, D, E, G are the vertices of the polyline. The segments AB, BC, CD, DE, EG are the links of the broken line. G is a figure that consists of points A1, A2,……A n and segments A1A2, A2A3,…..A n A n connecting them.

Slide 24

Main property: The length of the polyline is not less than the length of the segment connecting its ends. The length of a broken line is the sum of the lengths of its links.

Slide 25

Examples of tasks What is the broken line that has the most links? Less links? Which polyline has 3 vertices? 4 peaks? How to find out which segment is larger?

Slide 26

How can you draw a right angle on unlined paper? How to make 4 right angles with just two segments? And now 2 sharp and 2 blunt?

Slide 27

Rectangle A quadrilateral with all right angles. - is a parallelogram with all right angles. B A C D

Slide 28

Diagonals of a rectangle are equal Opposite sides are equal Sides do not intersect Diagonals intersect and the point of intersection is bisected

Slide 29

A square - - - - is a rectangle whose adjacent sides are equal. is a rectangle whose diagonals are mutually perpendicular and equal. This is a rhombus that has a right angle. It is a parallelogram in which all sides are equal and the angles are right. B A C D

Slide 30

After drawing the diagonals, we get equal triangles. The diagonals are equal. The diagonals intersect and the intersection point is bisected. The sides do not intersect. Diagonals intersect at right angles.

Slide 31

Example tasks Is this figure a rectangle? Why? How to shift the sticks so that you get 3 identical squares? Which figure has the largest area? Why? Do the calculations.

Formation of mathematical concepts in elementary school

Formation of mathematical concepts in elementary school.

The study of mathematics is associated with the assimilation of a certain system of concepts. In order to master this system and then successfully apply the acquired knowledge and skills, teaching younger students and solving the problem of their development by means of mathematics, you must first understand what are the features of mathematical concepts, how their definitions, sentences expressing the properties of concepts are arranged. This knowledge is necessary for a primary school teacher because he is the first to introduce children into the world of mathematical knowledge, and the attitude of the child in the future depends on how competently and successfully he does this.

The appearance in mathematics of new concepts, and hence new terms denoting these concepts, presupposes their definition.

« Definition is a logical operation that reveals the content of the concept. The ways of definition are different: For example, perimeter - is the sum of the sides of some geometric figure.

Perimeter Sum

A = B, and is B

A B

I have no compulsion of the two concepts of the two concepts.