Mathematical concepts for children
The 4 Major Math Concepts Your Kids Learn in PreK & Kindergarten
There are so many different topics our children learn throughout the year, just keeping up with each night’s new piece of homework and its latest ideas can feel very overwhelming. As parents, we don’t get to see the major idea behind the “everyday” work and it can be frustrating to understand where each skill is going. In this first blog post of a continuing series, I will be highlighting the major math concepts that are taught at the different grade levels so we, as parents, can help to build and support these ideas at home.
Here are the four major math concepts taught in pre-kindergarten and kindergarten, along with exercises you can practice with your children to help reinforce their learning.
1. Counting. Students are beginning their experience with numbers through counting, number names and written numerals. Students are learning to count objects and understand a one-to-one correspondence. They are also starting to compare different sets of objects and use appropriate language.
Encourage your child to:
- Touch different objects and count out loud.
- Move objects from one group to another.
- Count a set of objects and “see” or “write” that corresponding number.
- Start to use comparing words: more than, less than, the same as.
2. Addition & Subtraction. This is the very early stage of adding and subtracting. The focus should be on developing an understanding of addition as “putting together and adding to,” and subtracting as “taking apart and taking from.” Students do not need to write equations at this young an age, but are encouraged to begin using them.
Encourage your child to:
- Tell stories about adding and subtracting. For example, for addition: Two bunnies sat on the grass. Three more bunnies hopped there. How many bunnies are on the grass now? For subtraction: Five apples were on the table.
I ate two apples. How many apples are on the table now? Draw pictures about putting together and taking apart. - Count to 10 and break apart numbers (decompose – math’s fancy word for “breaking apart”) into different combinations. For example, 5 can be seen as:
Image Credit: http://kindercraze.com
3. Measurement & Data. Young children are beginning to describe and compare their physical world. They are starting to classify, sort and group objects into categories.
Encourage your children to:
- Compare two different objects using appropriate language. For example:
“John is taller than Sarah.”
“This tree is shorter than that tree.”
“My bag is heavier than your bag.” - Sort objects by color, size, material, etc.
- Describe their physical world with directional words: in front of, behind, on top of, next to, below, etc.
4. Geometry. Students are starting to look at and compare two-dimensional (flat) and three-dimensional (solid) shapes.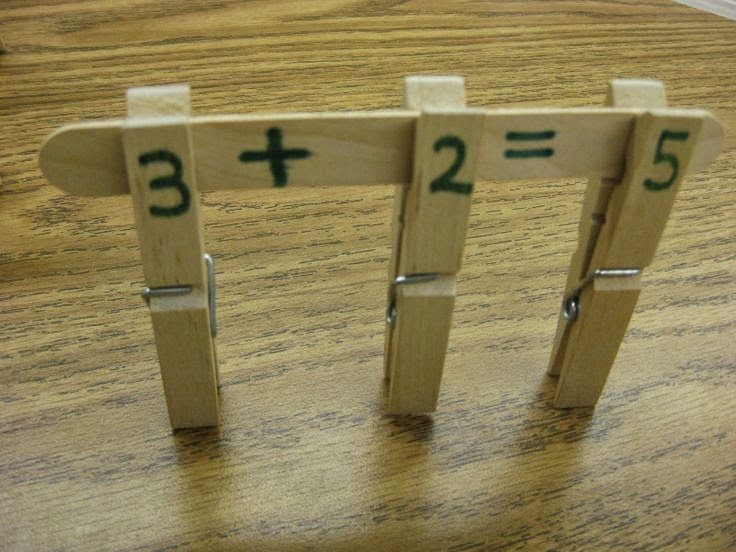
They are using appropriate language to recognize different shapes and talk about their attributes.
Encourage your child to:
- Find 2-D shapes in the world: squares, circles, triangles, rectangles, and hexagons.
- Find 3-D shapes in the world: cubes, cones, cylinders, and spheres.
- Count the different number of sides, vertices, angles, etc.Model different shapes using clay, sticks, pipe-cleaners, etc.
See all blog posts in this series for information on what your child will learn in math class from preschool all the up through 8th grade.
Help Your Child Develop Early Math Skills
Before they start school, most children develop an understanding of addition and subtraction through everyday interactions. Learn what informal activities give children a head start on early math skills when they start school.
Children are using early math skills throughout their daily routines and activities. This is good news as these skills are important for being ready for school.
But early math doesn’t mean taking out the calculator during playtime. Even before they start school, most children develop an understanding of addition and subtraction through everyday interactions. For example, Thomas has two cars; Joseph wants one. After Thomas shares one, he sees that he has one car left (Bowman, Donovan, & Burns, 2001, p. 201). Other math skills are introduced through daily routines you share with your child—counting steps as you go up or down, for example. Informal activities like this one give children a jumpstart on the formal math instruction that starts in school.
What math knowledge will your child need later on in elementary school? Early mathematical concepts and skills that first-grade mathematics curriculum builds on include: (Bowman et al., 2001, p. 76).
- Understanding size, shape, and patterns
- Ability to count verbally (first forward, then backward)
- Recognizing numerals
- Identifying more and less of a quantity
- Understanding one-to-one correspondence (i.
e., matching sets, or knowing which group has four and which has five)
Key Math Skills for School
More advanced mathematical skills are based on an early math “foundation”—just like a house is built on a strong foundation. In the toddler years, you can help your child begin to develop early math skills by introducing ideas like: (From Diezmann & Yelland, 2000, and Fromboluti & Rinck, 1999.)
Number Sense
This is the ability to count accurately—first forward. Then, later in school, children will learn to count backwards. A more complex skill related to number sense is the ability to see relationships between numbers—like adding and subtracting. Ben (age 2) saw the cupcakes on the plate. He counted with his dad: “One, two, three, four, five, six…”
Representation
Making mathematical ideas “real” by using words, pictures, symbols, and objects (like blocks). Casey (aged 3) was setting out a pretend picnic. He carefully laid out four plastic plates and four plastic cups: “So our whole family can come to the picnic!” There were four members in his family; he was able to apply this information to the number of plates and cups he chose.
Spatial sense
Later in school, children will call this “geometry.” But for toddlers it is introducing the ideas of shape, size, space, position, direction and movement. Aziz (28 months) was giggling at the bottom of the slide. “What’s so funny?” his Auntie wondered. “I comed up,” said Aziz, “Then I comed down!”
Measurement
Technically, this is finding the length, height, and weight of an object using units like inches, feet or pounds. Measurement of time (in minutes, for example) also falls under this skill area. Gabriella (36 months) asked her Abuela again and again: “Make cookies? Me do it!” Her Abuela showed her how to fill the measuring cup with sugar. “We need two cups, Gabi. Fill it up once and put it in the bowl, then fill it up again.”
Estimation
This is the ability to make a good guess about the amount or size of something. This is very difficult for young children to do. You can help them by showing them the meaning of words like more, less, bigger, smaller, more than, less than.
Nolan (30 months) looked at the two bagels: one was a regular bagel, one was a mini-bagel. His dad asked: “Which one would you like?” Nolan pointed to the regular bagel. His dad said, “You must be hungry! That bagel is bigger. That bagel is smaller. Okay, I’ll give you the bigger one. Breakfast is coming up!”
Patterns
Patterns are things—numbers, shapes, images—that repeat in a logical way. Patterns help children learn to make predictions, to understand what comes next, to make logical connections, and to use reasoning skills. Ava (27 months) pointed to the moon: “Moon. Sun go night-night.” Her grandfather picked her up, “Yes, little Ava. In the morning, the sun comes out and the moon goes away. At night, the sun goes to sleep and the moon comes out to play. But it’s time for Ava to go to sleep now, just like the sun.”
Problem-solving
The ability to think through a problem, to recognize there is more than one path to the answer. It means using past knowledge and logical thinking skills to find an answer.
Carl (15 months old) looked at the shape-sorter—a plastic drum with 3 holes in the top. The holes were in the shape of a triangle, a circle and a square. Carl looked at the chunky shapes on the floor. He picked up a triangle. He put it in his month, then banged it on the floor. He touched the edges with his fingers. Then he tried to stuff it in each of the holes of the new toy. Surprise! It fell inside the triangle hole! Carl reached for another block, a circular one this time…
Math: One Part of the Whole
Math skills are just one part of a larger web of skills that children are developing in the early years—including language skills, physical skills, and social skills. Each of these skill areas is dependent on and influences the others.
Trina (18 months old) was stacking blocks. She had put two square blocks on top of one another, then a triangle block on top of that. She discovered that no more blocks would balance on top of the triangle-shaped block. She looked up at her dad and showed him the block she couldn’t get to stay on top, essentially telling him with her gesture, “Dad, I need help figuring this out.
” Her father showed her that if she took the triangle block off and used a square one instead, she could stack more on top. She then added two more blocks to her tower before proudly showing her creation to her dad: “Dada, Ook! Ook!”
You can see in this ordinary interaction how all areas of Trina’s development are working together. Her physical ability allows her to manipulate the blocks and use her thinking skills to execute her plan to make a tower. She uses her language and social skills as she asks her father for help. Her effective communication allows Dad to respond and provide the helps she needs (further enhancing her social skills as she sees herself as important and a good communicator). This then further builds her thinking skills as she learns how to solve the problem of making the tower taller.
What You Can Do
The tips below highlight ways that you can help your child learn early math skills by building on their natural curiosity and having fun together.
(Note: Most of these tips are designed for older children—ages 2–3. Younger children can be exposed to stories and songs using repetition, rhymes and numbers.)
Shape up.
Play with shape-sorters. Talk with your child about each shape—count the sides, describe the colors. Make your own shapes by cutting large shapes out of colored construction paper. Ask your child to “hop on the circle” or “jump on the red shape.”
Count and sort.
Gather together a basket of small toys, shells, pebbles or buttons. Count them with your child. Sort them based on size, color, or what they do (i.e., all the cars in one pile, all the animals in another).
Place the call.
With your 3-year-old, begin teaching her the address and phone number of your home. Talk with your child about how each house has a number, and how their house or apartment is one of a series, each with its own number.
What size is it?
Notice the sizes of objects in the world around you: That pink pocketbook is the biggest.
The blue pocketbook is the smallest. Ask your child to think about his own size relative to other objects (“Do you fit under the table? Under the chair?”).
You’re cookin’ now!
Even young children can help fill, stir, and pour. Through these activities, children learn, quite naturally, to count, measure, add, and estimate.
Walk it off.
Taking a walk gives children many opportunities to compare (which stone is bigger?), assess (how many acorns did we find?), note similarities and differences (does the duck have fur like the bunny does?) and categorize (see if you can find some red leaves). You can also talk about size (by taking big and little steps), estimate distance (is the park close to our house or far away?), and practice counting (let’s count how many steps until we get to the corner).
Picture time.
Use an hourglass, stopwatch, or timer to time short (1–3 minute) activities. This helps children develop a sense of time and to understand that some things take longer than others.
Shape up.
Point out the different shapes and colors you see during the day. On a walk, you may see a triangle-shaped sign that’s yellow. Inside a store you may see a rectangle-shaped sign that’s red.
Read and sing your numbers.
Sing songs that rhyme, repeat, or have numbers in them. Songs reinforce patterns (which is a math skill as well). They also are fun ways to practice language and foster social skills like cooperation.
Start today.
Use a calendar to talk about the date, the day of the week, and the weather. Calendars reinforce counting, sequences, and patterns. Build logical thinking skills by talking about cold weather and asking your child: What do we wear when it’s cold? This encourages your child to make the link between cold weather and warm clothing.
Pass it around.
Ask for your child’s help in distributing items like snacks or in laying napkins out on the dinner table. Help him give one cracker to each child. This helps children understand one-to-one correspondence.
When you are distributing items, emphasize the number concept: “One for you, one for me, one for Daddy.” Or, “We are putting on our shoes: One, two.”
Big on blocks.
Give your child the chance to play with wooden blocks, plastic interlocking blocks, empty boxes, milk cartons, etc. Stacking and manipulating these toys help children learn about shapes and the relationships between shapes (e.g., two triangles make a square). Nesting boxes and cups for younger children help them understand the relationship between different sized objects.
Tunnel time.
Open a large cardboard box at each end to turn it into a tunnel. This helps children understand where their body is in space and in relation to other objects.
The long and the short of it.
Cut a few (3–5) pieces of ribbon, yarn or paper in different lengths. Talk about ideas like long and short. With your child, put in order of longest to shortest.
Learn through touch.
Cut shapes—circle, square, triangle—out of sturdy cardboard.
Let your child touch the shape with her eyes open and then closed.
Pattern play.
Have fun with patterns by letting children arrange dry macaroni, chunky beads, different types of dry cereal, or pieces of paper in different patterns or designs. Supervise your child carefully during this activity to prevent choking, and put away all items when you are done.
Laundry learning.
Make household jobs fun. As you sort the laundry, ask your child to make a pile of shirts and a pile of socks. Ask him which pile is the bigger (estimation). Together, count how many shirts. See if he can make pairs of socks: Can you take two socks out and put them in their own pile? (Don’t worry if they don’t match! This activity is more about counting than matching.)
Playground math.
As your child plays, make comparisons based on height (high/low), position (over/under), or size (big/little).
Dress for math success.
Ask your child to pick out a shirt for the day.
Ask: What color is your shirt? Yes, yellow. Can you find something in your room that is also yellow? As your child nears three and beyond, notice patterns in his clothing—like stripes, colors, shapes, or pictures: I see a pattern on your shirt. There are stripes that go red, blue, red, blue. Or, Your shirt is covered with ponies—a big pony next to a little pony, all over your shirt!
Graphing games.
As your child nears three and beyond, make a chart where your child can put a sticker each time it rains or each time it is sunny. At the end of a week, you can estimate together which column has more or less stickers, and count how many to be sure.
References
Bowman, B.T., Donovan, M.S., & Burns, M.S., (Eds.). (2001). Eager to learn: Educating our preschoolers. Washington, DC: National Academy of Sciences.
Diezmann, C., & Yelland, N. J. (2000). Developing mathematical literacy in the early childhood years. In Yelland, N.J. (Ed.), Promoting meaningful learning: Innovations in educating early childhood professionals.
(pp.47–58). Washington, DC: National Association for the Education of Young Children.
Fromboluti, C. S., & Rinck, N. (1999 June). Early childhood: Where learning begins. U.S. Department of Education, Office of Educational Research and Improvement, National Institute on Early Childhood Development and Education. Retrieved on May 11, 2018 from https://www2.ed.gov/pubs/EarlyMath/title.html
Basic mathematical concepts
The FEMP methodology in the system of pedagogical sciences is designed to help prepare preschool children for the perception and assimilation of mathematics - one of the most important subjects in school and the comprehensive development of the child.
The FEMP technique has a specific, purely mathematical terminology .
This is:
- set;
- number;
- counting and computing activities;
- value;
- geometric figures;
- time;
- space.
SET is a collection of objects that are considered as a single whole .
The world in which a person lives is represented by a variety of sets: a lot of stars in the sky, plants, animals around him, a lot of different sounds, parts of his own body.
Sets consist of elements. The elements of the set are the objects that make up the set. It could be real objects (things, toys, drawings), as well as sounds, movements, numbers, etc. .
The elements of a set can be not only individual objects, but also their combinations . For example, when counting in pairs, triplets, tens. In these cases, the elements of the set are not one object, but two, three, ten - a set.
Thus, the set is considered as a set, a set , a collection of any objects and objects, united by a common, for all characteristic property .
Any property can be considered as belonging to some objects.
Attention!
If you need help writing a paper, we recommend that you contact professionals.
Over 70,000 authors are ready to help you right now. Free corrections and improvements. Find out the value of your work.
Calculation CostGuaranteesReviews
For example, has the property of being red for some flowers, berries, cars and other objects. The property of being round is possessed by the moon, the ball, the wheels of bicycles and cars, parts of various machines and machine tools, etc.
Thus, each property is associated with a set (objects) that have this property. It is also said that the set is characterized by the given property - or the set is given by specifying the characteristic property.
Under the characteristic property of a set is meant such a property, which all objects belonging to a given set (elements of this set) have, and not a single object that does not belong to it, i.e. this item is not its element.
If some set A is specified by specifying the characteristic property P , then this is written as follows:
A = { x | P ( x )}
and reads like this: “ A is the set of all x such that x has the property P ”, or, in short, “A is the set of all 9003 having property P ".
When they say: "the set of all objects that have the property P", they mean those and only those objects that have this property.
Thus, if the set A is given by the characteristic property P , this means that it consists of all objects that have this property, and only of them. If some a has the property P , then it belongs to the set A , and vice versa, if the object a belongs to the set A , then it has the property P .
An infinite set of objects can have some property, only a finite set can have another. Therefore, the sets are subdivided into end and end .
A finite set can be specified by direct enumeration of all its elements in an arbitrary order. For example, the set of children of a given group living on Sadovaya Street can be described using a characteristic property: { x | x - lives on Sadovaya Street) or listing all its elements in an arbitrary order: {Lena, Sasha, Vitya, Ira, Kolya}.
It is quite clear that an infinite set cannot be defined by listing all of its elements .
Mathematics mostly deals with infinite sets (numbers, points, figures and other objects), but basic mathematical ideas and logical structures can be modeled on finite sets.
Naturally, in pre-mathematical preparation usually deals with finite sets .
COUNT - first and main mathematical activity based on element-by-element comparison of finite sets.
NUMBER is the general invariable category of the set , which is an indicator of the cardinality of the set. This is just a sound designation.
Theoretical foundations for the formation of elementary mathematical concepts in preschoolers include a detailed study of only the system of natural numbers . Therefore, when we say "numbers", we mean natural numbers.
NUMBERS - a system of characters (“letters”) for writing numbers (“words”) (numerical characters).
The word “digit” without qualification usually means one of the following ten characters: 0 1 2 3 4 5 6 7 8 9 (so-called “Arabic numerals”). Combinations of these numbers generate two (or more) digit numbers.
The number has 2 values : number and ordinal.
With a quantitative value of , we are interested in the number of elements in the set. We use the question HOW MUCH? and we start counting with the cardinal number ONE.
When the ordinal value is , we are interested in the place of the number among others or the ordinal number of the element in the set. The question is WHICH COUNTS? and set the direction of the account. Ordinal numbers are used, counting begins with the word FIRST.
When we talk about quantity, it does not matter the direction of the count, the object from which the count began. The final number does not change. With an ordinal count, the final number may change.
COUNTING is considered as an activity with specific elements of the set, in which a relationship is established between objects and numerals.
The study of numerals and sets of objects leads to the assimilation of counting activities.
CALCULATION ACTIVITY - is an activity with abstract numbers, carried out through addition and subtraction. The simple naming of numerals will not be called counting activity. The system of computational actions is formed on the basis of quantitative knowledge.
VALUE is the quality and property of an object, with the help of which we compare objects with each other and establish a quantitative characteristic of the compared objects.
The concept , the value in mathematics is considered as the main one.
A direct answer to the question “what is a quantity?” no, since the general concept of magnitude is a direct generalization of more specific concepts: length, area, volume, mass, speed, etc.
The size of an object is its relative characteristic , emphasizing the length of individual parts and determining its place among homogeneous ones.
The value is a property of an object perceived by various analyzers: visual, tactile and motor. In this case, the size of an object is most often perceived simultaneously by several analyzers: visual-motor, tactile-motor, etc.
Item size, i.e. item size , determined by only based on comparison . It is impossible to say whether it is a large or a small object, it can only be compared with another.
The perception of magnitude depends on the distance from which the object is perceived, and also on the magnitude of the object with which it is compared . The farther an object is from the one who perceives it, the smaller it seems, and vice versa, the closer it is, the larger it seems.
The characteristic of the size of the object also depends on its location in space . The same object can be characterized either as high (low), or as long (short). This depends on whether it is in a horizontal or vertical position.
So, for example, in the figure, objects are located in a vertical position and are characterized as high and low, , and in another figure (in a horizontal position), these same objects are characterized as long and short.
The value of an item is always relative to , it is dependent on which item it is compared to . Comparing an object with a smaller one, we characterize it as a larger one, and comparing the same object with a larger one, we call it a smaller one.
So, the magnitude of a particular object is characterized by the following features : comparability, variability and relativity.
1) comparability carried out:
- overlay,
- application,
- measurement using a conditional measure,
- comparison by eye.
2) relativity - depends on the object with which we are comparing, on the distance at which we are comparing, on the location in space.
3) variability . Size is closely related to size. And size is a property of magnitude variability. Each item has its own generic purpose. It can change its dimensions without changing its essence.
GEOMETRIC FIGURE is an abstract concept with the help of which we personify all the objects around us in form.
A geometric figure is the presence of points on a plane, limited by space.
Figures are flat (circle, square, triangle, polygon…) and spatial (ball, cube, parallelepiped, cone...), which are also called geometric bodies.
GEOMETRIC BODY is a closed part of space, limited by flat and curved surfaces.
If the surface bounding the body consists of planes, then the body is called a polyhedron . These planes intersect along straight lines, which are called edges, and form the faces of the body. Each of the faces is a polygon whose sides are the edges of the polyhedron; the vertices of this polygon are called the vertices of the polyhedron.
Some polyhedra with a certain number of faces have special names : tetrahedron - tetrahedron, hexahedron - exahedron, octahedron - octahedron, dodecahedron - dodecahedron, twenty-sided - icosahedron.
What is a geometric FORM?
SHAPE is the outline, the outer appearance of the object.
Form (lat. forma - shape, appearance) – the mutual arrangement of the boundaries (contours) of the subject, object, as well as the relative position of the points of the line.
TIME is a philosophical concept that is characterized by the change of events and phenomena and the duration of their existence.
Time has properties :
- fluidity (time cannot be stopped)
- irreversibility and uniqueness
- duration .
SPACE is the quality by which relationships such as neighborhoods and distances are established.
Orientation in space implies orientation towards oneself, away from oneself, from other objects, orientation on the plane and orientation on the ground.
We will help you write any work for a similar one subject
-
Abstract
Basic mathematical concepts
From 250 rubles
-
Control job
Basic mathematical concepts
From 250 rubles
-
Coursework
Basic mathematical concepts
From 700 rubles
Get a job done or expert advice on your educational project
Get a quote
Mathematics for the little ones (from 0 to 3) – Development Academy
Experts in the field of early child development have established the fact that children's thinking absorbs all information.
In their opinion, all facts are deposited in the child's memory, which in the future are transformed into knowledge, but only if the material is presented at a high emotional level, exciting and tempting, without excessive perseverance.
This approach is absolutely justified in relation to the basics of mathematics, which the baby must certainly master. Such information enables the child to navigate in space, perform simple mathematical operations, logical tasks, and also determines the ability to use mathematical concepts such as size, shape. If the child is not familiar with the basic concepts, it will be more difficult for him to perceive the environment. Performing mathematical and logical tasks activates the mental activity of the baby, contributes to the development of thinking.
Where to start?
The first mathematical lessons should be started almost from the first days of life, namely in games that contribute to the development of tactile abilities. A newborn from the first days, thanks to vision, touch, learns to perceive the features of objects: size, texture, color.
It is important not to forget to name these qualities for the child and demonstrate the properties during the game or everyday activities. Teach your child to compare objects around him. As illustrative examples, you can use toys, clothing, dishes, body parts. For example, you can describe your favorite toy like this: “Look at that big, brown bear. Try how shaggy and soft he is. Where is our little ball? The ball is blue, round. Let's touch it, how smooth it is. He jumps higher than you."
For a child who is able to explore space while crawling, adults can suggest directions in the horizontal plane. This should be done not intrusively, commenting on the movements of the child or joint movements with adults. When the child has reached the goal, he begins to persistently master the subject, using all the possibilities (feels, tries on the tooth, moves). At this moment, a small person activates the work of the brain, starts the processes of analysis. Adults must necessarily suggest what is in front of the child, what properties are characteristic of this object, and say the baby's feelings.
(This cube is small, plastic, red, hard, and the pencil is long, thin, yellow, wooden).
At the age of one, the foundations are laid for the further development of cognitive abilities. Parents should be patient and try not to limit the baby in his desire for knowledge of the world around him. It is necessary to prepare a house or apartment for the appearance of a baby, so that his movement around the home becomes safe, and also remove valuables away. G. Doman, a well-known American theorist of the early development of a child, is sure that difficulties and problems in learning appear later in those children who were limited by space during the crawling period, sat in the arena, and were not able to freely move around the house. Physiologists who specialize in pediatrics know that a child acquires certain knowledge or skills in the proper period of time, when the body is capable of it and has reached the appropriate level of development.
At the age of one year, when a child begins to walk, it is important for him not only to feel the object, but also to understand the relationship between them.
At this age, a real mathematical boom begins in the development of the baby. The child activates his skills of analysis and synthesis. For learning, as a visual aid, toys still occupy the main place.
Sufficiently complex concepts quickly fit into the baby's head thanks to a variety of bright pyramids, cubes and nesting dolls, balls, dolls, plush animals. When a child builds castles using building blocks, he gradually learns shapes and colors. But only if the parents comment on the implementation and name the geometric shapes. Simple exploration of toys will help the child master their basic qualities and their most striking properties. For example, a toddler will enjoy watching a ball roll down an incline, while blocks will not be able to roll around corners. Invite your child to feed the toy animals with colorful cookies, pick up caps for felt-tip pens of the appropriate colors. If the child constantly performs such tasks, he will quickly master the colors and the combination of the words “by color” will no longer be frightening.
By organizing a game with a pyramid, the child will understand the ratio "more - less".
Studying numbers
There is no need to rush to study numbers. Until the age of three, children have concrete thinking. They perceive only those objects that can be touched and seen with their own eyes. Whereas numbers are something incomprehensible, meaningless, simple hooks and sticks. Toddlers perceive numbers in the same way that adults perceive Chinese characters. Since the memory of children is sufficiently formed, the child will be able to capture the meaning of these symbols, if necessary, reproduce and name numbers. But at an older age, the baby will re-master the material, learns to correlate the signs and the number of objects. For training, you can use nuts or sweets.
It should be noted that depending on the type of perception, children easily or difficultly memorize numbers. For example, visual kids (in whom vision prevails in the perception of the world around them) already at the age of two years reproduce numbers and letters.
To teach a child or not at this age should be decided by parents, taking into account the interests of the child in symbols. If he has a desire to master incomprehensible signs, give the baby such an opportunity and satisfy his interest. But it is worth remembering that such features are not typical for all children of this age. It is important not to force the child to such activities if he does not show interest. Persistence of parents can cause rejection of information and lack of desire to master the material in the future.
Three-year-olds must master the concept of the number of objects, as well as understand the relationship “many-few”. The best option for kids is learning from their own experience.
The American theorist of early childhood development G.Dogma, like Nikitin, suggests using dots to indicate the number of objects, Maria Montessori recommends using beads. Do not take such recommendations as a rule. Replace the beads with buttons, and the dots with sticks or matches.
Count with your child everything that comes to hand: balls, cars in the parking lot, animals, pencils in cups, spoons, birds on a tree. You can start studying numbers after three years.
Children will also be taught to count in kindergarten. Moreover, the child learns information much better if he is with his friends. If you are unable to send your child to a preschool, try placing him in a part-time kindergarten group.
We count everything
As a visual aid for a small child, you can use any children's book that is full of beautiful high-quality illustrations. You can train in the account by determining the number of objects depicted: butterflies, squirrels, berries, flowers, guys. Ask questions to the child so that he focuses his attention on the quantity. How many pens does the girl have? How many hands does a boy and a girl have together? How many paws does a cat have? How many paws does a dog have? How many shoes does the girl have? How many socks does a dog need? How many hats does the mushroom have? How many fish are in the aquarium? How many legs does a fish, octopus, spider, butterfly, bug have?
Do not try to stop a child by looking at other children if they are trying to learn to count.
You can learn to count not only within a dozen. If this is interesting and easy for a child, try to master counting to one hundred. You can count in direct order, through a number, or in reverse. Such exercises contribute to the development of logical thinking, memory. Try to make tasks varied: compare the number of items, perform elementary mathematical operations, play supermarket, dominoes, dice. Focus not on the information you are trying to offer the child, but on the process and methods of learning. The main criterion for an impeccable process of education and upbringing is the positive emotions of the baby and the child.
Sorting game. The game contributes to the development and training of mathematical logic, thinking. To organize the game, you can use improvised materials, for example, spoons, forks, cubes, toys, and other materials. You can get creative with the sorting process. Arrange special containers for items with appropriate openings. For example, a round hole for beans, a narrow oblong hole for buttons.
Taking into account the individual abilities of the child, tasks can be complicated by adding additional sorting signs. Tasks should be feasible for the child in order to create a situation of success. Try to constantly name household items in the kitchen, in the nursery, in the hallway. Name items of clothing when going for a walk, toys, cleaning the room, dishes, setting the table.
To increase the effectiveness of training, you should combine training with the activation of large and fine motor skills. This approach is especially important for children, who more clearly perceive the world around them through tactile sensations. For kinesthetic children, classes without movement have no benefit and result.
Mathematics also requires an integrated approach, taking into account the characteristics of children. You can play sorting not sitting in one place, but on the run. You can complicate the game by equipping an additional obstacle course in the room. While jogging, count steps, keep score, exercise, throw the ball.
