Number and counting
What are Counting Numbers? Definition, Chart, Examples, Facts
What is Counting?
In math, ‘to count’ or counting can be defined as the act of determining the quantity or the total number of objects in a set or a group. In other words, to count means to say numbers in order while assigning a value to an item in group, basis one to one correspondence. Counting numbers are used to count objects.
Here, for instance, we have used counting numbers to determine the number of animals or birds. The table also shows how we can use our fingers to count objects to ten.
Related Games
Counting Numbers
Numbers that we use to count things are called counting numbers. They are also called natural numbers. These numbers start from 1 and are infinite. That is why no one knows where to end these numbers. Zero is not a natural number since we cannot count zero. 1, 2, 3, 4, and so on are examples of counting numbers.
Counting is a topic that we have learned in kindergarten. Each one of you must have different ways to count. Some understand it by counting natural numbers on their fingers and others by counting things around them. But one thing common among us is that the first thing we all learn in math is counting. These numbers are the basis of all mathematics.
Where do we use these numbers?
We use counting in performing different activities in our day-to-day life. For instance,
- Counting money
- Counting balloons in a bunch
- Counting students in a class
Representing numbers with finger arrangements allows children to learn and incorporate the fundamental properties of natural numbers. The figure below shows how we can use our fingers to represent the numbers from one to ten.
Related Worksheets
Number Names of Numbers 1–20
The following table gives the number names of numbers from 1 to 20.
Different Ways to Count Numbers
- We can count the numbers forward.
For example,
1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
You can count numbers backward. For example,
10, 9, 8, 7, 6, 5, 4, 3, 2, 1.
- You can use skip counting as well.
Skip counting is the method of counting forward by numbers other than 1.
Counting by 2: 2, 4, 6…
Counting by 3: 3, 6, 9…
Counting by 4: 4, 8, 12…
How to Count?
Counting On – We can count on by saying by numbers while touching on each object once.
Here, for instance, we can count the buttons by touching each button once.
Counting on also requires us to count forward. Forward counting is counting by adding one more, every time.
Here, we forward count while putting the buttons in the jar, to find the number of the buttons.
Counting Back – We can count down or back by saying by numbers in reverse order while touching on each object once.
Here, for instance, we can reverse count the buttons by touching each button once.
Counting back requires us to count backwards. Backward counting is counting by removing one, every time.
Here, we reverse count while taking out the buttons from the jar, to find the number of the buttons.
Fun Facts
1. Did you know that numbers were invented by people using their fingers.
2. Do you know what comes after a million, billion and trillion? A quadrillion, quintillion, sextillion, septillion, octillion, nonillion, decillion and undecillion.
Let’s sing!One for the sun shining in the sky.
Two for the little birds that fly by.
Three for the tiny seashells in the sand.
Four for the sticks I hold in my hand.
Five for the petals of the flower I see.
Six for the bees as busy as can be.
Seven for the colors in the rainbow.
Eight for the snails crawling so slow.
Nine for the squirrels climbing up the tree.
Ten for the little puppies on a running spree.
Let’s do it!
Ask your children to observe and count things around them, for instance, the numbers of flowers they see, the number of crayons they have, the number of pages of the book he has read. Further to explain more explicitly,
you can use counters such as buttons, jelly beans to help them count up and count back and ask them to write addition and subtraction facts or sentences.
Solved Examples
Example 1. Write the missing numbers between 30 and 40.
31, 32, 33, ___, 35, ___, 37, ___, ___
Solution: Number between 30 and 40 are: 31, 32, 33, 34, 35, 36, 37, 38, 39
Therefore, the missing numbers are 34, 36, 38, and 39.
Example 2. Count by 2s and find the missing numbers.
8, __, 12, __, 16
Solution: Skip counting is counting forward by numbers other than 1.
So, skip counting by 2s from 8 to 16. We get
8, 10, 12, 14, and 16.
Therefore, the missing numbers are 10 and 14.
Example 3. Write the even counting numbers less than 10.
Solution: Even numbers are divisible by 2.
Counting numbers less than 10: 1, 2, 3, 4, 5, 6, 7, 8, 9
So, even numbers less than 10: 2, 4, 6, 8
Example 4. In the figure below, observe the pattern and find the number of dots in the fourth box.
Solution:
Number of dots in the first box $= 3$
Number of dots in the second box $= 4$
Number of dots in the third box $= 5$
So, the number of dots in the fourth box must be 6.
Practice Problems
1
How many apples are there in the figure?
3
5
8
9
Correct answer is: 8
There are eight apples.
2
What is the sum of the two missing numbers?
3
5
7
10
Correct answer is: 10
The given figure, between 1 and 10, 3 and 7, are missing.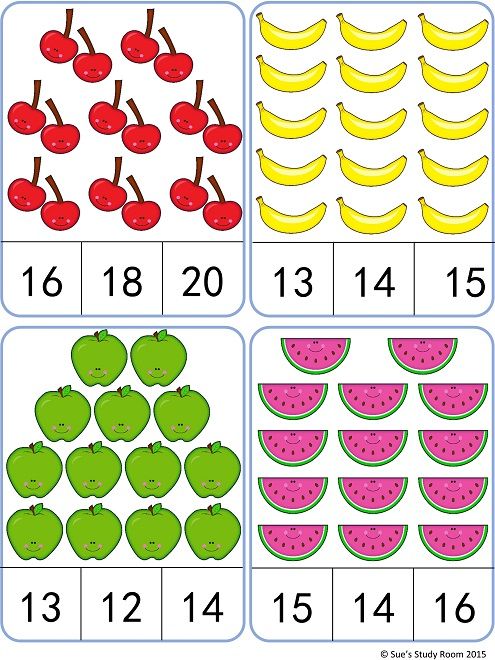
So, the sum of the missing numbers is $3 + 7 or 10$.
3
Which of the following is not a counting number?
10008
23
2
Correct answer is: 0
Natural numbers start with 1; zero is not a counting number.
4
Find the missing number.
$55, \underline{} , \underline{}, 58$
34, 36
23, 26
56, 57
39, 40
Correct answer is: 56, 57
55, 56, 57, 58
Frequently Asked Questions
Are negative numbers also counting numbers?
No. We don’t use negative numbers for counting.
What is the importance of counting numbers on fingers?
Counting on fingers is a constructive strategy to teach students math concepts. Representing numbers with finger arrangements allows children to learn and incorporate the fundamental properties of natural numbers.
What is the difference between counting numbers and whole numbers?
Numbers that we can use to count things are called counting numbers, for example 1, 2, 3, and so on.
They are also called natural numbers.
All counting numbers along with zero are the whole numbers.
What is the importance of counting?
Counting makes us understand that numbers have an order. In real life, we can relate numbers to quantities. Counting is used to find the number of elements of a finite set of objects by continually increasing a counter by 1 in some order. Counting is used to demonstrate knowledge of the number system.
Counting Numbers - Definition, Counting Chart, Examples
Counting numbers are the natural numbers that can be used in counting. They start from 1 and the series continues as 1, 2, 3, 4, and so on. Zero is not included in counting numbers because we cannot count 0. Let us learn more about counting numbers in this article.
| 1. | What are Counting Numbers? |
| 2. | Counting Numbers from 1 to 20 |
3. |
Counting Numbers from 1 to 100 |
| 4. | Counting Numbers with Hands |
| 5. | FAQs on Counting Numbers |
What are Counting Numbers?
Counting is the process of expressing the number of elements or objects that are given. Counting numbers include natural numbers which can be counted and which are always positive. Counting is essential in day-to-day life because we need to count the number of hours, the days, money, and so on. Numbers can be counted and written in words like one, two, three, four, and so on. They can be counted in order and backward too. Sometimes, we use skip counting, reverse counting, counting by 2s, counting by 5s, and many more.
Counting Numbers from 1 to 20
The counting of numbers always starts from 1 because zero cannot be counted. Let us start counting numbers from 1 to 20 and read their number names so that they can be identified.
Counting Numbers from 1 to 100
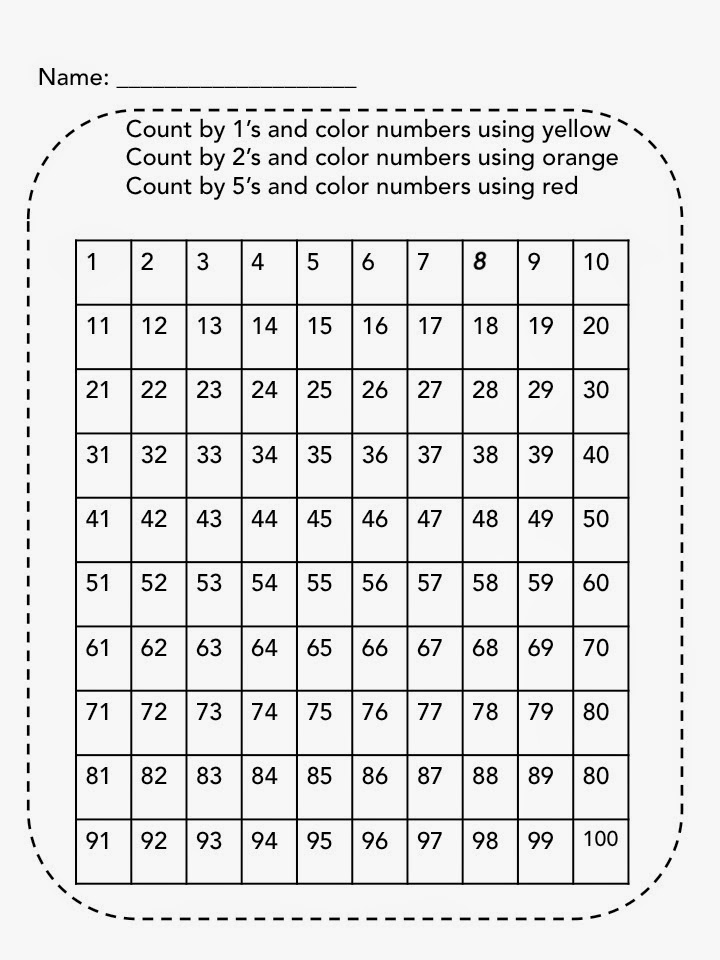
Repeated counting of numbers is very essential for children because it helps to know the sound and the order of numbers. Using simple techniques and real-life examples, like counting the number of cookies on a plate can help them memorize numbers easily. Counting numbers from 1 to 100 in words is quite helpful because it helps to grasp the number sense of increasing numbers. The following chart shows numbers from 1 to 100.
Counting in Numbers with Hands
Counting numbers from 1 to 10 can also be done using our hands and fingers. It is a known fact that visual maths helps children develop math skills faster. Using hands and fingers acts as a link between numbers and their symbolic representation. The following figure shows how the numbers from 1 to 10 can be easily represented with fingers.
Related Articles:
- Numbers
- Numbers in words
- Even Numbers
- Odd Numbers
FAQs on Counting Numbers
What are Counting Numbers in Math?
Counting numbers include natural numbers that can be counted.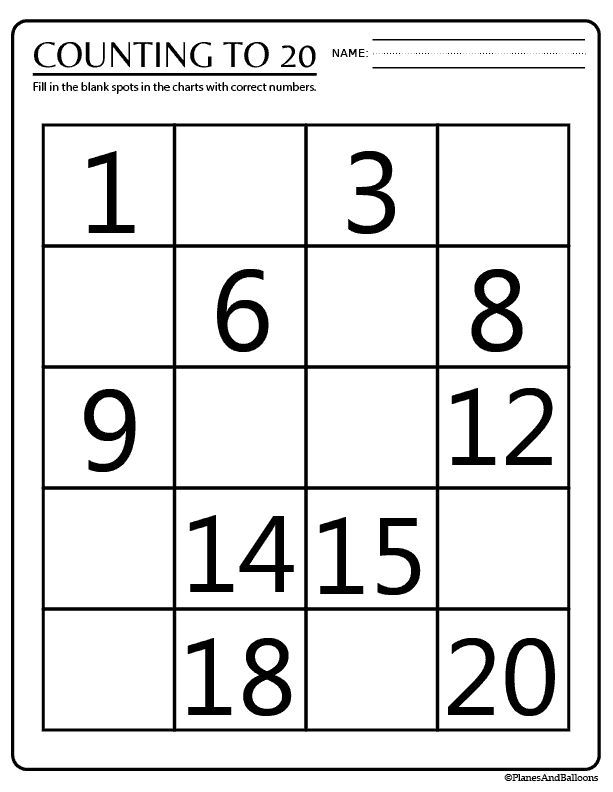
They start from 1 and the series continues as 1, 2, 3, 4, and so on. Zero is not included in counting numbers because we cannot count 0.
What are Counting Numbers Less than 10?
Counting numbers less than 10 can be listed as, 1, 2, 3, 4, 5, 6, 7, 8, 9.
How Many Counting Numbers are there?
There is no limit for counting numbers because they start from 1 and go on till infinity, like 1, 2, 3, 4, 5, and so on. Therefore, it can be said that there are infinite counting numbers.
What Counting Numbers are also Whole Numbers?
All counting numbers are whole numbers because counting numbers start from 1, 2, 3, 4, and so on. However, it should be noted that all whole numbers are not counting numbers because whole numbers include 0, and 0 is not considered to be a counting number since it cannot be counted.
What is the mean of the first 100 Counting Numbers?
The mean of the first 100 counting numbers can be calculated by finding the sum of the first 100 counting numbers, which is, 1 + 2 + 3 +.
........100. This sums up to 5050. Then, this sum is divided by the number of counting numbers, that is 100 in this case. So, 5050 ÷ 100 = 50.5. Therefore, the mean is 50.5
Give 5 examples of Counting in Numbers.
There can be many examples of counting numbers:
- Counting numbers from 1 to 5 can be listed as: 1, 2, 3, 4, 5
- Odd Counting numbers from 1 to 10 can be listed as: 1, 3, 5, 7, 9
- Even Counting numbers from 11 to 20 can be listed as: 12, 14, 16, 18, 20
- Counting numbers from 21 to 25 can be listed as: 21, 22, 23, 24, 25
- Counting numbers from 51 to 55 can be listed as: 51, 52, 53, 54, 55
What Is Another Name for Counting Numbers?
Counting numbers can also be called natural numbers because they do not include zero and are positive numbers that start from 1, 2, 3 and the series continues till infinity.
Write the Odd Counting Numbers Between 6 and 16.
Odd numbers are those numbers that are not divisible by 2.
So, the odd counting numbers between 6 and 16 are 7, 9, 11, 13, 15.
Write the Even Counting Numbers less than 12.
Even numbers are those numbers that are divisible by 2. So, the even counting numbers less than 12 are 2, 4, 6, 8, and 10.
NUMBER AND COUNT
Main page => library => table of contents
METHOD OF FORMING ELEMENTARY MATHEMATICAL REPRESENTATIONS IN CHILDREN
Repetition of the past. In the middle group, children were taught to count objects within 5. Consolidation of the relevant ideas and methods of action serves as the basis for the further development of counting activities.
Comparison of two sets containing an equal and unequal (more or less by 1) number of objects within 5 allows you to remind children how the numbers of the first heel are formed. In order to bring to the consciousness of children the meaning of counting and methods of piece-by-piece comparison of objects of two groups one to one to clarify the relationship “equal”, “not equal”, “more”, “less”, tasks are given to equalize the aggregates.
(“Bring so many cups so that all the dolls have enough and there are no extra ones,” etc.)
Much attention is paid to strengthening counting skills; children are taught to count objects from left to right, pointing to objects in order, agree on numerals with nouns in gender and number, name the result of the count.
If one of the children does not understand the final value of the last number named when counting, then he is invited to circle the counted objects with his hand. A circular generalizing gesture helps the child to correlate the last numeral with the entire set of objects. But in working with children of 5 years old, as a rule, it is no longer needed. Children can now be offered to count objects at a distance, silently, that is, to themselves.
In the older group, they begin to develop memory for numbers. To do this, gradually complicate the exercises in the counting of objects. For example, children are simultaneously called 2 numbers, immediately offered to count 2 types of objects or objects of the same type, but differing in color or size.
The names of objects are associated with their location.
Children learn to memorize numbers, take objects one at a time, clearly correlate numbers with each object taken, and report on the completed task. The teacher explains: “In order to remember the number, you need to carefully listen to the task, repeat it first in a whisper, and then to yourself.”
Children are reminded of techniques for counting sounds and objects by touch. They reproduce a certain number of movements in a pattern and a specified number.
In parallel with the work aimed at consolidating the skills of counting and counting objects, children are trained to distinguish between geometric shapes and compare the sizes of objects. They fix some spatial representations: the location of the object in relation to itself: in front, behind, left, right; the position of objects depicted on a sheet of paper: top, bottom, left, right, middle.
To repeat the past, combined exercises are used, allowing you to simultaneously work on 2-3 program tasks.
For example, children are trained simultaneously in counting sounds and in comparing and equalizing two sets of objects, in the formation of numbers. 4-5 lessons are not enough to repeat the entire program of the middle group. In these classes, they mainly consolidate the material of the section "Quantity and Count", ideas about the form, magnitude, etc .; continue to consolidate in the course of learning to count up to 10.
Counting within 10. To obtain the numbers of the second heel and learn to count up to 10, use techniques similar to those used in the middle group to obtain the numbers of the first heel.
The formation of numbers is demonstrated on the basis of a comparison of two sets of objects. Children must understand the principle of obtaining each subsequent number from the previous one and the previous one from the next (i ± 1). In this regard, in one lesson it is advisable to consistently receive 2 new numbers, for example, 6 and 7. As in the middle group, the display of the formation of each next number is preceded by a repetition of how the previous number was obtained.
Thus, at least 3 consecutive numbers are always compared. Children sometimes confuse numbers 7 and 8. Therefore, it is advisable to conduct more exercises in comparing sets consisting of 7 and 8 elements.
It is useful to compare not only collections of objects of different types (for example, Christmas trees, mushrooms, etc.), but also to break groups of objects of the same type into parts and compare them with each other (large and small apples), finally, a collection of objects can be compared with its part. (“Who is more: gray bunnies or gray and white bunnies together?”) Such exercises enrich the experience of children with multiple objects.
When assessing the numbers of sets of objects, five-year-old children are still disoriented by the pronounced spatial properties of objects. However, now it is not necessary to devote special classes to showing the independence of the number of objects from their size, shape, location, and the area they occupy. It is possible to simultaneously teach children to see the independence of the number of objects from their spatial properties and to receive new numbers.
The ability to compare sets of objects of different sizes or occupying different areas creates the prerequisites for understanding the meaning of counting and methods for piece-by-piece correlation of elements of two compared sets (one to one) in identifying the relationships “equal”, “greater”, “less”. For example, in order to find out which apples are more - small or large, which flowers are more - marigolds or daisies, if the latter are located at greater intervals than the former, it is necessary either to count the objects and compare their number, or to compare the objects of 2 groups (subgroups) one to alone. Different methods of comparison are used: overlay, application, use of equivalents. Children see: in one of the groups there was an extra object, which means there are more of them, and in the other - one object was not enough, which means there are fewer of them. Based on a visual basis, they compare numbers (so 8 > 7, and 7 < 8).
By equalizing groups by adding one item to a smaller number or removing one item from a larger number, children learn how to get each of the compared numbers.
Considering the relationship of the relationship "more", "less" will help them further understand the reciprocal nature of the relationship between numbers (7> 6, 6 < 7).
Children should tell how each number was received, that is, to what number of objects and how much was added, or from what number of objects and how much was taken away (removed). For example, 1 apple was added to 8 apples, it became 9apples. They took 1 out of 9 apples, 8 apples remained, etc. If the guys find it difficult to give a clear answer, you can ask leading questions: “How much was it? How much was added (removed)? How much has it become?
Change of didactic material, variation of tasks help children to better understand how to get each number. When they receive a new number, they first act as directed by the teacher (“Add 1 apple to 7 apples”), and then independently transform the aggregates. Achieving conscious actions and answers, the teacher varies the questions. He asks, for example: “What needs to be done to make 8 cylinders? If you add 1 to 7 cylinders, how many will there be?
To consolidate knowledge, it is necessary to alternate team work with independent work of children with handouts.
The child matches 2 sets by laying out items on a card with 2 free strips. Demonstration of methods for obtaining a new number (comparison of 3 neighboring members of the natural series) usually takes at least 8-12 minutes, so that the performance of monotonous tasks does not tire the children, similar work with handouts is carried out more often in the next lesson.
To consolidate counting skills within 10, a variety of exercises are used, for example, “Show the same number.” Children find a Card on which the same number of objects are drawn as the teacher showed. (“Find as many toys as there are circles on the card”, “Who will quickly find what kind of toys we have b (7, 8, 9, 10)?”.) To complete the last 2 tasks, the teacher makes groups of toys in advance.
Object count within 10. Exercises in object count continue to get more difficult. Along with tasks for reproducing 2 groups of objects of different types at once (“Count 6 cones and 7 chestnuts”) or 2 groups of objects of the same type, but differing either in color, or shape, or size (7 large and 8 small buttons), they give tasks not only count 2 groups of objects, but also place them in a certain place, for example, in a specified part of a sheet of paper: top, bottom, left, right, middle.
A little later, at the direction of the teacher, the children place objects along the top or bottom, right or left edge of the sheet, in the upper right, in the lower left corners. Before giving such tasks, the teacher specially trains the children in finding the corresponding parts of the sheet of paper. Children are taught to listen carefully to the task, memorize it, perform it accurately and talk about what they did and how. At first, it is difficult for them to give a complete clear answer. The teacher helps with leading questions. For example, he asks a child: “How many squares and where did you put them? How many rectangles and where did you put them? Now tell me everything you've done!" The answer in parts turns into a holistic story about the completed task. If the child finds it difficult to complete the task, the teacher, helping him, begins the answer: “I put 6 squares ...”, and the child finishes. In the speech of children, the connections between the number of objects, their qualitative characteristics and spatial arrangement must certainly be reflected.
Changing the quantitative ratios between the same objects, as well as their location, abstracts the number from the qualitative and spatial features of sets of objects. Children begin to be taught to repeat the task until it is completed, ensuring the development of the planning function of speech.
Account with different analyzers. For the development of the activity of the account, exercises in the account with. active participation of different analyzers: counting sounds, movements, counting objects to the touch.
After I-2 lessons after getting acquainted with the formation of the next number, children are offered tasks related to counting sounds, movements, etc. within a given number. So the amount of the account gradually increases to 10.
Account by touch. In the older Troupe, the exercises in counting objects by touch make it somewhat more difficult. For example, as in the middle group, the children count the buttons sewn onto the card, but they keep the card behind their backs.
Sew on card b - 10 buttons in 2 rows. Use smaller buttons. Children are given tasks to count the buttons by touch with their eyes closed, count the pebbles, shifting them from hand to hand. It is advisable to conduct exercises in a form that would ensure the inclusion of all children in the work. So, all children simultaneously practice counting by touch in the game "Let's go, go, go ...".
Sound count. In the older group, the counting of sounds is associated with the counting and counting of objects. The nature of the tasks gradually complicate. For example, at first, children are asked to count the sounds, then count the same number of toys, later simultaneously count the sounds and put the toys away, and after finishing the count, say how many sounds they heard and how many toys they put. The counting of sounds is often associated with the performance of movements. (“Jump as many times as you hear sounds.”) Five-year-olds can be encouraged to count sounds with their eyes closed.
As in the middle group, sounds are extracted on different instruments: for example, on a drum, metallophone; knock on the table with a stick, etc.
In the third quarter, children are introduced to the composition of the number of units. It is useful to conduct such an exercise: the teacher extracts 3 (4, 5) sounds on different instruments and asks: “Guess which instrument and how many sounds I made.” The child lists: “1 time you hit a stick with a stick, 1 time - on a drum, 1 time - on a metallophone.” "How many sounds did you hear?" the teacher asks. “I heard only 3 sounds,” the child replies.
Counting and reproduction of movements. Children consider the movements performed by the teacher or other children. Reproduce the number of movements according to the pattern and according to the named number. (“Sit down as many times as there are circles on the card”, “Bend over so many times.”) To make the children more actively involved in work, the tasks are given a playful character: “Guess how many times I told Misha to throw the ball up.
” (Misha throws the ball, and the rest of the children count his movements.)
The teacher organizes the exercises in such a way as to ensure the coverage of a large number of children at once. For example, children are built in 2 lines. While the children of one line perform the indicated number of movements, standing opposite, in the other line, they are checked. In the older group, tasks include more complex movements: toss the ball, jump with a rope. The most difficult task for the children is to take a certain number of steps in the indicated direction. For example, a child is offered: "Take 5 steps forward, turn to the right, take 3 more steps ..." Children, moving, simultaneously train in counting steps and in orientation in space. The establishment of quantitative relations between the sets perceived by different analyzers contributes to the generalization of counting activities.
It is important that the children's speech reflects the connections "between the number of movements, sounds, objects perceived visually or by touch.
" ("I jumped up 5 times because there are 5 circles on the card", "I threw the ball 6 times because I heard b sounds ", etc.)
Exercises in counting by touch, in counting sounds and movements are associated with a difference comparison of numbers. Children perform tasks: "Sit down 1 time more than you heard sounds", "Find a card on which 1 circle , more (less) than there were sounds”, “Name how many buttons Serezha has on the card if he jumps 1 time more”.
HP Metlin. Mathematics in kindergarten. M.: Prosveshchenie, 1984.
Main page => library => table of contents
abstract "Number and count" | Plan-summary of a lesson in mathematics (senior group):
Abstract of GCD in mathematics in the senior group "Number and Counting"
Purpose: To teach children to solve problems, promote the formation of logical thinking, develop children's speech, the ability to reason and draw conclusions.
Tasks
Educational:
- exercise children in quantitative counting from 1 to 10;
- to consolidate ideas about spatial relationships: between, on the right, on the left;
- to form an idea of addition as a union of groups of objects, introduce the "+" sign.
Educational:
- to cultivate interest in mathematics.
Developing:
- develop the imagination, logical thinking of children
- develop the ability to understand the learning task and perform it independently
Methodological techniques:
-Conducting
-Slovers (instructions, issues, reminders)
-Igravoy (Surprise)
-Analysis of the lesson
Demonstration:
-“Letter”
-numbers -numbers -numbers -numbers -numbers -numbers -numbers -numbers -numbers from 1 to 10
- "envelopes"
- "maze"
- dummies of vegetables for problem
Handout:
- "find the extra" cards
- cards for writing the conditions of problem
- a set of numbers and signs for solving problems
- counting sticks
NOD:
Educator: -Guys! We received a letter today. Shall we read it?
Children: -Yes
Educator: “Dear children! Please, help! I ended up in the city of Tsifrograd and got lost.
To get out of the city you need to complete the tasks correctly. Please, help! Hints in envelopes. The first task in the envelope number 1. Dunno." Well, guys, let's help Dunno find his way home?
Children: we will help
Task No. 1. “Build numbers in a row”
Educator: - Guys, the numbers “ran up” and “walk” around the “city”, you need to find them and build them in order.
Children: in a group they look for numbers and put them in order on the table
Educator: - and now let's count them in order and in reverse order.
- What are the neighbors of the number "5". What number is to the left of it? Which one is right? What is the previous number in relation to the number 5? What's next?
(you can repeat for several numbers so that each child can practice)
- Well done! Now let's find envelope No. 2
Task number 2. “Find the extra”
Educator: -Guys, there are different cards with pictures in this envelope, you need to carefully look and determine what is superfluous on the card from the drawings and explain why.
Children: everyone looks at their card and, in turn, explains what is superfluous on the card and why.
Educator: - Well done! Let's open envelope #3.
Task No. 3. "Smart problems"
Educator: -And now you have to solve problems, so let's first learn how to do it. Listen to the problem: Natasha and Pasha went with their mother to the vegetable store. Natasha asked to buy her 2 cucumbers, and Pasha asked for 3 tomatoes. Mom bought 2 cucumbers and 3 tomatoes and put everything in a bag. (put the dummies in a transparent bag)
- what word can replace the word "folded"?
Children: put together, united, etc.
Educator: in mathematics, the action performed by the mother is called "addition" and is replaced with a "+" - plus sign. See what happened as a result of addition: attach cards 2 + 3 = 5 on the board.
Physical education minute:
One – get up, stretch
Two – bend down, straighten up
Three – three hands clapping
Three nods with the head.
Four - arms wider,
Five - wave your arms,
Six quietly sit on chairs
Educator: - Sit down at the tables, each of you has pictures with a different number of vegetables and fruits, a set of numbers and signs, counting sticks. You need to compose a problem from pictures, solve it with counting sticks and lay out the mathematical notation of the solution using numbers and signs.
Checking. Well done. (correct if there are errors). And now envelope number 4.
Task number 4. "Labyrinth"
Educator: Guys, we have a maze in front of us, if we can get through it correctly, then we will help Dunno find the way from the city of Tsifrograd, and he will be able to get home. Everything is very confused, all roads are intertwined, there are many traps, different numbers and letters; but there is one hint - if we consistently connect the numbers with each other, we can find the right path, and help Dunno. Let's try.
Children: each in turn connects the number with the next one
Educator: Well done! You have found a way out of Tsifrograd! Now let's send Dunno this clue, and he can get home! (we seal in an envelope)
- Guys! You are great.
